Experimental Study of the Cavitation Effects on Hydrodynamic Behavior of a Circular Cylinder at Different Cavitation Regimes

Abstract

In this work, we experimentally investigated the cavitation effects on the hydrodynamic behavior of a circular cylinder at different cavitating flows. We analyzed the cavitation dynamics behind the circular cylinder using a high-speed camera and also measured the associated hydrodynamic forces on the circular cylinder using a load cell. We studied the cavitation dynamics around the cylinder at various types of the cavitating regimes such as cloud cavitation, partial cavitation and cavitation inception. In addition, we analyzed the cavitation dynamics at three different Reynolds numbers: 1 × 10${}^5$, 1.25 × 10${}^5$ and 1.5 × 10${}^5$. The results showed that the hydrodynamics force on the circular cylinder can be increased with the formation of the cavitation behind the cylinder compared with the cylinder at cavitation inception regime. The three-dimensional flow caused complex cavitation behavior behind the cylinder and a strong interaction between vortex structures and cavity shedding mechanism. In addition, the results revealed that the effects of the Reynolds number on the cavitation dynamics and amplitude of the shedding frequency is significant. However the effects of the cavitation number on the enhancement of the amplitude of the shedding frequency in the cavitating flow with a constant velocity is slightly higher than the effects of Reynolds number on the enhancement of the amplitude of the shedding frequency at a constant cavitation number.

1. Introduction

With the development of the marine applications and hydraulic machinery components, such as high-speed underwater vehicles, propeller-rudder systems and central flow pumps, the negative effects of cavitation and control of this phenomenon on the solid structure have became a matter of attention. The high velocity of flow around an immersible body can induce a low pressure region below the vapor pressure of the liquid and generate a phenomenon known as cavitation. The cavitation can grow on the surface of the immersible bodies and ultimately the extended cavity can be collapsed near the solid boundaries in the high pressure region and induce noise, vibration, erosion and mitigation of the performance of the systems [1,2,3,4,5]. As a non-linear system, the cavitation dynamics formed on an immersible body can be affected by different factors, such as surface roughness [6,7], material properties [8], cavitation nuclei density and nuclei radius [9], liquid temperature [10,11,12], and etc. Based on how the cavitation is created and oscillation mechanism of the cavitation dynamics, the cavitation can be classified into different types such as sheet cavitation, partial cavitation, cloud cavitation and super-cavitation on the marine operating systems and hydraulic components. The cavity structures around the immersible bodies have different volumes which can induce various hydrodynamic forces or vibration on the system. The sheet cavity can appear directly after the cavitation inception close to the leading edge of a hydrofoil with decreasing of the cavitation number. The cloud cavity structure can be formed after the detachment of the attached cavity from the solid surface and may collapse near the trailing edge of the hydrofoil.

Coutier-Delgosha et al. [13] investigated the internal structure of the attached cavity on a two dimensional hydrofoil by using the novel endoscopic and X-ray technology. They found the void fraction distribution inside the sheet cavitation and presented the vapor/liquid morphology for different cavitation shapes. Furthermore, Barre et al. [14] used the optical probe to measure the void ratio of a ‘quasi-stable’ sheet cavitation in a venturi-geometry and compared their results with their numerical simulation. They presented that the sheet cavitation dynamics is quasi stable, however small cavity structures are detached from the surface at the aft region of the sheet cavity due to the effects of the re-entrant jet. Pelz et al. [15] developed an analytical model to investigate the transition from the sheet to cloud cavitation by describing the growth of the attached sheet cavitation and the extension of the re-entrant jet. They modelled the re-entrant jet as a spreading film under the cavity and their work helped us to understand the transition between sheet and cloud cavitation phenomenon. Their results showed that sheet to cloud cavitation can be affected by the cavitation nuclei density, the viscous effect of flow and the Reynolds number. The cloud cavitation has been identified as the most dangerous type of cavitation because of the collapse of large scale of cloud cavity on the surface of immersible bodies at different cavitating regimes with lower cavitation numbers [16].

In the various previous studies, the fundamental of the shedding mechanism of different cavitation dynamics have been investigated experimentally and numerically. To understand the behavior of the partial cavitation, Le et al. [17] observed the cavity structure on a plano-convex hydrofoil placed in the cavitation tunnel and measured the wall pressure distribution around the hydrofoil. Their findings showed that the re-entrant jet is the main reason of the shedding mechanism of the cloud cavitation and the cavitation instability which may induce a periodic cavitation structure. Stutz and Reboud [18] studied experimentally the shedding mechanism of the cavitation and the phase transition in a venturi-type test section. They pointed out that in addition to the re-entrant jet, a local pressure reduction can be formed by the large turbulence fluctuation in the partial cavitation regime. The visualization of the re-entrant jet and the cavitation periodic behaviour around a hydrofoil was obtained by Callenaere et al. [19]. In their work, some essential factors for the generation of re-entrant jet have been discussed: 1. the large adverse pressure at the cavity closure region; 2. the thickness of the cavity structure should be large enough, which can also present the attached cavity length. They showed that the re-entrant jet can play as the primary shedding mechanism in the partial and cloud cavitation regimes.

Leroux et al. [20] studied experimentally and numerically the partial cavitation shedding on a two-dimensional hydrofoil to understand the periodic shedding mechanism of the cavity structure. Their results revealed that a shock wave can be appeared by the cloud cavity collapse at low cavitation numbers. They found that the extension of the shock wave can also change the cavity shedding dynamics near the leading-edge of the hydrofoil. The role of the shock wave on the cavity oscillation was investigated by different researchers Genesh et al. [21] and Wu et al. [22]. They studied the shock wave propagation on a wedge-apex geometry and around a two dimensional hydrofoil by using the high speed X-ray densitometry. They both observed that the large scale of the shedding cavity can be collapsed subsequently near the solid surface and a type of pressure pulsation can be generated at the low cavitation numbers. In addition, they found that the pressure pulsation can affect the growth of the attached partial cavitation on the solid boundary. Their results showed that the shock wave front on the downstream region has been formed which was the symbol of the shock wave in the cavity shedding mechanism. Furthermore, they indicated that the pressure pulsation inside the cavitation structure can play as a dominant role for the cavity shedding mechanism. Karathanassis et al. [23] performed high-speed X-ray phase-contrast imaging of the cavitating flow developing within an axisymmetric throttle orifice using high-flux synchrotron radiation. Karathanassis et al. [24] studied X-ray phase contrast and absorption imaging for the quantification of transient cavitation in high-speed nozzle flows. Their results revealed that the X-ray phase-contrast imaging is suitable for capturing fine morphological fluctuations of transient cavitation structures. However, the technique may not provide information on the quantity of vapor within the orifice. Kadivar et al. [25,26] studied the effects of the pressure fluctuations in the cavitation surge regime around a two dimensional hydrofoil and a flat plate with semi-circular leading edge. They presented that the cavitation dynamics on the hydrofoil was driven mainly by the re-entrant jet in the cloud cavitation regime. However, the pressure pulsations formed around the flat plate can generate pressure waves inside the cavitation structure which may play as a dominant role for the cavity shedding mechanism.

The relationship between cavitation and the turbulent flows on different geometries such as wedge-type geometries, circular cylinders and propellers were investigated. The experimental work from Kermen & Parkin [27] showed that the formation of the cavitation inception phenomenon on a circular disk depend on the Reynolds number. In addition, Arndt [28] extended the experimental studies around a disk and confirmed the relationship between cavitation inception number and the Reynolds number. The work from Kermen & Parkin and Arndt presented the counting near-wake vortices and the visualization of coherent structures behind the circular disk. However, the size and the rotation rate of the vortices haven’t been clarified. In study of Belahadji et al. [29] with a two dimensional wedge, the near-wake vortices and Benard-Karman vortices were observed. One model between the cavitation inception number and Reynolds number was corroborated with the experimental data and they explained the transition of vortices from near-wake region to the far-wake region. Recently Wu et al. [30] used an advance void-fraction method, a high-speed X-ray densitometry, to observe the cavitation vortices behind a wedge geometry. They examined the cavitation structure and corresponded void fraction behind the wedge and found out that the cavitation void and the local Mach number increased with reducing the cavitation numbers. They found that the sound speed in the mixture region can be reduced by increasing the void fraction. Besides the investigations of cavitating flows behind a standard bluff body such as wedge, the investigations of cavitation behind circular cylinders play also an important roll in the hydraulic and ship industries.

The single phase flows behind a circular cylinder has been studied extensively by different researchers (Roshko [31]; Bearman [32]; Wei & Smith [33]; Williamson [34]; Szepessy & Bearman [35]; Norberg [36]). However, only few studies are considered the cavitating flows around the circular cylinder and the hydrodynamics effect of cavitation regimes. Fry [37] performed an experiment of cavitation behind a cylinder in a free stream flow and captured the cavitation-induced noise spectra together with the cavitation dynamic observation. His results showed that the noise peaks was related to the cavity collapse intensity and the cavity/wake dynamics. Matsudaira et al. [38] measured the bubble collapse pressure in the wake dynamics and studied the relationship between the bubble collapse-induced pressure and the separation of Karmen-vortex cavity from a cylinder with Reynolds number region from 4.5 × 10${}^5$ to 6.0 × 10${}^5$ and cavitation numbers from 0.9 to 1.6. Their work showed that by the reduction of the cavitation number and increasing of the Reynolds number, the maximum bubble collapse induced pressure can be increased. In addition, they showed that more severe cavitation-induced erosion can be observed on the solid boundaries at higher Reynolds numbers. The effects of the erosion from the bubble collapse-induced pressure on the circular cylinder were investigated by Saito & Sato [39] mounting an aluminum plate behind the cylinder in the cavitating flows. They observed that the cavity shedding structures near the aluminum plate and measured the erode pits to get a ratio between the passing cavity shedding and the pits formed on the aluminum plate.

Recently some investigations around the cylinder in the cavitating flows were performed experimentally and numerically to study the relationship between cavitation regime, vortex shedding behind cylinder and the relationship between cavitation and transition from laminar to turbulence flows. Franc & Michel [40] developed a semi-empirical approach for the prediction of the location of cavity detachment in laminar separation for circular and elliptical cylinder and validated their approach with the experimental data. Gnanaskandan & Mehesh [41] studied the cavitating flows over a circular cylinder numerically and compared the results of the cavitating regimes with the results of the single phase flows. Their results showed that the cavitation suppressed the turbulence in the near-wake region and modified the vortex shedding mechanism significantly by the vorticity dilatation due to the phase changing inside the laminar separation. They investigated also the Reynolds number effect on the cavity length and found out that the cavity volume in vortex shedding process can be increased at higher Reynolds numbers. Kumar et al. [42] investigated the cavitation dynamics around a circular cylinder at the Reynolds number of 64,000 and the relationship between cavity life time and the cavitation number. The results from their work showed that the shedding frequency can be reduced and the pressure fluctuation due to the cavitation around the cylinder can be increased when the cavitation number decreased. Ghahramani et al. [43] performed experimental and numerical investigations about three-dimensional cavitating flow around a semi-cylinder at high Reynolds numbers and low cavitation numbers. They found that different vortices pattern formed and started to grow behind the semi-cylinder with the reduction of the cavitation numbers. In addition, their results revealed that at the lowest cavitation number, the cavitation dynamics affected the vorticity and vertical vortex structure significantly.

Brandao et al. [44] performed a numerical study on the cavitation around a circular cylinder based on the work done by Gnanaskandan & Mehesh [41] and extended the water-vapor model to include non-condensable gas effects. They considered the shock wave propagation inside the wake flow after the cavity collapse and presented the influence of non-condensable gas on delaying the transition to the low cavity shedding frequency. In addition, their results showed that the growth of two-dimensional cavity reduced the vortex stretching and baroclinic torque. Dobroselsky [45] investigated cavitation dynamics around a circular cylinder with the Reynolds number effect by using the Particle Image Velocimetry (PIV) measurement technology. His results presented the details of the transition from laminar to turbulent flow and the dependence of kinematic characteristics and the separation angle of the boundary layer on the Reynolds number at non-cavitating regime. In addition, different wake patterns and vortex shedding over a long period have been observed behind the cylinder. Sadri and Kadivar [46] performed a numerical simulation using a high-order compact finite-difference scheme to study cavitating flow and the cavitation-induced noise around one and two circular cylinders. They studied the cavitating flow for different gaps of two side-by-side cylinders. Their results revealed that the wakes behind the side-by-side cylinders are merged together and a single vortex street is generated by the gap reduction between two cylinders.

Previous works on cavitation dynamics around cylinder are mostly investigated the cavitating flows behind two dimensional cylinder with a very small gap between the cylinder and the test section. In this work, we focused on the highly three-dimensional cavitating flow around a stainless steel circular cylinder. In addition, we considered the Reynolds number effect on the cavitation dynamics and visualized two different cavitation regimes as cloud—and partial cavitations at high sampling frequency. We measured the synchronized hydrodynamics forces on the cylinder, which presented the effects of Reynolds numbers on the cavitation and vortex structures behind the cylinder. The remainder of this paper is arranged as follows: In Section 2, the experimental setup, experimental conditions and the test cases will be described. The main results of the cavitation around circular cylinders at different cavitating regimes and various Reynolds numbers are then discussed in Section 3. Finally, the main conclusions will be listed in Section 4.

2. Experimental Set-Up

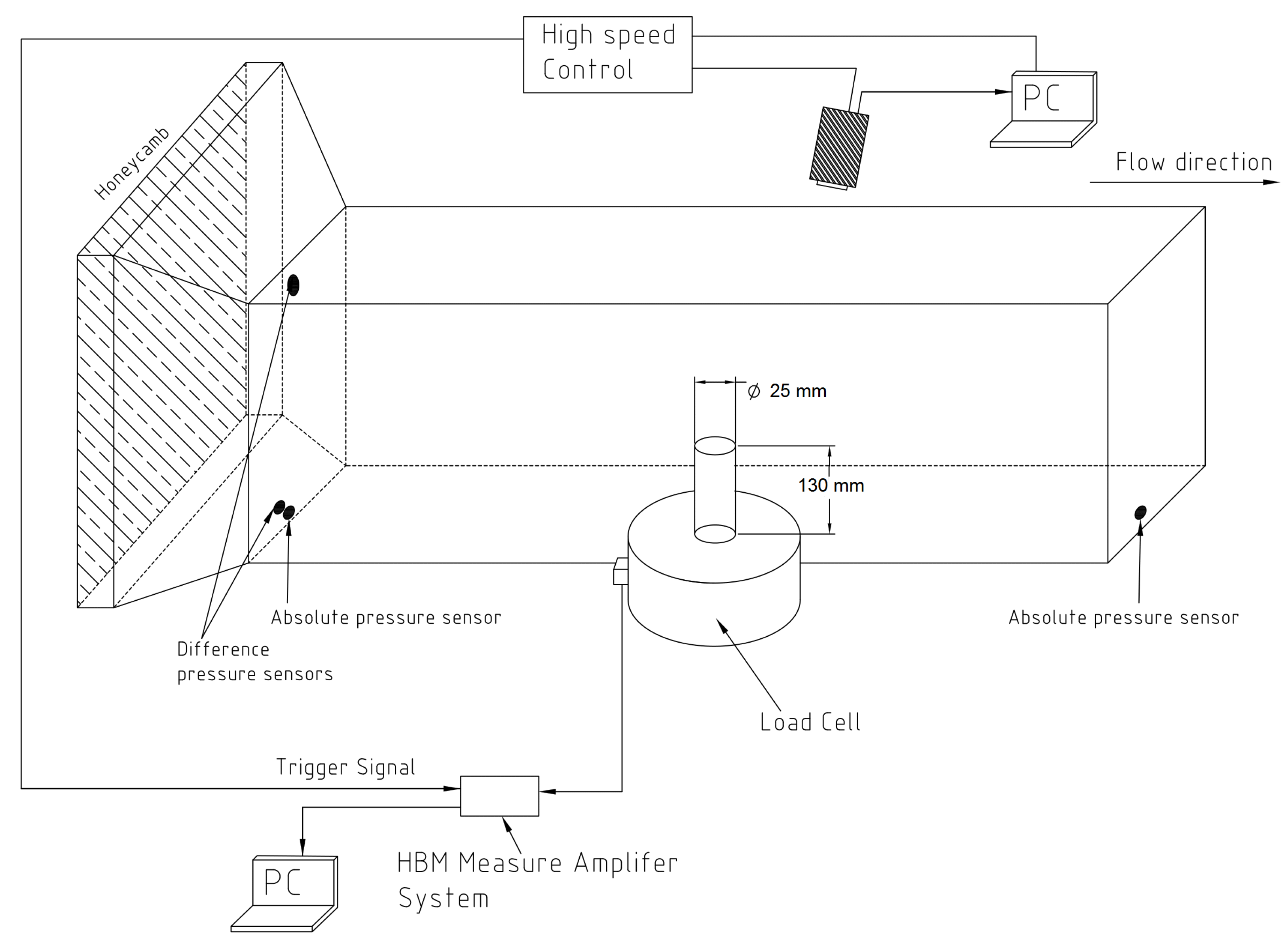
The experimental investigation was carried out in the cavitation tunnel K23 of Institute of Ship Technology, Ocean Engineering and Transport Systems at the University of Duisburg-Essen. In this cavitation tunnel, the absolute pressure range from 0.1 to 2 bar and the maximum velocity of 9 m/s can be achieved. Figure 1 showed the experimental setup of the present work. The test case is a circular cylinder which was mounted on one of the Plexiglas wall of the cavitation tunnel test section. The test section of the tunnel has a cross-section of 0.3 × 0.3 m${}^2$ and a length of 1.1 m. The velocity of the inlet section was measured using a differential pressure sensor and the inlet-/outlet absolute pressures are measured using the absolute pressure sensors mounted on the test section of the tunnel. The initial turbulence intensity for the inlet flow of was about 2%. The high-speed camera Phantom V9.1 was placed on the side of cavitation tunnel test section to capture the side view of the cavitation dynamics around the circular cylinder. For the visualization, the sampling frequency was adjusted 1000 Hz and the exposure time for each image was 30 ms. One user trigger signal was generated at the begin of the visualization and the force measurement was started to recording the data to achieve the synchronization between visualization and force measurement. The force measurement was carried out using a force sensor mounted between the tunnel test section and the cylinder. The recording frequency of the force measurement was adjusted to 4800 Hz.

In this investigation, we visualized cavitation dynamics around the circular cylinder and measured the hydrodynamics forces on the cylinder. The circular cylinder has a diameter of 25 mm and the length of 130 mm. We performed the experiments for three different Reynolds numbers ranging from 1.0 to $1.5\times {10}^5$ in this work. The experimental environment such as water temperature was maintained in a constant level for different Reynolds numbers to adjust the same situation for capturing the cavitation dynamics. The air content was between 1.2 and 1.4 mg/L and the water temperature was about 16 °C. The Reynolds number and cavitation number are defined as follows:

$$\begin{array}{c}\hfill \sigma =\frac{p_{ref}-p_v}{1/2{\rho }_{ref}{V}_{ref}^2}\end{array}$$

(1)

$$\begin{array}{c}\hfill Re=\frac{V_{ref}{l}_{ref}}{\nu }\end{array}$$

(2)

where $p_{ref}$ and $p_v$ are the reference static pressure at the middle of the inlet section and the saturation vapor pressure of the operating liquid, respectively, $V_{ref}$ is the incoming flow velocity, and ${\rho }_{ref}$ and $\nu$ are the reference density and kinematic viscosity of the operating liquid, respectively.

The absolute error of measurement of saturation vapor pressure depends on the water temperature during the experimental testing in the cavitation tunnel which can be estimated indirectly using a temperature measurement system. The water temperature was 16 ${}^{\circ }\mathrm{C}$ with an uncertainty of $0.1{}^{\circ }\mathrm{C}$ during the experiment. The measurement error of vapor pressure was estimated about $24\mathrm{Pa}$ for temperature variation of $0.1{}^{\circ }\mathrm{C}$. The uncertainty of the inlet pressure was in the range of 100–200 $\mathrm{Pa}$. The uncertainty of the measured cavitation number for different testings was in the range of 0.05–0.1 during the experiment. The uncertainty of the inlet velocity was obtained for different experiments and at different flow conditions. The measurement uncertainty of the Reynolds number based on the cylinder diameter and the mean flow velocity is proportional to the absolute error of the inlet velocity. The uncertainties of the inlet velocity were about 0.07 at the inlet velocity of 4 m/s, 0.09 at inlet velocity of 5 m/s and 0.1 at inlet velocity of 6 m/s. Therefore, the maximum measurement error of the inlet velocity was about 1% for different experiments which led to an uncertainty of the measured Reynolds number of about 1–2%.

3. Results

In this section, the results of two different cavitating regimes around the circular cylinder are presented. Figure 2 and Figure 3 illustrate one cyclic behavior of the cloud cavitation and partial cavitation dynamics around the circular cylinder with inlet flow velocity of 4 m/s, respectively. The Reynolds number for this velocity is 1.0 × 10${}^5$.

Table 1. The initial conditions of each experiment of the present work.

Inlet Velocity (m/s)	Cavitation Number (-)	Reynolds Number (-)	Outlet Pressure (bar)
4.0	1.1	1 × 10${}^5$	0.104
	1.6	1 × 10${}^5$	0.121
5.0	1.02	1.25 × 10${}^5$	0.135
	1.55	1.25 × 10${}^5$	0.199
6.0	1.05	1.49 × 10${}^5$	0.189
	1.55	1.49 × 10${}^5$	0.277

shows a summary of initial conditions such as inlet velocity, cavitation number, Reynolds number and outlet pressure for different experiments of the present work.

3.1. Cavitation Dynamics behind the Cylinder

As the results of cloud cavitation dynamics show, relative large vortex structures behind the cylinder were formed and developed downstream of the cylinder with the flow during a cyclic behavior of cavitation in the cloud cavitation regime. In addition, a quasi strong tip vortex cavitation can be seen at the free-end of the cylinder. The attached cavity on the cylinder was detached from the cylinder surface only after a short distance of about 4–6 mm on the surface. The flow moving downstream of the cylinder can interact with the cavity structures behind the circular cylinder and affect the cavitation dynamics. The interaction between the tip vortex cavitation and detached cavitation occurred at the position approximately 50 mm vertically from the tip and 25–30 mm horizontally behind the cylinder. This interaction can modify the cavitation shedding mechanism and affect on the pressure distribution of the cavitation and leading to a change of the cavity shedding frequency. The pressure wave propagation inside the cavity resulting from the cavity collapse may be the main reason of the cavity shedding in this case.

In Figure 3, the side-view of the partial cavitation behind the cylinder was presented. As it can be seen from the results, the cavity volume was significantly reduced with increasing of the cavitation number compared with the case of cloud cavitation. In addition, the images show that the cavity structures appeared behind the cylinder mostly initiated from the tip vortex cavitation and has a tendency from the top side to the bottom. In other words, a substantial amount of the cavitation can be induced in the region close to the tip of the cylinder. The main reason can be the formation of the low pressure region near the cylinder tip the where the flow with higher velocity passing from the cylinder tip. Therefore, in the partial cavitation regime, the cavity structures which can be started from the middle of the cylinder surface was much lower compared with the cavity structures in the cloud cavitation regime.

Figure 4 illustrates the cavitation dynamics around the cylinder at velocity of 5 m/s with the Reynolds number of 1.25 × 10${}^5$ and the cavitation number of 1.0. As the results show, a larger volume of the cavity structure behind the cylinder can be seen compared to the cavity structure at a velocity of 4 m/s in the cloud cavitating flow. The reason of larger cavity structure could be due to the larger low pressure region formed behind the cylinder due to the higher flow velocity compared to the case with lower Reynolds number.The tip vortex cavitation dynamics in the experiment with the velocity 5 m/s was remained mostly unchanged and the attached cavity on the upper side of cylinder appeared persisted for the entire period of cloud cavitation. The mean width of the cavity structure from the cylinder tip was about 50–55 mm. In addition, the attached cavity on the front view of the cylinder has a ‘finger’ shape. In this regime, both the cavity from the cylinder tip and from the cylinder surface crossed behind the cavitation vortex structure and created a strip-shape cavity (see the yellow squares in the images). These strip-shape cavitation structures can be observed in most of the time steps in the horizontal direction. Considering the vortex shedding mechanism behind the cylinder, the opposite direction of strip-shape cavities could be explained by detachment of the vortex structures from top and bottom of the cylinder which generated the low pressure regions at two parallel vortex streets. In the wake region of the cylinder, most cavitation structure collapse after a distance of about 5 cylinder diameters behind the cylinder. The reason could be due to the pressure enhancement in the region far from the cylinder. However, the details of flow pressure distribution needs a further investigation to understand this physical phenomenon inside the cavitation dynamics. The partial cavitation regime around the cylinder was presented in Figure 5 and the cavity structure exhibited a similar movement pattern as cavity dynamics seen in Figure 3. The main cavity structure could be generated by the flow passing over the cylinder tip. Simultaneously, the results reveal the detachment of the some cavities from the bottom section of the cylinder near the wall. These cavity structures have a movement diagonally upwards to the region near the middle of the cylinder.

In this work, we also studied the cavity dynamics on the circular cylinder at a velocity of 6 m/s, which presented in Figure 6 and Figure 7. The results show that the cloud cavitation structures on the cylinder at this velocity have the largest volume of cavity among all cases. Therefore, larger vortical structures can be generated behind the cylinder. In addition, the near wake region behind the cylinder extended over a larger range from about 4 cylinder diameters. The cavity structure condensed quickly at a distance of approximately 6 cylinder diameters. Compared to the cavity at the velocity of 5 m/s, the detached cavity formed behind the cylinder showed a parallel shedding structure from the whole cylinder surface in the downstream direction. This aspect could be attributed to the weaker influence of the tip vortex cavitation on the larger cavity structure which can increase the cavitation stability behind the cylinder.

In the Figure 7, the partial cavitation dynamics behind the circular cylinder at Reynolds number of $1.5\times {10}^5$ was presented. In this regime, the effects of the tip vortex cavitation on the dynamics of the cavitation formed behind the cylinder is dominant. As it can be seen from the images, the main part of the cavity volume is from the tip vortex cavitation which can be formed during the shedding process. In addition, the detached cavity from cylinder in the downstream has a similar parallel structure to the cloud cavitation at this velocity. The reason for this parallel structure is the large vortex shedding process generated by the higher velocity field.

3.2. Hydrodynamics Forces on the Cylinder

The time histories of lift coefficients amplitude on the circular cylinder at three different velocities and in the cloud cavitation regime are presented in Figure 8. The lift coefficient is defined as follows:

$$\begin{array}{c}\hfill c_l=\frac{F_{lift}}{0.5·\mathrm{A}·\rho ·v^2}\end{array}$$

(3)

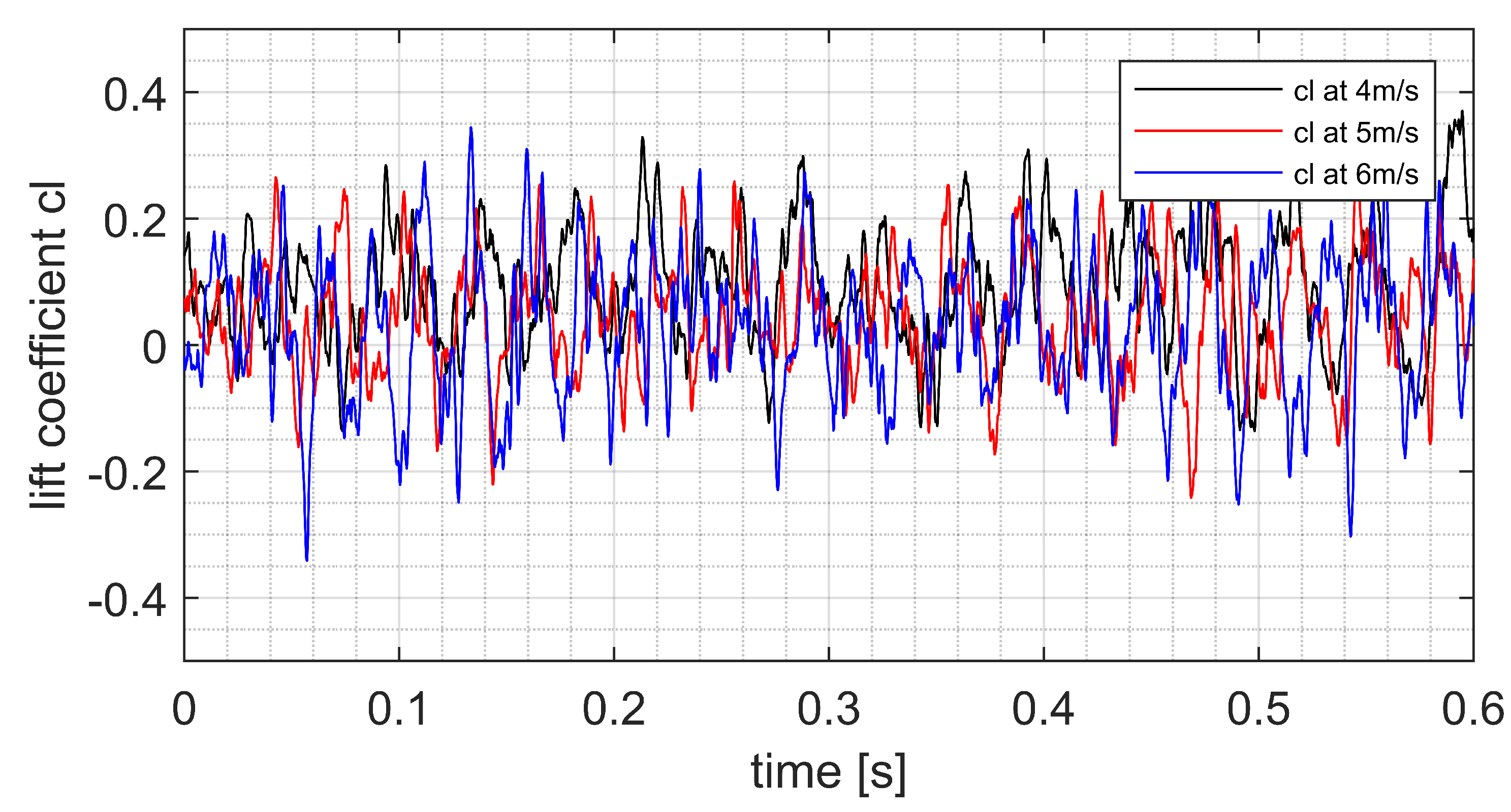
In the definition of the lift coefficient, the parameter is lift force and “A” is the relevant surface and calculated by the multiplication of the cylinder diameter and the cylinder height. The fluctuation of the lift coefficient at the Reynolds number $1.0\times {10}^5$ (velocity 4 m/s) demonstrates a strong repeatability with the peaks and troughs remaining at the same level during the recording period with no significant differences between each fluctuation. Based on the results, it can be deduced that the hydrodynamics force on the circular cylinder at the velocity of 4 m/s is continually repeated in the cloud cavitation regime. The lift coefficient on the cylinder at the velocity of 5 m/s presented a similar repeatability in its fluctuations, however with higher frequency vibration.

The time histories of the lift coefficients at the velocities of 4 m/s and 5 m/s have almost the same root mean square value which shows that the combined hydrodynamic force on the circular cylinder at these two velocities is at the same level. However, the lift coefficient on the cylinder at the velocity of 6 m/s shows a strong non-linear behavior characterized by a low frequency signal and multiple high frequency signals. The peak values exhibit multi similar fluctuations in high frequency region. This could be due to the highly instability behavior and the interaction between cloud cavitation collapse and tip vortex shedding behind the circular cylinder.

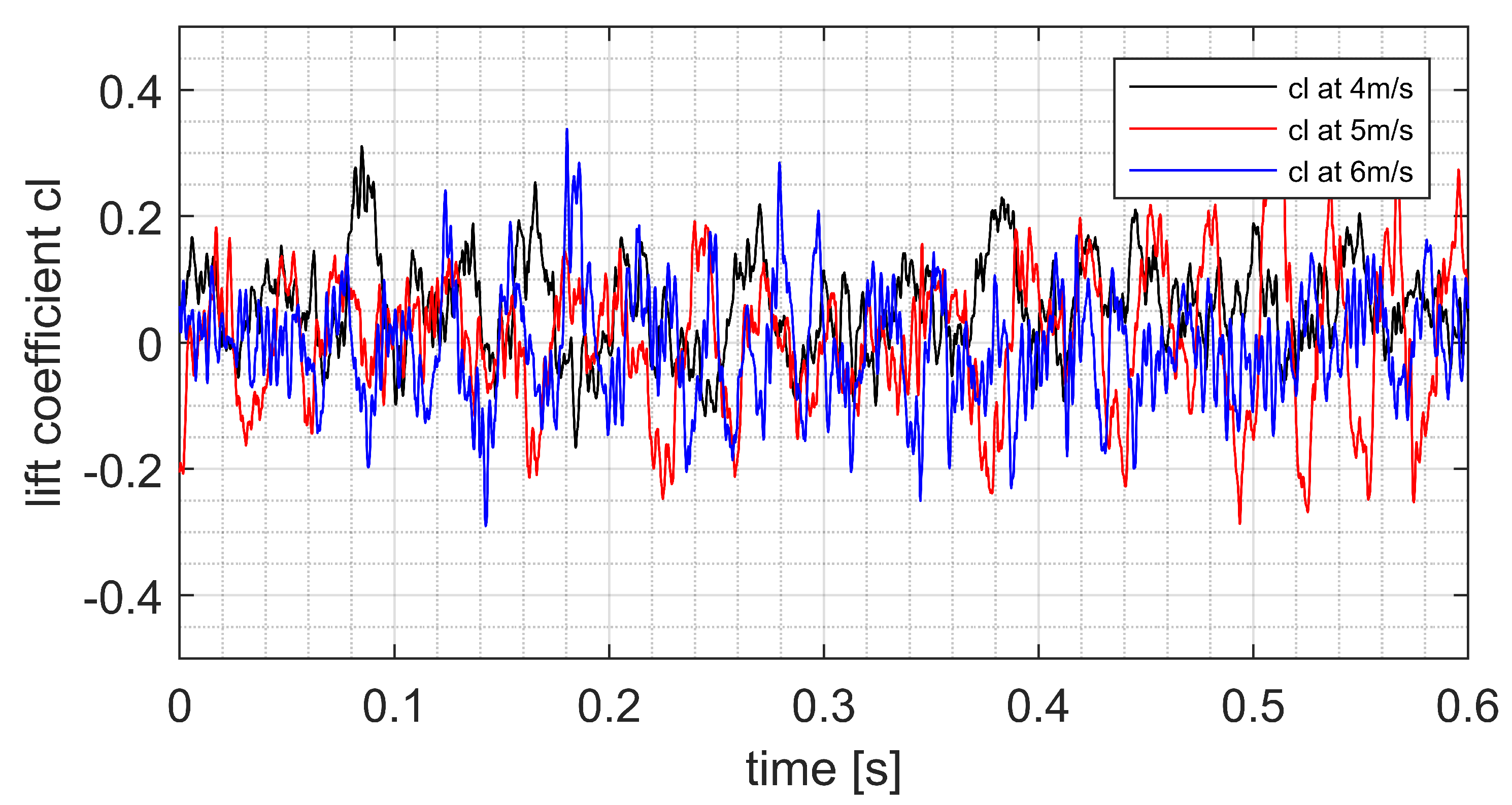
Figure 9 presents the time history of lift coefficient on the circular cylinder at three different velocities in the partial cavitation regime. In this regime, the tip vortex cavitation plays a dominant roll and the lift coefficient on the cylinder was affected by the tip vortex cavitation periodically. The cavity volume was increased by the increasing of the velocity. This enhancement of cavity volume can be observed by the increasing of the root mean square value of the amplitude of the lift coefficient fluctuations. Generally, the lift coefficients of the cylinder in three different velocities present a non-linearity behavior due to the influence of the interaction between tip vortex generation and cavity shedding. Further discuss about the hydrodynamics effect would be carried out in the frequency domain.

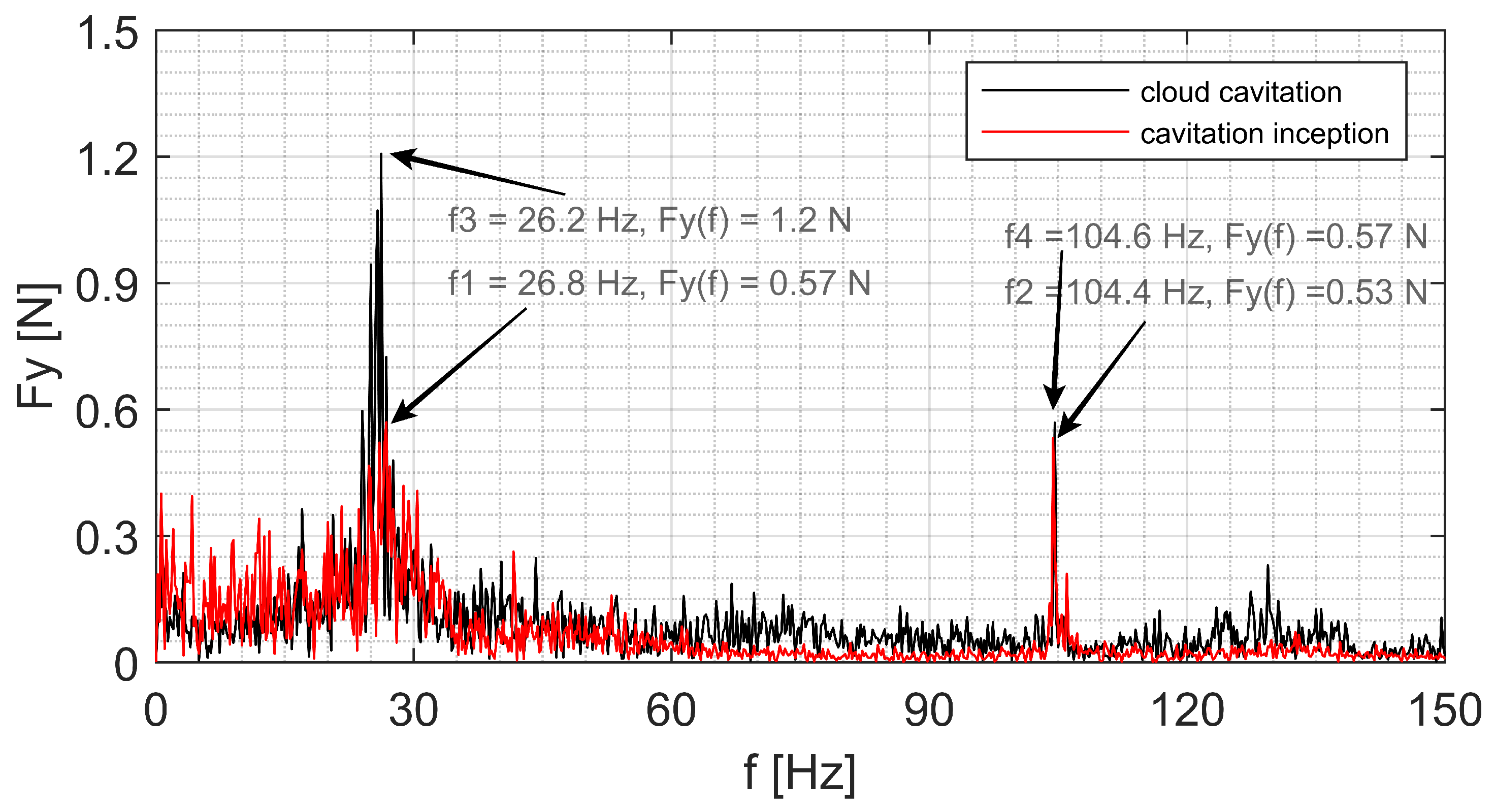
Figure 10 and Figure 11 present comparisons between lift forces in the frequency domain at cloud cavitation, partial cavitation and cavitation inception regimes at the velocity of 4 m/s. The cavitation inception dynamics on the circular cylinder appeared at the cavitation number of 2.4 but no visible cavitation structure was seen in this regime. Therefore, we ignored to present the results of the cavitation on the cylinder in the cavitation inception regime and focused on the cavitation effect on the hydrodynamic behavior of the partial- and cloud cavitation dynamics. Frequencies f1 to f6 and the corresponding amplitudes in the figures represented the peaks of the frequency amplitude in the fast Fourier transform (FFT) calculation.

The peaks at relative low frequency ranges can be corresponded to the shedding frequency of the large-scale cavity structures. The peaks at the high frequency range remained constant for all cases at different cavitation regimes. In addition, the peaks at relative low frequency ranges for each cases can be the reason of the flow induced hydrodynamics forces on the cylinder. The tip vortex shedding and small cavities shedding can affect the hydrodynamic forces in addition to the effects of the collapse of the large cavity structures behind the cylinder. The peaks at higher frequency range show not significant shift in the frequency range. From the Figure 10 can be seen that the peaks f1 and f3 represent the hydrodynamics lift forces at the low frequency range for the cavitation inception and cloud cavitation, respectively. The peaks f2 and f4 reveal the hydrodynamic lift forces at the high frequency domain for the cavitation inception and cloud cavitation, respectively. It can be deduced that the amplitude of the frequency f3 is about twice of the frequency f1 at a similar frequency. This means that the presence of the cavitation can affect the vibration behavior on the circular cylinder. In other words, the vibration amplitude of the cylinder can be increased at the cavitation cloud regime compared to the vibration amplitude of the cylinder at the cavitation inception regime. It can be deduced that the cavitation cloud can merged with Karman vortex street formed behind the cylinder at non-cavitating regime and induce much higher vibration amplitude acted on the cylinder. In this case, the frequency value and amplitude of frequency at relatively high frequency range show no significant difference at the cavitation inception and cloud cavitation regimes. Therefore, it can be included that the presence of the cavitation has less affect on the vibration amplitude of the cylinder at high frequency range in the cloud cavitation regime compared to the cavitation inception regime.

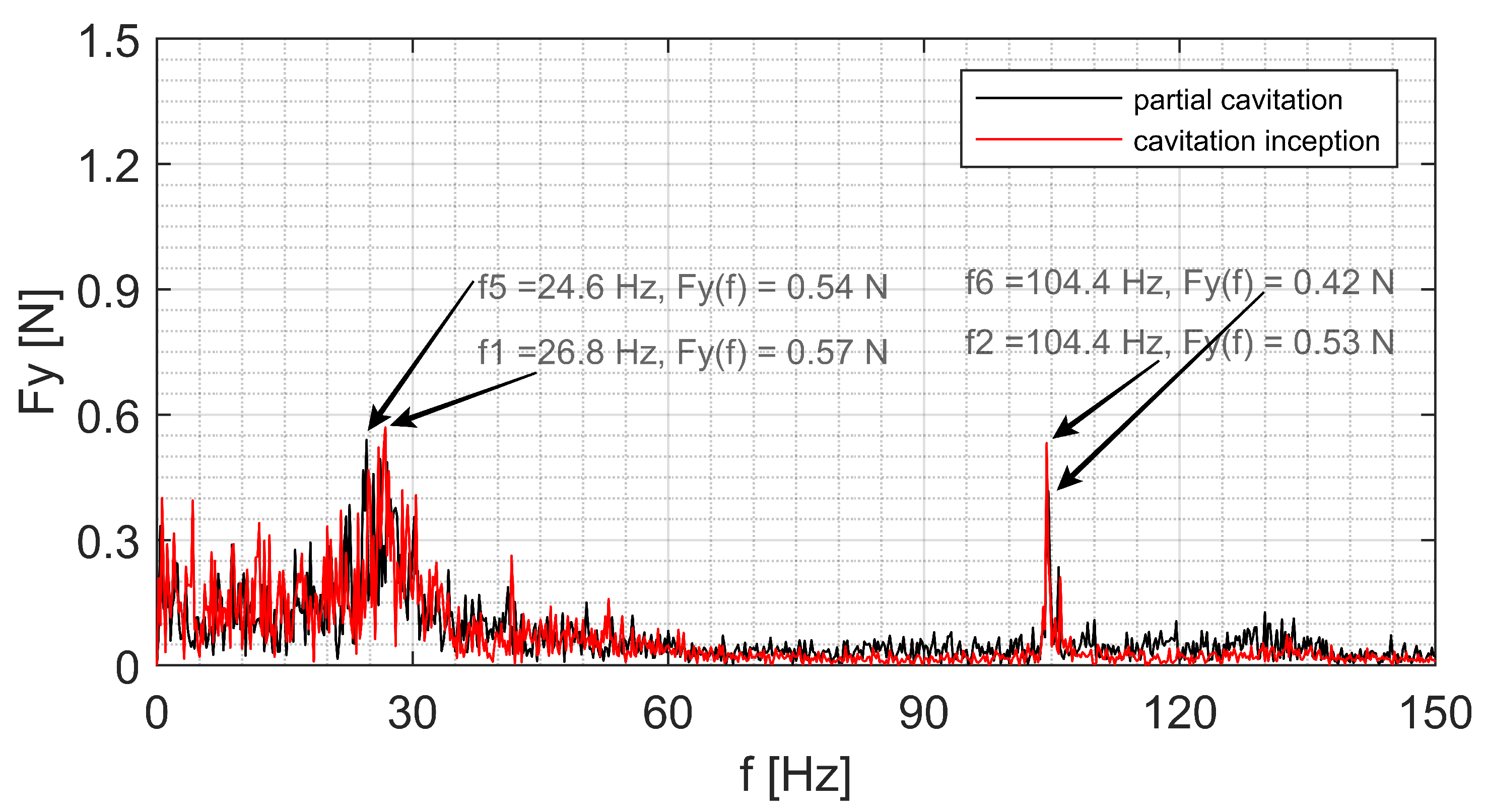
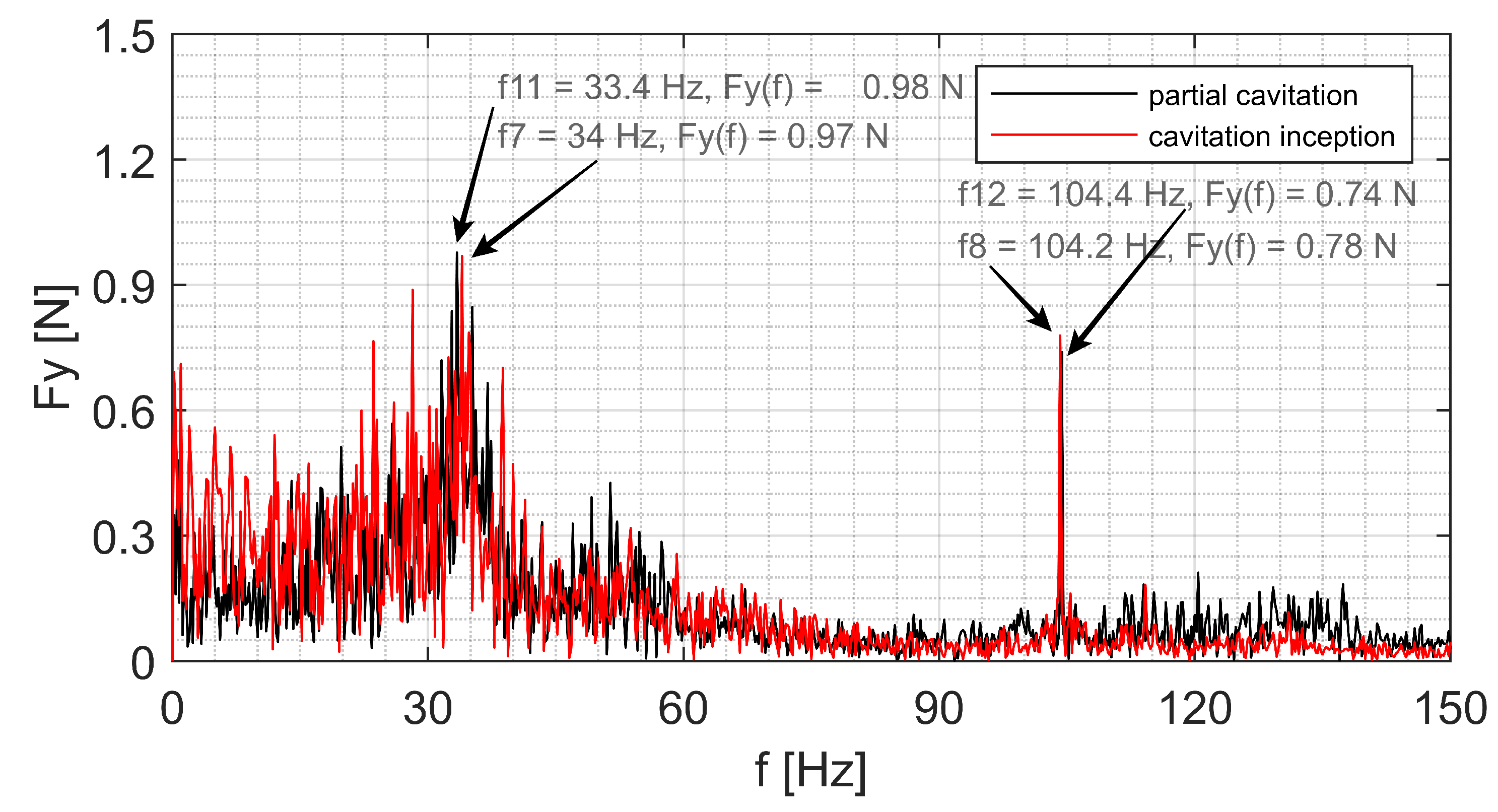
Figure 11 presents the comparison of the hydrodynamic lift forces on the cylinder in the frequency domain at partial cavitation regime (cavitation number = 1.5). The peaks at the low frequency domain, f1 and f5 have mostly the same amplitudes however an increasing of the frequency value about 2 Hz in the cavitation inception regime can be observed. The reason can be the low cavitation volume formed on the cylinder at cavitation inception regime and the large distance between the cavity collapse position and the cylinder surface. As it can be seen from the results, the cavitation has a influence on the vibration amplitude at the high frequency range in the partial cavitation regime. A reduction of about 20% for the vibration amplitude can be deduced due to the effects of the cavitation on the hydrodynamic force on the cylinder. One of the reason for this amplitude reduction could be the effects of the tip vortex cavitation shedding on the cavitation dynamics behind the cylinder.

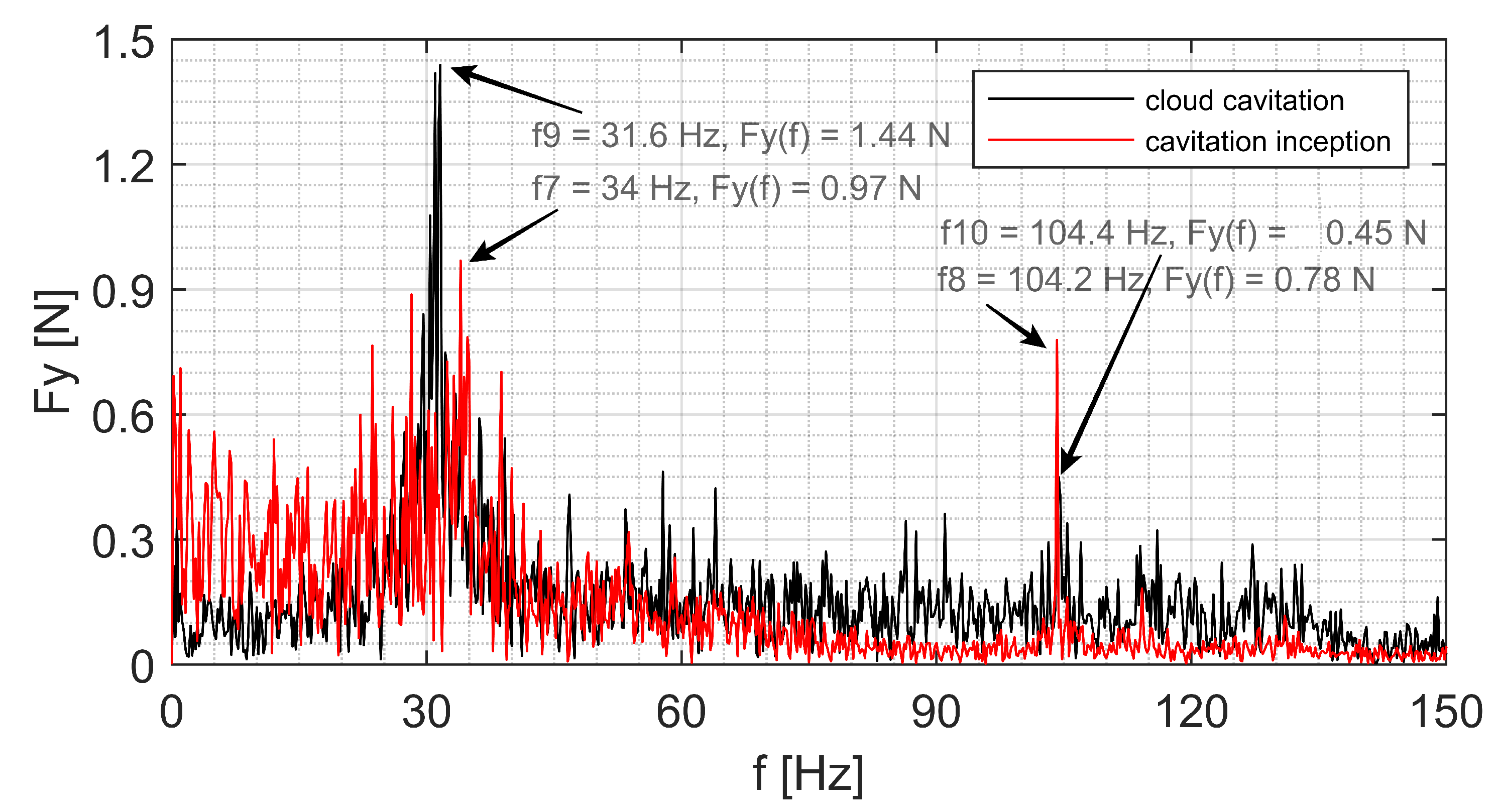
Figure 12 and Figure 13 show the hydrodynamic lift forces on the circular cylinder in the cloud cavitation regime ($\sigma$ = 1.0), partial cavitation regime ($\sigma$ = 1.5) and cavitation inception ($\sigma$ = 2.4) at velocity of 5 m/s. The lift force on the cylinder at this velocity shows a strong noise in the frequency range from 23 to 40 Hz. The vortex shedding at this range was affected by the small cavitation structures formed behind the cylinder. The peaks f7 and f9 represent the amplitude of the lift force on the cylinder in the cavitation inception and cloud cavitation regimes, respectively. In other words, the vibration amplitude in the cloud cavitation regime is about 1.5 times of the vibration amplitude on the cylinder in the cavitation inception regime. However, the vibration amplitude increasing rate at the flow velocity of 5 m/s is lower than the amplitude increasing rate at the flow velocity of 4 m/s in the low frequency range. In addition, the vibration amplitude on the cylinder at lower Reynolds number is higher than the vibration amplitude at higher Reynolds number. In relatively high frequency range from 45 to 135 Hz in the Figure 12, the lift force on the circular cylinder in the cloud cavitation regime has several small peaks with amplitudes over 0.3 N. These peaks were probably caused by the small cavitation structure shedding, which have also relatively higher frequency. Furthermore, the lift force peak of the frequency in the cloud cavitation regime (f10) is about 60% of the lift force peak in the cavitation inception regime (f8). In other words, the vibration amplitude for the cavitation inception regime at higher frequency is higher than the vibration amplitude for the case with the cloud cavitation. In Figure 13, the results show that the lift forces have similar vibration magnitude at the cavitation inception regime in the low frequency range compared to the partial cavitation regime at the same condition. In addition, the value and amplitude of the frequency for both cavitating regimes are similar to each other.

The results revealed, at the velocity of 4 m/s, the amplitude of the lift force at cloud cavitation regime (cavitation number of 1.0) is 2.2 times of the amplitude of the lift force at partial cavitation regime (cavitation number of 1.5). At the velocity of 5 m/s, the vibration amplitude at cloud cavitation regime (cavitation number of 1.0) is 1.46 times of the vibration amplitude at partial cavitation regime (cavitation number of 1.5). However, at a constant cavitation number of 1.0, the vibration amplitude at the velocity of 5 m/s is 1.2 times of the vibration amplitude at the velocity of 4 m/s. In addition, at a constant cavitation number of 1.5, the vibration amplitude at the velocity of 5 m/s is 1.8 times of the vibration amplitude at the velocity of 4 m/s.

4. Conclusions

We performed an experimental study on the cavitation structure and the corresponding hydrodynamic force on a circular cylinder at three Reynolds numbers and two different cavitating regimes. The cavity shedding mechanism, the time history of force coefficient and the lift force in frequency domain have been analyzed to understand the cavitation dynamics and the effects of cavitation on the hydrodynamic force on the circular cylinder. The results revealed that by increasing the flow velocity, larger cavity volume on the circular cylinder can be observed which lead to a stronger hydrodynamic forces. With increasing of the Reynolds number, the frequency of lift force on the cylinder shifted to a higher frequency position, indicating an increase in vortex and cavity shedding frequencies. At the same Reynolds number, changing the cavitation number affected the cavitation dynamics and the amplitude of the hydrodynamics forces on the circular cylinder. However, the cavitation regime had only a small influence on the frequency value of the lift force in the low frequency range. It can be concluded that the effects of the Reynolds number on the cavitation dynamics and amplitude of the shedding frequency is significant. However the effects of the cavitation number on the enhancement of the amplitude of the shedding frequency in a cavitating flow with a constant velocity is slightly higher than the effects of Reynolds number on the enhancement of the amplitude of the shedding frequency at a constant cavitation number.