Abstract
Erythrocyte enrichment is needed for blood disease diagnosis and research. DLD arrays with an I-shaped pillar (I-pillar) sort erythrocytes in a unique, accurate, and low-reagent method. However, the existing I-shaped pillar DLD arrays for erythrocyte sorting have the drawbacks of higher flow resistance and more challenging fabrication. A two-dimensional erythrocyte simulation model and the arbitrary Lagrangian–Euler equations at the cell–fluid boundary were built based on the fluid–solid coupling method to investigate the influencing factors of the erythrocyte flow path in an I-pillar DLD array and find its optimization method. Three different sizes of I-pillars were built and multiple sets of corresponding arrays were constructed, followed by finite element simulations to separately investigate the effects of these arrays on the induction of erythrocyte motion paths. This work demonstrates the motion paths of erythrocyte models in a series of I-pillar arrays with different design parameters, aiming to summarize the variation modes of erythrocyte motion paths, which in turn provides some reference for designing and optimizing the pillar size and array arrangement methods for I-pillar array DLD chips.
1. Introduction
Erythrocytes are an essential component of about 45% of human blood. Their deformability directly affects the hemorheology [1,2,3]. Erythrocyte biconcave shape and corresponding deformability are essential features of their biological function, and the deformability of erythrocytes can be seriously affected under the influence of various diseases [4,5,6]. This deformable change has been identified as an intrinsic indicator of some blood disorders. Therefore, sorting and enriching erythrocytes is necessary in researching and diagnosing various blood diseases. As a new technology, in recent years, the microfluidic method can potentially apply tiny biological particles. Instead of the existing bulky and complex blood-cell processing equipment, microfluidic technology is applied to sorting and enriching erythrocytes, which can provide a new, efficient, cheap method for studying blood diseases and erythrocyte properties.
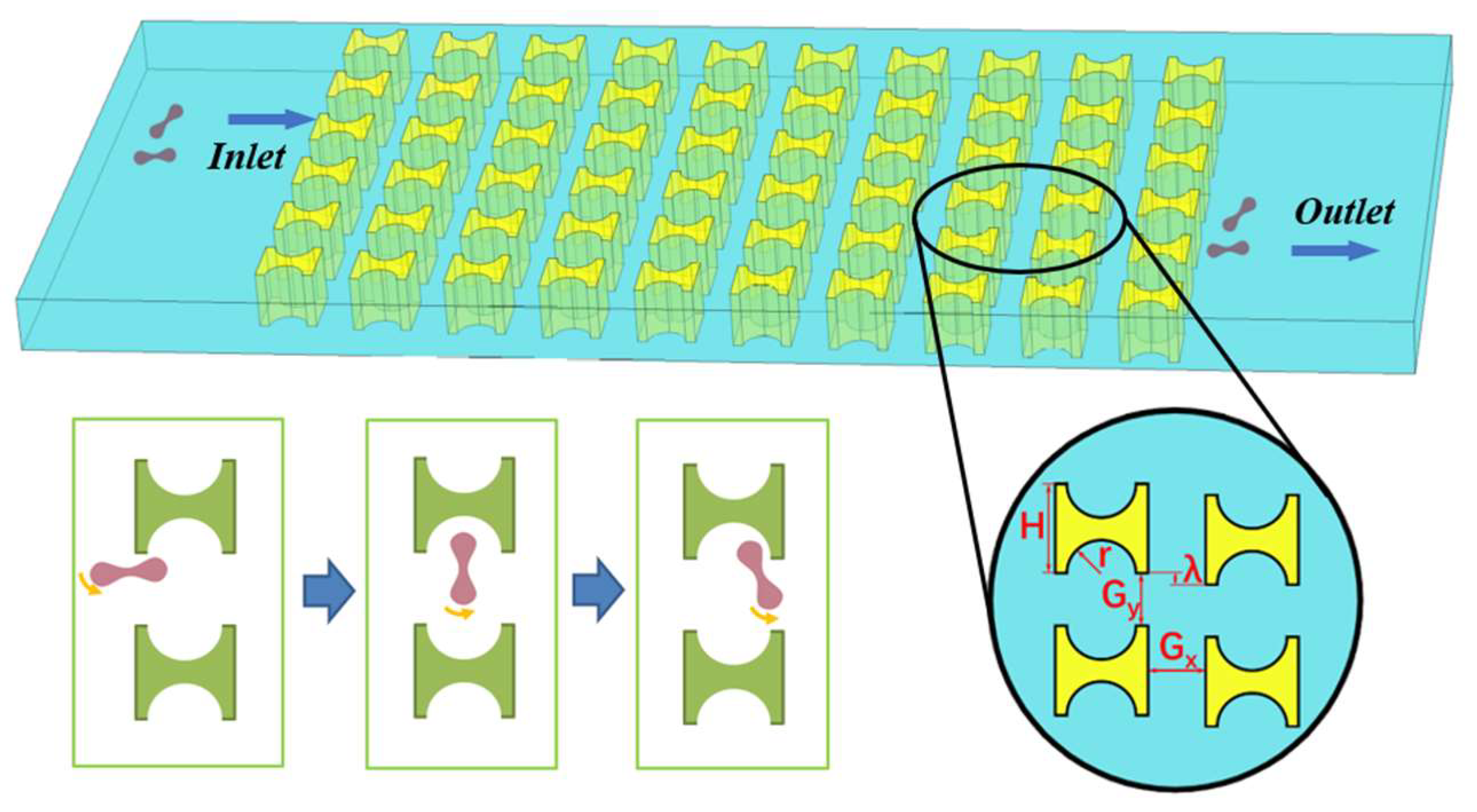
A microfluidic technique called deterministic lateral displacement (DLD) can separate and enrich micro-nano particles of various sizes [7,8]. An array of micro pillars is arranged in a flat microchannel to form a DLD chip, and the array is arranged at an angle to the main channel. The particle suspension flowing through the array is divided into a large number of microfluidic beams, and the particles are affected by the combined action of these beams and the pillars during their motion. The larger particles move in displacement flow mode along the pillar arrangement toward the side of the channel, while the smaller particles move in zigzag mode around the pillars in the same overall direction as the main channel. This eventually causes the two types of particles to be collected at different exits at the end of the chip [9].
DLD technology is well-suited for sorting small spherical particles in biological studies because of its function principle. Xavier, M. et al. [10] used the DLD technique to classify skeletal stem cells (SSCs) according to cell size and stiffness. Their results showed that the DLD particle size-based sorting method could provide a rich and diverse population of SSCs. DLD technology also shows excellent potential in isolating circulating tumor cells; CTCs are separated from the blood or urine [11,12] by a DLD chip and are diagnosed with related cancers. Tang, H. et al. [13] used a new design method of extension optimization to shorten the device and flexibly manipulate the cell motion path for efficient sorting of the circulating tumor cells (CTCs).
As the research progresses, many improved pillar designs and array layouts make the technique suitable for non-spherical particles, such as erythrocytes [14,15,16]. Davis, J.A. et al. [17] used circular pillars to construct a DLD array to separate leukocytes, erythrocytes, and platelets from almost undiluted contaminated blood, with sample processing speeds of up to 1 μL/min. Al-Fandi et al. [18] proposed wing-and-rhomboid pillar shapes and compared them with circular pillars. The results show that the wing-shaped pillar reduces the deformability of non-spherical biological particles, thus reducing the critical radius of the separation chip, improving the separation performance of blood cells and trypanosoma, and avoiding the clogging of the equipment caused by the random flow of the particles in the separation of deformable non-spherical biological particles. Zeming, K.K. et al. [14] demonstrated that using an I-shaped pillar structure can induce erythrocytes to flow continuously to the side of the main channel in a displacement mode. The unique shape of the I-shaped pillar can induce erythrocytes to roll as they flow, making more efficient use of the maximum size of the non-spherical particles than traditional pillars. However, the rugged appearance of the I-pillar is not conducive to reducing the flow resistance when the DLD chip is working. At the same time, the difficulty of processing chips also increases the experimental cost of such pillars.
To reduce the research cost of I-shaped pillar DLD arrays, we attempted to use numerical methods to study the dynamic behavior of erythrocytes in DLD devices. Timm Kruger et al. [19] simulated the displacement of erythrocytes with different deformabilities in a DLD device by using a three-dimensional immersed boundary finite element lattice Boltzmann method, showing that it is possible to separate different deformable erythrocytes with a DLD device. Kabacaoglu, G. et al. [20] used an internal integral equation solver to investigate the ordering of same-size erythrocytes based on deformability by DLD for a two-dimensional vesicle flow. It was found that cells moving at a sufficiently high positive angle relative to the direction of flow moved laterally, while those with a smaller angle moved with the flow line. The efficiency of the dense suspension technique was also evaluated, demonstrating that most cells in a dense suspension do not undergo lateral displacement. Jiao, Y.Y. et al. [21] created a numerical simulation of erythrocyte movement using DLD devices with different pillar shapes and gap configurations. The effects of pillar shape, row shift distance, and pillar diameter on erythrocyte separation performance were investigated. The numerical results show that erythrocytes enter the zigzag mode at low row shift (Δλ < 1.4 µm) and large row shift (Δλ > 1.5 µm).
A geometric model of red blood cells was established using parametric curves and a two-dimensional (2D) linear elastic red blood cell numerical model based on the continuous medium assumption. The motion of erythrocytes in the DLD chip was simulated by a finite element simulation using a fluid–solid coupling method. Following the experiments of Zeming, K.K et al. [14], an I-pillar with a side length of 15 μm was established and constituted a DLD array for the erythrocyte flow simulation. To confirm the simulation’s accuracy, the findings from the experiment and the simulation were compared. To reduce the flow resistance of the arrays and to optimize the performance of the chip, two more slender pillars were built. Subsequently, multiple arrays with different layouts were designed using the three pillar types, and the motion paths of the erythrocyte model in these arrays were observed. The comparison of these motion paths reflects the effect of parameters such as pillar size, distance between array rows, and fluid flow rate on the movement of red blood cells, and provides new and improved solutions for the design of I-pillar array.
2. Calculation Method
We adopted version 5.6 of COMSOL® Multiphysics software as the calculation tool, which is widely used for the computation of particle trajectories [22]. Typically, the I-pillar DLD arrays used for erythrocyte sorting are very narrow and long. In addition, the study of erythrocyte motion requires the longest possible arrays. The complexity of the three-dimensional (3D) problem in simulating the motion and deformation of particles in a DLD sorting chip stems from more than just the coupling itself. The interaction between the particles and the fluid and microcolumns can cause the particles to tumble and deform during their motion. This can lead to mesh distortion and overlap in the computational domain, which makes the computation non-convergent. To reduce the computational demand, a 2D approximation is usually used to simplify the 3D problem. Therefore, 2D arrays and erythrocyte models were established to simulate longer arrays. The proposed array height was 15 µm, and the erythrocyte model was driven by the fluid flow through ten rows of pillars leading to the outlet.
2.1. Fluid Flow Solver
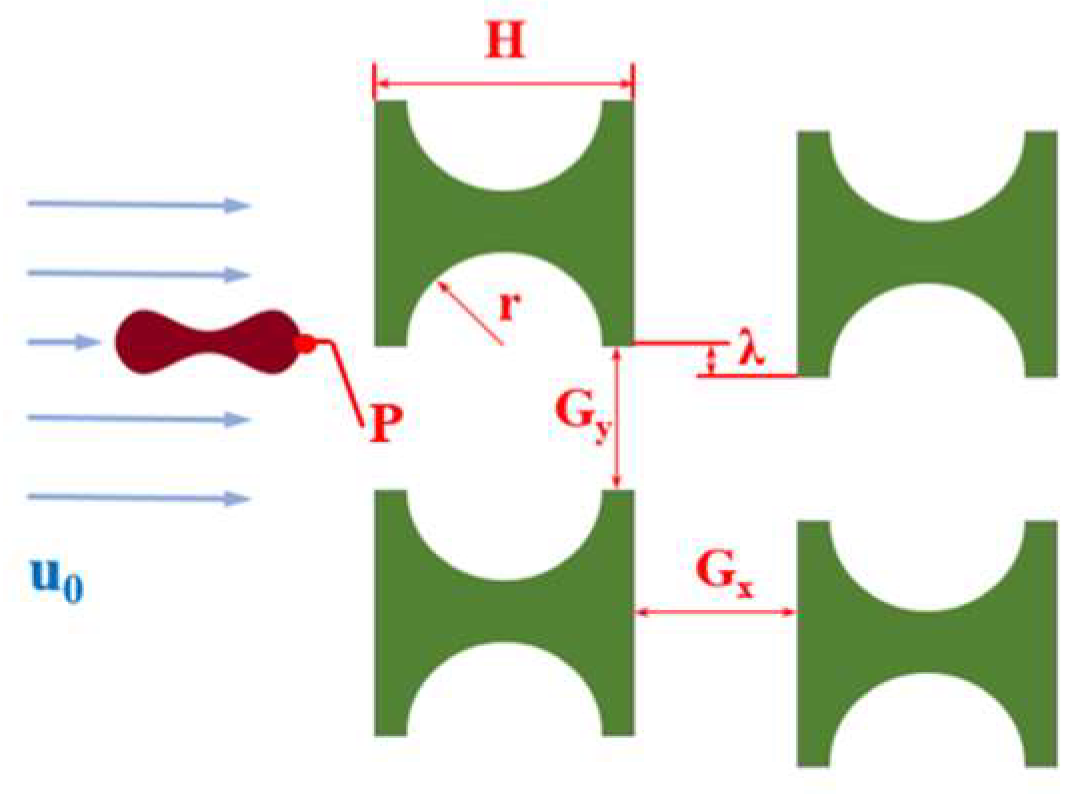
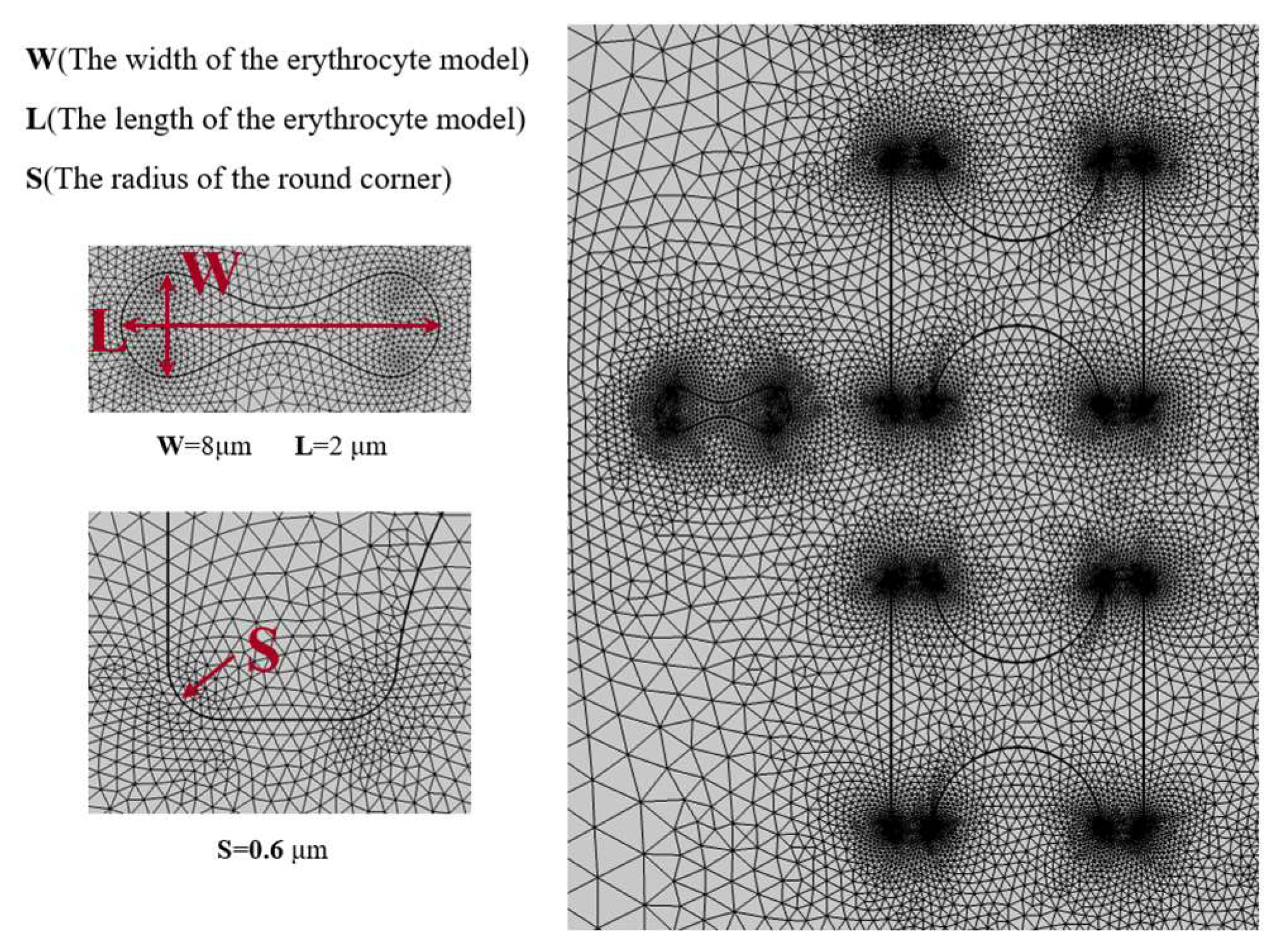
Figure 1 shows a partial schematic diagram of the I-pillar DLD chip, in which the red blood cells follow the suspension from the left inlet into the array and tumble under the combined effect of the fluid and the pillar. When flowing out from the array, the red cells are displaced in the direction perpendicular to the suspension flow. The main parameters affecting the effect of the array and pillar action are shown in Figure 1, where H is the side length of the I-pillar; r is the radius of the semicircle at the groove of the pillar; Gx and Gy denote the lateral and downstream pillar distances; and λ is the row shift distance of the array.
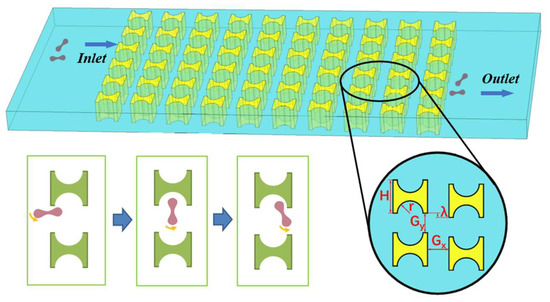
Figure 1.
I-pillar structure and its effect on the movement of erythrocytes.
In terms of the selection of chip material parameters, it was assumed that the DLD chip was composed of polydimethylsiloxane (PDMS), which is commonly used in microfluidic experiments, and its Young’s modulus was set as 1.5 MPa, Poisson’s ratio as 0.49, and dynamic viscosity as 0.001 Pa∙s [21,23,24]. The physical parameters of the proposed chip material, as well as the erythrocyte suspension, were all constants.
According to the law of conservation of mass, the continuity equation satisfied by the sample solution is:
where is the density of the fluid and is the fluid velocity. The erythrocyte suspension (saline, phosphate buffer, etc.) usually used in the process of DLD sorting experiments has a linear change in velocity gradient in the direction perpendicular to the flow, and can be considered as a Newtonian fluid. At the same time, the flow of fluid in the DLD chip is slow, the Reynolds number is very small (Re << 10) [25], and the flow state belongs to the laminar flow. According to the nature of the actual fluid, the fluid was set as an incompressible steady-state laminar fluid motion during the simulation. At this time, and were constants, and Equation (1) could be simplified as:
According to the law of conservation of momentum, the flow of fluid in the DLD sorting chip satisfied the Navier–Stokes (N–S) equation [26]:
where is the fluid viscosity, is the inertial force per unit volume of fluid, represents the pressure gradient, denotes the fluid’s deformation stress, represents the expansion stress of the viscous body, and is the mass force per unit volume of fluid.
The erythrocyte sample solution used for the DLD separation chip was in laminar flow state, where the viscous force had greater influence on the flow incompressible field than the inertial force [27]. This fluid was considered an incompressible flow, and its density and viscosity were uniform throughout the process. Equation (3) can be simplified as:
The other feature sizes in the flow field must be significantly less than the depth of the flow field in order for the two-dimensional simulation to be applied. In contrast, the main channel of a DLD chip must be generally flat, and its depth must be significantly smaller than its width. As a result, the simulation approach in this research applied the shallow groove approximation theory [28]. With this approach, the volume force representing the effect of the flat channel inner surface was added to the N–S equation:
In the transient flow simulation, the entire flow field changed with time, and the geometric boundaries and the grid in the physical plane changed with time. Considering the change in the grid boundary, the () coordinate system was introduced, and this coordinate system was used as the computational space. The grid in the computational space corresponded to the grid in the physical space one by one. When the grid in the physical space changed with time, the grid in the computational space was invariant, and at this time, the coordinate transformation quantity relationship was:
in Equation (6) is the Jacobian determinant:
The transformation relation of the volume when the corresponding grid was solved in two spaces was:
By bringing this relationship into the N–S equation and continuously calculating the value of J as the simulation proceeded, the physical space could be solved by calculating the differential equation in the space.
The sample solution in the DLD separation chip was driven by the injection pump, and the flow field in the chip reached a stable state after fully developing flow conditions. Therefore, the average flow velocity at the chip inlet was set as u0, and the pressure and viscous resistance at the outlet were defined according to Dirichlet conditions:
The injection pump injected the sample solution into the DLD chip. The pressure difference was formed between the inlet and outlet of the chip. With the pressure difference, the driving particles arrived at the outlet along with the flow of the fluid. The inner wall of the DLD sorting chip and the wall of the pillar obstacle were uniformly set as no-slip conditions. This paper does not consider the influence of the material properties of the pillar or wall on the motion trajectory of the object. If the acceleration motion of the particle at the entrance of the chip is considered, the initial values of its displacement field and velocity field are set to zero. If the particle has moved to a certain part of the chip, the initial value of velocity field can be set to the velocity at the corresponding position under the steady-state flow field.
2.2. Erythrocyte Structure Solver
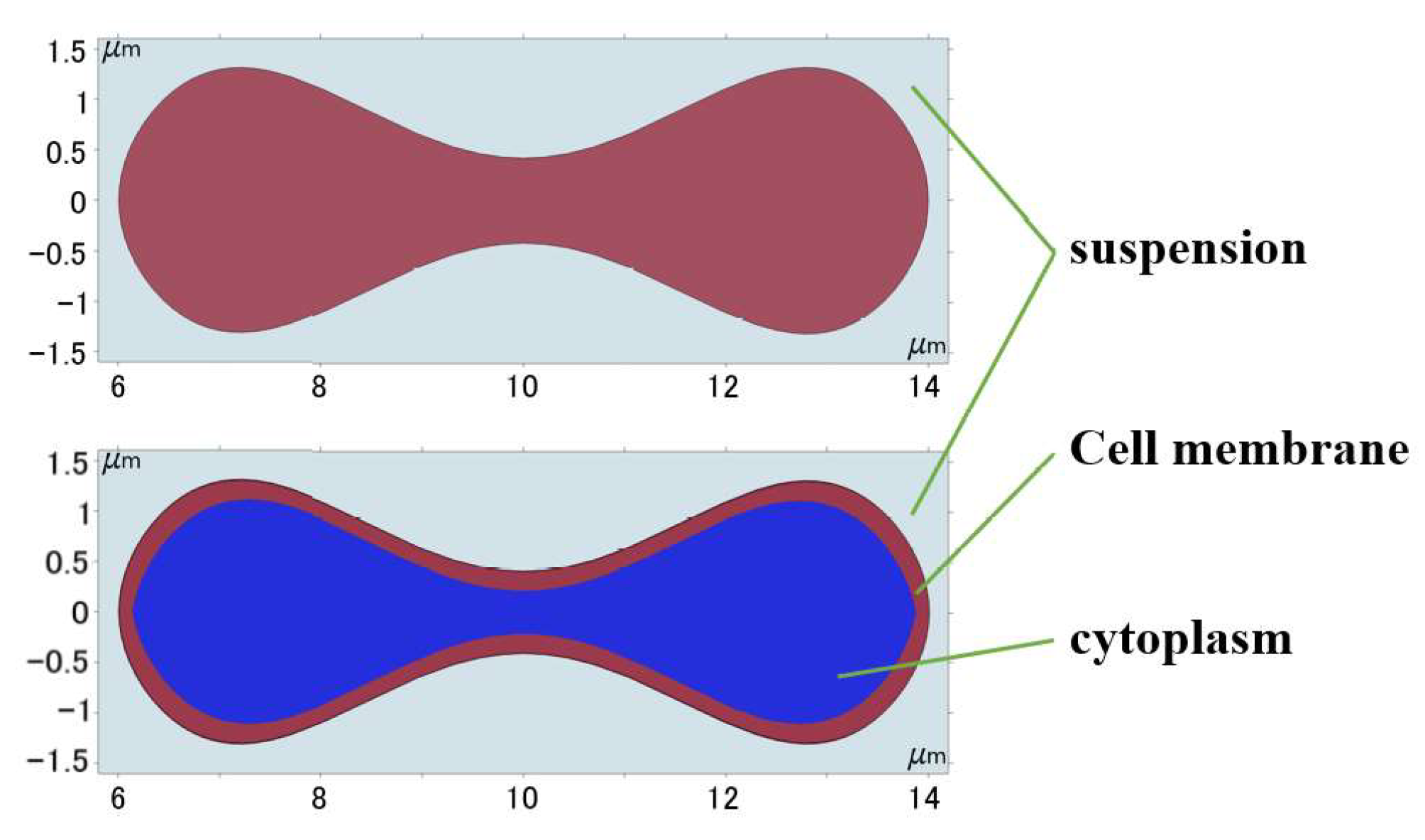
Evans and Feng [29] fitted an expression for the geometry of human erythrocytes based on empirical data:
where , , , , and μm is the radius of erythrocyte. Then the obtained curves were moved and scaled to establish the approximate shape of the erythrocytes with the cell membranes and cytoplasm, and the geometric shape was obtained as shown in Figure 2.
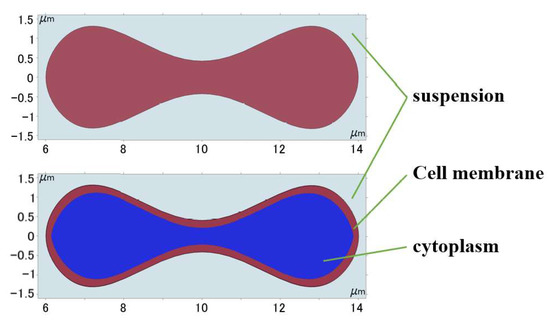
Figure 2.
Geometry of 2D erythrocyte model.
Erythrocytes can be thought of as an incompressible fluid encased in an elastic membrane that has a distinct elastic deformability and is primarily composed of a 5 nm thick phospholipid bilayer and a cytoskeleton embedded in the lipid layer [30]. If the erythrocyte model structure composed of the cell membrane and cytoplasm was used under the current continuum 2D model conditions, the degree of folding deformation created during the flow simulation was too great and a significant discrepancy with the actual experiment existed, as shown in Figure 3. This gap was brought about by structural flaws in the 2D model; hence the erythrocyte model had to be modified to account for these flaws.

Figure 3.
Deformation of 2D erythrocyte model with cytoplasmic structure.
The deformation of red blood cells during movement in the I-pillar array was small because the force during movement was low. Under a low shear rate and low fluid viscosity, the cell appeared as a solid [31], and its deformation and displacement satisfied the linear elastic momentum equation. Jiao et al. [21] verified the reliability of linearly elastic solids. Therefore, the whole erythrocyte model was simplified to a homogeneous elastic solid without a cell membrane by combining the Young’s modulus, E = 1 kPa, and Poisson’s ratio, 0.3 [21,32] of erythrocytes.
The linearly elastic material is characterized by the same deformability in all directions, and the controlling equation of its solid mechanics is:
where Equation (13) is the strain-displacement equation, Equation (14) is the Newtonian equation of motion, and Equation (15) is the linear elastic stress-strain equation, and is the Cauchy stress tensor, is the stiffness matrix, is the particle’s Young’s modulus, and is the Poisson’s ratio of the particle.
2.3. Coupling of Fluid and Erythrocyte Solvers
During the numerical calculation, the bidirectional coupling between the fluid and the solid was achieved through the interaction of the solid–liquid boundary [33,34]. On the boundary of the red cell model, the flow velocity of the fluid was equal to the motion velocity of the solid, and the boundary conditions can be expressed as:
where is the force of the fluid on the solid particle, is the distance the particle travels, and is the particle velocity. This calculation process firstly solves the parameters in the flow field to obtain the pressure and stress; secondly, the force is applied to the particle boundary to calculate the boundary motion of the particle; finally, the displacement and deformation of the particle are obtained and fed back to the flow field to repeat the previous process. Therefore, the relationship between the load on the particle boundary and the load applied by the fluid is [35]:
where the scale factors of the cell grid in the solid and fluid domains are represented by and , respectively.
In the domains with free displacement, the deforming domain feature and the free features in the moving mesh and deformed geometry interface solve an equation for the mesh displacement. This equation smoothly deforms the mesh, given the constraints placed on the boundaries.
Among the four types of mesh smoothing offered by version 5.6 of COMSOL® Multiphysics software, Yeoh smoothing is considered to generally produce the best results and allow for maximum boundary displacement before the mesh elements become inverted. It is more suitable for particle flow simulation within complex structural channels.
3. Model Verification and Flow Simulation
At the beginning of the simulation flow, as shown in Figure 4, the erythrocyte model was positioned close to the first pillar parallel to the flow direction at the start of the simulation flow to examine the rolling action. To match the fluid’s velocity, its starting velocity was adjusted to u0. For the convenience of grid independence verification later, the point P on the erythrocyte model’s edge was designated at its beginning position.
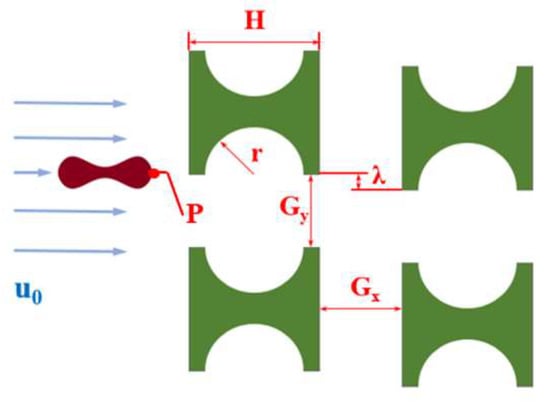
Figure 4.
Array layout and related parameters.
3.1. Verification of Simulation Accuracy
The initial array was established by mimicking the experiment of Zeming, K.K. et al. [14], using Pillar A (H = 15 μm, r = 5 μm), Gx = Gy = 10 μm, and λ = 1.25 μm.
During the establishment of the initial grid, to ensure the accuracy of the flow posture of the erythrocyte model, the erythrocyte model and the rest were divided into different free triangular grids. Then the curvature factor, the maximum cell growth rate, and other parameters were adjusted to construct multiple groups of initial grids for comparison. Skewness (based on the equiangular skew that penalizes elements with large or small angles as compared to the angles in an ideal element) was used as a reference for grid quality. Table 1 shows the partitioning methods of different mesh scales.

Table 1.
Meshing methods for different initial meshes.
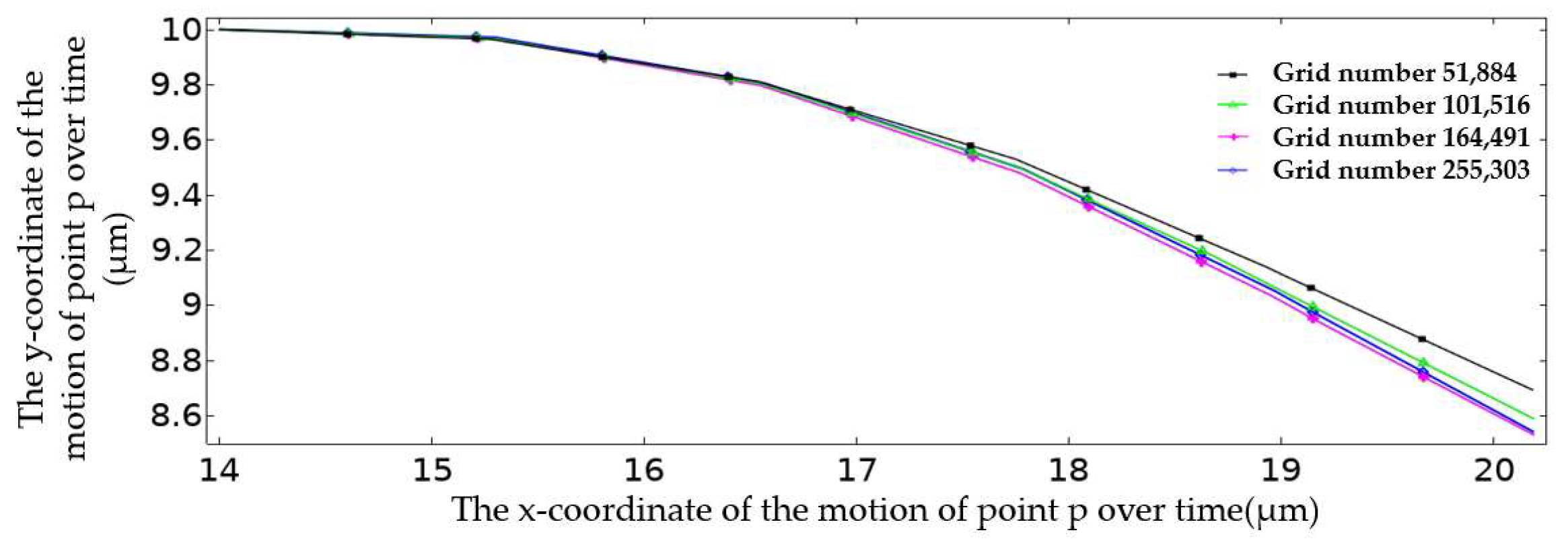
Figure 5 plots the movement trajectory of point P on the erythrocyte model at different grid scales within 5 ms. The trajectory of point P was roughly the same when the number of grids was 164,491 and 255,303. In order to consider the computational efficiency and the convergence of the solver, the grid division method was adopted when the number of grids was 164,491. At this time, the mesh division conformed to the law that the mesh quality is close to one; that is, the mesh quality was good.

Figure 5.
Motion trajectory of point P in the first 5 ms under different mesh division modes.
Figure 6 shows the grid division with a number of grid cells of 164,491, and it can be seen that the grid is finer at the flow–solid boundary. Especially at the sharper boundary, the grid is distributed most finely and gradually becomes loose towards the flat boundary. Similarly, the grid becomes sparser from the boundary to the fluid domain or inside the solid.
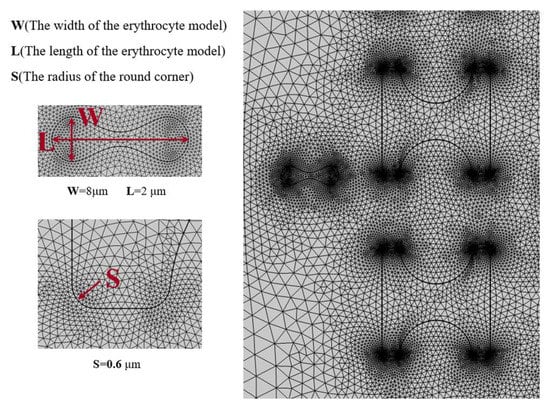
Figure 6.
Mesh 3-partition situation.
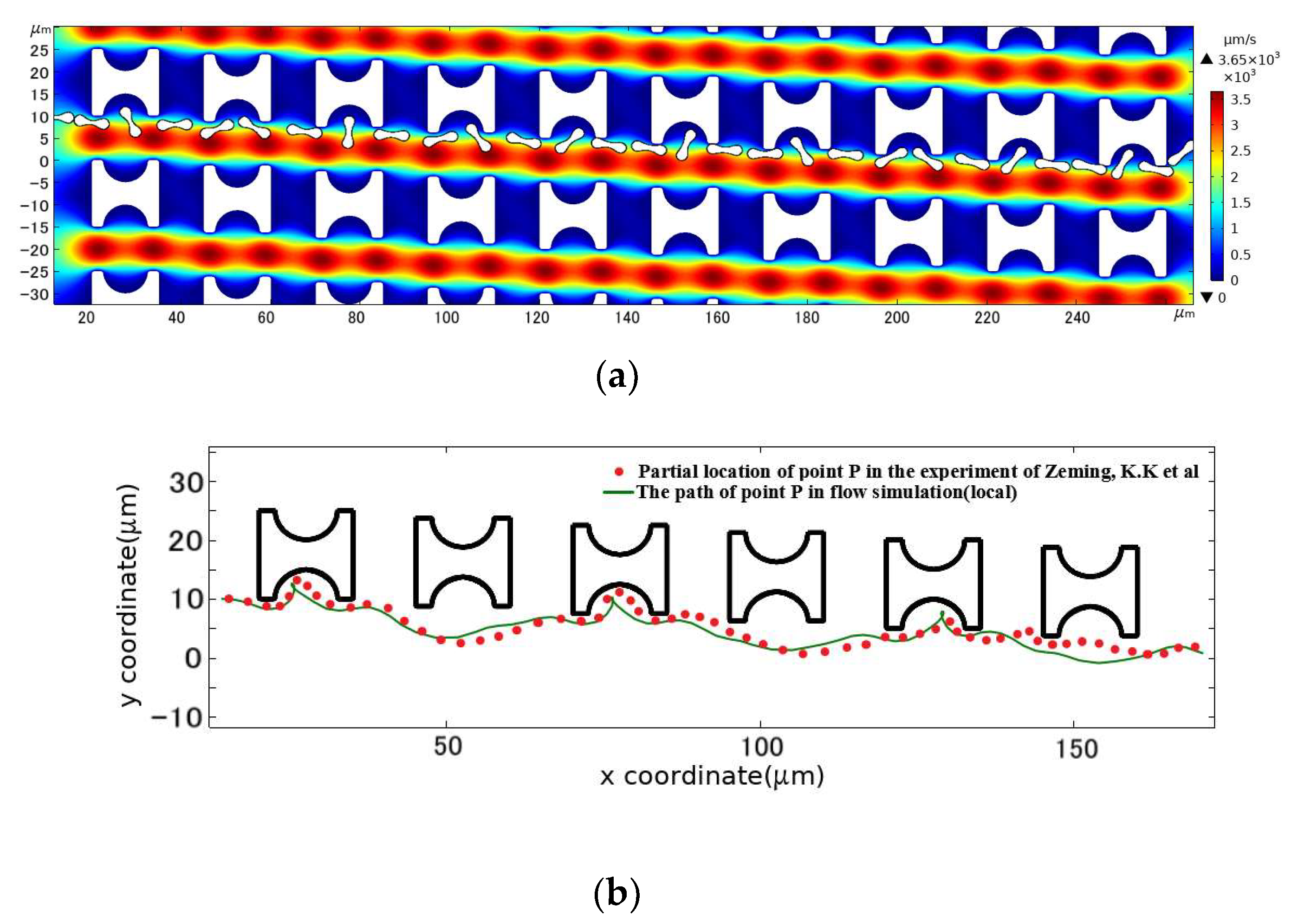
The above conditions were combined for the simulation calculations, and finally, the cell positions stored in the program were derived by interpolation time and reasonable sparsity to obtain the flow trajectory of the erythrocyte model in this DLD array, as shown in Figure 7. In comparison with the experimental results, the erythrocyte model flowed in the same displacement mode of continuous tumbling.
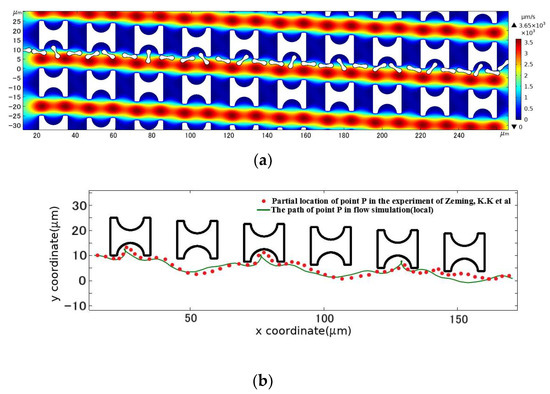
Figure 7.
Comparison between the motion path of the erythrocyte model in the initial array and the experimental results. (a) is the flow simulation results of the erythrocyte model; (b) is the path of point P in the simulated flow compared to the partial position of the corresponding point on the erythrocyte in the experimental results of Zeming, K.K et al. [14].
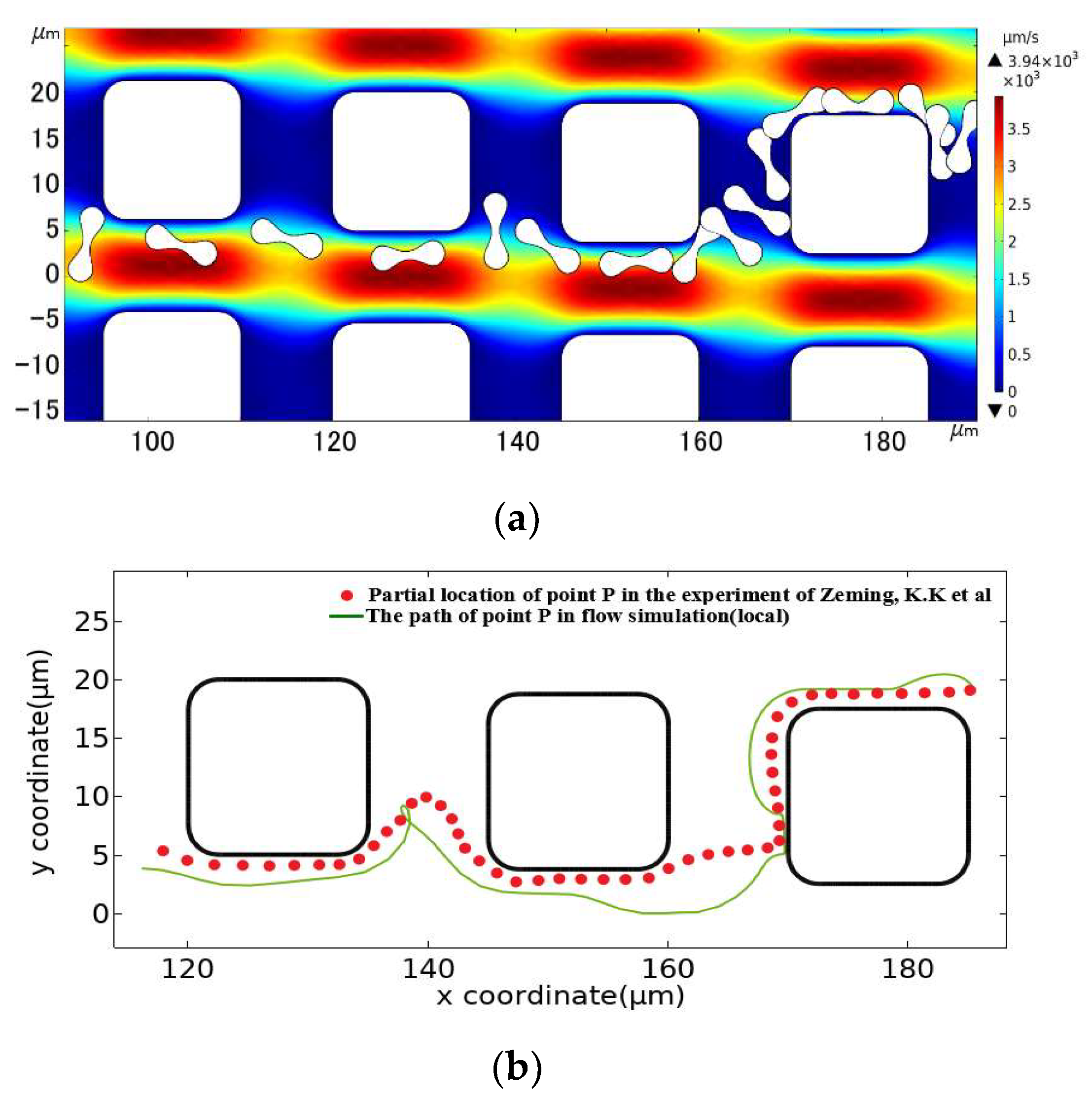
The square pillar array was also established by imitating the control group in the experiment. According to the pillar shape in the experiment, the section side length of the square pillar was set at 15 μm, and the radius of 2.5 μm was rounded at the square corner. We set array layout parameters of Gx = Gy = 10 μm, λ = 1.25 μm, and an initial flow rate of u0 = 1000 μm/s. As shown in Figure 8, The motion path of the erythrocyte model obtained after simulation calculation was also similar to that of the erythrocyte in the experiment. Therefore, the 2D linear elastic model is applicable to simulate the flow of erythrocyte in the DLD array.
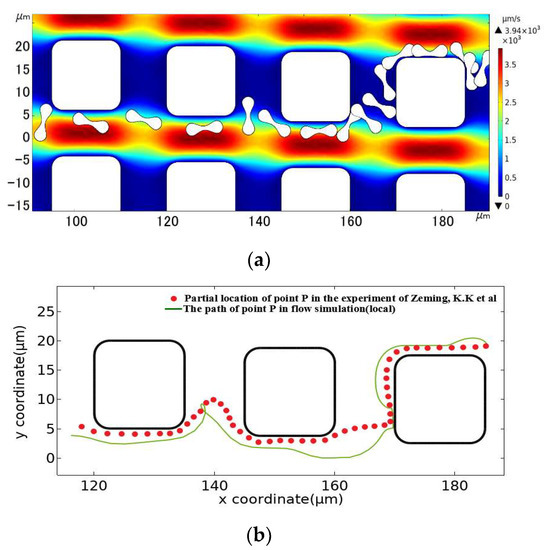
Figure 8.
Comparison between the motion path of the erythrocyte model in the square pillar array and the experimental results. (a) is the flow simulation results of the erythrocyte model, and (b) is the path of point P in the simulated flow compared to the partial position of the corresponding point on the erythrocyte in the experimental results of Zeming, K.K et al. [14].
3.2. Experimental Scheme Design
The pillar side lengths and the groove radius were decreased to form pillars B and C, taking advantage of the simulation model’s benefit of being unconstrained by chip processing technology. Table 2 displays the measurements of the three pillar shapes: A, B, and C.

Table 2.
Geometric parameters of the three pillar shapes.
After the pillar shape was established, respective corresponding DLD arrays were established. Considering that the change in Gy might make the period of arrays difficult to calculate, the downstream pillar distance Gy of all arrays was set to be 10 μm, and the following scheme was designed and simulated:
(1) Set the lateral pillar distance to Gx = 10 μm, and set the flow period of the array as 20. According to the pillar side length H and the lateral pillar distance Gy, the row shift distance λ of the three arrays was λa = 1.25 μm, λb = 1.1 μm, λc = 1 μm, respectively. Then the u0 value was increased at a rate of 100 μm/s each time, with 1000 μm/s as the initial value. Multiple experiments were conducted until u0 = 1500 μm/s;
(2) Keep the array period constant and fix u0 = 1000 μm/s. With Gx as the variable and Gx = 10 μm as the initial value, the lateral pillar distance Gx of each array was continuously increased by 2 μm length each time for the simulation until Gx = 30 μm;
(3) Fix u0 = 1000 μm/s, Gx = 10 μm, shorten the array period to 10, and find the row shift distance λ after three array changes to λA = 2.5 μm, λB = 2.2 μm, and λC = 2 μm, respectively, and perform the flow simulation.
4. Analysis of Simulation Results
4.1. Effects of Pillar Shape on Pressure Distribution within the Array
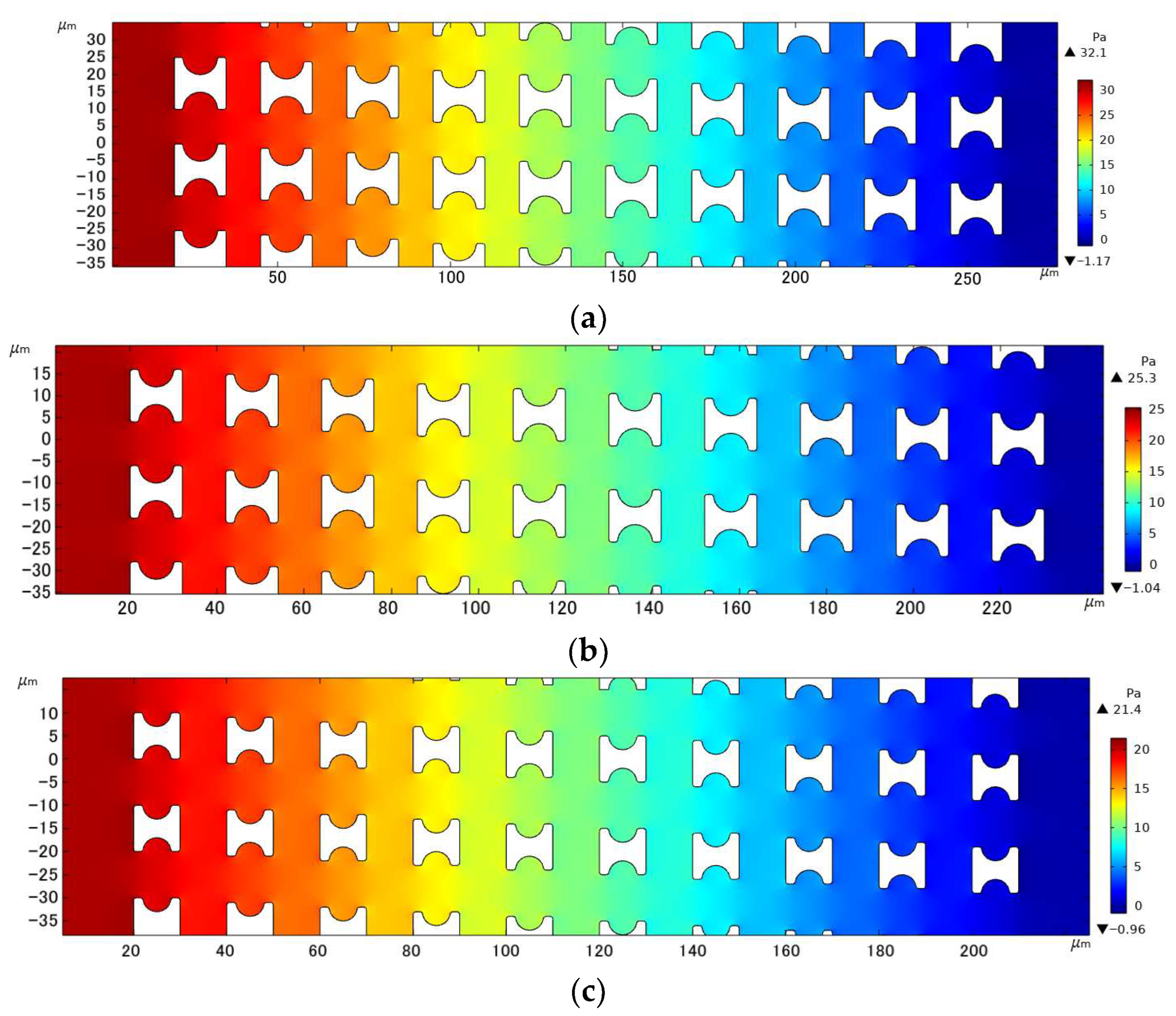
With the array arrangement parameters of Gx = Gy = 10 µm, u0 = 1000 µm/s, and a period of 20, Figure 9 shows the fluid pressure distribution clouds within the three different I-pillars. The resistance to fluid flow generated by the array decreased with decreasing pillar size for the same array gap. In contrast, the fluid pressure variation in the array with Pillar C was smoother, which facilitated faster sample processing of the chip by increasing the fluid flux, and also allowed a longer array arrangement to improve the accuracy of chip sorting under the same pressure limitation.
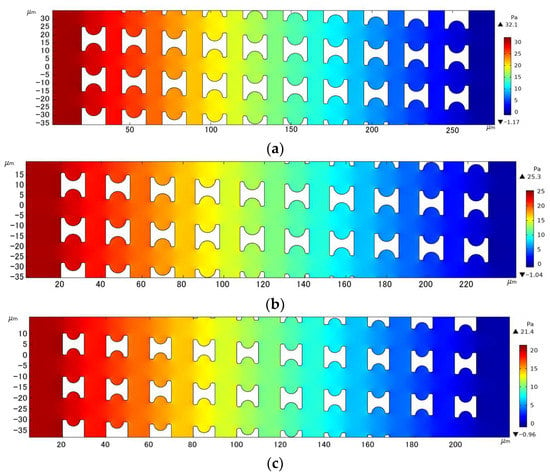
Figure 9.
Comparison of pressure drop in the three I-pillar arrays: (a) Pillar A, (b) Pillar B, and (c) Pillar C.
4.2. Movement of Erythrocyte Models in Each Array
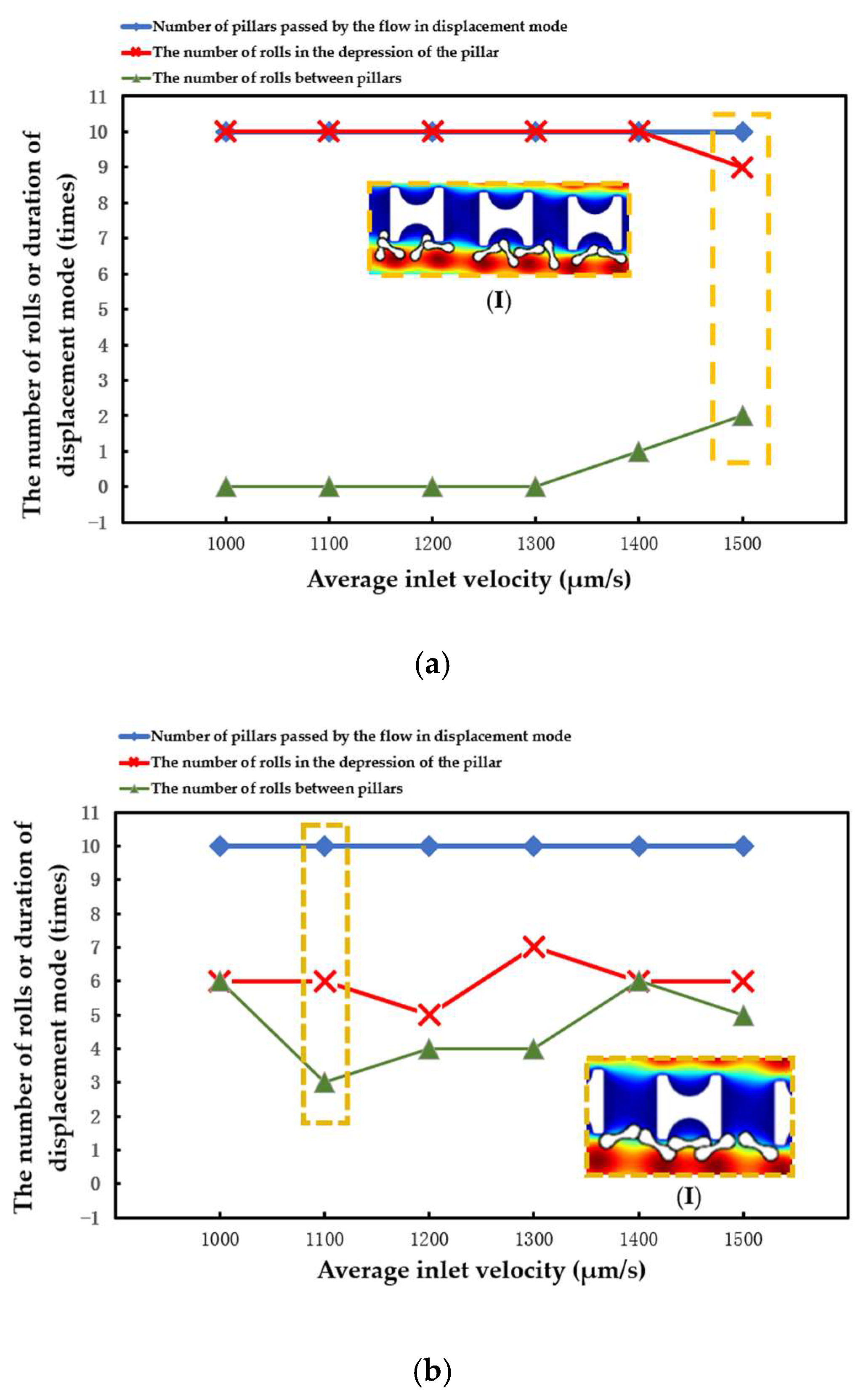
The number of array rows passed by erythrocytes in displacement mode, the number of times erythrocyte models rolled in the groove of I-pillars, and the number of times erythrocyte models rolled in the lateral channels were all recorded in each simulation. The three different types of data were contrasted to assess the stability of the erythrocyte model in the new array.
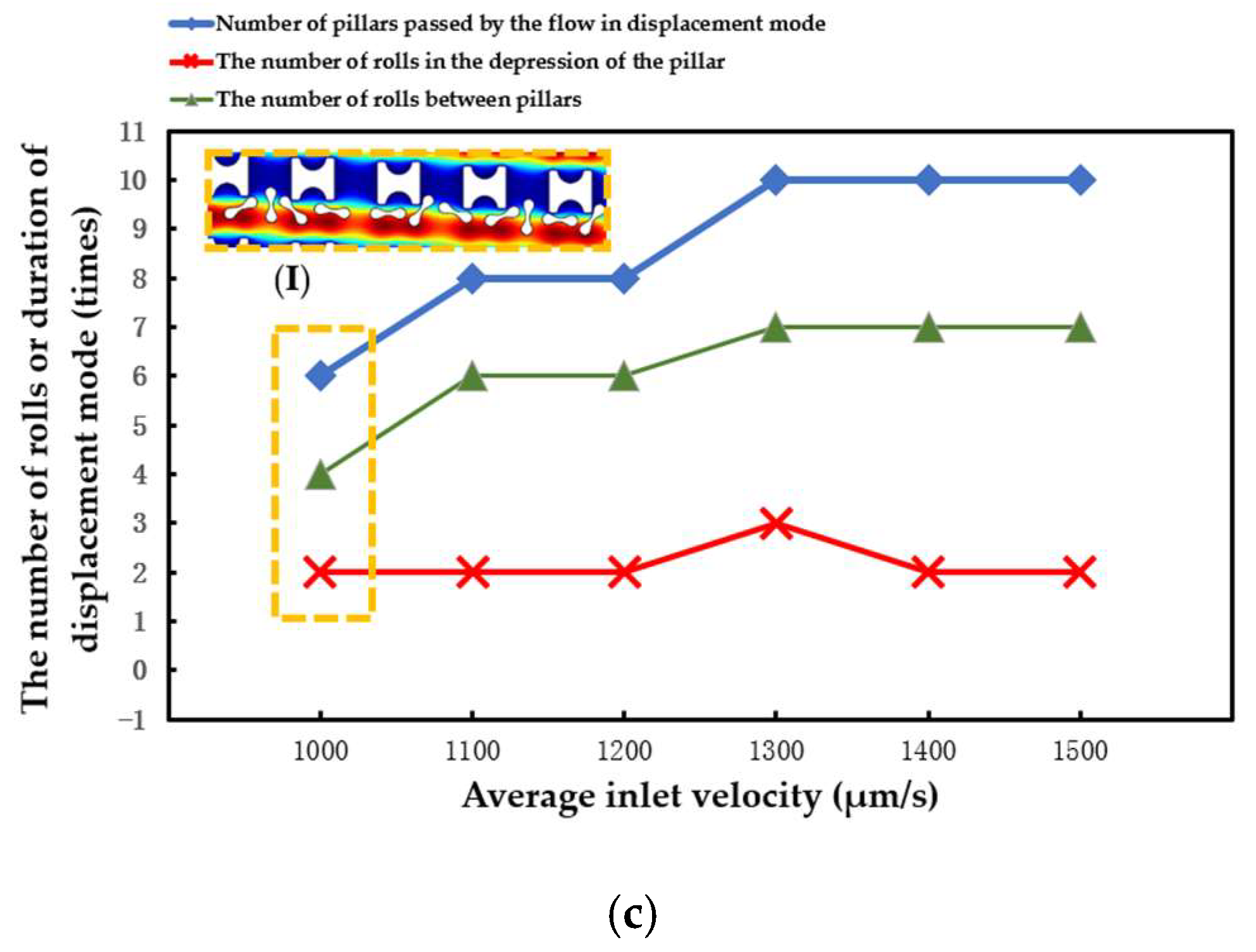
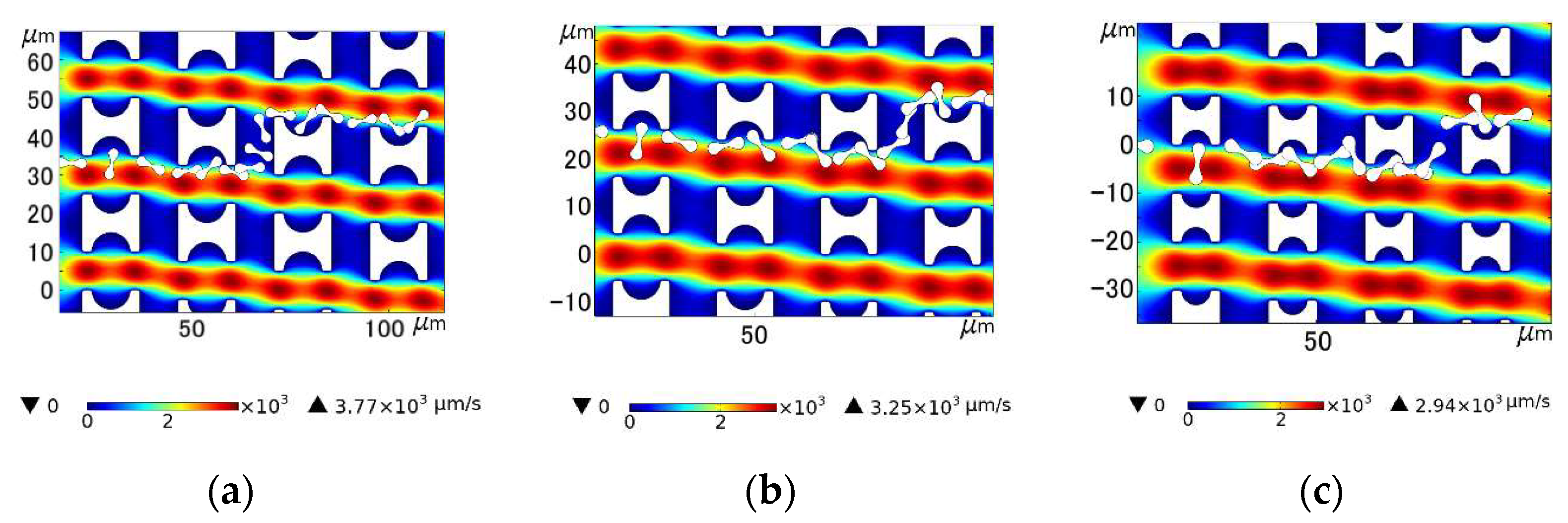
The statistical situation in the first group of flow simulation is shown in Figure 9. The size of the I-pillar directly affects the movement of erythrocytes in the array. In the array formed by the larger Pillar A, the erythrocyte model flowed in displacement mode within the range of velocity variation and could almost maintain rolling every time it passed through the groove of the I-pillar. However, in the Pillar B array, the position of erythrocyte tumbling was randomly distributed in the gap between the depression of the pillar and the array, indicating that the ability of the I-pillar to induce erythrocyte tumbling decreased after the size reduction, but the Pillar B array could still keep the erythrocyte moving in displacement mode. As the pillar size continued to shrink, the number of erythrocyte rolls in the pillar depression became less in the Pillar C array, indicating that Pillar C almost lost its ability to induce erythrocyte rolling at this size. In addition, with the increase in suspension flow rate, the position of erythrocyte tumbling became more random, and the ability of I-pillar to induce erythrocyte tumbling decreased. However, the increased flow rate made it easier for the red cell model to flow in displacement mode.
(I) in Figure 10a shows the local flow of the erythrocyte model in the Pillar A array at u = 1500 μm/s. (I) in Figure 10b shows the local flow of the erythrocyte model in the Pillar B array when u0 = 1100 μm/s. (I) in Figure 10c shows the local flow of the erythrocyte model in the Pillar C array at u0 = 1000 μm/s. In all three cases, the tumbling position of the erythrocyte model was abnormal and did not roll steadily in the depression of the pillar.
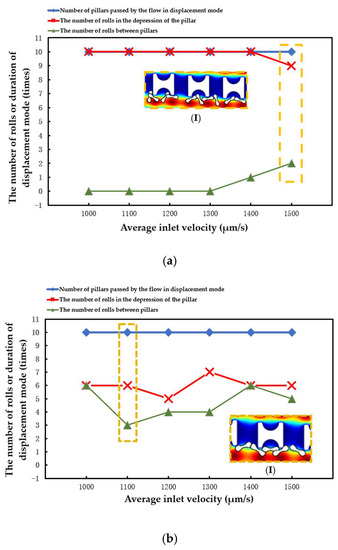
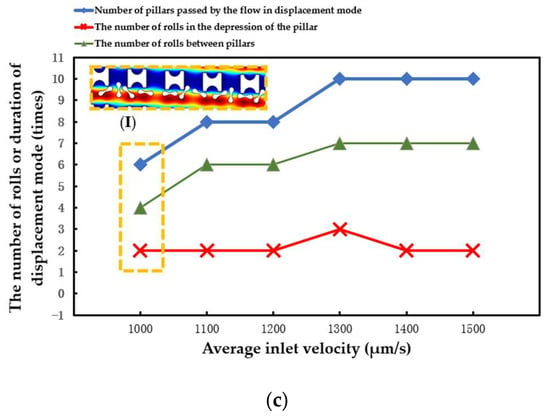
Figure 10.
Comparison of motion paths of erythrocyte models in the first set of flow simulations: (a) Pillar A array, (b) Pillar B array, and (c) Pillar C array.
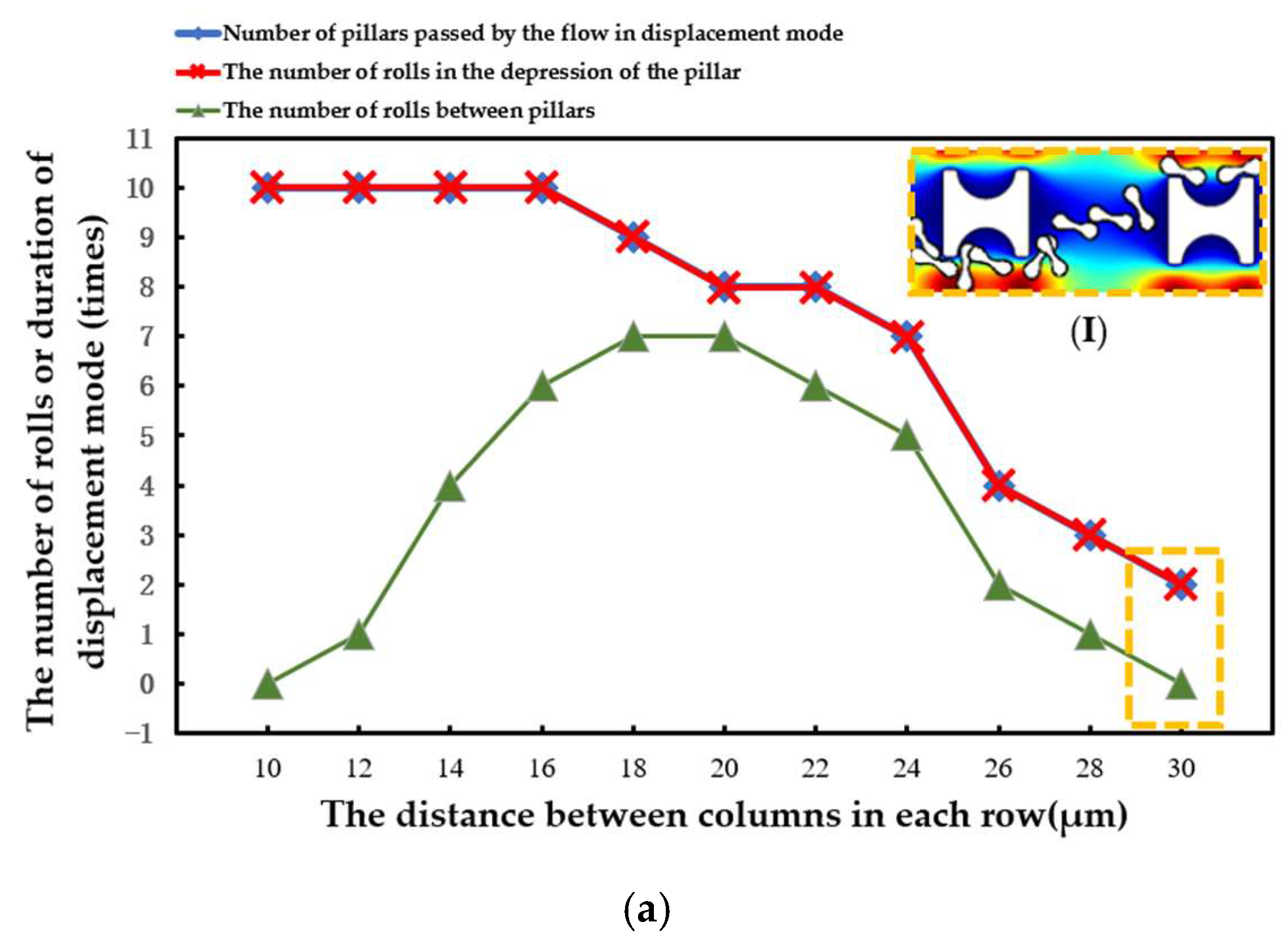
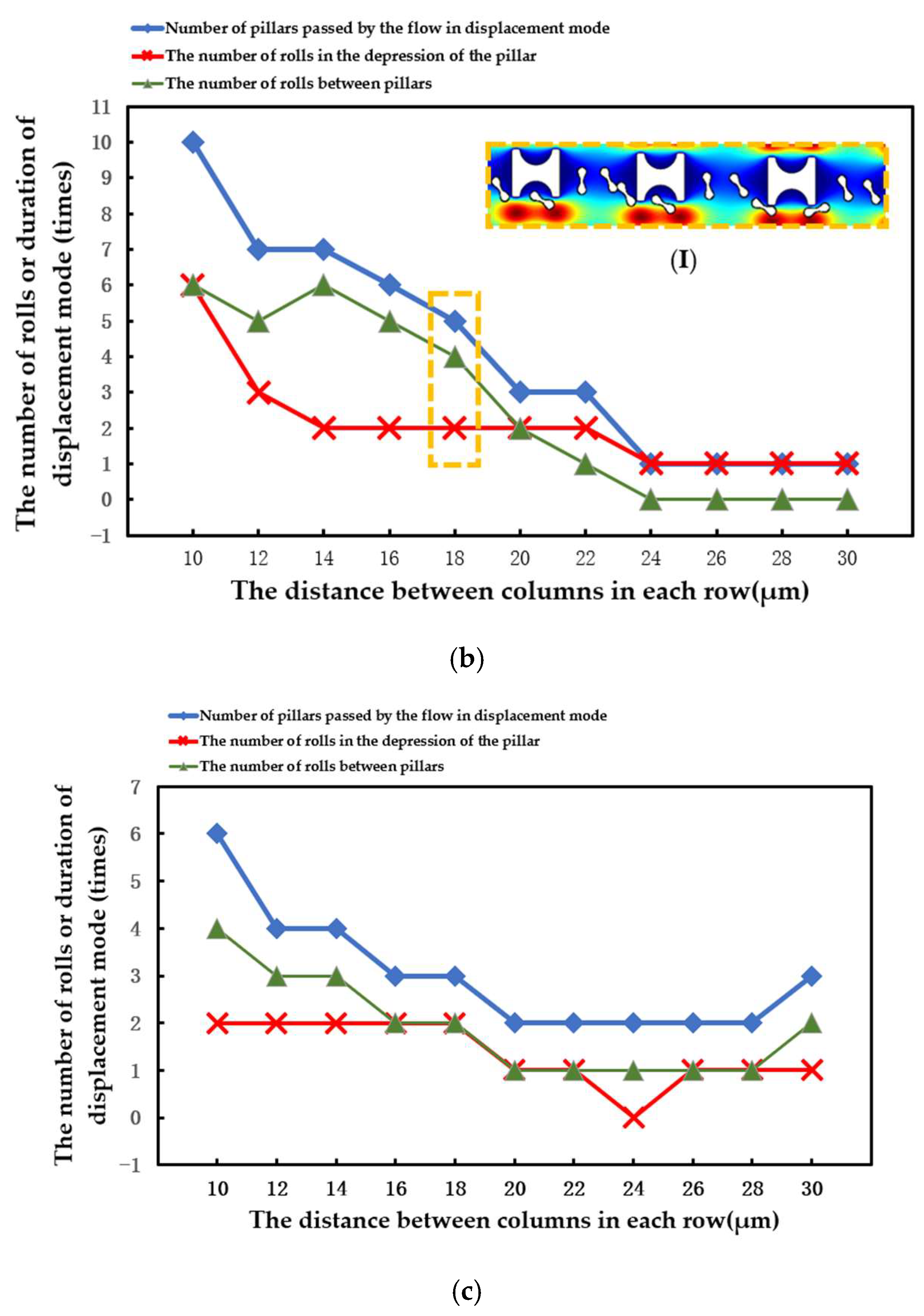
The statistical situation in the second group of flow simulations is shown in Figure 11. With the increase in array transverse spacing Gx, the red cell model flowed more easily in the word mode. As in the first simulation, the larger Pillar A had more control over the movement of the erythrocytes and caused the erythrocyte model to roll each time it passed through the groove of the pillar. However, with the increase in Gx, the smaller Pillar B and Pillar C rapidly lost the ability to make the erythrocyte model move in displacement mode, and the erythrocyte roll was very random.
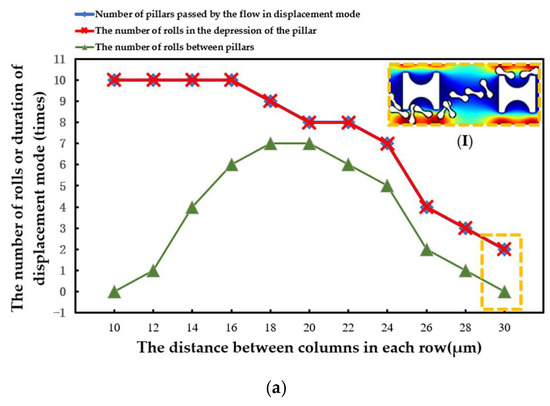
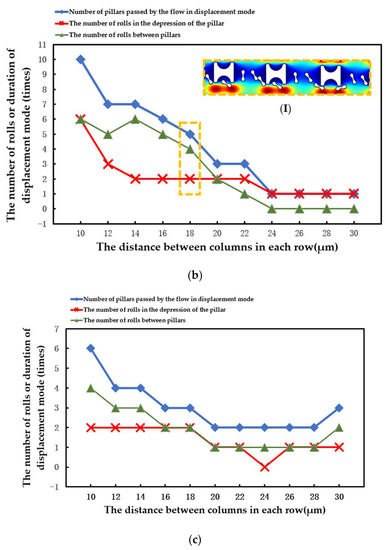
Figure 11.
Comparison of erythrocyte model motion paths in the second set of flow simulations: (a) Pillar A array, (b) Pillar B array, and (c) Pillar C array.
(I) in Figure 11a shows the local flow of the erythrocyte model in the Pillar A array at Gx = 30 μm. (I) in Figure 11b shows the local flow of the erythrocyte model in the Pillar B array at Gx = 18 μm. These two conditions show the movement of the red cell model after the array was unable to make the model flow in displacement mode as the value of Gx increased.
When the array period was shortened and the λ value was increased, the erythrocyte model in the array composed of three pillars flowed in the zigzag mode more easily. As shown in Figure 12, the transfer of erythrocytes from the Pillar A array to another lateral channel occurred behind the second row. In the array of the other two pillars, the shift occurs behind the third row.
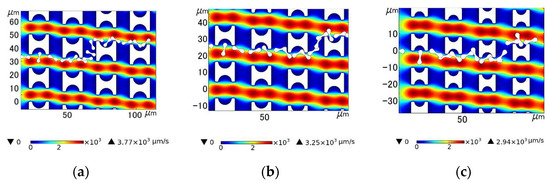
Figure 12.
Comparison of motion paths of erythrocyte models in the three arrays in the third set of flow simulations: (a) Pillar A array; (b) Pillar B array; and (c) Pillar C array.
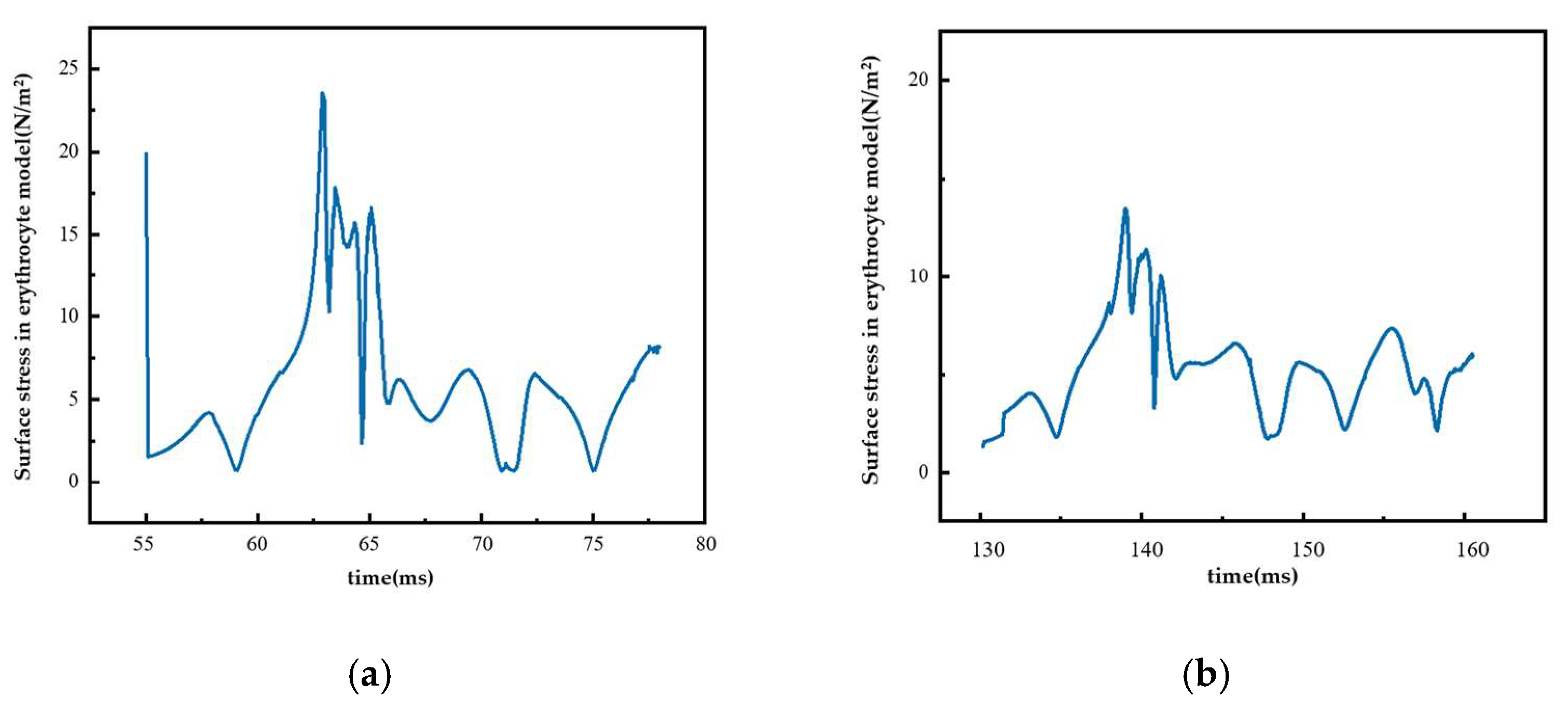
4.3. Surface Stress in the Erythrocyte Model
Figure 13 shows the surface stress change in the erythrocyte model in the second group of experiments when it moved in the Pillar B array with Gx = 18 μm. Figure 13a shows the surface stress change in the erythrocytes in the rolling process. During this process, the surface stress of erythrocytes increased and reached its maximum value. During the subsequent movement, the erythrocyte model was continuously affected by fluid, and the stress curve was in the shape of wavy lines, indicating that the fluid’s effect on the erythrocytes was constantly changing but relatively stable. Figure 13b shows the surface stress changes in the erythrocyte model when it entered the zigzag mode. In this process, the collision between the erythrocyte model and the pillar was weak, resulting in a small thrust of the erythrocyte model as it was returning to the flow channel, and the change in its surface stress was relatively more stable.
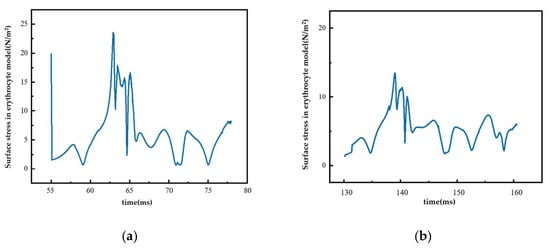
Figure 13.
Surface stress of red cell model under different movement modes: (a) rolling process and (b) zigzag mode.
5. Conclusions
In comparison with existing experimental results, it was found that under the condition of a low degree of deformation, the linear elastic 2D red cell model based on the finite element method could be used to simulate and analyze the motion path of red cells in I-shaped DLD arrays with fairly accurate results. After a comprehensive analysis of the research results in this paper, the following conclusions are drawn:
(1) The increase in row shift distance λ and lateral pillar distance Gx will affect the effect of I-pillar arrays, inducing erythrocytes to move in displacement mode. If the increase is too high, the array will lose the function of sorting and enriching erythrocytes.
(2) The decrease in pillar size and the increase in fluid velocity will make the effect of I-pillar-induced erythrocyte tumbling worse. When the pillar side length is reduced to 10 μm and the semicircle diameter at the pillar groove is reduced to 3 μm, it is difficult for the I-pillar to induce erythrocytes to roll stably. However, if appropriate array arrangement parameters are selected, smaller I-pillars can be used for sorting and enrichment of erythrocytes.
(3) The collision degree of erythrocytes in contact with the pillar affects the movement mode of the following erythrocytes, so that the erythrocytes carry out stable collisions at the pillar, which can be used as a method to optimize the performance of the I-pillar DLD chip.
In this paper, three I-pillars were designed, and the corresponding arrays were established. Through analytical simulations, it can be seen that the performance of DLD arrays composed of smaller I-beam columns can be further improved by using methods such as adjusting the period and offset distance and increasing the flow rate of the suspension, which provides a new design direction for the optimization of I-beam DLD chips.
Author Contributions
Conceptualization, Y.H. and X.D.; investigation, Y.H. and J.W; data curation, Y.L. and J.W.; visualization and writing—original draft, Y.L.; writing—review and editing, Y.H. and J.W.; funding acquisition, J.W. and X.D.; resources, J.L. and W.Z.; supervision, X.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Program of the National Natural Science Foundation of China, grant number 52130607; the Double First-Class Key Program of Gansu Provincial Department of Education, grant number GCJ2022-38; and the 2022 Gansu Provincial University Industry Support Plan Project, grant number 2022CYZC-21.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tsubota, K.-I.; Wada, S.; Yamaguchi, T. Particle method for computer simulation of red blood cell motion in blood flow. Comput. Methods Programs Biomed. 2006, 83, 139–146. [Google Scholar] [CrossRef] [PubMed]
- Mendez, S.; Chnafa, C.; Gibaud, E.; Sigueenza, J.; Moureau, V.; Nicoud, F. YALES2BIO: A Computational Fluid Dynamics Software Dedicated to the Prediction of Blood Flows in Biomedical Devices. In Proceedings of the 5th International Conference on the Development of Biomedical Engineering in Vietnam, Ho Chi Minh City, Vietnam, 16–18 June 2015; pp. 7–10. [Google Scholar]
- Ju, M.; Ye, S.S.; Namgung, B.; Cho, S.; Low, H.T.; Leo, H.L.; Kim, S. A review of numerical methods for red blood cell flow simulation. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 130–140. [Google Scholar] [CrossRef]
- Bizjak, D.A.; John, L.; Matits, L.; Uhl, A.; Schulz, S.V.W.; Schellenberg, J.; Peifer, J.; Bloch, W.; Weiss, M.; Gruner, B.; et al. SARS-CoV-2 Altered Hemorheological and Hematological Parameters during One-Month Observation Period in Critically Ill COVID-19 Patients. Int. J. Mol. Sci. 2022, 23, 15332. [Google Scholar] [CrossRef] [PubMed]
- Niesor, E.J.; Nader, E.; Perez, A.; Lamour, F.; Benghozi, R.; Remaley, A.; Thein, S.L.; Connes, P. Red Blood Cell Membrane Cholesterol May Be a Key Regulator of Sickle Cell Disease Microvascular Complications. Membranes 2022, 12, 1134. [Google Scholar] [CrossRef] [PubMed]
- Hareendranath, S.; Sathian, S.P. Dynamic response of red blood cells in health and disease. Soft Matter 2023, 19, 1219–1230. [Google Scholar] [CrossRef]
- Laxmi, V.; Joshi, S.S.; Agrawal, A. Extracting white blood cells from blood on microfluidics platform: A review of isolation techniques and working mechanisms. J. Micromech. Microeng. 2022, 32, 053001. [Google Scholar] [CrossRef]
- Salafi, T.; Zhang, Y.; Zhang, Y. A Review on Deterministic Lateral Displacement for Particle Separation and Detection. Nano-Micro Lett. 2019, 11, 77. [Google Scholar] [CrossRef]
- Hochstetter, A.; Vernekar, R.; Austin, R.H.; Becker, H.; Beech, J.P.; Fedosov, D.A.; Gompper, G.; Kim, S.C.; Smith, J.T.; Stolovitzky, G.; et al. Deterministic Lateral Displacement: Challenges and Perspectives. ACS Nano 2020, 14, 10784–10795. [Google Scholar] [CrossRef]
- Xavier, M.; Holm, S.H.; Beech, J.P.; Spencer, D.; Tegenfeldt, J.O.; Oreffo, R.O.C.; Morgan, H. Label-free enrichment of primary human skeletal progenitor cells using deterministic lateral displacement. Lab Chip 2019, 19, 513–523. [Google Scholar] [CrossRef]
- Rahmati, M.; Chen, X.L. Separation of circulating tumor cells from blood using dielectrophoretic DLD manipulation. Biomed. Microdevices 2021, 23, 49. [Google Scholar] [CrossRef]
- Wang, Y.P.; Gao, Y.F.; Song, Y.J. Microfluidics-Based Urine Biopsy for Cancer Diagnosis: Recent Advances and Future Trends. ChemMedChem 2022, 17, e202200422. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Niu, J.; Pan, X.; Jin, H.; Lin, S.; Cui, D. Topology optimization based deterministic lateral displacement array design for cell separation. J. Chromatogr. A 2022, 1679, 463384. [Google Scholar] [CrossRef] [PubMed]
- Zeming, K.K.; Ranjan, S.; Zhang, Y. Rotational separation of non-spherical bioparticles using I-shaped pillar arrays in a microfluidic device. Nat. Commun. 2013, 4, 1625. [Google Scholar] [CrossRef]
- Ranjan, S.; Zeming, K.K.; Jureen, R.; Fisher, D.; Zhang, Y. DLD pillar shape design for efficient separation of spherical and non-spherical bioparticles. Lab Chip 2014, 14, 4250–4262. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.; Liu, S.W.; Tang, W.L. Fabrication and Manipulation of Non-Spherical Particles in Microfluidic Channels: A Review. Micromachines 2022, 13, 1659. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.A.; Inglis, D.W.; Morton, K.J.; Lawrence, D.A.; Huang, L.R.; Chou, S.Y.; Sturm, J.C.; Austin, R.H. Deterministic hydrodynamics: Taking blood apart. Proc. Natl. Acad. Sci. USA 2006, 103, 14779–14784. [Google Scholar] [CrossRef]
- Al-Fandi, M.; Al-Rousan, M.; Jaradat, M.A.K.; Al-Ebbini, L. New design for the separation of microorganisms using microfluidic deterministic lateral displacement. Robot. Comput.-Integr. Manuf. 2011, 27, 237–244. [Google Scholar] [CrossRef]
- Kruger, T.; Holmes, D.; Coveney, P.V. Deformability-based red blood cell separation in deterministic lateral displacement devices-A simulation study. Biomicrofluidics 2014, 8, 054114. [Google Scholar] [CrossRef]
- Kabacaoglu, G.; Biros, G. Sorting same-size red blood cells in deep deterministic lateral displacement devices. J. Fluid Mech. 2019, 859, 433–475. [Google Scholar] [CrossRef]
- Jiao, Y.Y.; He, Y.Q.; Jiao, F. Two-dimensional Simulation of Motion of Red Blood Cells with Deterministic Lateral Displacement Devices. Micromachines 2019, 10, 393. [Google Scholar] [CrossRef]
- Li, Q.; Ito, K.; Wu, Z.S.; Lowry, C.S.; Loheide, S.P. COMSOL Multiphysics: A Novel Approach to Ground Water Modeling. Ground Water 2009, 47, 480–487. [Google Scholar] [CrossRef]
- Johnston, I.D.; McCluskey, D.K.; Tan, C.K.L.; Tracey, M.C. Mechanical characterization of bulk Sylgard 184 for microfluidics and microengineering. J. Micromech. Microeng. 2014, 24, 035017. [Google Scholar] [CrossRef]
- Johari, S.; Fazmir, H.; Anuar, A.F.M.; Zainol, M.Z.; Nock, V.; Wang, W. PDMS Young’s Modulus Calibration for Micropillar Force Sensor Application. In Proceedings of the IEEE Regional Symposium on Micro and Nanoelectronics (RSM), Kuala Terengganu, Malaysia, 19–21 August 2015; pp. 9–12. [Google Scholar]
- Dincau, B.M.; Aghilinejad, A.; Hammersley, T.; Chen, X.L.; Kim, J.H. Deterministic lateral displacement (DLD) in the high Reynolds number regime: High-throughput and dynamic separation characteristics. Microfluid. Nanofluid. 2018, 22, 59. [Google Scholar] [CrossRef]
- Kraposhin, M.V.; Ryazanov, D.A.; Elizarova, T.G. Numerical algorithm based on regularized equations for incompressible flow modeling and its implementation in OpenFOAM. Comput. Phys. Commun. 2022, 271, 108216. [Google Scholar] [CrossRef]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977–1026. [Google Scholar] [CrossRef]
- Xu, X.; Li, Z.; Nehorai, A. Finite element simulations of hydrodynamic trapping in microfluidic particle-trap array systems. Biomicrofluidics 2013, 7, 054108. [Google Scholar] [CrossRef] [PubMed]
- Evans, E.; Fung, Y.C. Improved measurements of the erythrocyte geometry. Microvasc. Res. 1972, 4, 335–347. [Google Scholar] [CrossRef]
- Zhu, Q.; Salehyar, S.; Cabrales, P.; Asaro, R.J. Prospects for Human Erythrocyte Skeleton-Bilayer Dissociation during Splenic Flow. Biophys. J. 2017, 113, 900–912. [Google Scholar] [CrossRef]
- Fischer, T.M. Shape Memory of Human Red Blood Cells. Biophys. J. 2004, 86, 3304–3313. [Google Scholar] [CrossRef]
- Tognoni, E.; Orsini, P.; Pellegrino, M. Nonlinear indentation of single human erythrocytes under application of a localized mechanical force. Micron 2019, 127, 102760. [Google Scholar] [CrossRef]
- Sun, P.T.; Zhang, C.S.; Lan, R.H.; Li, L. Monolithic Arbitrary Lagrangian-Eulerian Finite Element Method for a Multi-domain Blood Flow-Aortic Wall Interaction Problem. In Proceedings of the 20th Annual International Conference on Computational Science (ICCS), Amsterdam, The Netherlands, 3–5 June 2020; pp. 60–74. [Google Scholar]
- Khodaee, F.; Movahed, S.; Fatouraee, N.; Daneshmand, F. Numerical Simulation of Separation of Circulating Tumor Cells From Blood Steam in Deterministic Lateral Displacement (DLD) Microfluidic Channel. J. Mech. 2016, 32, 463–471. [Google Scholar] [CrossRef]
- Wang, Y.; Jimack, P.K.; Walkley, M.A.; Pironneau, O. An energy stable one-field monolithic arbitrary Lagrangian–Eulerian formulation for fluid–structure interaction. J. Fluids Struct. 2020, 98, 103117. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).