Performance of a Helical Microswimmer Traversing a Discrete Viscoelastic Network with Dynamic Remodeling

Abstract

Microorganisms often navigate a complex environment composed of a viscous fluid with suspended microstructures such as elastic polymers and filamentous networks. These microstructures can have similar length scales to the microorganisms, leading to complex swimming dynamics. Some microorganisms secrete enzymes that dynamically change the elastic properties of the viscoelastic networks through which they move. In addition to biological organisms, microrobots have been engineered with the goals of mucin gel penetration or dissolving blood clots. In order to gain insight into the coupling between swimming performance and network remodeling, we used a regularized Stokeslet boundary element method to compute the motion of a microswimmer consisting of a rotating spherical body and counter-rotating helical flagellum. The viscoelastic network is represented by a network of points connected by virtual elastic linkages immersed in a viscous fluid. Here, we model the enzymatic dissolution of the network by bacteria or microrobots by dynamically breaking elastic linkages when the cell body of the swimmer falls within a given distance from the link. We investigate the swimming performance of the microbes as they penetrate and move through networks of different material properties, and also examine the effect of network remodeling.

1. Introduction

The study of the fluid dynamics of microswimmers, both natural and engineered, has enjoyed great success in recent decades, through advances in imaging technologies, computational methods, microfluidic devices, and material science (e.g., [1,2,3,4,5,6,7]). In biological systems, flagella often beat or rotate in close proximity to (or through) passive elastic structures such as as mucosal strands embedded in the fluid environment. For example, mammalian fertilization requires a sperm to penetrate two layers surrounding the egg—an outer layer of cumulus cells and the zona pellucida, a thick extracellular matrix [8,9]. Scanning electron microscopic images in Schwartz et. al. [10] show that voids in the net-like, porous structure of the zona pellucida are of the same length as the diameter of the (human) sperm’s cell body. Another example is the Lyme disease spirochete B. burgdorferi that traverses epithelial cells, fluid environments, and polymeric networks—first within the tick and then through the skin of its mammalian host, causing infection [11]. It has been shown that spirochetes persist in both treated and untreated Lyme-disease-infected rhesus macaques in multiple tissues [12]. In both of these examples, the microswimmer must penetrate and navigate through a complex, heterogeneous polymeric network embedded in a viscous fluid.

Recent experiments were performed with Bacillus subtilis moving through shallow mucus films [13] with network pore sizes comparable to bacteria size. It was demonstrated that the anisotropic organization of the mucus filaments affected swimming performance, with velocity decreasing dramatically as the bacteria penetrated and moved through the mucus. Moreover, the bacteria altered the compliant environment, displacing polymeric strands in the mucus network as they progressed through it. In some cases, when a bacterium reversed direction, it was able to move backwards with an increased velocity through the self-created transient tunnel. This is an illustration of the elastohydrodynamic coupling in the system—not only is the performance of the microswimmer affected by the complex environment, the microswimmer’s motion also affects the polymeric network.

In addition to mechanical remodeling, bacteria can alter polymeric network rheological properties and connectivity through enzymatic activity. For instance, both E. coli and Vibrio cholerae secrete mucinase to help them penetrate the mucus barrier of the human gastrointestinal tract, and other Vibrio species are similarly able to traverse the mucus barriers of coral polyps in the marine environment [14]. Another well-studied example is that of Helicobacter pylori, which colonizes the harsh enviroment of the human stomach by producing urease, thus elevating the pH of its environment and locally de-gelling the gastric mucus layer [15,16]. Rheological measurements show that the viscoelasticity of samples of porcine gastric mucin decreases dramatically when incubated with H. pylori. These bacteria overcome “elastic confinement” by altering the material properties of their environment [15].

Recently, the use of helical nanorobots, driven by an external source, has emerged as an exciting possibility in biotechnology, with potential applications including targeted drug delivery [7] and lysis of blood clots [17]. In such applications, the microswimmer needs to be guided through complex viscoelastic environments, with added control challenges such as real-time imaging. Experiments have shown that helical nanopropellers that are magnetically actuated in a gel with a comparable mesh size to the size of the robot can be steered to progress effectively, while larger nanopropellers are unable to move through the gel [18]. Motivated by the enzymatic activity of H. pylori, Walker et al. [19] developed reactive micropropellers with immobilized urease on their surface. This strategy enabled the magntically driven synthetic swimmers to be propelled in acidified mucin gels that contain urea [19]. In fact, the propellers that were not coated with urease became entangled in the polymer chains of the mucin, and could not swim.

Each of the examples discussed above demonstrate the need to understand microswimming in complex, polymeric environments. Recently, there has been much progress in modeling the hydrodynamics of microorganisms swimming in a non-Newtonian fluid using continuum descriptions of a viscoelastic fluid (e.g., [20,21,22,23,24,25,26]). Instead, we advance our viscoelastic model of a non-Newtonian fluid environment [27] and use a discrete network to capture the length scale of voids in the fibrous environment. This approach allows for us to probe the dynamics of a swimmer as it moves from a Stokesian fluid into a polymeric region, and to measure both the progression of the swimmer and the deformations in the network. The discrete network can more easily represent heterogeneous environments, and its topology and material properties can be dynamically altered.

Motivated by biological and engineered helical propellers, here, we focus on the motility of a model bacteria-inspired organism composed of a helical flagellum and a cell body. The swimmer is driven by an applied torque between the cell body (a sphere for simplicity) and the flagellum (a helix), such that the two structures counter-rotate as in real bacteria [4]. Both the body and flagellum are assumed to be rigid structures and the swimmer’s shape does not deviate from this prescription, no matter what forces are felt from the viscous load or nearby polymeric boundaries. This is a good assumption for many artificial microswimmers (e.g., those discussed above), as well as for most bacterial cell bodies [28] and flagella not undergoing active reorientation behaviors [4]. As with other swimmers in this class of models (e.g., [22,29,30,31,32]), the force-free and torque-free constraints give rise to a translation and rotation of the swimmer. These models may be used to analyze the fluid flow generated by the given motion and the forces required to achieve the prescribed shape.

The viscoelastic network is modeled using a regularized Stokeslet framework that applies forces due to connections between network nodes and the surrounding fluid. The connections are assigned individual constitutive laws, and material properties can vary in space and evolve over time. Within the context of an immersed boundary method, a similar modeling approach was used by Bottino [33] to capture cytoskeletal structure, and, more recently, by Fai et al. [34]. While more complex stress–strain relationships may be used, here a connection is taken to be either a spring element or a spring and dashpot in series (Maxwell element). In [27], we demonstrated that when forces from these elements are coupled to the Stokes equations, the surrounding viscous fluid acts as a dashpot in parallel with the element. In addition, computational rheometry tests that characterized the viscoelastic structures, such as computing their frequency-dependent loss and storage moduli, showed that using Maxwell elements resulted in moduli that reflected many viscoelastic materials in biological structures [27].

In [35], we conducted computational studies of an undulating planar flagellum with prescribed kinematics swimming through discrete networks with different constitutive properties and connectivities. The work presented here extends this model in three important directions. Firstly, the swimmer considered here is driven by a prescribed constant torque between a cell body and a helical flagellum so that the relative rotational frequency between the two emerges from the simulation, consistent with experimental observations of bacterial flagellar motors [4]. Secondly, we capture network remodeling by dynamically dissolving links between nodes based upon the swimmer’s evolving position. Finally, here we choose a hybrid boundary integral-regularized Stokeslet method with high-resolution discretization of the cell body and flagellum. The numerical method and simulation results are presented below.

2. Methods

2.1. The Computational Framework

We assume that the viscoelastic network and the microswimmer are suspended in a Newtonian solvent. At these small scales, the fluid motion can be modeled by the Stokes equations. A regularized Stokeslet is the exact solution of the incompressible Stokes equations

$$0=-\nabla p+\mathsf{\mu }\Delta \mathit{u}+\mathit{f}{\varphi }_{ϵ}(\mathit{x}-{\mathit{x}}_0),\nabla ·\mathit{u}=0$$

(1)

where p is the pressure, $\mathit{u}$ is the fluid velocity, $\mathsf{\mu }$ is the viscosity, and $\mathit{f}{\varphi }_{ϵ}$ is external force per volume. The regularizing function, or blob, ${\varphi }_{ϵ}\left(r\right)$ is a smooth approximation to a delta distribution. A commonly used function has radial symmetry and is given by ${\varphi }_{ϵ}\left(r\right)=15{ϵ}^4/(8\pi {(r^2+{ϵ}^2)}^{7/2})$, where $ϵ$ is a small parameter which controls the width, or spreading [36,37]. For this function, the exact solution of Equation (1) is the regularized Stokeslet

$$\mathit{u}\left(\mathit{x}\right)=\mathbf{S}(\mathit{x},{\mathit{x}}_0,ϵ)\mathit{f}=\frac{\mathit{f}(R^2+{ϵ}^2)+(\mathit{f}·(\mathit{x}-{\mathit{x}}_0))(\mathit{x}-{\mathit{x}}_0)}{8\pi \mathsf{\mu }{R}^3}.$$

(2)

where we use the notation $R^2=r^2+{ϵ}^2$ with $r=\left|\mathit{x}-{\mathit{x}}_0\right|$. Due to the linearity of the Stokes equations, the flow induced by N forces is the superposition of regularized Stokeslets. In the model presented below, such forces will be supported both at nodes of the viscoelastic network and at surface points of the microswimmer’s helical flagellum and cell body. We describe the computational framework used in the simulations presented below. Here, we focus on the new elements of this computational framework and provide a brief description of the elements that have been introduced elsewhere.

2.2. The Network

We model the interactions between a microswimmer and a polymeric network embedded in a viscous fluid by creating a discrete network of viscoelastic linkages occupying a portion of the fluid domain (Figure 1). These virtual links between nodes are not material fibers, but are viewed as viscoelastic elements whose compression or extension exert forces on the nodes. As such, the network, introduced in [27], is a set of nodes ${\mathit{y}}_i$, some of which are connected to others by Maxwell elements (a spring and a dashpot in series). As the nodes ${\mathit{y}}_i$ and ${\mathit{y}}_j$ are advected by the flow, they develop forces given by

$$\tilde{\mathit{g}}({\mathit{y}}_i,{\mathit{y}}_j)=-\tilde{\mathit{g}}({\mathit{y}}_j,{\mathit{y}}_i)={\ell }_{0,ij}^2{E}_{ij}\left(\frac{∥{\mathit{y}}_j-{\mathit{y}}_i∥}{{\ell }_{ij}\left(t\right)}-1\right)\frac{{\mathit{y}}_j-{\mathit{y}}_i}{∥{\mathit{y}}_j-{\mathit{y}}_i∥}$$

where ${\ell }_{ij}\left(t\right)$ is the time-dependent resting length of the element, $E_{ij}$ is the spring stiffness constant, and ${\ell }_{0,ij}$ is the initial resting length. The action of the viscous dashpot within each link is modeled using

$$\frac{d{\ell }_{ij}\left(t\right)}{dt}=\frac{E_{ij}{\ell }_{0,ij}}{{\eta }_{ij}}\left(\frac{∥{\mathit{y}}_j-{\mathit{y}}_i∥}{{\ell }_{ij}\left(t\right)}-1\right)$$

(3)

where ${\eta }_{ij}$ is the dashpot constant, which affects how fast the spring resting length adjusts to stretching and compression. In a network of interconnected Maxwell elements, the total force on node ${\mathit{y}}_i\left(t\right)$ due to its links to other nodes is given by

$$\mathit{g}\left({\mathit{y}}_i\right)=\sum _{j\in L^i}\tilde{\mathit{g}}({\mathit{y}}_i,{\mathit{y}}_j)$$

where ${\mathit{y}}_j:j\in L^i$ are all the neighbor nodes connected to ${\mathit{y}}_i$.

The elastic potential energy contained in a network of $N_N$ nodes depends on how stretched or compressed each link is and is given by

$$PE\left(t\right)=\sum _{j>i}\sum _{i=1}^{N_N}{\ell }_{0,ij}^3{E}_{ij}{\left(\frac{∥{\mathit{y}}_j-{\mathit{y}}_i∥}{{\ell }_{ij}\left(t\right)}-1\right)}^2$$

(4)

2.3. The Swimmer

The bacterium-inspired microswimmer is modeled as a rigid spherical body of radius $R_S$ coupled to a rigid helical flagellum that is modeled as a uniform cylinder of diameter $d_f$ built around the centerline (see [30]) given by:

$$\begin{array}{cc}\hfill x_1^f\left(\zeta \right)& =\zeta \hfill \\ \hfill x_2^f\left(\zeta \right)& =a\left(1-e^{-K_E^2{\zeta }^2}\right)cos\left(k\zeta \right)\hfill \\ \hfill x_3^f\left(\zeta \right)& =a\left(1-e^{-K_E^2{\zeta }^2}\right)sin\left(k\zeta \right)\hfill \end{array}$$

(5)

The helix amplitude $a\left(1-e^{-K_E^2{\zeta }^2}\right)$ is approximately constant throughout the length of the flagellum except in a small region nearest the cell body, where it tapers to zero amplitude based on the parameter $K_E$. There is a small gap of $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.d_f$ between the body and base of the flagellum, as in [38,39], to avoid numerical problems due to the counter-rotation of the two surfaces. A discretization of the spherical cell body and of the surface of the cylindrical flagellum is used to compute surface forces that produce a prescribed velocity of the flagellum and cell body, as in [38,39]. Geometric parameter values of the model bacterium are given in

Table 1. Physical and numerical parameter values used in this work.

Type	Parameter	Value
Swimmer
Body	radius, $R_S$	0.6204 $\mathsf{\mu }$m
Flagellum	diameter $d_f$	0.16 $\mathsf{\mu }$m
	amplitude, a	0.4 $\mathsf{\mu }$m
	wavelength, $2\pi /k$	2.9 $\mathsf{\mu }$m
	# wavelengths	1.5
	exponential decay constant, $K_E$	1.543 $\mathsf{\mu }$m${}^{-1}$
Network
	length, width, height	6.2 $\mathsf{\mu }$m, 13.6 $\mathsf{\mu }$m, 13.6 $\mathsf{\mu }$m
	# layers in swimming direction	6
	connectivity	18 links per node (6 along x, y, z, 12 diagonal)
	spacing between layers, min ${\ell }_{0,ij}$	0.6204 $\mathsf{\mu }$m
	spring stiffness, E	0–100 mPa
	dashpot constant, $\eta$	0.1–10, ∞ mPa s
	fluid viscosity, $\mathsf{\mu }$	1 mPa s
Numerical
Swimmer	total number of nodes, $N_S$	1780
Body
	regularization parameter, ${ϵ}_S$	$4\times {10}^{-5}$$\mathsf{\mu }$m
	number of nodes and triangular elements	454 and 226
Flagellum
	regularization parameter, ${ϵ}_S$	$4\times {10}^{-5}$$\mathsf{\mu }$m
	number of nodes and triangular elements	1326 and 662
	applied motor torque, $\tau$	1000 fN $\mathsf{\mu }$m
Network
	regularization parameter, ${ϵ}_N$	0.0796 $\mathsf{\mu }$m
	total number of nodes ($N_N$) and links	864 and 6396
	number of anchored nodes, $N_A$	264
	dissolution distance ${\delta }_r{R}_S$	$0.1241$$\mathsf{\mu }$m

.

Since the body (B) and flagellum (F) are assumed to be rigid, the velocity $\mathit{u}\left(\mathit{x}\right)$ at any point on the swimmer is given by a translational velocity $\mathit{U}$, a rotational velocity ${\mathbf{\Omega }}^B$, and a rotational speed of the flagellum relative to the body ${\Omega }^F$:

$$\mathit{u}\left(\mathit{x}\right)=\left\{\begin{array}{cc}\mathit{U}+{\mathbf{\Omega }}^B\times \tilde{\mathit{x}}\hfill & \mathit{x}\in B\hfill \\ \mathit{U}+\left({\mathbf{\Omega }}^B-{\Omega }^F{\widehat{\mathit{e}}}^F\right)\times \tilde{\mathit{x}}\hfill & \mathit{x}\in F\hfill \end{array}\right.$$

(6)

where $\tilde{\mathit{x}}=\mathit{x}-\mathit{X}$, with reference point $\mathit{X}$ chosen as the center of the spherical body, and ${\widehat{\mathit{e}}}^F$ is a unit vector along the flagellar axis.

As in [39], we used the SALOME Platform software [40] with the Netgen 1D-2D meshing algorithm [41] to discretize the swimmer body and flagellum with second-order triangular surface meshes. Each curved triangular element has three corner vertex nodes and three nodes at the midpoints of each side. Figure 2 shows the nodes on the surface of the cell body and flagellum.

2.4. Repulsion and Anchoring Forces

In our discretization of the model swimmer, the no-slip, no-penetration boundary condition is enforced at the surface mesh nodes on the body and flagellum. To prevent network nodes from entering the swimmer body, we introduce an exponentially decaying repulsion force similar to that employed in previous studies [42,43,44,45]. Of particular importance are the forces at the network nodes near the swimmer. The force $\tilde{\mathit{g}}({\mathit{y}}_i,{\mathit{y}}_j)$ at node ${\mathit{y}}_i$ along a link of the network is decomposed into a component normal to the surface of the spherical body and a transverse component. Only when the normal component of the network node force points toward the center of the cell body do we introduce a repulsive force on network node ${\mathit{y}}_i$ and an equal and opposite force on the surface of the spherical cell body, at the point closest to ${\mathit{y}}_i$. The force is given by

$${\mathit{f}}_R\left({\mathit{y}}_i\right)=-e^{-\left(∥{\mathit{p}}_i∥-R_S\right)/\delta }\left(\sum _{j\in L^i}min\left[\tilde{\mathit{g}}({\mathit{y}}_i,{\mathit{y}}_j)·\frac{{\mathit{p}}_i}{∥{\mathit{p}}_i∥},0\right]\right)\frac{{\mathit{p}}_i}{∥{\mathit{p}}_i∥}$$

(7)

where $R_S$ is the spherical body radius, $\delta$ is a small length scale, and ${\mathit{p}}_i={\mathit{y}}_i-\mathit{X}$ is the vector from the center of the cell body to the network node. Hence, when a network node is on the cell body surface, the repulsion strength is equal to the total normal force, rapidly decreases in magnitude moving away from the surface, and increases in magnitude if a node manages to get inside. This repulsion method introduces no additional net force or torque on the system. Here, we chose $\delta$ such that the exponential scale factor $e^{-\left(∥{\mathit{p}}_i∥-R_S\right)/\delta }\approx 5·{10}^{-4}$ at a distance from the surface $∥{\mathit{p}}_i∥-R_S\approx 0.1R_S$. We found this model and choice of $\delta$ to be a good tradeoff between minimally altering the solution and keeping network nodes out of the swimmer body.

To prevent bulk movement of the entire network through the surrounding fluid due to the action of the swimmer, we also introduced additional anchoring forces ${\mathit{f}}_A\left({\mathit{y}}_i\right)$ to all the nodes along four of the outer faces of the rectangular network (in the $xy$ and $xz$ planes where x is the swimming direction). These forces were chosen such that the velocities of these nodes were always zero (see below).

The total force of each network node i on the fluid is, therefore,

$$\left\{\begin{array}{cc}{\mathit{f}}_N\left({\mathit{y}}_i\right)=\mathit{g}\left({\mathit{y}}_i\right)+{\mathit{f}}_R\left({\mathit{y}}_i\right)\hfill & i\notin Q\hfill \\ {\mathit{f}}_N\left({\mathit{y}}_i\right)=\mathit{g}\left({\mathit{y}}_i\right)+{\mathit{f}}_R\left({\mathit{y}}_i\right)+{\mathit{f}}_A\left({\mathit{y}}_i\right)\hfill & i\in Q\hfill \end{array}\right.$$

(8)

where ${\mathit{y}}_i:i\in Q$ are the $N_A$ network nodes on the aforementioned outer faces.

2.5. Regularized Stokeslet Solution

Given the distribution of forces on the viscoelastic network nodes and the swimmer, the velocity at any point $\mathit{x}$ in the fluid (including on the swimmer), due to these forces is:

$$\mathit{u}\left(\mathit{x}\right)=\frac{1}{8\pi \mathsf{\mu }}\underset{B\cup F}{\int }\mathbf{S}(\mathit{x},\xi ,{ϵ}_S){\mathit{f}}_S\left(\xi \right)d{S}_{\xi }+\frac{1}{8\pi \mathsf{\mu }}\sum _i\mathbf{S}\left(\mathit{x},{\mathit{y}}_i,{ϵ}_N\right){\mathit{f}}_N\left({\mathit{y}}_i\right)$$

(9)

The boundaries $B\cup F$ consist of the swimmer body B and helical flagellum F, $\mathsf{\mu }$ is the fluid viscosity, ${\mathit{f}}_{\mathbf{S}}\left(\xi \right)$ is the force per area, or traction, of the microswimmer on the fluid, and $\mathbf{S}(\mathit{x},\xi ,ϵ)$ is the regularized Stokeslet kernel with parameter $ϵ$ as in (2) above.

Here, ${ϵ}_S$ is chosen as a small numerical parameter in the computation of the boundary integral, while ${ϵ}_N$ is chosen as a geometric parameter related to the size of the viscoelastic network elements as in [27].

2.6. Instantaneous Kinematics

The state of the system at any instant in time is given by the configuration of the network nodes and the position of the swimmer. At the start of a simulation, the links between the network nodes are taken to be at their equilibrium lengths, so initially there are no elastic forces supported by the network. The motion is immediately driven by an applied motor torque at the base of the flagellum. This applied torque results in a translation of the entire swimmer and different rotations of the flagellum and cell body—all of which have to be computed. Moreover, the distribution of forces on the free swimmer that allow this rigid translation and rotation also need to be computed. These forces instantaneously result in fluid velocities at the network nodes (which move with the local fluid velocity), causing compression or extension of linkages, and, hence, a distribution of elastic forces on the network nodes which are no longer in equilibrium. Below, we describe the procedure for evolving this system.

To solve the instantaneous kinematics of the freely swimming organism traversing a viscoelastic network, we must solve a linear system of equations involving the unknown rigid-body velocities of the swimmer (vectors $\mathit{U}$, ${\mathbf{\Omega }}^B$, and scalar ${\Omega }^F$), as well as the traction ${\mathit{f}}_{S,j}$ at each of the $N_S$ collocation points that are chosen to be the mesh nodes on the body and flagellum, and finally the external force ${\mathit{f}}_{A,m}$ required to keep each of the $N_A$ anchored network nodes fixed in space. We describe this in three parts. First, we can evaluate (9) at each of the $N_S$ collocation points. Substituting (6) for $\mathit{u}\left(\mathit{x}\right)$ on the swimmer and (8) for ${\mathit{f}}_N\left({\mathit{y}}_i\right)$ yields $3N_S$ scalar equations. Note that, given the geometric configuration of the network and swimmer, we can directly compute $\mathit{g}\left({\mathit{y}}_i\right)$ and ${\mathit{f}}_R\left({\mathit{y}}_i\right)$.

$$\begin{array}{cc}\hfill -\frac{1}{8\pi \mathsf{\mu }}\sum _{i=1}^{N_N}\mathbf{S}\left({\mathit{x}}_j,{\mathit{y}}_i,{ϵ}_N\right)\left(\mathit{g}\left({\mathit{y}}_i\right)+{\mathit{f}}_R\left({\mathit{y}}_i\right)\right)=& \frac{1}{8\pi \mathsf{\mu }}\left(\sum _{i\in Q}\mathbf{S}\left({\mathit{x}}_j,{\mathit{y}}_i,{ϵ}_N\right){\mathit{f}}_A\left({\mathit{y}}_i\right)+\underset{B\cup F}{\int }\mathbf{S}({\mathit{x}}_j,\xi ,{ϵ}_S){\mathit{f}}_S\left(\xi \right)d{S}_{\xi }\right)\hfill \\ \hfill & -\left\{\begin{array}{cc}\left[\mathit{U}+{\mathbf{\Omega }}^B\times {\tilde{\mathit{x}}}_j\right]\hfill & {\mathit{x}}_j\in B\hfill \\ \left[\mathit{U}+\left({\mathbf{\Omega }}^B-{\Omega }^F{\widehat{\mathit{e}}}^F\right)\times {\tilde{\mathit{x}}}_j\right]\hfill & {\mathit{x}}_j\in F\hfill \end{array}\right.j=1,2,...,N_S\hfill \end{array}$$

(10)

An additional $3N_A$ equations are needed to solve the $N_A$ unknown vectors ${\mathit{f}}_A\left({\mathit{y}}_m\right)$, so we use the linear relationship between velocity and forces in (9) again, now specifying zero velocity at each anchored network node: $\mathit{u}\left({\mathit{y}}_m\right)=0:m\in Q$.

$$\begin{array}{c}-\frac{1}{8\pi \mathsf{\mu }}\sum _{i=1}^{N_N}\mathbf{S}\left({\mathit{y}}_m,{\mathit{y}}_i,{ϵ}_N\right)\left(\mathit{g}\left({\mathit{y}}_i\right)+{\mathit{f}}_R\left({\mathit{y}}_i\right)\right)=\hfill \\ \frac{1}{8\pi \mathsf{\mu }}\left(\sum _{i\in Q}\mathbf{S}\left({\mathit{y}}_m,{\mathit{y}}_i,{ϵ}_N\right){\mathit{f}}_A\left({\mathit{y}}_i\right)+\underset{B\cup F}{\int }\mathbf{S}({\mathit{y}}_m,\xi ,{ϵ}_S){\mathit{f}}_S\left(\xi \right)d{S}_{\xi }\right)m\in Q\hfill \end{array}$$

(11)

To approximate $\underset{B\cup F}{\int }\mathbf{S}({\mathit{x}}_j,\xi ,{ϵ}_S){\mathit{f}}_S\left(\xi \right)d{S}_{\xi }$ and $\underset{B\cup F}{\int }\mathbf{S}({\mathit{y}}_m,\xi ,{ϵ}_S){\mathit{f}}_S\left(\xi \right)d{S}_{\xi }$ in (10) and (11) respectively, we use an existing adaptive quadrature algorithm for simplices, ADSIMP [46]. The algorithm subdivides each triangular element until the desired error estimate is reached; we obtained the highest efficiency with the 5th order integration rule. The integrations are performed by mapping each curved element to a standard (flat) reference triangle according to standard methodology [47].

To close the linear system, seven additional scalar equations are included that enforce the conservation of linear and angular momentum, as well as the specified torque $\tau$ imposed between the body and the flagellum. Note that the constraint on force-free swimming includes the contributions of repulsive forces on the cell body. The equations are:

$$\begin{array}{cc}\hfill \mathbf{0}& =\sum _{i=1}^{N_N}{\mathit{f}}_R\left({\mathit{y}}_i\right)+{\int }_{B\cup F}{\mathit{f}}_S\left(\xi \right)d{S}_{\xi }\hfill \\ \hfill \mathbf{0}& ={\int }_{B\cup F}(\xi -\mathit{X})\times {\mathit{f}}_S\left(\xi \right)d{S}_{\xi }\hfill \\ \hfill \tau & ={\widehat{\mathit{e}}}^F·{\int }_F(\xi -\mathit{X})\times {\mathit{f}}_S\left(\xi \right)d{S}_{\xi }\hfill \end{array}$$

(12)

As the reference point $\mathit{X}$ is the center of the spherical body, the repulsive force, which points in the normal direction to the sphere, does not contribute to the total torque on the system.

We directly solve the $3N_S+3N_A+7$ by $3N_S+3N_A+7$ dense linear system given by (10)–(12). The solution of this system yields the traction over the swimmer surface, the anchoring forces at the frame of the network, the swimmer’s translational and rotational velocities, and the relative rotational velocity of the flagellum. Once the above linear system is solved for ${\mathit{f}}_{S,j}$, ${\mathit{f}}_{A,m}$, $\mathit{U}$, ${\mathbf{\Omega }}^B$, and ${\Omega }^F$, we directly compute the velocities at the network nodes with

$$\mathit{u}\left({\mathit{y}}_m\right)=\frac{1}{8\pi \mathsf{\mu }}\underset{B\cup F}{\int }\mathbf{S}({\mathit{y}}_m,\xi ,{ϵ}_S){\mathit{f}}_S\left(\xi \right)d{S}_{\xi }+\frac{1}{8\pi \mathsf{\mu }}\sum _{i=1}^{N_N}\mathbf{S}\left({\mathit{y}}_m,{\mathit{y}}_i,{ϵ}_N\right)\left(\mathit{g}\left({\mathit{y}}_i\right)+{\mathit{f}}_R\left({\mathit{y}}_i\right)\right)m=1,2,...,N_N$$

(13)

2.7. Temporal Evolution

To obtain the trajectory of the swimmer and evolution of the viscoelastic network, we evolve a system of ordinary differential equations for the center of the body $\mathit{X}\left(t\right)$, orientation ${\theta }^B\left(t\right)$ using Tait–Bryan angles as in [39], and flagellar phase angle ${\theta }^F\left(t\right)$ in addition to the locations of each network node ${\mathit{y}}_m\left(t\right)$ and rest length of each link ${\ell }_{ij}\left(t\right)$. The former are related to the kinematic vectors $\mathit{U}$, ${\mathbf{\Omega }}^B$, and scalar ${\Omega }^F$ by the ODEs

$$\begin{array}{cc}\hfill \dot{\mathit{X}}\left(t\right)& =\mathit{U}\left(t\right)\hfill \\ \hfill {\dot{\theta }}^B\left(t\right)& =\left[\begin{array}{ccc}\frac{sin\left({\theta }_2^B\left(t\right)\right)cos\left({\theta }_1^B\left(t\right)\right)}{cos\left({\theta }_2^B\left(t\right)\right)}& \frac{sin\left({\theta }_2^B\left(t\right)\right)sin\left({\theta }_1^B\left(t\right)\right)}{cos\left({\theta }_2^B\left(t\right)\right)}& 1\\ -sin\left({\theta }_1^B\left(t\right)\right)& cos\left({\theta }_1^B\left(t\right)\right)& 0\\ \frac{cos\left({\theta }_1^B\left(t\right)\right)}{cos\left({\theta }_2^B\left(t\right)\right)}& \frac{sin\left({\theta }_1^B\left(t\right)\right)}{cos\left({\theta }_2^B\left(t\right)\right)}& 0\end{array}\right]{\mathbf{\Omega }}^B\left(t\right)\hfill \\ \hfill {\dot{\theta }}^F\left(t\right)& ={\Omega }^F\left(t\right)\hfill \end{array}$$

(14)

Note that $\mathit{U}$, ${\mathbf{\Omega }}^B$, and ${\mathit{f}}_S$ are defined in the fixed frame (but ${\Omega }^F$ is the same in either frame). The network nodes move with the velocity given by Equation (13) and the network link rest lengths change according to Equation (3). The system of differential equations for the evolution of the swimmer and the network was numerically solved using MATLAB’s ode113. While this algorithm uses adaptive time-stepping, in the simulations presented below; usually, 80 time steps were used to resolve one flagellar rotation.

The swimming efficiency of the microswimmer is defined as

$$\psi \left(t\right)=\frac{6\pi \mathsf{\mu }{R}_S{∥\overline{\mathit{U}}\left(t\right)∥}^2}{\tau {\overline{\Omega }}^F\left(t\right)}$$

where the moving averages $\overline{\mathit{U}}\left(t\right)$ and ${\overline{\Omega }}^F\left(t\right)$ are taken over the approximate period of a swimmer body rotation.

2.8. Remodeling

We chose a simple model of chemical degradation of the network due to teh compounds released by the swimmer assuming an envelope around the swimmer cell body, in which such compounds are sufficiently concentrated. Since our swimmer body is spherical, this envelope is a sphere of radius $(1+{\delta }_r)R_S$. Note that in the simulations presented below, we chose ${\delta }_r=0.2$. If the line segment representing a link intersects this sphere, the link is considered to be permanently destroyed. In practice, when such an event occurs, the stiffness $E_{ij}$ of that destroyed link is set to zero for the remainder of the simulation, effectively converting the two nodes of the link to passive tracer particles.

3. Simulation Results

In all simulations presented here, we fix the swimmer geometry and lattice network geometry depicted in Figure 1, with geometric and numerical parameters listed in Table 1. For simplicity, we consider a network geometry that is a uniform lattice of $6\times 12\times 12$ nodes with all initial link rest lengths ${\ell }_{0,ij}$ at equilibrium. Each interior node is connected to its six neighbors in the coordinate directions, as well as its twelve nearest diagonal neighbors. A simulation begins with the leading edge of the microswimmer a short distance ahead of the leftmost face of the network, with the flagellar axis perpendicular to that face. As described above, the motion of the microswimmer is driven by an imposed torque $\tau$. Here, we chose all links in the network to be virtual Maxwell elements, with uniform stiffness constants $E_{i,j}=E$ and uniform dashpot constants ${\eta }_{i,j}=\eta$. We now investigate the swimming performance as a function of these material parameters, E and $\eta$, both with and without network dissolution. Note that the case of $E=0$ results in a purely Newtonian fluid with network nodes acting as passive tracers only. In addition, the case of $\eta =\infty$ results in purely Hookean spring elements, with no relaxation of the element’s rest length due to a dashpot.

3.1. No Remodeling of Network

To begin to understand the interactions between the microswimmer and surrounding viscoelastic network, we first illustrate the effects of the network link dashpot parameter $\eta$, keeping stiffness $E=25$ mPa fixed.

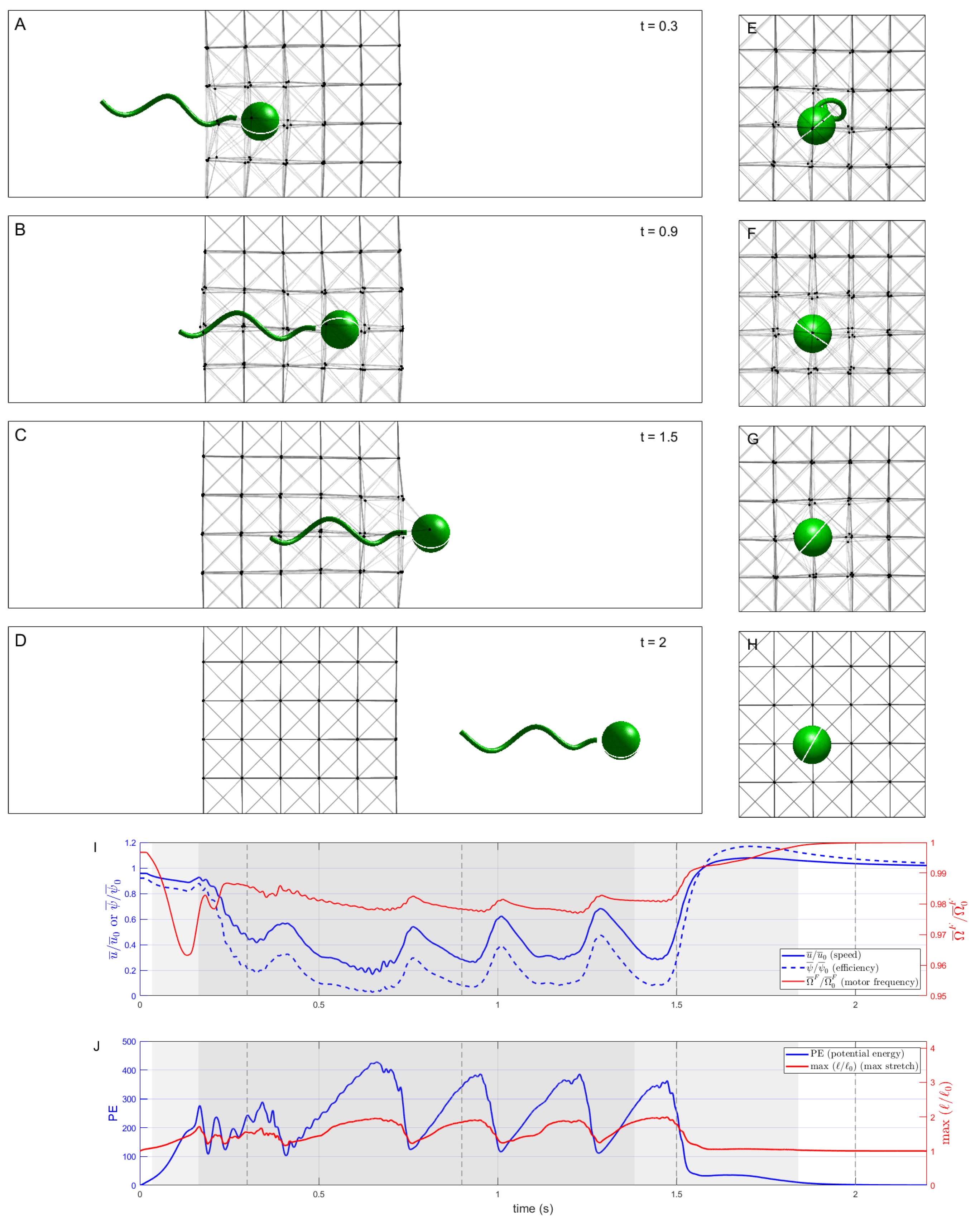
Figure 3 shows a sequence of snapshots of the microswimmer as it penetrates and moves through the network of nodes connected by elastic Hookean springs ($\eta =\infty$). Note that we are depicting two-dimensional side views in panels (A)–(D), as well as two-dimensional front views in panels (E)–(H), of this three-dimensional system. Figure 3I shows a timeseries of the swimming speed of the organism, normalized by its swimming speed in a Newtonian Stokes fluid, as well as motor frequency and power efficiency (also normalized by the Newtonian values). The swimmer is initialized with its cell body just outside the network, so even when it has not yet entered the network, the presence of this obstacle causes its normalized swimming speed to be slightly less than one. The swimmer then penetrates and traverses the network at a reduced swimming speed, at times even lower than $25\%$ of the Newtonian speed. Moreover, driven by the prescribed motor torque, the resulting motor frequency in the network is less than the achieved motor frequency in the Newtonian case, but by only about $2\%$. As such, the reduction in swimming efficiency, at times less than $10\%$ of the Newtonian case, is due to the retarded swimming speed and not to the hydrodynamic power needed to rotate the flagellum. Figure 3J shows a timeseries of the potential energy in the network as well as the maximal relative stretch of the springs. These timeseries illustrate that the swimmer slows down each time it encounters a successive discrete layer in the network, stretches the links attached to the nodes in front of it, and eventually pushes past, allowing for those links to contract back to rest. We do see a slight boost in swimming speed as the cell body exits the network, with a boost in efficiency of almost $20\%$, since the increase in swimming speed was accompanied by a reduction in motor frequency compared to the Newtonian case.

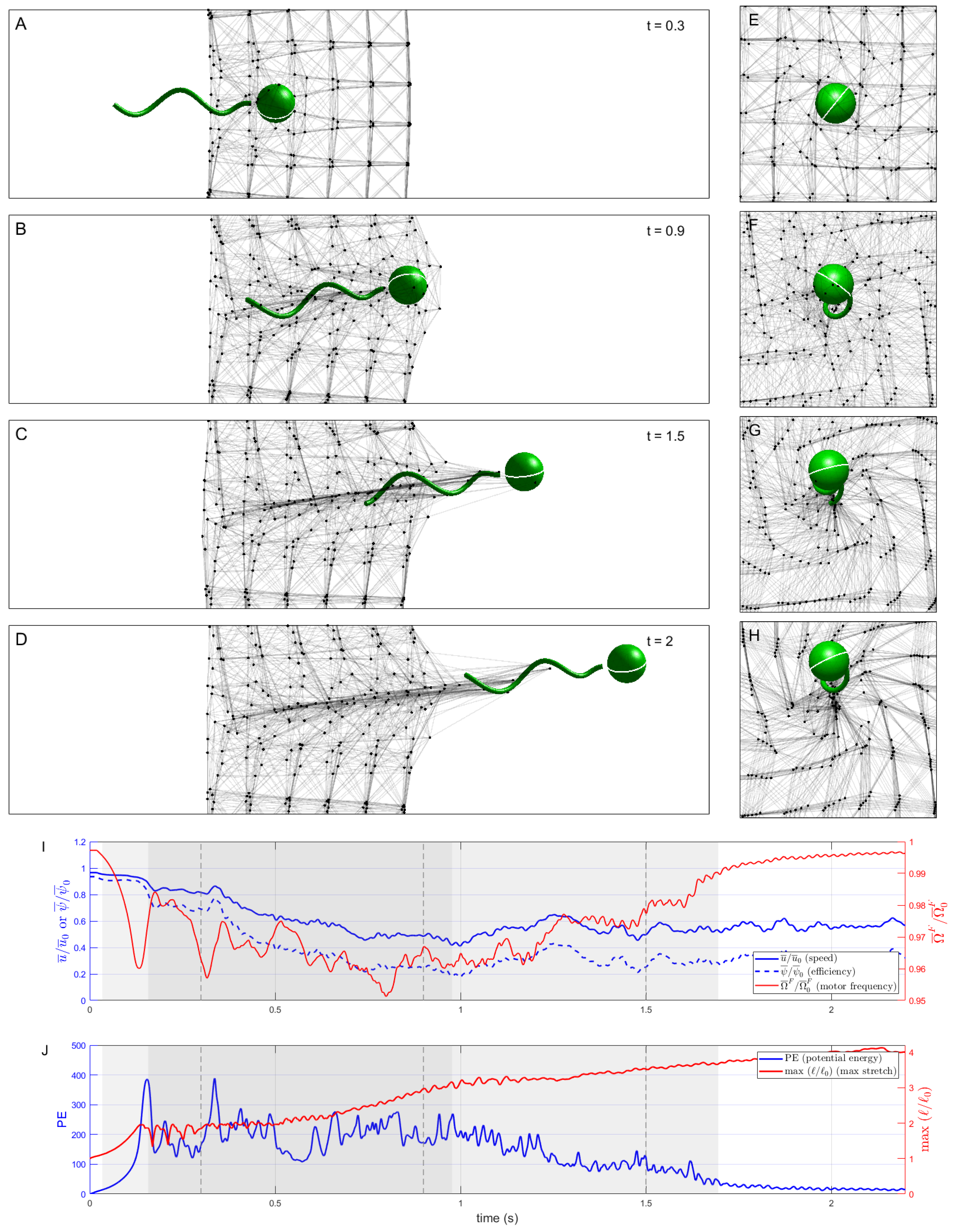
Figure 4 shows the swimming progression through a network with a moderate dashpot parameter $\eta =10$ mPa-s. Again, the swimmer is able to penetrate and traverse the network, but at a significantly reduced speed, swimming at around 30% of the network-free Newtonian case over much of this distance. The potential energy stored in the stretched links rapidly increases during initial penetration of the network, then stays roughly constant, and finally decreases back to zero when the swimmer leaves and each link returns to its new rest length—the latter is illustrated by the maximum relative stretch parameter $\ell /{\ell }_0$ reaching a steady state value above 1. In this example, as well as the previous Hookean case, the swimmer is effectively held back by a single network node as it exits the network (see $t=1.5$ s in Figure 4) but does escape. Once the body is completely free and the tail is mostly free, the swimmer again experiences a small increase in speed and efficiency versus the Newtonian case.

We now consider the case of $E=25$ mPa with the dashpot constant further reduced to $\eta =1$ mPa-s. In this case, link rest lengths quickly adapt upon being stretched or compressed (Figure 5). The ‘pusher’ velocity field induced by the swimmer draws network nodes toward it, deforming the network considerably and resulting in the swimmer becoming entangled in many nodes. Compared to the Hookean ($\eta =\infty$) and moderate $\eta =10$ mPa-s cases above, the swimmer takes much longer to fully escape the network (not shown in Figure 5). Despite this, the swimmer travels further by $t=2$ s than in either of these cases because the elastic forces exerted by the rapidly adapting network on the swimmer are relatively small.

We further explore the effect of the varying the dashpot parameter $\eta$ while fixing the spring stiffness $E=25$ mPa. Figure 6 shows the trajectory of the cell centroid in the swimming direction through the network for $E=25$ mPa and various values of $\eta$. In each case, the swimmer starts near the Newtonian swimming speed as it approaches the network, but slows down as the elastic link forces increase and it penetrates the network. Comparing the simulations, Figure 6 shows that from $t=0.25$ s to $t=1.25$ s, the swimming speed decreases as $\eta$ (and network resiliency) increases. Eventually, when the swimmer escapes the network, its swimming speed returns to the network-free Newtonian case. The transition does not take place until the swimmer completely separates itself from the network links, which takes longer for more deformable networks, i.e., for smaller values of $\eta$, as the swimmer drags portions of the network with it. In Figure 6, we see that for $\eta =1$ mPa-s, the transition to network-free swimming occurs at about $t=2.5$ s (right inset), while for $\eta =10$ mPa-s (red dashed line) the transition occurs at about $t=1.8$ s. For the Hookean case, the transition is at $t=1.5$ s (left inset).

3.2. Remodeling of Network Due to Dissolution

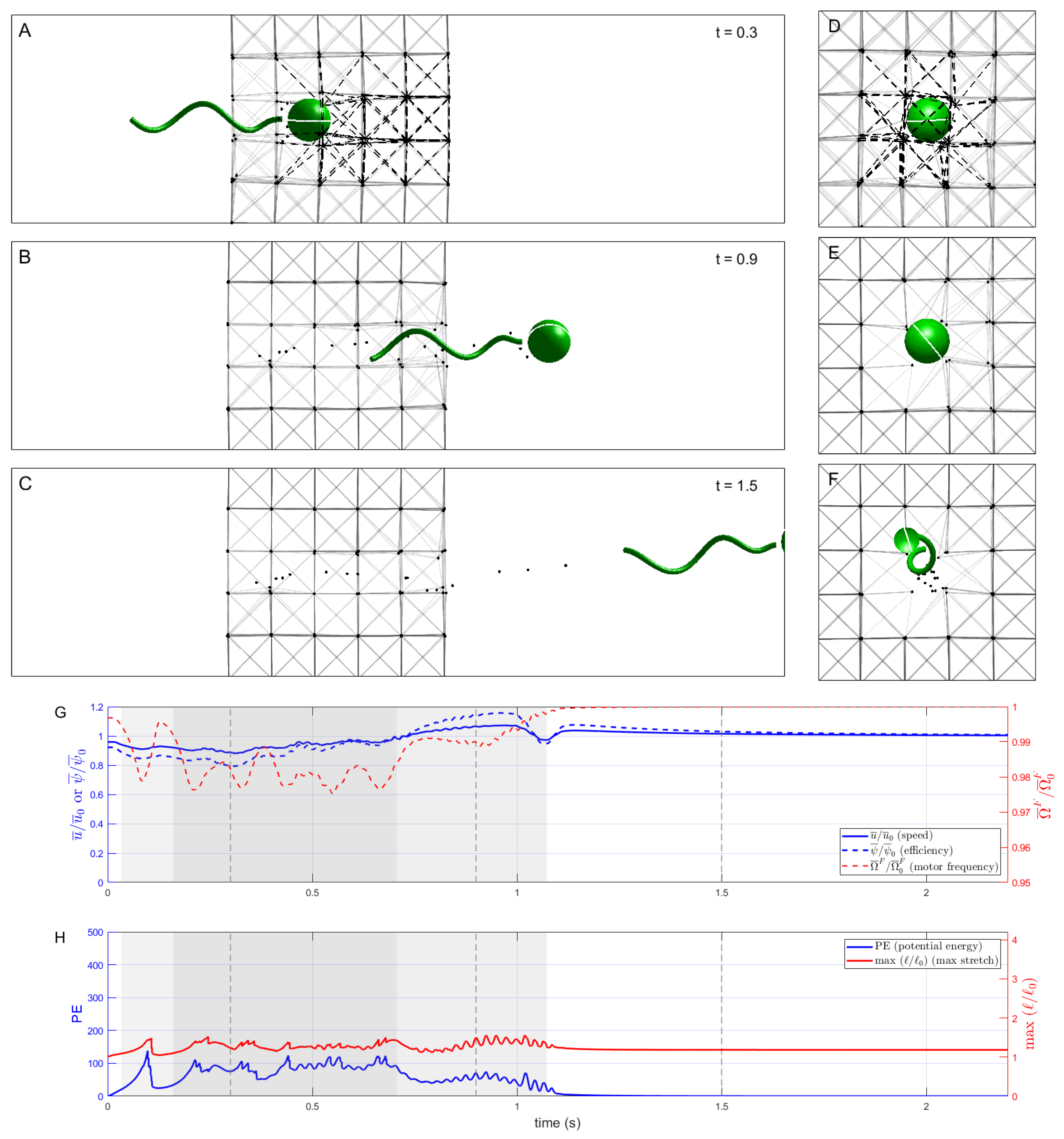
Figure 7 shows a sequence of snapshots and related timeseries in the case when network links are permanently dissolved when they come within ${\delta }_r=0.2R_S$ of the swimmer body surface. We see that the swimmer effectively clears a path around itself, leaving disconnected network nodes in its wake that become passive tracers. Due to the dissolution of network links, there is less interaction between the swimmer and the elastic elements, resulting in an increase in the swimmer’s average speed. The swimmer is able to traverse the network considerably faster than without remodeling (Figure 7 vs. Figure 4). As in the previous cases, the discrete nature of the network introduces small peaks and dips in speed (one seen at about $t=1.06$ s here). The potential energy of the network does not increase as much as in the cases without remodeling because the links that tend to stretch the most are also more likely to come close to the swimmer and be dissolved.

If we examine the effects of remodeling across a range of stiffness values, as E is increased, the number of links that are dissolved over the course of a simulation tends to increase to a relative maximum near $E=10$ mPa and then decrease sharply as stiffness is further increased (Figure 8A). Figure 8B,C depict the network links that were dissolved during two simulations with different network parameters chosen in the range of relatively high E values. The swimmer position shown is not part of the simulation; it is shown to provide a reference for the extent of the dissolved network links. The case $E=10$ mPa and $\eta =1$ mPa-s is a network that substantially deforms, making it more likely that larger numbers of links will come in close proximity to the swimmer. Therefore, more links are dissolved in the simulation compared to a more rigid network ($E=100$ mPa, $\eta =\infty$) where only those links that were initially very close to the swimmer path are dissolved.

3.3. Effects of Varying E, $\eta$

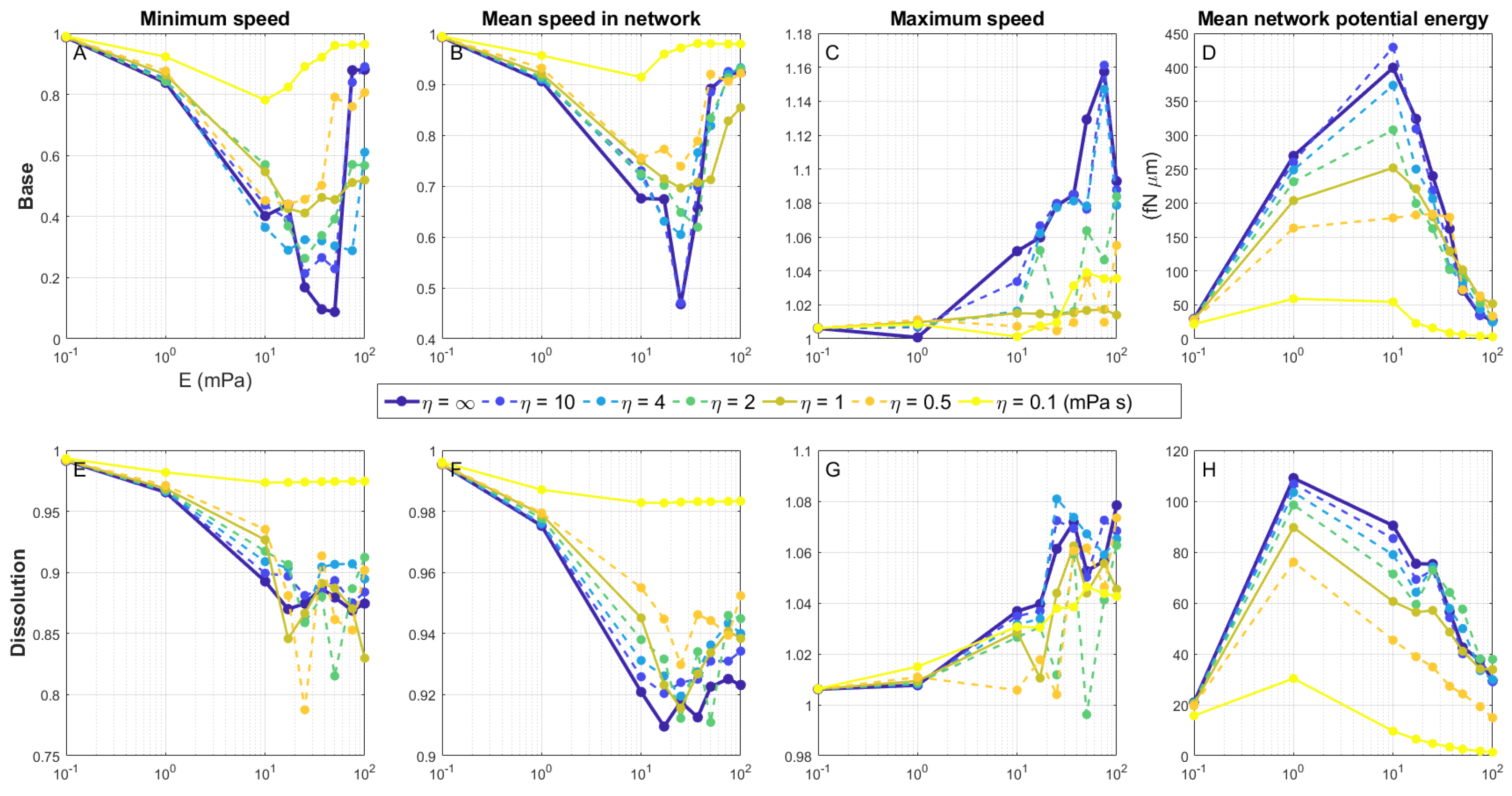
We performed simulations of the model swimmer penetrating, traversing and exiting the model viscoelastic network for a range of material parameters E and $\eta$. Figure 9 shows the metrics of swimmer velocities (Panels A–C; E–G) and average potential energy in the network (Panels D, H) for the base case with no link dissolution and for the case where network links were dissolved. In particular, we report the minimum speed (Panels A, E) and the maximum speed (Panels C, G) of the swimmer in a simulation, over the duration of time it took for the swimmer to break completely free of the network and regain its Newtonian swimming velocity. The mean speed in the network (Panels B, F) and the mean network potential energy (Panels D, H) were computed by averaging these quantities from $t=0$ until the center of the body reached the outermost network layer. Note that in the absence of remodeling, there is a relative minimum in both minimum and mean swimming speed, approximately between $25<E<50$ mPa, which becomes increasingly pronounced as $\eta$ increases toward the Hookean case, $\eta =\infty$. Intuitively, one might expect swimming speed to decrease monotonically with increasing E as the network exerts larger forces on the swimmer. However, since the gaps between network nodes are comparable in size to the swimmer cell body, a sufficiently large stiffness of the network links can result in less deformation of these channels and faster traversal by the swimmer, especially as the network is arranged as a uniform lattice.

The maximum speed reported in Figure 9C,G occurred overwhelmingly at the moment the swimmer’s cell body exited the network. Once the swimmer begins to exit the network and the body is no longer constrained, it tends to experience a modest increase in swimming speed compared to the Newtonian case due to the flagellum effectively pushing against the nodes behind it. This is most effective (up to a maximum of 16% faster than Newtonian) for high values of both E and $\eta$, when the network is most resilient to deformation. The microswimmer does impart elastic potential energy into the viscoelastic network as it moves through it. While the concept of the swimmer extracting some of this elastic energy to boost swimming speed is intriguing, we did not find evidence for this. Instead, we believe the speed boosts we observed as the swimmer exited the network were primarily due to the swimmer’s ability to push against the network nodes behind it to some extent. Indeed, simulations in which the flagellar torque was instantly lowered to zero as the swimmer exited the network resulted in a near-instantaneous cessation of all swimmer movement (data not shown).

When the swimmer can actively remodel the network, it achieves much higher swimming speeds across all E and $\eta$ as seen in both the minimum and mean speed metrics (Figure 9E,F). The local minima in these speeds do not drop as far below the Newtonian speed as those of the swimmers that are unable to dissolve links. While the swimmer traverses the network overall much faster with remodeling, its maximum speed while exiting is reduced (Figure 9G) due to a reduced ability to push against what were the nearest network nodes, which now effectively became passive tracers.

Finally, we comment on the potential energy (PE) stored in the network elements. Figure 9D shows the mean value of the PE per simulation for a range of values of E and $\eta$. The trends indicate that, for a fixed value of $\eta$, the mean PE increases with E to a maximum value, and then sharply decreases. Referring to Equation (4), the PE is proportional to the stiffness E and each term is proportional to the square of the strain, which, in turn, depends on the deformation of the network. These are competing effects because stiffer networks deform less. The concavity of the curves in Figure 9D shows that the reduction in strain as E increases dominates the effects of increasing stiffness. The mean potential energy across all simulations with remodeling (Figure 9H) is smaller than that without remodeling, since the most deformed links are dissolved. As in the base case, we do see the persistence of a relative maximum in network PE with respect to E, though it shifts to a lower value.

4. Discussion

We have presented a model for the simulation of the motion of a swimmer in Stokes flow as it approaches, traverses, and exits a viscoelastic region. The region represents a polymeric network characterized by gaps of a size comparable to the dimensions of the cell body, where continuum models do not apply. Our simulations are based on a hybrid boundary integral-regularized Stokeslet method which allows for high resolution in the discretization of the cell body and the flagellum. The network is composed of Maxwell elements characterized by a stiffness parameter and a dashpot constant. Throughout this work, we have assigned the same constants to all elements, although our model is not restricted to homogeneous material properties of network links.

We note that the discrete nature of the network has an effect on the dynamics. For instance, depending on its initial orientation with respect to the regular lattice of elements, a swimmer may run directly into a network node, causing the swimmer to slow down, while a swimmer that was initially lined up with the pores of the network may advance faster. Hence, such discrete events introduce seemingly random noise in many of the trends in velocities reported in Figure 9, although trends in network potential energy, which is aggregated over the entire network, are smoother than the trends in speed of the individual swimmer. While we found that sufficiently high stiffness values can facilitate faster traversal of the network, this result is dependent on the particular geometry of the system. In fact, in simulations not shown here, in some cases with network nodes arranged with little geometric order, as opposed to in regular lattices, faster swimming with increased stiffness was not observed. On the contrary, in some cases with perturbed networks with large E, the computational swimmer was not able to escape the viscoelastic network. This observation is consistent with the experiments on natural bacteria [13] and engineered nanopropellers [18], which demonstrate that, at times, the microswimmers are not able to progress through the viscoelastic environment. In fact, the experiments in [13] also show that pore sizes in a mucus network can be manipulated by squeezing the sample between parallel plates, which alters subsequent bacterial progression and flagellar bundling. This shear induced rearrangement of mucosal fibers could possibly open up the types of channels present in the regular-lattice simulations above.

5. Future Directions

While we have demonstrated that our model can capture the dynamic remodeling of network rheology by a microswimmer, here we chose a generic swimmer and used a very simple dissolution model of network links. Bacteria exhibit an enormous diversity of body shapes that affect motility in both Newtonian (e.g., [39]) and complex (e.g., [48]) fluids. The latter effects are less well studied than the former and it would be worth investigating other common body geometries (e.g., straight or curved rods, helices) interacting with viscoelastic networks in the future: this would be straightforward with our modeling framework. Likewise, in our treatment of network remodeling, we did not try to capture the details of enzymatic release and their relation to specific rheological properties of the polymeric network, central to systems such as $\mathit{H}.\mathit{pylori}$ [16]. Of course, when probing a particular system, details of the biochemistry should also be included.

Our method is formulated to model microswimmers that not only swim within discrete viscoelastic networks but also penetrate into and exit out of such regions of a bulk Newtonian environment. In many experimental studies of biological viscoelastic structures (e.g., [49]), it is difficult to ascertain the precise geometry of the transition between Newtonian and viscoelastic regions. In this study, we chose to model a sharp interface, since this is consistent with observations in several studies, e.g., the oocyte cumulus complex in mammalian reproduction [50], the mucus-periciliary layer interface in the respiratory tract [51], and experiments involving bacterial invasion of cervical mucus [13]. While we created a sharp interface between the Newtonian and viscoelastic region by assigning the same parameters to every link in the network, smoother transitions could be modeled in the future by assigning different properties to the network links near the edge of the network.

This study focused on a single microswimmer, but suspensions of many microswimmers are common in both natural and engineered systems [52]. At sufficiently dense concentrations, cell locomotion can no longer be considered on an individual basis due to hydrodynamic interactions. Intriguingly, [53] show how, even in dilute suspensions, individual bacteria are, in fact, frequently mechanically coupled by a weak viscoelastic matrix. It would be straightforward to extend our modeling framework to include multiple microswimmers embedded in a network, with the only limitation being an increased computational cost.