A Framework for Generating Radial and Surface-Oriented Regularized Stokeslets
Abstract
1. Introduction
2. Methods
2.1. The Stokeslet and Regularized Stokeslet
2.2. A Regularization Approach Utilizing the Vector Potential of the Stokeslet
2.3. Radially Symmetric Regularizations
2.3.1. Formulation of Smoothing Factors
2.3.2. Error Analysis
2.4. Surface-Oriented Regularizations
2.5. Test Case: A Translating Sphere
3. Results
3.1. Radial Regularizations
3.1.1. Example Smoothing Factors
3.1.2. Forward Problem
3.1.3. Inverse Problem
3.2. A Surface-Oriented Regularization
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MRS | Method of Regularized Stokeslets |
| IB | Immersed Boundary |
Appendix A. Moments of Radial Blob Functions
Appendix B. Expressions and Computational Cost of Regularized Stokeslets
| Label | Time | ||
|---|---|---|---|
| alg2 | |||
| alg4 | |||
| tanh | |||
| erf | |||
| alg2-c | |||
| alg4-c | |||
| tanh-c | |||
| erf-c |
Appendix C. Matrix Condition Numbers

References
- Elgeti, J.; Winkler, R.G.; Gompper, G. Physics of Microswimmers—Single Particle Motion and Collective Behavior: A Review. Rep. Prog. Phys. 2015, 78, 056601. [Google Scholar] [CrossRef] [PubMed]
- Fauci, L.J.; Dillon, R. Biofluidmechanics of Reproduction. Annu. Rev. Fluid Mech. 2006, 38, 371–394. [Google Scholar] [CrossRef]
- Gaffney, E.; Gadêlha, H.; Smith, D.; Blake, J.; Kirkman-Brown, J. Mammalian Sperm Motility: Observation and Theory. Annu. Rev. Fluid Mech. 2011, 43, 501–528. [Google Scholar] [CrossRef]
- Lauga, E.; Powers, T.R. The Hydrodynamics of Swimming Microorganisms. Rep. Prog. Phys. 2009, 72, 096601. [Google Scholar] [CrossRef]
- du Roure, O.; Lindner, A.; Nazockdast, E.N.; Shelley, M.J. Dynamics of Flexible Fibers in Viscous Flows and Fluids. Annu. Rev. Fluid Mech. 2019, 51, 539–572. [Google Scholar] [CrossRef]
- Goldstein, R.E.; van de Meent, J.W. A Physical Perspective on Cytoplasmic Streaming. Interface Focus 2015, 5, 20150030. [Google Scholar] [CrossRef]
- Mogilner, A.; Manhart, A. Intracellular Fluid Mechanics: Coupling Cytoplasmic Flow with Active Cytoskeletal Gel. Annu. Rev. Fluid Mech. 2018, 50, 347–370. [Google Scholar] [CrossRef]
- Nazockdast, E.; Rahimian, A.; Needleman, D.; Shelley, M. Cytoplasmic Flows as Signatures for the Mechanics of Mitotic Positioning. MBoC 2017, 28, 3261–3270. [Google Scholar] [CrossRef]
- Shinar, T.; Mana, M.; Piano, F.; Shelley, M.J. A Model of Cytoplasmically Driven Microtubule-Based Motion in the Single-Celled Caenorhabditis Elegans Embryo. Proc. Natl. Acad. Sci. USA 2011, 108, 10508–10513. [Google Scholar] [CrossRef]
- Stone, H.; Stroock, A.; Ajdari, A. Engineering Flows in Small Devices: Microfluidics Toward a Lab-on-a-Chip. Annu. Rev. Fluid Mech. 2004, 36, 381–411. [Google Scholar] [CrossRef]
- Sharan, P.; Nsamela, A.; Lesher-Pérez, S.C.; Simmchen, J. Microfluidics for Microswimmers: Engineering Novel Swimmers and Constructing Swimming Lanes on the Microscale, a Tutorial Review. Small 2021, 17, 2007403. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Karrila, S.J. Microhydrodynamics: Principles and Selected Applications; Butterworth-Heinemann Series in Chemical Engineering; Butterworth-Heinemann: Boston, MA, USA, 1991. [Google Scholar]
- Pozrikidis, C. Boundary Integral and Singularity Methods for Linearized Viscous Flow, 1st ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar] [CrossRef]
- Higdon, J.J.L. A Hydrodynamic Analysis of Flagellar Propulsion. J. Fluid Mech. 1979, 90, 685. [Google Scholar] [CrossRef]
- Lighthill, J. Flagellar Hydrodynamics. SIAM Rev. 1976, 18, 161–230. [Google Scholar] [CrossRef]
- Lighthill, J. Helical Distributions of Stokeslets. J. Eng. Math. 1996, 30, 35–78. [Google Scholar] [CrossRef]
- Keller, J.B.; Rubinow, S.I. Slender-Body Theory for Slow Viscous Flow. J. Fluid Mech. 1976, 75, 705–714. [Google Scholar] [CrossRef]
- Peskin, C.S. The Immersed Boundary Method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Cortez, R. The Method of Regularized Stokeslets. SIAM J. Sci. Comput. 2001, 23, 1204–1225. [Google Scholar] [CrossRef]
- Cortez, R.; Fauci, L.; Medovikov, A. The Method of Regularized Stokeslets in Three Dimensions: Analysis, Validation, and Application to Helical Swimming. Phys. Fluids 2005, 17, 031504. [Google Scholar] [CrossRef]
- Tlupova, S.; Beale, J.T. Nearly Singular Integrals in 3D Stokes Flow. Commun. Comput. Phys. 2013, 14, 1207–1227. [Google Scholar] [CrossRef][Green Version]
- Tlupova, S.; Beale, J.T. Regularized Single and Double Layer Integrals in 3D Stokes Flow. J. Comput. Phys. 2019, 386, 568–584. [Google Scholar] [CrossRef]
- Olson, S.D.; Suarez, S.S.; Fauci, L.J. Coupling Biochemistry and Hydrodynamics Captures Hyperactivated Sperm Motility in a Simple Flagellar Model. J. Theor. Biol. 2011, 283, 203–216. [Google Scholar] [CrossRef] [PubMed]
- Olson, S.D.; Fauci, L.J. Hydrodynamic Interactions of Sheets vs Filaments: Synchronization, Attraction, and Alignment. Phys. Fluids 2015, 27, 121901. [Google Scholar] [CrossRef]
- Simons, J.; Fauci, L.; Cortez, R. A Fully Three-Dimensional Model of the Interaction of Driven Elastic Filaments in a Stokes Flow with Applications to Sperm Motility. J. Biomech. 2015, 48, 1639–1651. [Google Scholar] [CrossRef]
- Lim, S.; Peskin, C.S. Fluid-Mechanical Interaction of Flexible Bacterial Flagella by the Immersed Boundary Method. Phys. Rev. E 2012, 85, 036307. [Google Scholar] [CrossRef] [PubMed]
- Ainley, J.; Durkin, S.; Embid, R.; Boindala, P.; Cortez, R. The Method of Images for Regularized Stokeslets. J. Comput. Phys. 2008, 227, 4600–4616. [Google Scholar] [CrossRef]
- Leiderman, K.; Bouzarth, E.L.; Cortez, R.; Layton, A.T. A Regularization Method for the Numerical Solution of Periodic Stokes Flow. J. Comput. Phys. 2013, 236, 187–202. [Google Scholar] [CrossRef]
- Leiderman, K.; Bouzarth, E.; Nguyen, H. A Regularization Method for the Numerical Solution of Doubly-Periodic Stokes Flow. In Biological Fluid Dynamics: Modeling, Computation, and Applications; Layton, A.O., Ed.; American Mathematical Society: Providence, RI, USA, 2014; Volume 628, pp. 73–90. [Google Scholar]
- Cortez, R.; Varela, D. A General System of Images for Regularized Stokeslets and Other Elements near a Plane Wall. J. Comput. Phys. 2015, 285, 41–54. [Google Scholar] [CrossRef]
- Wróbel, J.K.; Cortez, R.; Varela, D.; Fauci, L. Regularized Image System for Stokes Flow Outside a Solid Sphere. J. Comput. Phys. 2016, 317, 165–184. [Google Scholar] [CrossRef]
- Mannan, F.O.; Cortez, R. An Explicit Formula for Two-Dimensional Singly-Periodic Regularized Stokeslets Flow Bounded by a Plane Wall. Commun. Comput. Phys. 2018, 23, 142–167. [Google Scholar] [CrossRef]
- Barrero-Gil, A. Weakening Accuracy Dependence with the Regularization Parameter in the Method of Regularized Stokeslets. J. Comput. Appl. Math. 2013, 237, 672–679. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Cortez, R. Reduction of the Regularization Error of the Method of Regularized Stokeslets for a Rigid Object Immersed in a Three-Dimensional Stokes Flow. Commun. Comput. Phys. 2014, 15, 126–152. [Google Scholar] [CrossRef]
- Stotsky, J.A.; Bortz, D.M. A Posteriori Error Analysis of Fluid–Structure Interactions: Time Dependent Error. Comput. Methods Appl. Mech. Eng. 2019, 356, 1–15. [Google Scholar] [CrossRef]
- Martindale, J.D.; Jabbarzadeh, M.; Fu, H.C. Choice of Computational Method for Swimming and Pumping with Nonslender Helical Filaments at Low Reynolds Number. Phys. Fluids 2016, 28, 021901. [Google Scholar] [CrossRef]
- Zhao, B.; Lauga, E.; Koens, L. Method of Regularized Stokeslets: Flow Analysis and Improvement of Convergence. Phys. Rev. Fluids 2019, 4, 084104. [Google Scholar] [CrossRef]
- Tran-Cong, T.; Blake, J. General Solutions of the Stokes’ Flow Equations. J. Math. Anal. Appl. 1982, 90, 72–84. [Google Scholar] [CrossRef]
- Gimbutas, Z.; Greengard, L.; Veerapaneni, S. Simple and Efficient Representations for the Fundamental Solutions of Stokes Flow in a Half-Space. J. Fluid Mech. 2015, 776. [Google Scholar] [CrossRef]
- Yan, W.; Shelley, M. Universal Image Systems for Non-Periodic and Periodic Stokes Flows above a No-Slip Wall. J. Comput. Phys. 2018, 375, 263–270. [Google Scholar] [CrossRef]
- Mindlin, R.D. Note on the Galerkin and Papkovitch Stress Functions. Bull. Am. Math. Soc. 1936, 42, 373–376. [Google Scholar] [CrossRef]
- Smith, D.J. A Nearest-Neighbour Discretisation of the Regularized Stokeslet Boundary Integral Equation. J. Comput. Phys. 2018, 358, 88–102. [Google Scholar] [CrossRef]
- Beale, J.T.; Lai, M.C. A Method for Computing Nearly Singular Integrals. SIAM J. Numer. Anal. 2001, 38, 1902–1925. [Google Scholar] [CrossRef][Green Version]
- Beale, J.T. A Grid-Based Boundary Integral Method for Elliptic Problems in Three Dimensions. SIAM J. Numer. Anal. 2004, 42, 599–620. [Google Scholar] [CrossRef][Green Version]
- Beale, J.T.; Ying, W.; Wilson, J.R. A Simple Method for Computing Singular or Nearly Singular Integrals on Closed Surfaces. Commun. Comput. Phys. 2016, 20, 733–753. [Google Scholar] [CrossRef]
- Cortez, R. Regularized Stokeslet Segments. J. Comput. Phys. 2018, 375, 783–796. [Google Scholar] [CrossRef]
- Tyrrell, J.; Smith, D.J.; Dyson, R.J. Regularized Stokeslet Rings—An Efficient Method for Axisymmetric Stokes Flow, with Application to the Growing Pollen Tube. Phys. Rev. Fluids 2019, 4, 063102. [Google Scholar] [CrossRef]
- Swinbank, R.; James Purser, R. Fibonacci Grids: A Novel Approach to Global Modelling. Q. J. R. Meteorol. Soc. 2006, 132, 1769–1793. [Google Scholar] [CrossRef]
- Niederreiter, H.; Ian, H.S. Integration of Nonperiodic Functions of Two Variables by Fibonacci Lattice Rules. J. Comput. Appl. Math. 1994, 51, 57–70. [Google Scholar] [CrossRef]
- Bunch, J.R.; Kaufman, L. Some Stable Methods for Calculating Inertia and Solving Symmetric Linear Systems. Math. Comp. 1977, 31, 163–179. [Google Scholar] [CrossRef]
- Cortez, R.; Hoffmann, F. A Fast Numerical Method for Computing Doubly-Periodic Regularized Stokes Flow in 3D. J. Comput. Phys. 2014, 258, 1–14. [Google Scholar] [CrossRef]
- Cortez, R.; Cummins, B.; Leiderman, K.; Varela, D. Computation of Three-Dimensional Brinkman Flows Using Regularized Methods. J. Comput. Phys. 2010, 229, 7609–7624. [Google Scholar] [CrossRef]
- Leiderman, K.; Olson, S.D. Swimming in a Two-Dimensional Brinkman Fluid: Computational Modeling and Regularized Solutions. Phys. Fluids 2016, 28, 021902. [Google Scholar] [CrossRef]


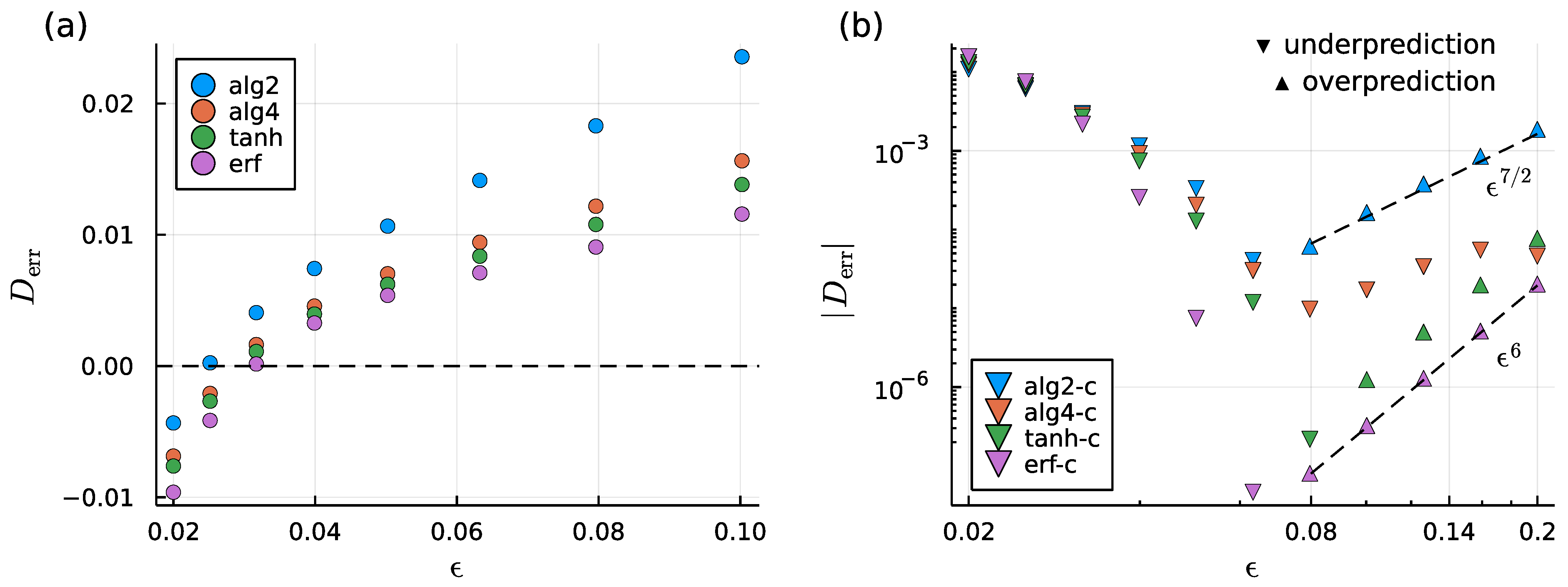
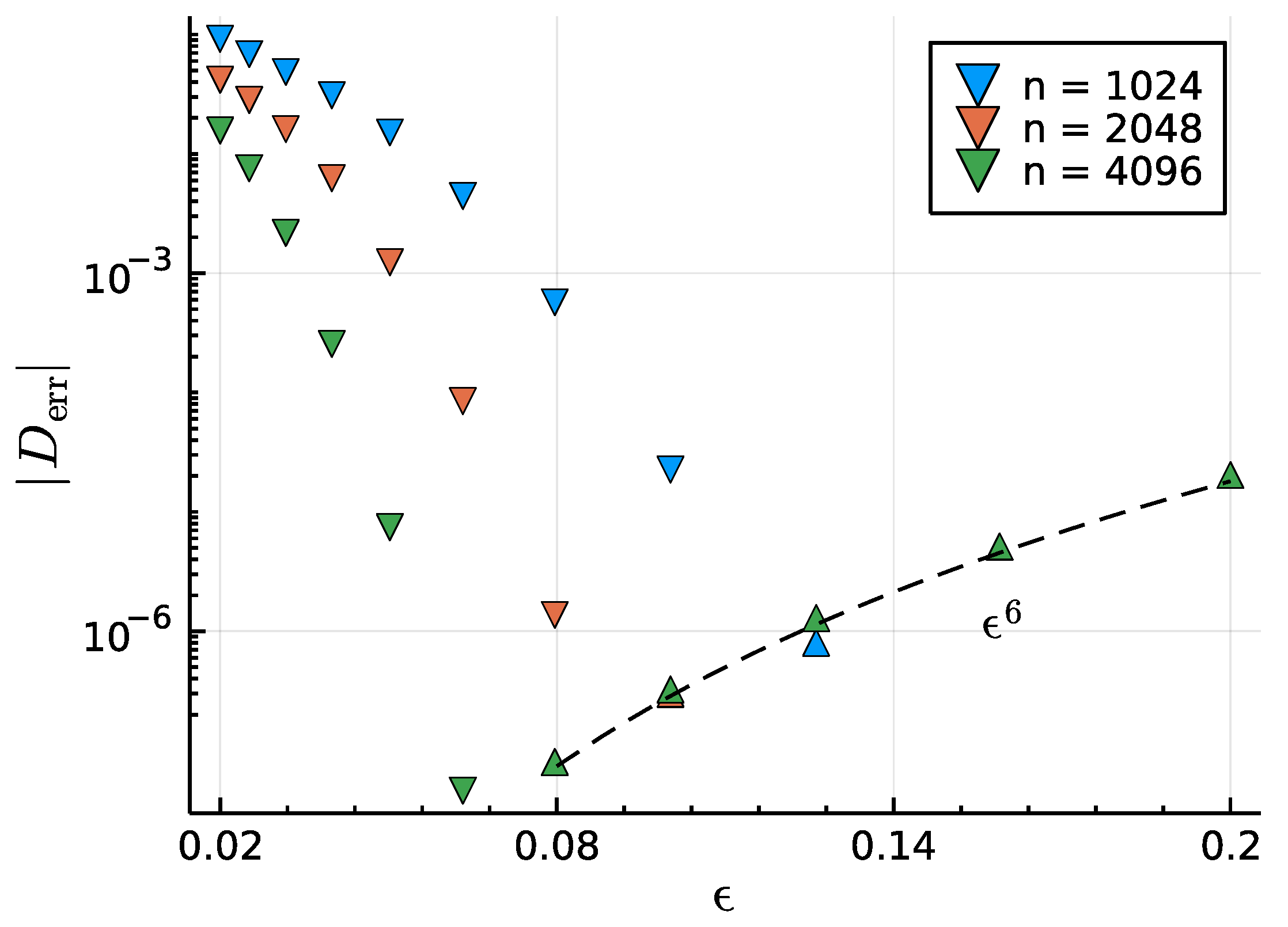


| Label | Correction Term | Correction Term | ||
|---|---|---|---|---|
| alg2 | ||||
| alg4 | ||||
| tanh | ||||
| erf | ||||
| (*) | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chisholm, N.G.; Olson, S.D. A Framework for Generating Radial and Surface-Oriented Regularized Stokeslets. Fluids 2022, 7, 351. https://doi.org/10.3390/fluids7110351
Chisholm NG, Olson SD. A Framework for Generating Radial and Surface-Oriented Regularized Stokeslets. Fluids. 2022; 7(11):351. https://doi.org/10.3390/fluids7110351
Chicago/Turabian StyleChisholm, Nicholas G., and Sarah D. Olson. 2022. "A Framework for Generating Radial and Surface-Oriented Regularized Stokeslets" Fluids 7, no. 11: 351. https://doi.org/10.3390/fluids7110351
APA StyleChisholm, N. G., & Olson, S. D. (2022). A Framework for Generating Radial and Surface-Oriented Regularized Stokeslets. Fluids, 7(11), 351. https://doi.org/10.3390/fluids7110351








