Experiments on Water Gravity Drainage Driven by Steam Injection into Elliptical Steam Chambers
Abstract
:1. Introduction
2. Basis of the Simple Model for Steam Flow in the Chamber
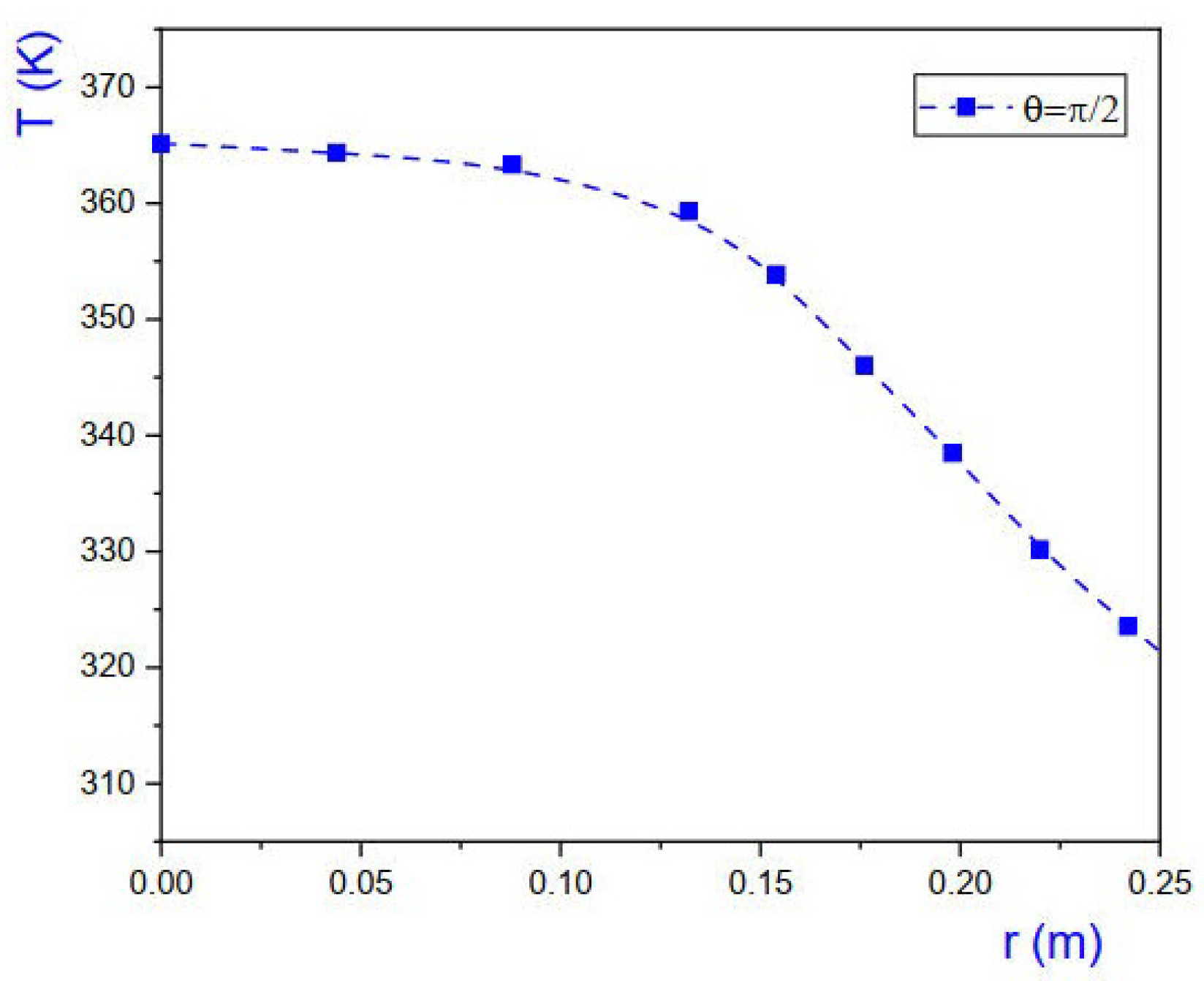
2.1. The Steam Condensation Problem
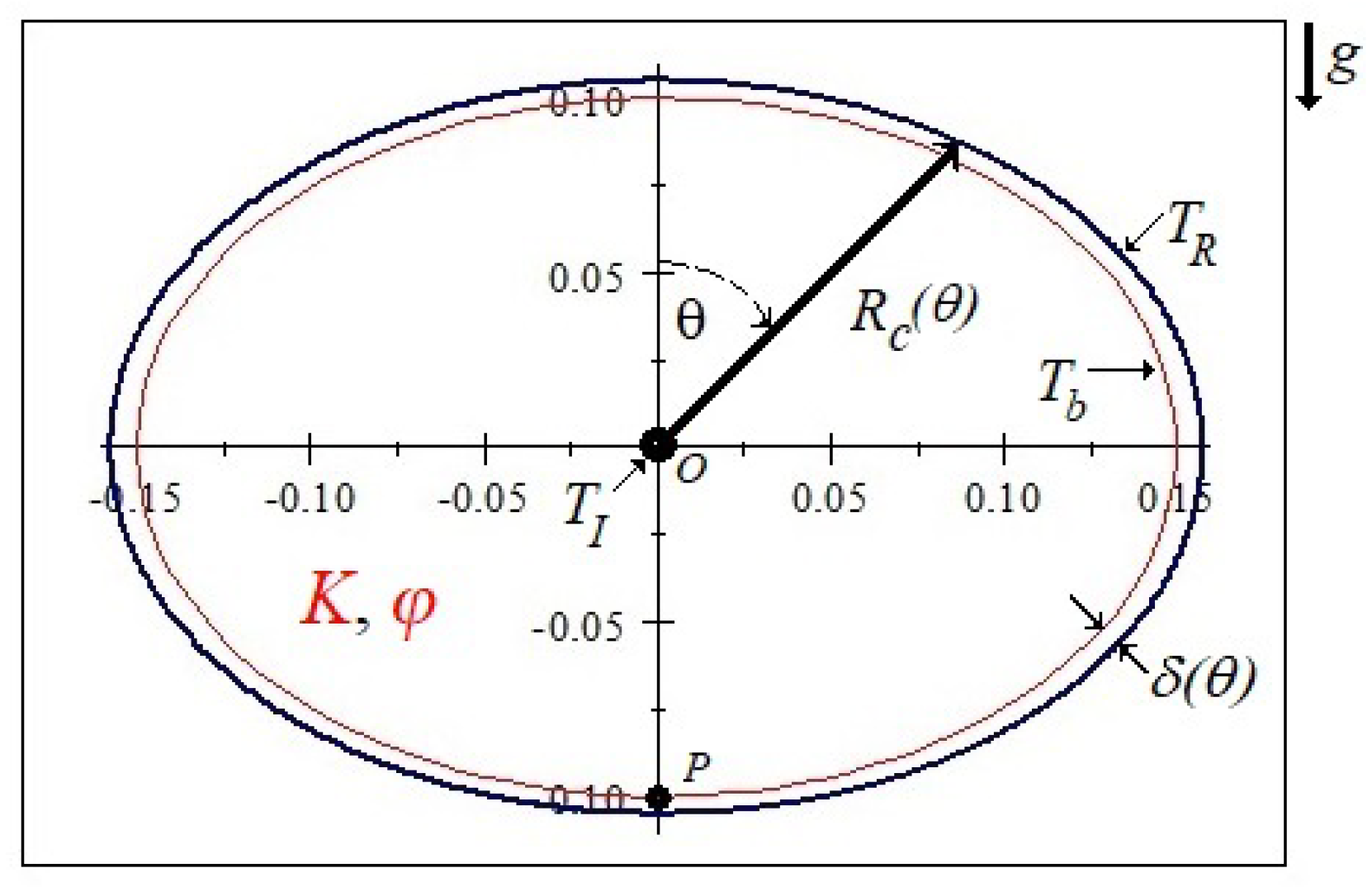
2.2. The Geometry of the Chamber
3. Experiments of Steam Injection into an Oil-Saturated Porous Medium in an Elliptical Chamber
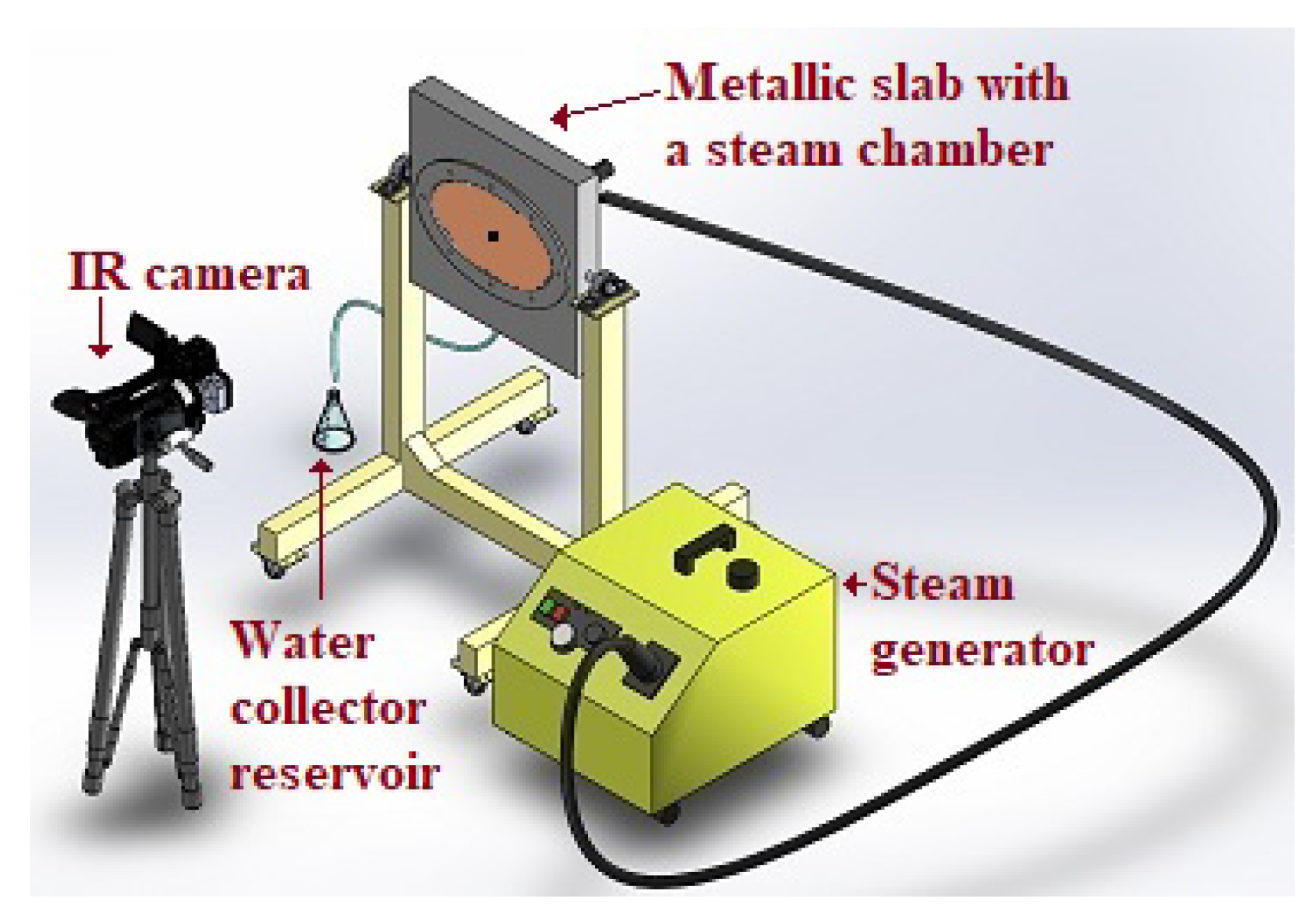
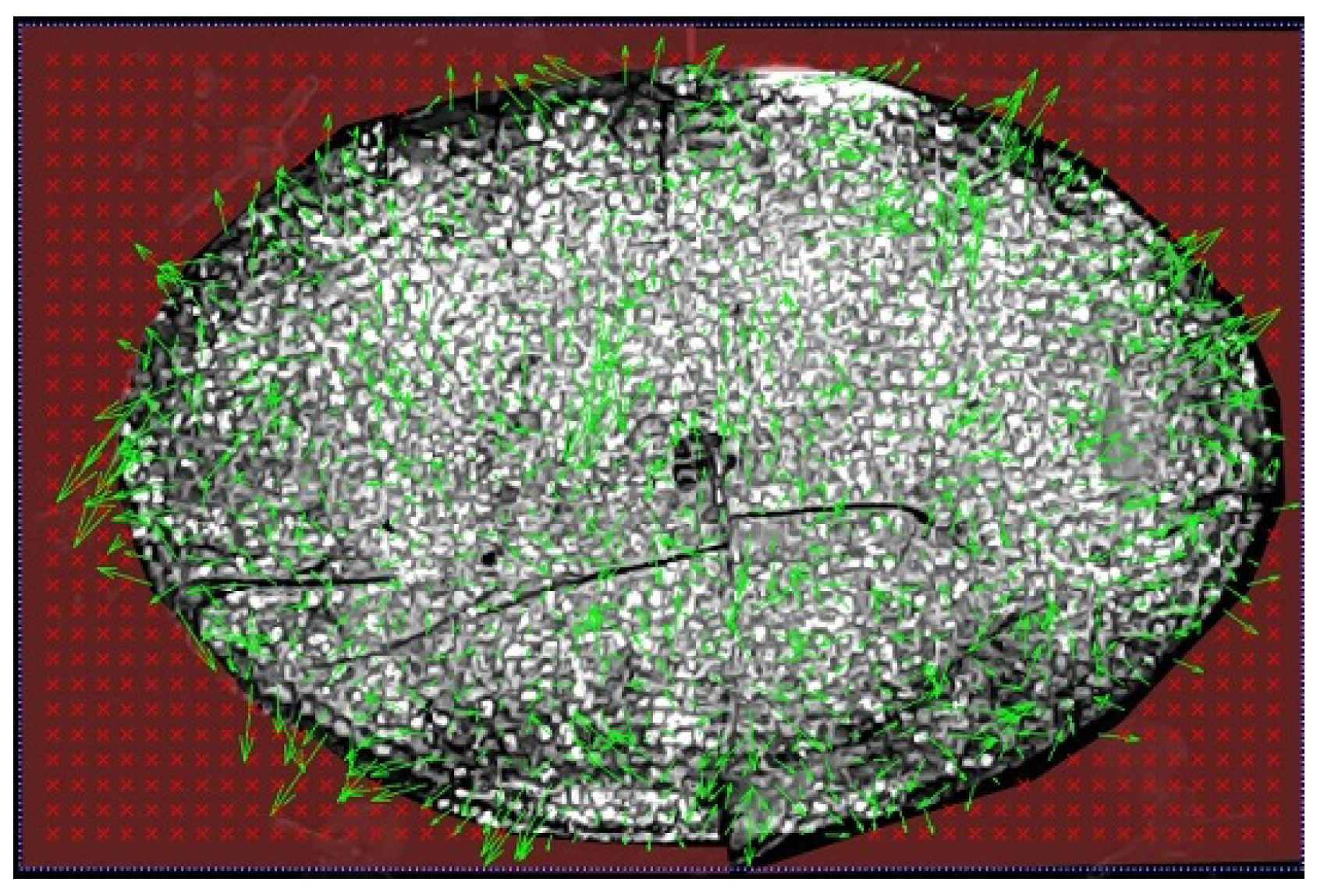
3.1. Experimental Setup
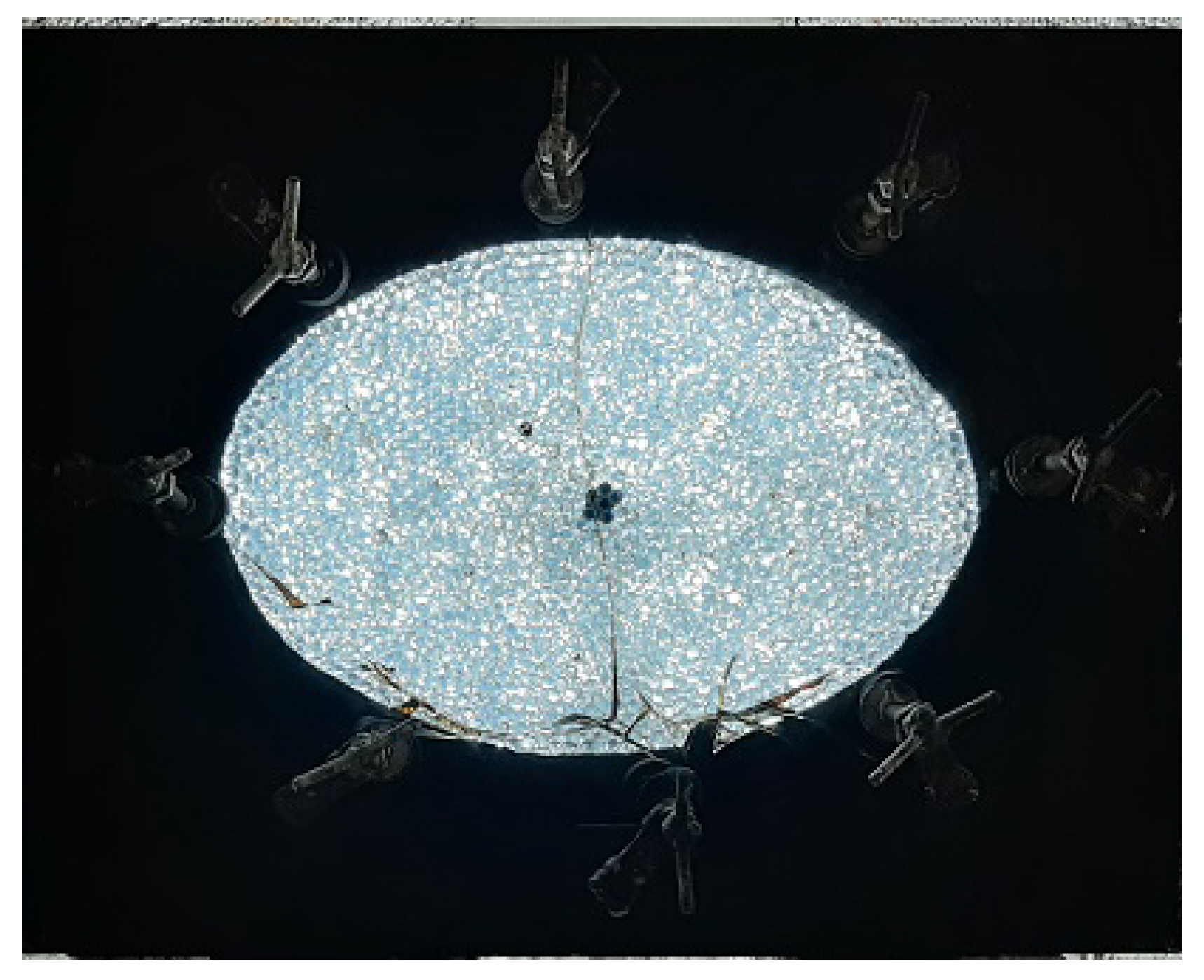
3.2. Extra-Heavy-Oil-Saturated Chamber
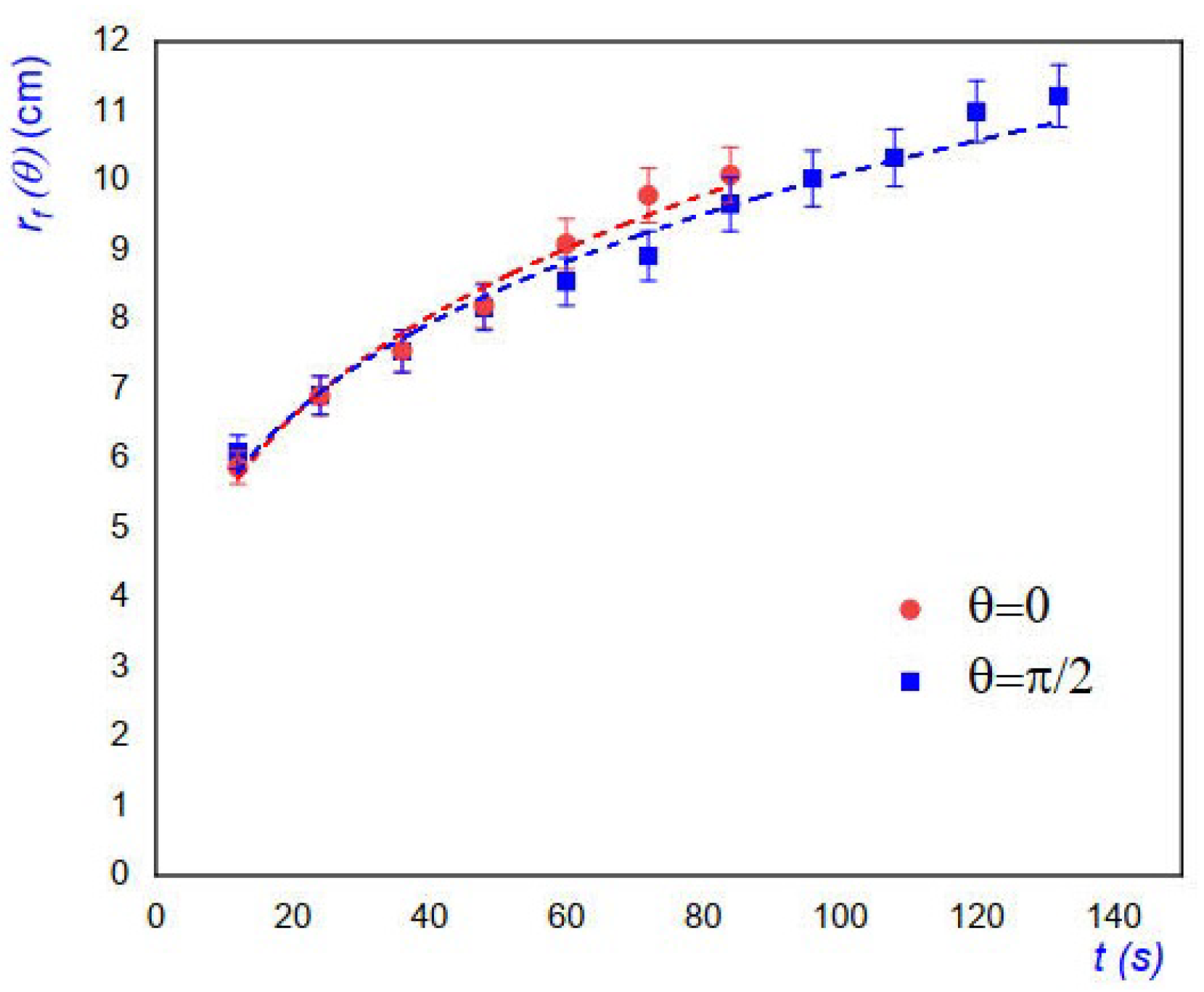
4. Elliptical Steam Chamber
4.1. Transient and Steady Steam Flows
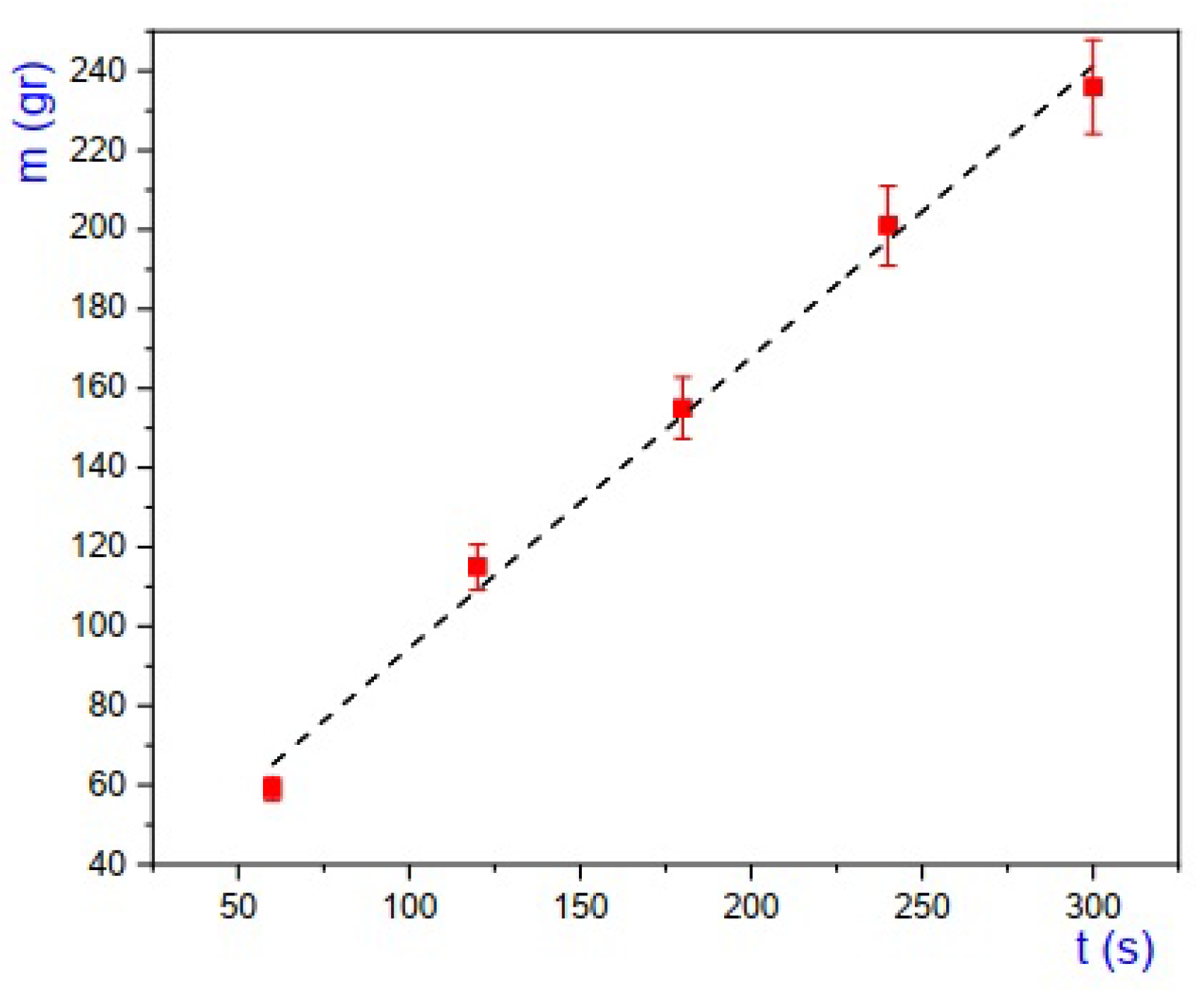
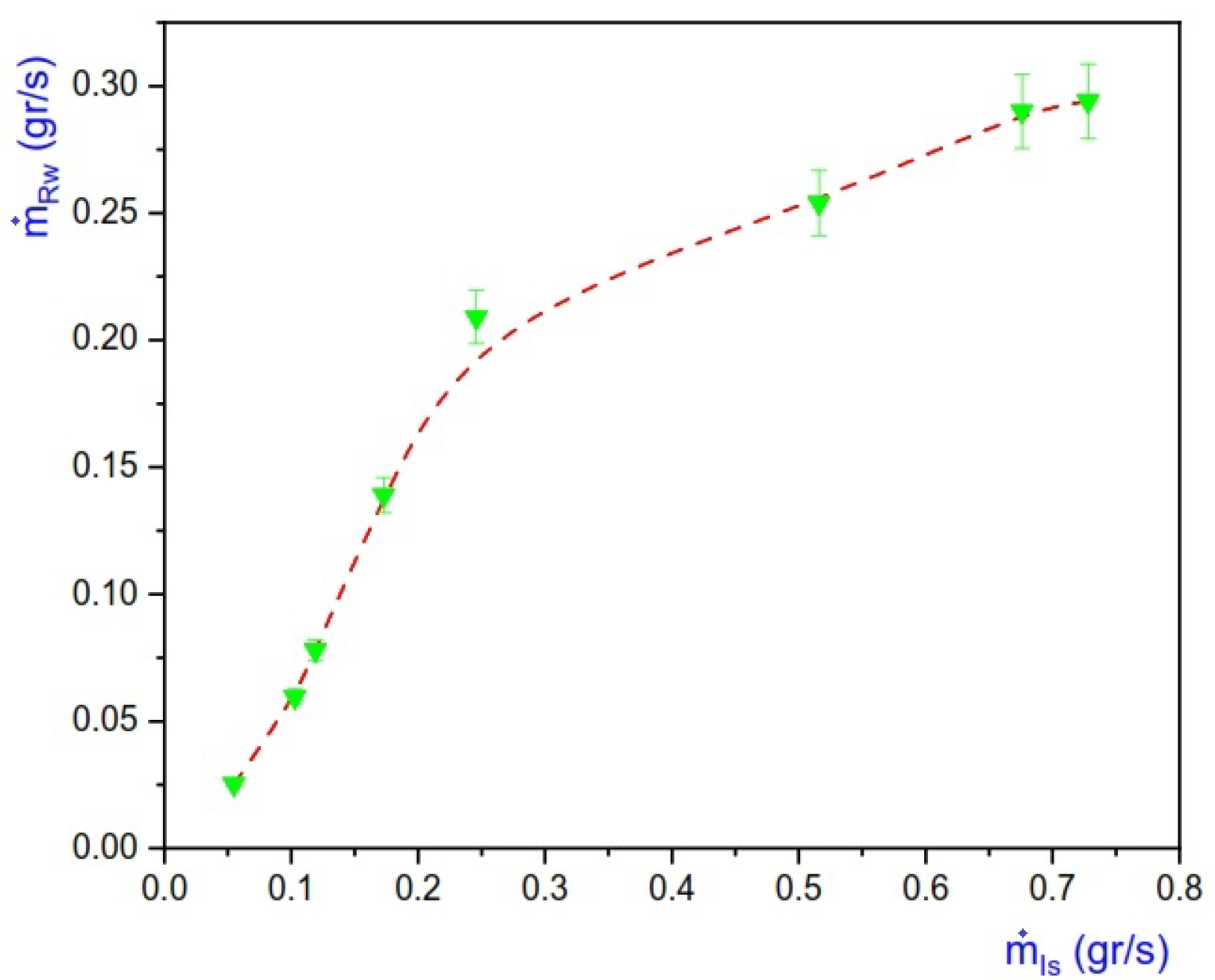
4.2. Accumulated Amounts of Injected and Recovered Fluids
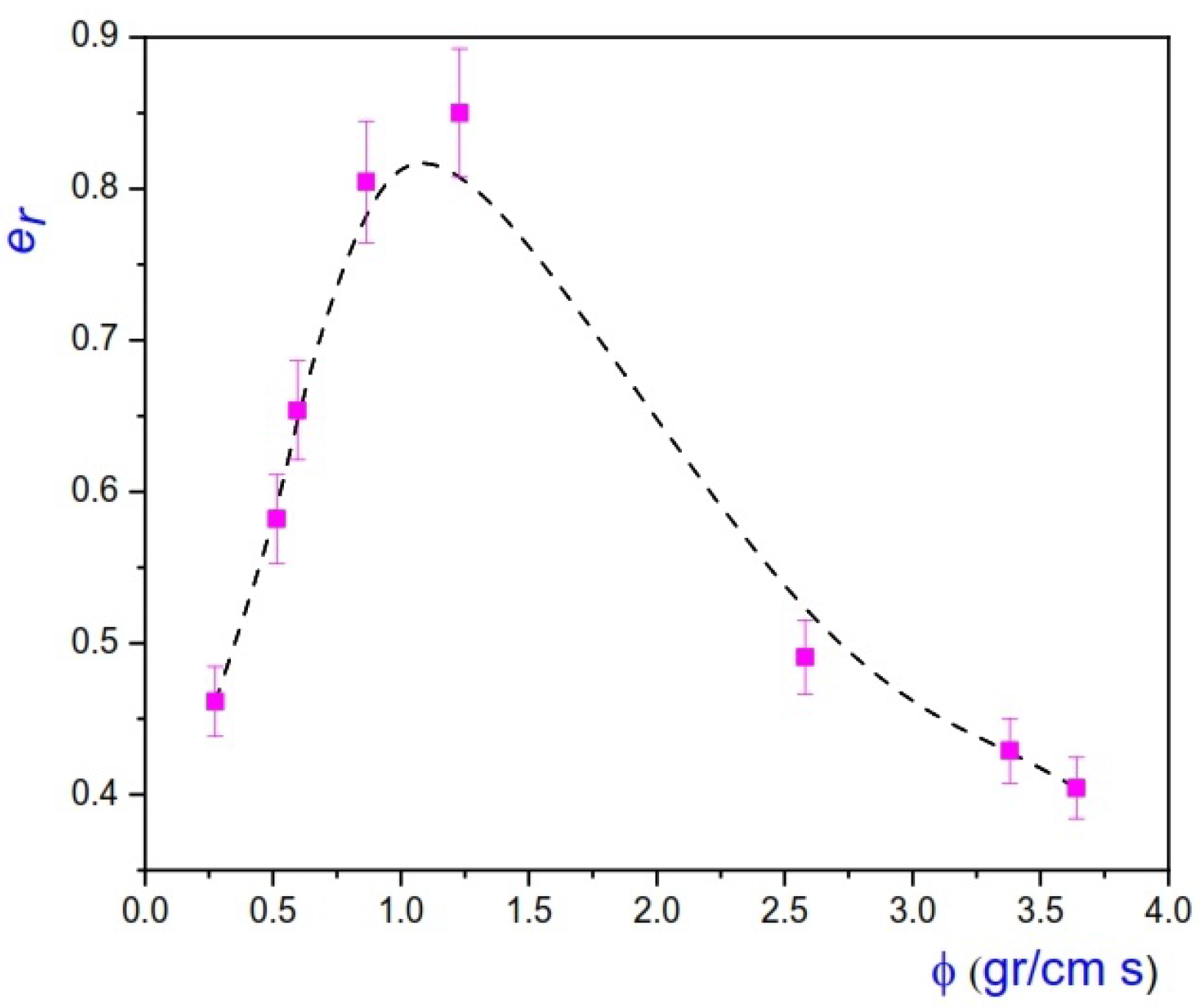
5. Discussion of the Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Z.; Wang, H.; Blackbourn, G.; Ma, F.; He, Z.; Wen, Z.; Wang, Z.; Yang, Z.; Luan, T.; Wu, Z. Heavy Oils and Oil Sands: Global Distribution and Resource Assessment. Acta Geol. Sin. 2019, 93, 199–212. [Google Scholar] [CrossRef] [Green Version]
- Grilc, M.; Likozar, B.; Levec, J. Hydrotreatment of solvolytically liquefied lignocellulosic biomass over NiMo/Al2O3 catalyst: Reaction mechanism, hydrodeoxygenation kinetics and mass transfer model based on FTIR. Biomass Bioenergy 2014, 63, 300–312. [Google Scholar] [CrossRef]
- Grilc, M.; Likozar, B.; Levec, J. Simultaneous Liquefaction and Hydrodeoxygenation of Lignocellulosic Biomass over NiMo/Al2O3, Pd/Al2O3, and Zeolite Y Catalysts in Hydrogen Donor Solvents. ChemCatChem 2016, 8, 180–191. [Google Scholar] [CrossRef]
- Pelkmans, L. IEA Bioenergy Countries’ Report—Update 2021, Implementation of Bioenergy in the IEA Bioenergy Member Countries. Technical Coordinator, IEA Bioenergy TCP. 2021. Available online: https://www.ieabioenergy.com/wp-content/uploads/2021/11/CountriesReport2021_final.pdf (accessed on 1 June 2022).
- Meyer, R.F.; Attanasi, E.D.; Freeman, P.A. Heavy Oil and Natural Bitumen Resources in Geological Basins of the World, Open File-Report 2007-1084; U.S. Geological Survey: Reston, VA, USA, 2007. [Google Scholar]
- Butler, R.M.; Stephens, D.J. The gravity drainage of steam-heated heavy oil to parallel horizontal wells. J. Can. Pet. Technol. 1981, 22, 90–96. [Google Scholar] [CrossRef]
- Butler, R.M. A new approach to the modelling of steam-assisted gravity drainage. J. Can. Pet. Technol. 1985, 24, 42–51. [Google Scholar] [CrossRef]
- Chung, K.H.; Butler, R.M. Geometrical effect of steam injection on the formation of emulsions in the steam-assisted gravity drainage process. J. Can. Pet. Technol. 1988, 27, 36–42. [Google Scholar] [CrossRef]
- Sasaki, K.; Akibayashi, S.; Yazawa, N.; Doan, Q.; Farouq Ali, S.M. Experimental modelling of the SAGD process 3/4 enhancing SAGD performance with periodic stimulation of the horizontal producer. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999. Paper SPE-56544-MS. [Google Scholar]
- Sasaki, K.; Akibayashi, S.; Yasawa, N.; Kaneko, F. Microscopic visualization with high resolution optical-fiber scope at steam chamber interface on initial stage of SAGD process. In Proceedings of the SPE/DOE Improved Oil Recovery Symposium, Tulsa, OK, USA, 16–18 April 2002. Paper SPE-75241. [Google Scholar]
- Mohammadzadeh, O.; Rezaei, N.; Chatzis, I. Pore-level investigation of heavy oil and bitumen recovery using hybrid SAGD process. In Proceedings of the 2010 SPE Improved Oil Recovery Symposium, Tulsa, OK, USA, 24–28 April 2010. Paper SPE 130011. [Google Scholar]
- Mohammadzadeh, O.; Chatzis, I. Pore-level investigation of heavy oil recovery using steam assisted gravity drainage (SAGD). Oil Gas Sci. Technol. Rev. IFP Energies Nouv. 2010, 65, 839–857. [Google Scholar]
- Li, S.; Yu, T.; Li, Z.; Zhang, K. Experimental investigation of nitrogen-assisted SAGD in heavy-oil reservoirs: A two-dimensional visual analysis. Fuel 2019, 257, 116013. [Google Scholar] [CrossRef]
- Velayati, A.; Nouri, A. Emulsification and emulsion flow in thermal recovery operations with a focus on SAGD operations: A critical review. Fuel 2020, 267, 117141. [Google Scholar] [CrossRef]
- Higuera, F.J.; Medina, A. A simple model of the flow in the steam chamber in SAGD oil recovery. In Supercomputing. ISUM 2019. Communications in Computer and Information Science; Torres, M., Klapp, J., Eds.; Springer: Cham, Switzerland, 2019; Volume 1151. [Google Scholar] [CrossRef]
- Edmunds, N.R.; Gittins, S.D. Effective application of steam assisted gravity drainage of bitumen to long horizontal well pairs. J. Can. Pet. Technol. 1993, 32, 49–55. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, T.; Wu, S.; Shi, L.; Du, X.; Wang, J. Models of steam-assisted gravity drainage (SAGD) steam chamber expanding velocity in double horizontal wells and its application. Petrol. Explor. Dev. 2019, 46, 347–354. [Google Scholar] [CrossRef]
- Fattahpour, V.; Mahmoudi, M.; Roostaei, M.; Wang, C.; Kotb, O.; Nouri, A.; Sutton, C.; Fermaniuk, B. Sand control testing for steam injection wells. In Proceedings of the SPE Canada Heavy Oil Technical Conference, Calgary, AB, Canada, 13–14 March 2018. Paper SPE-189766-MS. [Google Scholar]
- Phillips, O.M. Geological Fluid Dynamics: Sub-Surface Flow and Reactions; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: New York, NY, USA, 2013. [Google Scholar]
- Berryman, J.G. Random close packing of hard spheres and disks. Phys. Rev. A 1983, 27, 1053–1061. [Google Scholar] [CrossRef]
- Carman, O.C. Flow of Gases through Porous Media; Butterworths: London, UK, 1956. [Google Scholar]
- Chun, M.-H.; Kim, Y.-S.; Park, J.-W. An investigation of direct condensation of steam jet in subcooled water. Int. Commun. Heat Mass Transf. 1996, 23, 947–958. [Google Scholar] [CrossRef]
- Kim, H.Y.; Bae, Y.Y.; Song, C.H.; Park, J.K.; Choi, S.M. Experimental study on stable steam condensation in a quenching tank. Int. J. Energy Res. 2001, 25, 239–252. [Google Scholar] [CrossRef]
- Peralta, S.; Aragón, F.; Serrano, E.; Carbajal, I.; Medina, A. Visualization of steam injection into homogeneous porous media. J. Vis. 2017, 20, 277–288. [Google Scholar] [CrossRef]
- Properties of Saturated Steam—SI Units. Available online: https://www.engineeringtoolbox.com/saturated-steam-properties-d_101.html (accessed on 1 June 2022).
- Bruining, J.; Marchesin, D.; Schecter, S. Steam condensation waves in water-saturated porous rock. Qual. Theory Dyn. Syst. 2004, 4, 205–231. [Google Scholar] [CrossRef]
- Medina, A.; Higuera, F.J.; Pliego, M.; Gomez, G. Temperature profiles due to continuous hot water injection into homogeneous fluid-saturated porous media through a line source. Rev. Mex. Fís. 2021, 67, 365–368. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics (Volume 6 of Course of Theoretical Physics); Pergamon Press: Oxford, UK, 1987. [Google Scholar]
- Abramovich, G.N. The Theory of Turbulent Jets; The MIT Press: Cambridge, MA, USA, 1963. [Google Scholar]
- Zargar, Z.; Farouq Ali, S.M. Analytical modelling of steam chamber rise stage of Steam-Assisted Gravity Drainage (SAGD) process. Fuel 2018, 233, 732–742. [Google Scholar] [CrossRef]
- Jia, X.; Qu, T.; Chen, H.; Chen, Z. Transient convective heat transfer in a steam-assisted gravity drainage (SAGD) process. Fuel 2019, 247, 315–323. [Google Scholar] [CrossRef]
- Zargar, Z.; Razavi, S.M.; Farouq Ali, S.M. Analytical model of steam-assisted gravity drainage (SAGD) process in relation to constant injection rate. Fuel 2020, 265, 116772. [Google Scholar] [CrossRef]
- Nie, R.-S.; Wang, Y.-M.; Kang, Y.-L.; Jia, Y.-L. A steam rising model of steam assisted gravity drainage production for heavy oil reservoirs. Energy Explor. Exploit. 2020, 38, 801–818. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Chen, X.; Liu, H.; Xia, Y.; Jiang, J.; Cao, M.; Li, A.; Yang, M. Experimental and numerical study of steam-chamber evolution during solvent-enhanced steam flooding in thin heavy-oil reservoirs. J. Pet. Sci. Eng. 2019, 172, 776–786. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, H.; Zhou, Y. Development of a deep learning-based model for the entire production process of steam-assisted gravity drainage (SAGD). Fuel 2021, 287, 119565. [Google Scholar] [CrossRef]
- Yang, Z.; Sun, X.; Luo, C.; Xu, B.; Yang, B.; Li, B. Vertical-well-assisted SAGD dilation process in heterogeneous super-heavy oil reservoirs: Numerical simulations. Undergr. Space 2021, 6, 603–618. [Google Scholar] [CrossRef]
- Fernandez, B.; Ehlig-Economides, C.A.; Economides, M.J. Multilevel Injector/Producer Wells in Thick Heavy Crude Reservoirs. In Proceedings of the 1999 SPE Latin American and Caribbean Petroleum Engineering Conference, Caracas, Venezuela, 21–23 April 1999. Paper SPE 53950. [Google Scholar]
- Tao, L.; Yuan, X.; Cheng, H.; Li, B.; Huang, S.; Zhang, N. Experimental study on well placement optimization for steam-assisted gravity drainage to enhance recovery of thin layer oil sand reservoirs. Geofluids 2021, 2021, 9954127. [Google Scholar] [CrossRef]







| Material | Density (kg/m) | Thermal Conductivity k (W/m K) | Specific Heat c (J/kg K) | Thermal Diffusivity (m/s) |
|---|---|---|---|---|
| Glass spheres (soda lime) | 2500 | 1.4 | 750 | 0.74 |
| Cast iron | 7871 | 80.2 | 447 | 22.80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Gómez, J.E.; Medina, A.; Higuera, F.J.; Vargas, C.A. Experiments on Water Gravity Drainage Driven by Steam Injection into Elliptical Steam Chambers. Fluids 2022, 7, 206. https://doi.org/10.3390/fluids7060206
Martínez-Gómez JE, Medina A, Higuera FJ, Vargas CA. Experiments on Water Gravity Drainage Driven by Steam Injection into Elliptical Steam Chambers. Fluids. 2022; 7(6):206. https://doi.org/10.3390/fluids7060206
Chicago/Turabian StyleMartínez-Gómez, Jonathan Enrique, Abraham Medina, Francisco J. Higuera, and Carlos A. Vargas. 2022. "Experiments on Water Gravity Drainage Driven by Steam Injection into Elliptical Steam Chambers" Fluids 7, no. 6: 206. https://doi.org/10.3390/fluids7060206
APA StyleMartínez-Gómez, J. E., Medina, A., Higuera, F. J., & Vargas, C. A. (2022). Experiments on Water Gravity Drainage Driven by Steam Injection into Elliptical Steam Chambers. Fluids, 7(6), 206. https://doi.org/10.3390/fluids7060206






