Turbulent Non-Stationary Reactive Flow in a Cement Kiln
Abstract
:1. Introduction
2. Material
2.1. Geometry Definition
2.2. Mesh Generation
2.3. Imposed Boundary Conditions
3. Method
3.1. Flow of Mixture of Gasses in the Flue
3.1.1. Conservation of Mass of the Mixture
3.1.2. Conservation of Momentum of the Mixture
3.1.3. Conservation of Energy of the Mixture
3.1.4. Conservation of the Chemical Species
3.1.5. Computation of the Radiative Heat Flux
3.2. Zeldovich Thermal nitric oxide Post-Processing
4. Implementation in OpenFOAM
5. Numerical Results
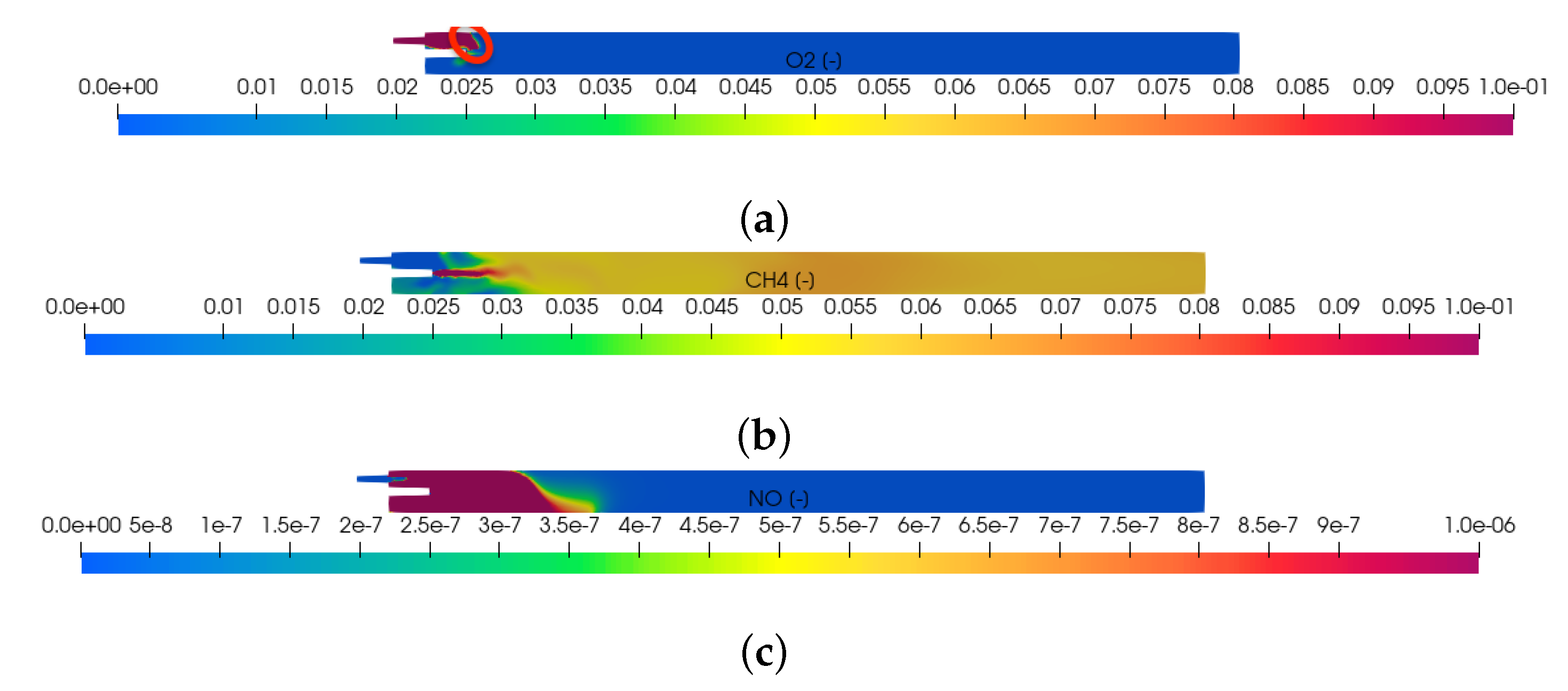
5.1. Computed Species Mass Fraction
5.2. Computed Wall Temperature
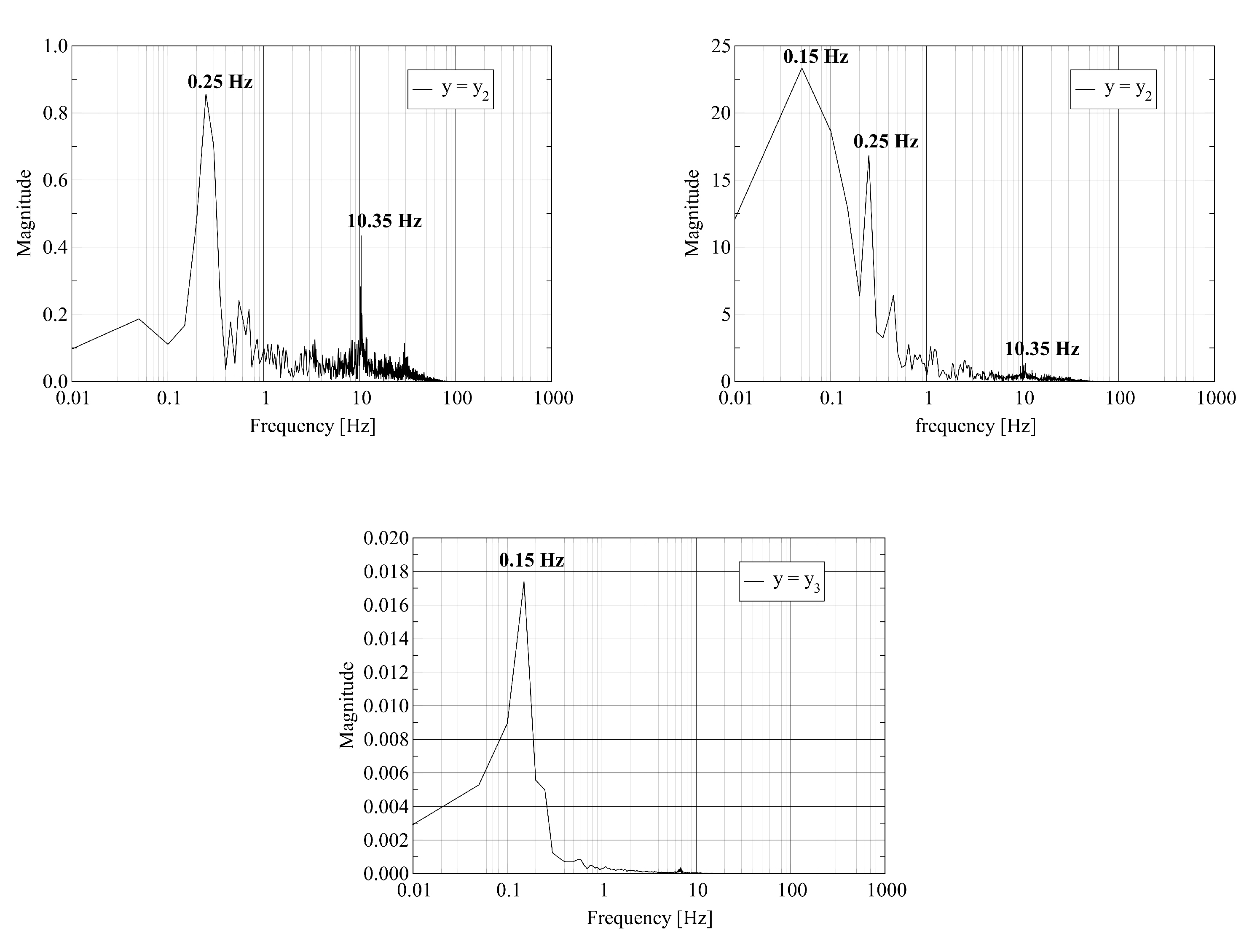
5.3. Frequency of Time Traces
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Details on the Mesh
References
- Boateng, A. Rotary Kilns: Transport Phenomena and Transport Processes; Elsevier Science, Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Giannopoulos, D.; Kolaitis, D.; Togkalidou, A.; Skevis, G.; Founti, M. Quantification of Emissions From the Co-Incineration of Cutting Oil Emulsions in Cement Plants: Part I: NOx, CO and VOC. Fuel 2007, 86, 1144–1152. [Google Scholar] [CrossRef]
- Larsson, I.S.; Lundström, T.S.; Marjavaara, B.D. Calculation of kiln aerodynamics with two RANS turbulence models and by DDES. Flow Turbul. Combust. 2015, 94, 859–878. [Google Scholar] [CrossRef]
- Elattar, H.F.; Specht, E.; Fouda, A.; Rubaiee, S.; Al-Zahrani, A.; Nada, S.A. Swirled Jet Flame Simulation and Flow Visualization Inside Rotary Kiln?CFD with PDF Approach. Processes 2020, 8, 159. [Google Scholar] [CrossRef] [Green Version]
- Gunnarsson, A.; Bckstrm, D.; Johansson, R.; Fredriksson, C.; Andersson, K. Radiative heat transfer conditions in a rotary kiln test furnace using coal, biomass, and cofiring burners. Energy Fuels 2017, 31, 7482–7492. [Google Scholar] [CrossRef]
- Edland, R.; Smith, N.; Allgurén, T.; Fredriksson, C.; Normann, F.; Haycock, D.; Johnson, C.; Frandsen, J.; Fletcher, T.H.; Andersson, K. Evaluation of NOx-Reduction Measures for Iron-Ore Rotary Kilns. Energy Fuels 2020, 34, 4934–4948. [Google Scholar] [CrossRef]
- Lahaye, D.; Abbassi, M.E.; Vuik, K.; Talice, M.; Juretić, F. Mitigating Thermal NOx by Changing the Secondary Air Injection Channel: A Case Study in the Cement Industry. Fluids 2020, 5, 220. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A Tensorial Approach to Computational Continuum Mechanics Using Object-oriented Techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Zhang, Y.; Vanierschot, M. Modeling capabilities of unsteady RANS for the simulation of turbulent swirling flow in an annular bluff-body combustor geometry. Appl. Math. Model. 2021, 89, 1140–1154. [Google Scholar] [CrossRef]
- Magnussen, B.F. The eddy dissipation concept: A bridge between science and technology. In Proceedings of the ECCOMAS Thematic Conference on Computational Combustion, Libson, Portugal, 24 June 2005; Volume 21, p. 24. [Google Scholar]
- Ertesvåg, I.S. Analysis of some recently proposed modifications to the Eddy Dissipation Concept (EDC). Combust. Sci. Technol. 2020, 192, 1108–1136. [Google Scholar] [CrossRef]
- Juretic, F. cfMesh Version 1.1 Users Guide; Creative Fields, Ltd.: Zagreb, Croatia, 2015. [Google Scholar]
- Ferziger, J.; Perić, M. Computational Methods for Fluid Dynamics; Springer: Berlin, Germany, 1999. [Google Scholar]
- Versteeg, H.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method, 2nd ed.; Pearson Education Limited: London, UK, 2007. [Google Scholar]
- Law, C. Combustion Physics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion, 2nd ed.; R.T. Edwards, Inc.: Bundaberg, QLD, Australia, 2005. [Google Scholar]
- Baukal, C. Industrial Combustion Pollution and Control; Environmental Science & Pollution; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Modest, M.F.; Haworth, D.C. Radiative Heat Transfer in Turbulent Combustion Systems: Theory and Applications; Springer: Berlin, Germany, 2016. [Google Scholar]
- Kadar, A.H. Modelling Turbulent Non-Premixed Combustion in Industrial Furnaces. Master’s Thesis, TU Delft, Delft, The Netherlands, 2015. [Google Scholar]
- Poinsot, T.; Lelef, S. Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]
- Pisaroni, M.; Sadi, R.; Lahaye, D. Counteracting ring formation in rotary kilns. J. Math. Ind. 2012, 2, 1–19. [Google Scholar] [CrossRef] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Talice, M.; Juretić, F.; Lahaye, D. Turbulent Non-Stationary Reactive Flow in a Cement Kiln. Fluids 2022, 7, 205. https://doi.org/10.3390/fluids7060205
Talice M, Juretić F, Lahaye D. Turbulent Non-Stationary Reactive Flow in a Cement Kiln. Fluids. 2022; 7(6):205. https://doi.org/10.3390/fluids7060205
Chicago/Turabian StyleTalice, Marco, Franjo Juretić, and Domenico Lahaye. 2022. "Turbulent Non-Stationary Reactive Flow in a Cement Kiln" Fluids 7, no. 6: 205. https://doi.org/10.3390/fluids7060205
APA StyleTalice, M., Juretić, F., & Lahaye, D. (2022). Turbulent Non-Stationary Reactive Flow in a Cement Kiln. Fluids, 7(6), 205. https://doi.org/10.3390/fluids7060205




