High-Order Accurate Numerical Simulation of Supersonic Flow Using RANS and LES Guided by Turbulence Anisotropy
Abstract
1. Introduction
2. Methodology
2.1. Nozzle Geometry and Boundary Conditions
2.2. PIV Experimental Data from Literature
2.3. Governing Equations
2.4. Baseline RANS
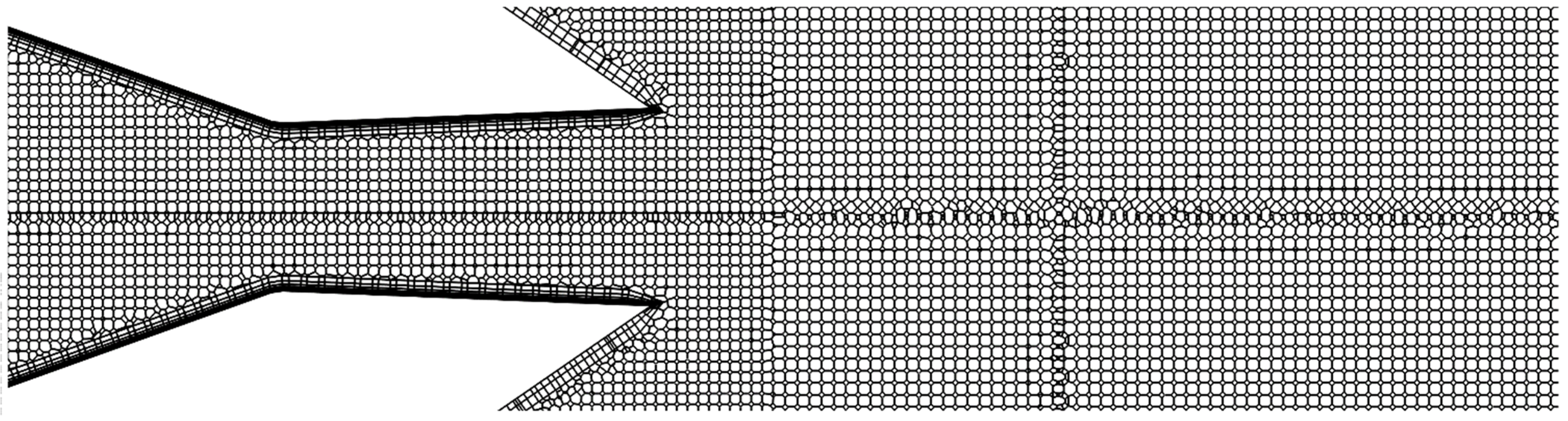
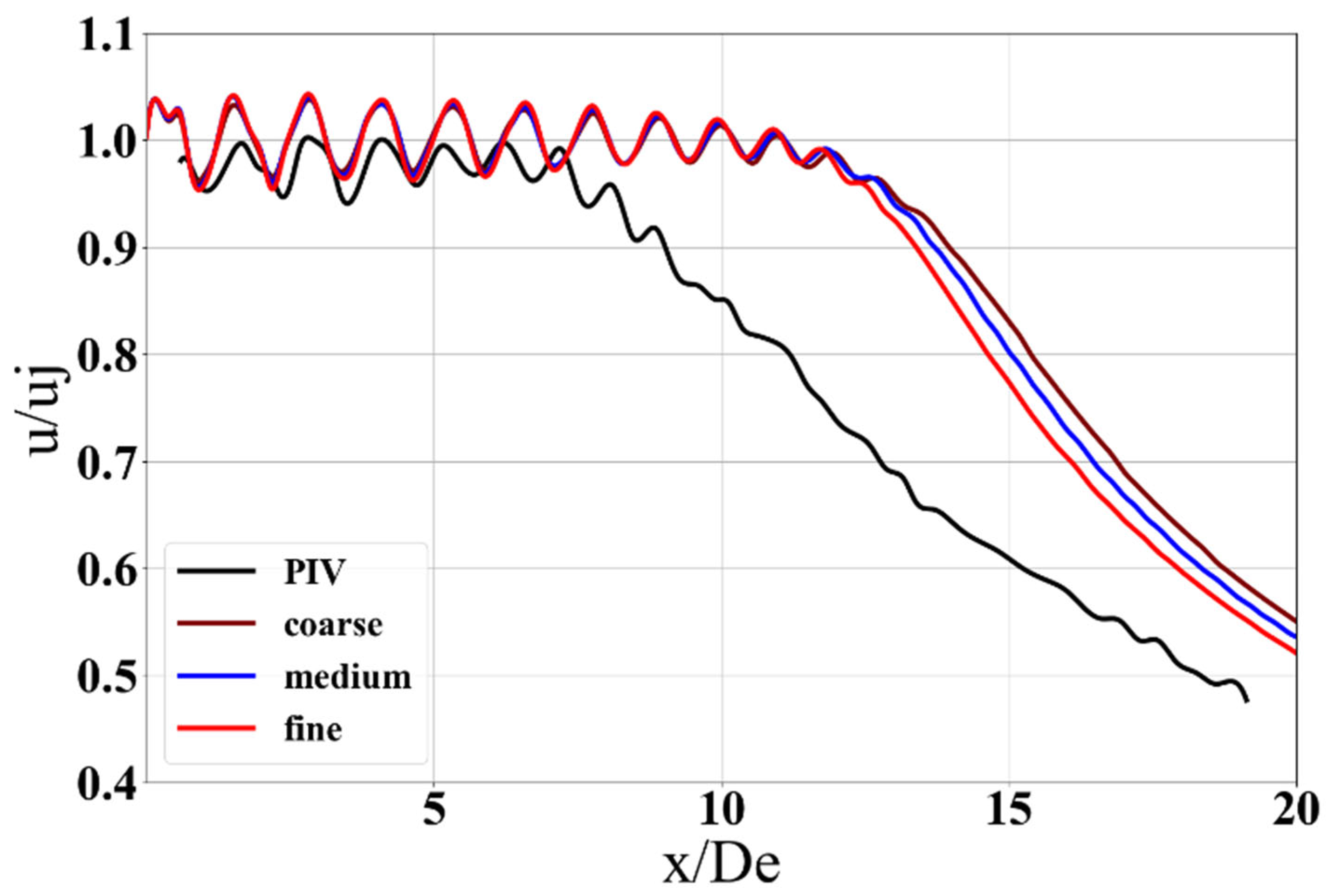
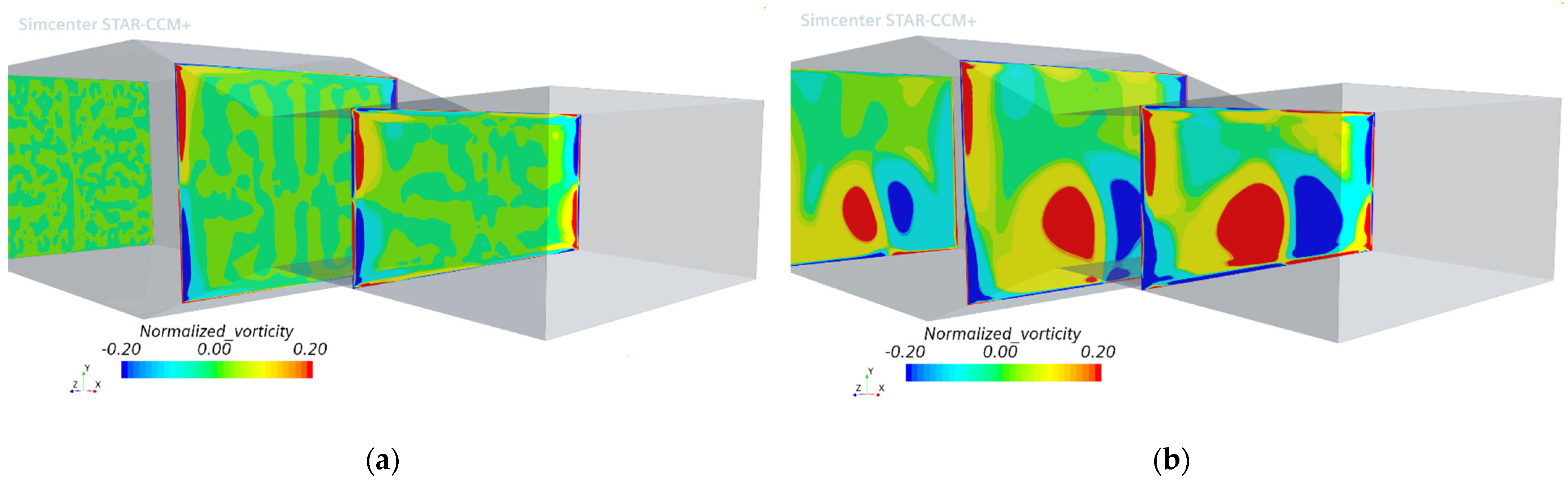
2.5. Mesh Sensitivity
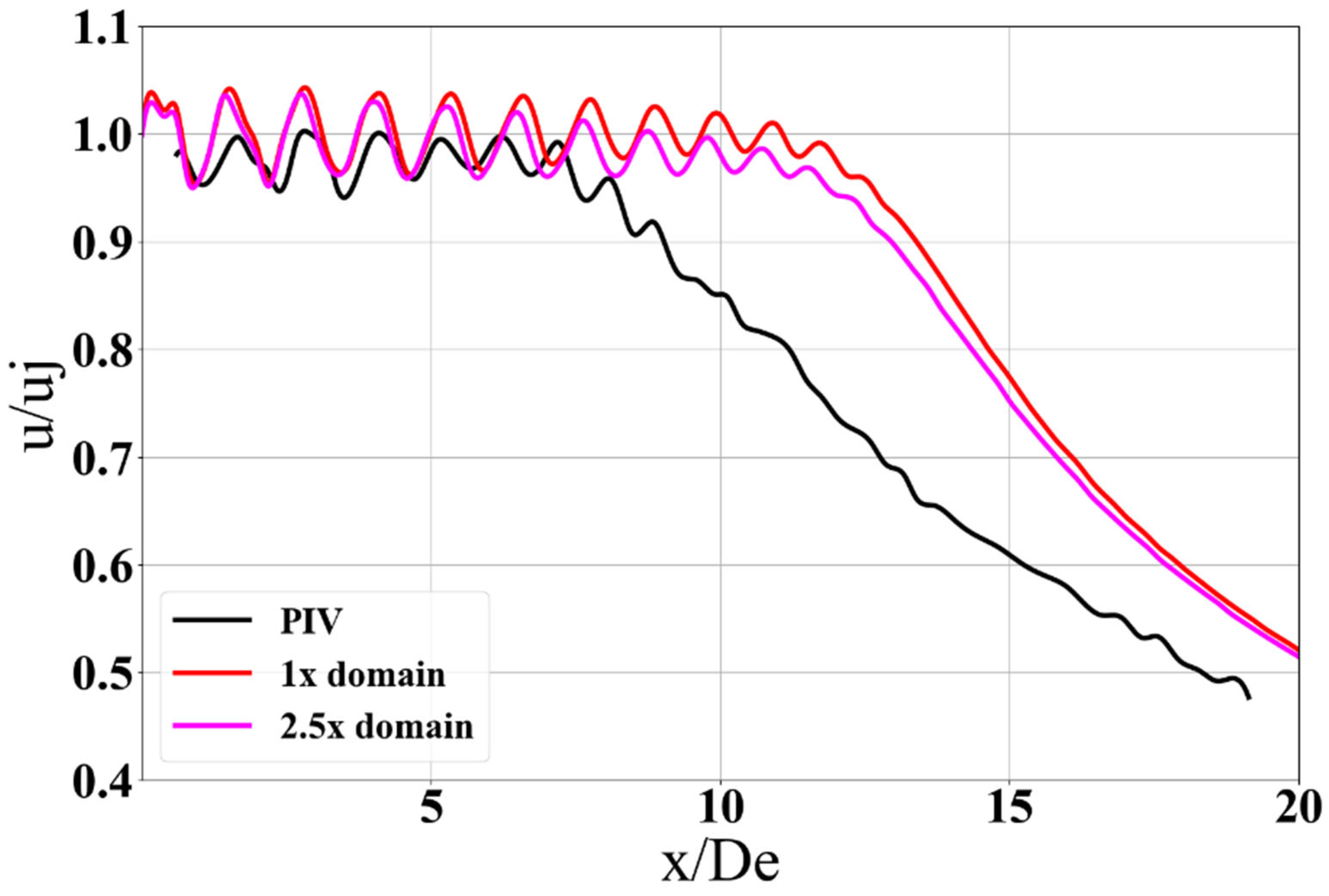
2.6. Effect of CFD Domain Size in RANS Simulations
3. Results—Improved Accuracy RANS
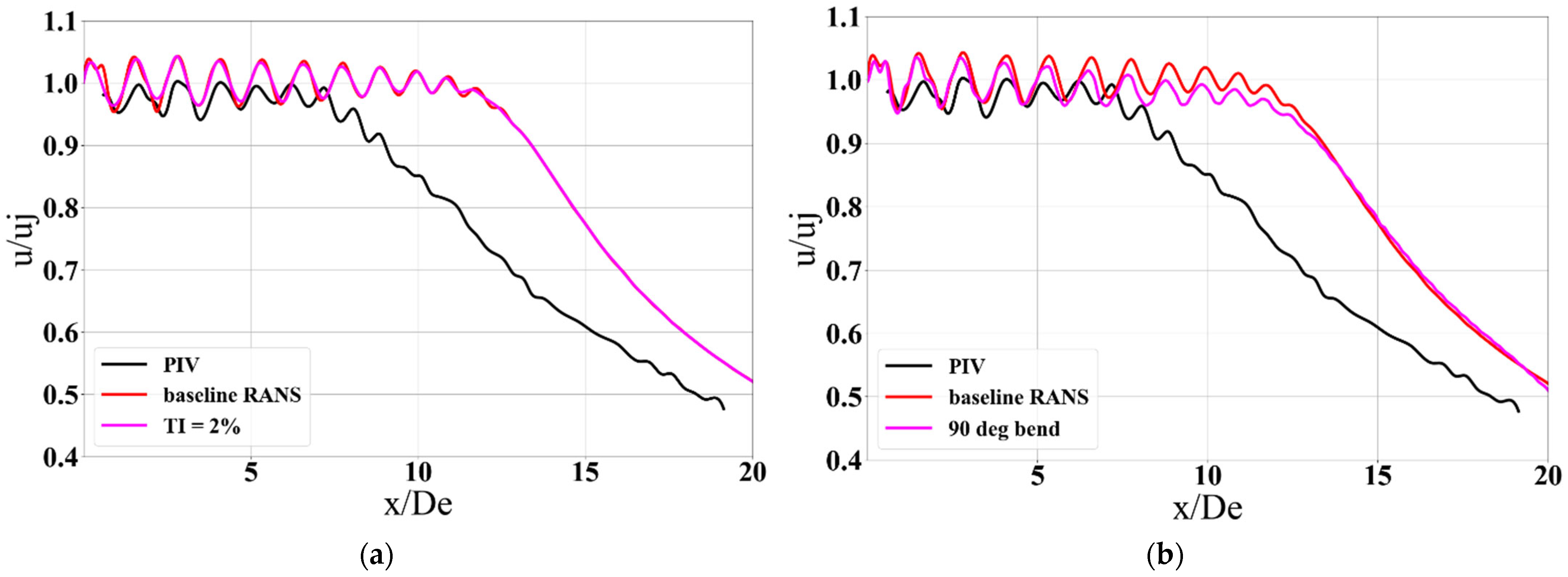
3.1. Inlet Modeling
3.1.1. Turbulence Intensity
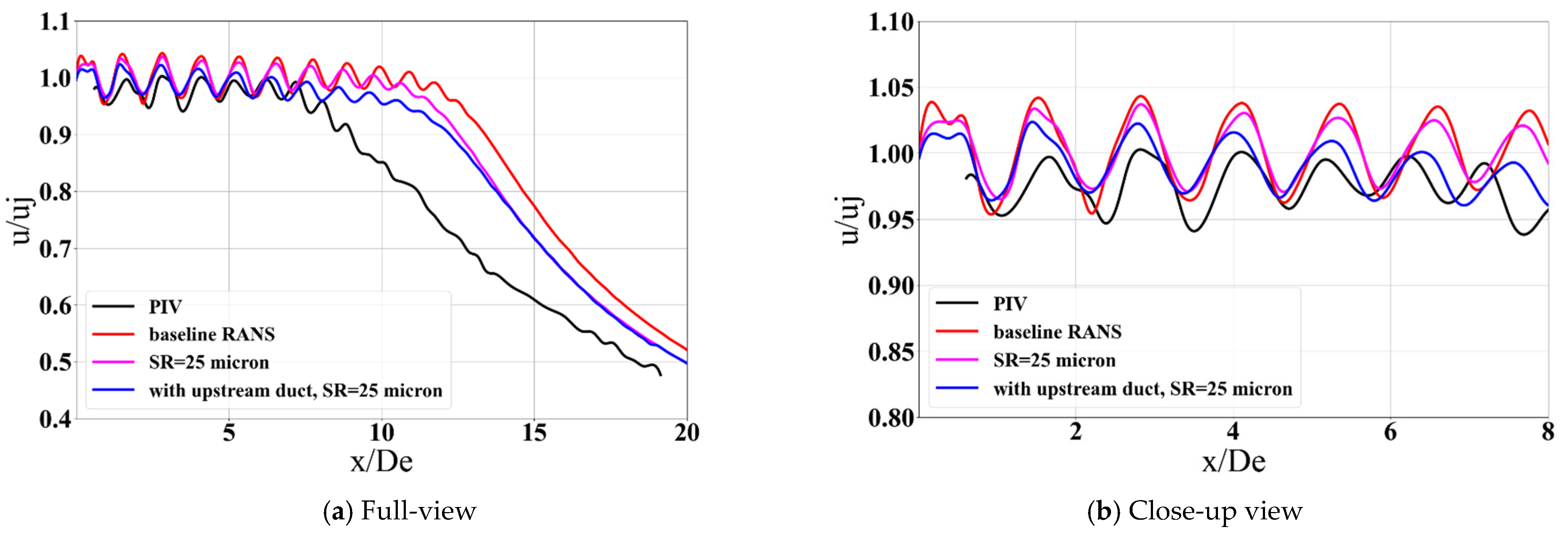
3.1.2. Effect of Upstream Air Supply Duct
3.2. Wall Modeling
3.2.1. Prism Layer Sensitivity
3.2.2. Adiabatic vs. Isothermal Walls
3.3. Wall Surface Roughness
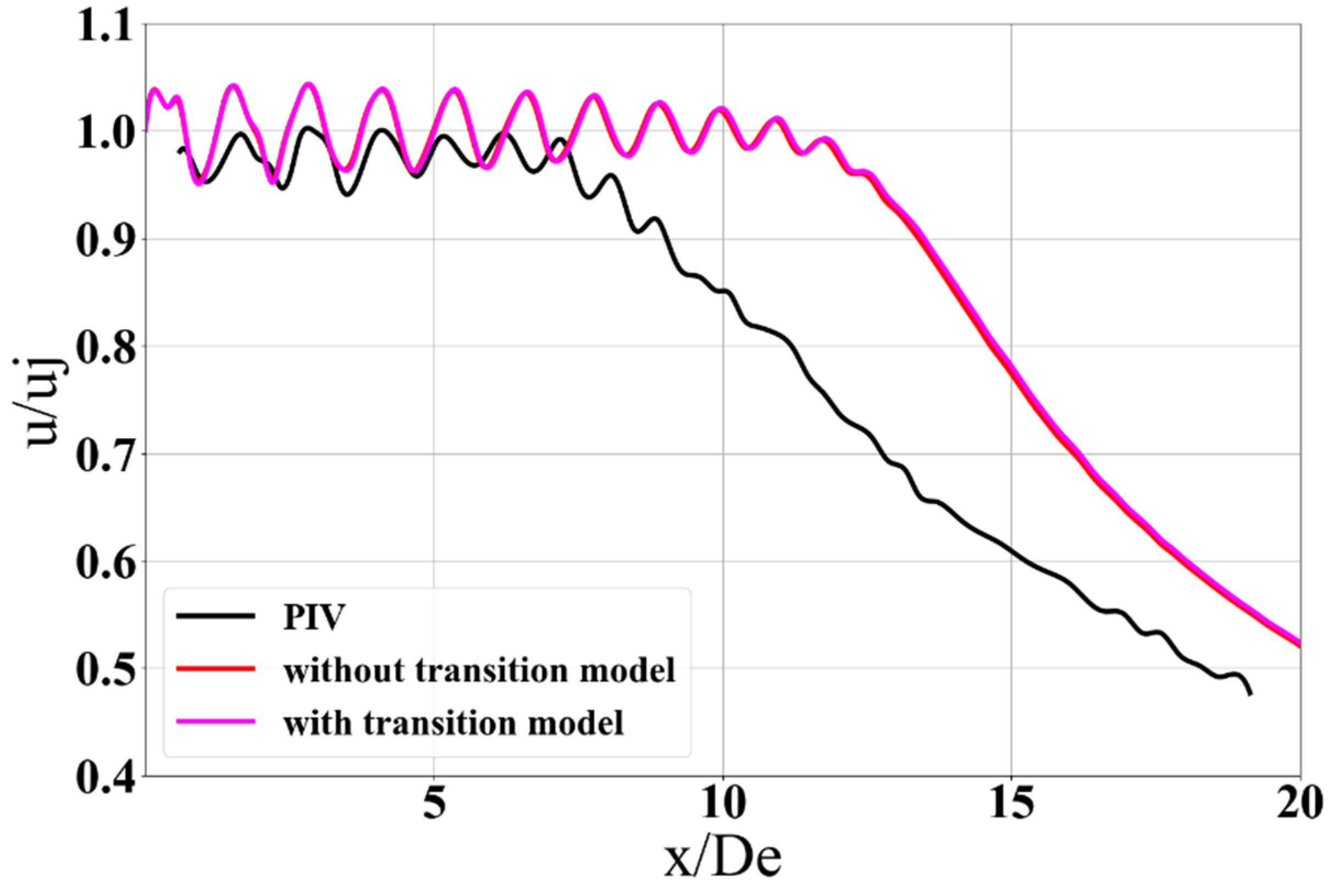
3.4. Laminar to Turbulent Transition
4. Results—LEVM, NLEVM, RSM and LES
4.1. Turbulence Capture in RANS
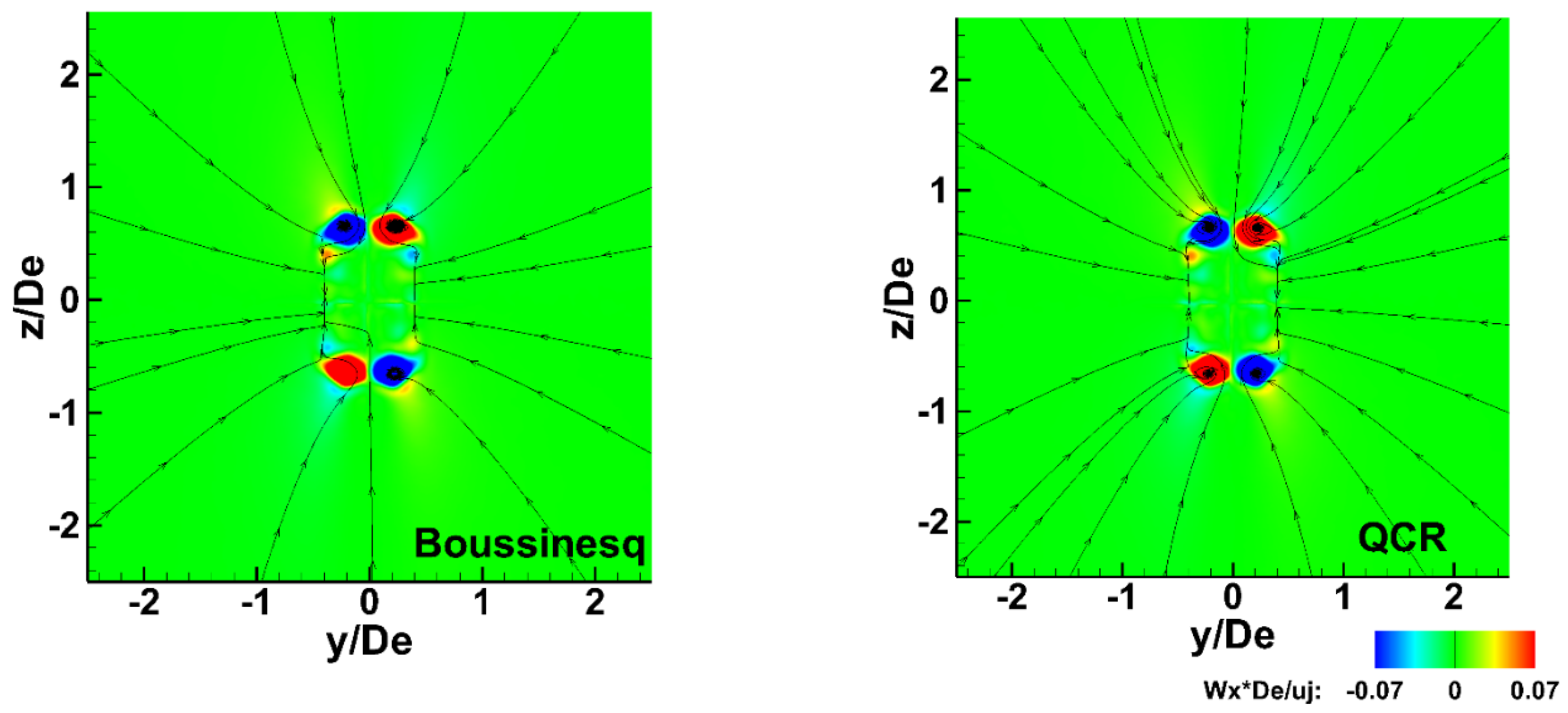
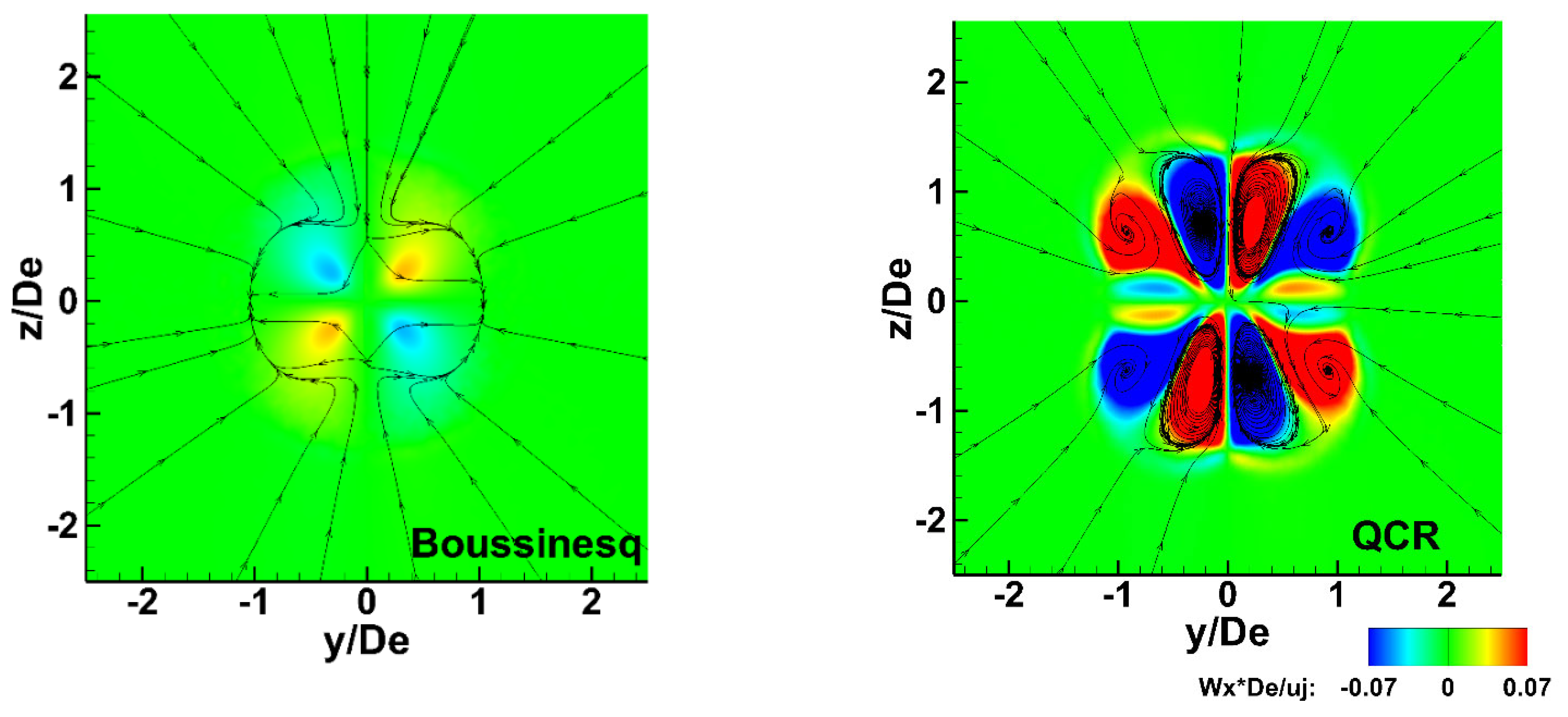
4.1.1. Streamwise Vorticity in Linear vs. Non-Linear Eddy Viscosity RANS
4.1.2. Turbulent Viscosity in RANS
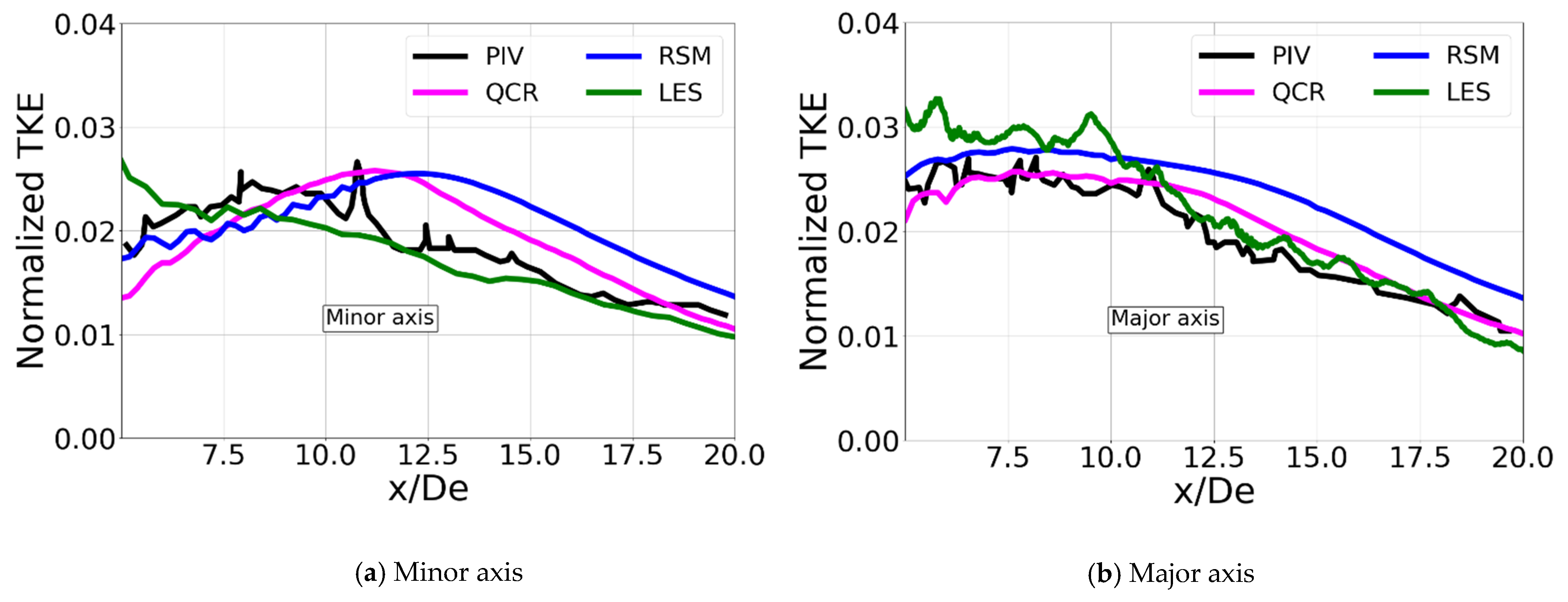
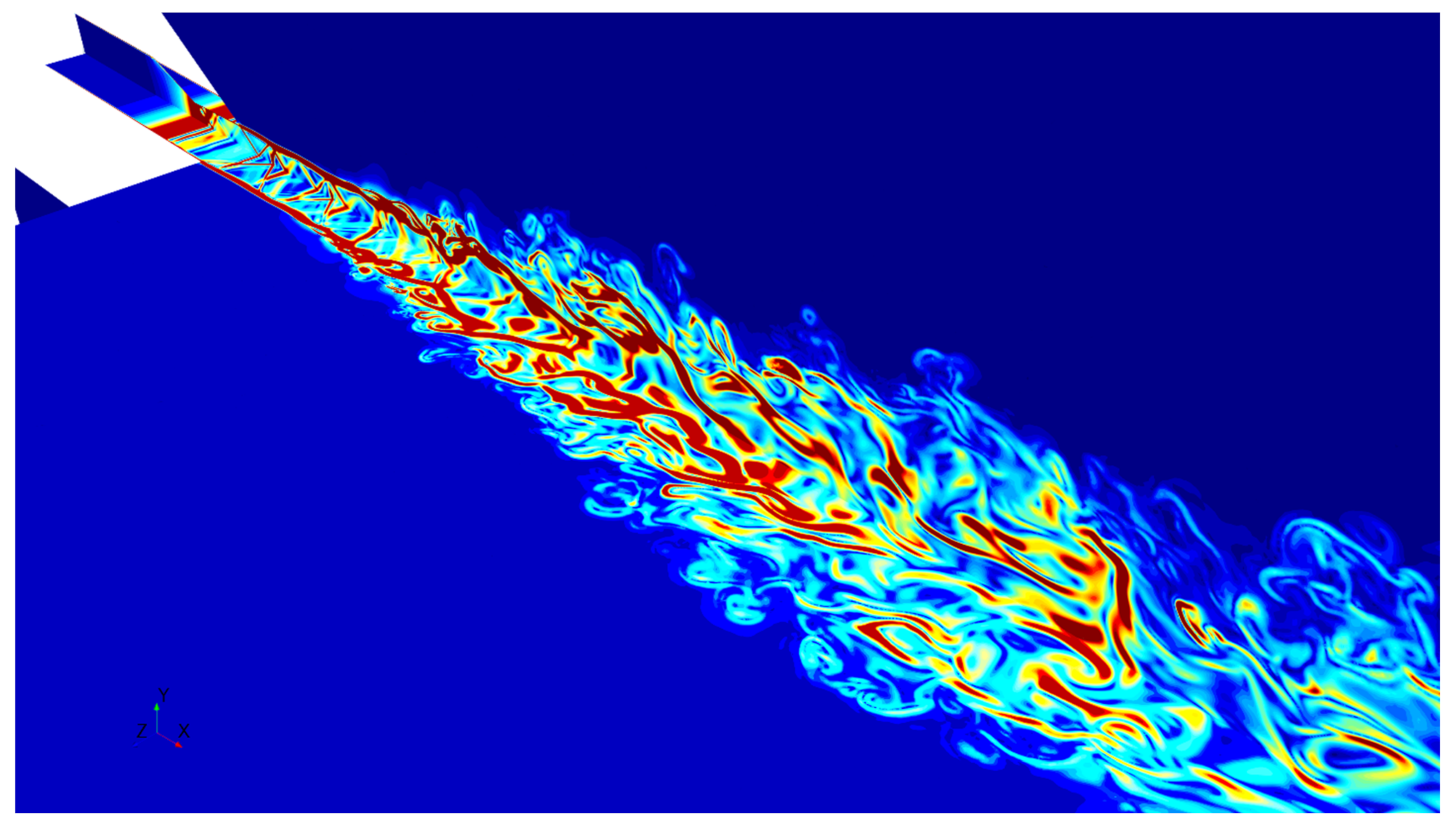
4.2. Comparisons with LES
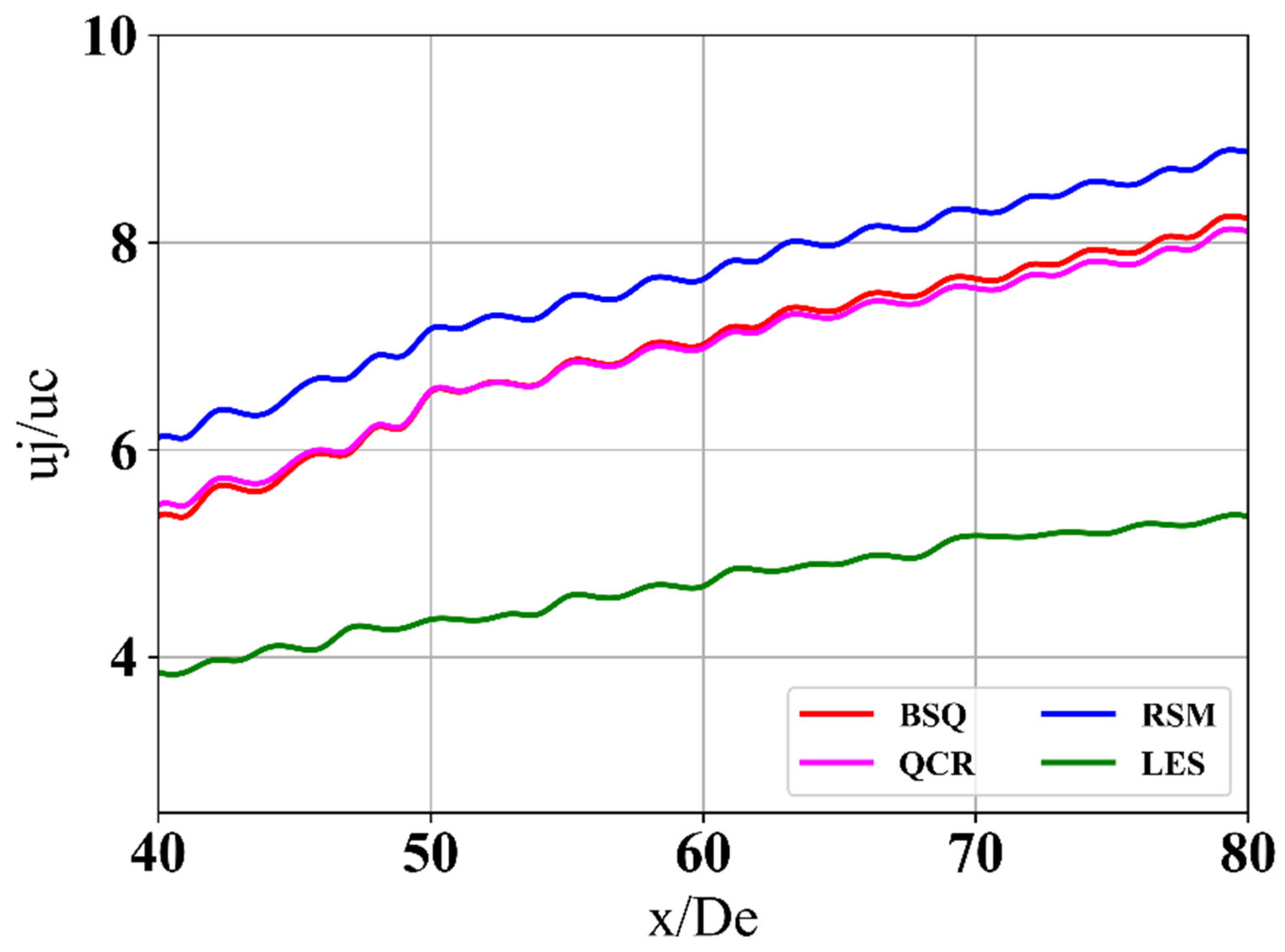
4.2.1. Jet Self-Similarity Assessment
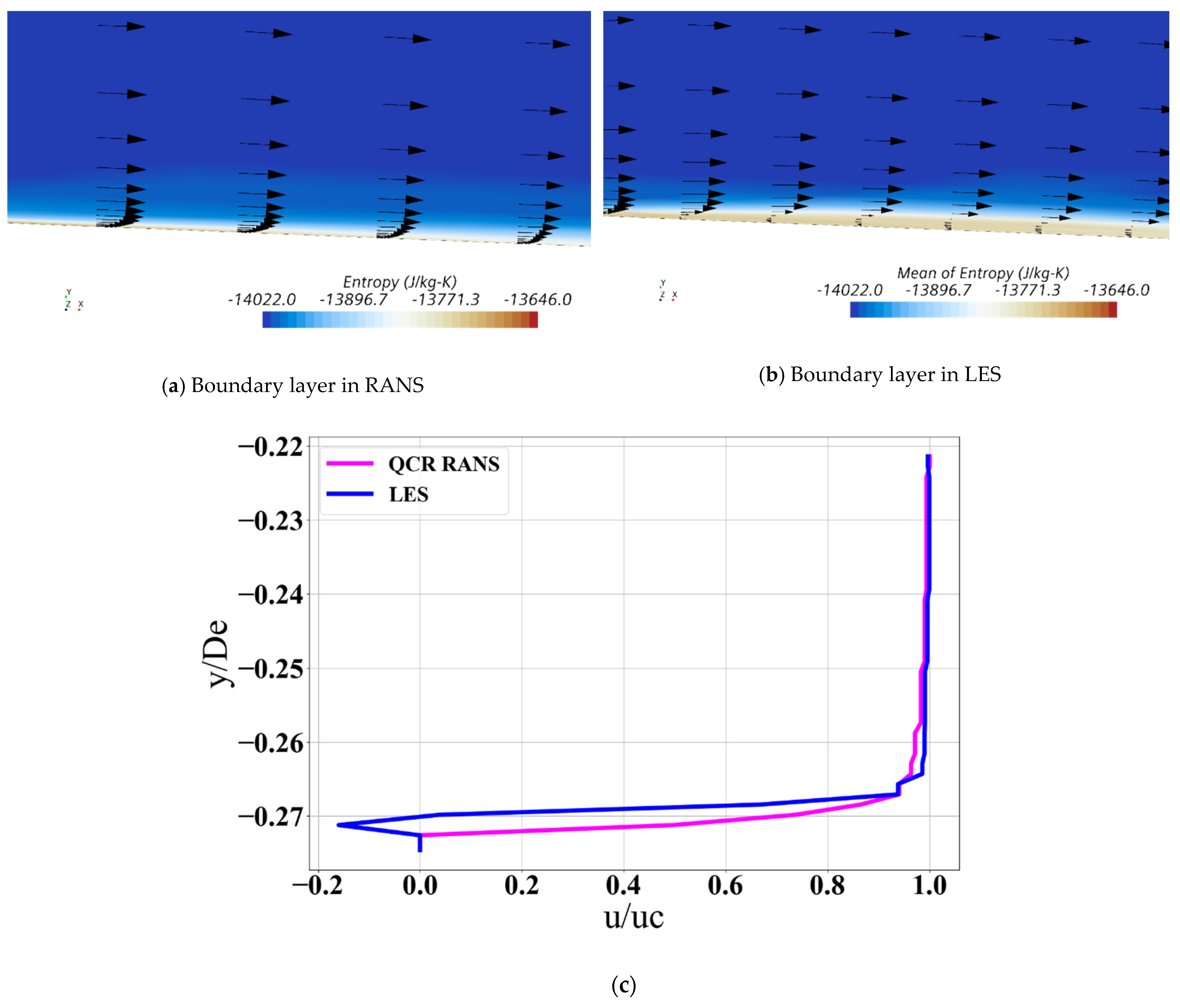
4.2.2. Boundary Layer Growth in RANS and LES
5. Discussion on Anisotropy
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| DNS | Direct numerical simulation |
| HPC | High performance computing |
| LES | Large Eddy Simulation |
| LEVM | Linear eddy viscosity model |
| NLEVM | Non-linear eddy viscosity model |
| PIV | Particle image velocimetry |
| QCR | Quadratic constitutive relation |
| TKE | Turbulent Kinetic Energy |
| RANS | Reynolds Averaged Navier Stokes |
| RSM | Reynolds stress model |
| SST | Shear Stress Transport |
| WALE | Wall adapting local eddy viscosity |
| WSS | Wall shear stress |
| u | Axial component of velocity |
| uj | Jet centerline velocity at nozzle exit |
| uc | Jet centerline velocity along jet axis |
| De | Nozzle equivalent diameter |
| h | Height at nozzle exit from minor axis plane view |
References
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Canada, CA, USA, 1998; Volume 2. [Google Scholar]
- Greitzer, E.M.; Tan, C.S.; Graf, M.B. Internal Flow: Concepts and Applications; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Schlichting, H.; Kestin, J. Boundary Layer Theory; McGraw-Hill: New York, NY, USA, 1961; Volume 121. [Google Scholar]
- Shapiro, A.H. The Dynamics and Thermodynamics of Compressible Fluid Flow; Ronald Press: New York, NY, USA, 1953. [Google Scholar]
- Bobba, C.R.; Ghia, K.N. A study of three-dimensional compressible turbulent jets. In 2nd Symposium on Turbulent Shear Flows; Imperial College of Science and Technology: London, UK, 1979; pp. 1–26. [Google Scholar]
- Georgiadis, N.J.; DeBonis, J.R. Navier–stokes analysis methods for turbulent jet flows with application to aircraft exhaust nozzles. Prog. Aerosp. Sci. 2006, 42, 377–418. [Google Scholar] [CrossRef]
- Mihaescu, M.; Semlitsch, B.; Fuchs, L.; Gutmark, E. Assessment of turbulence models for predicting coaxial jets relevant to turbofan engines. In Proceedings of the Conference on Modelling Fluid Flow (CMFF 12), the 15th International Conference on Fluid Flow Technologies, Budapest, Hungary, 4–7 September 2012; pp. 4–7. [Google Scholar]
- Araya, G. Turbulence model assessment in compressible flows around complex geometries with unstructured grids. Fluids 2019, 4, 81. [Google Scholar] [CrossRef]
- Rumsey, C.L.; Nishino, T. Numerical study comparing RANS and LES approaches on a circulation control airfoil. Int. J. Heat Fluid Flow 2011, 32, 847–864. [Google Scholar] [CrossRef]
- Mirjalily, S.A.A. Lambda shock behaviors of elliptic supersonic jets; a numerical analysis with modification of RANS turbulence model. Aerosp. Sci. Technol. 2021, 112, 106613. [Google Scholar] [CrossRef]
- DeBonis, J.R. Prediction of turbulent temperature fluctuations in hot jets. AIAA J. 2018, 56, 3097–3111. [Google Scholar] [CrossRef]
- DeBonis, J.R.; Oberkampf, W.L.; Wolf, R.T.; Orkwis, P.D.; Turner, M.G.; Babinsky, H.; Benek, J.A. Assessment of computational fluid dynamics and experimental data for shock boundary-layer interactions. AIAA J. 2012, 50, 891–903. [Google Scholar] [CrossRef]
- DeBonis, J.R. Evaluation of industry standard turbulence models on an axisymmetric supersonic compression corner. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, Florida, 5–9 January 2015; p. 0314. [Google Scholar]
- Wernet, M.P.; Georgiadis, N.J.; Locke, R.J. Raman temperature and density measurements in supersonic jets. Exp. Fluids 2021, 62, 61. [Google Scholar] [CrossRef]
- Menter, F.R. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int. J. Comput. Fluid Dyn. 2009, 23, 305–316. [Google Scholar] [CrossRef]
- Latin, R.M. The Influence of Surface Roughness on Supersonic High Reynolds Number Turbulent Boundary Layer Flow. Ph.D. Thesis, Air Force Institute of Technology, Dayton, OH, USA, 1998. [Google Scholar]
- Aronson, K.E.; Brezgin, D.V. Wall roughness effect on gas dynamics in supersonic ejector. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2016; Volume 1770, No. 1; p. 030087. [Google Scholar]
- Liu, J.; Ramamurti, R. Numerical study of supersonic jet noise emanating from an F404 nozzle at model scale. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 0807. [Google Scholar]
- Liu, J.; Khine, Y. Simulations of Nozzle Boundary-Layer Separation in Highly Overexpanded Jets. In Proceedings of the AIAA Aviation Forum, Virtual, 15–19 June 2020. [Google Scholar]
- Gubanov, D.A.; Dyadâkin, A.A.; Zapryagaev, V.I.; Kavun, I.N.; Rybak, S.P. Experimental investigation of the nozzle roughness effect on the flow parameters in the mixing layer of an axisymmetric subsonic high-velocity jet. Fluid Dyn. 2020, 55, 185–193. [Google Scholar] [CrossRef]
- Cresci, I.; Ireland, P.T.; Bacic, M.; Tibbott, I.; Rawlinson, A. Realistic velocity and turbulence intensity profiles at the combustor-turbine interaction (CTI) plane in a nozzle guide vane test facility. In Proceedings of the 11th European Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Madrid, Spain, 23–27 March 2015; European Turbomachinery Society: Florence, Italy, 2015. [Google Scholar]
- Brès, G.A.; Ham, F.; Nichols, J.W.; Lele, S.K. Nozzle wall modeling in unstructured large eddy simulations for hot supersonic jet predictions. In Proceedings of the 19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany, 27–29 May 2013; p. 2142. [Google Scholar]
- Bres, G.A.; Towne, A.; Lele, S.K. Investigating the effects of temperature non-uniformity on supersonic jet noise with large-eddy simulation. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019; p. 2730. [Google Scholar]
- Bogey, C.; Marsden, O.; Bailly, C. Influence of initial turbulence level on the flow and sound fields of a subsonic jet at a diameter-based Reynolds number of 105. J. Fluid Mech. 2012, 701, 352–385. [Google Scholar] [CrossRef]
- Upadhyay, P.; Zaman, K.Q. The effect of incoming boundary layer characteristics on the performance of a distributed propulsion system. In Proceedings of the AIAA SciTech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 1092. [Google Scholar]
- Hu, J.; Rizzi, A. Turbulent flow in supersonic and hypersonic nozzles. AIAA J. 1995, 33, 1634–1640. [Google Scholar] [CrossRef]
- Siddappaji, K.; Turner, M.G.; Dey, S.; Park, K.; Merchant, A. Optimization of a 3-Stage Booster: Part 2—The Parametric 3D Blade Geometry Modeling Tool. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: San Antonio, TX, USA, 2011; Volume 54679, pp. 1431–1443. [Google Scholar]
- Siddappaji, K. Parametric 3D Blade Geometry Modeling Tool for Turbomachinery Systems. Master’s Thesis, University of Cincinnati, Cincinnati, OH, USA, 2012. [Google Scholar]
- Siddappaji, K.; Turner, M.G. Versatile Tool for Parametric Smooth Turbomachinery Blades. Aerospace 2022, 9, 489. [Google Scholar] [CrossRef]
- Siddappaji, K.; Turner, M.G. An Advanced Multifidelity Multidisciplinary Design Analysis Optimization Toolkit for General Turbomachinery. Processes 2022, 10, 1845. [Google Scholar] [CrossRef]
- Semlitsch, B.; Cuppoletti, D.R.; Gutmark, E.J.; Mihăescu, M. Transforming the shock pattern of supersonic jets using fluidic injection. AIAA J. 2019, 57, 1851–1861. [Google Scholar] [CrossRef]
- Hafsteinsson, H.E.; Eriksson, L.E.; Andersson, N.; Cuppoletti, D.R.; Gutmark, E. Noise control of supersonic jet with steady and flapping fluidic injection. AIAA J. 2015, 53, 3251–3272. [Google Scholar] [CrossRef]
- Semlitsch, B.; Mihăescu, M. Fluidic injection scenarios for shock pattern manipulation in exhausts. AIAA J. 2018, 56, 4640–4644. [Google Scholar] [CrossRef]
- Schmitt, F.G. About Boussinesq’s turbulent viscosity hypothesis: Historical remarks and a direct evaluation of its validity. Comptes Rendus Mécanique 2007, 335, 617–627. [Google Scholar] [CrossRef]
- Spalart, P.R. Strategies for turbulence modelling and simulations. Int. J. Heat Fluid Flow 2000, 21, 252–263. [Google Scholar] [CrossRef]
- Gibson, M.M.; Launder, B.E. Ground effects on pressure fluctuations in the atmospheric boundary layer. J. Fluid Mech. 1978, 86, 491–511. [Google Scholar] [CrossRef]
- Speziale, C.G.; Sarkar, S.; Gatski, T.B. Modelling the pressure–strain correlation of turbulence: An invariant dynamical systems approach. J. Fluid Mech. 1991, 227, 245–272. [Google Scholar] [CrossRef]
- Sarkar, S.; Lakshmanan, B. Application of a Reynolds stress turbulence model to the compressible shear layer. AIAA J. 1991, 29, 743–749. [Google Scholar] [CrossRef]
- Mehdizadeh, O.Z.; Temmerman, L.; Tartinville, B.; Hirsch, C. Applications of earsm turbulence models to internal flows. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: San Antonio, TX, USA, 2012; Volume 44748, pp. 2079–2086. [Google Scholar]
- Nagapetyan, H.J. Development and Application of Quadratic Constitutive Relation and Transition Crossflow Effects in the Wray-Agarwal Turbulence Model; Washington University: St. Louis, MO, USA, 2018. [Google Scholar]
- Thomas, B.; Agarwal, R.K. Evaluation of various RANS turbulence models for predicting the drag on an Ahmed body. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 2919. [Google Scholar]
- Rumsey, C.L.; Carlson, J.R.; Pulliam, T.H.; Spalart, P.R. Improvements to the quadratic constitutive relation based on NASA juncture flow data. AIAA J. 2020, 58, 4374–4384. [Google Scholar] [CrossRef]
- Bosco, A.; Reinartz, B.; Brown, L.; Boyce, R. Investigation of a compression corner at hypersonic conditions using a reynolds stress model. In Proceedings of the 17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, San Francisco, CA, USA, 11–14 April 2011; p. 2217. [Google Scholar]
- Molchanov, A.M.; Myakochin, A.S. Numerical simulation of high-speed flows using the algebraic Reynolds stress model. Russ. Aeronaut. 2018, 61, 236–243. [Google Scholar] [CrossRef]
- Gao, F. Advanced Numerical Simulation of Corner Separation in a Linear Compressor Cascade. Ph.D. Thesis, Ecole Centrale de Lyon, Écully, France, 2014. [Google Scholar]
- Yoder, D.A. Assessment of Turbulence Models for a Single-Injector Cooling Flow. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 1812. [Google Scholar]
- Paysant, R.; Laroche, E.; Troyes, J.; Donjat, D.; Millan, P.; Buet, P. Scale resolving simulations of a high-temperature turbulent jet in a cold crossflow: Comparison of two approaches. Int. J. Heat Fluid Flow 2021, 92, 108862. [Google Scholar] [CrossRef]
- Paysant, R.; Laroche, E.; Millan, P.; Buet, P. RANS modelling of a high-temperature jet in a cold crossflow: From eddy viscosity models to advanced anisotropic approaches. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 & 19–21 January 2021; p. 1542. [Google Scholar]
- Boychev, K.; Barakos, G.N.; Steijl, R. Numerical simulations of multiple shock wave boundary layer interactions. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 & 19–21 January 2021; p. 1762. [Google Scholar]
- Bhide, K.; Siddappaji, K.; Abdallah, S.; Roberts, K. Improved Supersonic Turbulent Flow Characteristics Using Non-Linear Eddy Viscosity Relation in RANS and HPC-Enabled LES. Aerospace 2021, 8, 352. [Google Scholar] [CrossRef]
- Bhide, K.R.; Abdallah, S. Turbulence statistics of supersonic rectangular jets using Reynolds Stress Model in RANS and WALE LES. In Proceedings of the AIAA AVIATION 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022; p. 3344. [Google Scholar]
- Dhamankar, N.S.; Blaisdell, G.A.; Lyrintzis, A.S. Overview of turbulent inflow boundary conditions for large-eddy simulations. AIAA J. 2018, 56, 1317–1334. [Google Scholar] [CrossRef]
- Liu, J.; Corrigan, A.T.; Kailasanath, K.; Taylor, B.D. Impact of the specific heat ratio on the noise generation in a high-temperature supersonic jet. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 2125. [Google Scholar]
- El Rafei, M.; Könözsy, L.; Rana, Z. Investigation of numerical dissipation in classical and implicit large eddy simulations. Aerospace 2017, 4, 59. [Google Scholar] [CrossRef]
- Seifollahi Moghadam, Z.; Guibault, F.; Garon, A. On the evaluation of mesh resolution for large-eddy simulation of internal flows using OpenFOAM. Fluids 2021, 6, 24. [Google Scholar] [CrossRef]
- Bhide, K.; Abdallah, S. Anisotropic Turbulent Kinetic Energy budgets in compressible rectangular jets. Aerospace 2022, 9, 484. [Google Scholar] [CrossRef]
- Siddappaji, K. On the Entropy Rise in General Unducted Rotors Using Momentum, Vorticity and Energy Transport. Doctoral Dissertation, University of Cincinnati, Cincinnati, OH, USA, 2018. [Google Scholar]
- Siddappaji, K.; Turner, M. Multifidelity Analysis of a Solo Propeller: Entropy Rise Using Vorticity Dynamics and Kinetic Energy Dissipation. Fluids 2022, 7, 177. [Google Scholar] [CrossRef]
- Siddappaji, K.; Turner, M. Improved Prediction of Aerodynamic Loss Propagation as Entropy Rise in Wind Turbines Using Multifidelity Analysis. Energies 2022, 15, 3935. [Google Scholar] [CrossRef]
- Baier, F.; Mora, P.; Gutmark, E.; Kailasanath, K. Flow measurements from a supersonic rectangular nozzle exhausting over a flat surface. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 0932. [Google Scholar]
- Simcenter Star-CCM+. Siemens PLM Software, Star-CCM+; Version 15 04.008-R8; Siemens Digital Industries Software: Plano, TX, USA, 2020. [Google Scholar]
- Bhide, K.; Siddappaji, K.; Abdallah, S. Influence of fluid–thermal–structural interaction on boundary layer flow in rectangular supersonic nozzles. Aerospace 2018, 5, 33. [Google Scholar] [CrossRef]
- Cuppoletti, D.R. Supersonic Jet Noise Reduction with Novel Fluidic Injection Techniques. Doctoral Dissertation, University of Cincinnati, Cincinnati, OH, USA, 2013. [Google Scholar]
- Heeb, N.S. Azimuthally Varying Noise Reduction Techniques Applied to Supersonic Jets. Ph.D. Thesis, University of Cincinnati, Cincinnati, OH, USA, 2015. [Google Scholar]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Wilson, B.M.; Smith, B.L. Uncertainty on PIV mean and fluctuating velocity due to bias and random errors. Meas. Sci. Technol. 2013, 24, 035302. [Google Scholar] [CrossRef]
- Lazar, E.; De Blauw, B.; Glumac, N.; Dutton, C.; Elliott, G. A practical approach to PIV uncertainty analysis. In Proceedings of the 27th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, Chicago, IL, USA, 28 June–1 July 2010; p. 4355. [Google Scholar]
- Pope, S.B.; Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bogey, C.; Bailly, C. Turbulence and energy budget in a self-preserving round jet: Direct evaluation using large eddy simulation. J. Fluid Mech. 2009, 627, 129–160. [Google Scholar] [CrossRef]
- Krothapalli, A.; Baganoff, D.; Karamcheti, K. On the mixing of a rectangular jet. J. Fluid Mech. 1981, 107, 201–220. [Google Scholar] [CrossRef]













| Category | Parameters |
|---|---|
| Mesh sensitivity | Mesh refinements in nozzle and jet |
| Domain dependency | Baseline domain, full experimental facility size domain |
| Inlet modeling | Turbulence intensity Effect of upstream supply duct |
| Wall modeling | Prism layer sensitivity Isothermal vs. adiabatic walls |
| Surface roughness | Smooth vs. rough walls |
| Transition modeling | Gamma transition model |
| Turbulence capture | Boussinesq (linear) k-omega SST RANS, Quadratic Constitutive relation (non-linear) k-omega SST RANS Linear pressure–strain Reynolds stress model, WALE LES |
| Case Abbreviation | Number of Cells (Million) | Refinement Size (m) | Total Pressure at Nozzle Exit (Normalized by Pin) |
|---|---|---|---|
| Coarse | 6 | De/25 | 0.965 |
| Medium | 8 | De/30 | 0.964 |
| Fine | 10 | De/35 | 0.964 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhide, K.; Abdallah, S. High-Order Accurate Numerical Simulation of Supersonic Flow Using RANS and LES Guided by Turbulence Anisotropy. Fluids 2022, 7, 385. https://doi.org/10.3390/fluids7120385
Bhide K, Abdallah S. High-Order Accurate Numerical Simulation of Supersonic Flow Using RANS and LES Guided by Turbulence Anisotropy. Fluids. 2022; 7(12):385. https://doi.org/10.3390/fluids7120385
Chicago/Turabian StyleBhide, Kalyani, and Shaaban Abdallah. 2022. "High-Order Accurate Numerical Simulation of Supersonic Flow Using RANS and LES Guided by Turbulence Anisotropy" Fluids 7, no. 12: 385. https://doi.org/10.3390/fluids7120385
APA StyleBhide, K., & Abdallah, S. (2022). High-Order Accurate Numerical Simulation of Supersonic Flow Using RANS and LES Guided by Turbulence Anisotropy. Fluids, 7(12), 385. https://doi.org/10.3390/fluids7120385






