On Energy Redistribution for the Nonlinear Parabolized Stability Equations Method
Abstract
:1. Introduction
2. Basic States
3. Stability Analysis
3.1. Jokher
3.1.1. Linear Stability Theory
3.1.2. Parabolized Stability Equations
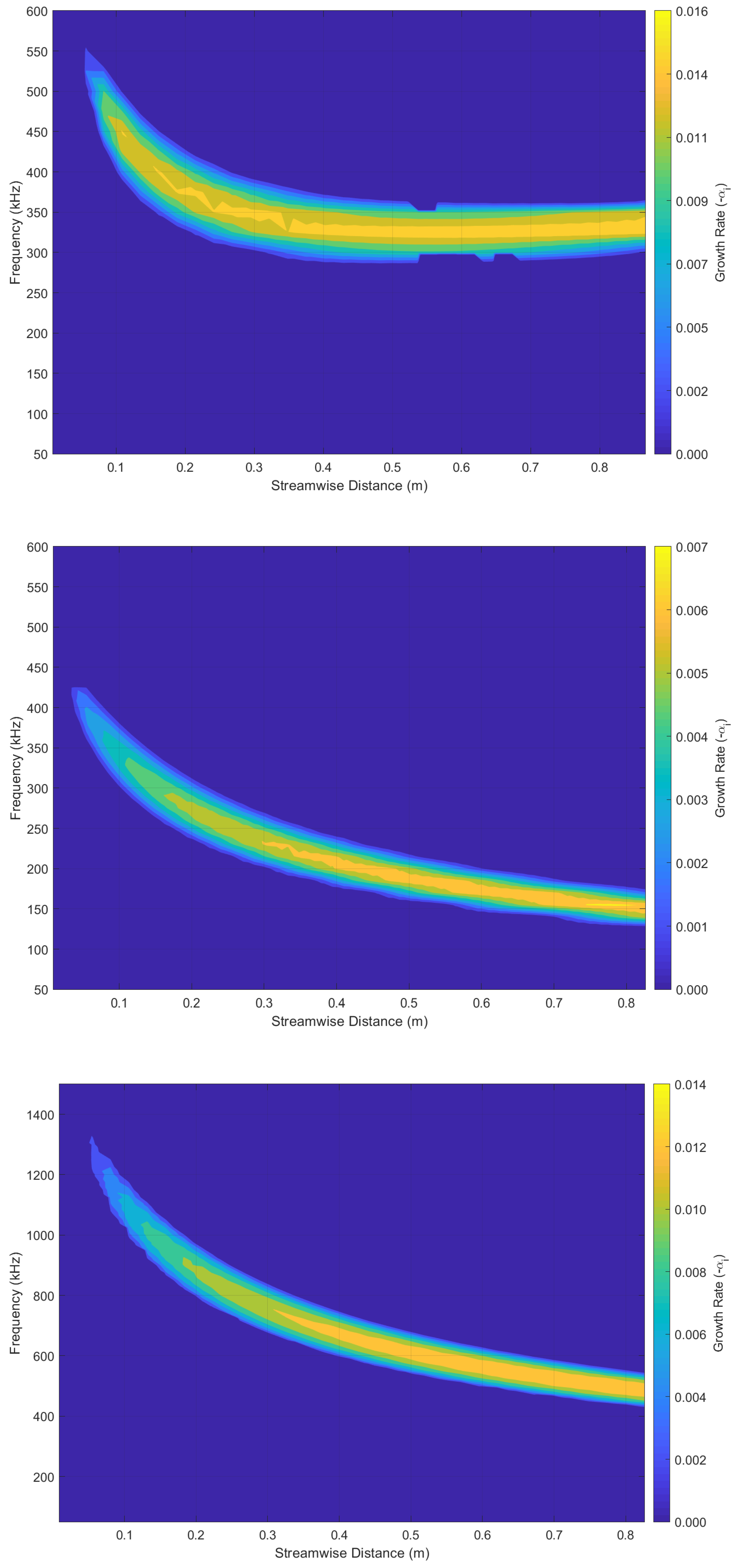
4. Linear Results
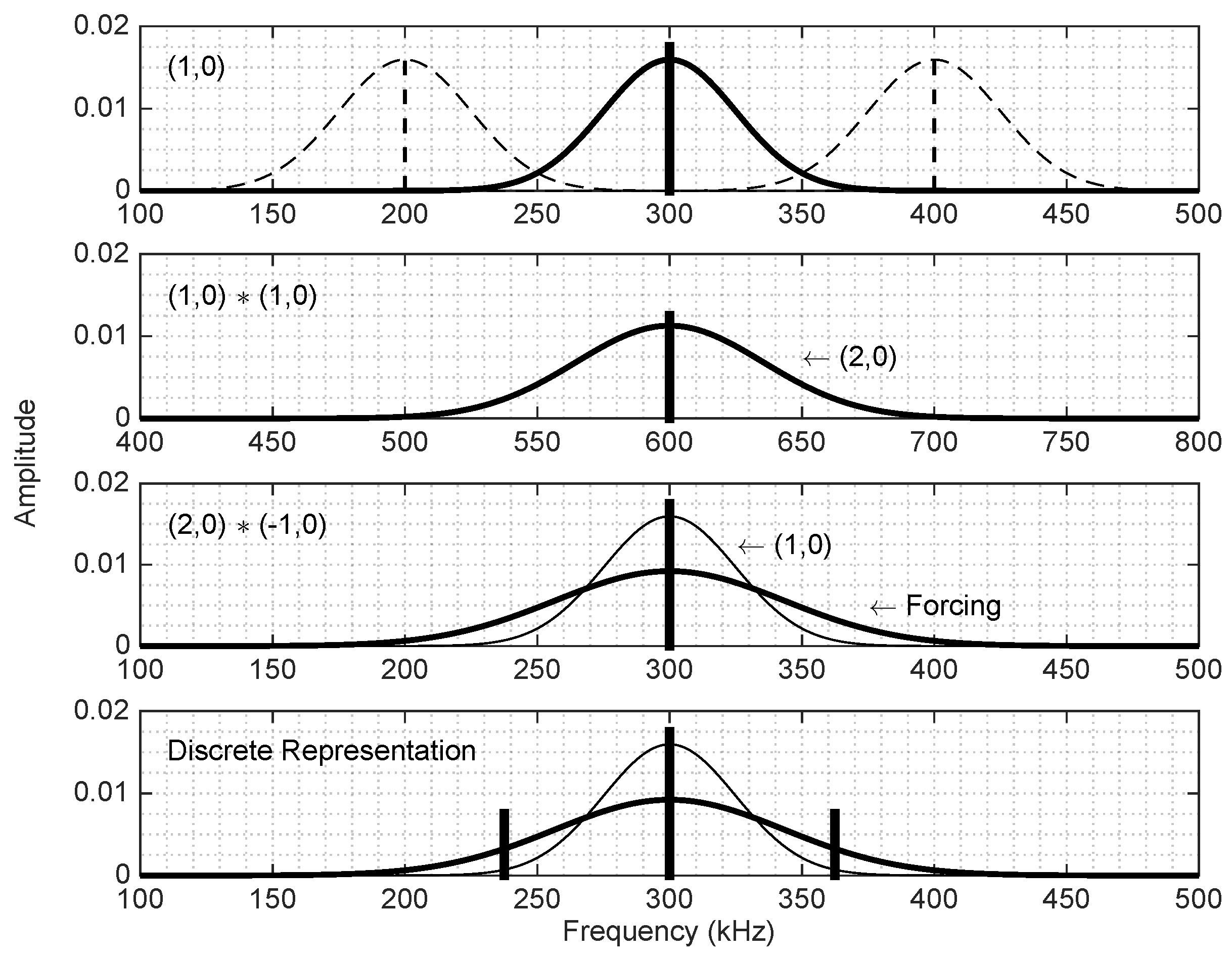
5. Nonlinear Energy Transfer Mechanism
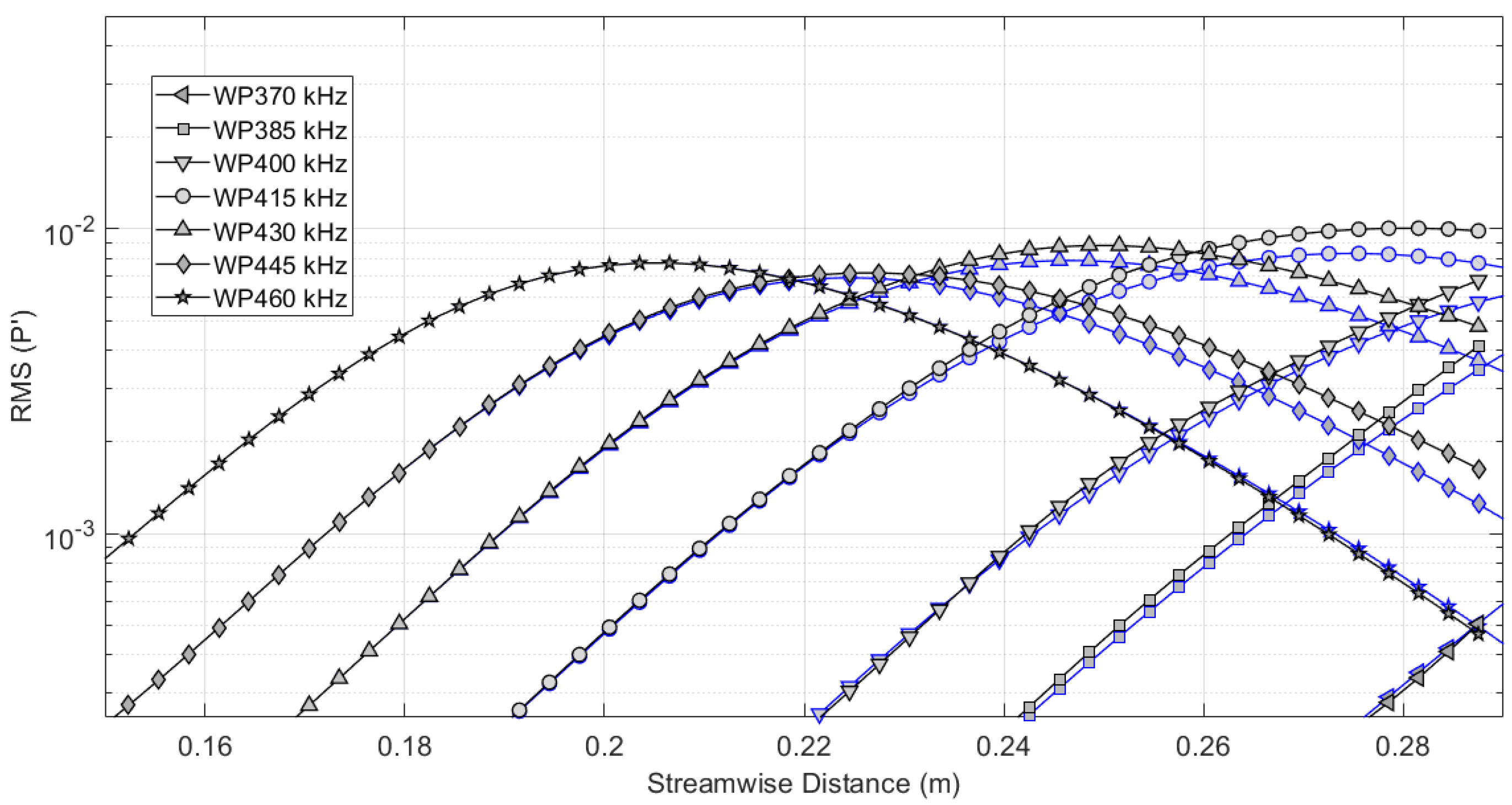
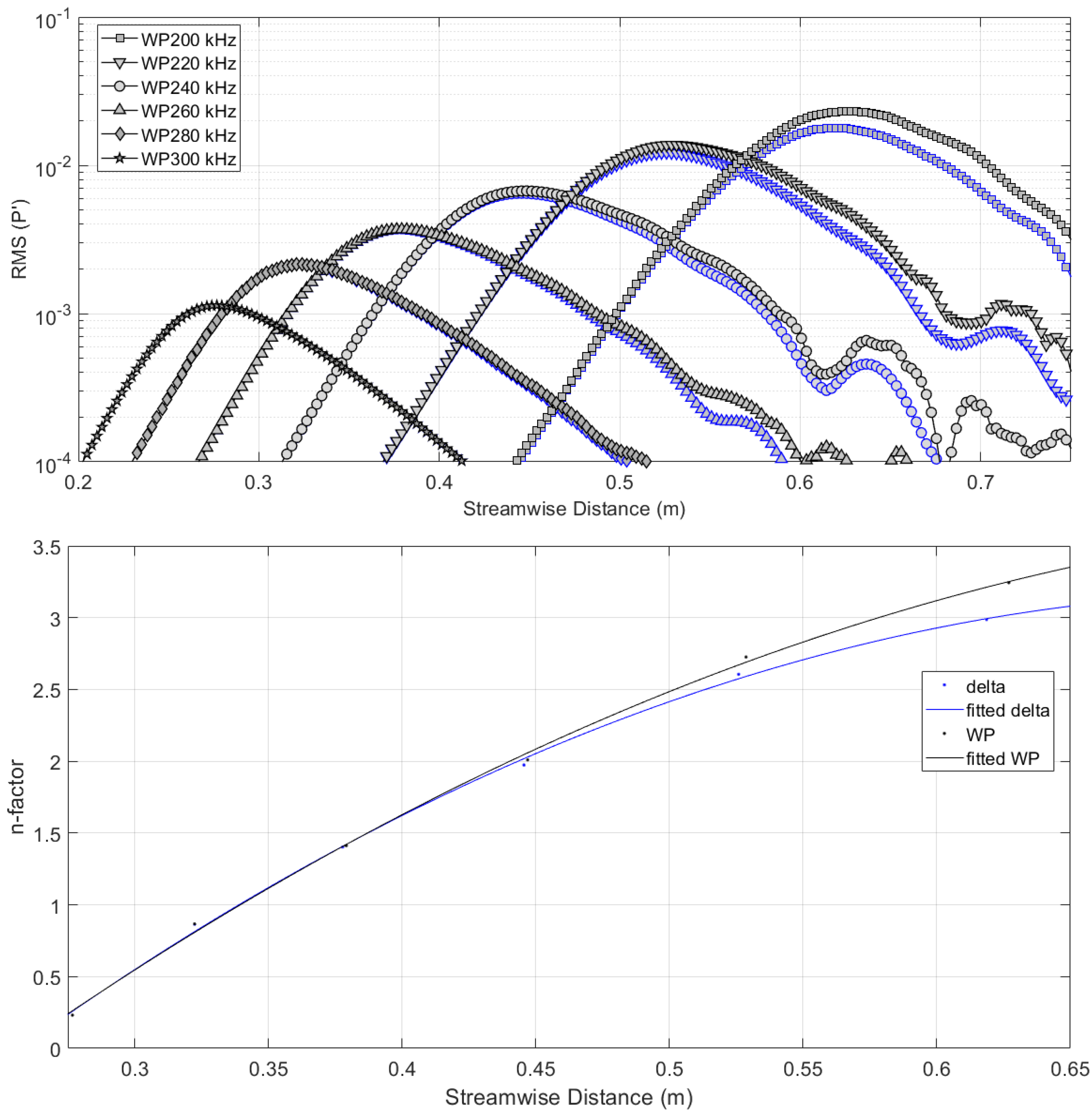
6. NPSE Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Hirschel, E.H. Basics of Aerothermodynamics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Anderson, J.D., Jr. Hypersonic and High-Temperature Gas Dynamics, 2nd ed.; AIAA Education Series; AIAA: Reston, VA, USA, 2006. [Google Scholar]
- Schmid, P.J.; Henningson, D.S. Stability and Transition in Shear Flows. Appl. Math. Sci. 2001, 142. [Google Scholar]
- Reed, H.L. Stability of Hypersonic Boundary—Layer Flows; AFOSR-TR-97 Report; Arizona State University: Tempe, AZ, USA, 1997. [Google Scholar]
- Lewis, M. Hypersonic Flight: Progress and Challenges on the Way to High Mach Systems; AIAA: Reston, VA, USA, 2018. [Google Scholar]
- Mack, L.M. Boundary-Layer Linear Stability Theory; AGARD Report 709; California Institute of Tech Pasadena Jet Propulsion Lab: Pasadena, CA, USA, 1984. [Google Scholar]
- Fedorov, A. Transition and stability of high-speed boundary layers. Annu. Rev. Fluid Mech. 2011, 43, 79–95. [Google Scholar] [CrossRef]
- Reshotko, E. Transient growth: A factor in bypass transition. Phys. Fluids 2001, 13, 1067–1075. [Google Scholar] [CrossRef]
- Reshotko, E.; Tumin, A. The Blunt Body Paradox—A Case for Transient Growth. Laminar-Turbulent Transition; IUTAM Symposia (International Union of Theoretical and Applied Mechanics); Springer: Berlin, Heidelberg, Germany, 2000; pp. 403–408. [Google Scholar]
- Batista, A.; Khan, A.A.; Kuehl, J. On the mechanism by which nose bluntness suppresses second-mode instability. Theor. Appl. Mech. Lett. 2020, 10, 230–240. [Google Scholar] [CrossRef]
- Batista, A.; Kuehl, J.J. Local Wall Temperature Effects on the Second-Mode Instability. J. Spacecr. Rocket. 2020, 57, 580–595. [Google Scholar] [CrossRef]
- Sakakeeny, J.; Batista, A.; Kuehl, J. How nose bluntness suppresses second-mode growth. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 3083. [Google Scholar]
- Stetson, K.F.; Kimmel, R.L. Example of second-mode instability dominance at a Mach number of 5.2. AIAA J. 1992, 30, 2974–2976. [Google Scholar] [CrossRef]
- Stetson, K.F. Nosetip Bluntness Effects on Cone Frustum Boundary Layer Transition in Hypersonic Flow. In Proceedings of the 16th AIAA Fluid and Plasmadynamics Conference, Danvers, MA, USA, 12–14 July 1983. AIAA Paper 1983–1763. [Google Scholar] [CrossRef]
- Tufts, M.; Kimmel, R.L. Analysis of Windward Side Hypersonic Boundary Layer Transition on Blunted Cones at Angle of Attack. AIAA Paper 2017-0764. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef] [Green Version]
- Hader, C.; Fasel, H.F. Laminar-Turbulent Transition on a Flared Cone at Mach 6. AIAA Paper 2016-3344. In Proceedings of the 46th AIAA Fluid Dynamics Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Hader, C.; Fasel, H.F. Fundamental Resonance Breakdown for a Flared Cone at Mach 6.AIAA Paper 2017-0765. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Unnikrishnan, S.; Gaitonde, D.V. First-mode-induced nonlinear breakdown in a hypersonic boundary layer. Comput. Fluids 2019, 191, 104249. [Google Scholar] [CrossRef]
- Kuehl, J. Nonlinear Saturation versus Nonlinear Detuning: Quantification on a Mach 6 Flared Cone.AIAA Paper 2017-0763. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Moyes, A.J.; Paredes, P.; Kocian, T.S.; Reed, H.L. Secondary instability analysis of crossflow on a hypersonic yawed straight circular cone. J. Fluid Mech. 2017, 812, 370–397. [Google Scholar] [CrossRef]
- Wheaton, B.M.; Berridge, D.C.; Wolf, T.D.; Stevens, R.T.; McGrath, B.E. Boundary layer transition (BOLT) flight experiment overview. In Proceedings of the 2018 Fluid Dynamics Conference, Atlanta, GA, USA, 25–29 June 2018; p. 2892. [Google Scholar]
- Berridge, D.C.; McKiernan, G.; Wadhams, T.P.; Holden, M.; Wheaton, B.M.; Wolf, T.D.; Schneider, S.P. Hypersonic ground tests in support of the boundary layer transition (BOLT) flight experiment. In Proceedings of the 2018 Fluid Dynamics Conference, Atlanta, GA, USA, 25–29 June 2018; p. 2893. [Google Scholar]
- Wheaton, B.M.; Berridge, D.C.; Wolf, T.; Araya, D.; Stevens, R.; McGrath, B.E.; Kemp, B.; Adamczak, D. Final Design of the Boundary Layer Transition (BOLT) Flight Experiment. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1041. [Google Scholar]
- Thome, J.; Dwivedi, A.; Nichols, J.W.; Candler, G.V. Direct numerical simulation of BOLT hypersonic flight vehicle. In Proceedings of the 2018 Fluid Dynamics Conference, Atlanta, GA, USA, 25–29 June 2018; p. 2894. [Google Scholar]
- Moyes, A.J.; Reed, H.L. Preflight Boundary-Layer Stability Analysis of BOLT Geometry. J. Spacecr. Rocket. 2020, 58, 78–89. [Google Scholar] [CrossRef]
- Kimmel, R.L.; Adamczak, D.; Paull, A.; Paull, R.; Shannon, J.; Pietsch, R.; Frost, M.; Alesi, H. HIFiRE-1 ascent-phase boundary-layer transition. J. Spacecr. Rocket. 2015, 52, 217–230. [Google Scholar] [CrossRef]
- Li, F.; Choudhari, M.; Chang, C.L.; Kimmel, R.; Adamczak, D.; Smith, M. Transition analysis for the ascent phase of HIFiRE-1 flight experiment. J. Spacecr. Rocket. 2015, 52, 1283–1293. [Google Scholar] [CrossRef]
- Juliano, T.J.; Kimmel, R.L.; Willems, S.; Gulhan, A.; Wagnild, R.M. HIFiRE-1 Boundary-Layer Transition: Ground Test Results and Stability Analysis. AIAA Paper 2015-1736. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Reed, H.L.; Perez, E.; Kuehl, J.; Kocian, T.; Oliviero, N. Verification and validation issues in hypersonic stability and transition prediction. J. Spacecr. Rocket. 2014, 52, 29–37. [Google Scholar] [CrossRef]
- Hofferth, J.; Saric, W.; Kuehl, J.; Perez, E.; Kocian, T.; Reed, H. Boundary-Layer Instability and Transition on a Flared Cone in a Mach 6 Quiet Wind Tunnel. Int. J. Eng. Syst. Model. Simul. 2013, 5, 109–124. [Google Scholar] [CrossRef]
- Chynoweth, B.; Schneider, S.P.; Fasel, H.; Hader, C.; Batista, A.; Kuehl, J.; Juliano, T.J.; Wheaton, B. A History and Progress of Research on Boundary-Layer Transition on a Mach 6 Flared Cone. J. Spacecr. Rocket. 2019, 56, 333–346. [Google Scholar] [CrossRef]
- Radespiel, R.; Schneider, S.P.; Adamczak, D.; Ali, S.; Andre, T.; Arndt, A.; Berger, K.T.; Borg, M.; Chaudry, R.; Choudhari, M.M.; et al. Hypersonic Boundary-Layer Transition Prediction; STO Technical Report TR-AVT-240; The NATO Science and Technology Organization: Brussels, Belgium, 2020; ISBN 978-92-837-2227-4. [Google Scholar]
- Kuehl, J.J. Discrete- and finite-bandwidth-frequency distributions in nonlinear stability applications. Phys. Fluids 2017, 29, 024101. [Google Scholar] [CrossRef]
- Yeo, K.S.; Zhao, X.; Wang, Z.Y.; Ng, K.C. DNS of wavepacket evolution in a Blasius boundary layer. J. Fluid Mech. 2010, 652, 333–372. [Google Scholar] [CrossRef]
- Sivasubramanian, J.; Fasel, H. Numerical Investigation of the Development of Three-Dimensional Wavepackets in a Sharp Cone Boundary Layer at Mach 6. J. Fluid Mech. 2014, 756, 600–649. [Google Scholar] [CrossRef]
- Duan, L.; Choudhari, M.; Li, F. DNS of laminar-turbulent transition in swept-wing boundary layers. In Proceedings of the Center for Turbulence Research Summer Program, Stanford, CA, USA, 6 July–1 August 2014; pp. 273–283. [Google Scholar]
- Cook, D.A.; Thome, J.; Brock, J.M.; Nichols, J.W.; Candler, G.V. Understanding effects of nose-cone bluntness on hypersonic boundary layer transition using input-output analysis. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 0378. [Google Scholar]
- Sheremet, V.; Ierley, G.; Kamenkovich, V. Eigenanalysis of the two-dimensional wind-driven ocean circulation problem. J. Mar. Res. 1997, 55, 57–92. [Google Scholar] [CrossRef]
- Ginsberg, J.H.; Ginsberg, J.H. Mechanical and Structural Vibrations: Theory and Applications; Wiley: New York, NY, USA, 2001; Volume 704. [Google Scholar]
- Luchini, P.; Bottaro, A. Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 2014, 46, 493–517. [Google Scholar] [CrossRef]
- Chandler, G.J.; Juniper, M.P.; Nichols, J.W.; Schmid, P.J. Adjoint algorithms for the Navier–Stokes equations in the low Mach number limit. J. Comput. Phys. 2012, 231, 1900–1916. [Google Scholar] [CrossRef]
- Marineau, E.C.; Moraru, C.G.; Lewis, D.R.; Norris, J.D.; Lafferty, J.F.; Wagnild, R.M.; Smith, J.A. Mach 10 Boundary-Layer Transition Experiments on Sharp and Blunted Cones. AIAA Paper 2014-3108. In Proceedings of the 19th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Marineau, E.C.; Moraru, G.C.; Lewis, D.R.; Norris, J.D.; Lafferty, J.; Johnson, H.B. Investigation of Mach 10 Boundary Layer Stability of Sharp Cones at Angle-of-Attack, Part 1: Experiments. AIAA Paper 2015-1737. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Marineau, E.C.; Morraru, G.C.; Daniel, D. Sharp cone boundary-layer transition and stability at Mach 14. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 0766. [Google Scholar]
- Schneider, S.P. Developing mechanism-based methods for estimating hypersonic boundary-layer transition in flight: The role of quiet tunnels. Prog. Aerosp. Sci. 2014, 72, 17–29. [Google Scholar] [CrossRef]
- McKiernan, G.; Chynoweth, B.; Schneider, S.P. Instability and Transition Experiments in the Boeing/AFOSR Mach 6 Quiet Tunnel. AIAA Paper 2015-1735. In Proceedings of the 45th AIAA Thermophysics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Lewis, D.R.; Alba, C.R.; Rufer, S.J.; Beresh, S.J.; Casper, K.M.; Berridge, D.C.; Schneider, S.P. Measurements and Computations of Second-Mode Instability Waves in Three Hypersonic Wind Tunnels; Technical Report; Sandia National Laboratories: Albuquerque, NM, USA, 2010. [Google Scholar]
- Berridge, D.; Casper, K.; Rufer, S.; Alba, C.; Lewis, D.; Beresh, S.; Schneider, S. Measurements and computations of second-mode instability waves in several hypersonic wind tunnels. In Proceedings of the 40th Fluid Dynamics Conference and Exhibit, Chicago, IL, USA, 28 June–1 July 2010; p. 5002. [Google Scholar]
- Khan, A.A.; Batista, A.; Kuehl, J. Nonlinear stability of straight cones with sharp and blunt noses at Mach 6. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1819. [Google Scholar]
- Batista, A.; Khan, A.A.; Kuehl, J. Variable Frequency Disturbances on a Flared Cone at Mach 6. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0589. [Google Scholar]
- Lakebrink, M.T.; Bowcutt, K.G.; Winfree, T.; Huffman, C.C.; Juliano, T.J. Optimization of a Mach-6 Quiet Wind Tunnel Nozzle. J. Spacecr. Rocket. 2018, 55, 315–321. [Google Scholar] [CrossRef]
- Nompelis, I.; Drayna, T.; Candler, G. Development of a Hybrid Unstructured Implicit Solver for the Simulation of Reacting Flows Over Complex Geometries. AIAA Paper 2004-2227. In Proceedings of the 34th AIAA Fluid Dynamics Conference and Exhibit, Portland, OR, USA, 28 June–1 July 2004. [Google Scholar]
- Nompelis, I.; Drayna, T.; Candler, G. A Parallel Unstructured Implicit Solver for Hypersonic Reacting Flow Simulation. In Parallel Computational Fluid Dynamics; Elsevier: Amsterdam, The Netherlands, 2005; pp. 389–395. [Google Scholar]
- Candler, G.V.; Johnson, H.B.; Nompelis, I.; Subbareddy, P.K.; Drayna, T.W.; Gidzak, V.; Barnhardt, M.D. Development of the US3D code for advanced compressible and reacting flow simulations. AIAA Paper 2015-1893. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Kocian, T.; Perez, E.; Oliviero, N.; Kuehl, J.; Reed, H. Hypersonic Stability Analysis of a Flared Cone. AIAA Paper 2013-0667. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar] [CrossRef]
- Chynoweth, B.; Schneider, S.P.; Fasel, H.; Hader, C.; Batista, A.; Kuehl, J.; Juliano, T.J.; Wheaton, B. A History and Progress of Research on Boundary-Layer Transition on a Mach 6 Flared Cone. AIAA Paper Scitech 2018-0060. In Proceedings of the AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Kuehl, J.J.; Paredes, P. Gortler Modified Mack-modes on a Hypersonic Flared Cone. AIAA Paper 2016-0849. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Sousa, V.C.B.; Batista, A.; Kuehl, J.; Scalo, C. Nonlinear Dynamics of Second Mode Waves on a Hypersonic Flared Cone; AIAA Aviation Forum Paper 2018-3852; AIAA: Reston, VA, USA, 2018. [Google Scholar]
- Paredes, P.; Theofilis, V.; Rodriguez, D.; Tendero, J.A. The PSE-3D instability analysis methodology for flows depending strongly on two and weakly on the third spatial dimension. AIAA Paper 2011-3752. In Proceedings of the 6th AIAA Theoretical Fluid Mechanics Conference, Honolulu, HI, USA, 27–30 June 2011. [Google Scholar] [CrossRef] [Green Version]
- Kuehl, J.; Reed, H.; Kocian, T.; Oliviero, N. Bandwidth effects on Mack-mode instability. AIAA Paper 2014-2777. In Proceedings of the 7th AIAA Theoretical Fluid Mechanics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar] [CrossRef]
- Batista, A.; Kuehl, J. A Mechanism for Spectral Broadening and Implications for Saturation Amplitude Estimates; AIAA Aviation Forum Paper 2017-3635. In Proceedings of the 47th AIAA Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Khan, A.A.; Kuehl, J.; Chelidze, D. Toward a unified interpretation of the “proper”/“smooth” orthogonal decompositions and “state variable”/“dynamic mode” decompositions with application to fluid dynamics. AIP Adv. 2020, 10, 035225. [Google Scholar] [CrossRef] [Green Version]
- Herbert, T. Parabolized stability equations. Annu. Rev. Fluid Mech. 1997, 29, 245–283. [Google Scholar] [CrossRef]
- Bertolotti, F.P. Compressible boundary layer stability analyzed with the PSE equations. AIAA Paper No. 91-1637. In Proceedings of the 22nd Fluid Dynamics, Plasma Dynamics and Lasers Conference, Honolulu, HI, USA, 24–26 June 1991. [Google Scholar] [CrossRef]
- Gaster, M. On the effects of boundary-layer growth on flow stability. J. Fluid Mech. 1974, 66, 465–480. [Google Scholar] [CrossRef]
- Chang, C.L.; Malik, M.R.; Erlebacher, G.; Hussaini, M.Y. Compressible stability of growing boundary layers using parabolized stability equations. AIAA Paper No. 91-1636. In Proceedings of the 22nd Fluid Dynamics, Plasma Dynamics and Lasers Conference, Honolulu, HI, USA, 24–26 June 1991. [Google Scholar] [CrossRef]
- Joslin, R.D.; Streett, C.L.; Chang, C.L. 3-D Incompressible Spatial Direct Numerical Simulation Code Validation Study: A Comparison with Linear Stability and Parabolic Stability Equation Theories in Boundary-Layer Transition on a Flat Plate; Report No. NASA TP-3205; NASA: Washington, DC, USA, 1992. [Google Scholar]
- Li, F.; Malik, M.R. On the nature of PSE approximation. Theor. Comput. Fluid Dyn. 1996, 8, 253–273. [Google Scholar] [CrossRef]
- Haynes, T.S.; Reed, H.L. Simulation of swept-wing vortices using nonlinear parabolized stability equations. J. Fluid Mech. 2000, 405, 325–349. [Google Scholar] [CrossRef]
- Stuckert, G.; Reed, H. Linear disturbances in hypersonic, chemically reacting shock layer. AIAA J. 1994, 32, 1384–1393. [Google Scholar] [CrossRef]
- Chang, C.L.; Vinh, H.; Malik, M.R. Hypersonic boundary-layer stability with chemical reactions using PSE. AIAA Paper No. 97–2012. In Proceedings of the 28th Fluid Dynamics Conference, Snowmass Village, CO, USA, 29 June–2 July 1997. [Google Scholar] [CrossRef]
- Chang, C.L. The Langley Stability and Transition Analysis Code (LASTRAC) Version 1.2 User Manual; Report No. NASA/TM-2004-213233; NASA Langley Research Center: Hampton, VA, USA, 2004. [Google Scholar]
- Malik, M.R. Hypersonic flight transition data analysis using parabolized stability equations with chemistry effects. J. Spacecr. Rocket. 2003, 40, 332–344. [Google Scholar] [CrossRef]
- Johnson, H.B.; Candler, G.V. Hypersonic boundary layer stability analysis using PSE-chem. AIAA Paper 2005–5023. In Proceedings of the 35th AIAA Fluid Dynamics Conference and Exhibit, Toronto, ON, Canada, 6–9 June 2005. [Google Scholar] [CrossRef]
- Li, F.; Choudhari, M.; Chang, C.L.; White, J. Analysis of instabilities in non-axisymmetric hypersonic boundary layers over cones. In Proceedings of the 10th AIAA/ASME Joint Thermophysics and Heat Transfer Conference, Chicago, IL, USA, 28 June–1 July 2010. [Google Scholar] [CrossRef] [Green Version]
- Theofilis, V. Global Linear Instability. Annu. Rev. Fluid Mech. 2011, 43, 319–352. [Google Scholar] [CrossRef]
- Kuehl, J.; Perez, E.; Reed, H.L. JoKHeR: NPSE simulations of hypersonic crossflow instability. AIAA Paper 2012–0921. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar] [CrossRef]
- Perez, E.; Kocian, T.S.; Kuehl, J.; Reed, H.L. Stability of Hypersonic Compression Cones. AIAA Paper AIAA Paper 2012–2962. In Proceedings of the 42nd AIAA Fluid Dynamics Conference and Exhibit, New Orleans, LO, USA, 25–28 June 2012. [Google Scholar] [CrossRef]
- Kuehl, J. Thermoacoustic Interpretation of Second-Mode Instability. AIAA J. 2018, 56, 3585–3592. [Google Scholar] [CrossRef]


| Mach | Re/m | [kg/m] | T [K] | u [m/s] | T [K] | |
|---|---|---|---|---|---|---|
| Tunnel | 6 | 11.0 × 10 | 0.0432 | 53.0488 | 875.9795 | 300 |
| Flight | 5.3 | 13.42 × 10 | 0.1190 | 201.4 | 1509.2075 | 393.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, A.A.; Liang, T.; Batista, A.; Kuehl, J. On Energy Redistribution for the Nonlinear Parabolized Stability Equations Method. Fluids 2022, 7, 264. https://doi.org/10.3390/fluids7080264
Khan AA, Liang T, Batista A, Kuehl J. On Energy Redistribution for the Nonlinear Parabolized Stability Equations Method. Fluids. 2022; 7(8):264. https://doi.org/10.3390/fluids7080264
Chicago/Turabian StyleKhan, Arham Amin, Tony Liang, Armani Batista, and Joseph Kuehl. 2022. "On Energy Redistribution for the Nonlinear Parabolized Stability Equations Method" Fluids 7, no. 8: 264. https://doi.org/10.3390/fluids7080264
APA StyleKhan, A. A., Liang, T., Batista, A., & Kuehl, J. (2022). On Energy Redistribution for the Nonlinear Parabolized Stability Equations Method. Fluids, 7(8), 264. https://doi.org/10.3390/fluids7080264






