Stability of a Regularized Casson Flow down an Incline: Comparison with the Bingham Case
Abstract
1. Introduction
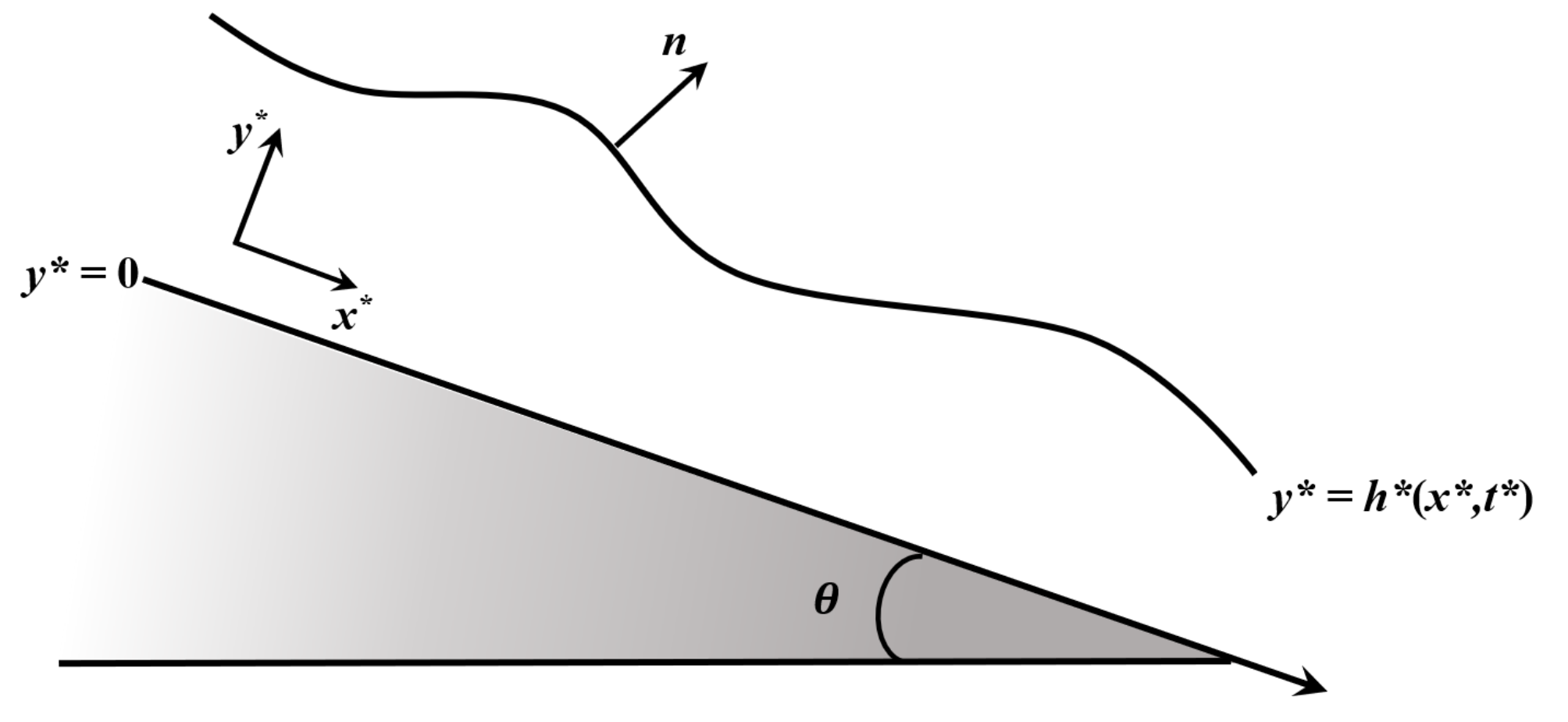
2. Mathematical Model
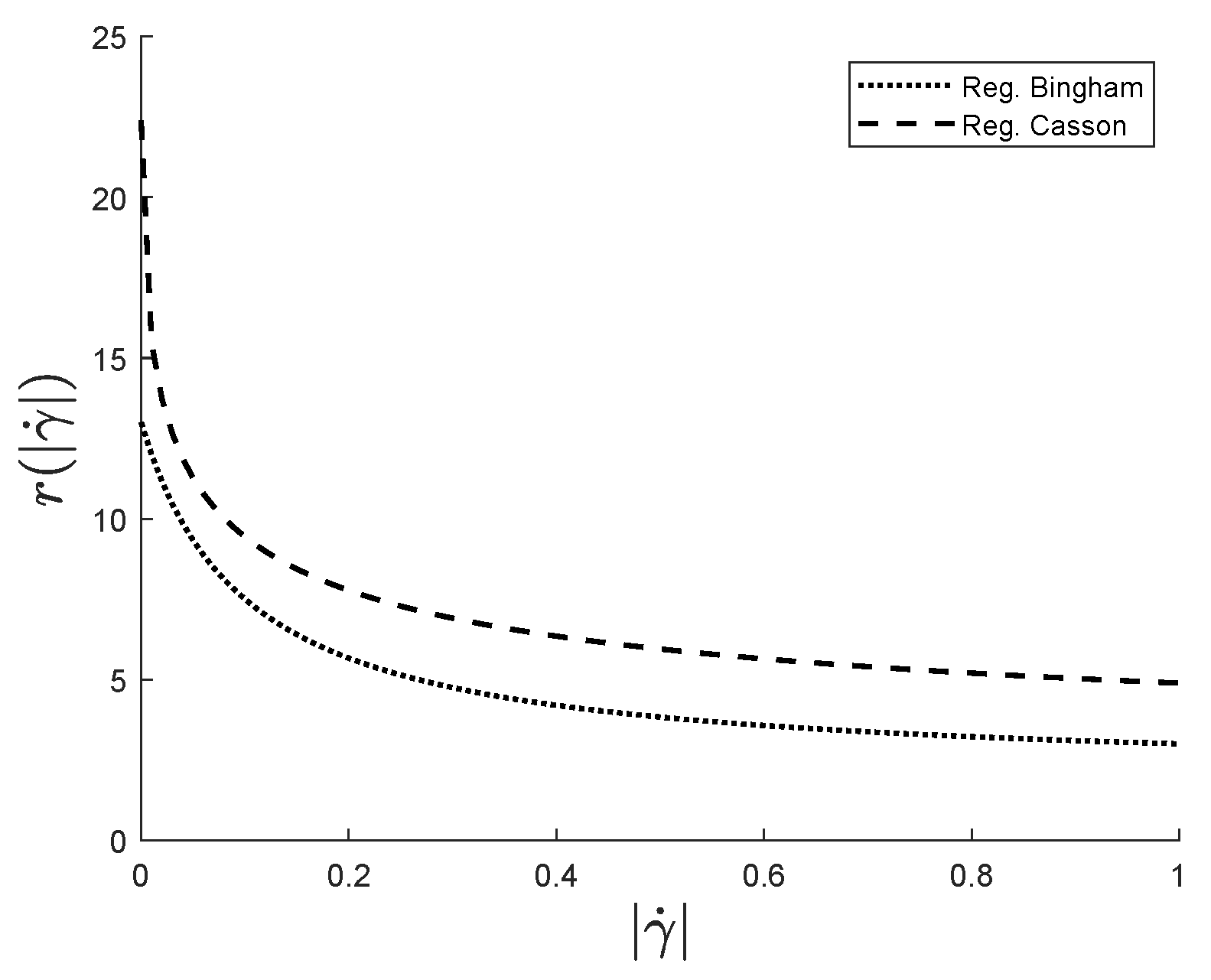
3. Regularized Casson
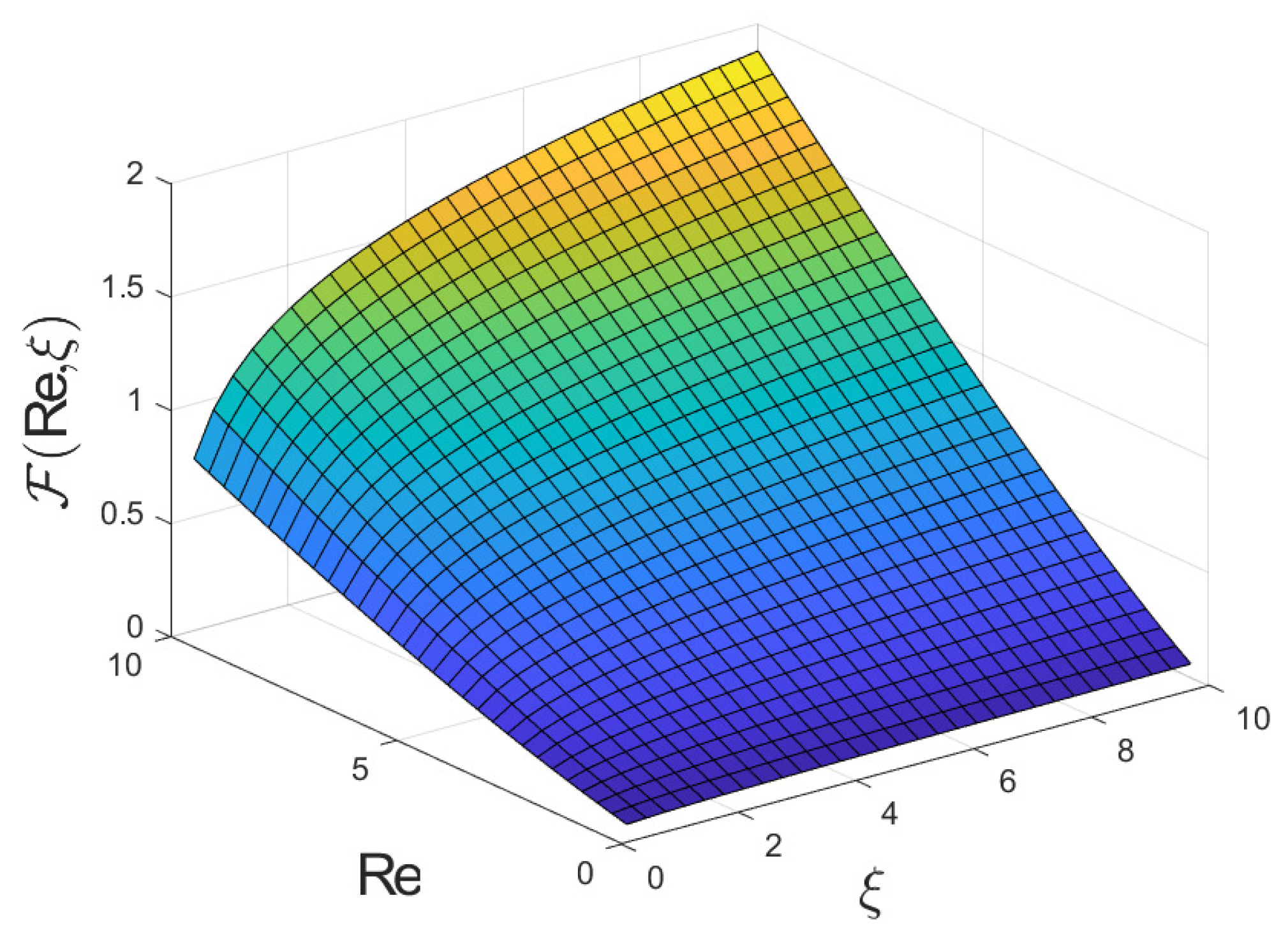
4. Linear Stability Furthermore, Long-Wave Approximation
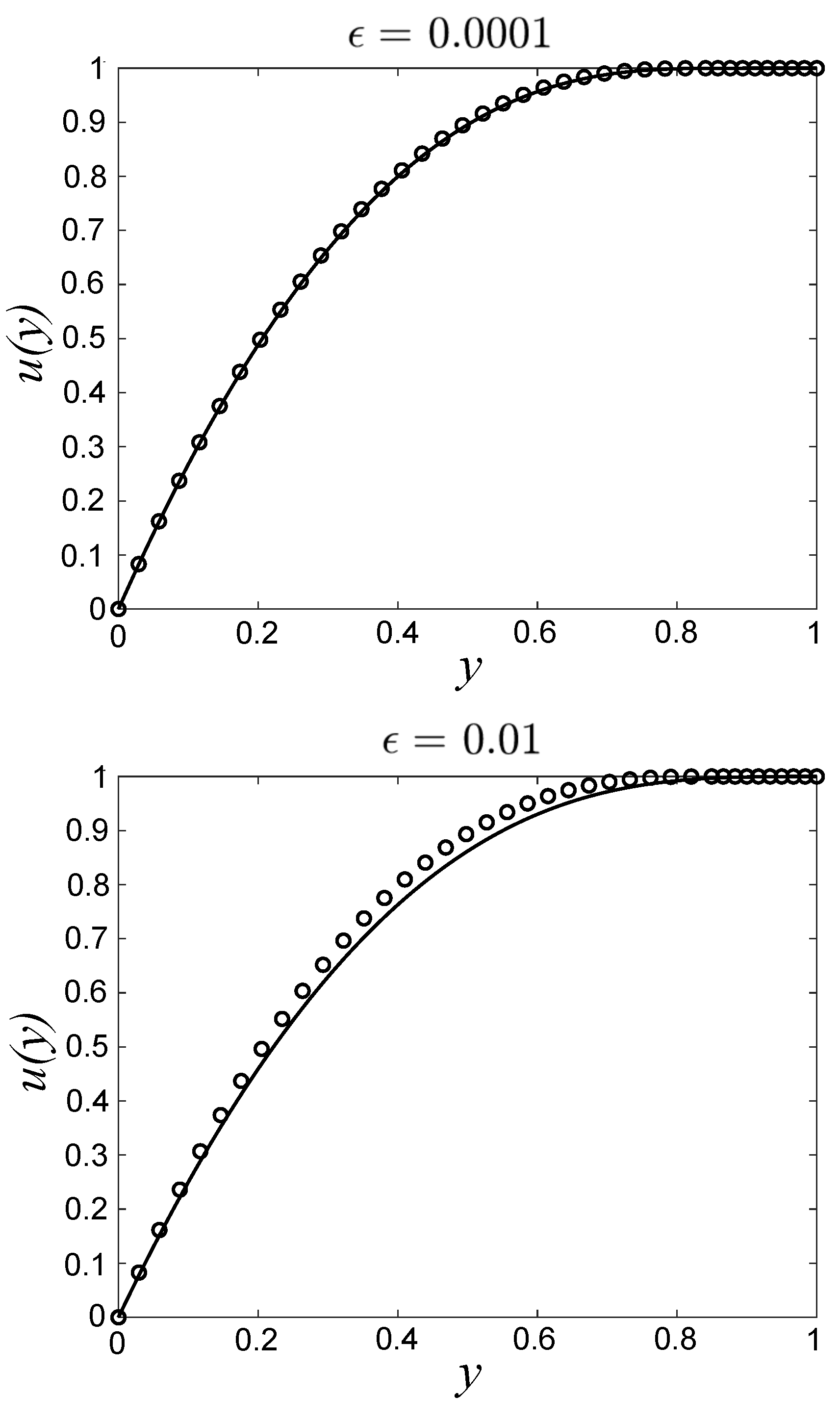
5. Results
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bingham, E.C. Fluidity and Plasticity; McGraw-Hill: New York, NY, USA, 1922. [Google Scholar]
- Herschel, W.H.; Bulkley, R. Konsistenzmessungen von gummi-benzollosungen. Kolloid-Z. 1926, 39, 291–300. [Google Scholar] [CrossRef]
- Casson, N. A Flow Equation for Pigment-oil Suspensions of the Printing Ink Type. In Rheology of Disperse Systems; Mill, C.C., Ed.; Pergamon Press: Oxford, UK, 1959; pp. 84–104. [Google Scholar]
- Benjamin, T.B. Wave formation in laminar flow down an inclined plane. J. Fluid Mech. 1957, 2, 554. [Google Scholar] [CrossRef]
- Yih, C.-S. Stability of liquid flow down an inclined plane. Phys. Fluids 1963, 6, 321. [Google Scholar] [CrossRef]
- Liu, J.; Paul, J.D.; Gollub, J.P. Measurements of the primary instabilities of film flows. J. Fluid Mech. 1993, 250, 69–101. [Google Scholar] [CrossRef]
- Allouche, M.H.; Millet, S.; Botton, V.; Henry, D.; Hadid, H.B.; Rousset, F. Stability of a flow down an incline with respect to two-dimensional and three-dimensional disturbances for Newtonian and non-Newtonian fluids. Phys. Rev. E 2015, 92, 063010. [Google Scholar] [CrossRef]
- Allouche, M.H.; Botton, V.; Millet, S.; Henry, D.; Dagois-Bohy, S.; Güzel, B.; Hadid, H. B. Primary instability of a shear-thinning film flow down an incline: Experimental study. J. Fluid Mech. 2017, 821, R1. [Google Scholar] [CrossRef]
- Balmforth, N.J.; Liu, J.J. Roll waves in mud. J. Fluid Mech. 2004, 519, 33–54. [Google Scholar] [CrossRef]
- Calusi, B.; Farina, A.; Fusi, L.; Rosso, F. Long-wave instability of a regularized Bingham flow down an incline. Phys. Fluids 2022, 34, 054111. [Google Scholar] [CrossRef]
- Chakraborty, S.; Sheu, T.W.-H.; Ghosh, S. Dynamics and stability of a power-law film flowing down a slippery slope. Phys. Fluids 2019, 31, 013102. [Google Scholar] [CrossRef]
- Falsaperla, P.; Giacobbe, A.; Mulone, G. Stability of the plane Bingham–Poiseuille flow in an inclined channel. Fluids 2020, 5, 141. [Google Scholar] [CrossRef]
- Fernandez-Nieto, E.D.; Noble, P.; Vila, J.-P. Shallow water equations for non-Newtonian fluids. J. Non-Newtonian Fluid Mech. 2010, 165, 712–732. [Google Scholar] [CrossRef]
- Forterre, Y.; Pouliquen, O. Long-surface-wave instability in dense granular flows. J. Fluid Mech. 2003, 486, 21–50. [Google Scholar] [CrossRef]
- Fusi, L. Channel flow of viscoplastic fluids with pressure-dependent rheological parameters. Phys. Fluids 2018, 30, 073102. [Google Scholar] [CrossRef]
- Fusi, L.; Calusi, B.; Farina, A.; Rosso, F. Stability of laminar viscoplastic flows down an inclined open channel. Eur. J. Mech.-B/Fluid 2022, 95, 137–147. [Google Scholar] [CrossRef]
- Hu, J.; Millet, S.; Botton, V.; Hadid, H.B.; Henry, D. Inertialess temporal and spatio-temporal stability analysis of the two-layer film flow with density stratification. Phys. Fluids 2006, 18, 104101. [Google Scholar] [CrossRef]
- Hu, J.; Yin, X.Y.; Hadid, H.B.; Henry, D. Linear temporal and spatiotemporal stability analysis of two-layer falling films with density stratification. Phys. Rev. E 2008, 77, 026302. [Google Scholar] [CrossRef]
- Hu, J.; Hadid, H.B.; Henry, D.; Mojtabi, A. Linear temporal and spatiotemporal stability analysis of a binary liquid film flowing down an inclined uniformly heated plate. J. Fluid Mech. 2008, 599, 269–298. [Google Scholar] [CrossRef][Green Version]
- Hu, T.; Fu, Q.F.; Xing, Y.; Yang, L.J.; Xie, L. Stability of a thin viscoelastic film falling down an inclined plane. Phys. Rev. Fluids 2021, 6, 083902. [Google Scholar] [CrossRef]
- Métivier, C.; Nouar, C. Stability of a Rayleigh–Bénard Poiseuille flow for yield stress fluids—Comparison between Bingham and regularized models. Int. J. Non-Linear Mech. 2011, 46, 1205–1212. [Google Scholar] [CrossRef]
- Millet, S.; Botton, V.; Rousset, F.; Hadid, H.B. Wave celerity on a shearthinning fluid film flowing down an incline. Phys. Fluids 2008, 20, 031701. [Google Scholar] [CrossRef]
- Millet, S.; Botton, V.; Hadid, H.B.; Henry, D.; Rousset, F. Stability of twolayer shear-thinning film flows. Phys. Rev. E 2013, 88, 043004. [Google Scholar] [CrossRef]
- Millet, S.; Usha, R.; Botton, V.; Rousset, F. The mechanism of long-wave instability in a shear-thinning film flow on a porous substrate. Acta Mech. 2019, 230, 2201–2220. [Google Scholar] [CrossRef]
- Mogilevskiy, E. Stability of a non-Newtonian falling film due to three-dimensional disturbances. Phys. Fluids 2020, 32, 073101. [Google Scholar] [CrossRef]
- Ng, C.-O.; Mei, C.C. Roll waves on a shallow layer of mud modelled as a power-law fluid. J. Fluid Mech. 1994, 263, 151–184. [Google Scholar] [CrossRef]
- Noble, P.; Vila, J.-P. Thin power-law film flow down an inclined plane: Consistent shallow-water models and stability under large-scale perturbations. J. Fluid Mech. 2013, 735, 29–60. [Google Scholar] [CrossRef]
- Mounkaila Noma, D.; Dagois-Bohy, S.; Millet, S.; Botton, V.; Henry, D.; Ben Hadid, H. Primary instability of a visco-plastic film down an inclined plane: Experimental study. J. Fluid Mech. 2021, 922, R2. [Google Scholar] [CrossRef]
- Nsom, B.; Ramifidisoa, L.; Latrache, N.; Ghaemizadeh, F. Linear stability of shear-thinning fluid down an inclined plane. J. Mol. Liquids 2019, 277, 1036–1046. [Google Scholar] [CrossRef]
- Pascal, J.P.; D’Alessio, S.J.D. Instability of power-law fluid flows down an incline subjected to wind stress. Appl. Math. Model. 2007, 31, 1229–1248. [Google Scholar] [CrossRef]
- Rousset, F.; Millet, S.; Botton, V.; Hadid, H.B. Temporal stability of carreau fluid flow down an incline. J. Fluids Eng. 2007, 129, 913–920. [Google Scholar] [CrossRef]
- Ruyer-Quil, C.; Chakraborty, S.; Dandapat, B.S. Wavy regime of a powerlaw film flow. J. Fluid Mech. 2012, 692, 220–256. [Google Scholar] [CrossRef]
- Merrill, E.W.; Margetts, W.G.; Cokelet, G.C.; Gilliland, E.R. The Casson equation and rheology of the blood near shear zero. In Proceedings Fourth International Congress on Rheology; Copley, A.L., Ed.; Interscience: New York, NY, USA, 1965; Part 4; pp. 135–143. [Google Scholar]
- Farina, A.; Fasano, A.; Rosso, F. Mathematical models for some aspects of blood microcirculation. Symmetry 2021, 13, 1020. [Google Scholar] [CrossRef]
- Fasano, A.; Sequeira, A. Hemomath: The Mathematics of Blood; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Charakopoulos, A.; Karakasidis, T.; Sarris, I. Analysis of magnetohydrodynamic channel flow through complex network analysis. Chaos 2021, 31, 043123. [Google Scholar] [CrossRef] [PubMed]
- Fusi, L. Lubrication flow of a generalized Casson fluid with pressure-dependent rheological parameters. J. Non-Newton. Fluid Mech. 2019, 274, 104199. [Google Scholar] [CrossRef]
- Guadagli, S.; Palade, L.I.; Fusi, L.; Farina, A. On a Casson Fluid Motion: Nonuniform Width Symmetric Channel and Peristaltic Flows. Fluids 2021, 6, 356. [Google Scholar] [CrossRef]
- Reddy, M.G.; Kumara, B.C.P.; Makinde, O.D. Cross Diffusion Impacts on Hydromagnetic Radiative Peristaltic Carreau-Casson Nanofluids Flow in an Irregular Channel. Defect Diffus. Forum 2017, 377, 62–83. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.; Spetsiotis, D. Molecular dynamics simulations of ion separation in nano-channel water flows using an electric field. Mol. Simul. 2019, 45, 1395–1402. [Google Scholar] [CrossRef]
- Song, L.; Huo, X.; Zhang, L.; Xie, Y.; Yang, M. Fast estimation on the pressure of detonation products of cyclotetramethylene tetranitramine through molecular dynamics simulations. Int. J. Mod. Phys. B 2021, 35, 2150106. [Google Scholar] [CrossRef]
- Astarita, G. Letter to the editor: The engineering reality of the yield stress. J. Rheol. 1990, 34, 275–277. [Google Scholar] [CrossRef]
- Barnes, H.A. The yield stress—A review or ‘πανταρϵι’—Everything flows? J. Non-Newton. Fluid Mech. 1999, 81, 133–178. [Google Scholar] [CrossRef]
- Barnes, H.A.; Walters, K. The yield stress myth? Rheol. Acta 1985, 24, 323–326. [Google Scholar] [CrossRef]
- Frigaard, I.; Nouar, C. On the usage of viscosity regularisation methods for visco-plastic fluid flow computation. J. Non-Newton. Fluid Mech. 2005, 127, 1–26. [Google Scholar] [CrossRef]
- Frigaard, I.A.; Paso, K.G.; de Souza Mendes, P.R. Bingham’s model in the oil and gas industry. Rheol. Acta 2017, 56, 259–282. [Google Scholar] [CrossRef]
- Fusi, L.; Farina, A.; Rosso, F. On the mathematical paradoxes for the flow of a viscoplastic film down an inclined surface. Int. J. Non-Linear Mech. 2014, 58, 139–150. [Google Scholar] [CrossRef]
- Fusi, L.; Farina, A.; Rosso, F. Roscani, S. Pressure driven lubrication flow of a Bingham fluid in a channel: A novel approach. J. Non-Newtonian Fluid Mech. 2015, 221, 66–75. [Google Scholar] [CrossRef]
- Bercovier, M.; Engleman, M. A finite-element method for incompressible non-Newtonian flows. J. Comput. Phys. 1980, 36, 313–326. [Google Scholar] [CrossRef]
- Papanastasiou, T.C. Flows of materials with yield. J. Rheol. 1987, 31, 385–404. [Google Scholar] [CrossRef]
- Pascal, J. P. Linear stability of fluid flow down a porous inclined plane. J. Phys. D Appl. Phys. 1999, 32, 417. [Google Scholar] [CrossRef]
- Allouche, M.; Frigaard, I.A.; Sona, G. Static wall layers in the displacement of two visco-plastic fluids in a plane channel. J. Fluid Mech. 2000, 424, 243–277. [Google Scholar] [CrossRef]


| Reg. Bingham | Reg. Casson | Reg. Bingham | Reg. Casson | |
|---|---|---|---|---|
| 0 | 14.29 | 14.29 | 2 | 2 |
| 0.01 | 14.08 | 15.61 | 2.03 | 2.15 |
| 0.1 | 12.45 | 19.08 | 2.34 | 2.52 |
| 0.5 | 9.05 | 28.13 | 4.31 | 3.30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calusi, B.; Farina, A.; Fusi, L.; Palade, L.I. Stability of a Regularized Casson Flow down an Incline: Comparison with the Bingham Case. Fluids 2022, 7, 380. https://doi.org/10.3390/fluids7120380
Calusi B, Farina A, Fusi L, Palade LI. Stability of a Regularized Casson Flow down an Incline: Comparison with the Bingham Case. Fluids. 2022; 7(12):380. https://doi.org/10.3390/fluids7120380
Chicago/Turabian StyleCalusi, Benedetta, Angiolo Farina, Lorenzo Fusi, and Liviu Iulian Palade. 2022. "Stability of a Regularized Casson Flow down an Incline: Comparison with the Bingham Case" Fluids 7, no. 12: 380. https://doi.org/10.3390/fluids7120380
APA StyleCalusi, B., Farina, A., Fusi, L., & Palade, L. I. (2022). Stability of a Regularized Casson Flow down an Incline: Comparison with the Bingham Case. Fluids, 7(12), 380. https://doi.org/10.3390/fluids7120380








