Single-Mode Solutions for Convection and Double-Diffusive Convection in Porous Media
Abstract
1. Introduction
2. Single-Mode Solutions for Double-Diffusive Convection in a Porous Medium
3. Comparisons of Single-Mode Solutions with Direct Numerical Simulations
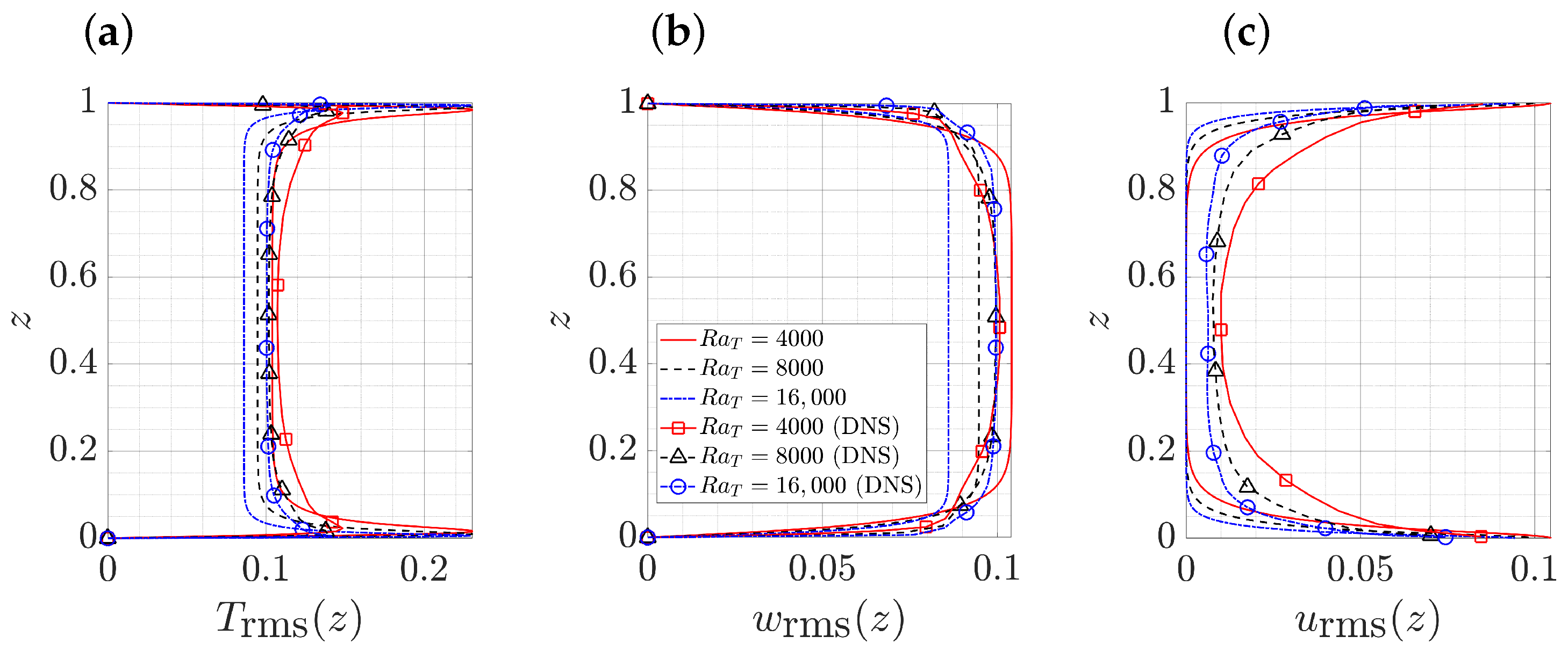
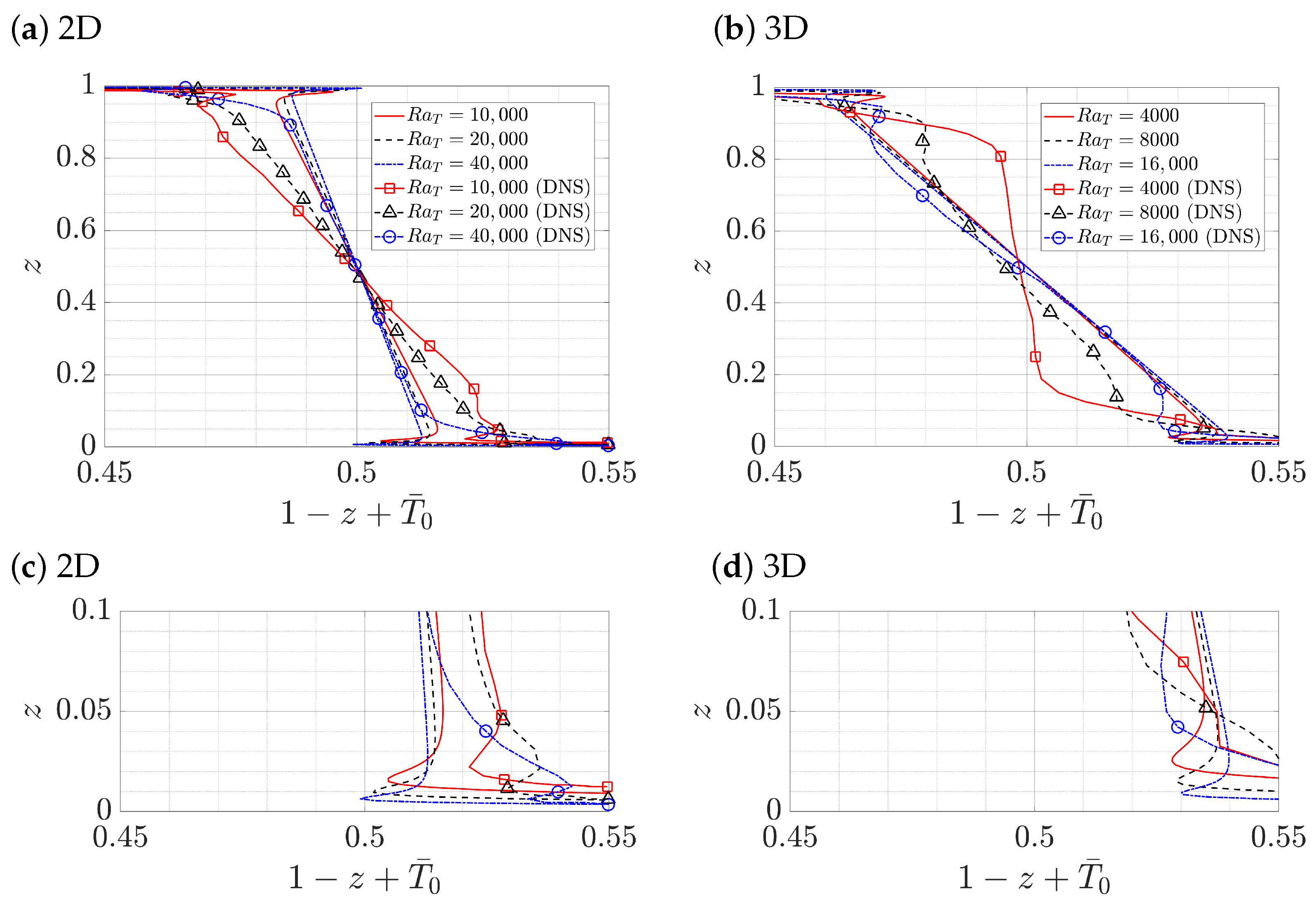
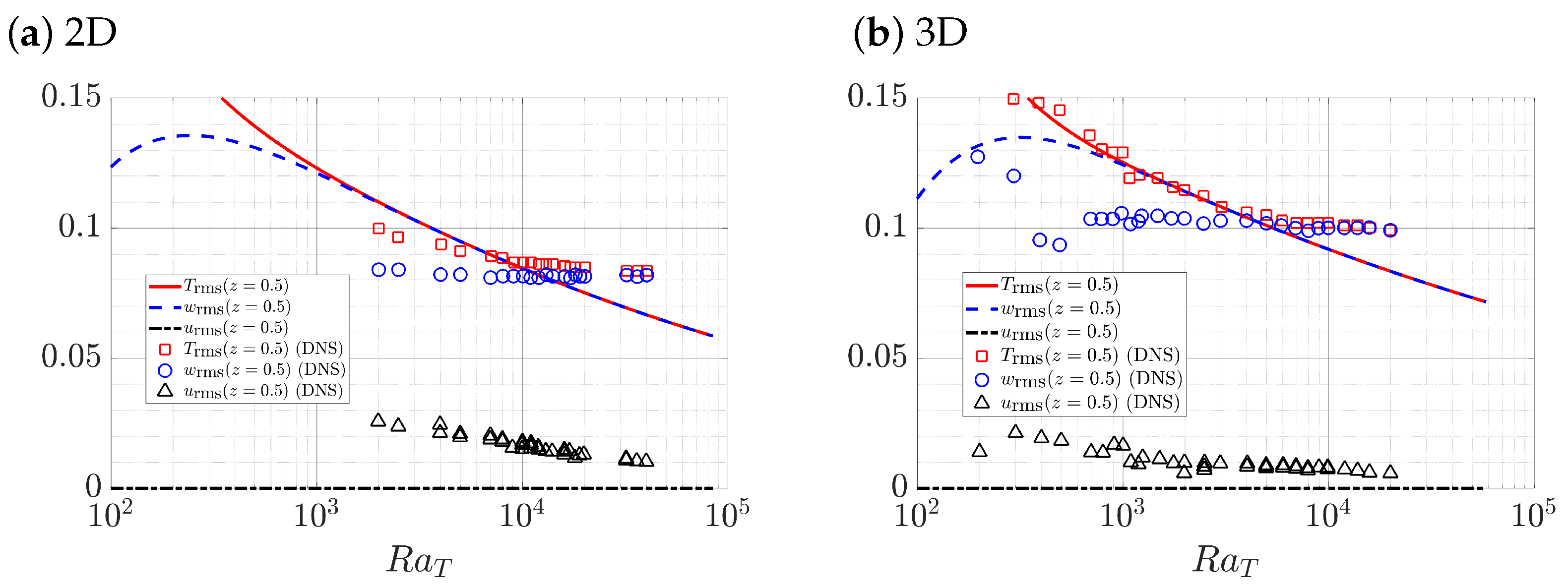
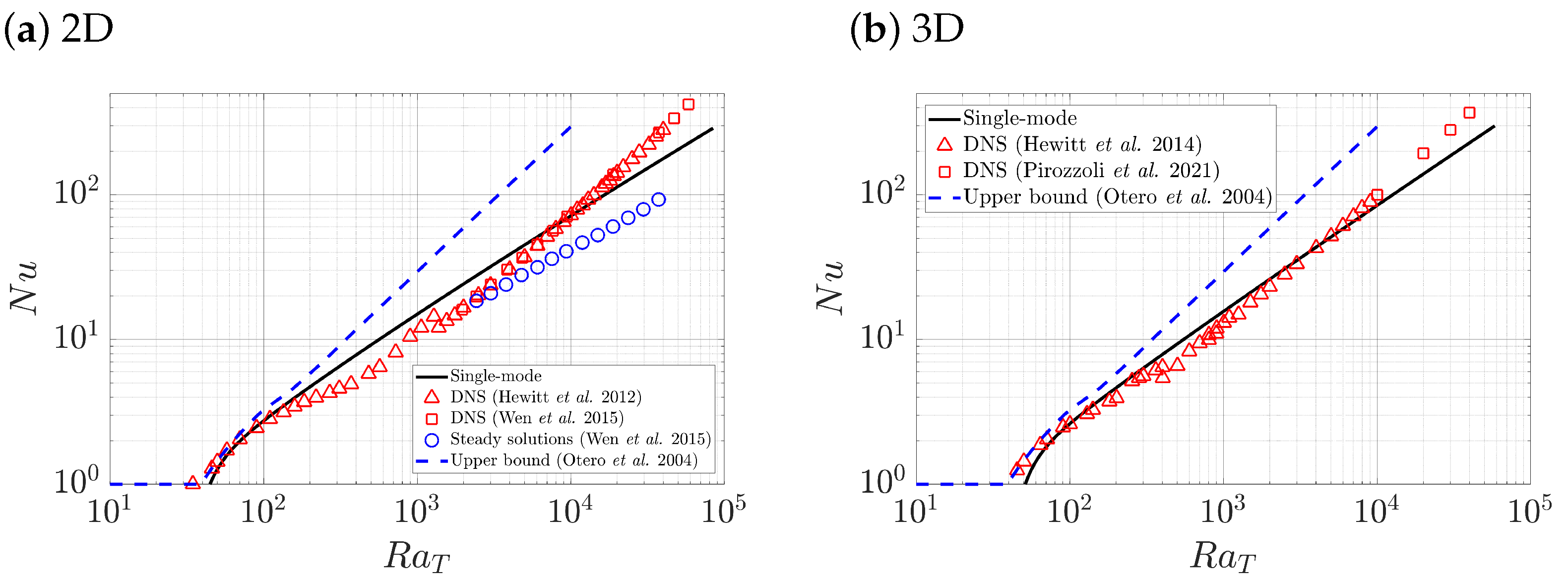
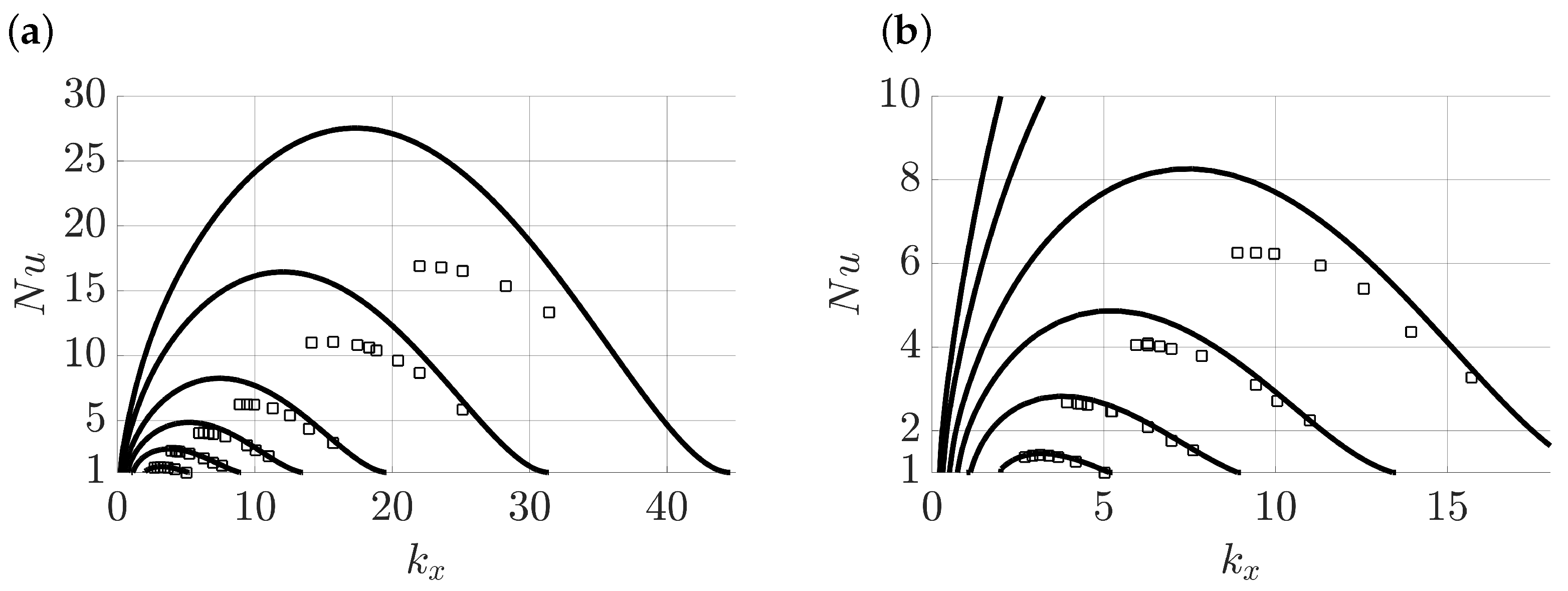
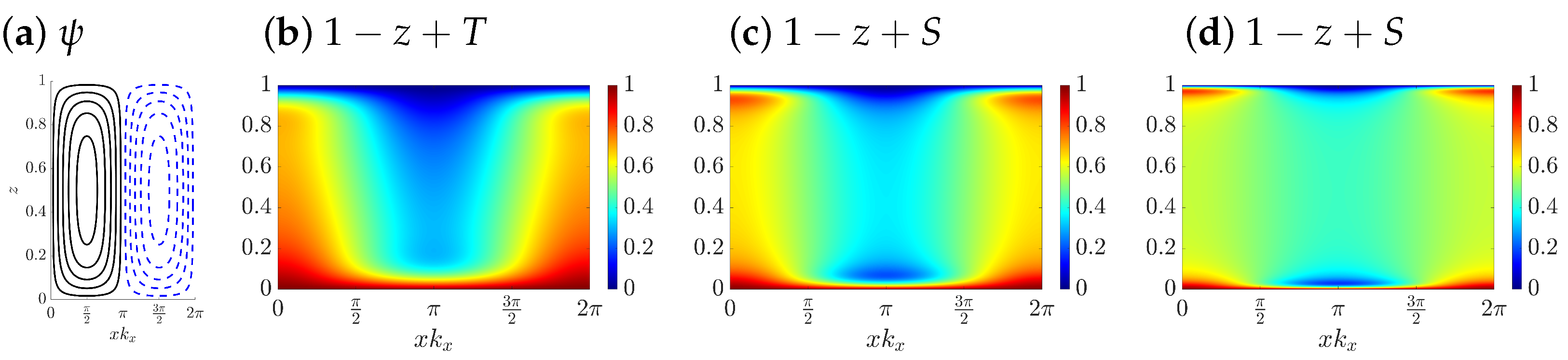
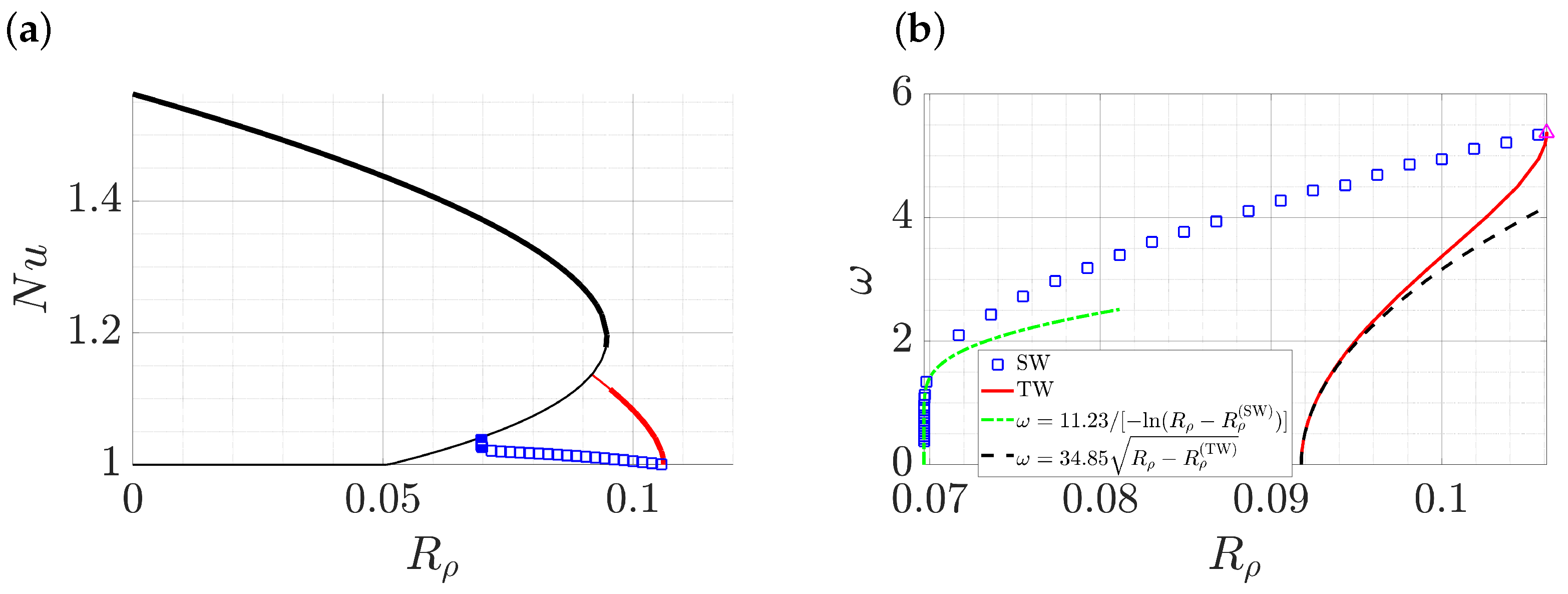
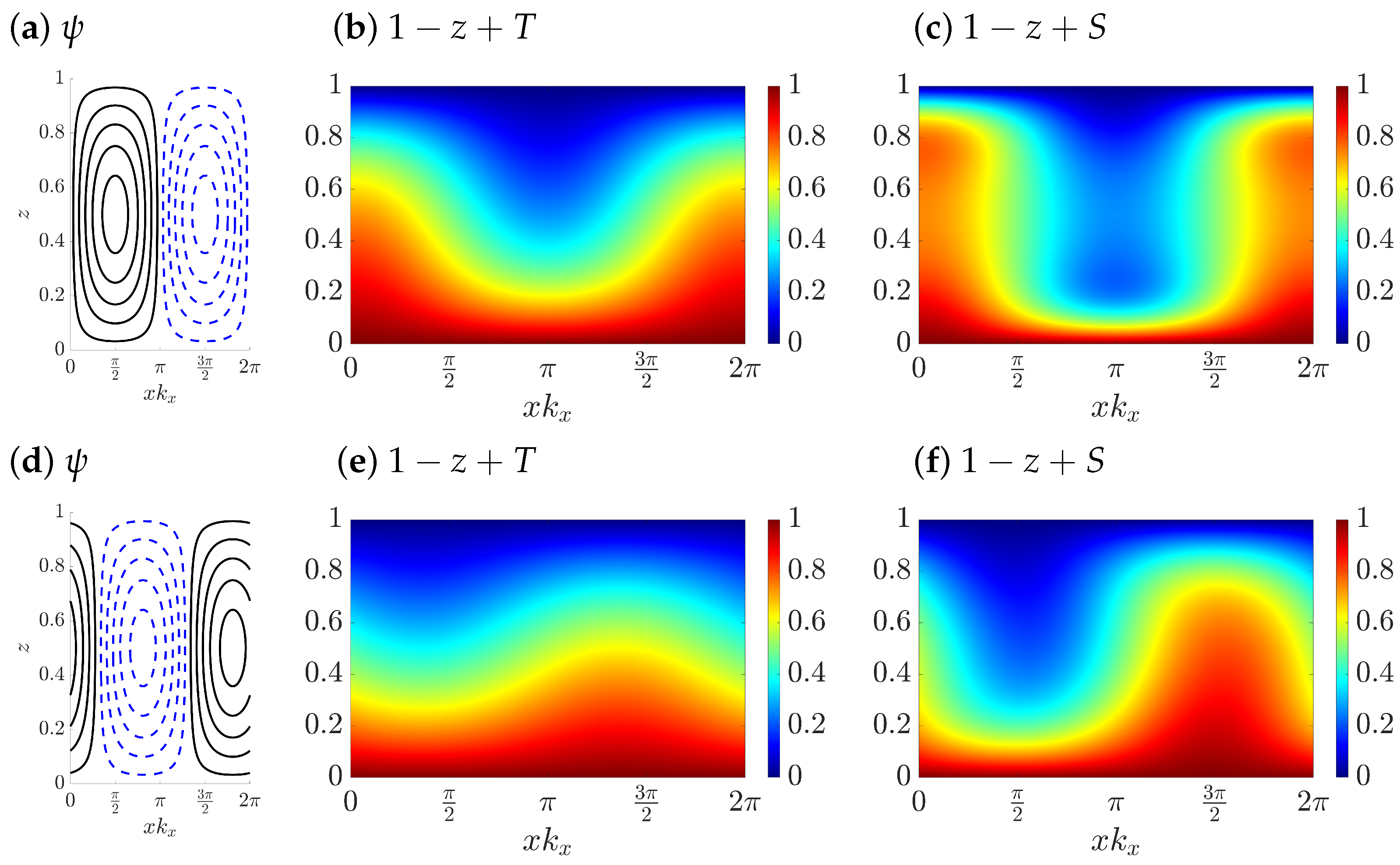
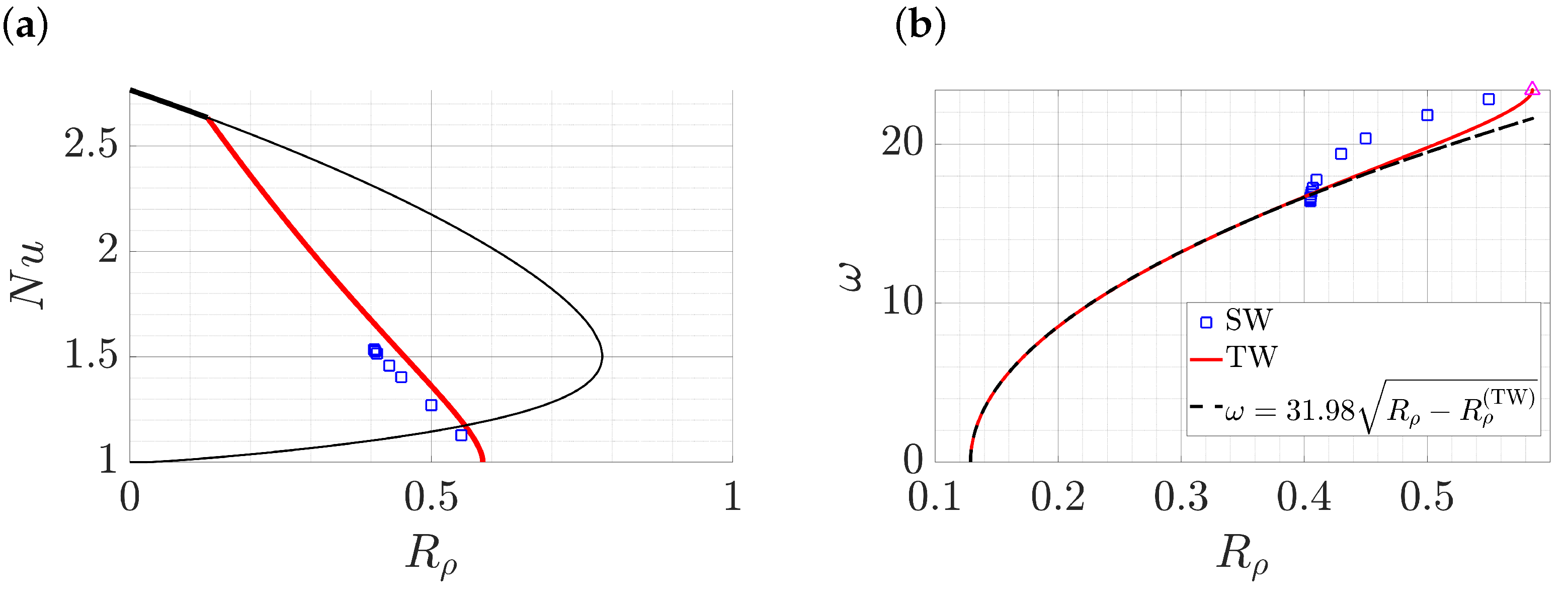
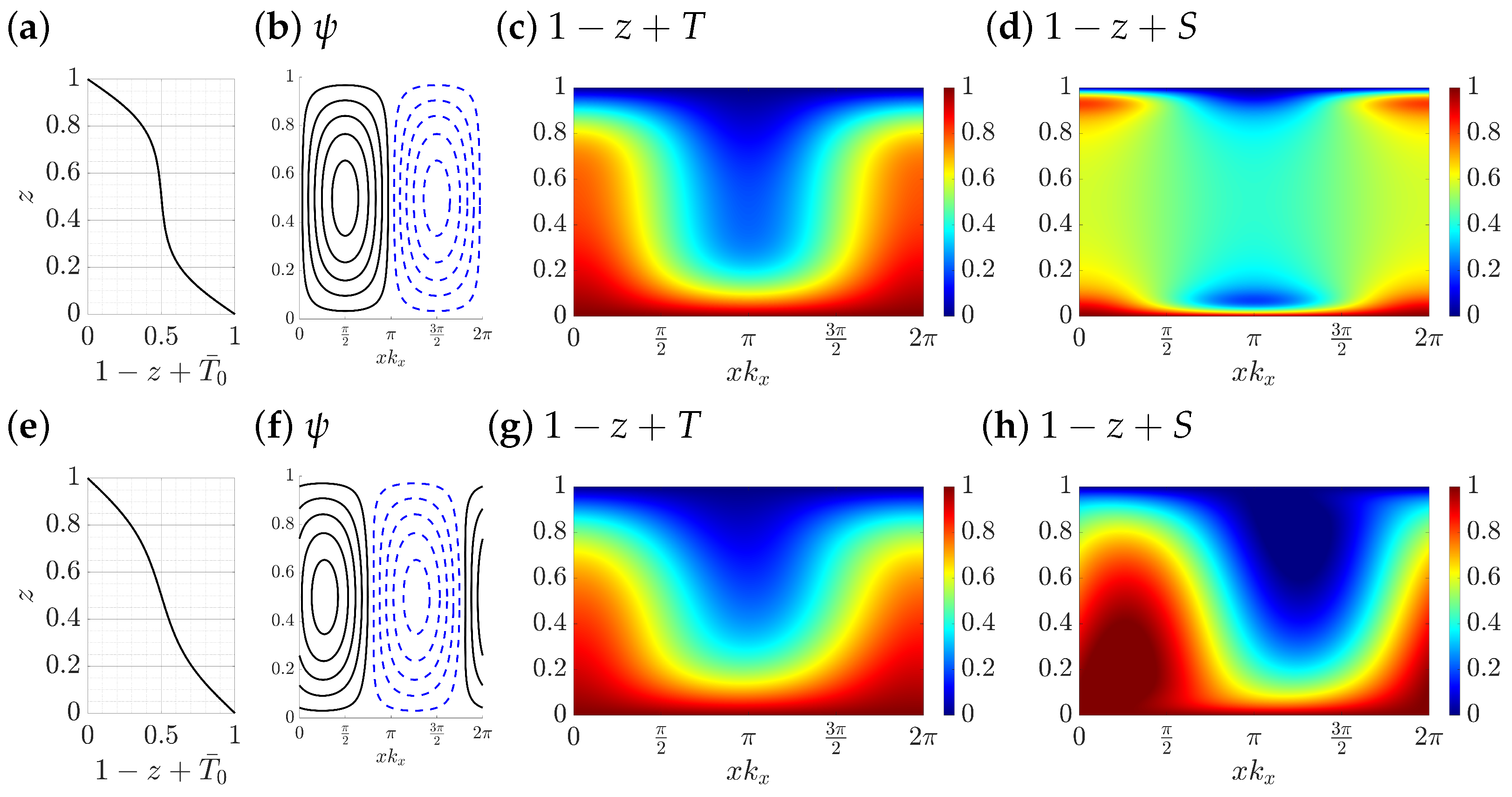
3.1. Thermal Convection with Passive Salinity
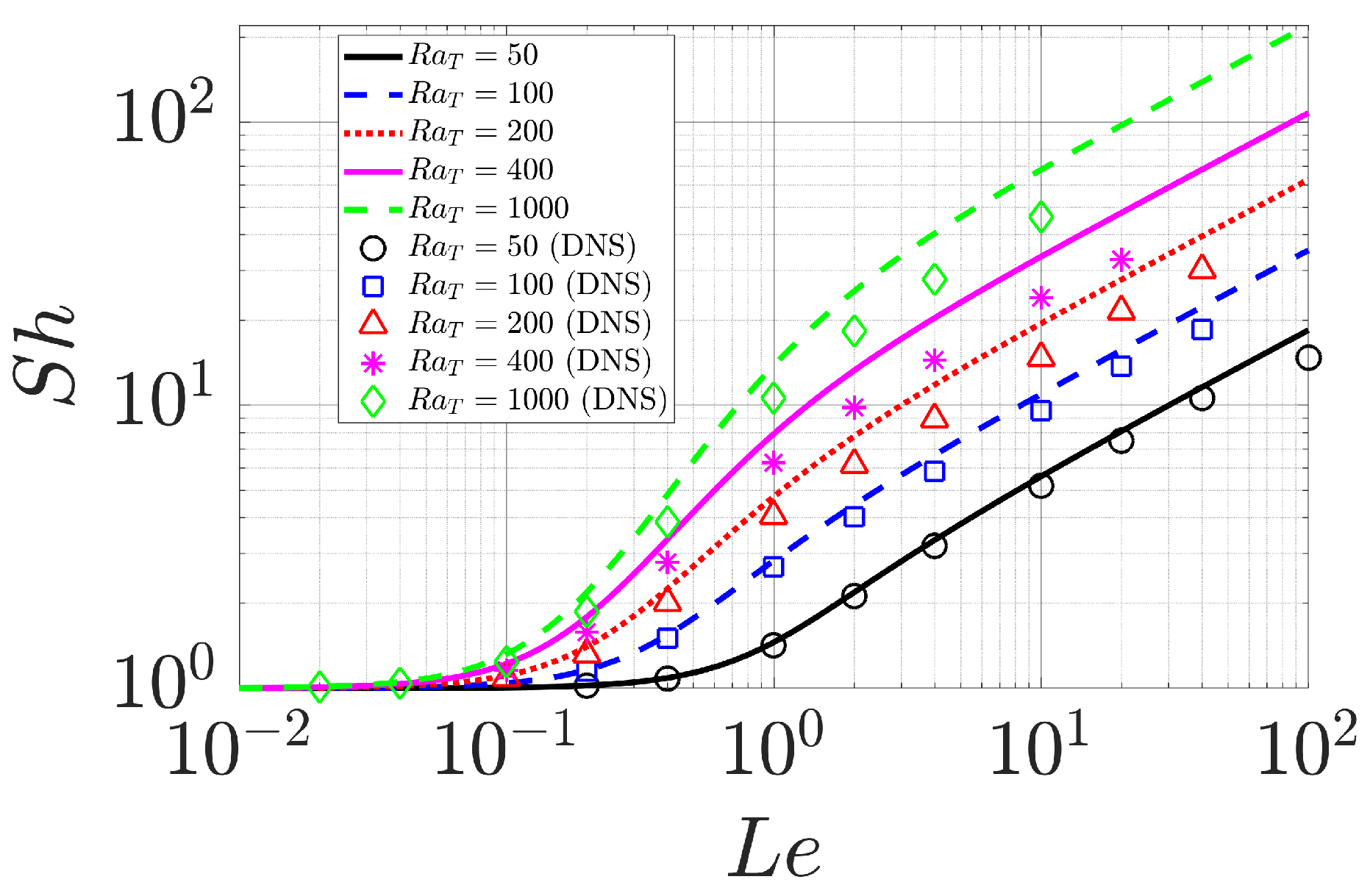
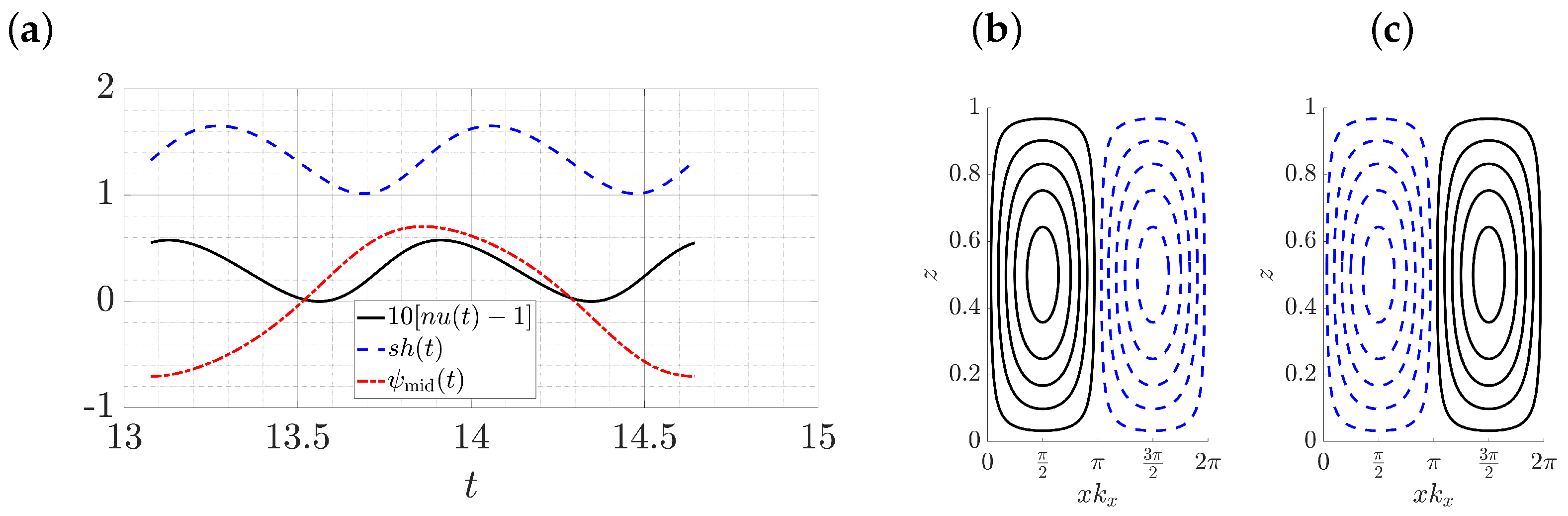
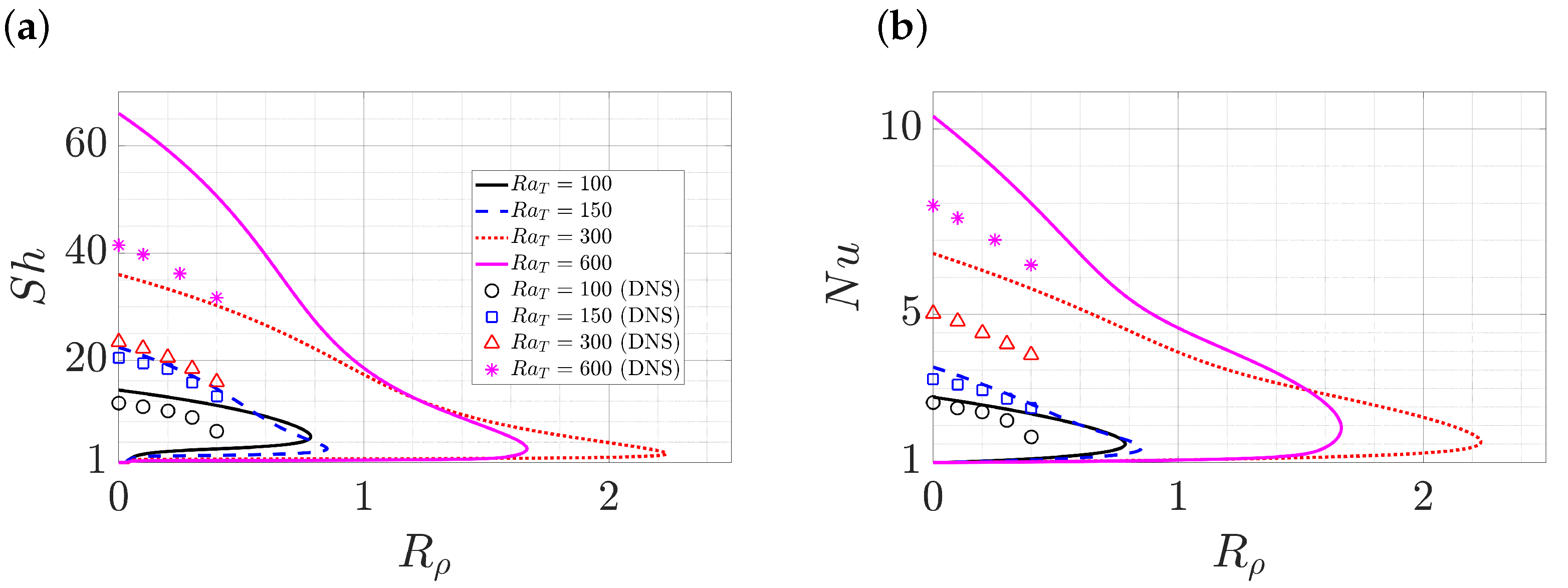
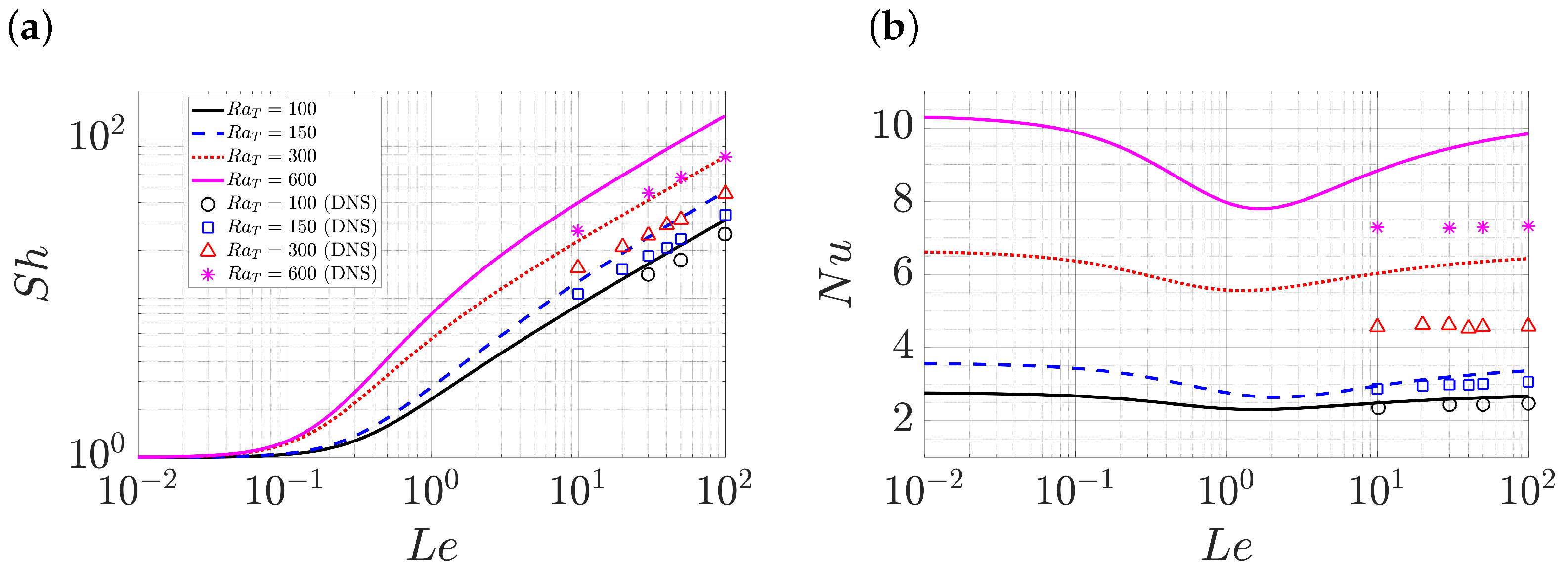
3.2. Double-Diffusive Convection with
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DNS | Direct numerical simulations |
| RBC | Rayleigh-Bénard convection |
| ODDC | Oscillatory double-diffusive convection |
| B.C. | Boundary conditions |
| NBC | Neumann boundary conditions |
| CO2 | Carbon dioxide |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| c.c. | complex conjugate |
| RMS | Root mean square |
| NLBVP | Nonlinear boundary value problem |
| SW | Standing waves |
| TW | Traveling waves |
References
- Herring, J.R. Investigation of problems in thermal convection. J. Atmos. Sci. 1963, 20, 325–338. [Google Scholar] [CrossRef]
- Herring, J.R. Investigation of problems in thermal convection: Rigid boundaries. J. Atmos. Sci. 1964, 21, 277–290. [Google Scholar] [CrossRef]
- Elder, J.W. The temporal development of a model of high Rayleigh number convection. J. Fluid Mech. 1969, 35, 417–437. [Google Scholar] [CrossRef]
- Gough, D.O.; Spiegel, E.A.; Toomre, J. Modal equations for cellular convection. J. Fluid Mech. 1975, 68, 695–719. [Google Scholar] [CrossRef]
- Toomre, J.; Gough, D.O.; Spiegel, E.A. Numerical solutions of single-mode convection equations. J. Fluid Mech. 1977, 79, 1–31. [Google Scholar] [CrossRef]
- Gough, D.O.; Toomre, J. Single-mode theory of diffusive layers in thermohaline convection. J. Fluid Mech. 1982, 125, 75–97. [Google Scholar] [CrossRef]
- Turner, J.S. The coupled turbulent transports of salt and and heat across a sharp density interface. Int. J. Heat Mass Transf. 1965, 8, 759–767. [Google Scholar] [CrossRef]
- Crapper, P.F. Measurements across a diffusive interface. Deep Sea Res. Oceanogr. Abstr. 1975, 22, 537–545. [Google Scholar] [CrossRef]
- Marmorino, G.O.; Caldwell, D.R. Heat and salt transport through a diffusive thermohaline interface. Deep Sea Res. Oceanogr. Abstr. 1976, 23, 59–67. [Google Scholar] [CrossRef]
- Paparella, F.; Spiegel, E.A.; Talon, S. Shear and mixing in oscillatory doubly diffusive convection. Geophys. Astrophys. Fluid Dyn. 2002, 96, 271–289. [Google Scholar] [CrossRef]
- Paparella, F.; Spiegel, E.A. Sheared salt fingers: Instability in a truncated system. Phys. Fluids 1999, 11, 1161–1168. [Google Scholar] [CrossRef]
- Liu, C.; Julien, K.; Knobloch, E. Staircase solutions and stability in vertically confined salt-finger convection. J. Fluid Mech. 2022, 952, A4. [Google Scholar] [CrossRef]
- Blennerhassett, P.J.; Bassom, A.P. Nonlinear high-wavenumber Bénard convection. IMA J. Appl. Math. 1994, 52, 51–77. [Google Scholar] [CrossRef]
- Lewis, S.; Rees, D.A.S.; Bassom, A.P. High wavenumber convection in tall porous containers heated from below. Q. J. Mech. Appl. Math. 1997, 50, 545–563. [Google Scholar] [CrossRef]
- Proctor, M.R.E.; Holyer, J.Y. Planform selection in salt fingers. J. Fluid Mech. 1986, 168, 241–253. [Google Scholar] [CrossRef]
- Julien, K.; Knobloch, E. Reduced models for fluid flows with strong constraints. J. Math. Phys. 2007, 48, 065405. [Google Scholar] [CrossRef]
- Taylor, G.I. Motion of solids in fluids when the flow is not irrotational. Proc. R. Soc. Lond. Ser. A 1917, 93, 99–113. [Google Scholar]
- Proudman, J. On the motion of solids in a liquid possessing vorticity. Proc. R. Soc. Lond. Ser. A 1916, 92, 408–424. [Google Scholar]
- Sprague, M.; Julien, K.; Knobloch, E.; Werne, J. Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 2006, 551, 141–174. [Google Scholar] [CrossRef]
- Grooms, I.; Julien, K.; Weiss, J.B.; Knobloch, E. Model of convective Taylor columns in rotating Rayleigh-Bénard convection. Phys. Rev. Lett. 2010, 104, 224501. [Google Scholar] [CrossRef]
- Calkins, M.A.; Julien, K.; Tobias, S.M.; Aurnou, J.M.; Marti, P. Convection-driven kinematic dynamos at low Rossby and magnetic Prandtl numbers: Single mode solutions. Phys. Rev. E 2016, 93, 023115. [Google Scholar] [CrossRef] [PubMed]
- Calkins, M.A.; Long, L.; Nieves, D.; Julien, K.; Tobias, S.M. Convection-driven kinematic dynamos at low Rossby and magnetic Prandtl numbers. Phys. Rev. Fluids 2016, 1, 083701. [Google Scholar] [CrossRef]
- Yang, Y.; van der Poel, E.P.; Ostilla-Mónico, R.; Sun, C.; Verzicco, R.; Grossmann, S.; Lohse, D. Salinity transfer in bounded double diffusive convection. J. Fluid Mech. 2015, 768, 476–491. [Google Scholar] [CrossRef]
- Xie, J.H.; Julien, K.; Knobloch, E. Jet formation in salt-finger convection: A modified Rayleigh–Bénard problem. J. Fluid Mech. 2019, 858, 228–263. [Google Scholar] [CrossRef]
- Hewitt, D.R.; Neufeld, J.A.; Lister, J.R. Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 2012, 108, 224503. [Google Scholar] [CrossRef]
- Wen, B.; Corson, L.T.; Chini, G.P. Structure and stability of steady porous medium convection at large Rayleigh number. J. Fluid Mech. 2015, 772, 197–224. [Google Scholar] [CrossRef]
- Hewitt, D.R.; Neufeld, J.A.; Lister, J.R. High Rayleigh number convection in a three-dimensional porous medium. J. Fluid Mech. 2014, 748, 879–895. [Google Scholar] [CrossRef]
- Pirozzoli, S.; De Paoli, M.; Zonta, F.; Soldati, A. Towards the ultimate regime in Rayleigh–Darcy convection. J. Fluid Mech. 2021, 911, R4. [Google Scholar] [CrossRef]
- Hewitt, D.R. Vigorous convection in porous media. Proc. R. Soc. A 2020, 476, 20200111. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Vafai, K. Handbook of Porous Media; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Mojtabi, A.; Charrier-Mojtabi, M.C. Double-diffusive convection in porous media. In Handbook of Porous Media; CRC Press: Boca Raton, FL, USA, 2005; pp. 287–338. [Google Scholar]
- Cheng, P. Heat transfer in geothermal systems. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1979; Volume 14, pp. 1–105. [Google Scholar]
- Wooding, R.A.; Tyler, S.W.; White, I. Convection in groundwater below an evaporating salt lake: 1. Onset of instability. Water Resour. Res. 1997, 33, 1199–1217. [Google Scholar] [CrossRef]
- Wooding, R.A.; Tyler, S.W.; White, I.; Anderson, P.A. Convection in groundwater below an evaporating salt lake: 2. Evolution of fingers or plumes. Water Resour. Res. 1997, 33, 1219–1228. [Google Scholar] [CrossRef]
- Huppert, H.E.; Neufeld, J.A. The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 2014, 46, 255–272. [Google Scholar] [CrossRef]
- Neufeld, J.A.; Hesse, M.A.; Riaz, A.; Hallworth, M.A.; Tchelepi, H.A.; Huppert, H.E. Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 2010, 37, L22404. [Google Scholar] [CrossRef]
- Caltagirone, J.P. Thermoconvective instabilities in a horizontal porous layer. J. Fluid Mech. 1975, 72, 269–287. [Google Scholar] [CrossRef]
- Trevisan, O.V.; Bejan, A. Mass and heat transfer by high Rayleigh number convection in a porous medium heated from below. Int. J. Heat Mass Transf. 1987, 30, 2341–2356. [Google Scholar] [CrossRef]
- Rosenberg, N.D.; Spera, F.J. Thermohaline convection in a porous medium heated from below. Int. J. Heat Mass Transf. 1992, 35, 1261–1273. [Google Scholar] [CrossRef]
- Goyeau, B.; Songbe, J.P.; Gobin, D. Numerical study of double-diffusive natural convection in a porous cavity using the Darcy-Brinkman formulation. Int. J. Heat Mass Transf. 1996, 39, 1363–1378. [Google Scholar] [CrossRef]
- Mamou, M.; Vasseur, P.; Bilgen, E. Double-diffusive convection instability in a vertical porous enclosure. J. Fluid Mech. 1998, 368, 263–289. [Google Scholar] [CrossRef]
- Mamou, M.; Vasseur, P. Thermosolutal bifurcation phenomena in porous enclosures subject to vertical temperature and concentration gradients. J. Fluid Mech. 1999, 395, 61–87. [Google Scholar] [CrossRef]
- Mahidjiba, A.; Mamou, M.; Vasseur, P. Onset of double-diffusive convection in a rectangular porous cavity subject to mixed boundary conditions. Int. J. Heat Mass Transf. 2000, 43, 1505–1522. [Google Scholar] [CrossRef]
- Bahloul, A.; Boutana, N.; Vasseur, P. Double-diffusive and Soret-induced convection in a shallow horizontal porous layer. J. Fluid Mech. 2003, 491, 325–352. [Google Scholar] [CrossRef]
- Knobloch, E.; Deane, A.E.; Toomre, J.; Moore, D.R. Doubly diffusive waves. Contemp. Math. 1986, 56, 203–216. [Google Scholar]
- Deane, A.E.; Knobloch, E.; Toomre, J. Traveling waves and chaos in thermosolutal convection. Phys. Rev. A 1987, 36, 2862–2869. [Google Scholar] [CrossRef] [PubMed]
- Knobloch, E. Oscillatory convection in binary mixtures. Phys. Rev. A 1986, 34, 1538–1549. [Google Scholar] [CrossRef]
- Knobloch, E.; Moore, D.R. Minimal model of binary fluid convection. Phys. Rev. A 1990, 42, 4693–4709. [Google Scholar] [CrossRef]
- Predtechensky, A.A.; McCormick, W.D.; Swift, J.B.; Rossberg, A.G.; Swinney, H.L. Traveling wave instability in sustained double-diffusive convection. Phys. Fluids 1994, 6, 3923–3935. [Google Scholar] [CrossRef]
- Predtechensky, A.A.; McCormick, W.D.; Swift, J.B.; Noszticzius, Z.; Swinney, H.L. Onset of traveling waves in isothermal double diffusive convection. Phys. Rev. Lett. 1994, 72, 218–221. [Google Scholar] [CrossRef]
- Otero, J.; Dontcheva, L.A.; Johnston, H.; Worthing, R.A.; Kurganov, A.; Petrova, G.; Doering, C.R. High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 2004, 500, 263–281. [Google Scholar] [CrossRef]
- Stern, M.E. Collective instability of salt fingers. J. Fluid Mech. 1969, 35, 209–218. [Google Scholar] [CrossRef]
- Holyer, J.Y. The stability of long, steady, two-dimensional salt fingers. J. Fluid Mech. 1984, 147, 169–185. [Google Scholar] [CrossRef]
- Radko, T. Double-Diffusive Convection; Cambridge University Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Uecker, H.; Wetzel, D.; Rademacher, J.D.M. pde2path-A Matlab package for continuation and bifurcation in 2D elliptic systems. Numer. Math. Theory Methods Appl. 2014, 7, 58–106. [Google Scholar] [CrossRef]
- Uecker, H. Numerical Continuation and Bifurcation in Nonlinear PDEs; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Weideman, J.A.; Reddy, S.C. A MATLAB differentiation matrix suite. ACM Trans. Math. Software 2000, 26, 465–519. [Google Scholar] [CrossRef]
- Uecker, H. pde2path without Finite Elements. 2021. Available online: http://www.staff.uni-oldenburg.de/hannes.uecker/pde2path/tuts/modtut.pdf (accessed on 12 December 2021).
- Burns, K.J.; Vasil, G.M.; Oishi, J.S.; Lecoanet, D.; Brown, B.P. Dedalus: A flexible framework for numerical simulations with spectral methods. Phys. Rev. Res. 2020, 2, 023068. [Google Scholar] [CrossRef]
- Bassom, A.P.; Zhang, K. Strongly nonlinear convection cells in a rapidly rotating fluid layer. Geophys. Astrophys. Fluid Dyn. 1994, 76, 223–238. [Google Scholar] [CrossRef]
- Rademacher, J.D.M.; Uecker, H. Symmetries, Freezing, and Hopf Bifurcations of Traveling Waves in pde2path. 2017. Available online: https://www.staff.uni-oldenburg.de/hannes.uecker/pde2path/tuts/symtut.pdf (accessed on 15 December 2021).
- Turner, J.S. Buoyancy Effects in Fluids; Cambridge University Press: Cambridge, UK, 1979. [Google Scholar]
- Lecoanet, D.; Le Bars, M.; Burns, K.J.; Vasil, G.M.; Brown, B.P.; Quataert, E.; Oishi, J.S. Numerical simulations of internal wave generation by convection in water. Phys. Rev. E 2015, 91, 063016. [Google Scholar] [CrossRef]
- Lecoanet, D.; Quataert, E. Internal gravity wave excitation by turbulent convection. Mon. Not. R. Astron. Soc. 2013, 430, 2363–2376. [Google Scholar] [CrossRef]
- Lecoanet, D.; Schwab, J.; Quataert, E.; Bildsten, L.; Timmes, F.X.; Burns, K.J.; Vasil, G.M.; Oishi, J.S.; Brown, B.P. Turbulent chemical diffusion in convectively bounded carbon flames. Astrophys. J. 2016, 832, 71. [Google Scholar] [CrossRef]
- Couston, L.A.; Lecoanet, D.; Favier, B.; Le Bars, M. Dynamics of mixed convective–stably-stratified fluids. Phys. Rev. Fluids 2017, 2, 094804. [Google Scholar] [CrossRef]
- Le Bars, M.; Lecoanet, D.; Perrard, S.; Ribeiro, A.; Rodet, L.; Aurnou, J.M.; Le Gal, P. Experimental study of internal wave generation by convection in water. Fluid Dyn. Res. 2015, 47, 045502. [Google Scholar] [CrossRef]
- Couston, L.A.; Lecoanet, D.; Favier, B.; Le Bars, M. The energy flux spectrum of internal waves generated by turbulent convection. J. Fluid Mech. 2018, 854, R3. [Google Scholar] [CrossRef]
- Bouffard, M.; Favier, B.; Lecoanet, D.; Le Bars, M. Internal gravity waves in a stratified layer atop a convecting liquid core in a non-rotating spherical shell. Geophys. J. Int. 2022, 228, 337–354. [Google Scholar] [CrossRef]
- Léard, P.; Favier, B.; Le Gal, P.; Le Bars, M. Coupled convection and internal gravity waves excited in water around its density maximum at 4° C. Phys. Rev. Fluids 2020, 5, 024801. [Google Scholar] [CrossRef]
- Le Bars, M.; Couston, L.A.; Favier, B.; Léard, P.; Lecoanet, D.; Le Gal, P. Fluid dynamics of a mixed convective/stably stratified system—A review of some recent works. Comptes Rendus. Phys. 2020, 21, 151–164. [Google Scholar] [CrossRef]
- Aidun, C.K.; Steen, P.H. Transition to oscillatory convective heat transfer in a fluid-saturated porous medium. J. Thermophys. Heat Transf. 1987, 1, 268–273. [Google Scholar] [CrossRef]
- Graham, M.D.; Steen, P.H. Plume formation and resonant bifurcations in porous-media convection. J. Fluid Mech. 1994, 272, 67–90. [Google Scholar] [CrossRef]
- Graham, M.D.; Steen, P.H. Strongly interacting travelling waves and quasiperiodic dynamics in porous medium convection. Phys. D 1992, 54, 331–350. [Google Scholar] [CrossRef]
- Julien, K.; Knobloch, E. Fully nonlinear oscillatory convection in a rotating layer. Phys. Fluids 1997, 9, 1906–1913. [Google Scholar] [CrossRef][Green Version]
- Knobloch, E.; Silber, M. Travelling wave convection in a rotating layer. Geophys. Astrophys. Fluid Dyn. 1990, 51, 195–209. [Google Scholar] [CrossRef]
- Knobloch, E.; Proctor, M.R.E. Nonlinear periodic convection in double-diffusive systems. J. Fluid Mech. 1981, 108, 291–316. [Google Scholar] [CrossRef]
- Dangelmayr, G.; Knobloch, E. The Takens-Bogdanov bifurcation with O(2)-symmetry. Philos. Trans. R. Soc. Lond. Ser. A 1987, 322, 243–279. [Google Scholar]
- Greene, J.M.; Kim, J.S. The steady states of the Kuramoto-Sivashinsky equation. Phys. D 1988, 33, 99–120. [Google Scholar] [CrossRef]
- Batiste, O.; Knobloch, E.; Alonso, A.; Mercader, I. Spatially localized binary-fluid convection. J. Fluid Mech. 2006, 560, 149–158. [Google Scholar] [CrossRef]
| Period | ||||
|---|---|---|---|---|
| Standing waves from DNS [43] | 0.670 | 1.052 | 1.594 | 1.535 |
| Standing wave from single-mode | 0.705 | 1.058 | 1.652 | 1.568 |
| c | ||||
|---|---|---|---|---|
| Steady convection rolls from DNS [43] | 1.924 | 1.371 | 3.320 | 0 |
| Steady convection rolls from single-mode | 1.812 | 1.341 | 3.387 | 0 |
| Traveling wave from DNS [43] | 0.869 | 1.087 | 1.865 | −1.03 |
| Traveling wave from single-mode | 0.848 | 1.083 | 1.828 | −1.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Knobloch, E. Single-Mode Solutions for Convection and Double-Diffusive Convection in Porous Media. Fluids 2022, 7, 373. https://doi.org/10.3390/fluids7120373
Liu C, Knobloch E. Single-Mode Solutions for Convection and Double-Diffusive Convection in Porous Media. Fluids. 2022; 7(12):373. https://doi.org/10.3390/fluids7120373
Chicago/Turabian StyleLiu, Chang, and Edgar Knobloch. 2022. "Single-Mode Solutions for Convection and Double-Diffusive Convection in Porous Media" Fluids 7, no. 12: 373. https://doi.org/10.3390/fluids7120373
APA StyleLiu, C., & Knobloch, E. (2022). Single-Mode Solutions for Convection and Double-Diffusive Convection in Porous Media. Fluids, 7(12), 373. https://doi.org/10.3390/fluids7120373






