Thin Liquid Film Dynamics on a Spinning Spheroid
Abstract
1. Introduction
2. The Lubrication Model
2.1. Generic Equation
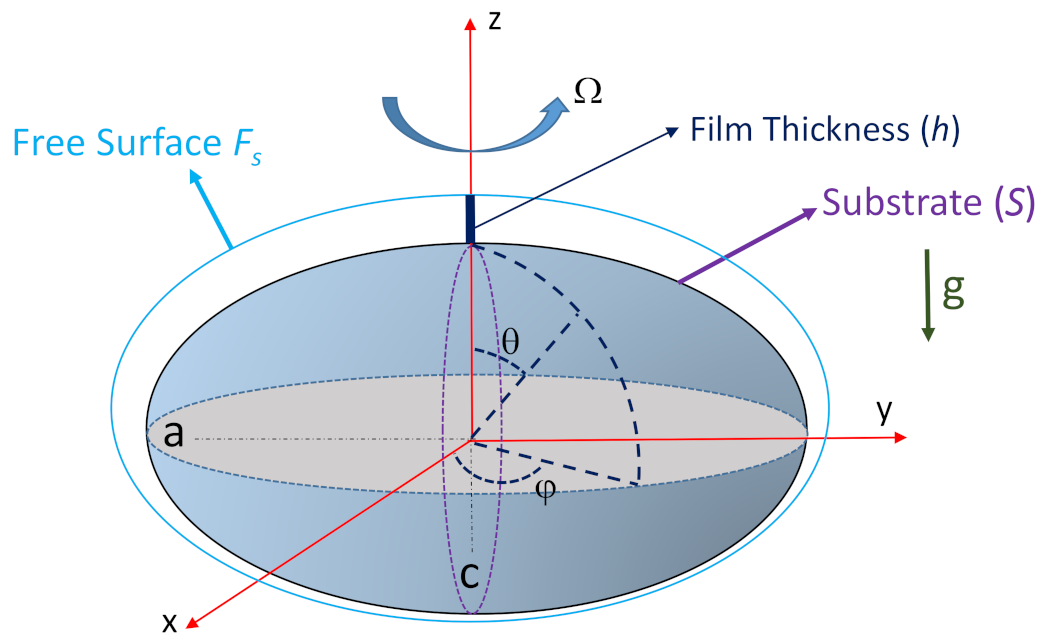
2.2. Lubrication Model for the Spheroid
- Equation (5) can be reduced to the model of a thin liquid film on a sphere of radius . Setting , we recover the evolution equation governing the dynamics of a thin film on a rotating sphere derived in [14,15] using a different approach.For small deviations from a sphere, i.e., for semi-axes satisfying , the equation at leading order in is also identical to the one derived for the spherical geometry. Nonetheless, depending on the choice of all the physical parameters together with the choice of the film parameter (which is also assumed to be small), the equation at the leading order might not reflect the actual dynamics, since is not the only small parameter of the problem. Therefore, the upcoming numerical investigations were all performed using the non-reduced version, even for .
- For the non-rotating case, it is straightforward that Equation (5) does not admit any constant solution (such as , which would indicate a uniform film thickness), unless the function is a constant. For substrates of uniform curvature, this function reduces to , which implies the possibility of a uniform coating for the zero gravity case (). On the other hand, for substrates of non-uniform curvature, it is not possible to develop a uniform film thickness, even in a zero gravity field.
3. Solution Methodology and Validation
3.1. Solution Methodology
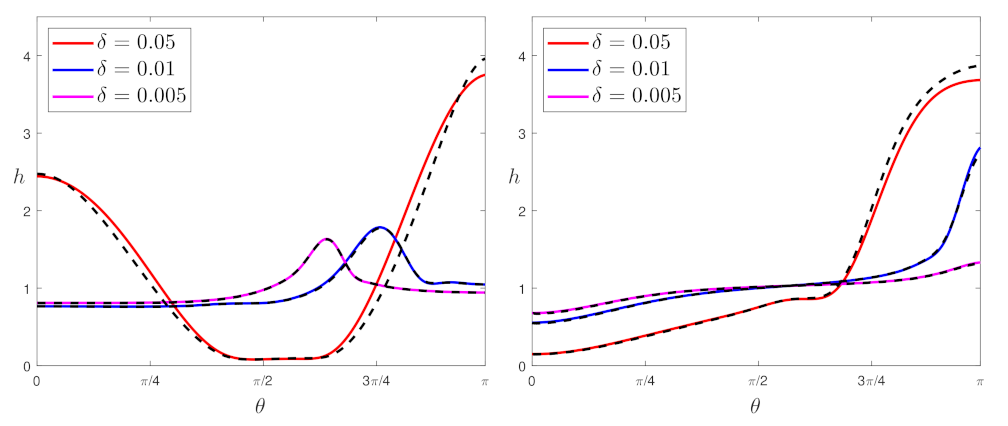
3.2. Validation
4. Results and Discussion
4.1. Capillary Dominated Flow with Constant Viscosity
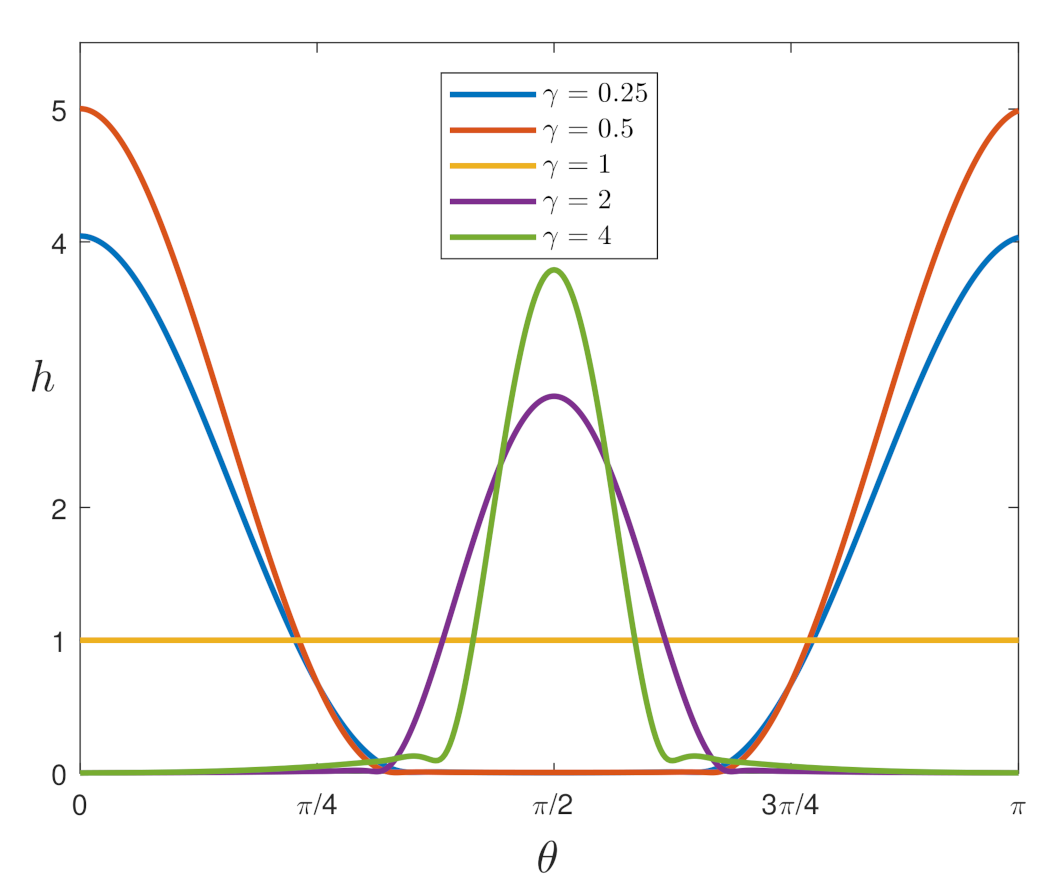
4.2. Combined Effects of Substrate Shape, Capillarity, Gravity, and Rotation
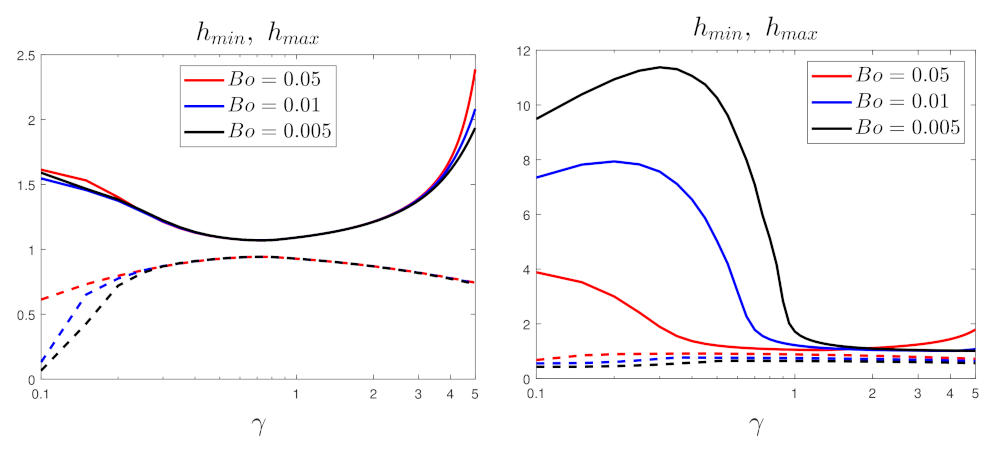
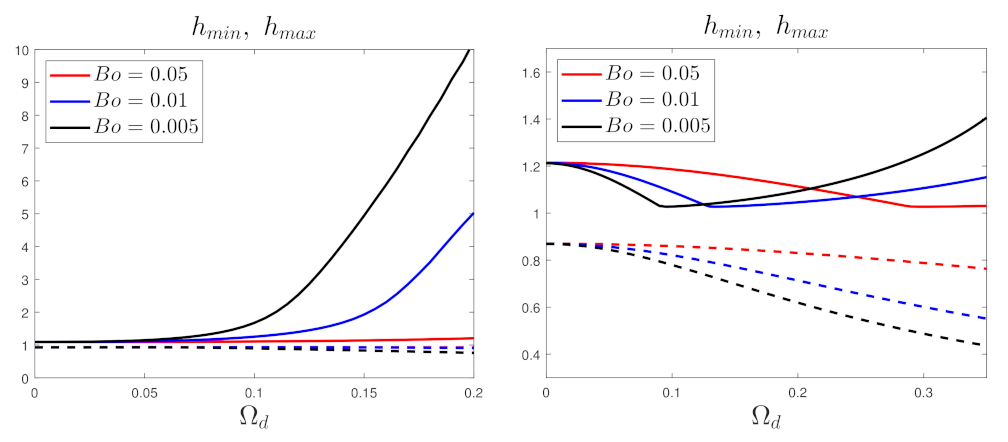
4.3. Minimum and Maximum Film Thickness
4.4. Free Surface Profiles
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sahu, N.; Parija, B.; Panigrahi, S. Fundamental understanding and modeling of spin coating process: A review. Indian J. Phys. 2009, 83, 493–502. [Google Scholar] [CrossRef]
- Feng, X.G.; Sun, L.C. Mathematical model of spin-coated photoresist on a spherical substrate. Opt. Express 2005, 13, 7070–7075. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.J.; Liang, Y.Y.; Luo, J.B.; Zhang, C.H.; Yang, G.G. Mathematical modeling and experimental study on photoresist whirl-coating in convex-surface laser lithography. J. Opt. A Pure Appl. Opt. 2009, 11, 105408. [Google Scholar] [CrossRef]
- Liu, H.; Fang, X.; Meng, L.; Wang, S. Spin Coating on Spherical Surface with Large Central Angles. Coatings 2017, 7, 124. [Google Scholar] [CrossRef]
- Hayes, M.A.; O’Brien, S.B.G. The fluid profile during spin-coating over a small sinusoidal topography. Int. J. Math. Math. Sci. 2004, 2004, 2279–2298. [Google Scholar] [CrossRef]
- Leslie, G.A.; Wilson, S.K.; Duffy, B. Three-dimensional coating and rimming flow: A ring of fluid on a rotating horizontal cylinder. J. Fluid Mech. 2013, 716, 51–82. [Google Scholar] [CrossRef][Green Version]
- Morad, A.M.; Zhukov, M.Y. The motion of a thin liquid layer on the outer surface of a rotating cylinder. Eur. Phys. J. Plus 2015, 130, 1–8. [Google Scholar] [CrossRef]
- Badali, D.; Chugunova, M.; Pelinovsky, D.E.; Pollack, S. Regularized shock solutions in coating flows with small surface tension. Phys. Fluids 2011, 23, 093103. [Google Scholar] [CrossRef]
- Takagi, G.; Huppert, H. Flow and instability of thin films on a cylinder and sphere. J. Fluid Mech. 2010, 647, 221–238. [Google Scholar] [CrossRef]
- D’Alessio, S.; Pascal, J. The dynamics of the globe fountain. Int. J. Comp. Meth. Exp. Meas. 2016, 4, 131–141. [Google Scholar] [CrossRef]
- Balestra, G.; Brun, P.-T.; Gallaire, F. Rayleigh-Taylor instability under curved substrates: An optimal transient growth analysis. Phys. Rev. Fluids 2016, 1.8, 083902. [Google Scholar] [CrossRef]
- Balestra, G.; Nguyen, D.M.P.; Gallaire, F. Rayleigh-Taylor instability under a spherical substrate. Phys. Rev. Fluids 2018, 8, 084005. [Google Scholar] [CrossRef]
- Qin, J.; Xia, Y.; Gao, P. Axisymmetric evolution of gravity-driven thin films on a small sphere. J. Fluid Mech. 2020, 907, A4.1. [Google Scholar] [CrossRef]
- Kang, D.; Nadim, A.; Chugunova, M. Dynamics and equilibria of thin viscous coating films on a rotating sphere. J. Fluid Mech. 2016, 791, 495–518. [Google Scholar] [CrossRef]
- Shepherd, R.; Sellier, M.; Boujo, E. Modelling and Simulation of Spin Coating on a Spherical Substrate. In Proceedings of the 22nd Australasian Fluid Mechanics Conference AFMC2020, Brisbane, Australia, 7–10 December 2020. [Google Scholar]
- Schwartz, L.W.; Weidner, D.E. Modeling of coating flows on curved surfaces. J. Eng. Math. 1995, 29, 91–103. [Google Scholar] [CrossRef]
- Roy, R.; Roberts, A.; Simpson, M.E. A lubrication model of coating flows over a curved substrate in space. J. Fluid Mech. 2002, 454, 235–261. [Google Scholar] [CrossRef]
- Myers, T.G.; Charpin, J.P.F.; Chapman, S.J. The flow and solidification of a thin fluid film on an arbitrary three-dimensional surface. Phys. Fluids 2002, 14, 2788–2803. [Google Scholar] [CrossRef]
- Ruschak, K.J.; Weinstein, S.J. Laminar, gravitationally driven flow of a thin film on a curved wall. J. Fluids Eng. 2003, 125, 10–17. [Google Scholar] [CrossRef]
- Howel, P.D. Surface-tension-driven flow on a moving curved surface. J. Eng. Math. 2002, 45, 283–308. [Google Scholar] [CrossRef]
- Mayo, L.C.; McCue, S.W.; Moroney, T.C.; Forster, W.A.; Kempthorne, D.M.; Belward, J.A.; Turner, I.W. Simulating droplet motion on virtual leaf surfaces. R. Soc. Open Sci. 2015, 2, 140528. [Google Scholar] [CrossRef]
- Weidner, D.E. Analysis of the flow of a thin liquid film on the surface of a rotating, curved, axisymmetric substrate. Phys. Fluids 2018, 30, 082110. [Google Scholar] [CrossRef]
- Weidner, D.E. Numerical Simulation of the Spin Coating of the Interior of Metal Beverage Cans. In Methods for Film Synthesis and Coating Procedures; IntechOpen: London, UK, 2019. [Google Scholar]
- Lee, A.; Brun, P.T.; Marthelot, J.; Balestra, G.; Gallaire, F.; Reis, P.M. Fabrication of slender elastic shells by the coating of curved surfaces. Nat. Commun. 2016, 7, 11155. [Google Scholar] [CrossRef] [PubMed]
- Bourne, E.; Kendall, P.C. Vector Analysis and Cartesian Tensors, 3rd ed.; Chapman and Hall: Boca Raton, FL, USA; CRC: London, UK, 2018. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duruk, S.; Boujo, E.; Sellier, M. Thin Liquid Film Dynamics on a Spinning Spheroid. Fluids 2021, 6, 318. https://doi.org/10.3390/fluids6090318
Duruk S, Boujo E, Sellier M. Thin Liquid Film Dynamics on a Spinning Spheroid. Fluids. 2021; 6(9):318. https://doi.org/10.3390/fluids6090318
Chicago/Turabian StyleDuruk, Selin, Edouard Boujo, and Mathieu Sellier. 2021. "Thin Liquid Film Dynamics on a Spinning Spheroid" Fluids 6, no. 9: 318. https://doi.org/10.3390/fluids6090318
APA StyleDuruk, S., Boujo, E., & Sellier, M. (2021). Thin Liquid Film Dynamics on a Spinning Spheroid. Fluids, 6(9), 318. https://doi.org/10.3390/fluids6090318





