Pore-Scale Simulation of the Interaction between a Single Water Droplet and a Hydrophobic Wire Mesh Screen in Diesel
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Model
2.2. Geometry and Computational Grids
2.3. Initial and Boundary Conditions
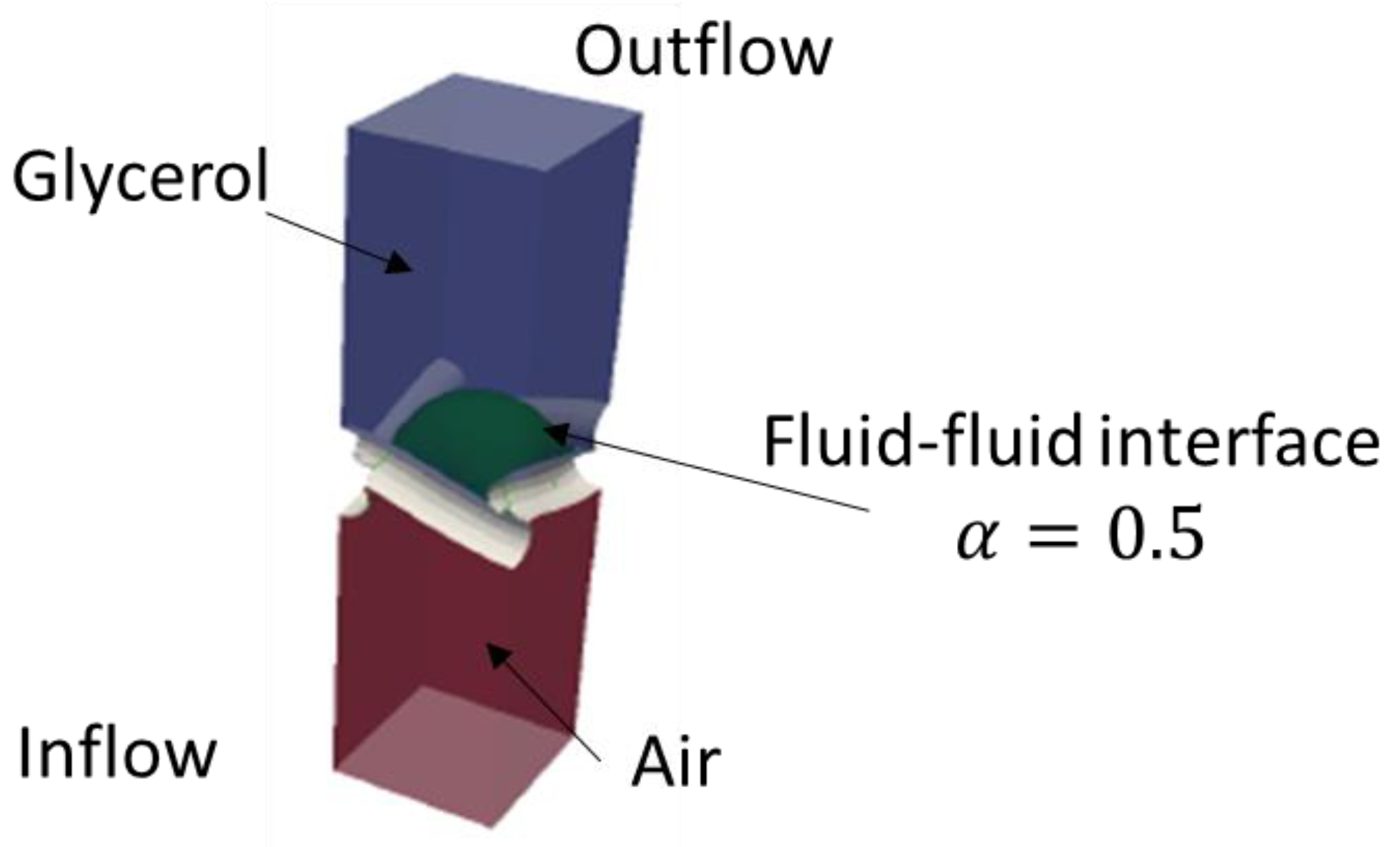
2.3.1. Bubble Point Test
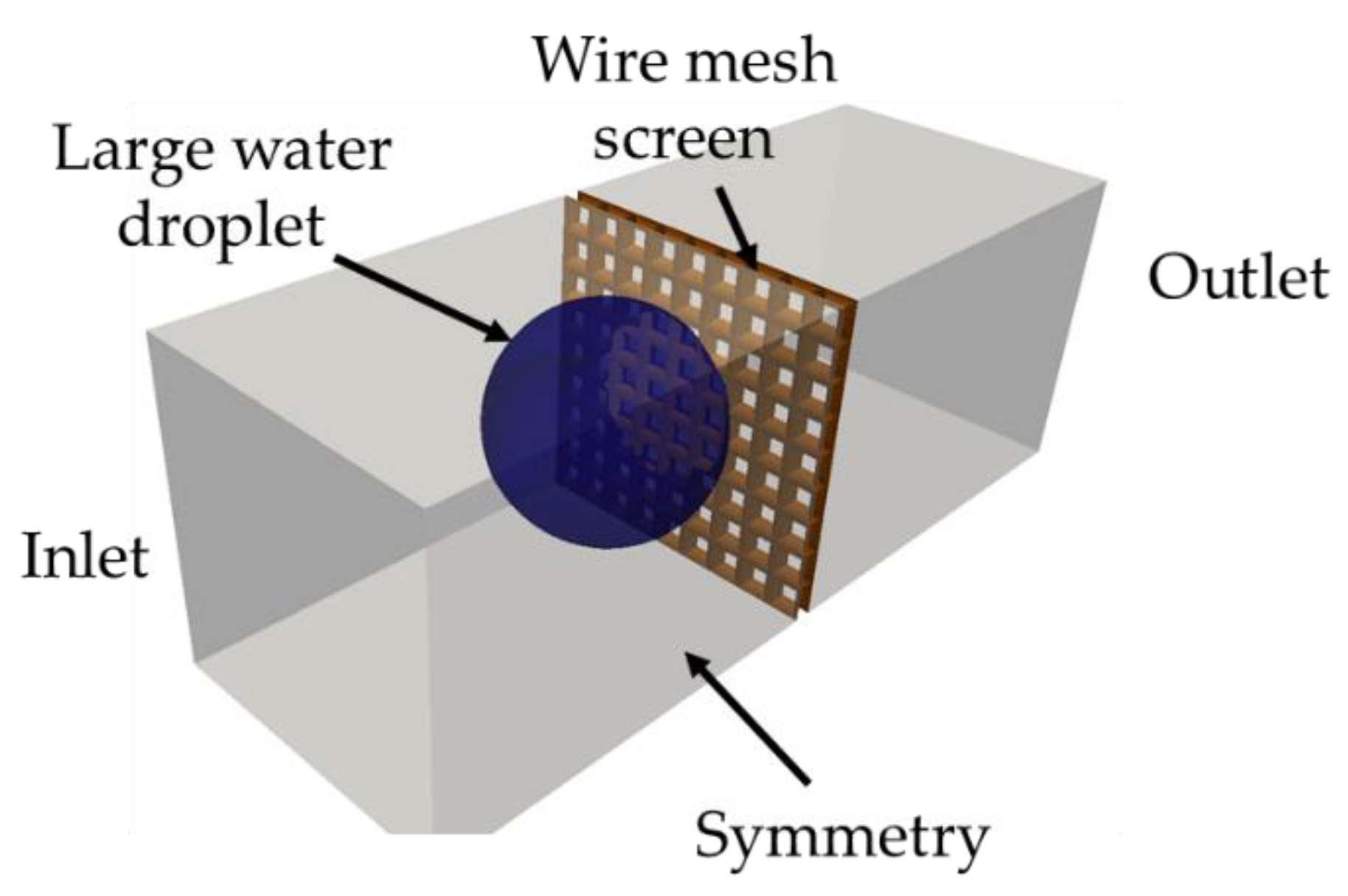
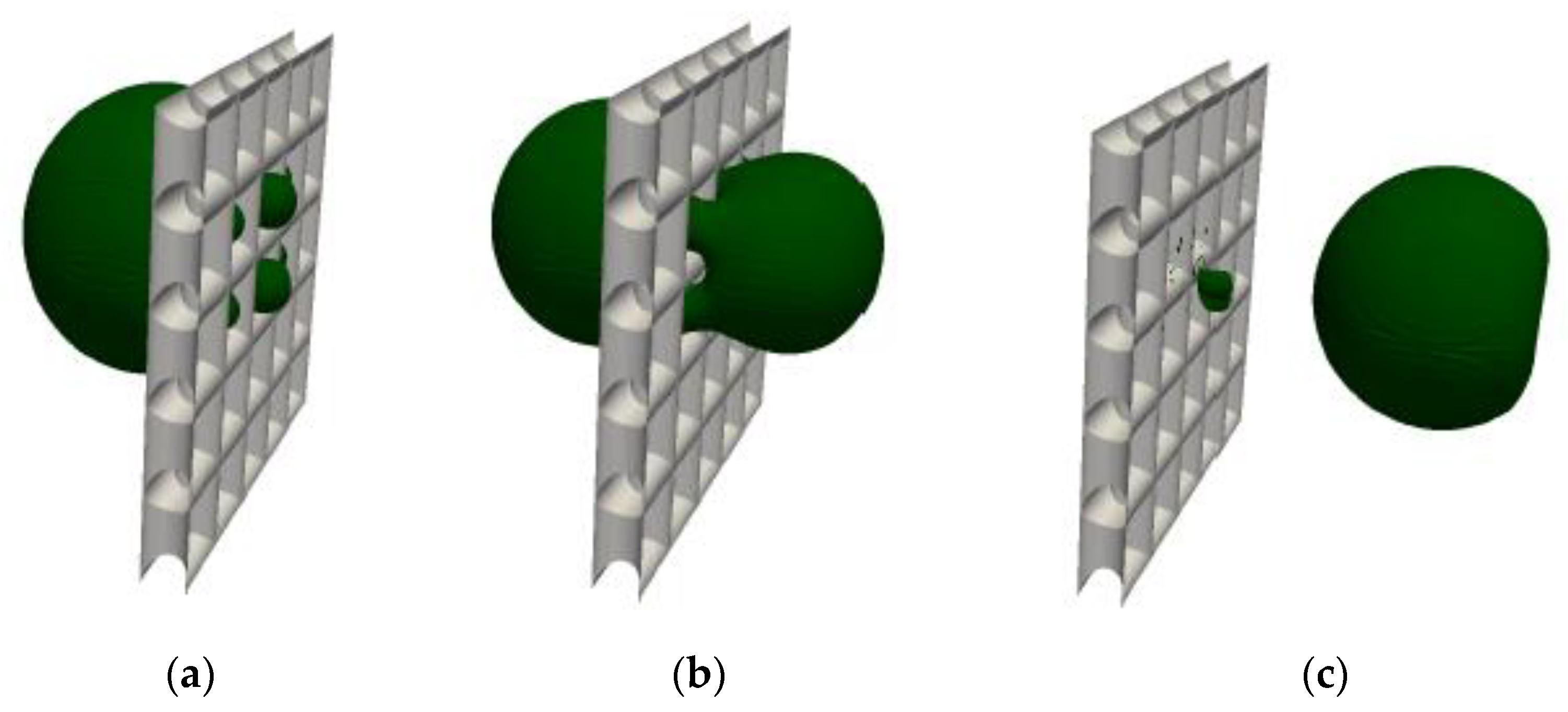
2.3.2. Droplet–Mesh Interaction
2.4. Discretization Schemes and Solution Control
2.5. Experimental Setup
3. Results and Discussion
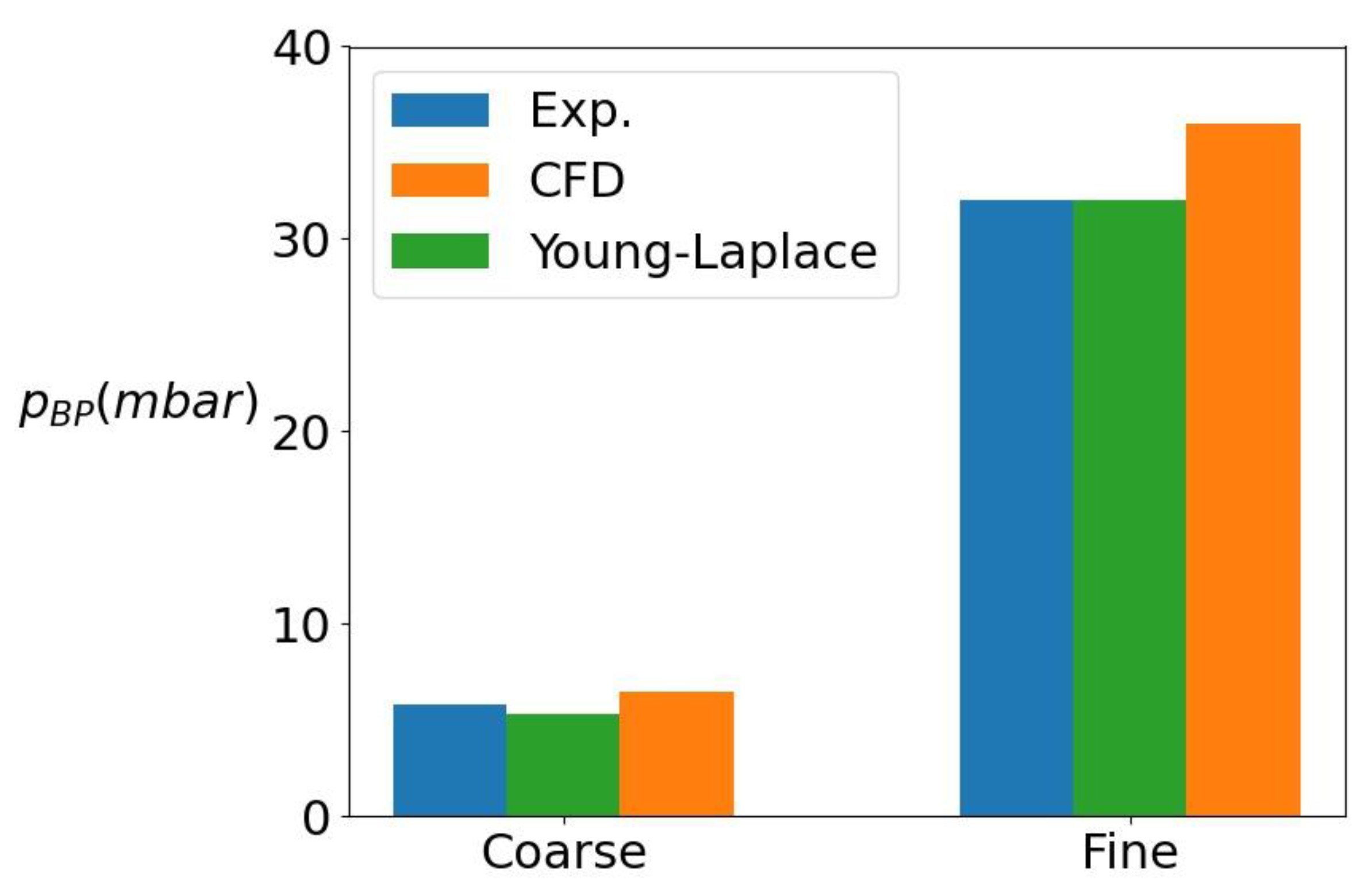
3.1. Bubble Point Test: Validation Case
3.2. Single Water Droplet Interaction with Wire Mesh Screen
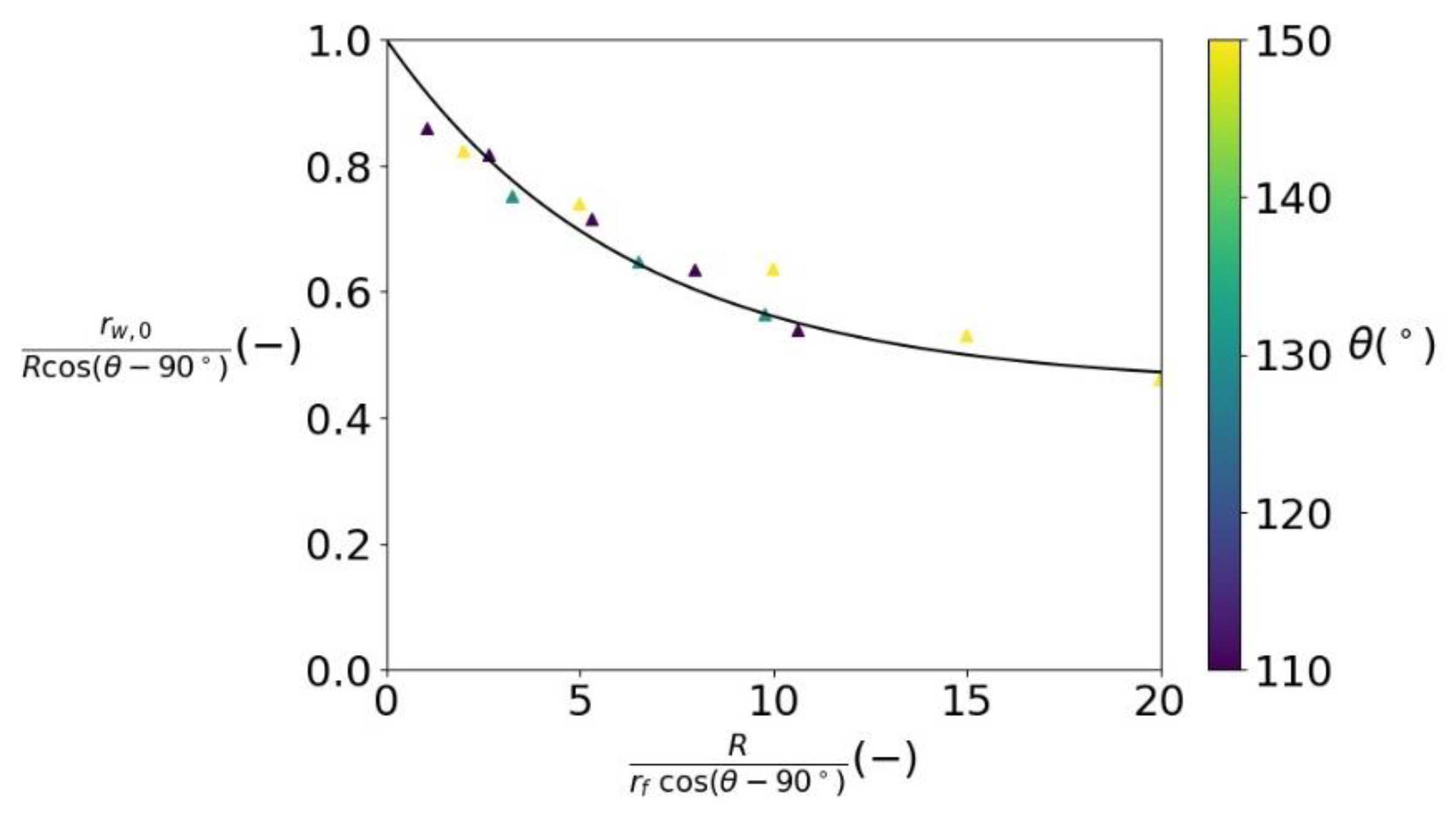
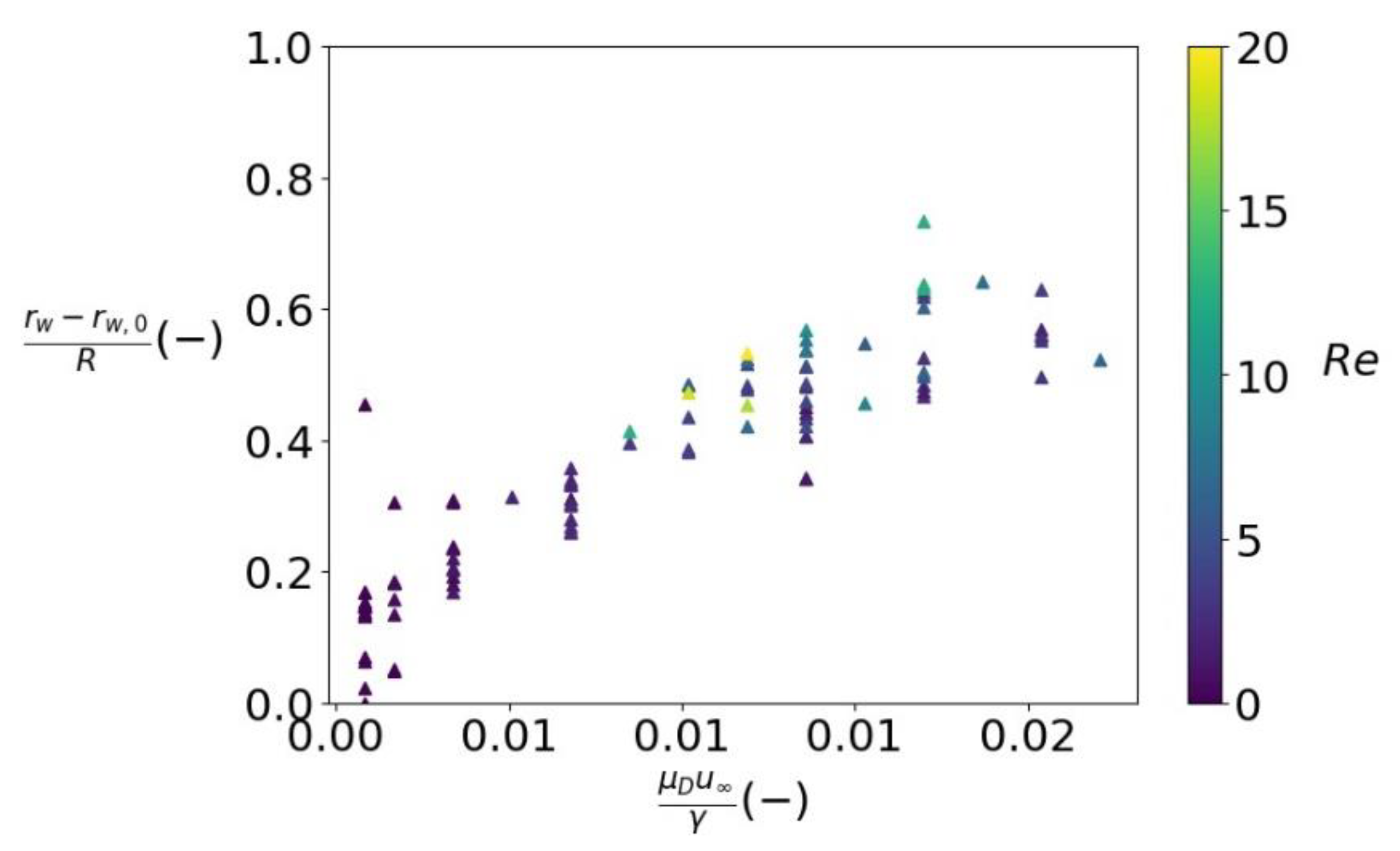
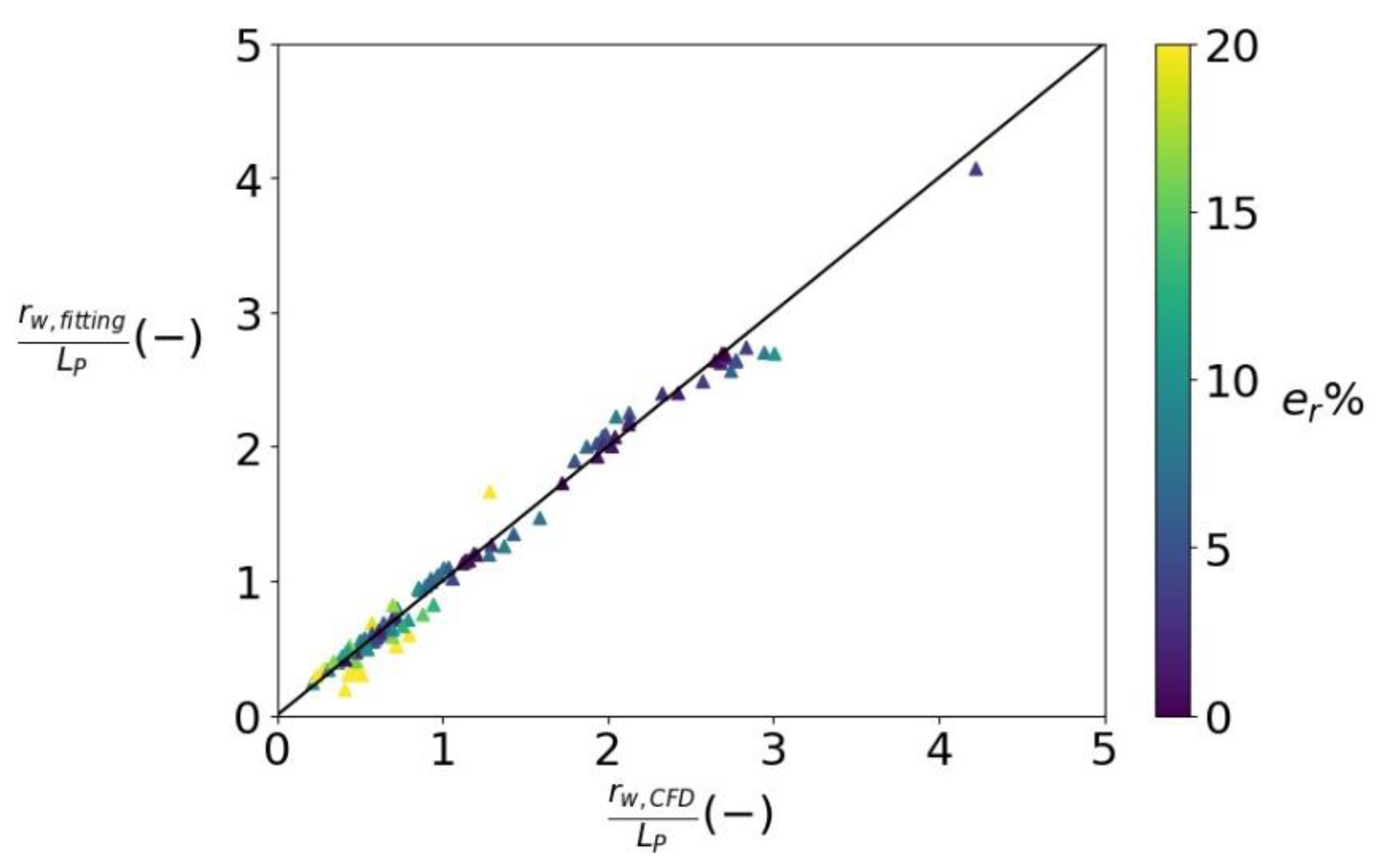
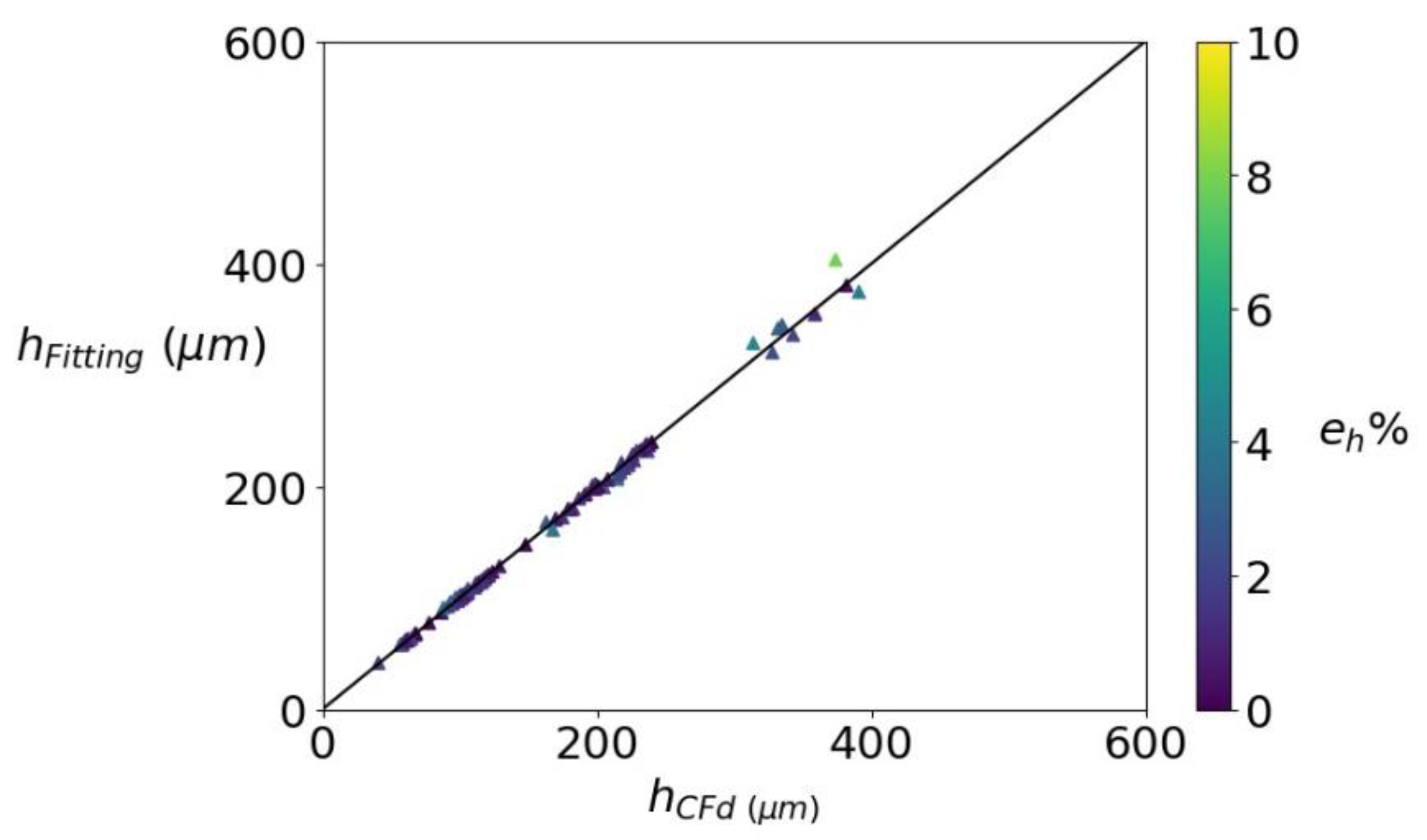
3.2.1. Spreading Radius
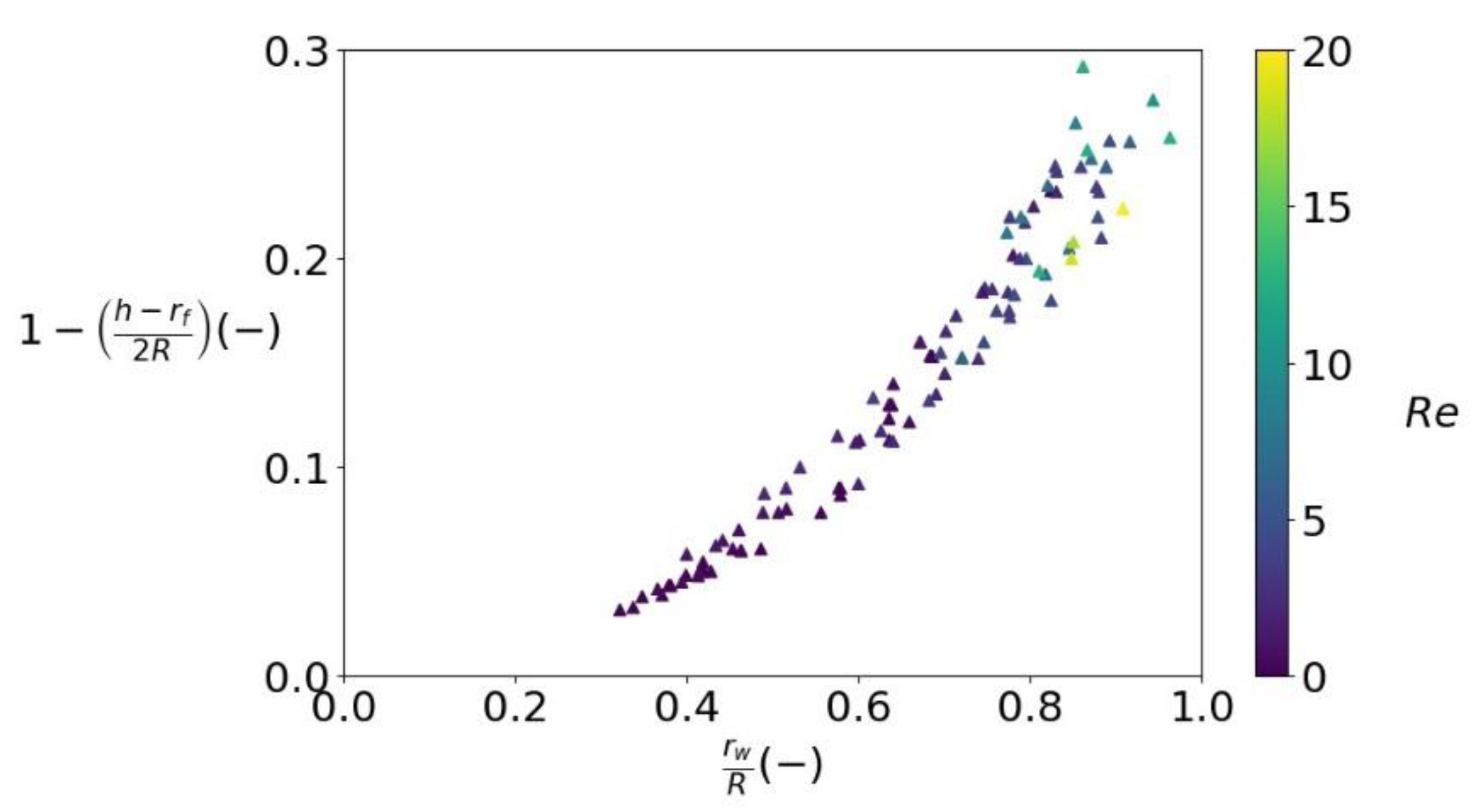
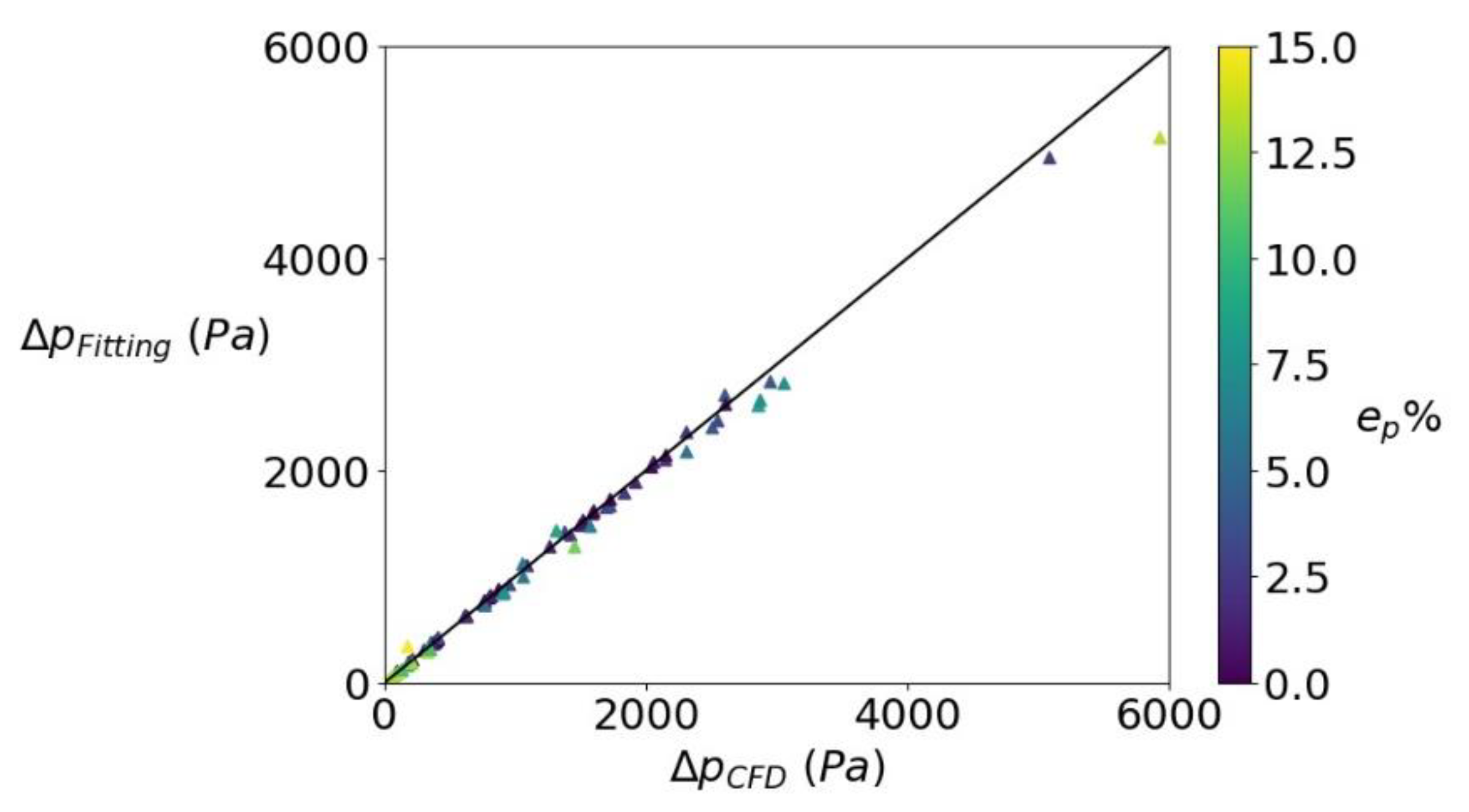
3.2.2. Pressure Drop
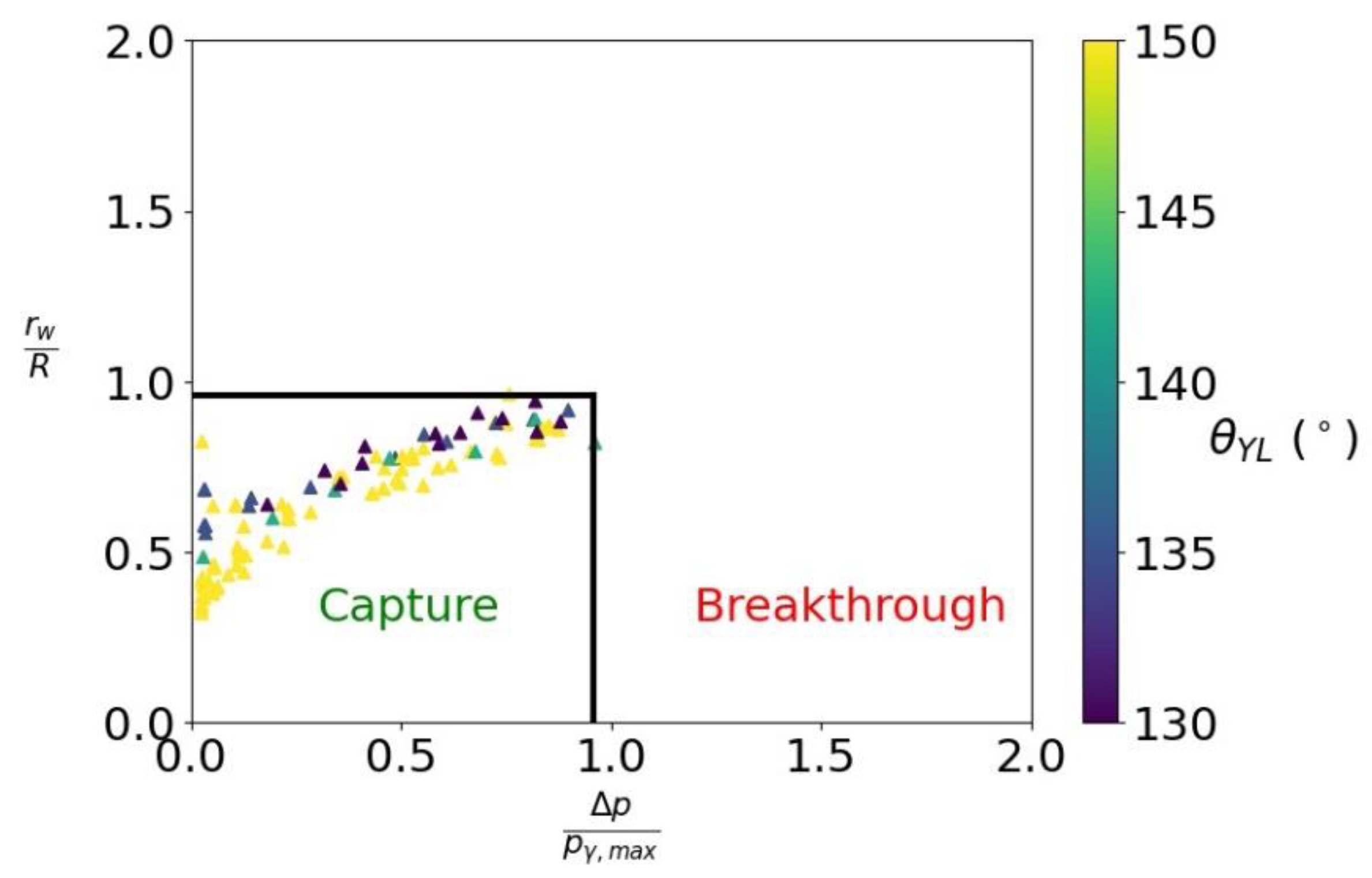
3.2.3. Breakthrough
4. Conclusions
- 1.
- Validation of the two-phase flow simulations by comparing the bubble point test simulations with experiments. The bubble point test is usually used to find an empirical parameter which fits the Young–Laplace equation to the measurement. The simulations showed validity and predictability in computing the threshold pressure. Hence, the fitting coefficient can be computed with good agreement from direct numerical simulations.
- 2.
- Quantification of the interaction of a single water droplet with a hydrophobic wire mesh screen in diesel. The simulations covered a wide range of capillary and Reynolds numbers. The obtained results were used to find correlations, which describe the radius of the clogging (wetting) contact line, the change in the droplet height, the pressure drop because of the reduction of the open surface area, and the criteria for droplet breakthrough.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stanfel, C. Fuel filtration: Protecting the diesel engine. Filtr. Sep. 2009, 46, 22–25. [Google Scholar] [CrossRef]
- Liu, X.; Guan, B.; Liu, X. Experimental Study on the Filtration Efficiency of Structured Packing Air Handling Processors. Procedia Eng. 2015, 121, 2037–2043. [Google Scholar] [CrossRef] [Green Version]
- Brown, R.; Wake, D. Loading filters with monodisperse aerosols: Macroscopic treatment. J. Aerosol Sci. 1999, 30, 227–234. [Google Scholar] [CrossRef]
- Kim, C.; Pui, D.Y. Experimental study on the filtration efficiency of activated carbons for 3–30 nm particles. Carbon 2015, 93, 226–229. [Google Scholar] [CrossRef]
- Japuntich, D.; Stenhouse, J.; Liu, B. Experimental results of solid monodisperse particle clogging of fibrous filters. J. Aerosol Sci. 1994, 25, 385–393. [Google Scholar] [CrossRef]
- Konda, A.; Prakash, A.; Moss, G.A.; Schmoldt, M.; Grant, G.D.; Guha, S. Response to Letters to the Editor on Aerosol Filtration Efficiency of Common Fabrics Used in Respiratory Cloth Masks: Revised and Expanded Results. ACS Nano 2020, 14, 10764–10770. [Google Scholar] [CrossRef] [PubMed]
- Iliev, O.; Kirsch, R.; Osterroth, S. Combined Depth and Cake Filtration Model Coupled with Flow Simulation for Flat and Pleated Filters. Chem. Eng. Technol. 2018, 41, 70–78. [Google Scholar] [CrossRef]
- Iliev, O.R.; Kirsch, Z.; Lakdawala, S.R.; Steiner, K. Currents in Industrial Mathematics: From concepts to research to education. In Currents in Industrial Mathematics; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–403. [Google Scholar]
- Kulkarni, P.S.; Patel, S.U.; Chase, G.G. Layered hydrophilic/hydrophobic fiber media for water-in-oil coalescence. Sep. Purif. Technol. 2012, 85, 157–164. [Google Scholar] [CrossRef]
- Kulkarni, P.S.; Patel, S.U.; Patel, S.U.; Chase, G.G. Coalescence filtration performance of blended microglass and electrospun polypropylene fiber filter media. Sep. Purif. Technol. 2014, 124, 1–8. [Google Scholar] [CrossRef]
- Patel, S.U.; Chase, G.G. Separation of water droplets from water-in-diesel dispersion using superhydrophobic polypropylene fibrous membranes. Sep. Purif. Technol. 2014, 126, 62–68. [Google Scholar] [CrossRef]
- Lu, H.; Yang, Q.; Liu, S.; Xie, L.-S.; Wang, H.-L. Effect of fibrous coalescer redispersion on W/O emulsion separation. Sep. Purif. Technol. 2016, 159, 50–56. [Google Scholar] [CrossRef]
- Kampa, D.; Wurster, S.; Buzengeiger, J.; Meyer, J.; Kasper, G. Pressure drop and liquid transport through coalescence filter media used for oil mist filtration. Int. J. Multiph. Flow 2014, 58, 313–324. [Google Scholar] [CrossRef]
- Lao, C.T.; Akroyd, J.; Eaves, N.; Smith, A.; Morgan, N.; Bhave, A.; Kraft, M. Modelling particle mass and particle number emissions during the active regeneration of diesel particulate filters. Proc. Combust. Inst. 2019, 37, 4831–4838. [Google Scholar] [CrossRef] [Green Version]
- Song, M.; Steiff, A.; Weinspach, P.-M. A very effective new method to solve the population balance equation with particle-size growth. Chem. Eng. Sci. 1997, 52, 3493–3498. [Google Scholar] [CrossRef]
- Cheung, S.C.; Yeoh, G.; Tu, J. On the modelling of population balance in isothermal vertical bubbly flows—Average bubble number density approach. Chem. Eng. Process. Process. Intensif. 2007, 46, 742–756. [Google Scholar] [CrossRef] [Green Version]
- Cheung, S.C.; Yeoh, G.H.; Tu, J. A Review of Population Balance Modelling for Isothermal Bubbly Flows. J. Comput. Multiph. Flows 2009, 1, 161–199. [Google Scholar] [CrossRef] [Green Version]
- Koch, B.M.L.; Amirfazli, A.; Elliott, J.A.W. Modeling and Measurement of Contact Angle Hysteresis on Textured High-Contact-Angle Surfaces. J. Phys. Chem. C 2014, 118, 18554–18563. [Google Scholar] [CrossRef]
- Chibowski, E.; Jurak, M. Comparison of contact angle hysteresis of different probe liquids on the same solid surface. Colloid Polym. Sci. 2013, 291, 391–399. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Wu, Y.; Cao, Y.; Li, G.; Liao, Y. Influence of surface roughness on contact angle hysteresis and spreading work. Colloid Polym. Sci. 2020, 298, 1107–1112. [Google Scholar] [CrossRef]
- Elhaj, M.A.; Hossain, M.E.; Imtiaz, S.A.; Naterer, G.F. Hysteresis of wettability in porous media: A review. J. Pet. Explor. Prod. Technol. 2020, 10, 1897–1905. [Google Scholar] [CrossRef] [Green Version]
- Wenzel, R.N. Resistance of Solid Surfaces to Wetting by Water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Elzaabalawy, A.; Meguid, S.A. Effect of surface topology on the wettability of superhydrophobic surfaces. J. Dispers. Sci. Technol. 2020, 41, 470–478. [Google Scholar] [CrossRef]
- Zhao, H.; Park, K.-C.; Law, K.-Y. Effect of Surface Texturing on Superoleophobicity, Contact Angle Hysteresis, and “Robustness”. Langmuir 2012, 28, 14925–14934. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Pugno, N.M.; Ryu, S. Wetting theory for small droplets on textured solid surfaces. Sci. Rep. 2016, 6, 37813. [Google Scholar] [CrossRef] [PubMed]
- Chatain, D.; Lewis, D.; Baland, J.-P.; Carter, W.C. Numerical Analysis of the Shapes and Energies of Droplets on Micropatterned Substrates. Langmuir 2006, 22, 4237–4243. [Google Scholar] [CrossRef] [PubMed]
- Amrei, M.; Davoudi, M.; Chase, G.; Tafreshi, H.V. Effects of roughness on droplet apparent contact angles on a fiber. Sep. Purif. Technol. 2017, 180, 107–113. [Google Scholar] [CrossRef] [Green Version]
- He, L.; Sui, X.; Liang, W.; Wang, Z.; Akbarzadeh, A. Numerical analysis of anisotropic wetting of chemically striped surfaces. RSC Adv. 2018, 8, 31735–31744. [Google Scholar] [CrossRef] [Green Version]
- Jamali, M.; Tafreshi, H.V.; Pourdeyhimi, B. Droplet Mobility on Hydrophobic Fibrous Coatings Comprising Orthogonal Fibers. Langmuir 2018, 34, 12488–12499. [Google Scholar] [CrossRef]
- Brakke, K.A. The surface evolver. Exp. Math. 1992, 1, 141–165. [Google Scholar] [CrossRef]
- Lorenceau, É.; Clanet, C.; Quéré, D. Capturing drops with a thin fiber. J. Colloid Interface Sci. 2004, 279, 192–197. [Google Scholar] [CrossRef]
- Sher, E.; Haim, L.; Sher, I. Off-centered impact of water droplets on a thin horizontal wire. Int. J. Multiph. Flow 2013, 54, 55–60. [Google Scholar] [CrossRef]
- Lorenceau, E.; Clanet, C.; Quéré, D.; Vignes-Adler, M. Off-centre impact on a horizontal fibre. Eur. Phys. J. Spec. Top. 2009, 166, 3–6. [Google Scholar] [CrossRef]
- Dressaire, E.; Sauret, A.; Boulogne, F.; Stone, H.A. Drop impact on a flexible fiber. R. Soc. Soft Matter. 2016, 1, 200–216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Comtet, J.; Keshavarz, B.; Bush, J.W.M. Drop impact and capture on a thin flexible fiber. R. Soc. Soft Matter. 2016, 1, 149–156. [Google Scholar] [CrossRef]
- Ramstad, T.; Berg, C.F.; Thompson, K. Pore-Scale Simulations of Single- and Two-Phase Flow in Porous Media: Approaches and Applications. Transp. Porous Media 2019, 130, 77–104. [Google Scholar] [CrossRef]
- Carrillo, F.J.; Bourg, I.C.; Soulaine, C. Multiphase flow modeling in multiscale porous media: An open-source micro-continuum approach. J. Comput. Phys. X 2020, 8, 100073. [Google Scholar] [CrossRef]
- Alamooti, A.H.M.; Azizi, Q.; Davarzani, H. Direct numerical simulation of trapped-phase recirculation at low capillary number. Adv. Water Resour. 2020, 145, 103717. [Google Scholar] [CrossRef]
- Shams, M.; Raeini, A.Q.; Blunt, M.J.; Bijeljic, B. A numerical model of two-phase flow at the micro-scale using the volume-of-fluid method. J. Comput. Phys. 2018, 357, 159–182. [Google Scholar] [CrossRef]
- Fakhari, A.; Li, Y.; Bolster, D.; Christensen, K.T. A phase-field lattice Boltzmann model for simulating multiphase flows in porous media: Application and comparison to experiments of CO2 sequestration at pore scale. Adv. Water Resour. 2018, 114, 119–134. [Google Scholar] [CrossRef]
- Das, S.; Patel, H.V.; Milacic, E.; Deen, N.G.; Kuipers, J.A.M. Droplet spreading and capillary imbibition in a porous medium: A coupled IB-VOF method based numerical study. Phys. Fluids 2018, 30, 012112. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Xiao, W.; Zhang, H.; Luo, K.; Mao, C.; Fan, J. Immersed boundary method for multiphase transport phenomena. Rev. Chem. Eng. 2020. [Google Scholar] [CrossRef]
- Cummins, S.J.; Francois, M.M.; Kothe, D.B. Estimating curvature from volume fractions. Comput. Struct. 2005, 83, 425–434. [Google Scholar] [CrossRef]
- Raeini, A.Q.; Blunt, M.; Bijeljic, B. Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method. J. Comput. Phys. 2012, 231, 5653–5668. [Google Scholar] [CrossRef]
- Hoang, D.A.; van Steijn, V.; Portela, L.M.; Kreutzer, M.; Kleijn, C.R. Benchmark numerical simulations of segmented two-phase flows in microchannels using the Volume of Fluid method. Comput. Fluids 2013, 86, 28–36. [Google Scholar] [CrossRef]
- Elsayed, O.; Kirsch, R.; Osterroth, S.; Antonyuk, S. An improved scheme for the interface reconstruction and curvature approximation for flow simulations of two immiscible fluids. Int. J. Multiph. Flow 2021, 103805. [Google Scholar] [CrossRef]
- GKD. Improved accuracy in bubble point measurement. Filtr. Sep. 2017, 54, 38–41. [Google Scholar] [CrossRef]
- BSI. Method for Measurement of the Equivalent Pore Size of Fabrics (Bubble Pressure Test); British Standards Institution: London, UK, 1986. [Google Scholar]
- Goldman, R. Curvature formulas for implicit curves and surfaces. Comput. Aided Geom. Des. 2005, 22, 632–658. [Google Scholar] [CrossRef]
- Mayost, D. Applications of the Signed Distance Function to Surface Geometry. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2014. Available online: http://www.math.toronto.edu/mccann/papers/Mayost_Daniel_201406_PhD_thesis.pdf (accessed on 1 August 2021).
- Geodict, The Virtual Material Laboratory. ©2001–2011 Fraunhofer ITWM, ©2012–2021 Math2Market GmbH, 2001. Available online: https://www.math2market.com/ (accessed on 1 June 2021).
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Jasak, H. Error Analysis and Estimation for Finite Volume Method with Applications to Fluid Flow. Ph.D. Thesis, Imperial College, London, UK, 1996. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics the Finite Volume Method, 2nd ed.; Pearson Prentice Hall: Hoboken, NJ, USA, 2007. [Google Scholar]
- Courant, R.; Friedrichs, K.; Lewy, H. Über die partiellen Differenzengleichungen der mathematischen Physik. Math. Ann. 1928, 100, 32–74. [Google Scholar] [CrossRef]
- Roenby, J.; Bredmose, H.; Jasak, H. A computational method for sharp interface advection. R. Soc. Open Sci. 2016, 3, 160405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Topas-Gmbh. PSM 165—Capillary Flow Pore Size Meter. Available online: https://www.topas-gmbh.de/en/produkte/psm-165/ (accessed on 1 June 2021).
- Rivkind, V.Y.; Ryskin, G.M. Flow structure in motion of a spherical drop in a fluid medium at intermediate Reynolds numbers. Fluid Dyn. 1977, 11, 5–12. [Google Scholar] [CrossRef]

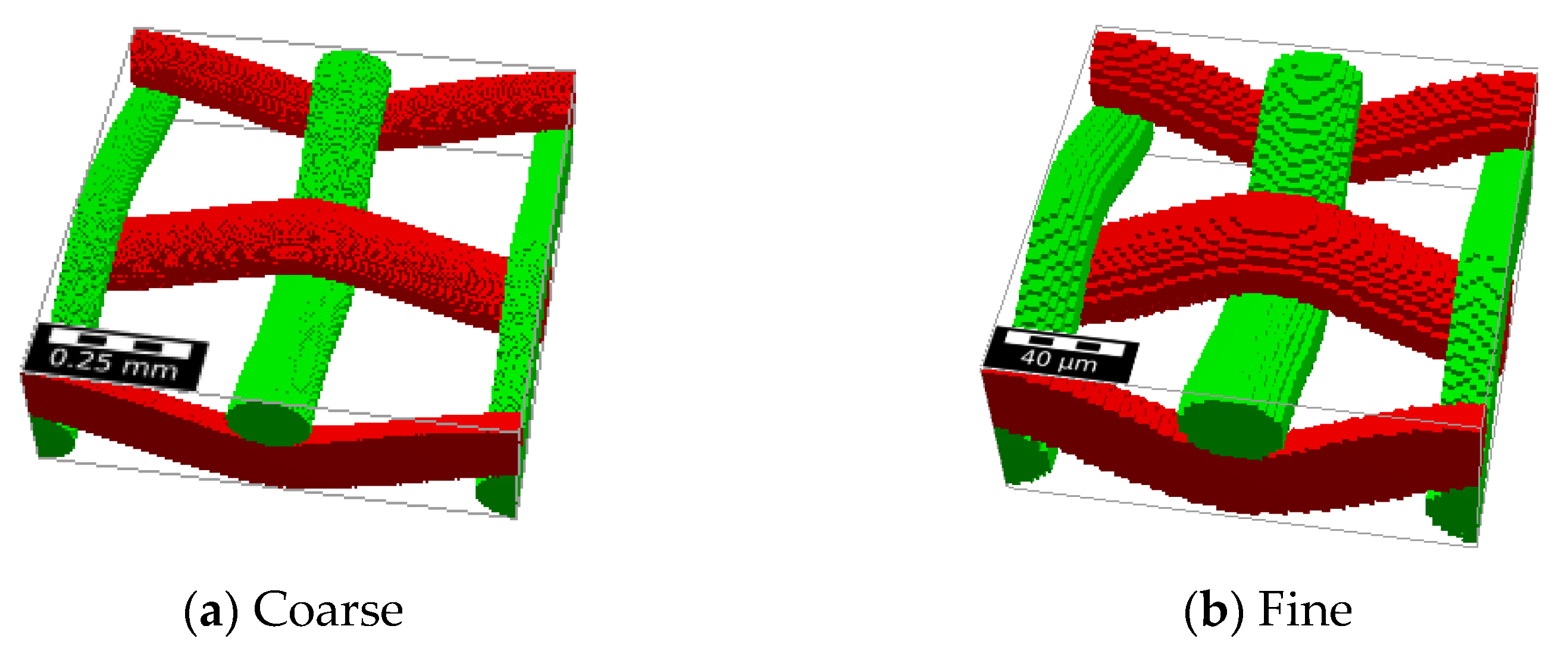








| Screen | Yarn Radius | Yarn Pitch | Mesh Thickness |
|---|---|---|---|
| Coarse | |||
| Fine |
| Total Number of Pores | |
|---|---|
| Fiber radius | |
| Open area ratio |
| Temporal Derivatives | First-Order Explicit (Euler) |
|---|---|
| Advection of volume fraction | Geometric scheme (isoAdvector) [57] |
| Convection of momentum | Second-order upwind [54] |
| Diffusion of momentum (shear stress) | Explicit central difference |
| Gradient | Least-squares |
| Interpolation | Linear |
| Density | |
|---|---|
| Dynamic viscosity | |
| Surface tension coefficient |
| Diesel Density | |
|---|---|
| Diesel dynamic viscosity | |
| Water density | |
| Water dynamic viscosity |
| Inlet Velocity | |
|---|---|
| Droplet radius | |
| Ratio between droplet radius and mesh pitch | |
| Surface tension coefficient | and |
| Young–Laplace contact angle | , and |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elsayed, O.; Kirsch, R.; Krull, F.; Antonyuk, S.; Osterroth, S. Pore-Scale Simulation of the Interaction between a Single Water Droplet and a Hydrophobic Wire Mesh Screen in Diesel. Fluids 2021, 6, 319. https://doi.org/10.3390/fluids6090319
Elsayed O, Kirsch R, Krull F, Antonyuk S, Osterroth S. Pore-Scale Simulation of the Interaction between a Single Water Droplet and a Hydrophobic Wire Mesh Screen in Diesel. Fluids. 2021; 6(9):319. https://doi.org/10.3390/fluids6090319
Chicago/Turabian StyleElsayed, Omar, Ralf Kirsch, Fabian Krull, Sergiy Antonyuk, and Sebastian Osterroth. 2021. "Pore-Scale Simulation of the Interaction between a Single Water Droplet and a Hydrophobic Wire Mesh Screen in Diesel" Fluids 6, no. 9: 319. https://doi.org/10.3390/fluids6090319
APA StyleElsayed, O., Kirsch, R., Krull, F., Antonyuk, S., & Osterroth, S. (2021). Pore-Scale Simulation of the Interaction between a Single Water Droplet and a Hydrophobic Wire Mesh Screen in Diesel. Fluids, 6(9), 319. https://doi.org/10.3390/fluids6090319






