Improvement of a Diagnostic Urban Wind Model for Flow Fields around a Single Rectangular Obstacle in Micrometeorology Simulation
Abstract
1. Introduction
2. The MASCON Field Model and Existing Algebraic Models for the Flow Field
2.1. The MASCON Field Model
2.2. Existing Algebraic Models for the Initial Flow Fields
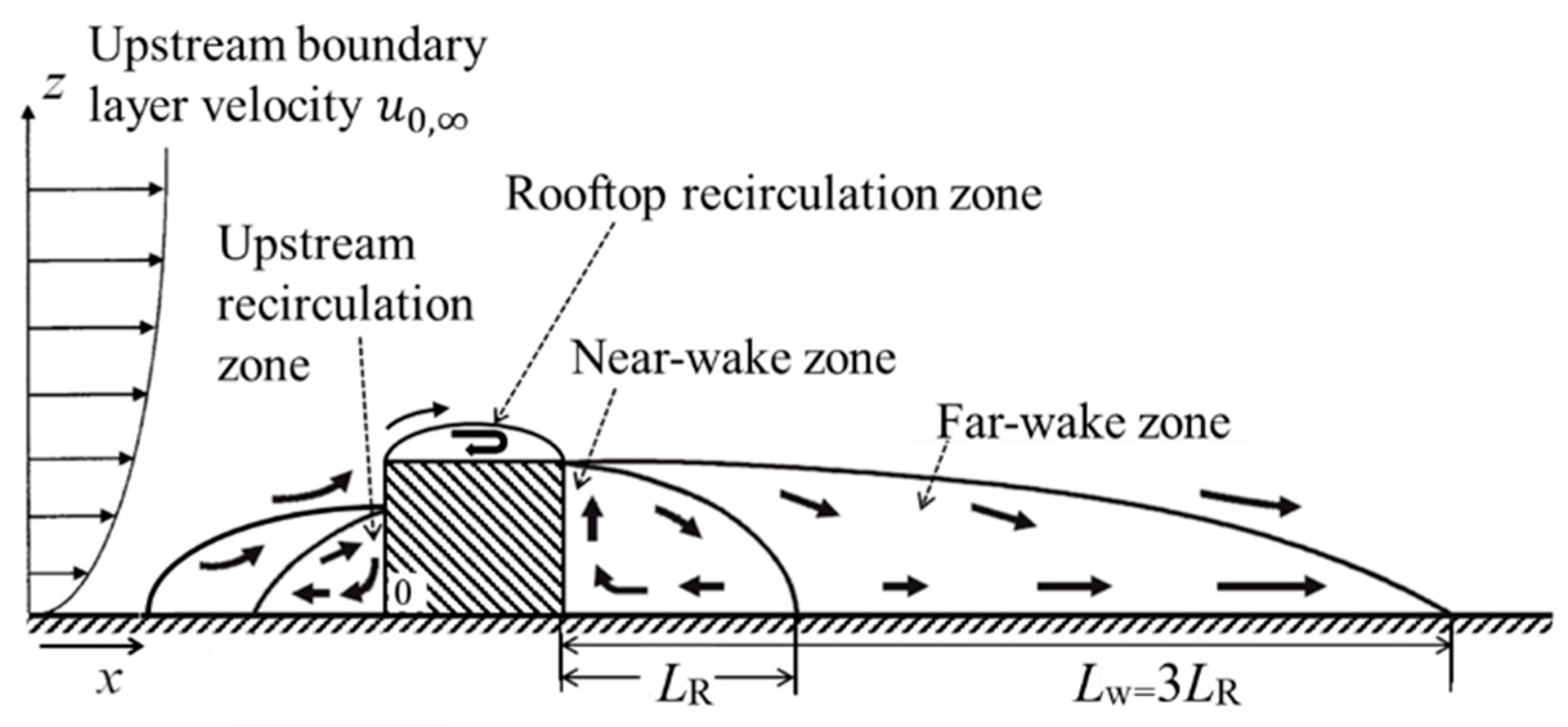
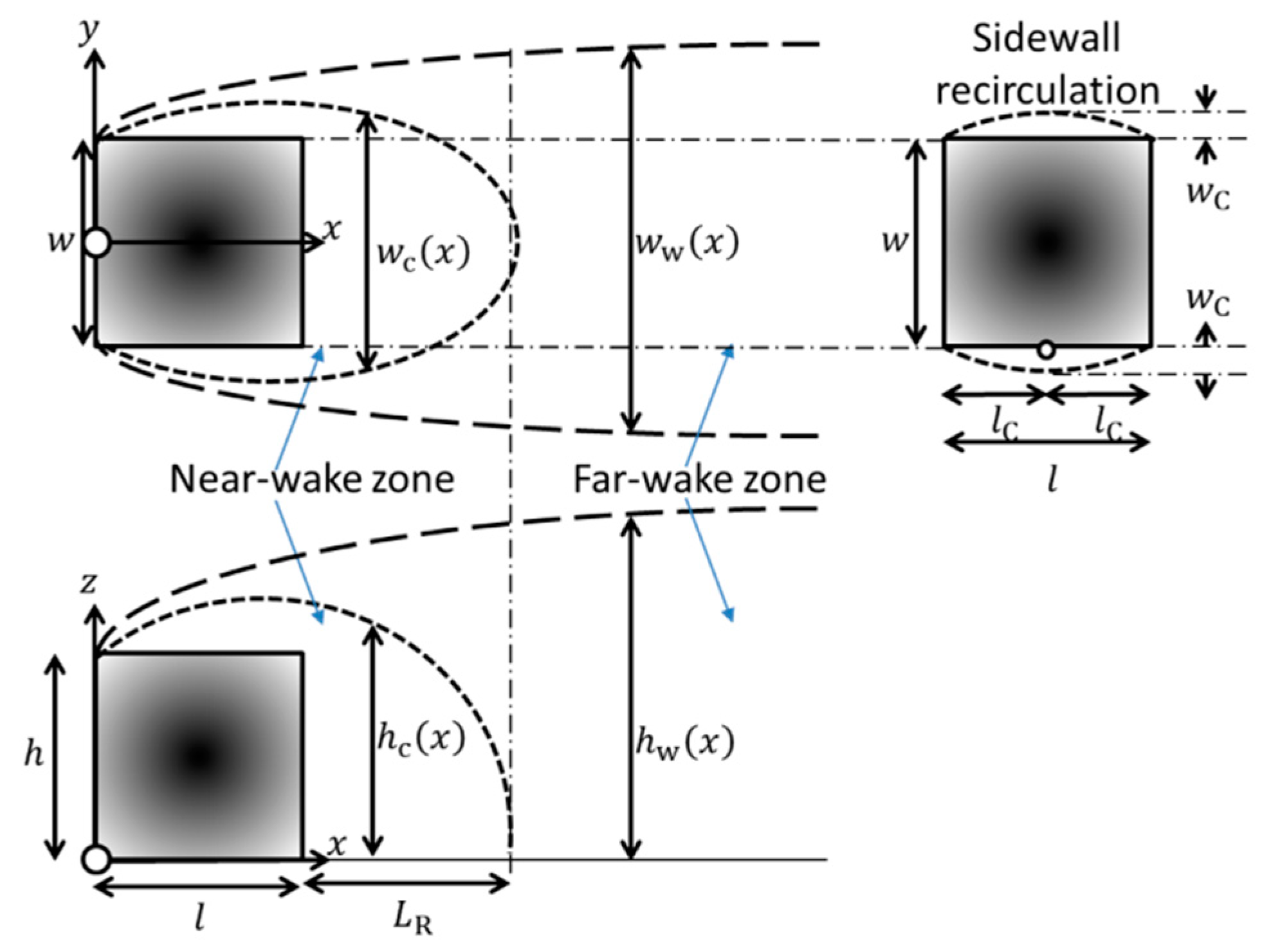
2.2.1. Modified Röckle Model
- (1)
- Rooftop recirculation zone
- (2)
- Near-wake zone
- (3)
- Far-wake zone
2.2.2. Shelter Model
3. Methodology
3.1. Improved Algebraic Models for Flow Fields Using MASCON Field Model
3.1.1. ADMS-Build Wake Model
3.1.2. PRIME Model
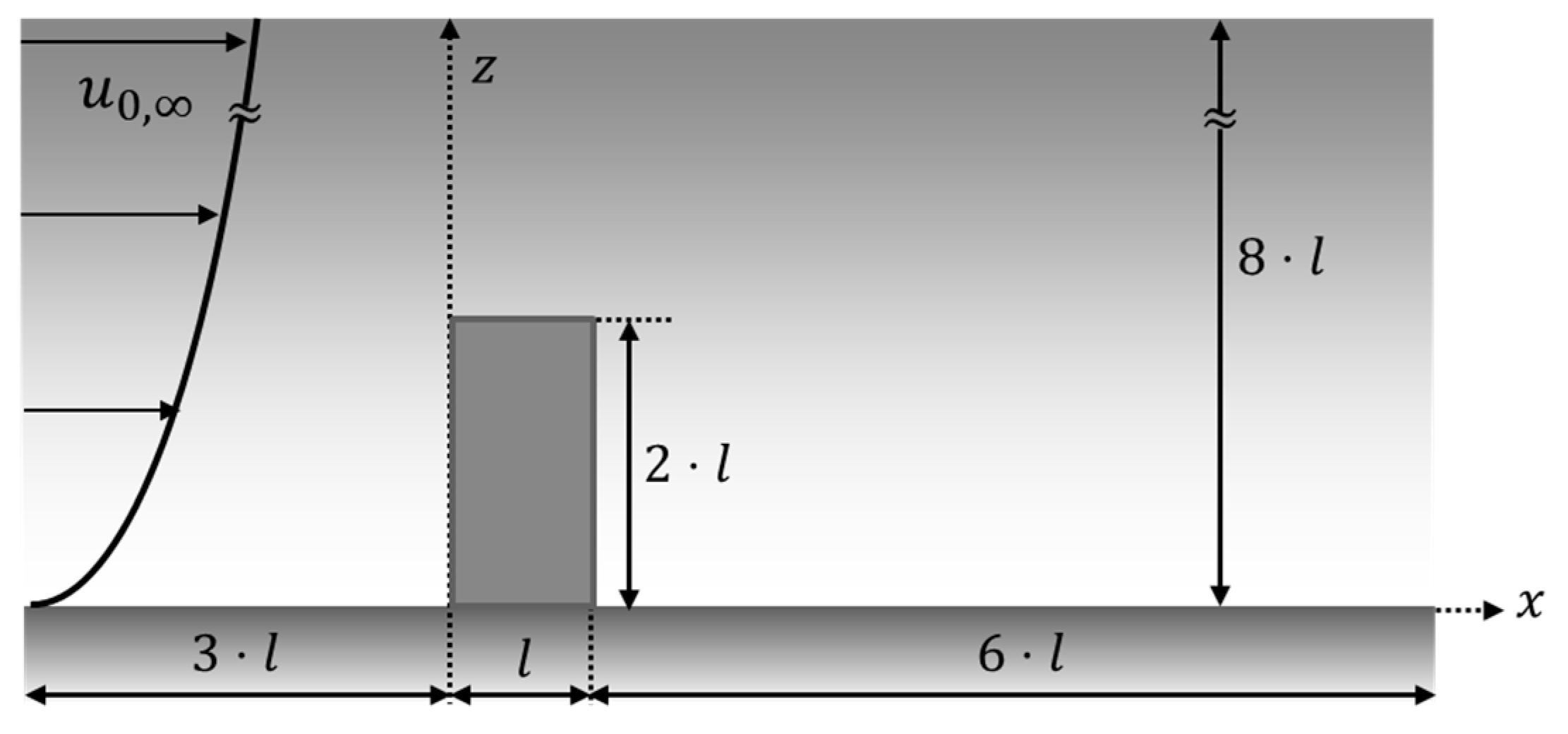
3.2. Wind-Tunnel Measurement Data
3.2.1. Outline of the Experiment by Wang et al. and Computational Condition
3.2.2. Outline of the Experiment by Meng et al. and Computational Condition
4. Results and Discussion
4.1. Comparison with Experiment by Wang et al.
4.2. Comparison with Experiment by Meng et al.
5. Concluding Remarks
- The new set of wake zone models based on ADMS-build and PRIME wake models can provide the initial velocity in the near-wake zone and take into consideration the effect of momentum diffusion in the far-wake region.
- Streamlines obtained from the experiment around the obstacle representing the flow field on the mid-height horizontal plane show the complicated recirculation flow formed by the union of the sidewall recirculation zone and the near-wake zone. The present wake zone model based on the PRIME model that includes the parameterization of the sidewall recirculation zones can reproduce such a recirculation flow.
- In the far-wake zone, the flow fields according to the present models considering the effect of momentum diffusion are all in general agreement with the experimental results. In particular, the wake zone model based on the PRIME model provides the excellent flow field that precisely reproduces the profile of the vertical velocity distribution of the experimental results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Singh, B.; Hansen, B.; Brown, M.J.; Pardyjak, E.R. Evaluation of the QUIC-URB fast response urban wind model for a cubical building array and wide building street canyon. Environ. Fluid. Mech. 2008, 8, 281–312. [Google Scholar] [CrossRef]
- Gowardhan, A.A.; Brown, M.J.; Pardyjak, E.R. Evaluation of a fast response pressure solver for flow around an isolated cube. Environ. Fluid Mech. 2010, 10, 311–328. [Google Scholar] [CrossRef]
- Hayati, A.N.; Stoll, R.; Kim, J.J.; Harman, T.; Nelson, M.A.; Brown, M.J.; Pardyjak, E.R. Comprehensive Evaluation of Fast-Response, Reynolds-Averaged Navier–Stokes, and Large-Eddy Simulation Methods Against High-Spatial-Resolution Wind-Tunnel Data in Step-Down Street Canyons. Bound.-Layer Meteorol. 2017, 164, 217–247. [Google Scholar] [CrossRef]
- Kimura, A.; Asami, M.; Oka, H.; Oka, Y. Development of an Algebraic Model of Empirical Parameterization of Near Wakes around a Vehicle. Fluids 2021, 6, 75. [Google Scholar] [CrossRef]
- Peña, A.; Bechmann, A.; Conti, D.; Angelou, N. The fence experiment—Full-scale lidar-based shelter observations. Wind Energ. Sch. Discuss. 2016, 1, 101–114. [Google Scholar] [CrossRef]
- Röckle, R. Bestimmung der Stomungsverhaltnisse im Bereich Komplexer Bebauugsstruckturen. Ph.D. Thesis, Vom Fachbereich Mechanik, der Technischen Hochschule Darmstadt, Darmstadt, Germany, 1990. [Google Scholar]
- Sherman, C.A.A. Mass-Consistent Model for Wind Fields Over Complex Terrain. J. Appl. Meterol. 1978, 17, 312–319. [Google Scholar] [CrossRef]
- Kanda, I.; Yamao, Y.; Ohara, T.; Uehara, K. An Urban Atmospheric Diffusion Model for Traffic-Related Emission Based on Mass-Conservation and Advection-Diffusion Equations. Environ. Model Assess. 2013, 18, 221–248. [Google Scholar] [CrossRef]
- Brown, M.J.; Williams, M.D.; Nelson, M.A.; Werley, K.A. QUIC Transport and Dispersion Modeling of Vehicle Emissions in Cities for Better Public Health Assessments. Environ. Health Insights 2015, 9, 55–65. [Google Scholar] [CrossRef] [PubMed]
- Hanna, S.; White, J.; Trolier, J.; Vernot, R.; Brown, M.; Gowardhan, A.; Kaplan, H.; Alexander, Y.; Moussafir, J.; Wang, Y.; et al. Comparisons of JU2003 observations with four diagnostic urban wind flow and Lagrangian particle dispersion models. Atmos. Environ. 2011, 45, 4073–4081. [Google Scholar] [CrossRef]
- Pardyjak, E.R.; Brown, M.J.; Bagal, N. Improved Velocity Deficit Parameterizations for a Fast Response Urban Wind Model. In Proceedings of the 84th AMS Annual Meeting, Seattle, WA, USA, 10–16 January 2004. [Google Scholar]
- Singh, B.; Pardyjak, E.R.; Brown, M.J. Testing of a Far-wake Parameterization for a Fast Response Urban Wind Model. In Proceedings of the 6th AMS Urban Environment Symposium, Atlanta, GA, USA, 28 January–3 February 2006. [Google Scholar]
- Gross, G.; Röckle, R.; Janssen, U. ASMUS-Ein numerisches model zur berechnung der strömung und der schadstoffverteilung im bereich einzelner gebäude. I Das strömungsfeld. Meteorol. Z. 1994, 3, 267–274. [Google Scholar] [CrossRef]
- Hosker, R.P. Flow and Diffusion near Obstacles. In Atmospheric Science and Power Production; Randerson, D., Ed.; Technical Information Center, Office of Scientific and Technical Information, United States Department of Energy: Springfield, VA, USA, 1984; pp. 241–326. [Google Scholar]
- Fröhlich, D. Development of a Microscale Model for the Thermal Environment in Complex Areas. Inaugural-Dissertation zur Erlangung der Doktorwürde der Fakultät für Umwelt und Natürliche Ressourcen der Albert-Ludwigs-Universität Freiburg im Breisgau. 2016. Available online: https://freidok.uni-freiburg.de/fedora/objects/freidok:11614/datastreams/FILE1/content (accessed on 1 June 2021).
- Taylor, P.A.; Salmon, J.R. A Model for the Correction of Surface Wind Data for Sheltering by Upwind Obstacles. J. Appl. Meteorol. 1993, 32, 1683–1694. [Google Scholar] [CrossRef][Green Version]
- Robins, A.G.; Apsley, D.D. Modelling of Building Effects in ADMS; Technical Report P16/01W/18; Cambridge Environmental Research Consultant: Cambridge, UK, 2018. [Google Scholar]
- CERC ADMS-Urban User Guide. Available online: http://www.cerc.co.uk (accessed on 1 January 2021).
- Robins, A.; McHugh, C. Development and evaluation of the ADMS building effects module. J. Environ. Pollut. 2001, 16, 161–174. [Google Scholar] [CrossRef]
- Schulman, L.; Strimaitis, D.G.; Scire, J.S. Development and Evaluation of the PRIME Plume Rise and Building Downwash Model. J. Air Waste Manag. Assoc. 1995, 50, 378–390. [Google Scholar] [CrossRef] [PubMed]
- 1997 ASHRAE Handbook—Fundamentals; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 1997.
- Wilson, D.J.; Britter, R.E. Estimates of building surface concentrations from nearby point sources. Atmos. Environ. 1982, 16, 2631–2646. [Google Scholar] [CrossRef]
- Snyder, W.H.; Lawson, R.E., Jr. Wind-tunnel measurements of flow fields in the vicinity of buildings. In Proceedings of the Eighth Joint Conference on Applications of Air Pollution Meteorology with A&WMA, Boston, MA, USA, 23–28 January 1994; pp. 244–250. [Google Scholar]
- Wang, F.; Lam, K.M. Geometry effects on mean wake topology and large-scale coherent structures of wall-mounted prisms. Phys. Fluids 2019, 31, 125109. [Google Scholar] [CrossRef]
- Meng, Y.; Hibi, K. Turblent measurements of the flow field around a high-rise building. J. Wind Eng. 1998, 76, 55–64. [Google Scholar] [CrossRef]
- Yoshie, R.; Mochida, A.; Tominaga, Y.; Kataoka, H.; Harimoto, K.; Nozu, T.; Shirasawa, T. Cooperative project for CFD prediction of pedestrian wind environment in the Architectural Institute of Japan. J. Wind Eng. Ind. Aerodyn. 2007, 95, 1551–1578. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M. Note on Pressure and Incompressibility. In Computational Methods for Fluid Dynamics, 3rd ed.; Splinger: Berlin, Germany, 2002; pp. 202–204. [Google Scholar]

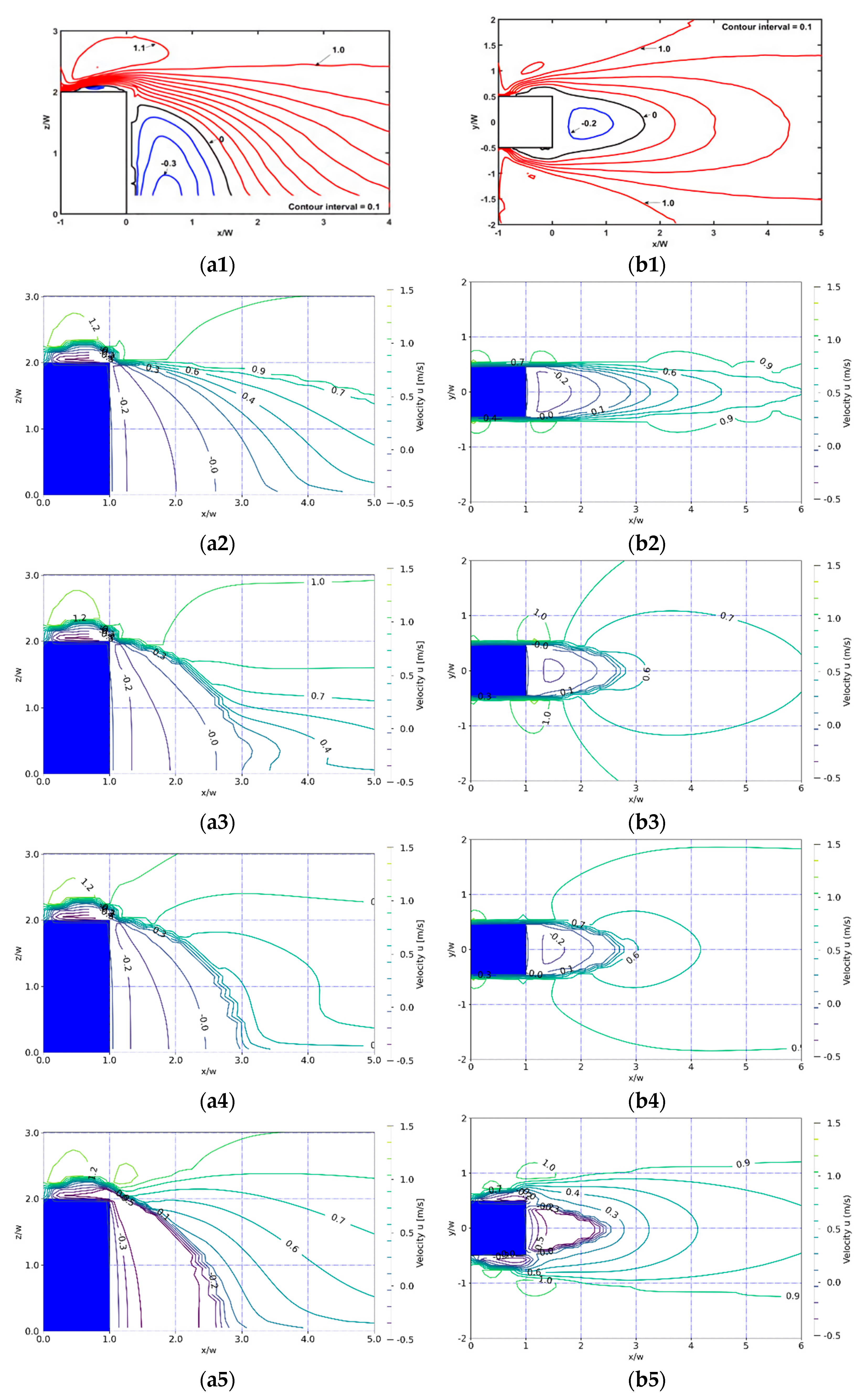
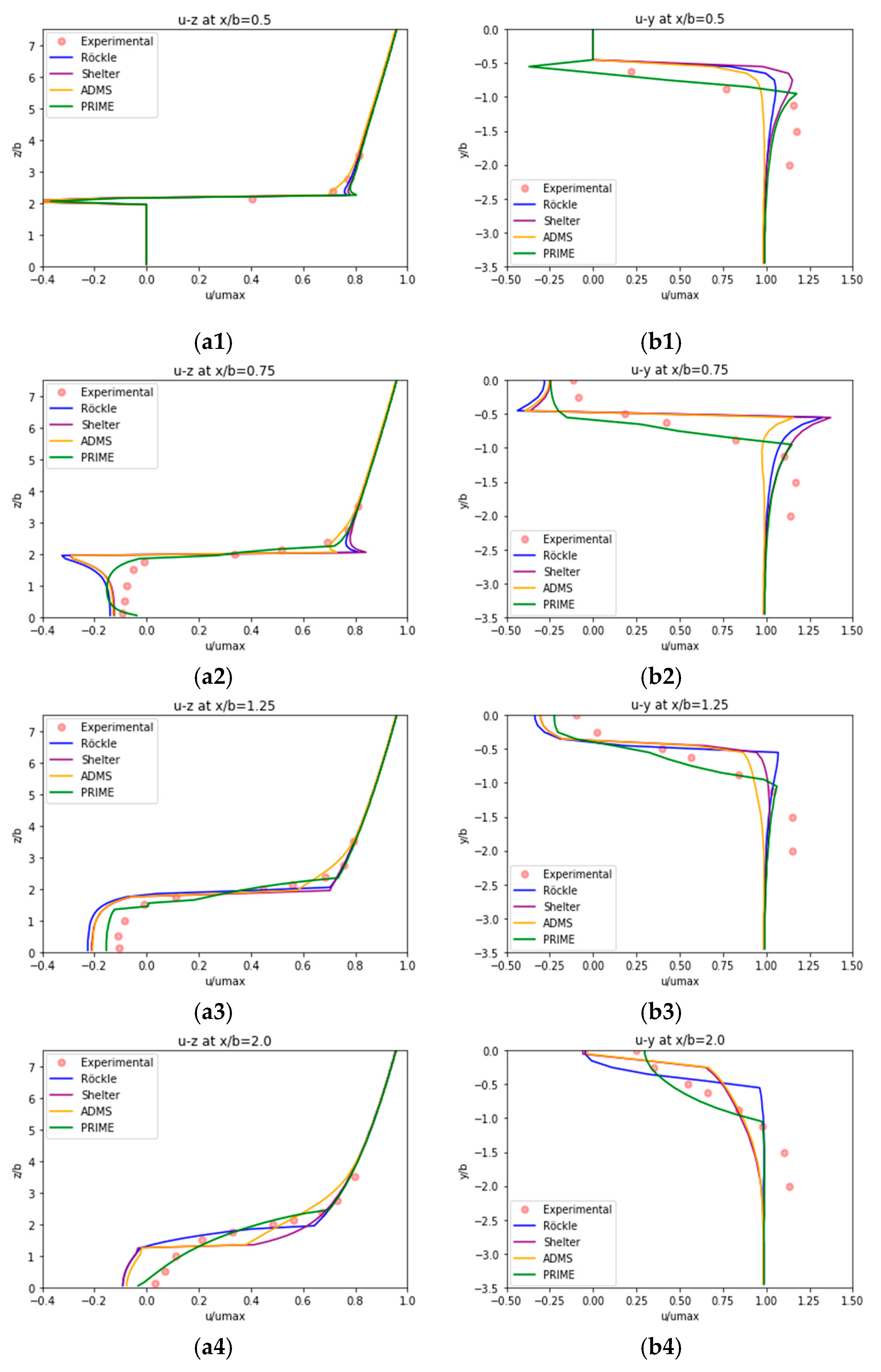
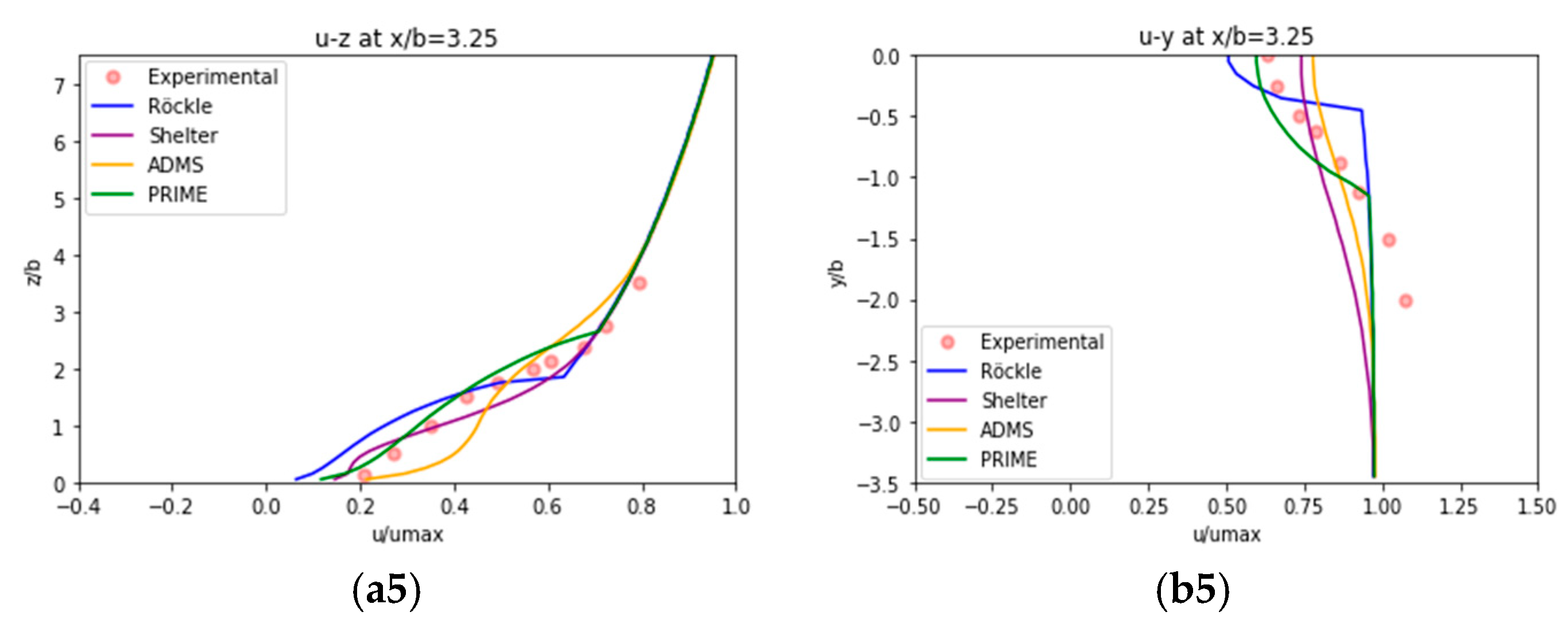
| Aspect Ratio of the Obstacle | Experiment/MASCON Model | Central Vertical Plane | Mid-Height Horizontal Plane | |||
|---|---|---|---|---|---|---|
| Vortex Core | Saddle Point | Vortex Core | Saddle Point | |||
| 1:1:2 | Experiment [24] | |||||
| MASCON | Röckle | |||||
| Shelter | ||||||
| ADMS | ||||||
| PRIME | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asami, M.; Kimura, A.; Oka, H. Improvement of a Diagnostic Urban Wind Model for Flow Fields around a Single Rectangular Obstacle in Micrometeorology Simulation. Fluids 2021, 6, 254. https://doi.org/10.3390/fluids6070254
Asami M, Kimura A, Oka H. Improvement of a Diagnostic Urban Wind Model for Flow Fields around a Single Rectangular Obstacle in Micrometeorology Simulation. Fluids. 2021; 6(7):254. https://doi.org/10.3390/fluids6070254
Chicago/Turabian StyleAsami, Mitsufumi, Arata Kimura, and Hideyuki Oka. 2021. "Improvement of a Diagnostic Urban Wind Model for Flow Fields around a Single Rectangular Obstacle in Micrometeorology Simulation" Fluids 6, no. 7: 254. https://doi.org/10.3390/fluids6070254
APA StyleAsami, M., Kimura, A., & Oka, H. (2021). Improvement of a Diagnostic Urban Wind Model for Flow Fields around a Single Rectangular Obstacle in Micrometeorology Simulation. Fluids, 6(7), 254. https://doi.org/10.3390/fluids6070254





