CFD Model for Aircraft Ground Deicing: Verification and Validation of an Extended Enthalpy-Porosity Technique in Particulate Two Phase Flows
Abstract
:1. Introduction
- Convection fusion (natural or forced): It occurs if a solid is placed in a fluid domain with certain pressure and temperature fields. In natural convection, no flow is imposed, the pressure or/and temperature gradients generated at the solid-fluid interface induces the movement. This movement prevents the solid from having a cold layer of fluid around it. This movement persists until a point of equilibrium is reached by melting the solid [17]. In forced convection, the flow lowers the pressure and/or increases the temperature at the solid-fluid interface, causing it to melt [18].
- Close Contact Fusion: It occurs if a heat source and a solid are brought into contact with each other during the solid fusion. The physical situation involves the movement of the heat source or the solid, which prevents the accumulation of the melt between the source and the solid [19].
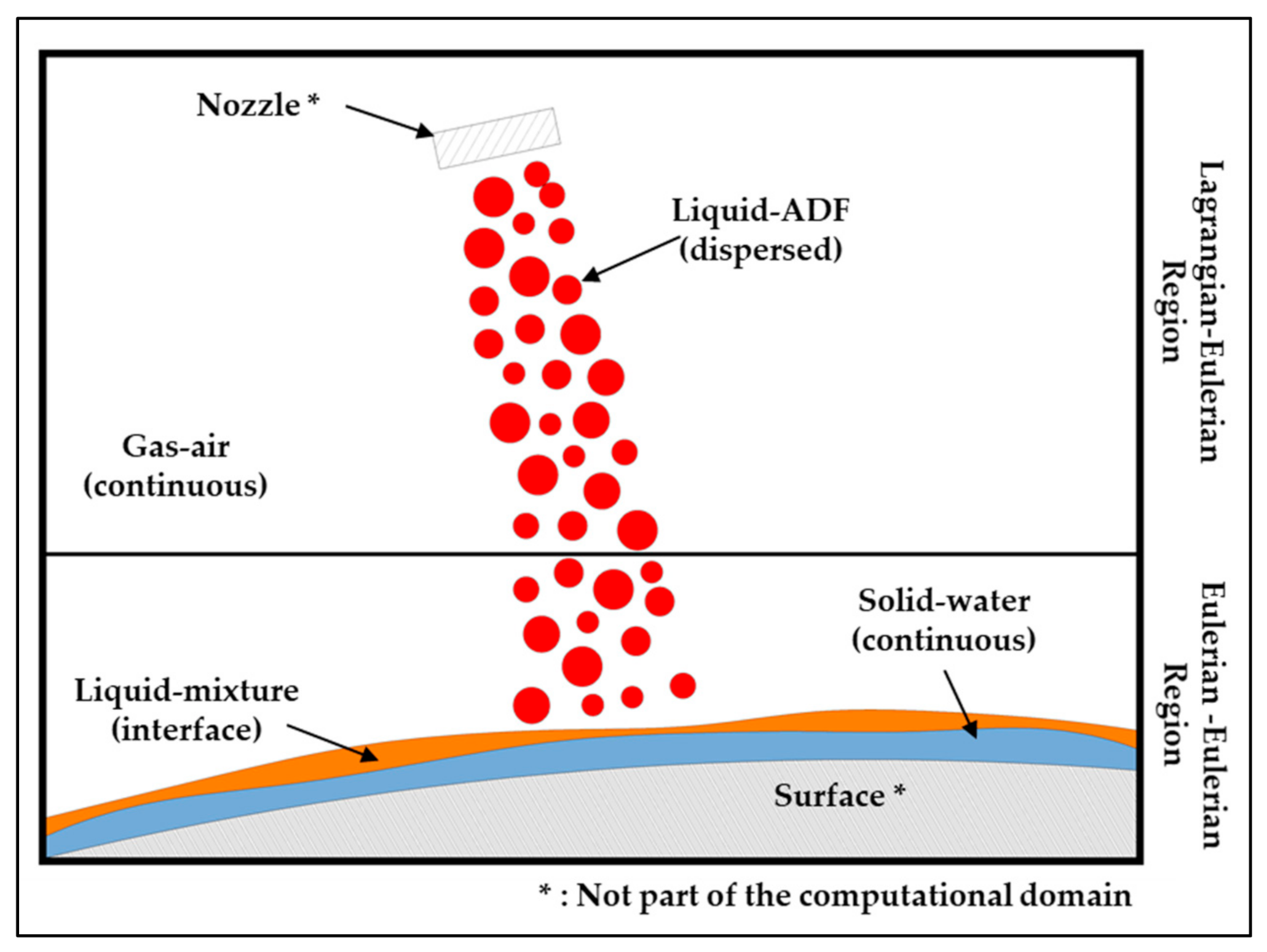
2. Conceptual Model
2.1. Mathematical Model
2.1.1. Mass Conservation
2.1.2. Momentum Conservation
2.1.3. Energy Conservation
2.1.4. Solidification/Melting Source Terms
2.2. Numerical Methods
2.2.1. Numerical Treatment
2.2.2. Numerical Schemes and Algorithm Controls
3. Verification, Validation and Calibration
3.1. Diffusion Verification Test
3.2. Miscibility -Energy Validation Test
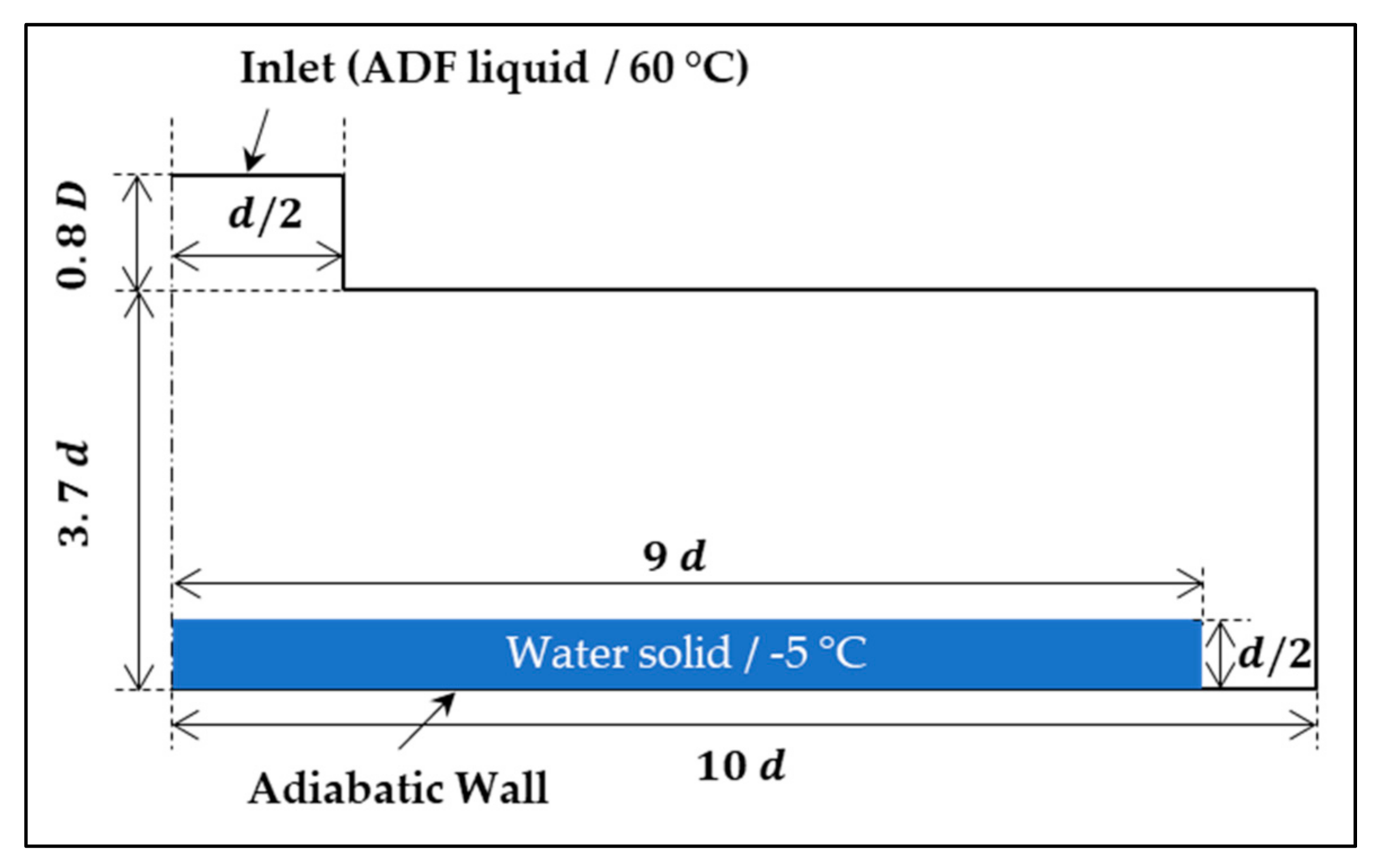
3.3. Impinging Jet Validation
3.4. Permeability Coefficient Calibration
4. Discussion and Conclusions
- The developed solver predicts unsteady temperature evolution of a two-phase flow in which one phase is a mixture of two species with a precision of 95%. This precision is observed in a 2D dam-break simulation involving mixture.
- The proposed solver predicts the convective heat transfer between liquid formed by an impinging jet and a heated wall with a maximal error of 12%. This result is comparable to the existing models.
- The permeability coefficient of the extended enthalpy-porosity technique is calibrated through a sensitivity study proposed in [24]. The results are insensitive to the permeability coefficient with an Extra-Fine mesh. The ice shape evolution can be well predicted with a Coarse mesh with a permeability coefficient of , which is within the interval stated by Ebrahimi, Kleijn and Richardson [24].
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Fields | |
| Volume fraction | |
| Phase density | |
| Velocity | |
| Time | |
| Specie mass fraction | |
| D | Species diffusion coefficients |
| Kinematic viscosity | |
| Schmidt number | |
| Specific heat capacity | |
| Thermal diffusivity/conductivity | |
| Pressure | |
| Gravity acceleration vector | |
| Dynamic viscosity | |
| Drag coefficient for a dispersed flow | |
| Drag coefficient for an interface flow | |
| Enthalpy | |
| Kinetic energy | |
| Effective thermal diffusivity | |
| Inter-phase heat transfer coefficient | |
| Temperature | |
| Solid volume fraction | |
| latent heat of fusion | |
| Source terms | |
| Inter-phase momentum transfer | |
| Momentum transfer between the solid phase and phase | |
| Inter-phase momentum transfer due to drag force | |
| Inter-phase momentum transfer due to virtual mass | |
| Energy sink term modelling phase change of phase | |
| Momentum transfer between the solid phase and phase modelling buoyancy | |
| Momentum transfer between the solid phase and phase modelling drag | |
| Parameters | |
| Permeability coefficient | |
| Enthalpy-porosity model coefficient | |
| Under-relaxation factor | |
| Indexes | |
| Phase | |
| Liquid phase | |
| Gaseous phase | |
| Species 1 | |
| Species 2 | |
| Species | |
Appendix A
| Generalized Model [39] | ||
| Fluidization [39] | ||
| Fluid flow through packed columns [39] | ||
| Dense dispersed flows (Generalized Model) [40] | : surface tension Eotvos number: | |
| [41] | ||
| Model for interface | ||
| For regions with no obvious dispersed phase [25] | ||
| Analytical model | |
| Correlation for turbulent heat transfer from the surface of a sphere to the surrounding fluid [42] |
References
- Al-Khalil, K.; Potapczuk, M. Numerical modeling of anti-icing systems and comparison to test results on a NACA 0012 airfoil. In Proceedings of the 31st Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1993. [Google Scholar]
- Morency, F.; Tezok, F.; Parashivoiu, I. Heat and Mass Transfer in the Case of Anti-Icing System Simulation. J. Aircr. 2000, 37, 245–252. [Google Scholar] [CrossRef]
- Liu, H.-T.; Hua, J. Three-Dimensional Integrated Thermodynamic Simulation for Wing Anti-Icing System. J. Aircr. 2004, 41. [Google Scholar] [CrossRef]
- Moshansky, T.H.V.P. Commission of Inquiry into the Air Ontario Crash at Dryden, Ontario: Final Report: Technical Appendices; Minister of Supply and Services: Ottawa, ON, Canada, 1992. [Google Scholar]
- National Transportation Safety Board, Aircraft Accident Report Washington, DC. 20594 AIRCRAFT, Takeoff Stall in Icing Conditions USAIR Flight 405 FOKKER F-28, New York 22 March 1992. 1993. Available online: http://www.ntsb.gov/investigations/AccidentReports/Reports/AAR0003.pdf (accessed on 2 July 2017).
- Transport Canada, Guidelines for Aircraft Ground Icing Operations (Chapter 13), Ottawa. 2005. Available online: http://www.tc.gc.ca/publications/en/tp14052/pdf/hr/tp14052e.pdf (accessed on 4 February 2018).
- ACRP Fact Sheets, De/Anti-Icing Optimization, Transportation Research Board of the National Academies, Sponsored by the FAA. 2016. Available online: http://onlinepubs.trb.org/onlinepubs/acrp/acrp_rpt_045factsheets.pdf (accessed on 21 May 2021).
- ICAO. Manual of Aircraft Ground De-Icing/Anti-Icing Operations. 2018. Available online: https://store.icao.int/en/manual-of-aircraft-ground-de-icing-anti-icing-operations-doc-9640 (accessed on 21 May 2021).
- ICAO. International Standards and Recommended Practices: Annex 6—Operation Of Aircraft—Part 1—International Commercial Air Transport—Aeroplanes: Paragraph 4.3.5.4. 2018. Available online: https://store.icao.int/en/annex-6-operation-of-aircraft-part-i-international-commercial-air-transport-aeroplanes (accessed on 21 May 2021).
- SAE. Aircraft Ground Deicing/Anti-Icing Processes AS6285D, Aerosp. Stand. 2021. Available online: https://www.sae.org/standards/content/as6285d/ (accessed on 21 May 2021).
- Visaria, M.; Mudawar, I. Theoretical and experimental study of the effects of spray inclination on two-phase spray cooling and critical heat flux. Int. J. Heat Mass Transf. 2008, 51, 2398–2410. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, M.; Liu, D.; Xu, K.; Chen, Y. Experimental study on the effects of spray inclination on water spray cooling performance in non-boiling regime. Exp. Therm. Fluid Sci. 2010, 34, 933–942. [Google Scholar] [CrossRef]
- Yan, Z.B.; Duan, F.; Wong, T.N.; Toh, K.C.; Choo, K.F.; Chan, P.K.; Chua, Y.S.; Lee, L.W. Large area impingement spray cooling from multiple normal and inclined spray nozzles. Heat Mass Transf. 2013, 49, 985–990. [Google Scholar] [CrossRef]
- Chen, B.; Wang, L.-W.; Gong, R.; Wang, S.-K. Numerical simulation and experimental validation of aircraft ground deicing model. Adv. Mech. Eng. 2016, 8, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Yakhya, S.; Ernez, S.; Morency, F. Computational Fluid Dynamics Investigation of Transient Effects of Aircraft Ground Deicing Jets. J. Thermophys. Heat Transf. 2019, 33, 117–127. [Google Scholar] [CrossRef]
- Ernez, S.; Morency, F. Eulerian-Lagrangian CFD Model for Prediction of Heat Transfer Between Aircraft Deicing Liquid Sprays and a Surface. Int. J. Numer. Methods Heat Fluid Flow. 2019, 29, 2450–2475. [Google Scholar]
- Bertrand, O.; Binet, B.; Combeau, H.; Couturier, S.; Delannoy, Y.; Gobin, D.; Lacroix, M.; le Quéré, P.; Médale, M.; Mencinger, J.; et al. Melting driven by natural convection a comparison exercise: First result. Int. J. Therm. Sci. 1999, 38, 5–26. [Google Scholar] [CrossRef]
- Ma, Z.W.; Zhang, P.; Wang, R.Z.; Furui, S.; Xi, G.N. International Journal of Heat and Mass Transfer Forced flow and convective melting heat transfer of clathrate hydrate slurry in tubes. Int. J. Heat Mass Transf. 2010, 53, 3745–3757. [Google Scholar] [CrossRef]
- Groulx, D.; Lacroix, M. Study of close contact melting of ice from a sliding heated flat plate. Int. J. Heat Mass Transf. 2006, 49, 4407–4416. [Google Scholar] [CrossRef]
- Tan, Z.; Lim, K.M.; Khoo, B.C. An adaptive mesh redistribution method for the incompressible mixture flows using phase-field model. J. Comput. Phys. 2007, 225, 1137–1158. [Google Scholar] [CrossRef]
- Voller, V.R.; Prakash, C. A fixed grid numerical modelling methodology for convection-diffusion mushy region phase-change problems. Int. J. Heat Mass Transf. 1987, 30, 1709–1719. [Google Scholar] [CrossRef]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions, Imperial College of Science, Technology & Medicine. 2002. Available online: http://hdl.handle.net/10044/1/8110 (accessed on 21 February 2019).
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics, 4th ed.; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Kolev, N.I. Multiphase Flow Dynamics 2, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Marschall, H. Towards the Numerical Simulation of Multi-Scale Two-Phase Flow; Technische Universität München: Munich, Germany, 2011. [Google Scholar]
- Manni, A. An Introduction to twoPhaseEulerFoam with Addition of an Heat Exchange Model. In CFD with OpenSource Softw. Gothenburg, Sweden, 2014. Available online: http://www.tfd.chalmers.se/~hani/kurser/OS_CFD_2014/AlessandroManni/ReportAM.pdf (accessed on 3 March 2020).
- Ebrahimi, A.; Kleijn, C.R.; Richardson, M.I. Sensitivity of numerical predictions to the permeability coefficient in simulations of melting and solidification using the enthalpy-porosity method. Energies 2019, 12, 4360. [Google Scholar] [CrossRef] [Green Version]
- Holzmann, T. Mathematics, Numerics, Derivations and OpenFOAM.; Holzmann CFD: Loeben, Germany, 2016; Volume 156. [Google Scholar] [CrossRef]
- Greenshields, C.J. OpenFOAM User Guide V5. 2017. Available online: http://foam.sourceforge.net/docs/Guides-a4/OpenFOAMUserGuide-A4.pdf (accessed on 25 May 2018).
- CFDDirect. OpenFOAM v5 User Guide: 3.4 Running Applications in Parallel. 2017. Available online: https://cfd.direct/openfoam/user-guide/running-applications-parallel/ (accessed on 22 April 2018).
- Greenshields, C.J.; OpenFOAM Programmer’s Guide v3.0.1; OpenFOAM Found. Ltd. 2015 100. Available online: http://foam.sourceforge.net/docs/Guides-a4/ProgrammersGuide.pdf (accessed on 21 April 2018).
- Rodríguez-Ocampo, P.E.; Ring, M.; Hernández-Fontes, J.V.; Alcérreca-Huerta, J.C.; Mendoza, E.; Silva, R. CFD simulations of multiphase flows: Interaction of miscible liquids with different temperatures. Water 2020, 12, 2581. [Google Scholar] [CrossRef]
- Stevens, J. Measurements of Local Heat Transfer Coefficients: Results for an Axisymmetric, Single-Phase Water Jet Impinging Normally on a Flat Plate with Uniform Heat Flux. Master’s Thesis, Brigham Young University, Provo, UT, USA, 1988. [Google Scholar]
- Noriega, H. Une Étude de Cas de Vérification Pour un Code À Source Ouvert de Simulation Numérique; Université de Montréal: Montreal, QC, Canada, 2016; Available online: https://publications.polymtl.ca/2407/ (accessed on 21 March 2021).
- Hermosilla, M.B. Study of Heat and Mass Transfer Applications in the Field of Engineering by Using OpenFOAM; Universitat Politècnica de Catalunya: Barcelona, Spain, 2016; Available online: https://upcommons.upc.edu/bitstream/handle/2117/98893/REPORT_260.pdf?sequence=2&isAllowed=y (accessed on 21 March 2021).
- Mironova, M. Numerical Study of Steady State and Transient Heat Conduction Using OpenFOAM; Montanuniversität Leoben: Leoben, Austria, 2018; Available online: https://pure.unileoben.ac.at/portal/files/3161767/AC15203764n01.pdf (accessed on 21 March 2021).
- Tong, A.Y. A Numerical Study on The Hydrodynamics and Heat Transfer of a Circular Liquid Jet Impinging Onto a Substrate. Numer. Heat Transf. Part A Appl. 2003, 44, 1–19. [Google Scholar] [CrossRef]
- Edin, B.; Šefko, Š. Computational Modeling and Simulation of Nonisothermal Free-surface Flow of a Liquid Jet Impinging on a Heated Surface. Procedia Eng. 2015, 100, 115–124. [Google Scholar] [CrossRef]
- Enwald, H.; Peirano, E.; Almstedt, A.-E. Eulerian two-phase flow theory applied to fluidization. Int. J. Multiph. Flow. 1996, 22, 21–66. [Google Scholar] [CrossRef]
- Ishii, M.; Zuber, N. Drag coefficient and relative velocity in bubbly, droplet or particulate flows. AIChE J. 1979, 25, 843–855. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions, 1st ed.; Elsevier: New York, NY, USA, 1994. [Google Scholar]
- Ranz, W.; Marshall, W. Evaporation from Drops. Chem. Eng. Prog. 1952, 48, 141–146. [Google Scholar]














| Thermophysical Properties | Expression |
|---|---|
| Density | |
| Dynamic viscosity | |
| Heat capacity | |
| Thermal diffusivity (for temperature) |
| Time Step | ||||||
|---|---|---|---|---|---|---|
| 0.61 | 7.96 | 0.39 | 9.19 | 0.41 | 8.59 | |
| 0.33 | 2.01 | 0.06 | 1.59 | 0.04 | 0.98 | |
| 0.32 | 1.53 | 0.06 | 0.73 | 0.004 | 0.90 | |
| 0.32 | 1.54 | 0.06 | 0.64 | |||
| Time Step | ||||||
| 1.3 | 1.06 | 5.21 | 3.40 | 4.12 | 1.14 | |
| 1.3 | 1.12 | 5.25 | 3.60 | 4.19 | 1.21 | |
| 1.3 | 1.13 | 4.12 | 3.63 | 3.08 | 1.21 | |
| 1.3 | 1.13 | 4.10 | 3.64 | 2.00 | 1.22 | |
| Direction | Cell Number | Cell Size (mm) | |
|---|---|---|---|
| Coarse Mesh | X | 50 | 10/4 |
| Y | 30 | 10/4 | |
| Medium Mesh | X | 100 | 10/8 |
| Y | 60 | 10/8 | |
| Fine Mesh | X | 200 | 10/16 |
| Y | 120 | 10/16 | |
| Extra-Fine Mesh | X | 400 | 10/32 |
| Y | 240 | 10/32 |
| CFL | Coarse Mesh | Medium Mesh | Fine Mesh | Extra-Fine Mesh | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | ||||||||
| 4.68 | 8.21 | 3.49 | 5.77 | 3.30 | 4.76 | 3.34 | 4.95 | |
| 4.80 | 7.66 | 3.47 | 6.34 | 3.56 | 5.53 | 3.75 | 5.61 | |
| 5.21 | 9.52 | 3.86 | 6.83 | 3.56 | 5.61 | 4.67 | 6.73 | |
| 6.89 | 11.83 | 3.54 | 6.15 | 3.56 | 5.61 | 3.97 | 6.98 | |
| Nozzle diameter | ||
| Kinematic viscosity | ||
| Reynolds number | ||
| Wall heat flux |
| Mesh | Cell Edge Length | Cells Number |
|---|---|---|
| Coarse | d/10 | 3740 |
| Medium | d/20 | 14,960 |
| Fine | d/40 | 59,840 |
| Extra-Fine | d/80 | 239,360 |
| Properties | Symbol | Unity | Phases/Species | ||
|---|---|---|---|---|---|
| Gas Phase | Liquid Phase | ||||
| Equation of state | |||||
| Species | Air | ADF | Water | ||
| Mol weight | |||||
| Fluid constant | |||||
| Reference density | |||||
| heat capacity | |||||
| Dynamic viscosity | |||||
| Prandtl number | / | ||||
| Solidificationtemperature | / | ||||
| Latent heat of fusion | / | ||||
| Schmidt number | / | 720 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ernez, S.; Morency, F. CFD Model for Aircraft Ground Deicing: Verification and Validation of an Extended Enthalpy-Porosity Technique in Particulate Two Phase Flows. Fluids 2021, 6, 210. https://doi.org/10.3390/fluids6060210
Ernez S, Morency F. CFD Model for Aircraft Ground Deicing: Verification and Validation of an Extended Enthalpy-Porosity Technique in Particulate Two Phase Flows. Fluids. 2021; 6(6):210. https://doi.org/10.3390/fluids6060210
Chicago/Turabian StyleErnez, Sami, and François Morency. 2021. "CFD Model for Aircraft Ground Deicing: Verification and Validation of an Extended Enthalpy-Porosity Technique in Particulate Two Phase Flows" Fluids 6, no. 6: 210. https://doi.org/10.3390/fluids6060210
APA StyleErnez, S., & Morency, F. (2021). CFD Model for Aircraft Ground Deicing: Verification and Validation of an Extended Enthalpy-Porosity Technique in Particulate Two Phase Flows. Fluids, 6(6), 210. https://doi.org/10.3390/fluids6060210








