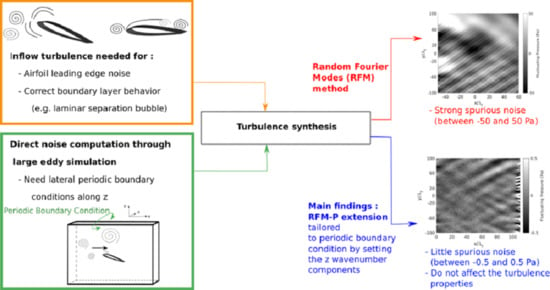
Low-Noise Synthetic Turbulence Tailored to Lateral Periodic Boundary Conditions
Abstract
:1. Introduction
2. Numerical Methods: Flow Solver and Inflow Synthetic Turbulence
2.1. Flow Solver
2.2. Inflow Synthetic Turbulence
2.2.1. Classical Random Fourier Modes Method
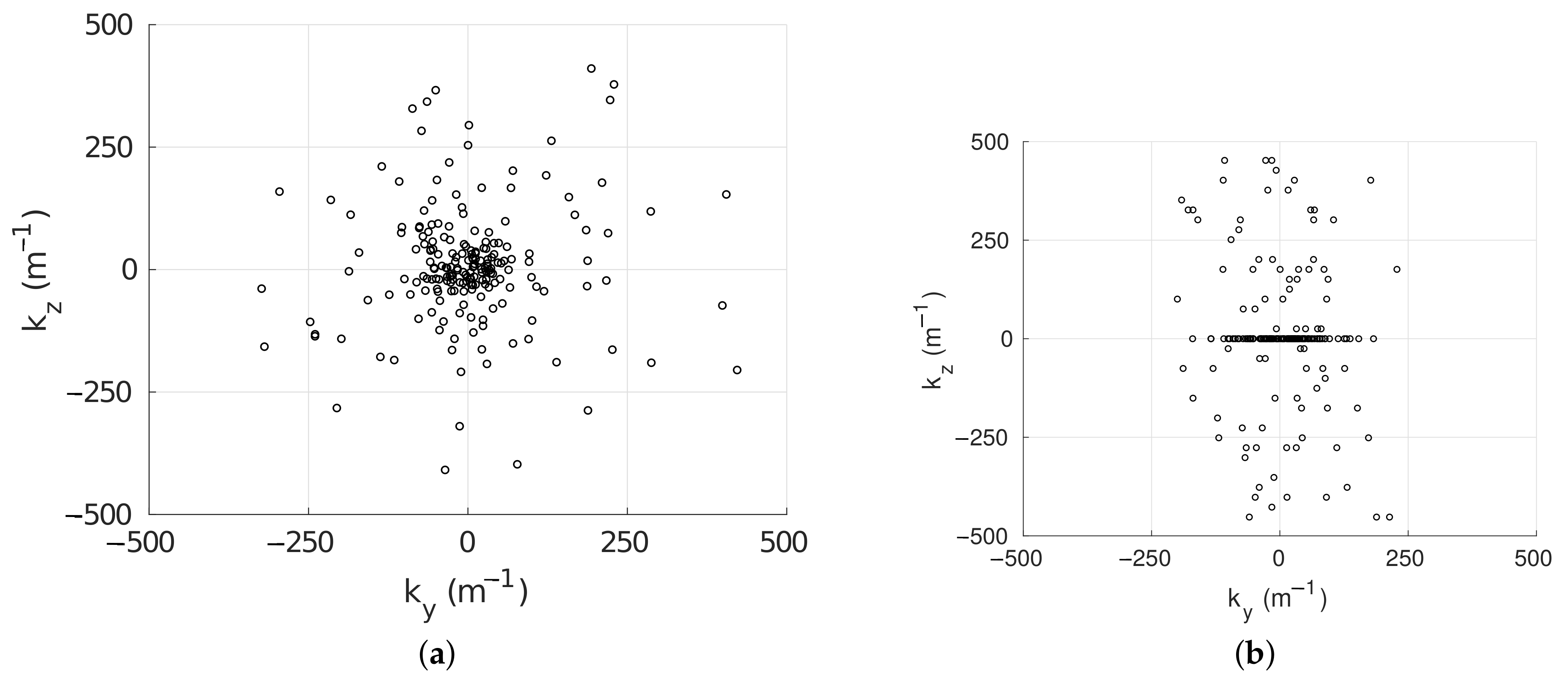
2.2.2. Random Fourier Modes Method Tailored to Periodic Boundary Conditions
3. Simulations of Spatially Decaying Homogeneous Isotropic Turbulence
3.1. Studied Configurations and Numerical Setups
3.1.1. Configurations
3.1.2. Simulation Parameters
3.1.3. Probes and Processing Method
3.1.4. Computation Platform and MPI Decomposition
3.2. Comparison of the RFM and RFM-P Approaches for Both Configurations
3.2.1. Instantaneous Velocity and Pressure Fields
3.2.2. Turbulent Kinetic Energy Evolution
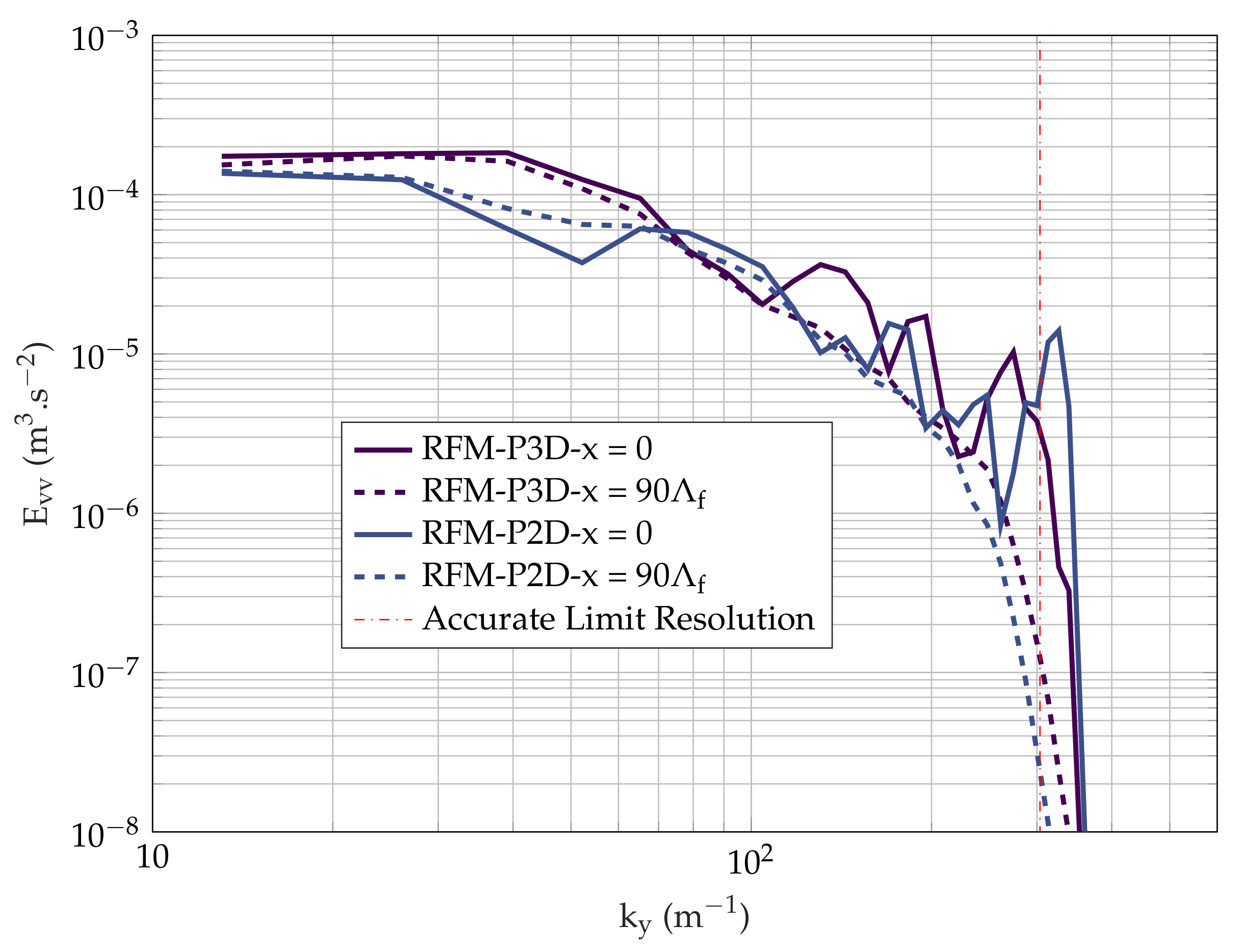
3.2.3. One-Dimensional Spectra
3.2.4. Computational Cost
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LSB | Laminar separation bubble |
| LES | Large eddy simulation |
| DNC | Direct noise computation |
| RFM | Random Fourier modes |
| RFM-P | Random Fourier modes method tailored to lateral periodic boundary conditions |
| SEM | Synthetic eddy method |
| RPM | Random particle mesh |
| PISO | Pressure-Implicit with Splitting of Operators |
| DRP | Dispersion-relation-preserving |
| MPI | Message passing interface |
| HIT | Homogeneous isotropic turbulence |
| CFL | Courant–Friedrichs–Lewy number |
| CINES | Centre Informatique National de l’Enseignement Supérieur |
Appendix A. Details about the Random Fourier Modes method
References
- Mueller, T.J.; DeLaurier, J.D. Aerodynamics of small vehicles. Annu. Rev. Fluid Mech. 2003, 35, 89–111. [Google Scholar] [CrossRef]
- Alam, M.M.; Zhou, Y.; Yang, H.; Guo, H.; Mi, J. The ultra-low Reynolds number airfoil wake. Exp. Fluids 2010, 48, 81–103. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, Z.; Alam, M.M.; Yang, H. Turbulent intensity and Reynolds number effects on an airfoil at low Reynolds numbers. Phys. Fluids 2014, 26, 115107. [Google Scholar] [CrossRef]
- Yauwenas, Y.; Fischer, J.; Moreau, D.; Doolan, C. The effect of inflow disturbance on drone propeller noise. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019. [Google Scholar]
- Casalino, D.; van der Velden, W.; Romani, G. Aeroacoustics Analysis of Urban Air Operations using the LB/VLES Method. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019. [Google Scholar]
- Oerlemans, S.; Schepers, J.G. Prediction of wind turbine noise and validation against experiments. Int. J. Aeroacoustics 2009, 8, 555–584. [Google Scholar] [CrossRef]
- Tian, Y.; Cotté, B. Wind turbine noise modeling based on Amiet’s theory: Effects of wind shear and atmospheric turbulence. Acta Acust. United Acust. 2016, 4, 626–639. [Google Scholar] [CrossRef] [Green Version]
- Buck, S.; Oerlemans, S.; Palo, S. Experimental validation of a wind turbine turbulent inflow noise prediction code. AIAA J. 2018, 56, 1495–1506. [Google Scholar] [CrossRef]
- Hosseinverdi, S.; Balzer, W.; Fasel, H.F. Direct Numerical Simulations of the Effect of Free-Stream Turbulence on “Long” Laminar Separation Bubbles. In Proceedings of the 42nd AIAA Fluid Dynamics Conference and Exhibit, New Orleans, LA, USA, 25–28 June 2012. [Google Scholar]
- Schmidt, S.; Breuer, M. Source term based synthetic turbulence inflow generator for eddy-resolving predictions of an airfoil flow including a laminar separation bubble. Comput. Fluids 2017, 147, 1–22. [Google Scholar] [CrossRef]
- Dhamankar, N.S.; Blaisdell, G.A.; Lyrintzis, A.S. Overview of Turbulent Inflow Boundary Conditions for Large-Eddy Simulations. AIAA J. 2018, 56, 1317–1334. [Google Scholar] [CrossRef]
- Gloerfelt, X.; Robinet, J.C. Silent inflow condition for turbulent boundary layers. Phys. Rev. Fluids 2017, 2, 124603. [Google Scholar] [CrossRef] [Green Version]
- Kraichnan, R.H. Diffusion by a random velocity field. Phys. Fluids 1970, 13, 22–31. [Google Scholar] [CrossRef]
- Smirnov, A.; Shi, S.; Celik, I. Random flow generation technique for Large Eddy Simulations and particle-dynamics modeling. ASME J. Fluids Eng. 2001, 123, 359–371. [Google Scholar] [CrossRef]
- Batten, P.; Goldberg, U.; Chakravarthy, S. Interfacing statistical turbulence closures with Large-Eddy Simulation. AIAA J. 2004, 42, 485–492. [Google Scholar] [CrossRef]
- Karweit, M.; Blanc-Benon, P.; Juvé, D.; Comte-Bellot, G. Simulation of the propagation of an acoustic wave through a turbulent velocity field: A study of phase variance. J. Acoust. Soc. Am. 1991, 89, 52–62. [Google Scholar] [CrossRef] [Green Version]
- Bechara, W.; Bailly, C.; Lafon, P. Stochastic Approach to Noise Modeling for Free turbulent flows. AIAA J. 1994, 32, 455–463. [Google Scholar] [CrossRef] [Green Version]
- Sescu, A.; Hixon, R. Toward low-noise synthetic turbulent inflow conditions for aeroacoustic calculations. Int. J. Numer. Methods Fluids 2013, 73, 1001–1010. [Google Scholar] [CrossRef]
- Clair, V.; Polacsek, C.; Garrec, T.L.; Rebou, G. Experimental and Numerical Investigation of Turbulence-Airfoil Noise Reduction Using Wavy Edges. AIAA J. 2013, 51, 2695–2713. [Google Scholar] [CrossRef] [Green Version]
- Jarrin, N.; Benhamadouche, S.; Laurence, D.; Prosser, R. A Synthetic-Eddy-Method for generating inflow conditions for large eddy simulations. Int. J. Heat Fluid Flow 2006, 27, 585–593. [Google Scholar] [CrossRef] [Green Version]
- Pamiès, M.; Weiss, P.; Garnier, E.; Deck, S.; Sagaut, P. Generation of synthetic turbulent inflow data for large eddy simulation of spatially evolving wall-bounded flows. Phys. Fluids 2009, 21, 045103. [Google Scholar] [CrossRef]
- Kim, J.W.; Haeri, S. An advanced synthetic eddy method for the computation of aerofoil-turbulence interaction noise. J. Comput. Phys. 2015, 287, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Klein, M.; Sadiki, A.; Janicka, J. A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulations. J. Comput. Phys. 2003, 186, 652–665. [Google Scholar] [CrossRef]
- Ewert, R. Broadband slat noise prediction based on CAA and stochastic sound sources from a fast random particle-mesh (RPM) method. Comput. Fluids 2008, 37, 369–387. [Google Scholar] [CrossRef]
- Xie, Z.T.; Castro, I.P. Efficient generation of inflow conditions for large eddy simulation of street-scale flows. Flow Turbul. Combust. 2008, 81, 449–470. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Castro, I.P.; Xie, Z.T. Divergence-free turbulence inflow conditions for large-eddy simulations with incompressible flow solvers. Comput. Fluids 2013, 84, 56–68. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Xie, Z.T. Modelling the effect of freestream turbulence on dynamic stall of wind turbine blades. Comput. Fluids 2016, 129, 53–66. [Google Scholar] [CrossRef] [Green Version]
- Gea-Aguilera, F.; Gill, J.; Zhang, X. Synthetic turbulence methods for computational aeroacoustic simulations of leading edge noise. Comput. Fluids 2017, 157, 240–252. [Google Scholar] [CrossRef]
- Atassi, H.M. Unsteady Aerodynamics of Vortical Flows: Early and Recent Developments. In Aerodynamics and Aeroacoustics; Fung, K.-Y., Ed.; World Scientific: Singapore, 1994; pp. 121–172. [Google Scholar]
- Daude, F.; Berland, J.; Emmert, T.; Lafon, P.; Crouzet, F.; Bailly, C. A high-order finite-difference algorithm for direct computation of aerodynamic sound. Comput. Fluids 2012, 61, 46–63. [Google Scholar] [CrossRef]
- Fauconnier, D.; Bogey, C.; Dick, E. On the performance of relaxation filtering for large-eddy simulation. J. Turbul. 2013, 14, 22–49. [Google Scholar] [CrossRef] [Green Version]
- Berland, J.; Lafon, P.; Daude, F.; Crouzet, F.; Bogey, C.; Bailly, C. Filter shape dependance and effective scale separation in large-eddy simulations based on relaxation filtering. Comput. Fluids 2011, 47, 65–74. [Google Scholar] [CrossRef]
- Bogey, C.; Bailly, C. A family of low dispersive and low dissipative explicit schemes for flow and noise computations. J. Comput. Phys. 2004, 194, 194–214. [Google Scholar] [CrossRef]
- Tam, C.; Webb, J. Dispersion-Relation-Preserving Finite Difference Schemes for Computational Acoustics. J. Comput. Phys. 1993, 107, 262–281. [Google Scholar] [CrossRef]
- Bogey, C.; de Cacqueray, N.; Bailly, C. A shock-capturing methodology based on adaptative spatial filtering for high-order non-linear computations. J. Comput. Phys. 2009, 228, 1447–1465. [Google Scholar] [CrossRef]
- Bogey, C.; Bailly, C. Three-dimensional non-reflective boundary conditions for acoustic simulations: Far field formulation and validation test cases. Acta Acust. United Acust. 2002, 88, 463–471. [Google Scholar]
- Tam, C.K.W. Advances in numerical boundary conditions for computational aeroacoustics. J. Comput. Acoust. 1998, 6, 377–402. [Google Scholar] [CrossRef] [Green Version]
- Henshaw, W.D. Mappings for Overture a Description of the Mapping Class and Documentation for Many Useful Mappings; Centre for Applied Scientific Computing, Lawrence Livermore National Laboratory: Livermore, CA, USA, 2011. [Google Scholar]
- Gloerfelt, X.; Garrec, T.L. Generation of inflow turbulence for aeroacoustic applications. In Proceedings of the 14th AIAA/CEAS Aeroacoustics Conference, Vancouver, BC, Canada, 5–7 May 2008. [Google Scholar]
- Comte-Bellot, G.; Corrsin, S. Simple Eulerian time correlation fo full and narrow-band velocity signals in grid-generated, isotropic turbulence. J. Fluid Mech. 1971, 48, 273–337. [Google Scholar] [CrossRef]
- Eljack, E. High-fidelity numerical simulation of the flow field around a NACA-0012 aerofoil from the laminar separation bubble to a full stall. Int. J. Comput. Fluid Dyn. 2017, 31, 230–245. [Google Scholar] [CrossRef]
- Thomareis, N.; Papadakis, G. Effect of trailing edge shape on the separated flow characteristics around an airfoil at low Reynolds number: A numerical study. Phys. Fluids 2017, 29, 014101. [Google Scholar] [CrossRef] [Green Version]
- Moreau, S.; Roger, M.; Jurdic, V. Effect of angle of attack and airfoil shape on turbulence interaction noise. In Proceedings of the 11th AIAA/CEAS Aeroacoustics Conference (26th AIAA Aeroacoustics Conference), Monterey, CA, USA, 23–25 May 2005. [Google Scholar]
- Bogey, C.; Bailly, C. On the application of explicit spatial filtering to the variables or fluxes of linear equations. J. Comp. Phys. 2007, 225, 1211–1217. [Google Scholar] [CrossRef]
- Sharan, N.; Pantano, C.; Bodony, D.J. Time-stable overset grid method for hyperbolic problems using summation-by-parts operators. J. Comp. Phys. 2018, 361, 199–230. [Google Scholar] [CrossRef]
- Rigall, T.; Cotté, B.; Lafon, P. Airfoil Noise Numerical Simulations with Direct Noise Computation and Hybrid Methods Using Inflow Synthetic Turbulence. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019. [Google Scholar]
- Mohamed, M.S.; Larue, J.C. The decay power law in grid-generated turbulence. J. Fluid Mech. 1990, 219, 195–214. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bailly, C.; Juvé, D. A stochastic Approach to compute subsonic noise using linearized Euler’s equations. In Proceedings of the 5th AIAA/CEAS Aeroacoustics Conference and Exhibit, Bellevue, WA, USA, 10–12 May 1999. [Google Scholar]


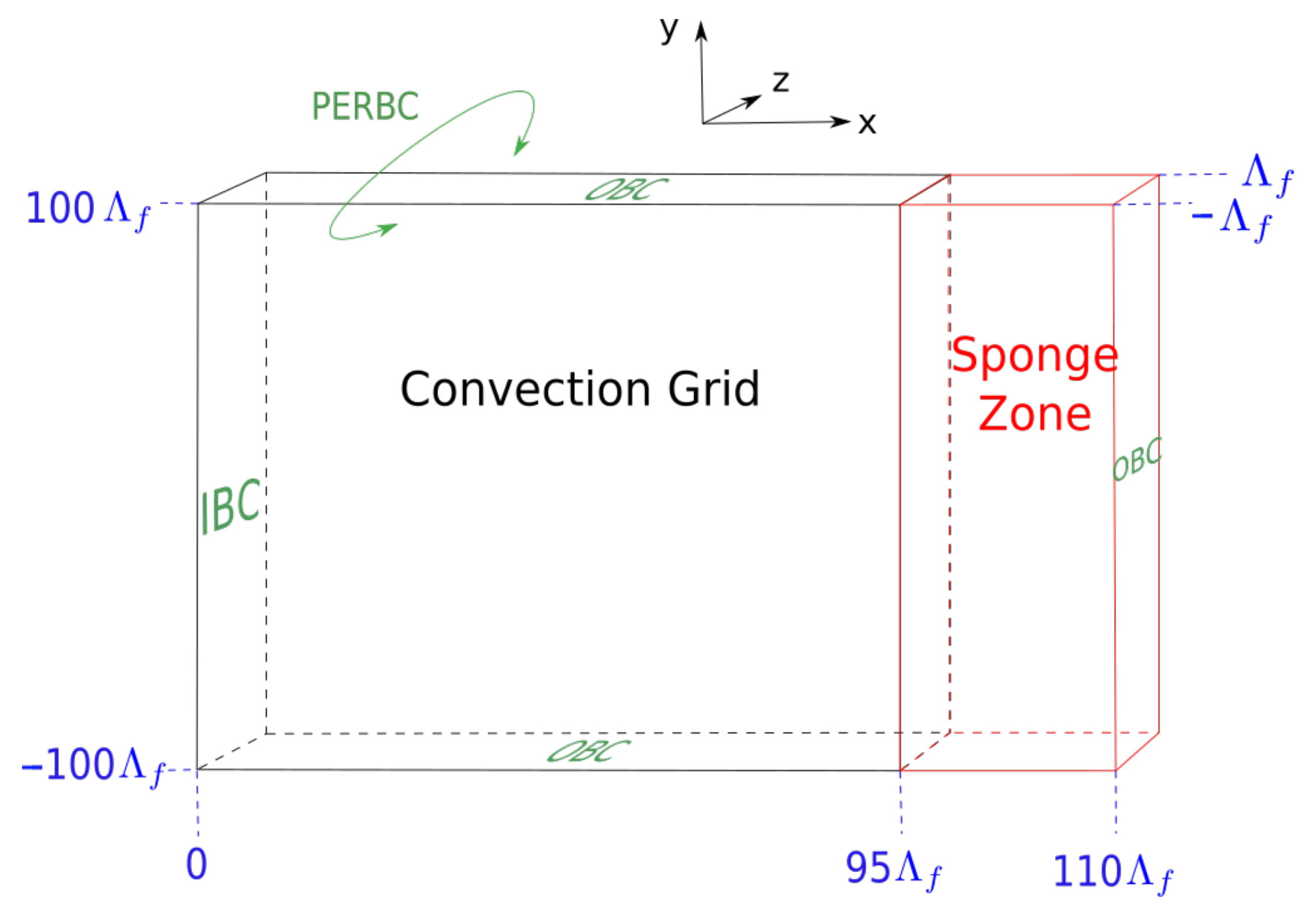
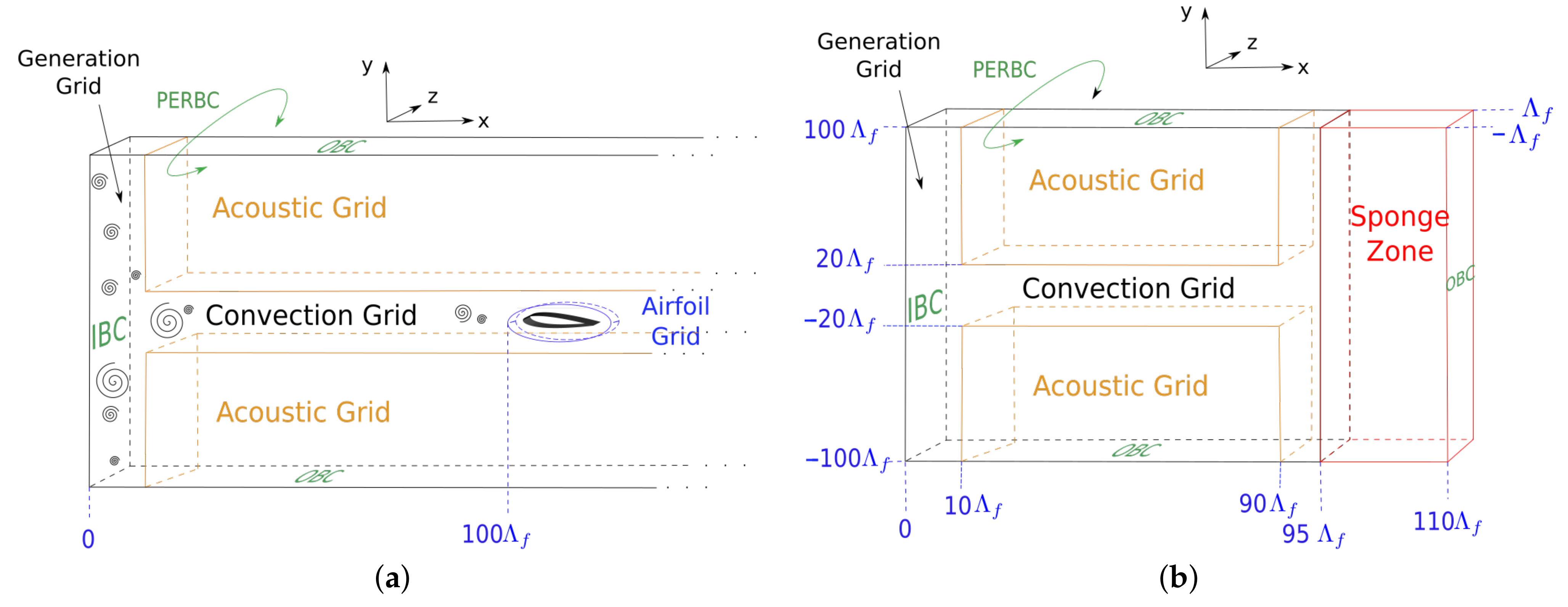
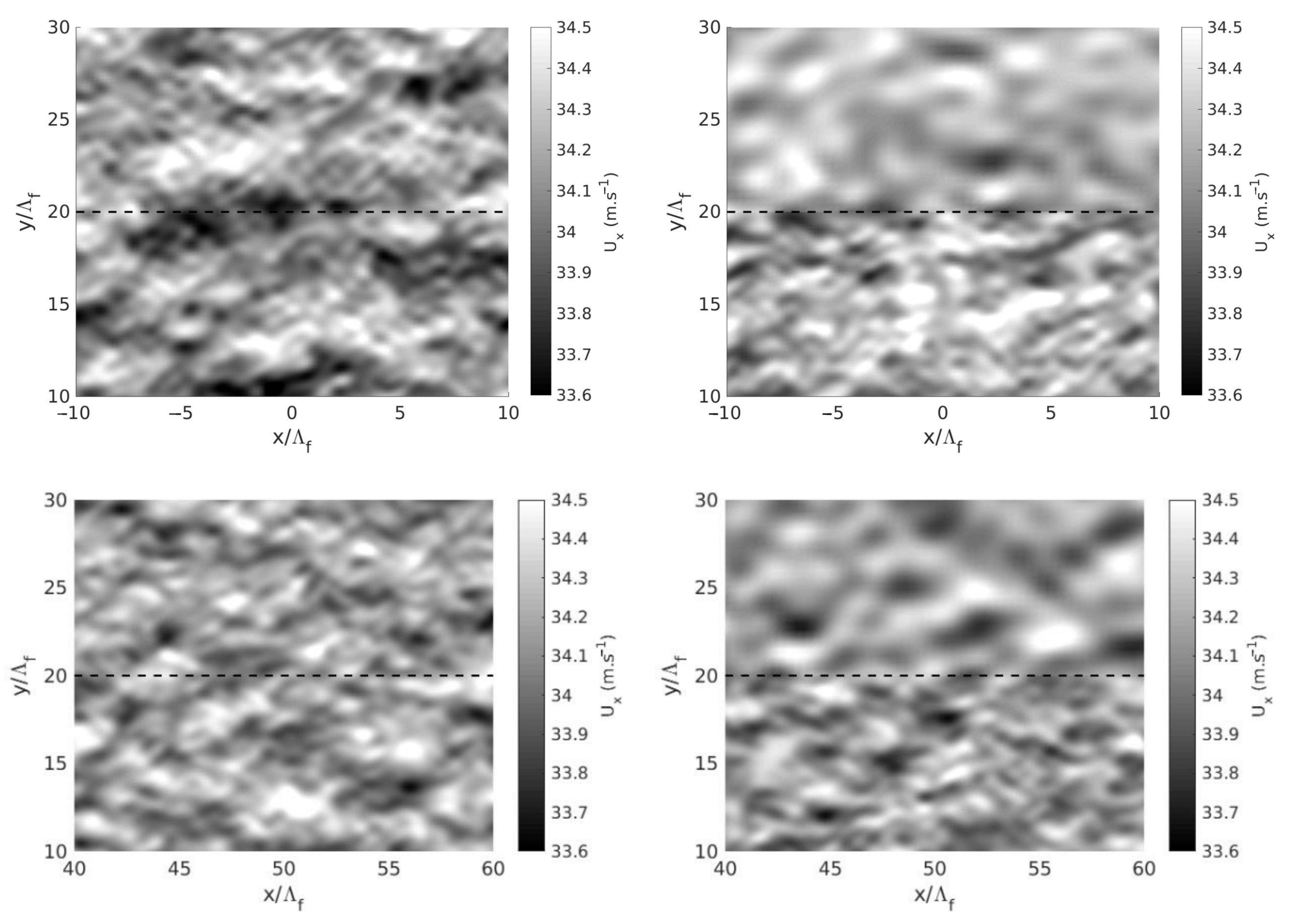
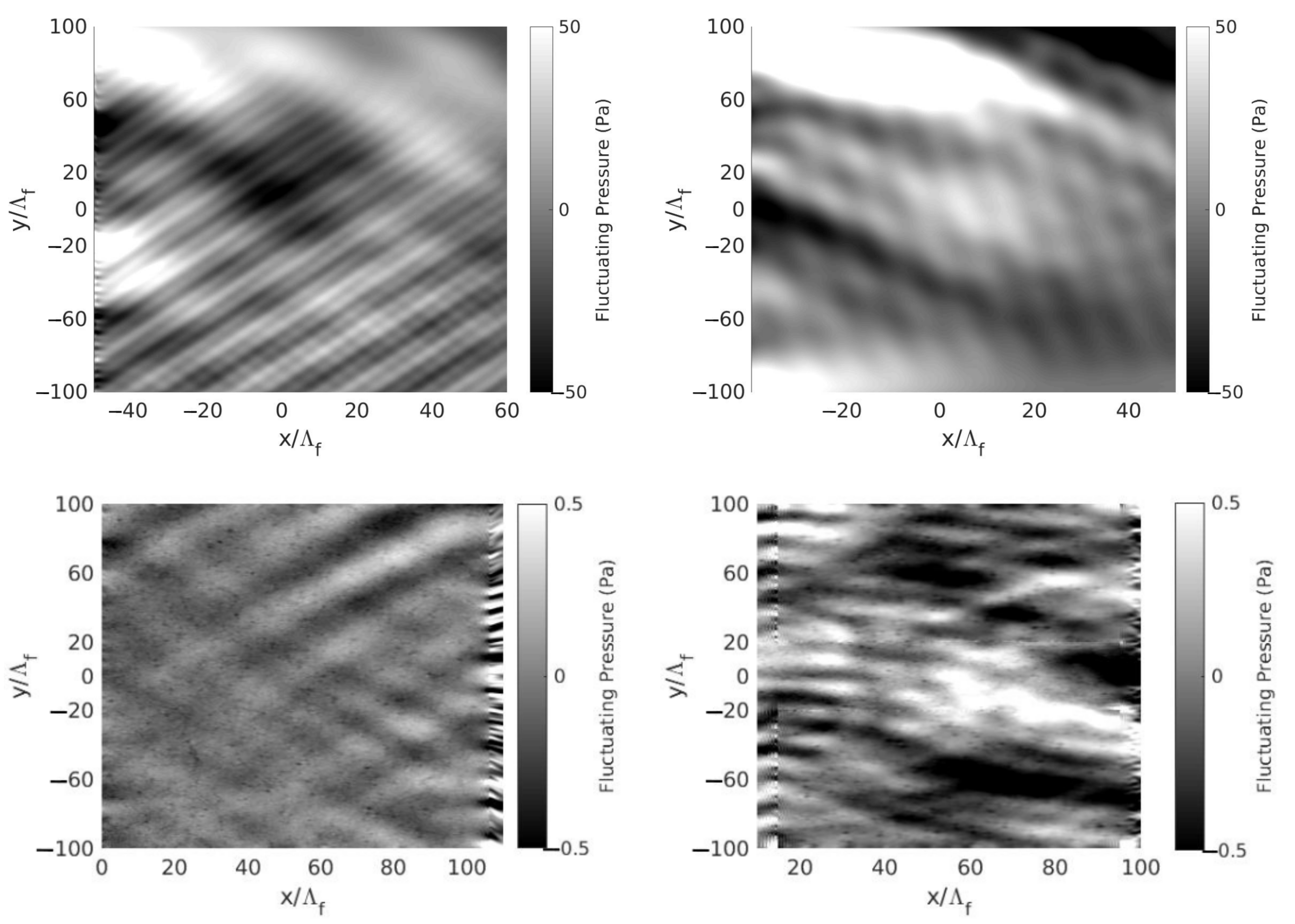
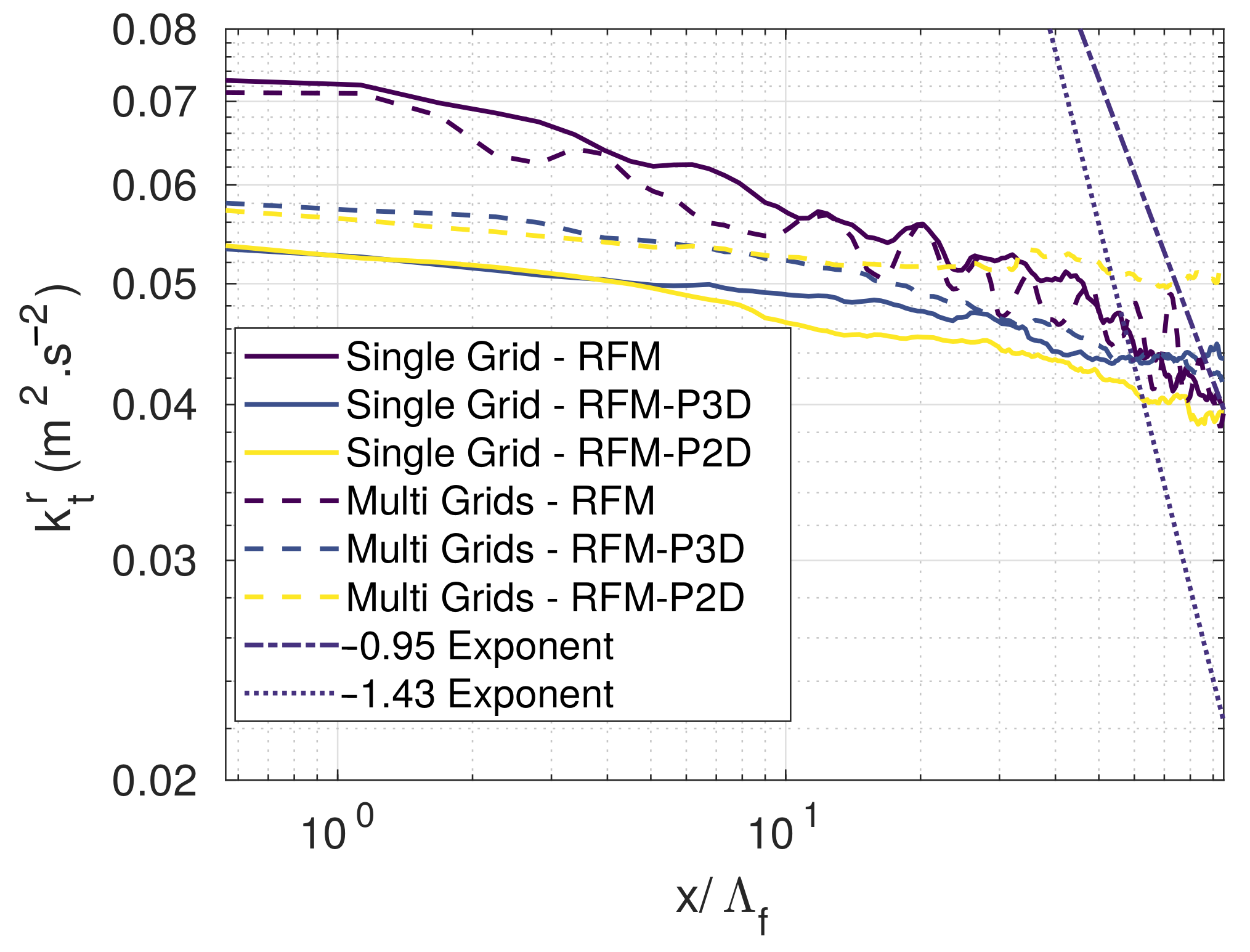
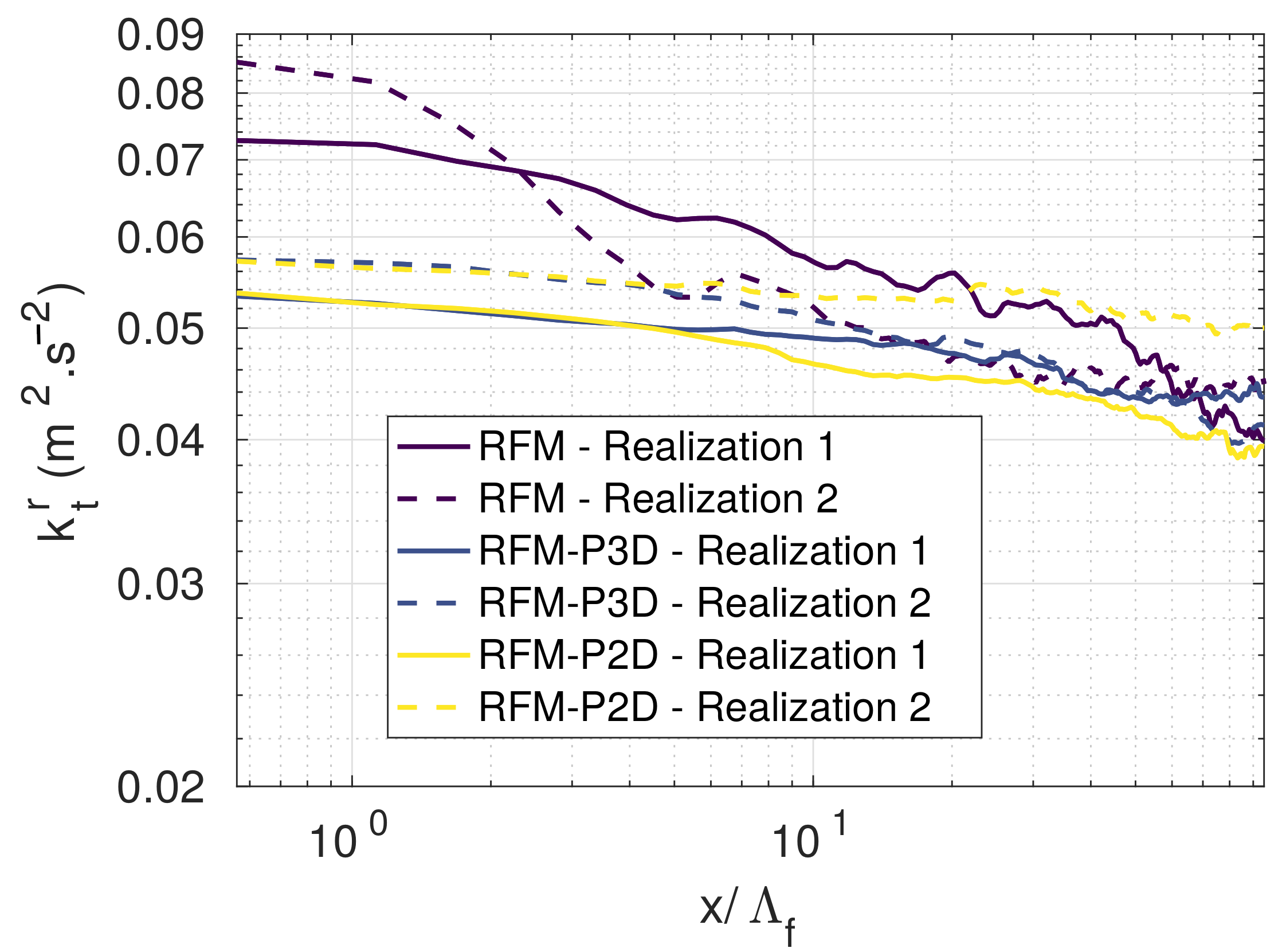


| Configuration | , , | Mesh Size in Convection Grid | Mesh Size in Acoustic Grids | Number of Mesh Points | Number of Interpolation Points |
|---|---|---|---|---|---|
| Single Grid | 95, 200, 2 | / | 6.79 × 106 | 1.07 × 105 | |
| Multi Grids | 95, 200, 2 | 3.34 × 106 | 2.08 × 105 |
| Simulation | N | ||
|---|---|---|---|
| RFM_Single_Grid | 200 | 200 | 200 |
| RFM-P3D_Single_Grid | 200 | 198 | 68 |
| RFM-P2D_Single_Grid | 200 | 196 | 0 |
| RFM_Multi_Grids | 200 | 200 | 200 |
| RFM-P3D_Multi_Grids | 200 | 199 | 62 |
| RFM-P2D_Multi_Grids | 200 | 196 | 0 |
| RFM_Single_Grid_Realization2 | 200 | 200 | 200 |
| RFM-P3D_Single_Grid_Realization2 | 200 | 200 | 67 |
| RFM-P2D_Single_Grid_Realization2 | 200 | 196 | 0 |
| Single Grid | Multi Grids | |||||
|---|---|---|---|---|---|---|
| x | y | z | x | y | z | |
| Convection Grid | 60 | 60 | 11 | 48 | 43 | 11 |
| Sponge Zone | 40 | 60 | 11 | 40 | 53 | 11 |
| Acoustic Grids | / | / | / | 48 | 53 | 6 |
| Generation Grid | / | / | / | 81 | 53 | 11 |
| Simulation | Cost (Core Hours) |
|---|---|
| RFM_Single_Grid | 6150 |
| RFM-P3D_Single_Grid | 6150 |
| RFM-P2D_Single_Grid | 6300 |
| RFM_Multi_Grids | 4700 |
| RFM-P3D_Multi_Grids | 4750 |
| RFM-P2D_Multi_Grids | 4600 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rigall, T.; Cotté, B.; Lafon, P. Low-Noise Synthetic Turbulence Tailored to Lateral Periodic Boundary Conditions. Fluids 2021, 6, 193. https://doi.org/10.3390/fluids6060193
Rigall T, Cotté B, Lafon P. Low-Noise Synthetic Turbulence Tailored to Lateral Periodic Boundary Conditions. Fluids. 2021; 6(6):193. https://doi.org/10.3390/fluids6060193
Chicago/Turabian StyleRigall, Tommy, Benjamin Cotté, and Philippe Lafon. 2021. "Low-Noise Synthetic Turbulence Tailored to Lateral Periodic Boundary Conditions" Fluids 6, no. 6: 193. https://doi.org/10.3390/fluids6060193
APA StyleRigall, T., Cotté, B., & Lafon, P. (2021). Low-Noise Synthetic Turbulence Tailored to Lateral Periodic Boundary Conditions. Fluids, 6(6), 193. https://doi.org/10.3390/fluids6060193