4.1. Uni-Directional Flow
Experiments in a wind tunnel were conducted under a Reynolds number of 4.5 × 10
4 for the flow around a circular cylinder placed at various heights above a plane boundary [
16]. It was revealed that regular vortex shedding persisted at the Strouhal number
St =
Uf/D for all gaps down to G/D = 0.3. For all values of G/D < 0.3, strong regular vortex shedding began to be suppressed, and when the cylinder touched the wall, there was no regular shedding of vortices.
As the cylinder was moved away from the wall, the pressure distribution around the cylinder became more symmetric near the stagnation point and at G/D = 0.4 it was perfectly symmetric. At small gaps, the separation point on the side nearest to the wall moved down stream to the narrowest point of the gap. The flow around a cylinder close to a wall can be considered to be analogous to the flow around two cylinders in a side-by-side arrangement. For G/D > 0.5 the two flows were similar. However, the flow around two cylinders becomes bi-stable for G/D < 0.5, whereas a cylinder near a wall shows no such in-stability.
The flow pattern of a cylinder near a wall at various gaps of 0, 0.2, and 0.4 diameters were reproduced from the experiment results [
12]. It is shown in
Figure 3, copyright by [
12], that suggested this reduction is mainly caused by the interference of the wall with the vortex shedding and the immersion of the cylinder in the lower energy wall-boundary layer flow.
However, their data appears to reveal an upward trend in the recorded values of the Strouhal number of approximately 5% at a gap of 0.75 diameters. It is argued that this effect is caused by a reduction of the scale of the vortex formation region due to the proximity of the wall, and that when the shear layers are brought closer together, their interaction is facilitated, and the shedding period is shortened [
17]. Variation of vortex shed-ding frequency as a function of wall distance from the cylinder are plotted in
Figure 4, which shows that the shedding frequency gradually increased as the gap decreased. A 10% increase of shedding frequency is expected when the gap is very small.
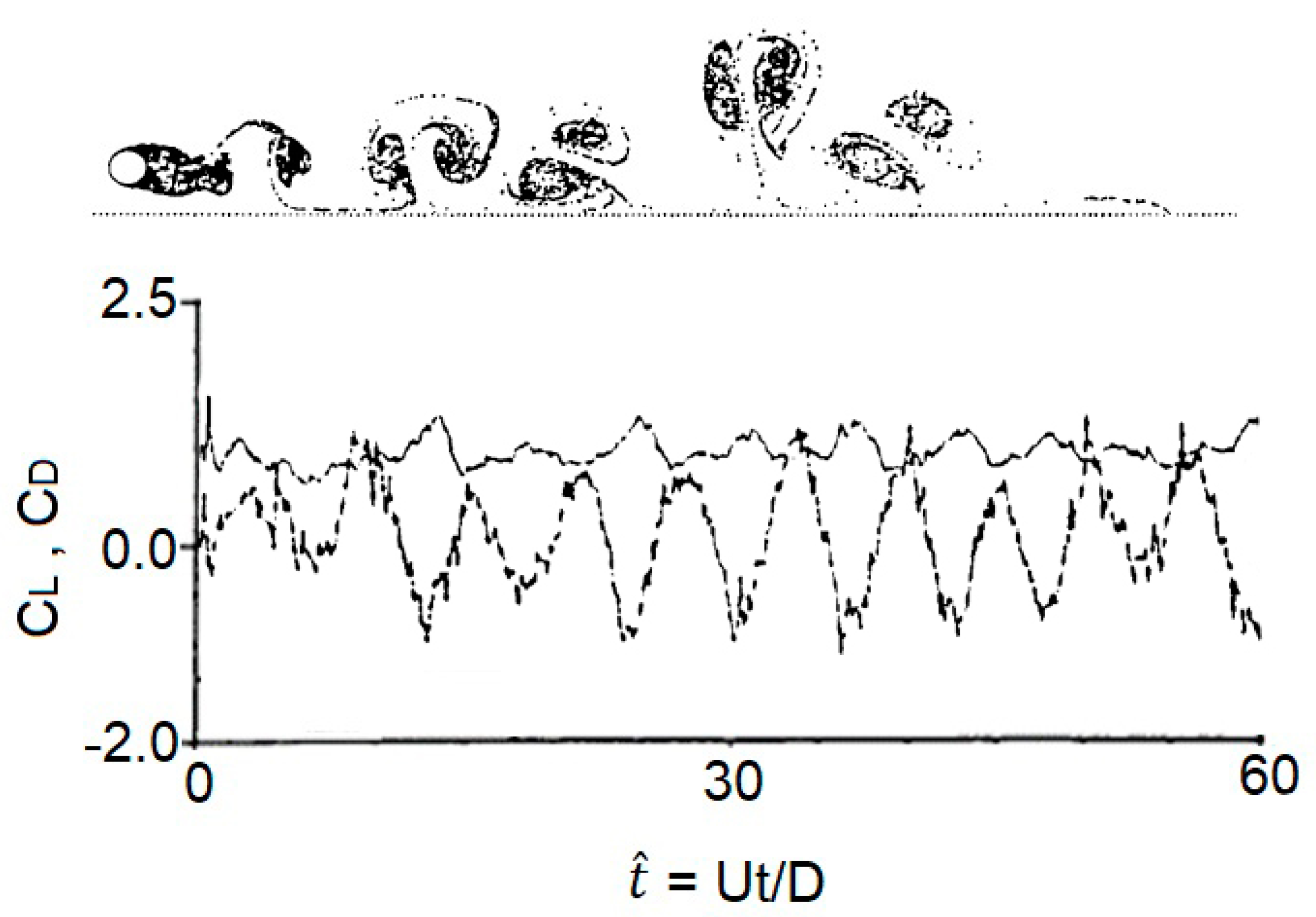
It is shown that when the gap ratio G/D is greater than 2, the cylinder behaves similar to an isolated cylinder due to the influence of the wall being relatively low. Based on these experimental studies, the model was tested at a high Reynolds number of 100,000 and at several gap ratio values of 2.0, 1.5, 1.0, 0.5, 0.25, 0.1. At the first gap ratio G/D = 2 and at the non-dimensional times of 1 and 5, the flow behind the cylinder is shown in
Figure 5.
In this study, the separation point close to the wall is shifted downstream to about 125 degrees, while the one on the top side of the cylinder surface is shifted upstream to about 135 degrees, measured from the positive X-axis. The shear layer emanating from the lower half of the cylinder seems to stretch longer than the upper one, even though no forced asymmetry was implemented. The formation region also seems to be slightly longer than that of an isolated cylinder by about 5 to 7%. This is due to the fact that the close presence of the wall creates an asymmetric velocity field around the circumference of the cylinder in which the velocity of the fluid particles close to the wall are relatively higher than the rest. The asymmetric velocity field around the cylinder also promotes the roll-up of the vortices earlier than that of the isolated cylinder.
As the flow further develops, a regular vortex shedding is clearly established, and this is also reflected in the graph of the force coefficients. The drag coefficient is slightly less than 1.14, which is the value for an isolated cylinder, and the lift coefficient oscillates around a mean value of about 0.15 with the Strouhal number relatively unchanged from 0.2. The steady flow implies that a repulsive force exists in the direction which tend to displace the cylinder away from the wall. The obvious difference between this flow pattern and that of an isolated cylinder is that the vortices close to the wall tend to approach it tangentially, follow it and then leave it tangentially as well, while those on the other side are freely convected, similar to an isolated cylinder. Numerically, this is obviously due to the source distribution along the wall. It tends to reflect the vortices close to it back to the fluid domain.
This is also shown in the calculation in that generally, when the vortices are close enough to the wall, the strength of the sources in that region are positive (sources), while those in the region sparsely populated by vortices show negative values (sinks).
The CPU time taken at each section is shown in
Table 1. It is shown that the percentage of time taken to calculate the vortex velocity is the greatest, up to 73.97%. The second biggest CPU time is the calculation of the cylinder surface velocity, as much as 16.03%.
The influence of the wall on the hydrodynamic characteristics of the cylinder increases as the gap ratio is reduced to 1.5, 1, 0.75, 0.5 and 0.25, as shown in
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10 and
Figure 11. The drag coefficient decreases to 1.13 and the mean value of the lift coefficient is around zero, in which these values are those of the isolated cylinder.
The cylinder can be seen to be increasingly deflected in a tangential direction as the gap between the cylinder and the wall is decreased. It is also shown in these figures that as the velocity in the gap region increases, vortices with high strengths are created, which in turn produces a strong mutual interaction. This results in a higher velocity in the region along the wall behind the cylinder, which then causes the vortex street to be deflected as the vortices close to the wall move further away from those located further into the flow.
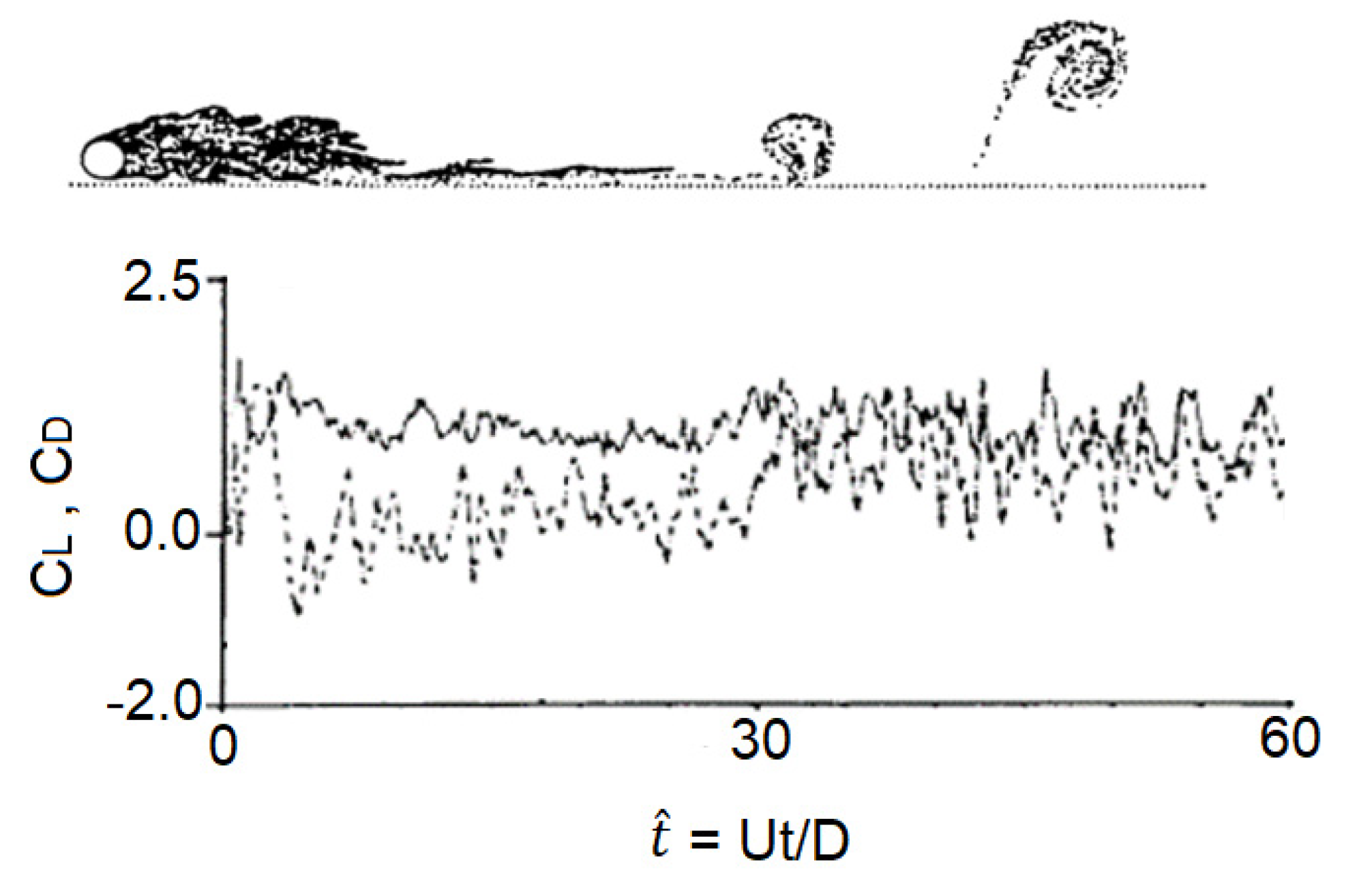
An asymmetric effect further occurs when the gap ratio G/D is reduced to 0.25 and the influence of the wall as described above is further pronounced. The vortex street becomes more skew-symmetric due to the greater influence of the wall, which is reflected in the higher velocity in the gap region, as shown in
Figure 11. It can also be seen that the repulsive force, shown as the average lift coefficient, is higher and reaches 0.75 with a Strouhal number equal to 0.17 and the drag coefficient slightly increases to 1.45. Experimental evidence shows that when the gap ratio G/D < 0.15, regular vortex shedding is suppressed due to the complicated behavior of the turbulent boundary layer interaction in the gap region.
Flow visualization, hot film and PIV experiments have been conducted to investigate the flow around a circular cylinder with a close proximity to a wall for Reynolds numbers in the range of 1200 ≤ Re ≤ 4960 [
18]. The results revealed that four distinct regions may be identified for describing the flow within the observed flow dynamics. For very small gap ratios, G/D ≤ 0.125, the gap flow is either suppressed or extremely weak, and no regular vortex shedding occurs downstream of the cylinder. This condition is not tested in this present study. The flow field for small gap ratios, 0.254 ≤ G/D ≤ 0.375, is very similar to that for very small gap ratios, except that there is now a pairing between the inner shear-layer shed from the cylinder and the separated wall boundary layer. Intermediate gap ratios—0.54 ≤ G/D ≤ 0.75—are characterized by the onset of vortex shedding from the cylinder. In addition, there is a significant decrease in the size of the upstream separation region. For the final region, characterized by the largest gap ratio considered, G/D ≥ 1.0, there is no separation of the wall boundary layer, either upstream or downstream of the cylinder. In addition, the flow around the cylinder is now essentially the same as the flow around an isolated circular cylinder. The variations of the Strouhal numbers with respect to the gap ratio is very dependent on the Reynolds number. For low Reynolds number flows, Re = 2600, the Strouhal number for G/D ≤ 2.0 is significantly greater than that of an isolated circular cylinder. However, for higher Reynolds numbers (Re = 4000) St seems to be insensitive to G/D. In contrast to other studies, there does not seem to be a minimum value of G/D below which periodicities are not detected in the wake. However, for G/D ≤ 0.25, the wake Strouhal number is more properly associated with periodicities in the outer shear-layer from the cylinder, as opposed to classical vortex shedding.
This affects the formation region which is lengthened to about eight times the cylinder diameter. Although there is no turbulence model applied in this study, numerically, the regular vortex shedding was still suppressed by the cancellation of the vortices shed from the lower part of the cylinder as they move closer than 0.05D from the wall, the minimum distance in which a vortex is still considered ‘alive’. The result for a gap ratio of 0.1D is presented in
Figure 12. The loss of circulation due to the vortex cancellation is then compensated in the next calculation of the surface vorticity for the next time step. At this gap ratio, the mean value of the lift and drag coefficients are increased unrealistically, even though the suppressed oscillating flow pattern is achieved. This unrealistic result is attributed to the strong interaction between the closest elements of the cylinder and the wall, and the resultant interaction could not model the interaction between the wall and the cylinder boundary layer correctly.
The effects of the Reynolds number at a fixed gap ratio value of G/D = 1 are also investigated in this study and the results are presented in
Figure 12,
Figure 13,
Figure 14 and
Figure 15. At Reynolds number 100, the resolution of the flow pattern is not as high as anticipated due to the dominant influence of the Random Walk diffusion scheme. The drag coefficient is found to be around 2.3 and the mean value of the lift coefficient is around 0.4.
The value of the Strouhal number is difficult to ascertain due to the numerical noise. This shows that the presence of the wall causes the drag coefficient to increase by about 10% and this can be attributed to the higher velocity in the gap region, which in turn creates stronger vortices that have a greater influence on the drag characteristics of the cylinder when they accumulate and interact in the formation region. At a higher Reynolds number of 500, a better picture of the flow pattern is observed; this is also reflected in the increased definition of the lift coefficient, as shown in
Figure 12.
The drag coefficient is reduced to around 1.9, which is slightly higher than the value of the isolated cylinder, while the mean value of the lift coefficient is around 0.3. The mean maximum value of the lift coefficient is around 0.8 with the Strouhal number value around 0.17. The drag coefficient continuously decreases at higher Reynolds numbers, greater than 1000, with values of around 1.6, 1.2 and 1.15, as shown in
Figure 13,
Figure 14 and
Figure 15, respectively. The mean maximum lift coefficient increases to around 0.9 with the Strouhal number reaching 0.2, which are both around the value obtained for the isolated cylinder. A summary of the results for the force coefficients of a cylinder placed at various distances from the wall with a Reynolds number of 100,000 is shown in
Table 2 below. The effect of the variation of the Reynolds number, in the range of 100 to 50,000, on the force coefficients at a gap ratio value of G/D = 1 is shown in
Table 3.
In a constant flow regime, the upper separation point moves upwards by decreasing G/D, indicating that the separation angle, θ, decreases too. This can be described by the growing stream-wise pressure gradient induced by the gap flow [
4].
4.2. Oscillatory Flow
The range of validity of the present model and the parameters defining it were discussed. The object of this section of the study is to examine the influence of the proximity of a cylinder to a plane surface bounding an oscillatory flow in the context of the limitations of the model used.
It was concluded that the present model could only produce results in reasonable agreement with the experimental results when the β value lies in a range in which the ‘boundary layer thickness’ is around half to twice the length of the local element. The Keulegan–Carpenter number Kc is a parameter which shows the scale of the motion of the water particles relative to the cylinder diameter. It is necessary to investigate the behavior of the present model upon the variation of the diameter of the first ring with respect to the cylinder diameter and also of the time step.
Using the cylinder parameters (the number of elements Ne is 64, the time step Δt is 0.15, and vortices are released from the first ring out) the hydrodynamic behavior of the cylinder and its flow pattern at the Keulegan–Carpenter number of 40, with gap ratios G/D of 2, 1, 0.5, 0.2, 0.1, and values of Reynolds number Re of 25,000, 50,000, 75,000, 100,000, are investigated. is the maximum velocity and the equation is .
At the first gap ratio of G/D = 2, the flow pattern and the force coefficient are displayed in
Figure 16. At
= 22.5, the pseudo-Karman vortex type of flow is produced behind the cylinder. The influence of the wall that is expressed in the suppression of the vortex street is not apparent in the region close to the cylinder. This is mainly due to the relatively wide gap between the cylinder and the wall. When the flow is reversed, more vortices will move closer again to the cylinder, compared to that of the isolated cylinder, as they are unable to spread in a downward direction due to the presence of the wall. It is seen that the vortices approach the wall tangentially. However, any vortices crossing the wall have been removed.
The in-line force coefficient is only slightly less than the experiment results by about 5% [
19,
20]. The values for the drag and inertia coefficients of the experimental results are 1.43 and 1.17, while those obtained from the present study are 1.56 and 1.89, respectively.
At the lower gap ratio of G/D = 1, the pseudo-Karman vortex street type flow also appeared behind the cylinder. The stronger influence of the wall is reflected in a more curved shape of the vortex street when it approaches the wall. This can also be seen in the higher amplitude of the drag coefficient which increases by about 5% compared to the previous case. As also displayed in
Figure 17, the amplitude of the drag coefficient is higher than the experimental results by about 4% [
20], whereas the phase is in quite good agreement.
As the gap ratio is reduced to G/D = 0.5, the difference in the amplitude of the drag coefficient compared to that of the experimental results is narrowed to about 3% and the phase of the flows are again in good agreement, as shown in
Figure 18. The flow pattern still has similarities with the unbounded oscillatory flow, but the trend of a deflected wake on the wall side of the cylinder is increasingly pronounced.
The flow becomes even more distorted when the cylinder is placed closer with G/D = 0.2. A drag coefficient with amplitude around 1.9 is produced, which is within 2% of the experimental results, as shown in
Figure 19. As reported by a number of studies [
21,
22], when the gap ratio is close to the wall, the turbulent boundary layers created on the wall and cylinder surface and their interaction causes the drag coefficient of the cylinder to drop to about 1.3.
As has been discussed already, the present study model cannot reproduce the effects, and although the results are surprisingly close to experimental results for the larger gap ratios, for G/D less than 0.2, they become increasingly unrealistic, as shown in
Figure 20. The effect of the wall proximity on the lift coefficient of a circular cylinder is shown in
Figure 21.
CLA and
CLT are the mean peak of the lift coefficients in directions against and towards the wall, respectively.
The effect of wall proximity becomes insignificant, however, when the turbulence either in the form of organized motion (namely, vortex shedding in the case of a wall-free cylinder) or in the form of disorganized wake flow in the case of a wall-mounted cylinder, is considered [
7].