Numerical Computation of Dufour and Soret Effects on Radiated Material on a Porous Stretching Surface with Temperature-Dependent Thermal Conductivity
Abstract
:1. Introduction
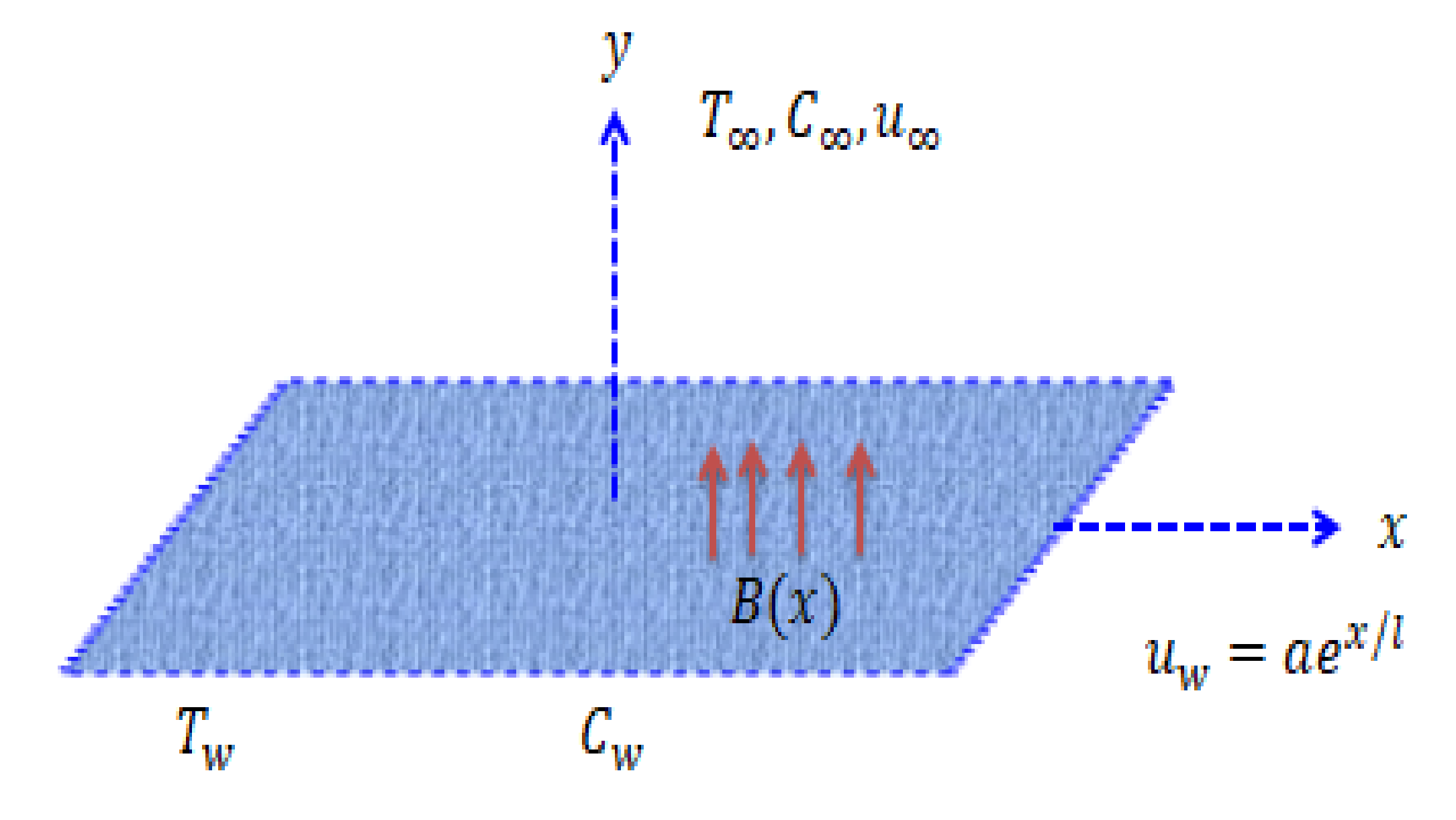
2. Governing Equations
3. Numerical Method for Solution
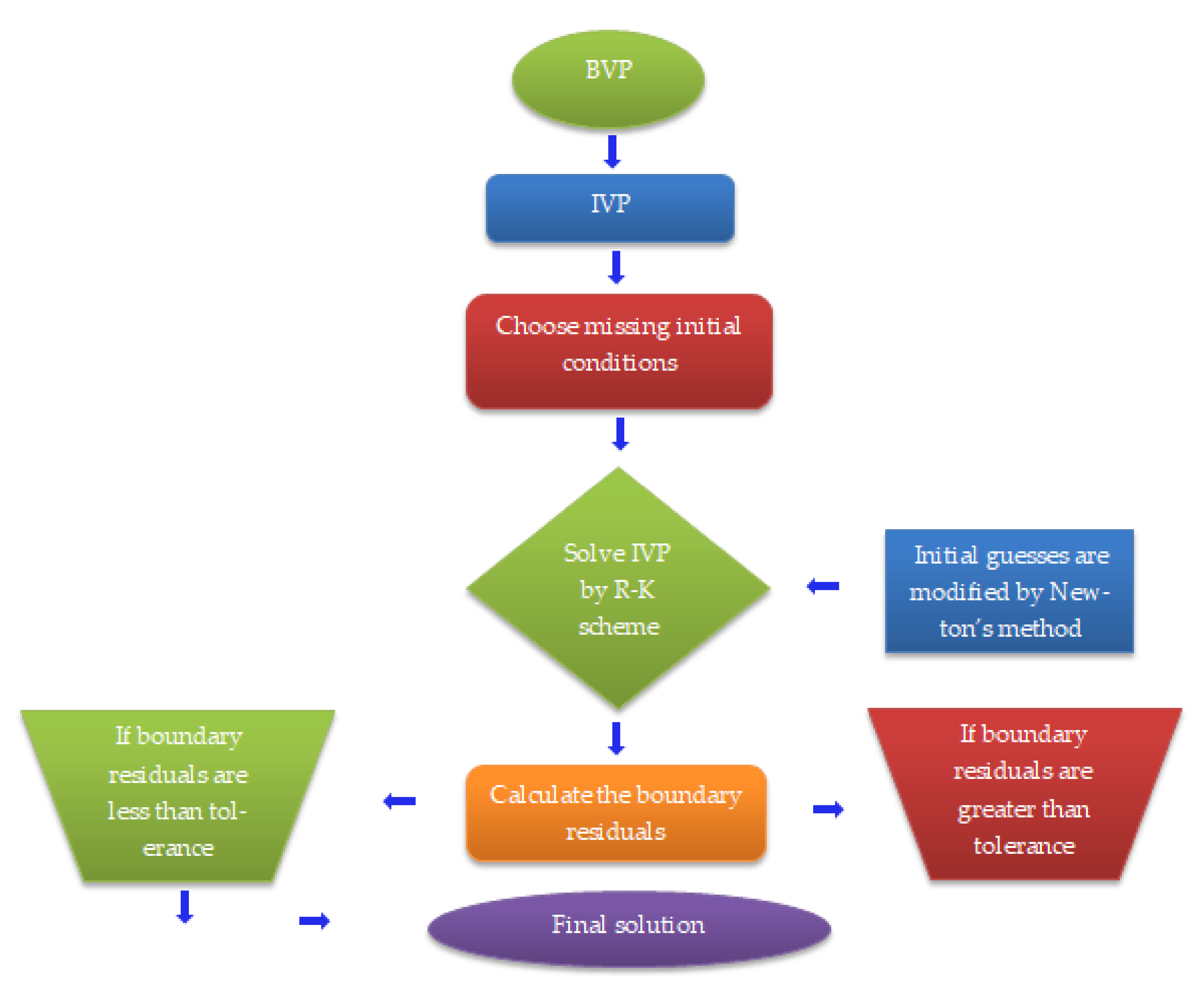
4. Results and Discussion
5. Conclusions
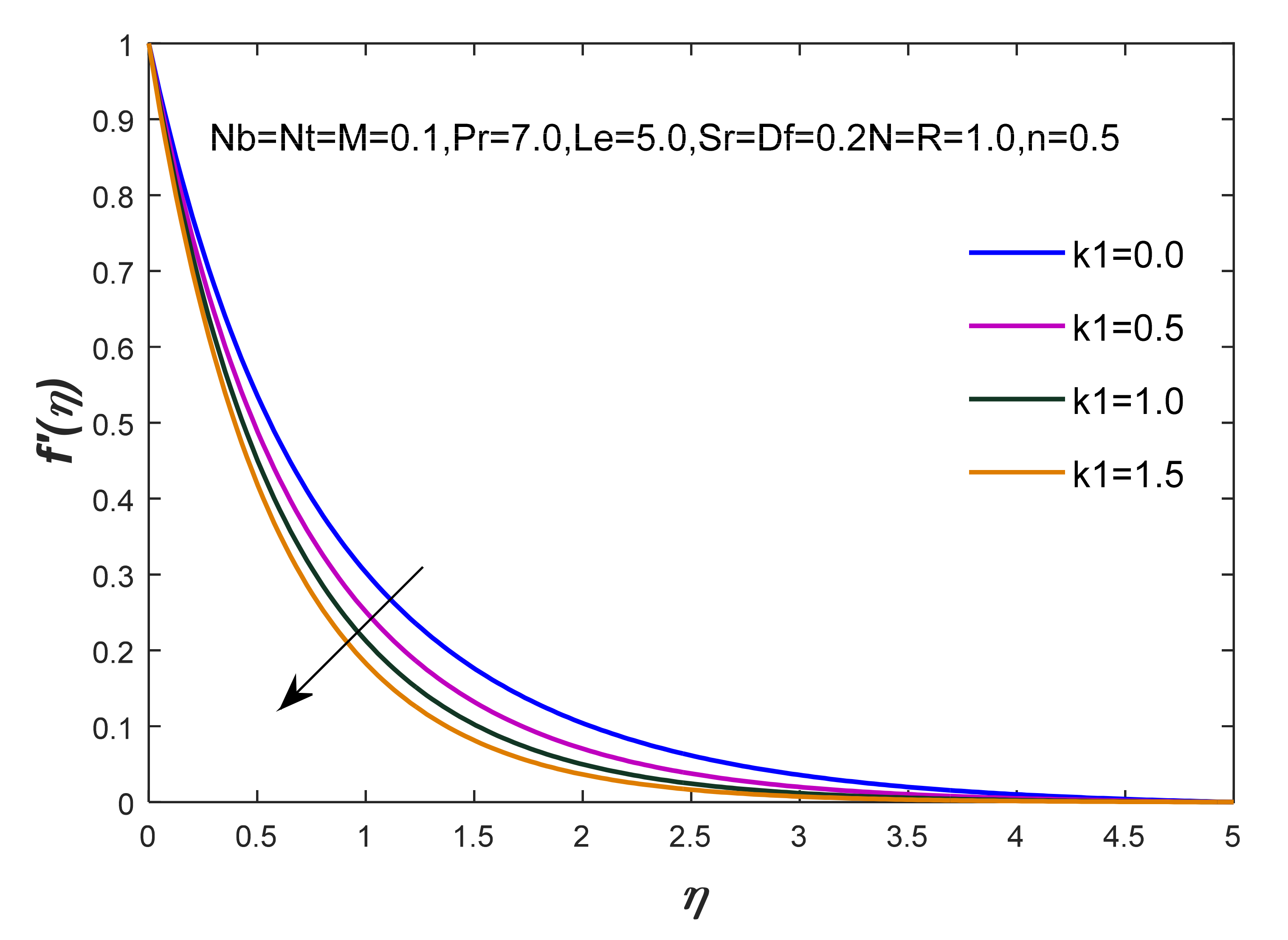
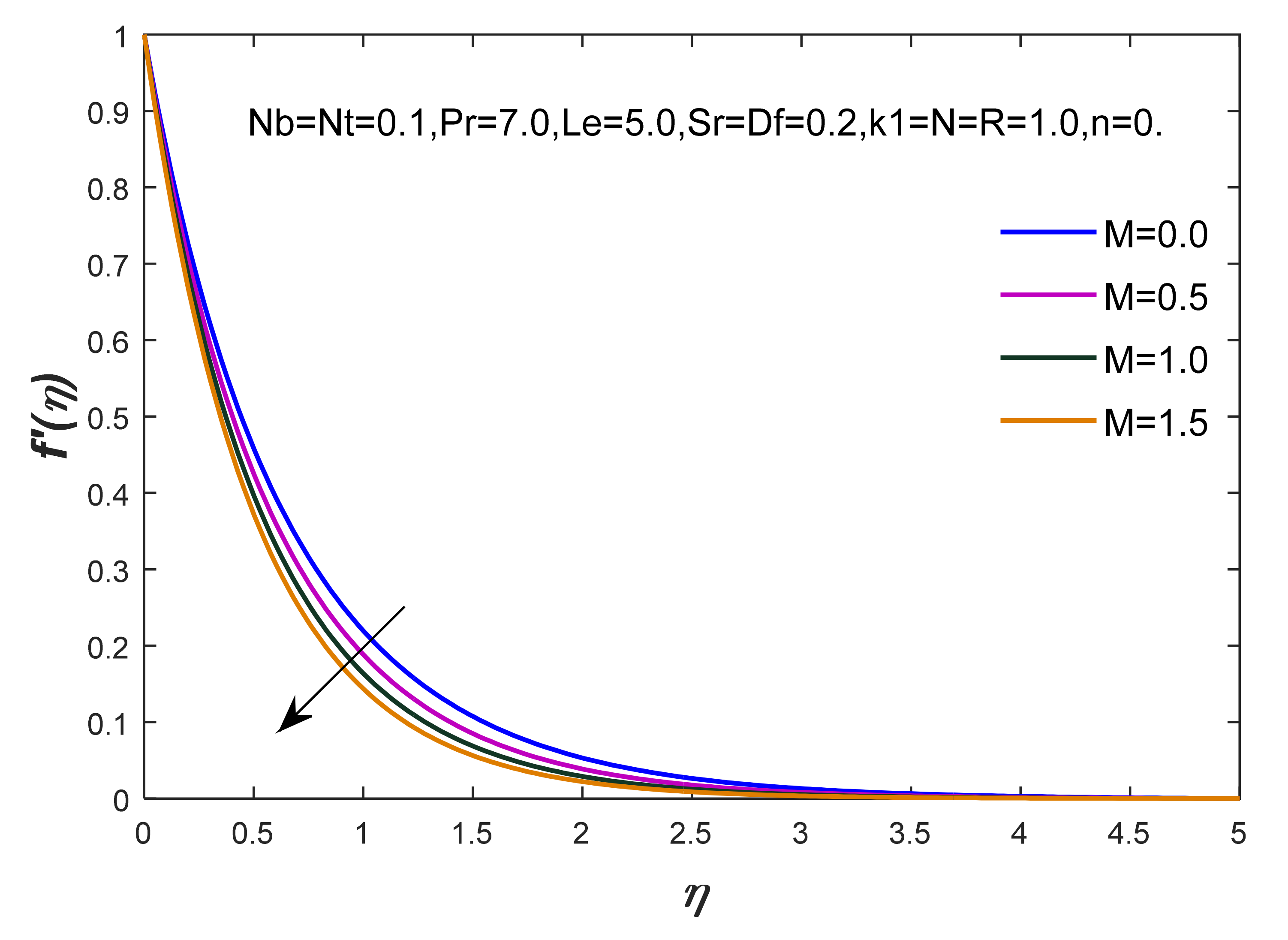
- The flow of nanoparticles on a hot surface is managed through the variation of magnetic field and porosity numbers. It is simulated that the motion of nanoparticles becomes slower versus growing values of the magnetic field and porosity numbers. The thickness of the MBL is investigated in view of this reduction;
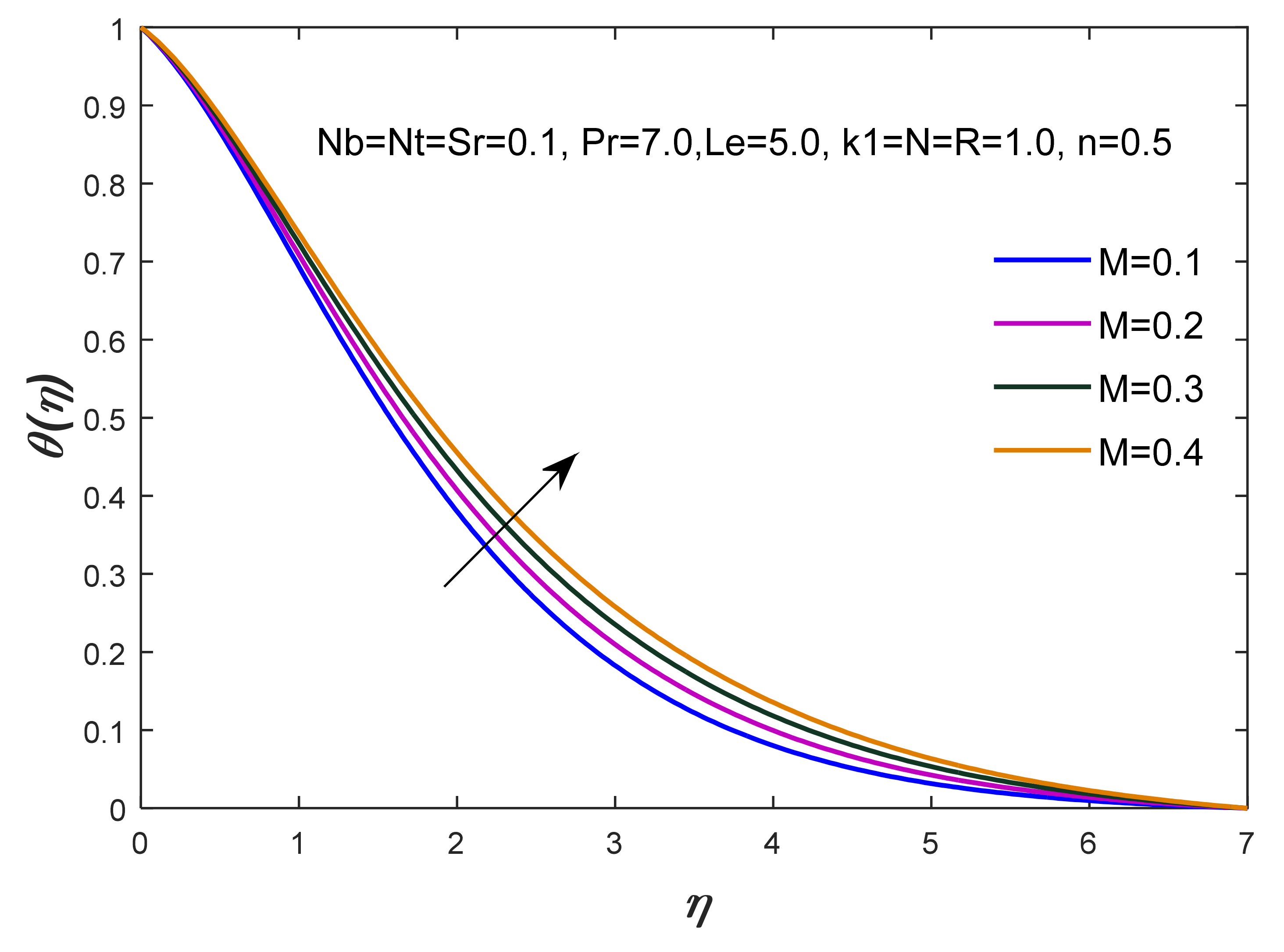
- The intensity of magnetic field plays a vital role on heat energy and the TBL because thermal performance has improved under the action of a magnetic field. Moreover, the transportation of temperature becomes slowr versus an increment in the Prandtl number called ration of MBL to TBL;
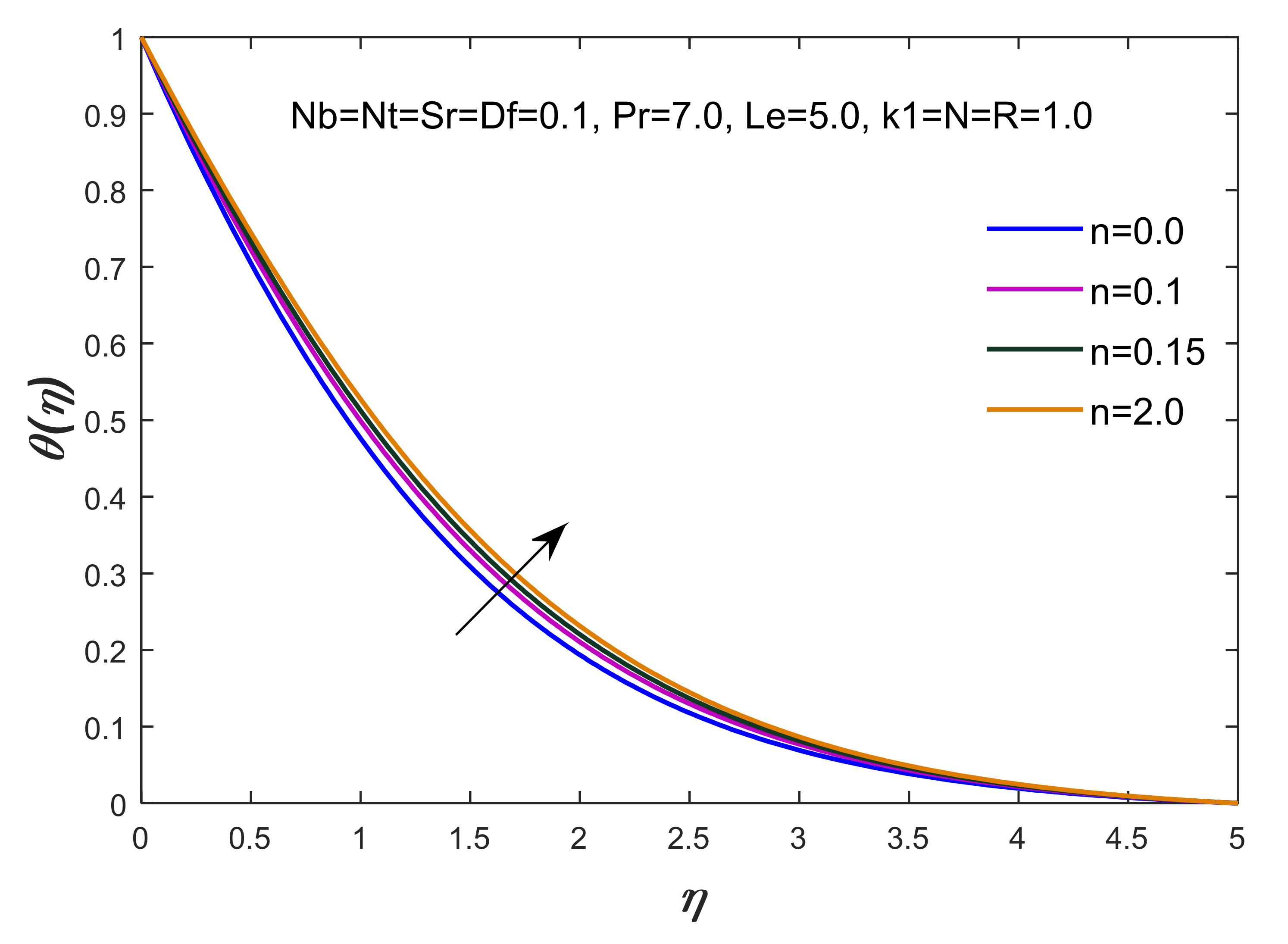
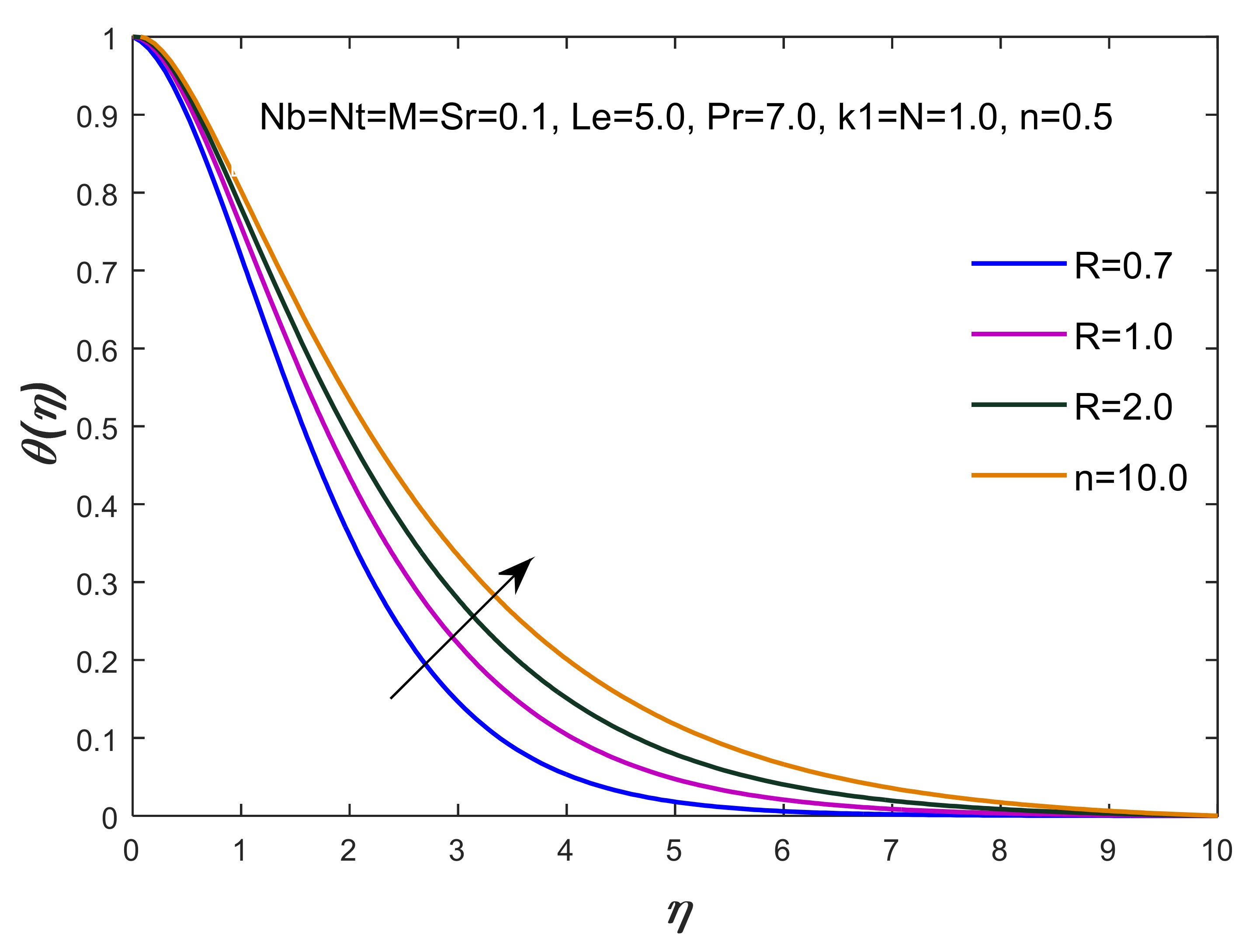
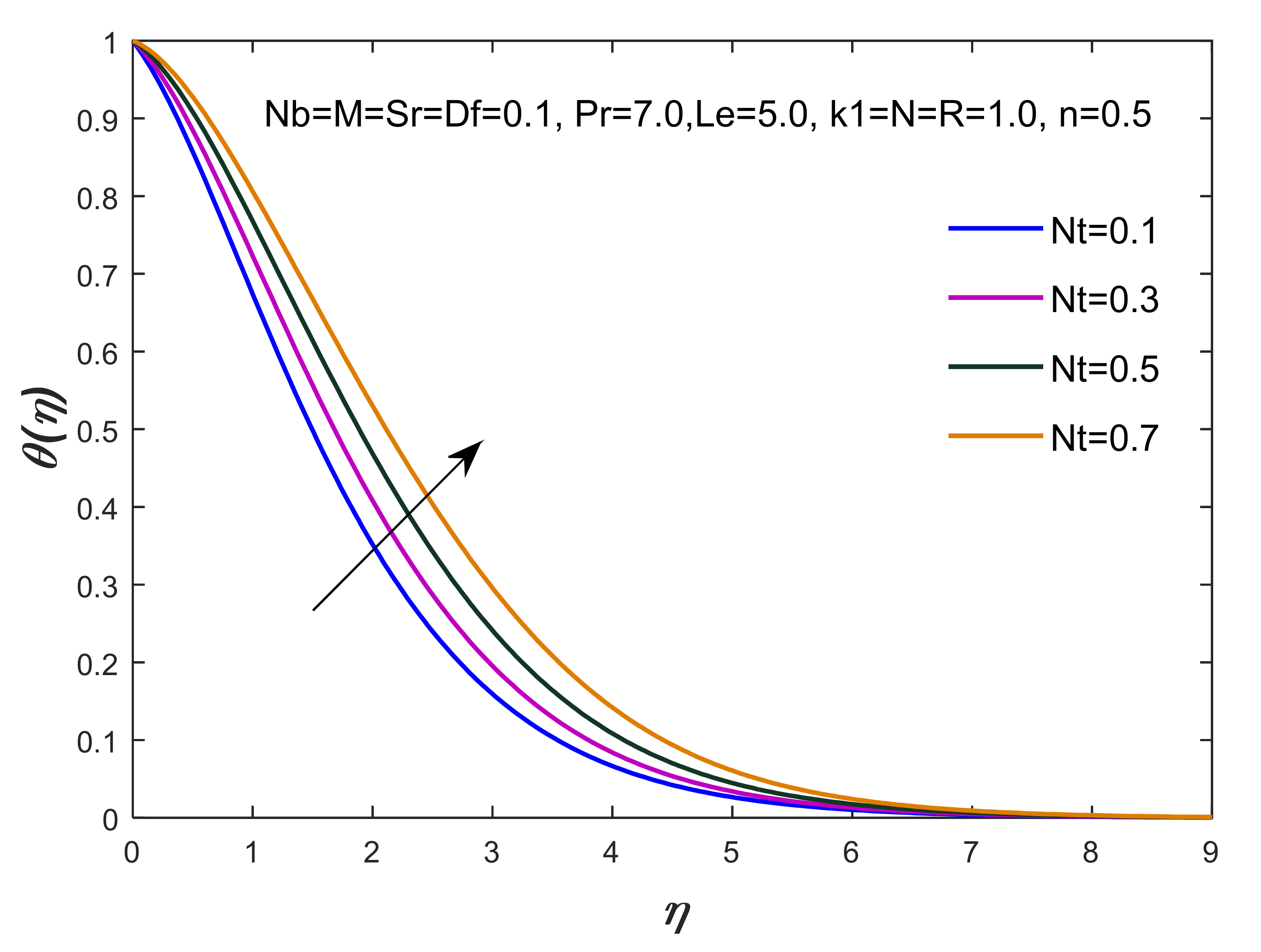
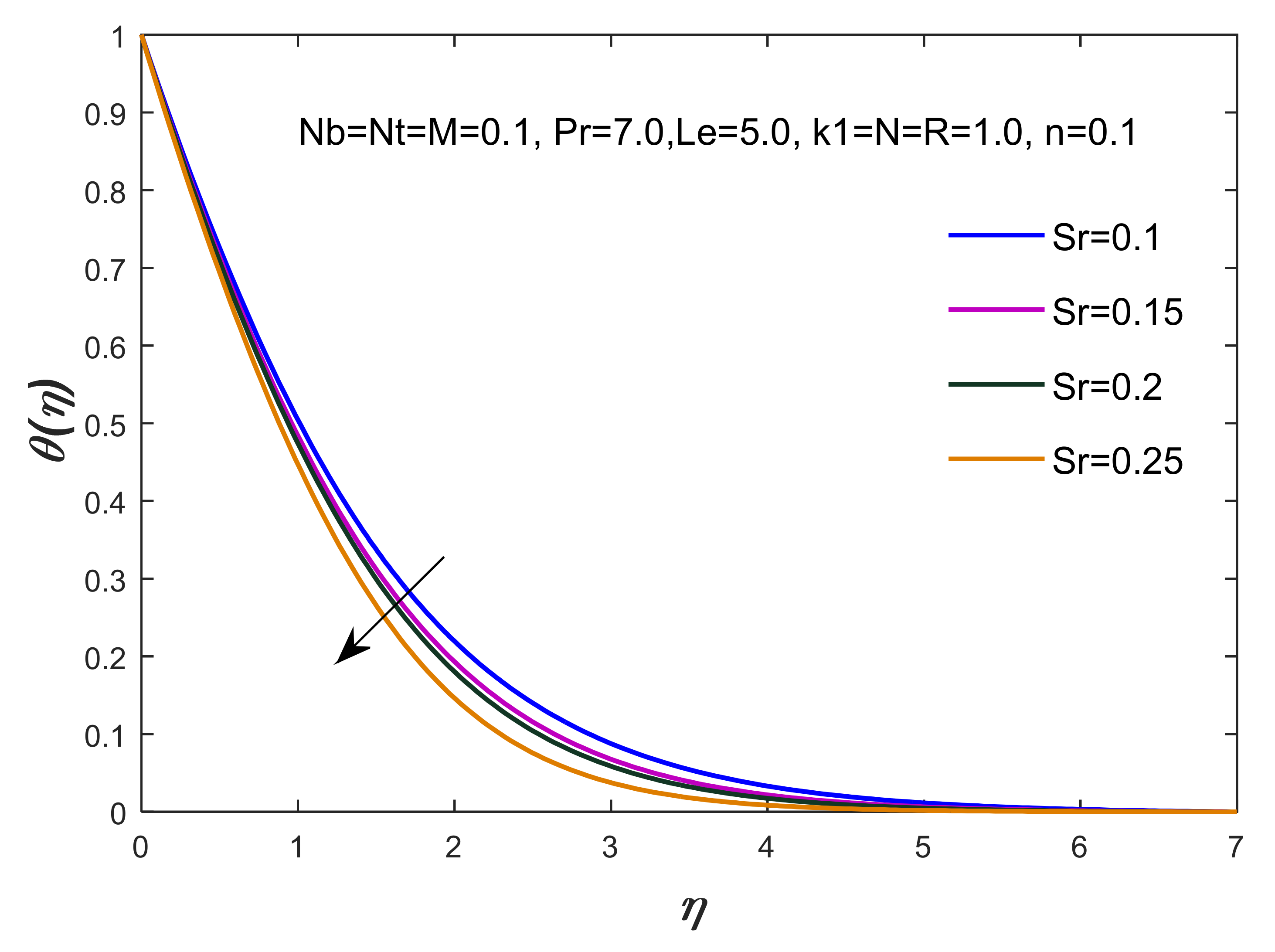
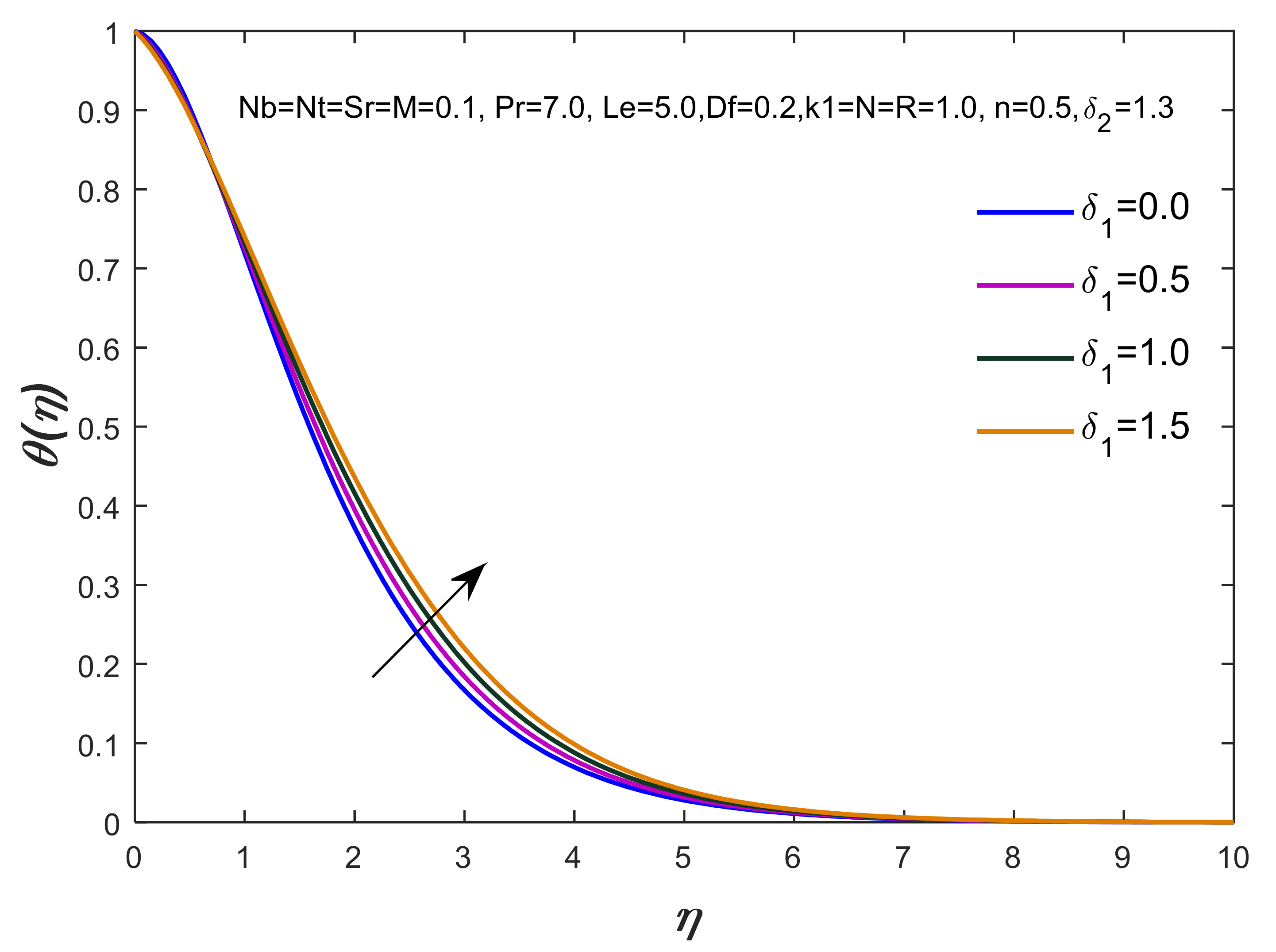
- The maximum production of thermal energy has been observed with respect to the variation of the thermal radiation, thermophoresis, Brownian motion and Dufour numbers, whereas thickness of the TBL declines by changing the values of the Dufour number;
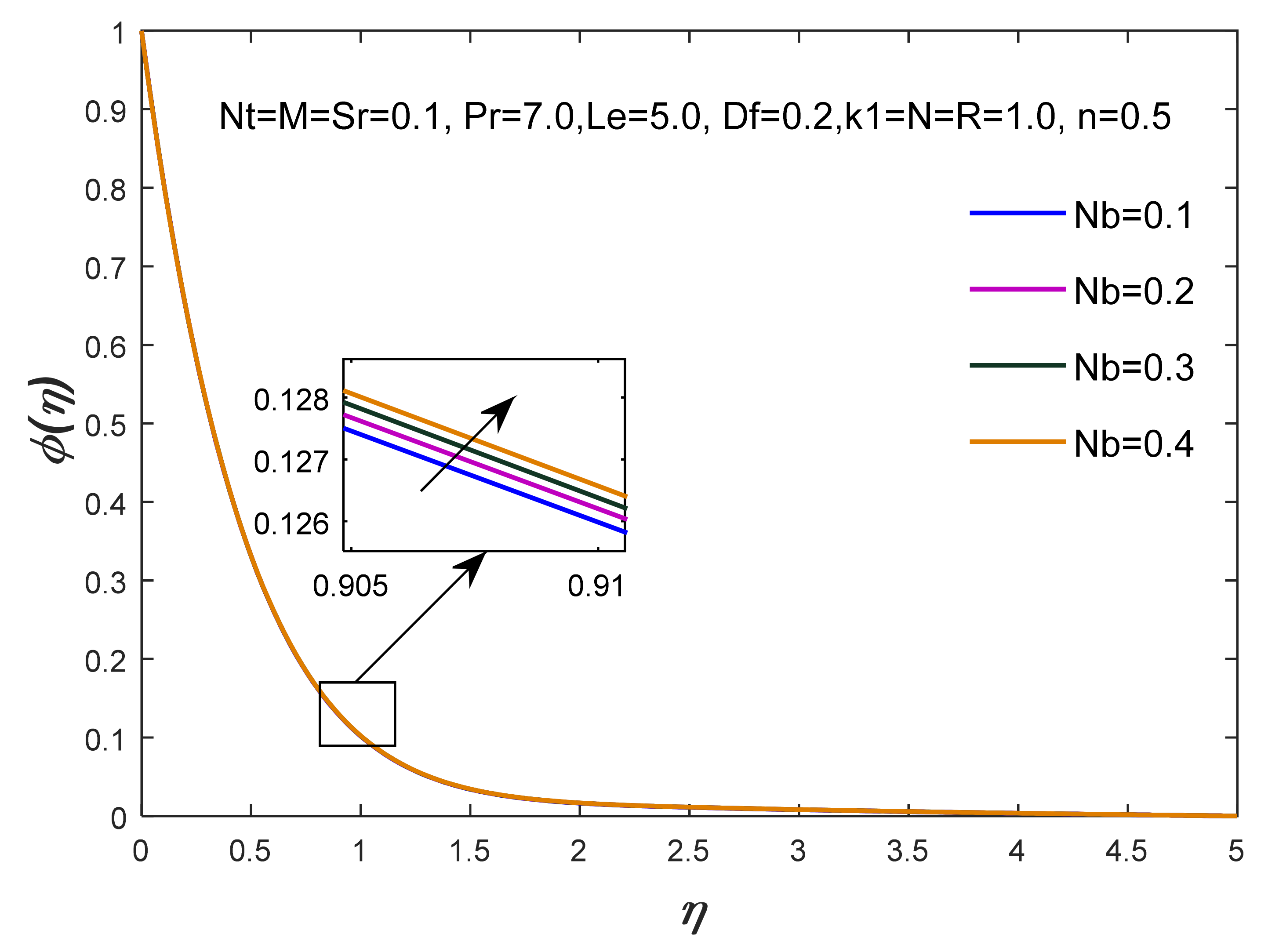
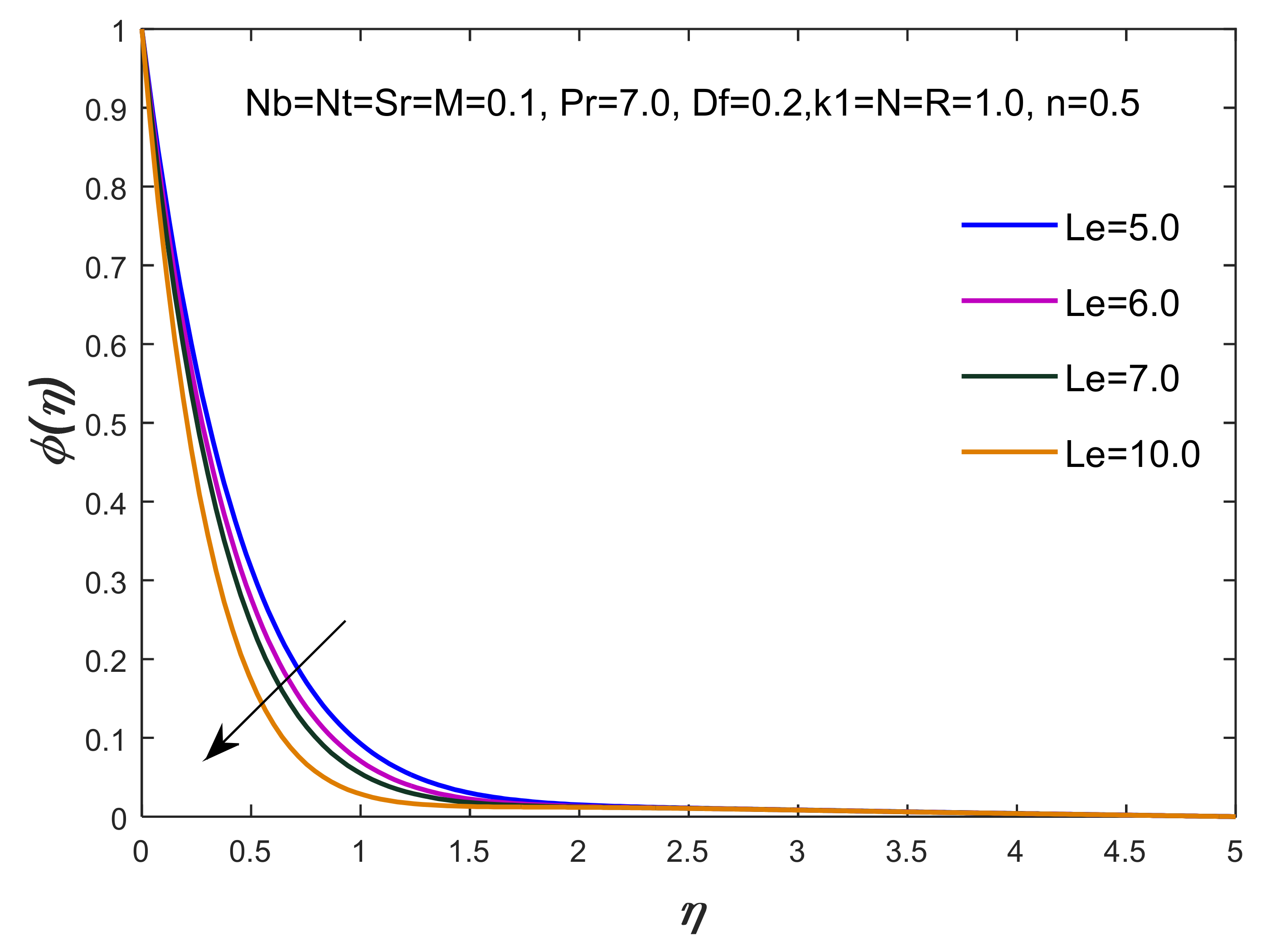
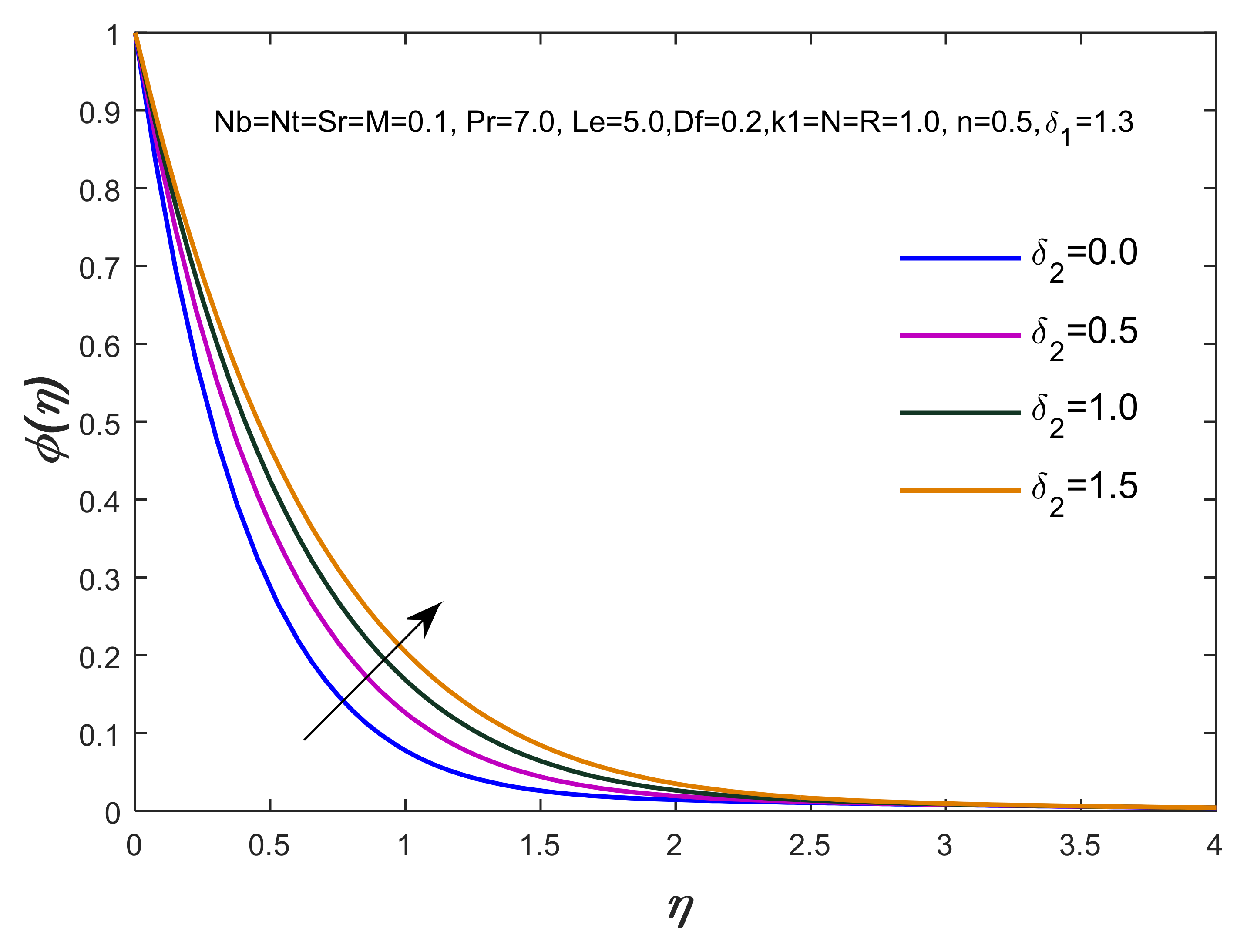
- The diffusion of fluid particles has been observed significantly against the variation of thermophoresis, Brownian motion, magnetic field, thermal relaxation time and concentration relaxation time numbers;
- The divergent velocity speeds up versus the Prandtl number, magnetic field, and the thermal radiation numbers, but reduces in speed in view of divergent flow against large values of the thermal radiation number.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Velocity field | |
| Temperature | |
| Fluid density | |
| Small parameters | |
| Dimensionless temperature | |
| Porosity parameter | |
| Lewis number | |
| Mass transfer rate | |
| Radiation parameter | |
| Stream function | |
| Temperature dependent diffusion coefficient | |
| Wall concentration/ambient concentration | |
| Space coordinates | |
| Concentration | |
| Chemical reaction parameter | |
| Magnetic parameter | |
| Dimensionless concentration | |
| Dimensionless velocity | |
| Chemical reaction parameter | |
| Heat transfer rate | |
| Temperature dependent thermal conductivity | |
| Dimensionless independent variable | |
| Wall temperature/ambient temperature | |
| Wall stress |
References
- Sohail, M.; Naz, R.; Bilal, S. Thermal performance of an MHD radiative Oldroyd-B nanofluid by utilizing generalized models for heat and mass fluxes in the presence of bioconvective gyrotactic microorganisms and variable thermal conductivity. Heat Transfer Asian Res. 2019, 48, 2659–2675. [Google Scholar] [CrossRef]
- Khan, M.I.; Kiyani, M.Z.; Malik, M.Y.; Yasmeen, T.; Khan, M.W.A.; Abbas, T. Numerical investigation of magnetohydrodynamic stagnation point flow with variable properties. Alex. Eng. J. 2016, 55, 2367–2373. [Google Scholar] [CrossRef] [Green Version]
- Sohail, M.; Ali, U.; Al-Mdallal, Q.; Thounthong, P.; Sherif, E.S.M.; Alrabaiah, H.; Abdelmalek, Z. Theoretical and numerical investigation of entropy for the variable thermophysical characteristics of couple stress material: Applications to optimization. Alex. Eng. J. 2020, 59, 4365–4375. [Google Scholar] [CrossRef]
- Khan, M.I.; Waqas, M.; Hayat, T.; Alsaedi, A. Chemically reactive flow of micropolar fluid accounting viscous dissipation and Joule heating. Results Phys. 2017, 7, 3706–3715. [Google Scholar] [CrossRef]
- Hayat, T.; Ahmad, S.; Khan, M.I.; Alsaedi, A. A frame work for heat generation/absorption and modified homogeneous–heterogeneous reaction in flow based on non-Darcy–Forchheimer medium. Nucl. Eng. Technol. 2018, 50, 389–395. [Google Scholar] [CrossRef]
- Sohail, M.; Shah, Z.; Tassaddiq, A.; Kumam, P.; Roy, P. Entropy generation in MHD Casson fluid flow with variable heat conductance and thermal conductivity over non-linear bi-directional stretching surface. Sci. Rep. 2020, 10, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Shah, Z.; Sheikholeslami, M.; Kumam, P.; Shafee, A. Modeling of entropy optimization for hybrid nanofluid MHD flow through a porous annulus involving variation of Bejan number. Sci. Rep. 2020, 10, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Shah, Z.; McCash, L.B.; Dawar, A.; Bonyah, E. Entropy optimization in Darcy–Forchheimer MHD flow of water based copper and silver nanofluids with Joule heating and viscous dissipation effects. AIP Adv. 2020, 10, 065137. [Google Scholar] [CrossRef]
- Khan, U.; Shafiq, A.; Zaib, A.; Sherif, E.S.M.; Baleanu, D. MHD Radiative Blood Flow Embracing Gold Particles via a Slippery Sheet through an Erratic Heat Sink/Source. Mathematics 2020, 8, 1597. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A. Numerical exploration of the features of thermally enhanced chemically reactive radiative Powell–Eyring nanofluid flow via Darcy medium over non-linearly stretching surface affected by a transverse magnetic field and convective boundary conditions. Appl. Nanosci. 2020, 53, 1–18. [Google Scholar]
- Al-Khaled, K.; Khan, S.U. Thermal Aspects of Casson Nanoliquid with Gyrotactic Microorganisms, Temperature-Dependent Viscosity, and Variable Thermal Conductivity: Bio-Technology and Thermal Applications. Inventions 2020, 5, 39. [Google Scholar] [CrossRef]
- Mandal, I.C.; Mukhopadhyay, S. Heat transfer analysis for fluid flow over an exponentially stretching porous sheet with surface heat flux in porous medium. Ain Shams Eng. J. 2013, 4, 103–110. [Google Scholar] [CrossRef] [Green Version]
- Khan, S.U.; Ali, N.; Abbas, Z. Hydromagnetic flow and heat transfer over a porous oscillating stretching surface in a viscoelastic fluid with porous medium. PLoS ONE 2015, 10, e0144299. [Google Scholar]
- Alam, A.; Marwat, D.N.K. Heat and mass transfer on a stretching/shrinking and porous sheet of variable thickness with suction and injection. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 0954406220982333. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Sohail, M. Numerical approach of variable thermophysical features of dissipated viscous nanofluid comprising gyrotactic micro-organisms. Pramana J. Phys. 2020, 94, 1–12. [Google Scholar] [CrossRef]
- Sohail, M.; Naz, R.; Shah, Z.; Kumam, P.; Thounthong, P. Exploration of temperature dependent thermophysical characteristics of yield exhibiting non-Newtonian fluid flow under gyrotactic microorganisms. AIP Adv. 2019, 9, 125016. [Google Scholar] [CrossRef] [Green Version]
- EL-Kabeir, S.M.; El-Zahar, E.R.; Rashad, A.M. Effect of chemical reaction on heat and mass transfer by mixed convection flow of casson fluid about a sphere with partial slip. J. Comput. Theor. Nanosci. 2016, 13, 5218–5226. [Google Scholar] [CrossRef]
- Sohail, M.; Naz, R. Modified heat and mass transmission models in the magnetohydrodynamic flow of Sutterby nanofluid in stretching cylinder. Phys. A Stat. Mech. Appl. 2020, 549, 124088. [Google Scholar] [CrossRef]
- Anwar, M.I.; Ali, M.; Rafique, K.; Shehzad, S.A. Soret–Dufour and radiative aspects in hydromagnetized nanofluid flow in stratified porous medium. SN Appl. Sci. 2019, 1, 1430. [Google Scholar] [CrossRef] [Green Version]





| Pr | M | R | −θ′(0) [19] | −θ′(0) Present Results |
|---|---|---|---|---|
| 1.0 | 0.0 | 0.0 | 0.9548 | 0.95484878 |
| 2.0 | 0.0 | 0.0 | 1.4714 | 1.4714548 |
| 3.0 | 0.0 | 0.0 | 1.8691 | 1.86906988 |
| 1.0 | 0.0 | 1.0 | 0.5315 | 0.53530132 |
| 1.0 | 1.0 | 0.0 | 0.8611 | 0.86150565 |
| 1.0 | 1.0 | 1.0 | 0.4505 | 0.46196426 |
| Nb | Nt | Pr | Le | M | k1 | R | Γ | Df | Sr | n | δ1 | δ2 | −f″(0) | −θ′ (0) | −∅′(0) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 1.3 | 1.3 | 1.358958 | 1.203130 | 1.692398 |
| 0.5 | 0.1 | 7.0 | 5.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 1.3 | 1.3 | 1.358958 | 0.745205 | 1.730309 |
| 0.1 | 0.3 | 7.0 | 5.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 1.3 | 1.3 | 1.358958 | 0.993797 | 1.705696 |
| 0.1 | 0.1 | 8.0 | 5.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 1.3 | 1.3 | 1.358958 | 1.260018 | 1.691140 |
| 0.1 | 0.1 | 7.0 | 10.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 1.3 | 1.3 | 1.358958 | 1.020337 | 2.459589 |
| 0.1 | 0.1 | 7.0 | 5.0 | 2.5 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 1.3 | 1.3 | 2.063846 | 1.080128 | 1.514741 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 2.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 1.3 | 1.3 | 1.93865 | 1.103093 | 1.545366 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 0.1 | 3.0 | 0.1 | 0.1 | 0.1 | 0.1 | 1.3 | 1.3 | 1.358958 | 0.628864 | 3.137834 |
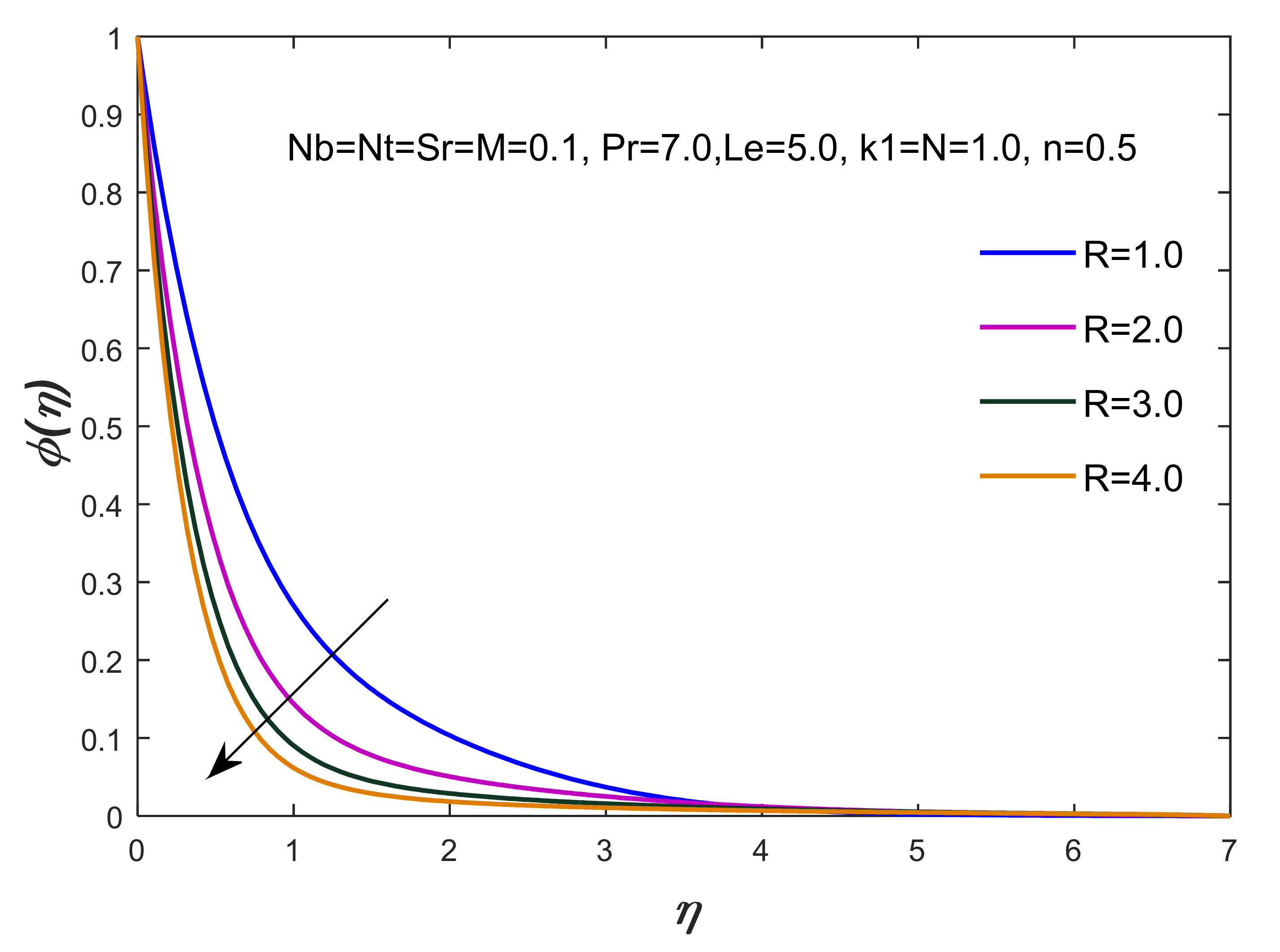
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 0.1 | 0.1 | 5.0 | 0.1 | 0.1 | 0.1 | 1.3 | 1.3 | 1.358958 | 0.458712 | 1.664456 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.3 | 0.1 | 0.1 | 1.3 | 1.3 | 1.358958 | 0.688129 | 1.720053 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.3 | 0.1 | 1.3 | 1.3 | 1.358958 | 1.287439 | 1.347656 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.2 | 1.3 | 1.3 | 1.358958 | 1.045916 | 1.696398 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 1.5 | 1.3 | 1.358958 | 1.179728 | 1.694022 |
| 0.1 | 0.1 | 7.0 | 5.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 1.3 | 1.5 | 1.358958 | 1.216942 | 1.635957 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naseem, T.; Nazir, U.; El-Zahar, E.R.; Algelany, A.M.; Sohail, M. Numerical Computation of Dufour and Soret Effects on Radiated Material on a Porous Stretching Surface with Temperature-Dependent Thermal Conductivity. Fluids 2021, 6, 196. https://doi.org/10.3390/fluids6060196
Naseem T, Nazir U, El-Zahar ER, Algelany AM, Sohail M. Numerical Computation of Dufour and Soret Effects on Radiated Material on a Porous Stretching Surface with Temperature-Dependent Thermal Conductivity. Fluids. 2021; 6(6):196. https://doi.org/10.3390/fluids6060196
Chicago/Turabian StyleNaseem, Tahir, Umar Nazir, Essam R. El-Zahar, Ahmed M. Algelany, and Muhammad Sohail. 2021. "Numerical Computation of Dufour and Soret Effects on Radiated Material on a Porous Stretching Surface with Temperature-Dependent Thermal Conductivity" Fluids 6, no. 6: 196. https://doi.org/10.3390/fluids6060196
APA StyleNaseem, T., Nazir, U., El-Zahar, E. R., Algelany, A. M., & Sohail, M. (2021). Numerical Computation of Dufour and Soret Effects on Radiated Material on a Porous Stretching Surface with Temperature-Dependent Thermal Conductivity. Fluids, 6(6), 196. https://doi.org/10.3390/fluids6060196







