Abstract
In the present analysis, an unsteady MHD mixed convection flow is scrutinized for a non-Newtonian Casson hybrid nanofluid in the stagnation zone of a rotating sphere, resulting from the impulsive motion of the angular velocity of the sphere and the velocity of the free stream. A set of linearized equations is derived from the governing ones, and these differential equations are solved numerically using the hybrid linearization–differential quadrature method. The surface shear stresses in the - and -directions and the surface heat transfer rate are improved due to the Casson , mixed convection , rotation and magnetic field parameters. In addition, as nanoparticles, the solid volume fraction (parameter ) increases, and the surface shear stresses and the rate of heat transfer are raised. A comparison between earlier published data and the present numerical computations is presented for the limiting cases, which are noted to be in very good agreement.
1. Introduction
The investigation of heat transfer and flow on rotary bodies of rotation in a forced flow has importance in many engineering applications, such as fiber coating, projectile motion, re-entry rocket design of rotary machinery, etc. [1,2,3,4,5], investigating heat transfer and flow on a rotating sphere in a regular flow stream where the free stream velocity is parallel to its axis of rotation. Rajasekaran and Palekar [6] addressed the impact of the forces of buoyancy on a stable forced convection flow over a rotating sphere. When the impulsive movement of a body in an otherwise surrounding fluid leads to instability in the flow field, there is an instantaneous development in the inviscid flow over the body. Inside the viscous layer, the flow is developed slowly, and, after a certain period of time, the flow becomes completely developed and stable. Over a short time, the unstable acceleration and the viscous forces are controlled in terms of the flow and, in general, the flow is independent of the conditions at the stagnation point and at the leading edge or far upstream. For a long time, the pressure gradient, convective acceleration, and the viscous force are dominated by the flow. The impacts of the conditions at the stagnation point or at the leading edge are important during this stage. Hall [7], Stewartson [8,9], and Watkins [10] showed the development of the flow of the boundary layer on a semi-infinite flat sheet due to impulsive movement. Due to the rheological characteristics of a Casson fluid, it is categorized as a non-Newtonian fluid in relation to the shear stress–strain relationship.
Casson fluid behaves like an elastic solid when the values of the shear strain are small, and it behaves like a Newtonian fluid when it is over a critical stress value. We can image Casson fluid as a shear thin liquid with zero viscosity at the rate of shear without limits, and a viscosity without limit at a zero shear rate. Soup, human blood, honey, tomato sauce, and orange juice are some common examples of liquids that show characteristics of a Casson fluid. The boundary layer flow of a Casson fluid is close to the stagnation point on a stretching flat surface and was analyzed by Mustafa et al. [11] using the homotopy analysis method (HAM) when the Casson parameter tends to infinity, and the results were shown for the limiting state. The thermal boundary layer and the momentum development in the flow of a Casson fluid over a semi-infinite flat sheet were studied by Mustafa et al. [12] when both the flat plate and the surrounding fluid were set in motion at the same time and the temperature of the flat sheet was suddenly raised from that of ambient fluid. They derived parabolic (PDE) partial differential equations that were analytically solved using the homotopy analysis method. A similar solution was presented by Nadeem et al. and was used to find the solution of the equations of the governing flow of an electrically conducting Casson fluid flow in two directions over a porous linear expansion sheet [13]. A stable and wavering blood flow, a Casson fluid, was analyzed by Boyd et al. [14]. Unsteady MHD heat and mass transfer from a mixed convection flow in the forward stagnation region of a rotating sphere under different wall conditions was studied by Chamkha et al. [15]. The magnetohydrodynamics of non-Newtonian Casson fluid flow between two revolving cylinders was provided by Eldabe et al. [16]. An improvement in the mass and heat transfer of a three-dimensional non-Newtonian Casson nanofluid was depicted by Nadeem et al. [17] and the hot liquid was adjusted on the lower face of a wall through a convective boundary case. They indicated that Newtonian nanofluids lead to a decline in skin friction at the wall with respect to the Casson nanofluid, and they achieved a decrease in the thermal conductivity when the Prandtl number was higher. Casson fluid flow on an unsteady extension surface through the expansion of the sheet of Andersson et al. [18] was examined by Mukhopadhyay et al. [19]. The unstable mixed convection flow for a non-Newtonian Casson fluid at the slump point in a rotating sphere was reviewed by Ahmed and Mahdy [20]. The 2D magnetohydrodynamic stagnation region flow of a Casson fluid, which was electrically conducive and transferred heat over a stretched surface due to thermal radiation, was reported by Bhattacharyya [21]. They noticed that the thickness of the boundary layer of the Newtonian fluid velocity became smaller than that of the Casson fluid due to Casson fluid elasticity. A numerical solution for transferring the heat of a non-Newtonian Casson fluid outside an expanded porous cylinder under Dufour and Soret effects was presented by Mahdy [22]. Heat transfer and the hydromagnetic boundary layer flow in a non-Newtonian Casson fluid with a slump point over that of a stretching flat surface in the presence of velocity and thermal slip boundary conditions were examined by Nandy [23], and the results show that temperature and flow fields were greatly influenced by sliding parameters in terms of the velocity and thermal boundary conditions, respectively. The 2D flow and diffusion types that react chemically in Casson fluids from an unstable stretching sheet in the existence of a magnetic field were considered by Makanda et al. [24]. Mahdy and Ahmed [25] addressed mass and heat transfer flows for electrically conducive fluids at the point of stagnation for a revolving sphere under the effect of thermal radiation. For prompt progress in thermal and industrial engineering processes, more compact and more efficient heat transfer systems are required. These systems of liquids for heat transfer are used as cooling agents. In any case, such liquids badly affect cooling processes or the heat transfer rate due to them having a low thermal conductivity.
Actually, scientists have found it difficult to enhance the thermal conductivity of liquids. Therefore, Choi and Eastman [26] and Choi et al. [27] were the primary researchers who attempted to face this difficult task by presenting a nanofluid. Raju and Sandeep [28] investigated the properties of ferrous nanoparticles considering Casson model. Nanofluids are an excellent invention which work to increase the heat transfer rate and the thermal conductivity. They consist of nanoparticles with volume (1–100 nm) and base fluids. The mixture (nanoparticles and base fluid) is exposed to sound waves for homogenization. Generally, base fluids could also be organic fluids (such as tri-ethylene, ethylene, etc.), water, engine oil, bio-fluids, polymeric solutions and other basic fluids. Usually, the nanoparticles used include carbon in various forms (such as graphite, diamond and carbon nanotubes), metal oxides (such as zirconia, titania), metals (such as gold, silver, copper) and functionalized nanoparticles. Nanofluids are of great importance due to its use in many applications.
After several experiments, a replacement type named the ‘hybrid nanofluid’ was obtained by suspending two classes of nanoparticles within the base fluid. This is the newest nanofluid technology. Hybrid nanoparticles present an enormous benefit, excepting the increase in effective thermal conductivity when nanosized particles are distributed appropriately. Several experimental research papers concerning hybrid nanofluids have been printed. An experimental study of mixed convection with (Cu-Al2O3/H2O) hybrid nanofluid for laminar flow in a sloped tube was performed by Momin [29]. Suresh et al. [30] examined a study on the synthesis of (Cu-Al2O3/H2O) hybrid nanofluid. The consequences of (Cu-Al2O3/H2O) hybrid nanofluid in heat transfer were studied by Suresh et al. [31]. Suresh et al. [32] examined the properties of the turbulent heat transfer and pressure decline of dilute water-based (Cu-Al2O3/H2O) hybrid nanofluids. The impacts of MHD and variable wall temperatures on transient mixed Casson nanofluid flow within the stagnation point of a rotating sphere were studied by Mahdy [33].
In the current contribution, we scrutinized the unsteady MHD radiation mixed convection flow of Casson hybrid nanofluid in the stagnation region of an impulsively rotating sphere with a magnetic field. By employing a suitable transformation, the partial differential equations were transformed into dimensionless differential equations, then solved numerically using the hybrid linearization–differential quadrature method employed in a MATLAB environment [34]. The impact of miscellaneous parameters such as radiation, buoyancy and rotation parameters were examined on the flow where the impulsive motion results in the unsteadiness of the hybrid nanofluid and, therefore, the impulsive rotation of the sphere. The outcomes obtained are compared to validate the technique.
2. Problem Formulation
Let us address the unsteady boundary layer flow of an incompressible non-Newtonian Casson hybrid nanofluid through the stagnation domain of an impulsively rotating sphere. Water is set as the base fluid which contains two types of nanoparticles, silver (Ag) and titanium (TiO2). represents an angular velocity of the sphere around an axis parallel to , which is the surrounding free stream velocity, as illustrated in Figure 1. Through the current investigation, the following hypotheses have been set:
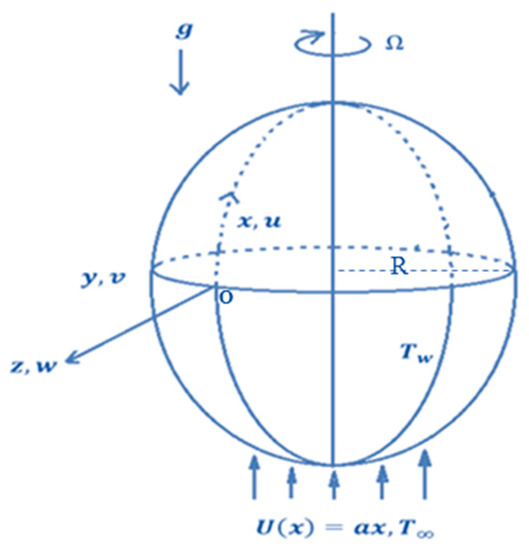
Figure 1.
Geometric model and coordinates system.
- The fluid is an electrical conductor in the existence of a fixed magnetic field applied in the z-direction.
- The sphere is at rest in the surrounding fluid prior to time , and the temperature of the surface is .
- At , the temperature of the surface for the sphere is unexpectedly increased to , where .
- It is assumed that the properties of the fluid are fixed, excluding the density, which is set based the Boussinesq approximation.
- The rheological equation for the non-compressible and isotropic flow state of a Casson fluid iswhere and which is the distortion rate components, µB refers to the dynamic viscosity of the non-Newtonian fluid, based on the non-Newtonian model is the critical value of , and indicates to the yield stress fluid.
- According to these suppositions, Joule heating impacts and the viscous dissipation are ignored. As depicted in Takhar at al. [35], the governing equations can be written:
The initial conditions are described as
associated with the following compatible boundary conditions:
where , and indicate the distance along a meridian from the forward point of the stagnation, the distance in the direction of the rotation and the vertical distance to the surface, respectively; is the time; is the component of Casson hybrid nanofluid velocity in -direction; is the component of Casson hybrid nanofluid velocity in -direction; is the component of Casson hybrid nanofluid velocity in -direction, is the Casson parameter, is the gravity acceleration, is the temperature, refers to the radius of the sphere, points out the strength of magnetic field, subscripts and stand for both conditions at the surface and in the free stream, respectively. represents the radiation flux, where and are the Stefan–Boltzmann constant and the coefficient of the mean absorption, respectively. Now, by extending about (Taylor expansion) and by ignoring the higher-order terms, we have [36].
, and , , , , and refer to the effective kinematic viscosity of the hybrid nanofluid, buoyancy coefficient, effective electrical conductivity, hybrid nanofluid density, hybrid nanofluid thermal conductivity and specific heat, which are expressed by the next formulae:
where , and subscript refers to the base fluid (water).
The properties of thermo-physical of the hybrid nanofluid are shown in Table 1 (see Firas et al. [37]).

Table 1.
Physical characteristics of the components of the hybrid fluid (see reference [37]).
Now, we present suitable non-similarity transformations which were used to convert the equations governing the flow and their proper boundary conditions into dimensionless forms:
By substituting Equation (13) into Equations (1)–(4), we notice that Equation (1) is satisfied and Equations (2)–(4) become:
and the boundary conditions become:
where the primes (′) denote the derivative with respect to , is the rotation parameter, is the mixed convection, stands for the magnetic field parameter, the radiation parameter, represents Grashof number, is the Renolds number.
Now, the shear stresses in the - and -directions are described as
The rate of surface heat transfer in terms of the Nusselt number takes the form of
3. Results and Discussion
In order to scrutinize the impacts of various governing parameters of Casson hybrid nanofluid behavior concerning the stagnation point of the rotating sphere with radiation, numerical computations are pointed out. To verify that the used method was working accurately, a comparison was made between our results and those previously published, and it became clear that our results are consistent with those obtained by Takhar et al. [35], as depicted in Figure 2 for , , , and . The ranges of such controlling parameters are the non-Newtonian Casson parameter (), rotation parameter , the mixed convection ), the magnetic field parameter , the nanoparticles volume parameter and the radiation parameter , as shown on Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11.
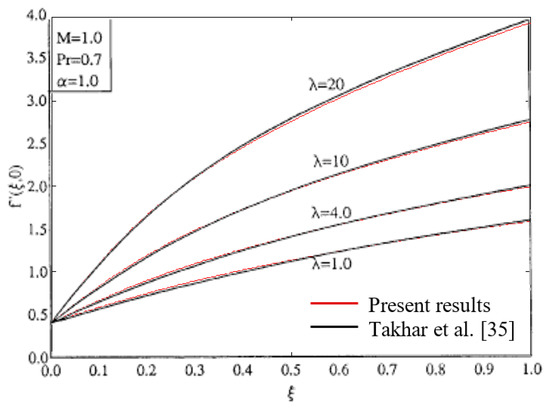
Figure 2.
Comparison between present results and Takhar et al. [35].
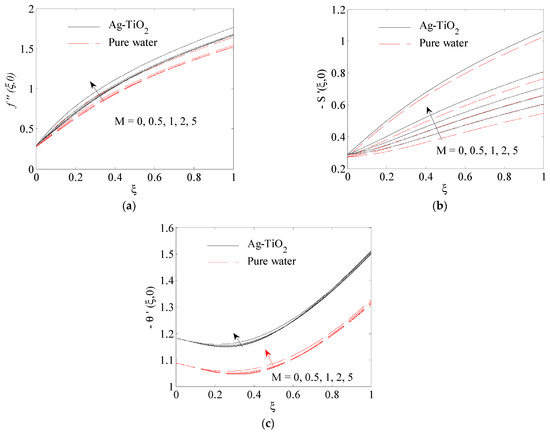
Figure 3.
Influence of magnetic field on (a) , (b) , (c) .
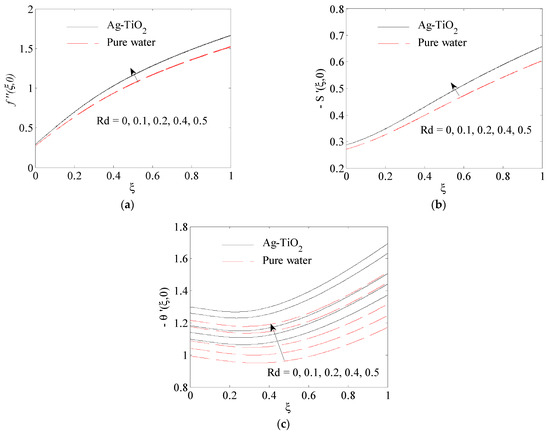
Figure 4.
Influence of radiation parameter on (a) , (b) , (c) .
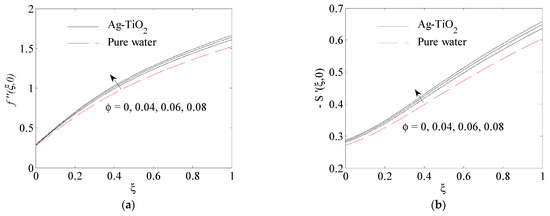
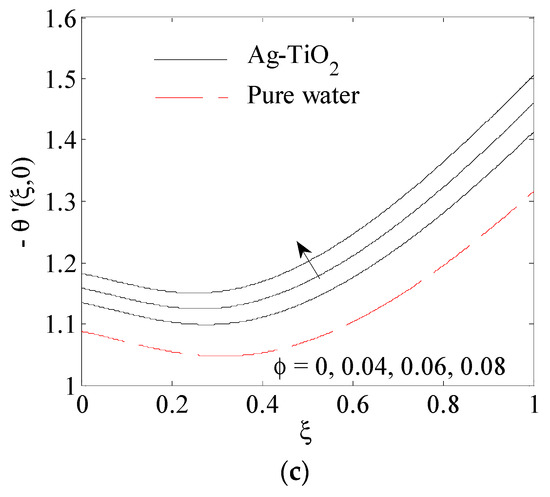
Figure 5.
Influence of nanoparticle volume fraction on (a) , (b) , (c) .
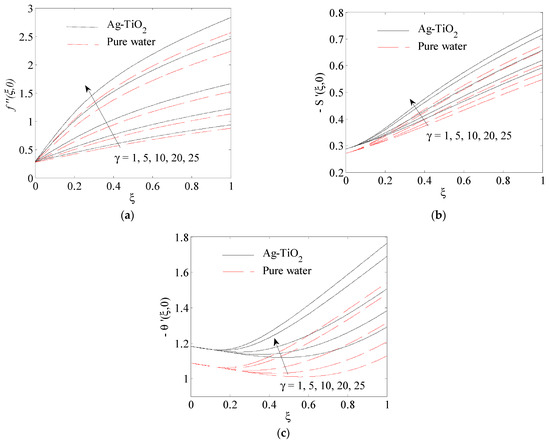
Figure 6.
Influence of rotation parameter on (a) , (b) , (c) .
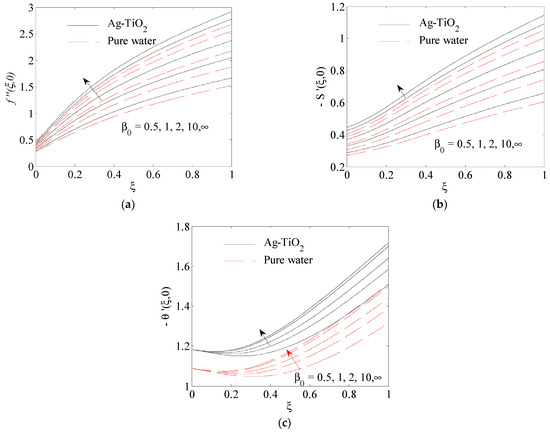
Figure 7.
Influence of Casson parameter on (a) , (b) , (c) .
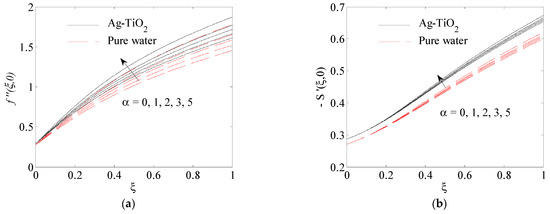
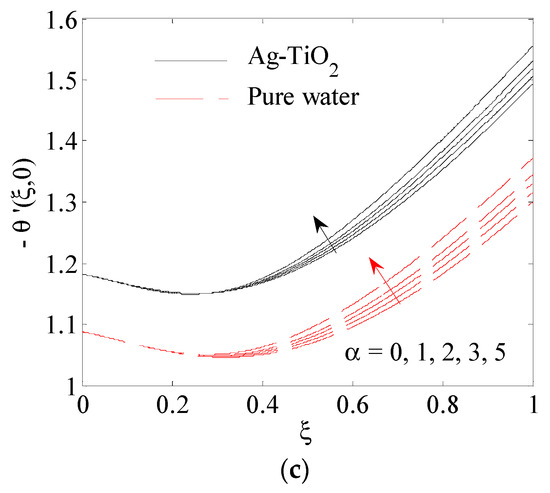
Figure 8.
Influence of mixed convection parameter on (a) , (b) , (c) .
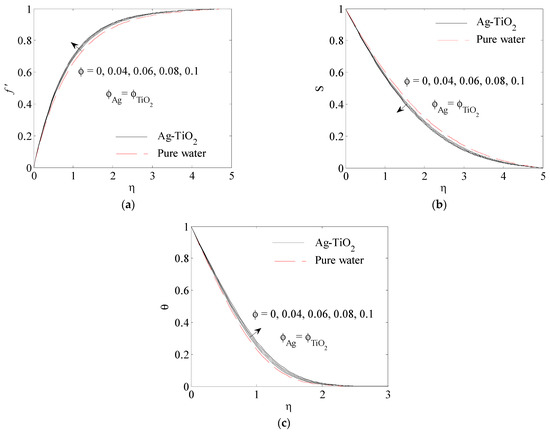
Figure 9.
Influence of nanoparticle volume fraction on (a) , (b) , (c) .
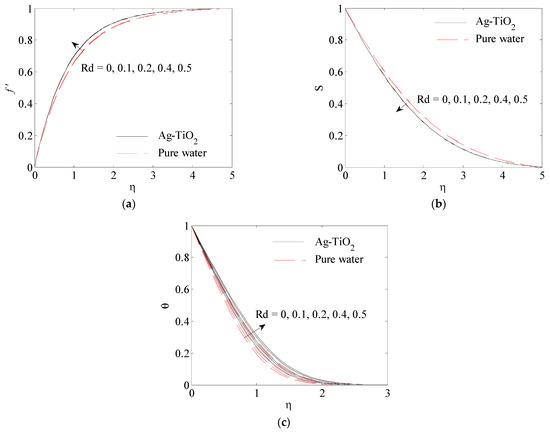
Figure 10.
Influence of radiation parameter on (a) , (b) , (c) .
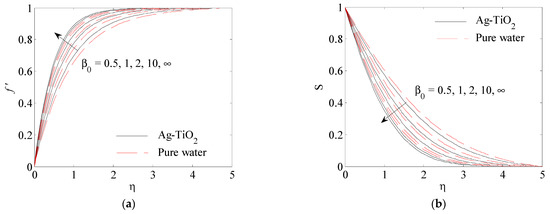
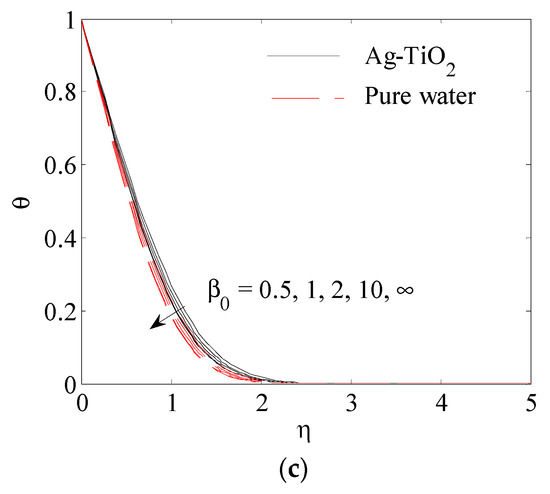
Figure 11.
Influence of Casson parameter on (a) , (b) , (c) .
The impact of the magnetic parameter on the surface shear stress in the -direction, , surface shear stress in the -direction, , and surface heat transfer rate is plotted in Figure 3a–c at , (for simplicity, we indicated the surface heat transfer rate as ). It is noticed that an increase in values of leads to a rise in the surface shear stress in the x-direction and y-direction and surface heat transfer rate due to the acceleration of the fluid in the boundary layer which was caused by the improvement of the Lorentz force. The reason for the weak impact of on the surface heat transfer, as shown in Figure 3c, is due to the fact that does not exist on the energy equation explicitly. From Figure 3a,b, it is found that the Ag-TiO2 hybrid nanofluid shows a higher drag as compared to the pure water. The influence of the radiation parameter on the surface shear stress , surface shear stress and the surface heat transfer rate for , is displayed in Figure 4a–c. Since the radiation only occurs in the energy equation, it greatly affects the heat transfer (see Figure 4c). In contrast to its effect on the surface shear stresses , it was observed that with increasing in , strengthened also. However, decreased. In Figure 4a,b, it is found that the Ag-TiO2 hybrid nanofluid shows a higher drag as compared to the pure water.
The impact of nanoparticle volume fraction on the surface shear stress , the surface shear stress and the surface heat transfer rate , at is presented in Figure 5a–c. These figures show that by the growth in nanoparticle volume fraction , the surface shear stress in the x and y-direction are improved, as shown in Figure 5a,b. The lower value of the surface shear stress on the x- and y-direction in the case of pure water is obtained at a smaller value of ξ in comparison with the Ag-TiO2 hybrid nanofluid. In Figure 5c, we observe that the wall heat transfer rate reduced as nanoparticles volume fraction increased. The existence of nanoparticles led to an increase in the rate of the wall heat transfer. The aspect of rotation parameter on the surface shear stress , the surface shear stress and the surface heat transfer rate for is illustrated in Figure 6b,c. It was observed that the effect of boosts with an increment of . , enhancing with . This increase is due to the reduction in both of the boundary layers of heat and the momentum which resulted from an increase in velocity and temperature gradients at the wall.
Figure 7a–c depicted the influence of the Casson parameter on the surface shear stress , the surface shear stress and the surface heat transfer rate These figures illustrate the enhancement of the surface shear stress in the and -direction and the surface heat transfer. The plasticity of the fluid is the reason for this increase, where the plasticity causes an improvement in the thickness of the boundary layer of thermal and velocity. The influence of the mixed convection parameter on the surface shear stress , the surface shear stress and the surface heat transfer rate is portrayed in Figure 8a–c. It is noticed that by an increase in the buoyancy parameter α, both the surface shear stresses in the - and -direction and the surface heat transfer are increased, because the buoyancy force works as a suitable pressure gradient which speeds up the fluid in the boundary layer. Therefore, the thickness of the boundary layer of momentum and thermal are decreased and thus improve the surface shear stress and the heat transfer.
Figure 9a–c display the influence of nanoparticle volume fraction on the velocity profile in x-direction , the velocity profile in -direction and the temperature profile for Figure 9a,c show that the velocity profile in x-direction and the temperature profile , respectively, are enhanced by an increase in the nanoparticle volume. This is because the main reason for the increase in the temperature is the rise in thermal conductivity of the hybrid nanoparticle. Again, it can be noted that since the conductivity of Ag-TiO2 is higher than that of water, the temperature distribution in Ag-TiO2 is higher than that in the base fluid, while Figure 9b shows that with an increase in the nanoparticle solid volume fraction, the velocity profile in y-direction is weakened. The influence of thermal radiation on the velocity profiles in the -direction , velocity profiles in the y-direction and the temperature profile are plotted in Figure 10a–c at By increasing the values of thermal radiation , the boundary layer thickness of velocity in x-direction and temperature are increased, as is clear in Figure 10a,c. The temperature field improves because of the rise in the radiation parameter, which results in a drop in the absorption coefficient, whilst in Figure 10b, by boosting the thermal radiation parameter , the velocity in -direction is decreased.
Figure 10a,c describe the influence of the Casson parameter on the velocity profile in x-direction , the velocity profile in -direction and the temperature profile at , . It is seen from Figure 11a that the velocity profile in the -direction is improved by an increase in the Casson parameter . Figure 11b,c show that the curve of Newtonian fluid is less than that in non-Newtonian fluid, so the thickness of the boundary layer of the velocity for the Casson fluid is greater than the Newtonian fluid. The explanation for this is due to the fact that the increase in Casson leads to an increase in the fluid elasticity; consequently, the thickness of the boundary layer increases in y-direction. Therefore, with increasing , the phenomenon of convection is reduced. Figure 12 illustrates the different relative distributions of particle species on the rate of heat transfer; as is shown, adding more solid volume fraction of titanium TiO2 leads to the better enhancement of the rate of heat transfer than by adding silver nanoparticles.
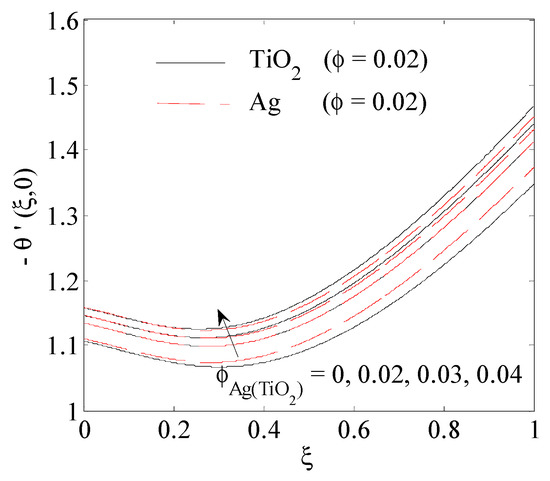
Figure 12.
Influence of different relative nanoparticles volume fraction on .
4. Conclusions
The impact of thermal radiation on the time-dependent MHD flow and heat transfer of a laminar incompressible viscous electrically conducting non-Newtonian Casson hybrid nanofluid (Ag-TiO2) within the stagnation region of a rotating sphere has been addressed in the present paper. Non-similar transformations and the hybrid linearization–differential quadrature method in a MATLAB environment have been applied to solve the flow governing equations. Some of the significant notes are listed as follows:
- The heat transfer rate and surface shear stress in x- and y-direction are enhanced by increasing the magnetic field, Casson, mixed convection and the sphere rotation parameters.
- The velocity profile in x-direction, temperature profile and surface shear stresses in x- and y-direction are enhanced by the increase in the thermal radiation, unlike the rate of heat transfer and the velocity profile in y-direction, which is decreased by boosting the thermal radiation parameter.
- Surface shear stresses in x- and y-direction, the velocity distribution in x-direction and temperature distribution of hybrid nanofluid (Ag-TiO2/H2O) is greater as compared to the base fluid.
- Both velocity distributions in y-direction and the temperature distribution in non-Newtonian hybrid nanofluid are greater than in Newtonian hybrid nanofluid, unlike the velocity distribution where it is noticed that the of non-Newtonian hybrid nanofluid is smaller than Newtonian fluid.
Author Contributions
Conceptualization, A.E.N.M., A.M.R. and W.S.; methodology, E.R.E.-Z., A.E.N.M., A.M.R., W.S. and L.F.S.; formal analysis, A.E.N.M., A.M.R. and W.S.; investigation, E.R.E.-Z., A.E.N.M., A.M.R., W.S. and L.F.S.; resources, A.E.N.M., A.M.R. and W.S.; writing—original draft preparation, E.R.E.-Z., A.E.N.M., A.M.R., W.S. and L.F.S.; writing—review and editing, E.R.E.-Z., A.E.N.M., A.M.R., W.S. and L.F.S.; supervision, A.E.N.M. and A.M.R.; project administration, A.E.N.M. and A.M.R.; funding acquisition, A.M.R., E.R.E.-Z. and L.F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge that this publication was supported by the Deanship of Scientific Research at Prince Sattam bin Abdulaziz University, Alkharj, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hoskin, N.E. The laminar boundary layer on a rotating sphere. In 50 Jahre Grenzschichfforschung; Vieweg Teubner Verlag: Wiesbaden, Germany, 1995; pp. 127–131. [Google Scholar]
- Sickmann, I. The calculation of the thermal laminar boundary layer on rotating sphere. Z. Angew. Math. Phys. 1962, 13, 468–482. [Google Scholar] [CrossRef]
- Chao, B.T.; Greif, R. Laminar forced convection over rotating bodies. J. Heat Transf. 1974, 96, 463–466. [Google Scholar] [CrossRef]
- Chao, B.T. An analysis of forced convection over nonisothermal surfaces via universal functions. In Recent Advances in Engineering Science; Lehigh University: Bethlehem, PA, USA, 1977; pp. 471–483. [Google Scholar]
- Lee, M.H.; Jang, D.R.; Dewitt, K.J. Laminar boundary layer heat transfer over rotating bodies in forced flow. J. Heat Transf. 1978, 100, 496–502. [Google Scholar] [CrossRef]
- Rajasekaran, R.; Palekar, M.G. Mixed convection about a rotating sphere. Int. J. Heat Mass Transf. 1985, 28, 959–968. [Google Scholar] [CrossRef]
- Hall, M.G. The boundary layer over an impulsively started flat plate. Proc. R. Soc. A 1969, 310, 401–414. [Google Scholar]
- Stewartson, K. On the impulsive motion of a flat plate in a viscous fluid. Part I. Q. J. Mech. Appl. Math. 1951, 4, 183–198. [Google Scholar] [CrossRef]
- Stewartson, K. On the impulsive motion of a flat plate in a viscous fluid. Part II. Q. J. Mech. Appl. Math. 1973, 26, 143–152. [Google Scholar] [CrossRef]
- Watkins, C.A. Heal transfer in the boundary layer over an impulsively started flat plate. J. Heat Transf. 1975, 97, 482–484. [Google Scholar] [CrossRef]
- Mustafa, M.; Hayat, T.; Pop, I.; Hendi, A. Stagnation-point flow and heat transfer of a Casson fluid towards a stretching sheet. Z. Nat. A 2012, 67, 70–76. [Google Scholar] [CrossRef]
- Mustafa, M.; Hayat, T.; Pop, I.; Aziz, A. Unsteady boundary layer flow of a Casson fluid due to an impulsively started moving flat plate. Heat Transf. 2011, 40, 563–576. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Akbar, N.S.; Khan, Z.H. MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet. Alex. Eng. J. 2013, 52, 577–582. [Google Scholar] [CrossRef]
- Boyd, J.; Buick, J.; Green, M.S. Analysis of the Casson and Carreau-Yasuda non-Newtonian blood models in steady and oscillatory flow using the lattice Boltzmann method. Phys. Fluids 2007, 19, 93–103. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Ahmed, S.E. Unsteady MHD heat and mass transfer by mixed convection flow in the forward stagnation region of a rotating sphere at different wall conditions. Chem. Eng. Commun. 2011, 199, 122–141. [Google Scholar] [CrossRef]
- Eldabe, N.T.M.; Saddeck, G.; El-Sayed, A.F. Heat transfer of MHD non-Newtonian Casson fluid flow between two rotating cylinders. Mech. Mech. Eng. 2001, 5, 237–251. [Google Scholar]
- Nadeem, S.; Haq, R.U.; Akbar, N.S. MHD three-dimensional boundary layer flow of Casson nanofluid past a linearly stretching sheet with convective boundary condition. IEEE Trans. Nanotechnol. 2014, 13, 109–115. [Google Scholar] [CrossRef]
- Andersson, H.I.; Aarseth, J.B.; Dandapat, B.S. Heat transfer in a liquid film on an unsteady stretching surface. Int. J. Heat Mass Transf. 2000, 43, 69–74. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; De Ranjan, P.; Bhattacharyya, K.; Layek, G.C. Casson fluid flow over an unsteady stretching surface. Ain Shams Eng. J. 2013, 4, 933–938. [Google Scholar] [CrossRef]
- Mahdy, A.; Ahmed, S.E. Unsteady MHD convective flow of non-Newtonian Casson fluid in the stagnation region of an impulsively rotating sphere. J. Aerosp. Eng. 2017, 30, 04017036. [Google Scholar] [CrossRef]
- Bhattacharyya, K. MHD stagnation-point flow of Casson fluid and heat transfer over a stretching sheet with thermal radiation. J. Thermodyn. 2013, 2013, 169674. [Google Scholar] [CrossRef]
- Mahdy, A. Heat transfer and flow of a Casson fluid due to a stretching cylinder with the Soret and Dufour effects. J. Eng. Phys. Thermophys. 2015, 88, 927–936. [Google Scholar] [CrossRef]
- Nandy, S.K. Analytical solution of MHD stagnation-point flow and heat transfer of Casson fluid over a stretching sheet with partial slip. Int. Sch. Res. Not. Thermodyn. 2013, 2013, 108264. [Google Scholar] [CrossRef]
- Makanda, G.; Shaw, S.; Sibanda, P. Diffusion of chemically reactive species in Casson fluid flow over an Unsteady Stretching surface in porous medium in the presence of a magnetic field. Math. Probl. Eng. 2015, 2015, 724596. [Google Scholar] [CrossRef]
- Mahdy, A.; Ahmed, S.E. Unsteady MHD double diffusive convection in the stagnation region of an impulsively rotating sphere in the presence of thermal radiation effect. J. Taiwan Inst. Chem. Eng. 2016, 58, 173–180. [Google Scholar]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. Dev. Appl. Non Newton. Flows 1995, 66, 99–105. [Google Scholar]
- Choi, S.U.S.; Zhang, Z.G.; Lockwood, F.E.; Gruike, E.A. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 2001, 79, 2252–2254. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Sandeep, N. Unsteady Casson nanofluid flow over a rotating cone in a rotating frame filled with ferrous nanoparticles: A numerical study. J. Magn. Magn. Mater. 2017, 421, 216–224. [Google Scholar] [CrossRef]
- Momin, G.G. Experimental investigation of mixed convection with water-Al2O3 & hybrid nanofluid in inclined tube for laminar flow. Int. J. Sci. Technol. Res. 2013, 2, 195–202. [Google Scholar]
- Suresh, S.; Venkitaraj, K.; Selvakumar, P.; Chandrasekar, M. Synthesis of Al2O3–Cu/water hybrid nanofluids using two step method and its thermo physical properties. Colloids Surf. A Physicochem. Eng. Asp. 2011, 388, 41–48. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.; Selvakumar, P.; Chandrasekar, M. Effect of Al2O3–Cu/water hybrid nanofluid in heat transfer. Exp. Therm. Fluid Sci. 2012, 38, 54–60. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Hameed, M.S.; Sarangan, J. Turbulent heat transfer and pressure drop characteristics of dilute water based Al2O3–Cu hybrid nanofluids. J. Nanosci. Nanotechnol. 2014, 14, 2563–2572. [Google Scholar] [CrossRef]
- Mahdy, A. Simultaneous impacts of MHD and variable wall temperature on transient mixed Casson nanofluid flow in the stagnation point of rotating sphere. Appl. Math. Mech. 2018, 39, 1327–1340. [Google Scholar] [CrossRef]
- EL-Zahar, E.R.; Rashad, A.M.; Seddek, L.F. The impact of sinusoidal surface temperature on the natural convective flow of a ferrofluid along a vertical plate. Mathematics 2019, 7, 1014. [Google Scholar] [CrossRef]
- Takhar, H.S.; Chamkha, A.J.; Nath, G. Unsteady laminar MHD flow and heat transfer in the stagnation region of an impulsively spinning and translating sphere in the presence of buoyancy forces. Heat Mass Transf. 2001, 37, 397–402. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Vishnu Ganesh, N.; Abdul Hakeem, A.K.; Ganga, B. Buoyancy effect on MHD flow of nanofluid over a stretching sheet in the presence of thermal radiation. J. Mol. Liq. 2014, 198, 234–238. [Google Scholar] [CrossRef]
- Alwawi, F.A.; Alkasasbeh, H.T.; Rashad, A.M.; Idris, R. A Numerical Approach for the Heat Transfer Flow of Carboxymethyl Cellulose-Water Based Casson Nanofluid from a Solid Sphere Generated by Mixed Convection under the Influence of Lorentz Force. Mathematics 2020, 8, 1094. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).