Gas–Liquid Two-Phase Flow and Heat Transfer without Phase Change in Microfluidic Heat Exchanger
Abstract
1. Introduction
2. Experimental Part
2.1. Microfluidic Heat Exchanger Design
2.2. Experimental Rig
3. Theoretical Part
4. Results and Discussion
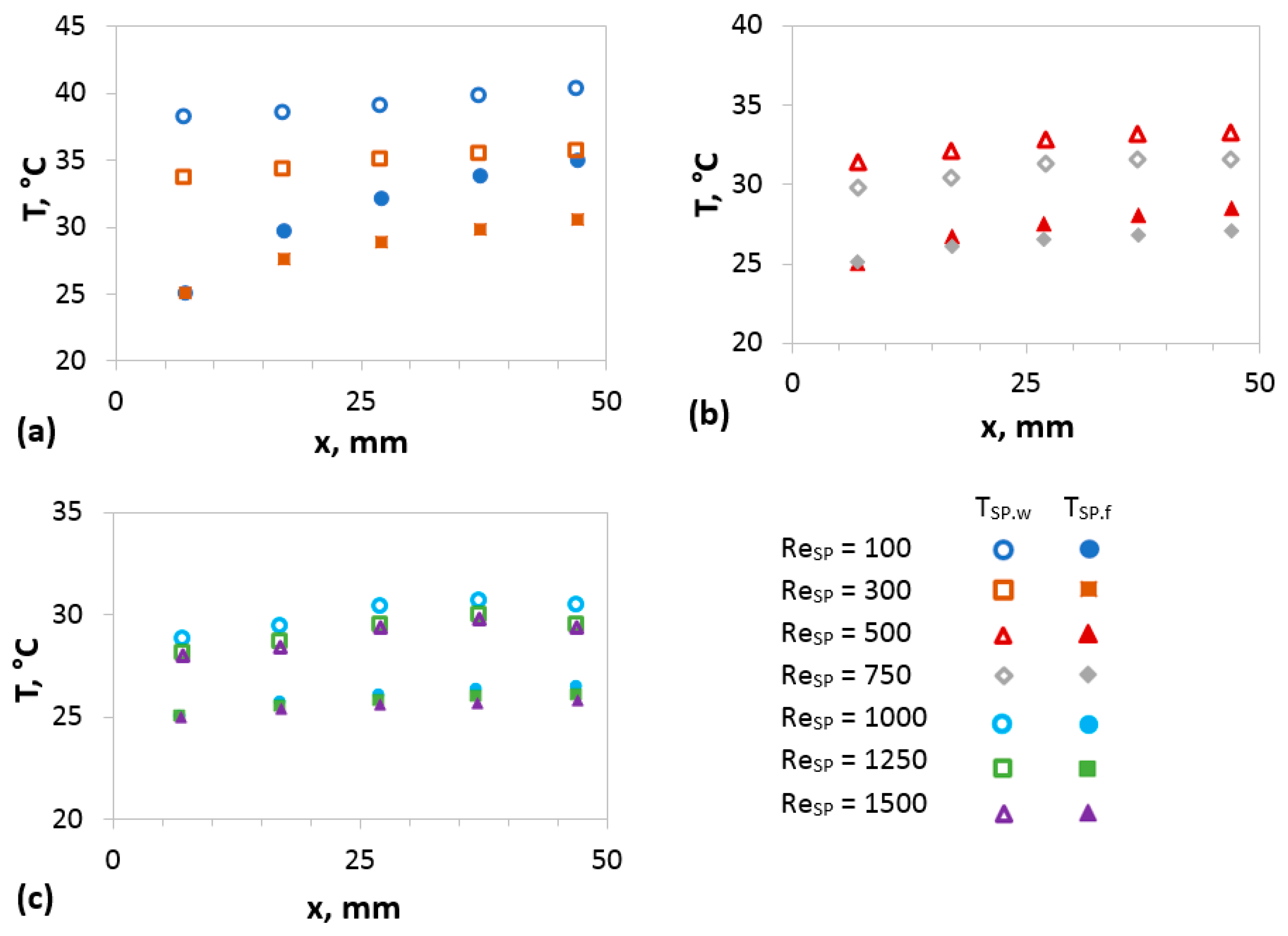
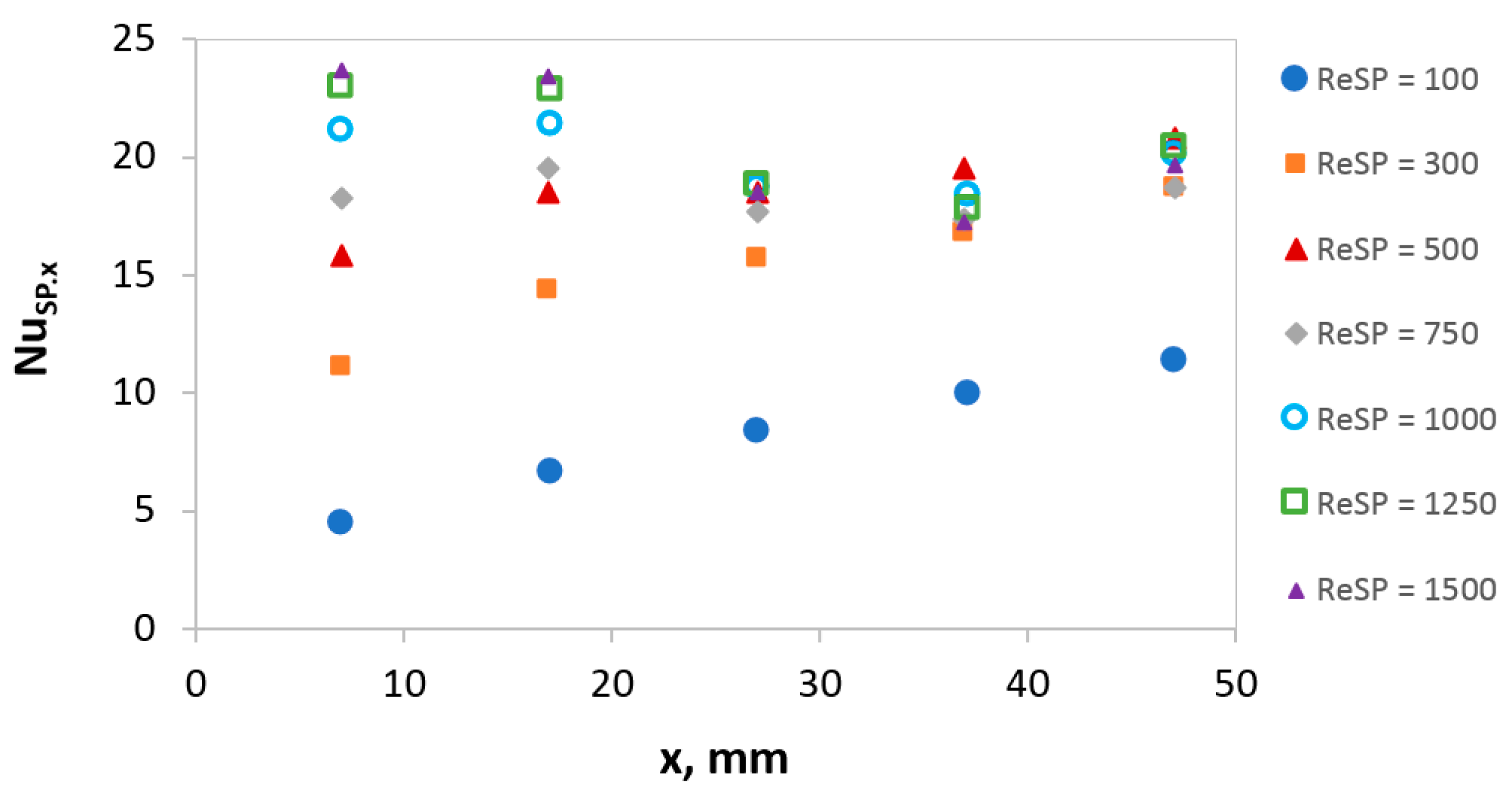
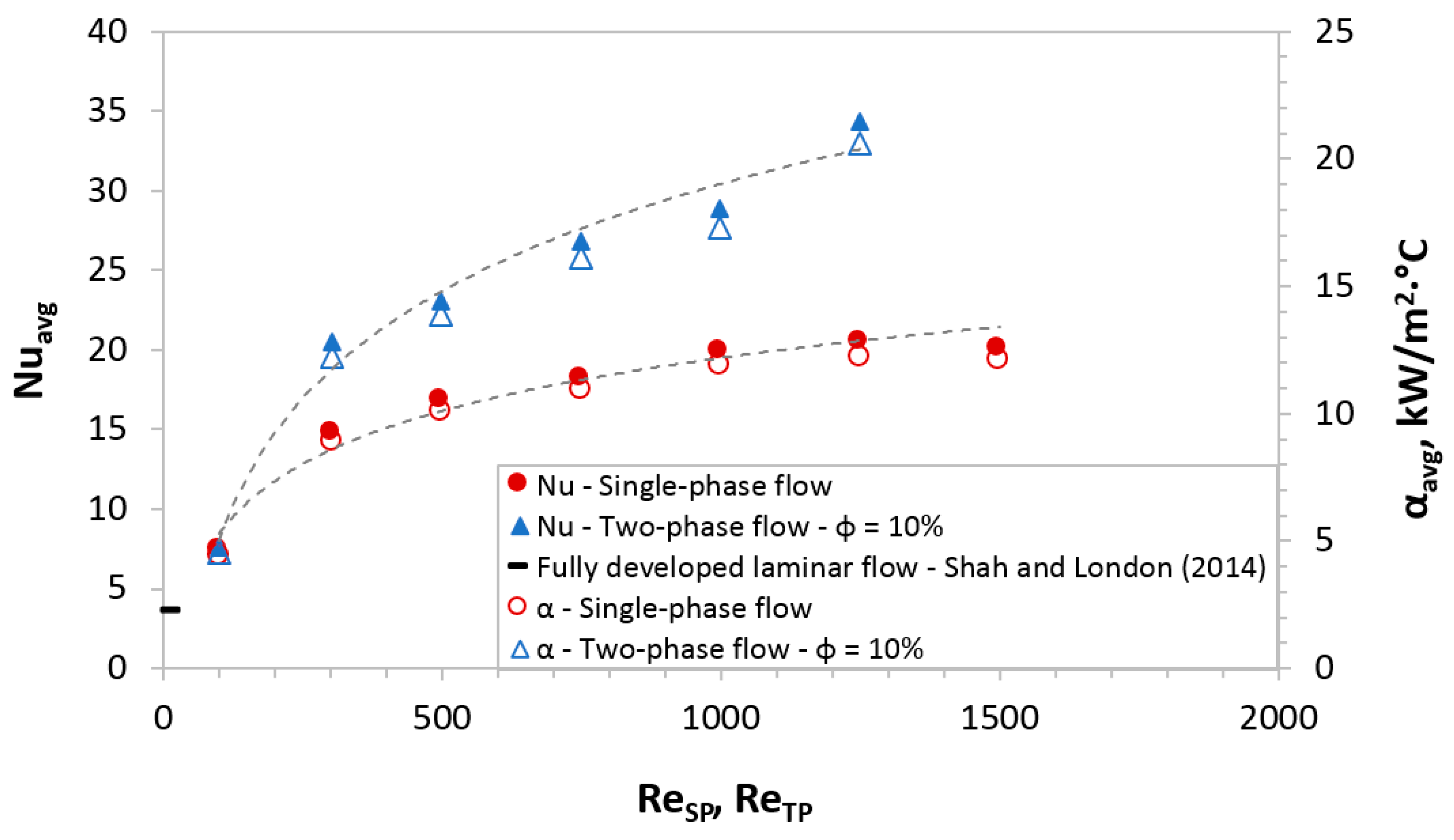
4.1. Heat Transfer in Single-Phase Flow in Microchannels
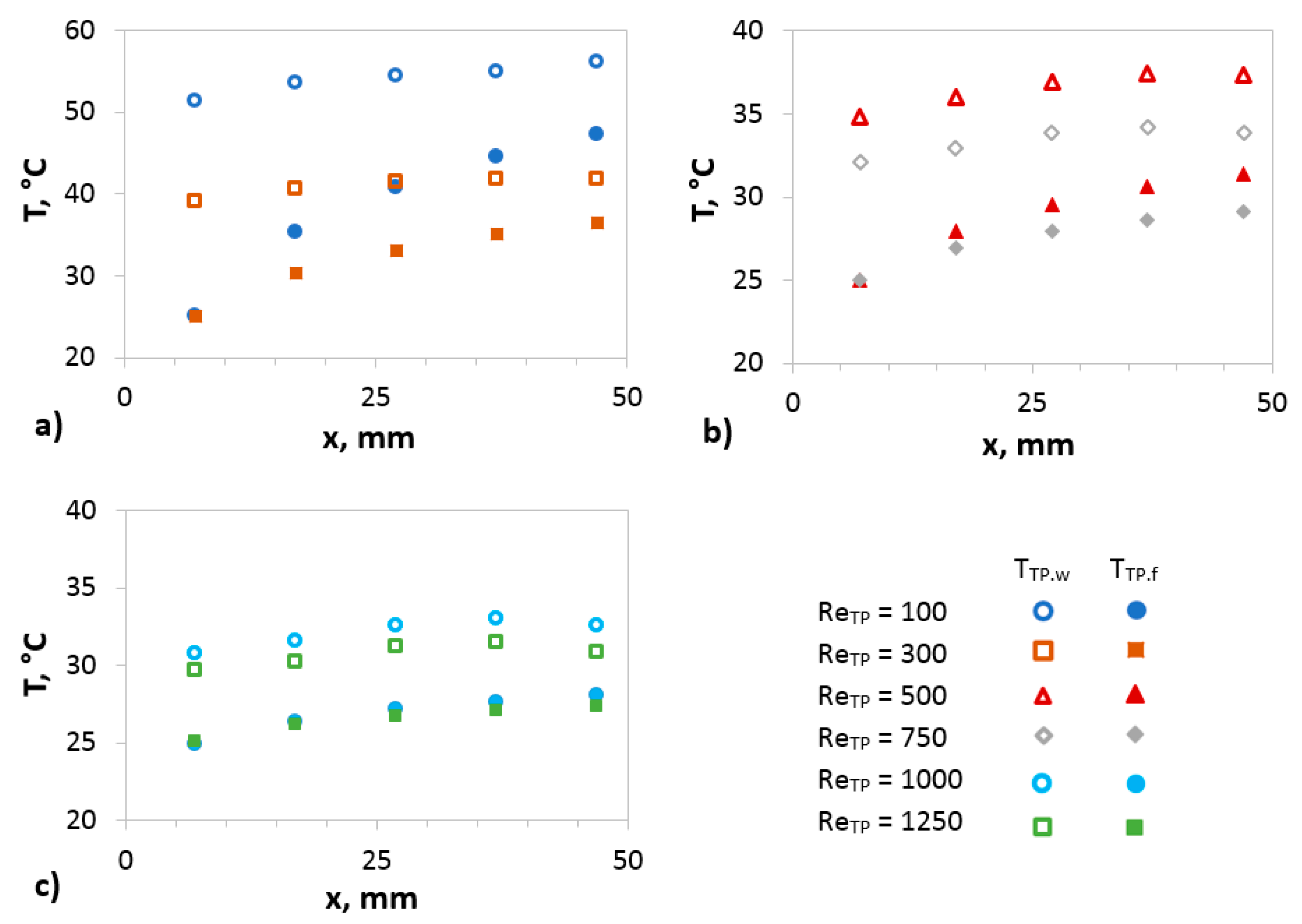
4.2. Heat Transfer in Two-Phase Flow in Microchannels
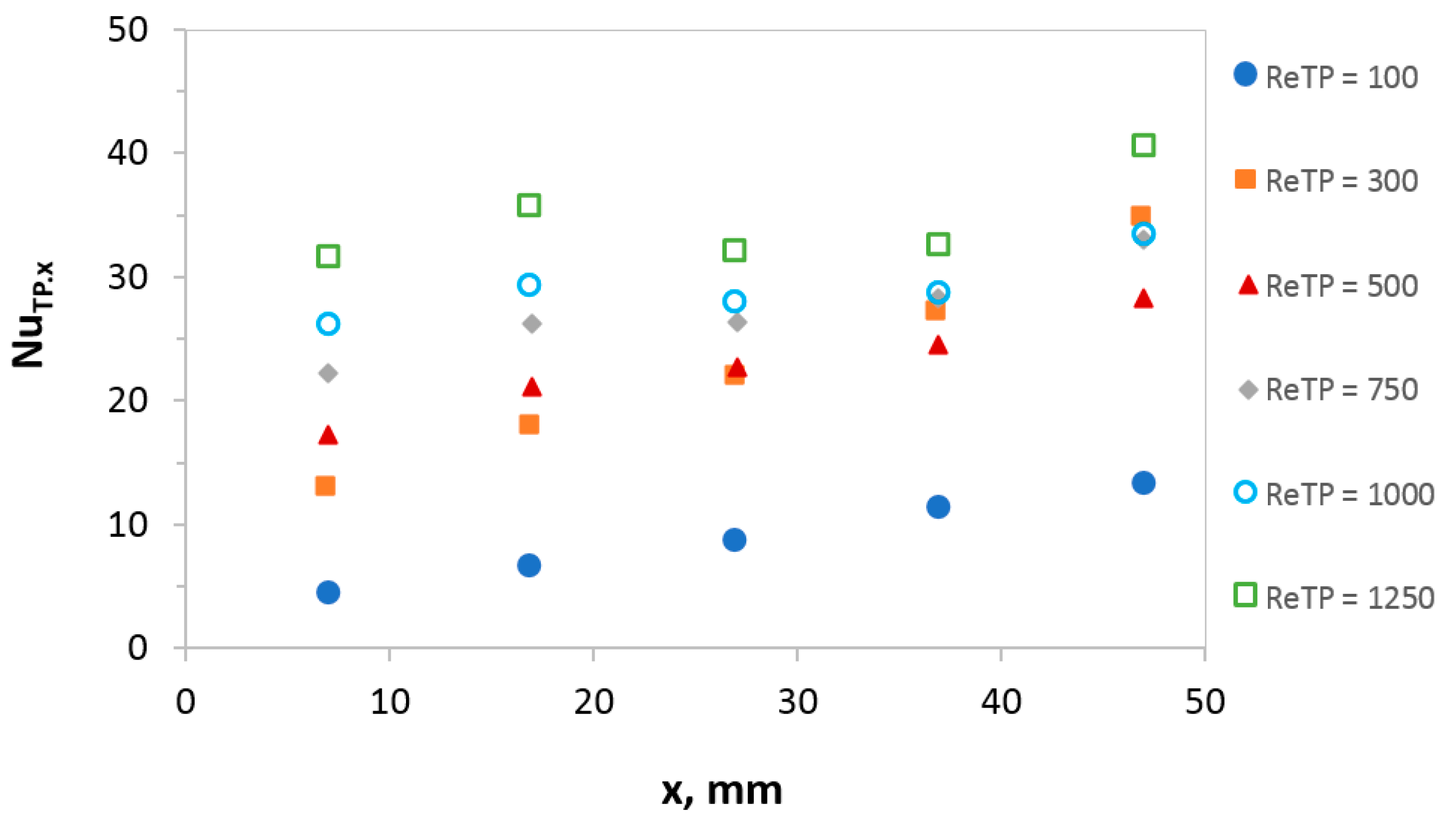
4.2.1. Influence of Reynolds Number on the Heat Transfer Efficiency in MFHE
4.2.2. Influence of Gas Hold-Up on the Heat Transfer Efficiency in MFHE
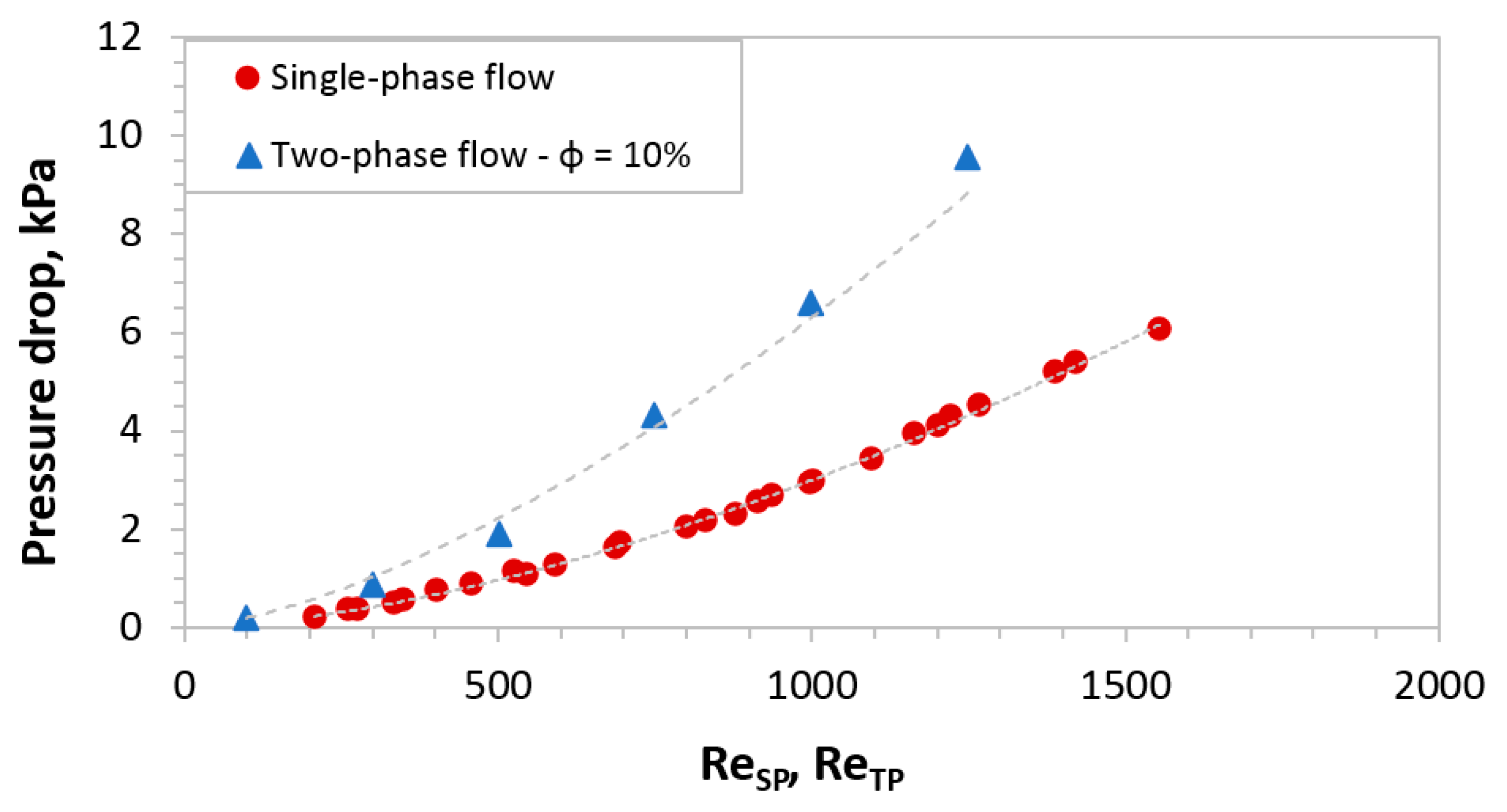
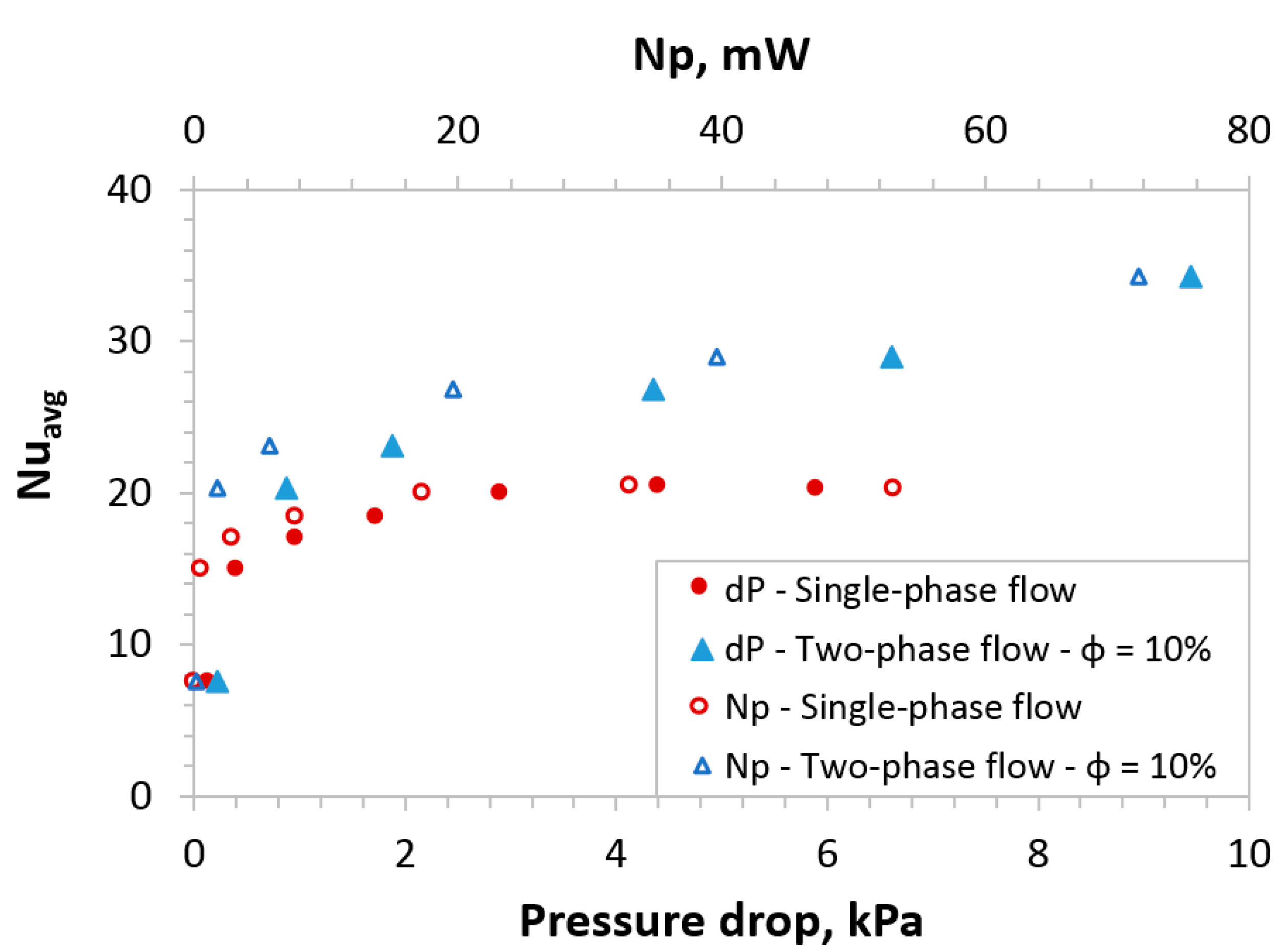
4.3. Single-Phase and Two-Phase Flow Hydrodynamics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Bar-Cohen, A.; Maurer, J.J.; Felbinger, J.G. Darpa’s intra/interchip enhanced cooling (icecool) program. In Proceedings of the 2013 International Conference on Compound Semiconductor Manufacturing Technology, CS MANTECH 2013, New Orleans, LA, USA, 13–15 May 2013. [Google Scholar]
- Karayiannis, T.; Mahmoud, M. Flow boiling in microchannels: Fundamentals and applications. Appl. Therm. Eng. 2017, 115, 1372–1397. [Google Scholar] [CrossRef]
- Lee, J.; Mudawar, I. Low-Temperature Two-Phase Microchannel Cooling for High-Heat-Flux Thermal Management of Defense Electronics. IEEE Trans. Components Packag. Technol. 2009, 32, 453–465. [Google Scholar] [CrossRef]
- Naqiuddin, N.H.; Saw, L.H.; Yew, M.C.; Yusof, F.; Ng, T.C. Overview of micro-channel design for high heat flux application. Renew. Sustain. Energy Rev. 2018, 82, 901–914. [Google Scholar] [CrossRef]
- Tuckerman, D.; Pease, R. High-performance heat sinking for VLSI. IEEE Electron. Device Lett. 1981, 2, 126–129. [Google Scholar] [CrossRef]
- Vasilev, M.; Abiev, R.; Kumar, R. Effect of microchannel heat sink configuration on the thermal performance and pumping power. Int. J. Heat Mass Transf. 2019, 141, 845–854. [Google Scholar] [CrossRef]
- Liu, H.-L.; Qi, D.-H.; Shao, X.-D.; Wang, W.-D. An experimental and numerical investigation of heat transfer enhancement in annular microchannel heat sinks. Int. J. Therm. Sci. 2019, 142, 106–120. [Google Scholar] [CrossRef]
- Kumar, R.; Yadav, V.; Abiev, R.S. Concurrent Removal of Heat Transfer and Mass Flow Rate Nonuniformities in Parallel Channels of Microchannel Heat Sink. Theor. Found. Chem. Eng. 2020, 54, 77–90. [Google Scholar] [CrossRef]
- Ansari, D.; Kim, K.-Y. Double-Layer Microchannel Heat Sinks with Transverse-Flow Configurations. J. Electron. Packag. 2016, 138, 031005. [Google Scholar] [CrossRef]
- Li, X.-Y.; Wang, S.-L.; Wang, X.-D.; Wang, T.-H. Selected porous-ribs design for performance improvement in double-layered microchannel heat sinks. Int. J. Therm. Sci. 2019, 137, 616–626. [Google Scholar] [CrossRef]
- Yan, Y.; He, Z.; Wu, G.; Zhang, L.; Yang, Z.; Li, L. Influence of hydrogels embedding positions on automatic adaptive cooling of hot spot in fractal microchannel heat sink. Int. J. Therm. Sci. 2020, 155, 106428. [Google Scholar] [CrossRef]
- Chein, R.; Chen, J. Numerical study of the inlet/outlet arrangement effect on microchannel heat sink performance. Int. J. Therm. Sci. 2009, 48, 1627–1638. [Google Scholar] [CrossRef]
- Kumar, R.; Abiev, R.; Ribatski, G.; Abdullah, S.; Vasilev, M. New Approach of Triumphing Temperature Nonuniformity and Heat Transfer Performance Augmentation in Micro Pin Fin Heat Sinks. J. Heat Transf. 2020, 142. [Google Scholar] [CrossRef]
- Vasilev, M.P.; Abiev, R.S.; Kumar, R. Effect of circular pin-fins geometry and their arrangement on the pressure drop and heat transfer in microchannel heat sink. Methods Eng. Technol. MMET 2020, 8, 60–62. [Google Scholar]
- Mudawar, I.; Bowers, M.B. Ultra-high critical heat flux (CHF) for subcooled water flow boiling—I: CHF data and parametric effects for small diameter tubes. Int. J. Heat Mass Transf. 1999, 42, 1405–1428. [Google Scholar] [CrossRef]
- Kandlikar, S.G. High Flux Heat Removal with Microchannels—A Roadmap of Challenges and Opportunities. Heat Transf. Eng. 2005, 26, 5–14. [Google Scholar] [CrossRef]
- Ma, H.; Cheng, P.; Boswell, J.A. Multiple Thermal Circuit Heat Spreader. U.S. Patent Application 13/640,758, 30 May 2013. [Google Scholar]
- Hardesty, R.E. Micro-Channel Pulsating Heat Pipe. U.S. Patent No. 8,919,426, 30 December 2014. [Google Scholar]
- Weinmueller, C.; Hotz, N.; Mueller, A.; Poulikakos, D. On two-phase flow patterns and transition criteria in aqueous methanol and CO2 mixtures in adiabatic, rectangular microchannels. Int. J. Multiph. Flow 2009, 35, 760–772. [Google Scholar] [CrossRef]
- Thorsen, T.; Roberts, R.W.; Arnold, F.H.; Quake, S.R. Dynamic Pattern Formation in a Vesicle-Generating Microfluidic Device. Phys. Rev. Lett. 2001, 86, 4163–4166. [Google Scholar] [CrossRef]
- Chen, W.; Twu, M.; Pan, C. Gas–liquid two-phase flow in micro-channels. Int. J. Multiph. Flow 2002, 28, 1235–1247. [Google Scholar] [CrossRef]
- Kreutzer, M.T.; Kapteijn, F.; Moulijn, J.A.; Heiszwolf, J.J. Multiphase monolith reactors: Chemical reaction engineering of segmented flow in microchannels. Chem. Eng. Sci. 2005, 60, 5895–5916. [Google Scholar] [CrossRef]
- Abiev, R.S.; Lavretsov, I. Intensification of mass transfer from liquid to capillary wall by Taylor vortices in minichannels, bubble velocity and pressure drop. Chem. Eng. Sci. 2012, 74, 59–68. [Google Scholar] [CrossRef]
- Abiev, R.S. Gas-liquid and gas-liquid-solid mass transfer model for Taylor flow in micro (milli) channels: A theoretical approach and experimental proof. Chem. Eng. J. Adv. 2020, 4, 100065. [Google Scholar] [CrossRef]
- Shah, R.K.; London, A.L. Laminar Flow Forced Convection in Ducts: A Source Book for Compact Heat Exchanger Analytical Data; Academic Press: Cambridge, MA, USA, 1978; ISBN 0120200511. [Google Scholar]
- Betz, A.R.; Attinger, D. Can segmented flow enhance heat transfer in microchannel heat sinks? Int. J. Heat Mass Transf. 2010, 53, 3683–3691. [Google Scholar] [CrossRef]
- Walsh, P.A.; Walsh, E.J.; Muzychka, Y.S. Heat transfer model for gas–liquid slug flows under constant flux. Int. J. Heat Mass Transf. 2010, 53, 3193–3201. [Google Scholar] [CrossRef]
- Gupta, R.; Fletcher, D.F.; Haynes, B.S. CFD modelling of flow and heat transfer in the Taylor flow regime. Chem. Eng. Sci. 2010, 65, 2094–2107. [Google Scholar] [CrossRef]
- Lee, J.; Mudawar, I. Implementation of Microchannel Evaporator for High-Heat-Flux Refrigeration Cooling Applications. J. Electron. Packag. 2005, 128, 30–37. [Google Scholar] [CrossRef]
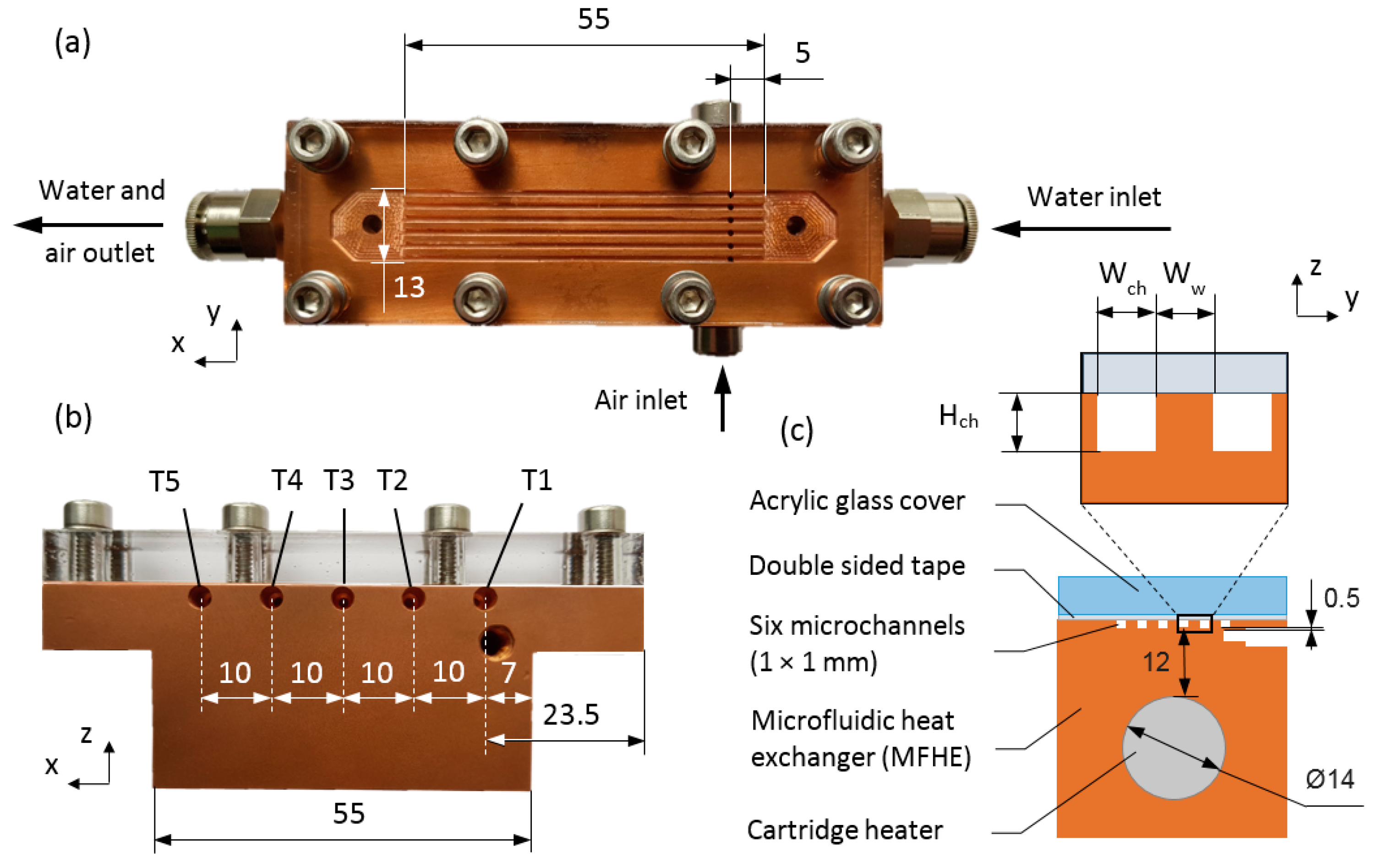






| Parameter | Lch, mm | Wch, mm | Ww, mm | Hch, mm |
|---|---|---|---|---|
| Value | 55 | 1 | 1 | 1 |
| Case | (a) | (b) | (c) | (d) |
|---|---|---|---|---|
| Gas hold-up (%) | 10 | 20 | 30 | 40 |
| Flow regime | slug | slug | slug | annular |
| Average length LB (mm) | 1.68 | 2.36 | 2.61 | – |
| Average length LS (mm) | 2.31 | 2.81 | 1.22 | – |
| Average length LUC (mm) | 3.99 | 4.17 | 3.83 | – |
(a) | (c) | |||
(b) | (d) | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasilev, M.P.; Abiev, R.S. Gas–Liquid Two-Phase Flow and Heat Transfer without Phase Change in Microfluidic Heat Exchanger. Fluids 2021, 6, 150. https://doi.org/10.3390/fluids6040150
Vasilev MP, Abiev RS. Gas–Liquid Two-Phase Flow and Heat Transfer without Phase Change in Microfluidic Heat Exchanger. Fluids. 2021; 6(4):150. https://doi.org/10.3390/fluids6040150
Chicago/Turabian StyleVasilev, Maksim P., and Rufat Sh. Abiev. 2021. "Gas–Liquid Two-Phase Flow and Heat Transfer without Phase Change in Microfluidic Heat Exchanger" Fluids 6, no. 4: 150. https://doi.org/10.3390/fluids6040150
APA StyleVasilev, M. P., & Abiev, R. S. (2021). Gas–Liquid Two-Phase Flow and Heat Transfer without Phase Change in Microfluidic Heat Exchanger. Fluids, 6(4), 150. https://doi.org/10.3390/fluids6040150







