Diffusion Mechanisms for the Occurrence of the Instability of Mechanical Equilibrium of a Ternary Gas Mixture Containing Carbon Dioxide

Abstract

Mixing of carbon dioxide dissolved in a multicomponent gas mixture at different pressures was researched. It was found that the mechanical equilibrium of the ternary gas mixture 0.4163H₂ (1) + 0.5837CO₂ (2) − N₂ (3) is violated at a pressure of p = 0.7 MPa and structured flows appear in the system. The pressure area (from 0.7 to 1.5 MPa) at which the conditions of priority transfer of components with the highest molecular weight in the mixture are realised in the system is fixed. To analyse the effect of pressure on the process of changing “diffusion–convection” modes, a mathematical model, which takes into account the kinetic features of multicomponent mixing, was applied. It was shown that the change in the modes of mass transfer is associated with a significant difference in the diffusion ability of the components. It is noted that the difference in the diffusion coefficients of components results in the nonlinearity of the concentration distribution, which leads to the inversion of the density gradient of the gas mixture, which is the cause of convective flows.

1. Introduction

Separation of substances during evaporation of solutions from a free surface, separation of vapour-gas mixtures into components with specified properties is a common process in nature and in many practical applications. Despite many researches on the study of pressure, temperature, and concentration distributions of the main mixing elements in specified technological segments, these issues require further study, including those related to the occurrence of concentration gravitational flows caused by diffusion. It should be noted that convective motions in one-component media with a monotonic dependence of density on temperature are well studied and described in [1,2,3]. In these works, a variety of approaches related to the study of natural gravitational convection in channels of various shapes were generalised. These generalisations make it possible to develop methods for determining the main parameters of heat and mass transfer connected with the properties of the substance under study, temperature head (Rayleigh number), hydraulic losses, and other factors, which allow for specific conditions to predict the modes of mixing.

Researches carried out in [4,5] showed that in the absence of an interphase boundary in the system under study, the reason for the occurrence of thermo-concentration gravitational currents is the inhomogeneity of the density of the medium caused by variations in temperature or composition. Development of convective instability depends on the mutual orientation of the density gradient and the direction of gravity. If the direction of the density gradient coincides with the direction of the gravity force, in this case a stable stratification of the medium occurs. The occurrence of convective motion in this situation is impossible. However, the extension of this approach to the case of non-isothermic binary and multicomponent mixtures showed that diffusion could have a destabilising influence on the development of convective flows in mixtures with different diffusion rates of the components [6,7,8]. The arising movement is an important mechanism for intensifying heat and mass transfer and selective separation of components [8,9].

One of the features of the researches carried out in [4,6,7,8,9] was the assumption that heat and solute act as components influencing the overall density distribution of the medium. It should be assumed that the effects of separation associated with the difference in the diffusion coefficients of the components, pressure, and composition can appear in multicomponent mixtures during isothermal mixing. The formation of density inversion, which causes gravitational convection in the isothermal case of multicomponent mixing, is probably associated with the appearance of effects that are not typical for non-isothermal diffusion. Experimental and computational theoretical researches, given in [10,11,12], showed that convective flows possibly occur in the case when the condition for a decrease in density with height is realised in isothermal multicomponent gas mixtures. In addition, the predominant transfer of the component with the highest molecular weight was recorded in [13], which is not typical for diffusion. Therefore, the solution of issues related to the study and refinement of the separation mechanisms in multicomponent gas mixtures is important for the problems of combined mass transfer.

The aim of the work is to experimentally study the change of “diffusion–convection” modes in a three-component gas mixture containing carbon dioxide at different pressures and isothermal conditions, for the situation in which the density of the mixture decreases with height. In this work, a calculation was carried out to determine the boundary of the change in the “diffusion–convection” modes. The density distribution in a vertical cylindrical channel at the transition pressure was analysed. The obtained results of the numerical research were compared with the experimental data.

2. Experimental Research

Separation of a multicomponent gas mixture 0.4163H₂ (1) + 0.5837CO₂ (2) − N₂ (3) was studied at different pressures. Numbers in front of the chemical element correspond to the initial concentration in mole fractions. The numbers in parentheses define the component numbering. 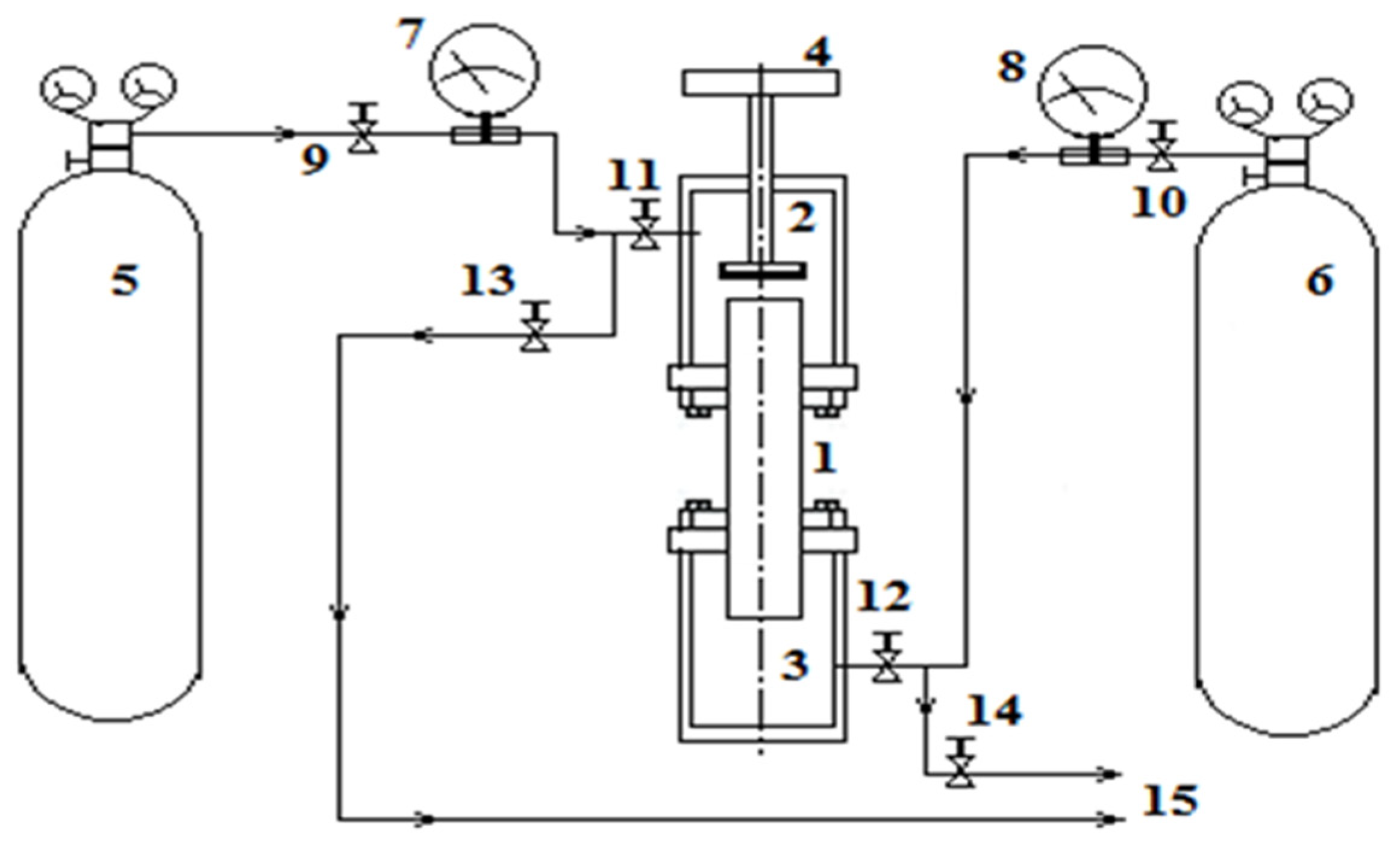Mixing of the components was carried out in a device representing a variation of the two-flask method, which is widely applied in experimental researches at various pressures and temperatures [14]. Flasks 2 and 3, connected by a vertical channel 1, represent a diffusion cell (Figure 1 [15]), in which multicomponent mixing is carried out under the given experimental conditions. The geometric characteristics of the diffusion cell are as follows: volumes of the upper and lower flasks are equal, and the amount of V_u = V_l = (55.0 ± 0.5) × 10⁻⁶ m³, the diameter and length of the vertical cylindrical channel are equal to d = (4.00 ± 0.05) × 10⁻³ m, L = (70.00 ± 0.05) × 10⁻³ m. The temperature in all experiments was constant and equal to T = 298.0 K. Mixing time for all experiments was 30 min. Experimental conditions assumed that the density of nitrogen in the lower flask 3 would be greater than the density of the mixture of hydrogen and carbon dioxide, which was located in flask 2.

The range of pressures under study is 0.2–1.7 MPa. The design features of the experimental stand determine the minimum pressure limit. The maximum pressure value is associated with the fact that at p ≥ 1.7 MPa due to a significant nonlinear dependence of the density of carbon dioxide on pressure [16] in the mixture under study, the sign of the density gradient changes, which does not correspond to the conditions of the problem. In this regard, the analysis of multicomponent mixing at pressures exceeding 1.7 MPa was not carried out. The concentration of a specified component was measured by the gas chromatography method by comparing the chromatograms by the height of the peaks of the components before and after mixing at a given pressure and temperature. For the mixture under study, the error in determining the component concentration was found by the estimation method of indirect measurement errors and was ±1%.

Experimental methods involved the implementation of certain procedures described, for example, in [17]. After evacuating the upper 2 and lower 3 flasks with the channel 1 connecting them with the valve 4 closed, the gases under study were fed into the diffusion cell. The upper flask 2 should be filled with a gas mixture of hydrogen and carbon dioxide from cylinder 5 through the opening of valves 9 and 11. Valve 13 must be closed. Pressurisation of the upper flask 2 was carried out up to the pressure of the experiment and was controlled by the manometer 7. After reaching the set pressure, valves 9 and 11 were closed. Similarly, the lower flask 3 was filled with nitrogen from the cylinder 6 through the open valves 10, 12 with the closed valve 14. The manometer 8 recorded the pressure of the experiment. Upon completion of the filling procedure, valves 10 and 12 were closed. Mixing of gases occurs when valve 4 is opened with synchronous recording of the mixing time. Valve 4 was closed at the end of the experiment. Then, the mixtures under study were fed through the outlets 15 to the chromatograph for analysis.

In the ternary mixture, the concentrations of carbon dioxide and hydrogen were directly measured. Concentration of nitrogen can be obtained from the condition of conservation number of particles ${\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{c}}_{\mathrm{i}}=1}$, where c_i is the concentration of i-th component. The experiment was repeated several times, and through averaging of the measured values, the specific value of the concentration of the components was determined. One of the main points of the experimental study is the registration of the boundary parameters that determine the transition from one state to another. Obviously, this can be done by comparing experimental data (for example, the concentrations of components) with those calculated by the Stefan-Maxwell equations [18] under the assumption of diffusion in ternary mixtures. If the experimental concentrations c_exp and the theoretical values c_theor calculated according to the Stefan-Maxwell equations are close to each other, this indicates a diffusion-mixing mode. The significant difference between the concentrations in experiment and theory shows the presence of other mixing mechanisms. The transition boundary can be fixed if we trace the ratio of the diffused concentrations of the components α = c_exp/c_theor. 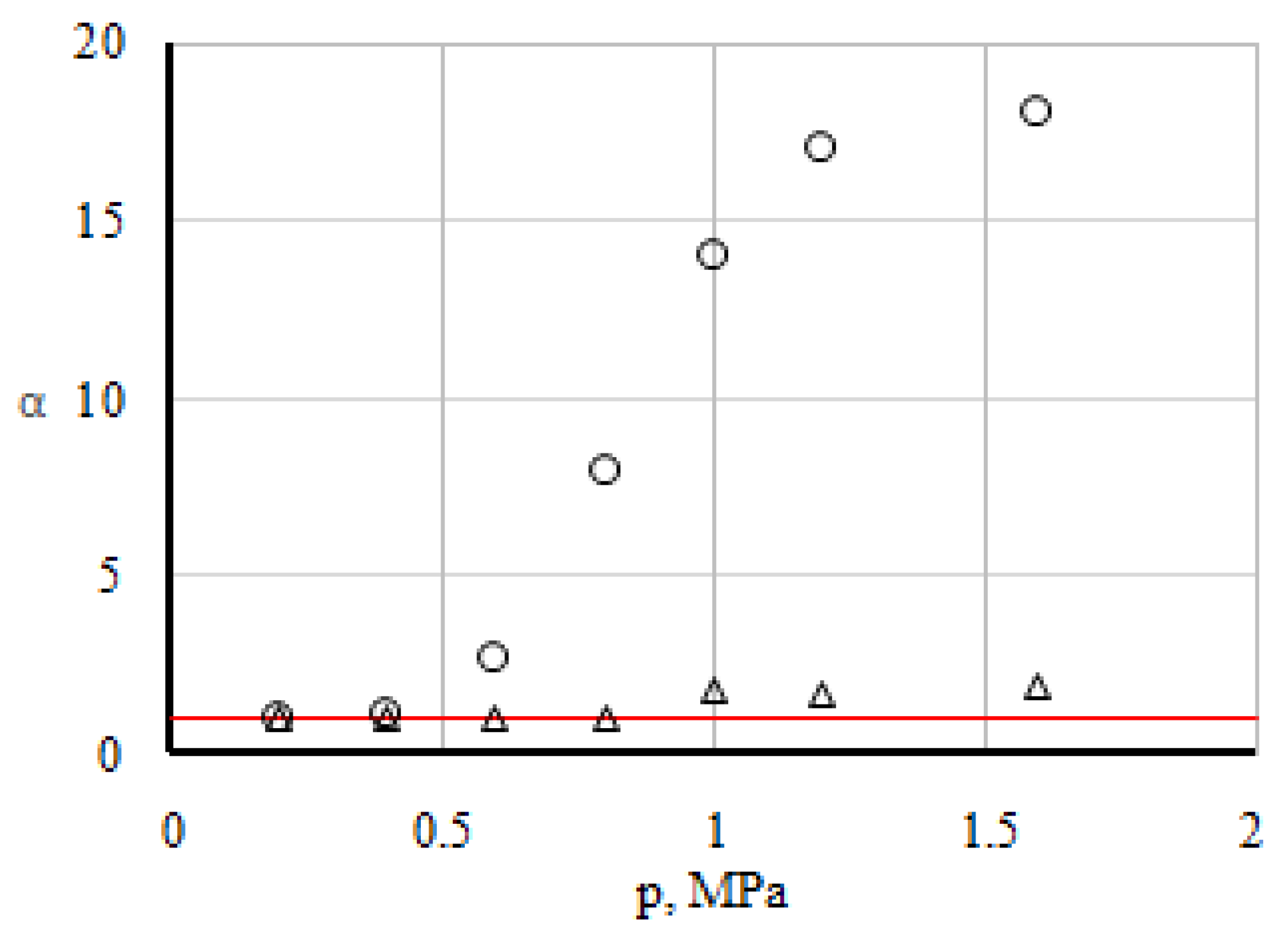Figure 2 shows the functional dependence of the dimensionless parameter α on pressure for the analysed system.

Analysis of the data, which is depicted in Figure 2, shows that diffusion is realised in the system in the pressure area of 0.1–0.6 MPa. This is evidenced by the equality to unity of the dimensionless parameter α_i for all three components of the mixture under research. Starting from a pressure of 0.6 MPa, an increase in α_i for all components in the system is fixed. Unusually significant increase was noted for CO₂ and to a lesser extent for the most diffusionally mobile H₂. Apparently, the pressure p_* ≥ 0.6 MPa provides a change in the transfer mode from diffusion to convective. Further increase of pressure leads to an increase in the intensity of convective currents. This mixing is not typical for diffusion, in which the mixing intensity decreases with increasing pressure. The highest values of α_i for CO₂ at pressures exceeding the transition pressure indicate that under the given conditions there is a predominant transfer of CO₂. With a further increase in pressure, the linear dependence is violated and the mixing intensity of the component behaves in a non-monotonic manner.

3. Determination of the Boundary of the Change of Diffusion-Convection Modes in Isothermal Ternary Gas Mixtures

Generalised description of the combined mass transfer for multicomponent mixtures seems to be a difficult problem. However, to determine the boundary of the change of “diffusion–convection” modes, some assumptions are possible. These assumptions allow performing numerical calculations to determine the characteristic features of partial mass transfer. Parameters determining the kinetic transition from diffusion to convective mixing can be obtained within the framework of stability theory [4,5] for the case of an isothermal ternary gas mixture.

In this case, the condition of independent diffusion is taken into account:

$${\displaystyle \sum _{\mathrm{i}=1}^3{\overrightarrow{\mathrm{j}}}_{\mathrm{i}}=0},{\displaystyle \sum _{\mathrm{i}=1}^3{\mathrm{c}}_{\mathrm{i}}=1}.$$

The system of equations describing convective mixing in three-component mixtures consists of the Navier-Stokes equation, the convective diffusion equation, and the equation for the conservation of the number of particles of the components [12]:

$$\begin{gathered} \mathsf{\rho }\left[\frac{\partial \overrightarrow{\mathrm{u}}}{\partial \mathrm{t}}+\left(\overrightarrow{\mathrm{u}}\nabla \overrightarrow{\mathrm{u}}\right)\right]=-\nabla \mathrm{p}+\mathsf{\eta }{\nabla }^2\overrightarrow{\mathrm{u}}+\left(\frac{\mathsf{\eta }}{3}+\mathsf{\xi }\right)\nabla \mathrm{div}\overrightarrow{\mathrm{u}}+\mathsf{\rho }\overrightarrow{\mathrm{g}} \\ \frac{\partial \mathrm{n}}{\partial \mathrm{t}}+\mathrm{div}\left(\mathrm{n}\overrightarrow{\mathrm{v}}\right)=0,\frac{\partial {\mathrm{c}}_{\mathrm{i}}}{\partial \mathrm{t}}+\overrightarrow{\mathrm{v}}\nabla {\mathrm{c}}_{\mathrm{i}}=-\mathrm{div}{\overrightarrow{\mathrm{j}}}_{\mathrm{i}}, \\ {\overrightarrow{\mathrm{j}}}_1=-\left({\mathrm{D}}_{11}^{*}\nabla {\mathrm{c}}_1+{\mathrm{D}}_{12}^{*}\nabla {\mathrm{c}}_2\right),{\overrightarrow{\mathrm{j}}}_2=-\left({\mathrm{D}}_{21}^{*}\nabla {\mathrm{c}}_1+{\mathrm{D}}_{22}^{*}\nabla {\mathrm{c}}_2\right), \end{gathered}$$

(1)

where ${\overrightarrow{\mathrm{j}}}_{\mathrm{i}}$ is the density of the diffusion flux of the i-th component, c_i is the concentration of the i-th component, p is the pressure, $\overrightarrow{\mathrm{g}}$ is the acceleration of gravity, $\overrightarrow{\mathrm{u}}=\frac{{\mathsf{\rho }}_1{\overrightarrow{\mathrm{u}}}_1+{\mathsf{\rho }}_2{\overrightarrow{\mathrm{u}}}_2+{\mathsf{\rho }}_3{\overrightarrow{\mathrm{u}}}_3}{\mathsf{\rho }}$ is the mass average velocity, $\overrightarrow{\mathrm{v}}=\frac{{\mathrm{n}}_1{\overrightarrow{\mathrm{u}}}_1+{\mathrm{n}}_2{\overrightarrow{\mathrm{u}}}_2+{\mathrm{n}}_3{\overrightarrow{\mathrm{u}}}_3}{\mathrm{n}}$ is the number average velocity of the ternary mixture, ρ is the density, and η and ξ are the coefficients of shear and bulk viscosity, respectively. Practical diffusion coefficients ${\mathrm{D}}_{\mathrm{i}\mathrm{j}}^{*}$ are determined as follows:

$$\begin{gathered} {\mathrm{D}}_{11}^{*}=\frac{{\mathrm{D}}_{13}\left[{\mathrm{c}}_1{\mathrm{D}}_{32}+\left({\mathrm{c}}_2+{\mathrm{c}}_3\right){\mathrm{D}}_{12}\right]}{\mathrm{D}},{\mathrm{D}}_{12}^{*}=-\frac{{\mathrm{c}}_1{\mathrm{D}}_{23}\left({\mathrm{D}}_{12}-{\mathrm{D}}_{13}\right)}{\mathrm{D}}, \\ {\mathrm{D}}_{22}^{*}=\frac{{\mathrm{D}}_{23}\left[{\mathrm{c}}_2{\mathrm{D}}_{13}+\left({\mathrm{c}}_1+{\mathrm{c}}_3\right){\mathrm{D}}_{12}\right]}{\mathrm{D}},{\mathrm{D}}_{21}^{*}=-\frac{{\mathrm{c}}_2{\mathrm{D}}_{13}\left({\mathrm{D}}_{12}-{\mathrm{D}}_{23}\right)}{\mathrm{D}}, \\ \mathrm{D}={\mathrm{c}}_1{\mathrm{D}}_{23}+{\mathrm{c}}_2{\mathrm{D}}_{13}+{\mathrm{c}}_3{\mathrm{D}}_{12}, \end{gathered}$$

(2)

where D_ij are the interdiffusion coefficients calculated within the framework of traditional kinetic concepts.

Equation (1) are completed by the equation of the medium state,

$$\mathsf{\rho }=\mathsf{\rho }\left({\mathrm{c}}_1,{\mathrm{c}}_2,\mathrm{p}\right),\mathrm{T}=\mathrm{const}.$$

(3)

To solve the system of Equations (1) and (3), we apply the method of small perturbations [4], which allows presenting c_i and p in the following way:

$${\mathrm{c}}_{\mathrm{i}}=\langle {\mathrm{c}}_{\mathrm{i}}\rangle +{\mathrm{c}}_{\mathrm{i}}^{/},\mathrm{p}=\langle \mathrm{p}\rangle +{\mathrm{p}}^{/},$$

where $\langle {\mathrm{c}}_{\mathrm{i}}\rangle$,$\langle \mathrm{p}\rangle$ are the constant average values taken as the point of origin, c_i^/, p^/ are the perturbed values which do not lead to a significant deviation of the density ρ^/ from the average value ρ₀. Furthermore, we assume that under the condition $\mathrm{L}\gg \mathrm{d}/2$ the differences between the perturbations of the number average $\overrightarrow{\mathrm{v}}$ and mass average $\overrightarrow{\mathrm{u}}$ velocities in the Navier-Stokes equation will be insignificant. Then, Equations (1) and (3) can be reduced to a system of equations for the perturbations undimensionalised relative to the given scales: distance d, time d²/ν, velocity D^*₂₂/d, concentration of the i-th component A_id, and pressure ρ₀νD^*₂₂/d². Finally, the system of perturbed dimensionless equations (the strokes are omitted) takes the form:

$$\begin{gathered} \mathrm{P}{\mathrm{r}}_{22}\frac{\partial {\mathrm{c}}_1}{\partial \mathrm{t}}-\left(\overrightarrow{\mathrm{u}}\overrightarrow{\mathsf{\gamma }}\right)={\mathsf{\tau }}_{11}{\nabla }^2{\mathrm{c}}_1+\frac{{\mathrm{A}}_2}{{\mathrm{A}}_1}{\mathsf{\tau }}_{12}{\nabla }^2{\mathrm{c}}_2, \\ \mathrm{P}{\mathrm{r}}_{22}\frac{\partial {\mathrm{c}}_2}{\partial \mathrm{t}}-\left(\overrightarrow{\mathrm{u}}\overrightarrow{\mathsf{\gamma }}\right)=\frac{{\mathrm{A}}_1}{{\mathrm{A}}_2}{\mathsf{\tau }}_{21}{\nabla }^2{\mathrm{c}}_1+{\nabla }^2{\mathrm{c}}_2, \\ \frac{\partial \overrightarrow{\mathrm{u}}}{\partial \mathrm{t}}=-\nabla \mathrm{p}+{\nabla }^2\overrightarrow{\mathrm{u}}+\left(\mathrm{R}{\mathrm{a}}_1{\mathsf{\tau }}_{11}{\mathrm{c}}_1+\mathrm{R}{\mathrm{a}}_2{\mathrm{c}}_2\right)\overrightarrow{\mathsf{\gamma }}, \\ \mathrm{div}\overrightarrow{\mathrm{u}}=0, \end{gathered}$$

(4)

where $\mathrm{P}{\mathrm{r}}_{\mathrm{i}\mathrm{i}}=\mathsf{\nu }/{\mathrm{D}}_{\mathrm{i}\mathrm{i}}^{*}$ is the diffusion Prandtl number, $\mathrm{R}{\mathrm{a}}_{\mathrm{i}}=\mathrm{g}{\mathsf{\beta }}_{\mathrm{i}}{\mathrm{A}}_{\mathrm{i}}{\mathrm{d}}^4/\mathsf{\nu }{\mathrm{D}}_{\mathrm{i}\mathrm{i}}^{*}$ is the partial Rayleigh number, ν is the kinematic viscosity coefficient, ${\mathsf{\beta }}_{\mathrm{i}}=-\frac{1}{{\mathsf{\rho }}_0}{\left(\frac{\partial \mathsf{\rho }}{\partial {\mathrm{c}}_{\mathrm{i}}}\right)}_{\mathrm{p},\mathrm{T}}$, ${\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}={\mathrm{D}}_{\mathrm{i}\mathrm{j}}^{*}/{\mathrm{D}}_{22}^{*}$ are the parameters determining the relationship between the practical diffusion coefficients, $\overrightarrow{\gamma }$ is the unit vector directed along the upward vertical. Parameters ${\mathsf{\tau }}_{\mathrm{i}\mathrm{j}}={\mathrm{D}}_{\mathrm{i}\mathrm{j}}^{*}/{\mathrm{D}}_{22}^{*}$ are calculated through ${\mathrm{D}}_{\mathrm{i}\mathrm{j}}^{*}$ defined by Formula (2). At p = 0.101 MPa and T = 273.0 K, the interdiffusion coefficients of gas vapour have the following values: ${\mathrm{D}}_{{\mathrm{H}}_2-{\mathrm{N}}_2}=$ 6.883 × 10⁻⁵ m²·s⁻¹, ${\mathrm{D}}_{{\mathrm{H}}_2-\mathrm{C}{\mathrm{O}}_2}=$ 5.75 × 10⁻⁵ m²·s⁻¹, ${\mathrm{D}}_{{\mathrm{N}}_2-\mathrm{C}{\mathrm{O}}_2}=$ 1.44 × 10⁻⁵ m²·s⁻¹ [16]. The calculations took into account the change of IDC (interdiffusion coefficient) as a function of pressure and temperature.

The solution of the system of Equation (4) can be conditionally divided into several stages [19]. At the first stage, taking into account the existence of three-dimensional motion in a cylindrical channel of finite length, an approximation of the velocity is written, considering all components of the vector $\overrightarrow{\mathrm{u}}$ to be nonzero. Furthermore, on the basis of the continuity equation, the ratio connecting the radial constituents of the velocity components is written. This ratio is determined through the n-order Bessel functions. At the second stage, from the first two equations of System (4), the concentrations of the components are determined by means of the Kantorovich method under boundary conditions that suggest the vanishing of perturbations of the velocity and flow of matter at the boundaries of the diffusion channel. At the third stage, the boundary of monotonic stability is determined.

On the basis of the described approach to solving the system of equations of concentration convection (4) for a vertical cylindrical channel of finite height with boundary conditions suggesting zero perturbations of the velocity and flow of matter at the boundaries, in [19] the boundary relation in terms of the Rayleigh numbers Ra_i, defining the change of “diffusion–convection” modes, was obtained in the form:

$${\displaystyle \int \overrightarrow{\mathrm{u}}{\nabla }^2\overrightarrow{\mathrm{u}}\mathrm{d}\mathrm{V}+\mathrm{R}{\mathrm{a}}_1{\mathsf{\tau }}_{11}{\displaystyle \int {\mathrm{u}}_z{\mathrm{c}}_1\mathrm{d}\mathrm{V}+\mathrm{R}{\mathrm{a}}_2{\displaystyle \int {\mathrm{u}}_z{\mathrm{c}}_2\mathrm{d}\mathrm{V}=0}}}.$$

(5)

Based on the obtained Solution (5), it is possible to determine a stability map in coordinates (Ra₁, Ra₂) and display the experimental data on it. Experimental data are restored through the partial Rayleigh numbers, for example, according to the formulas given in [19],

$$\mathrm{R}{\mathrm{a}}_1=\frac{\mathrm{g}\mathrm{n}{\mathrm{r}}^4\Delta {\mathrm{m}}_1}{\mathsf{\rho }\mathsf{\nu }{\mathrm{D}}_{11}^{*}}\cdot \frac{\partial {\mathrm{c}}_1}{\partial \mathrm{z}},\mathrm{R}{\mathrm{a}}_2=\frac{\mathrm{g}\mathrm{n}{\mathrm{r}}^4\Delta {\mathrm{m}}_2}{\mathsf{\rho }\mathsf{\nu }{\mathrm{D}}_{22}^{*}}\cdot \frac{\partial {\mathrm{c}}_2}{\partial \mathrm{z}},$$

where $\Delta {\mathrm{m}}_1={\mathrm{m}}_1-{\mathrm{m}}_2$, $\Delta {\mathrm{m}}_2={\mathrm{m}}_2-{\mathrm{m}}_3$, m_i is the molecular mass of i-th component, $\mathrm{n}=\mathrm{p}/{\mathrm{k}}_{\mathrm{B}}\mathrm{T}$, and then represented on the coordinate plane (Ra₁, Ra₂). Zero density gradient line, the position of which is determined by the following equation

$${\mathsf{\tau }}_{11}\mathrm{R}{\mathrm{a}}_1=-\mathrm{R}{\mathrm{a}}_2,$$

(6)

is also drawn on the cartogram (Ra₁, Ra₂).

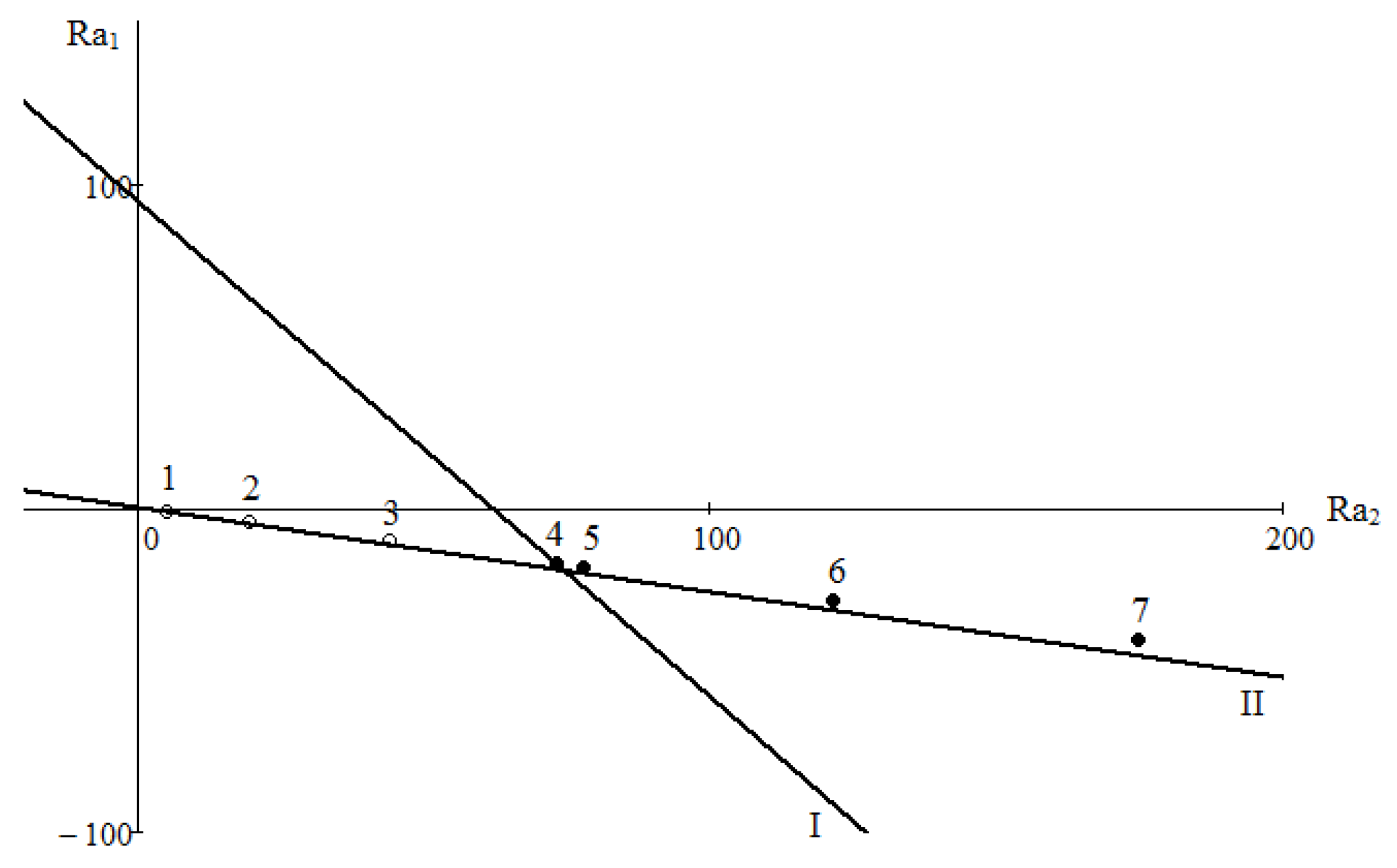
Crossing of the boundary line defined by Equation (5) with axes Ra₁ and Ra₂ allows obtaining two critical Rayleigh numbers. Results of a numerical study of the system 0.4163H₂ + 0.5837CO₂ − N₂ are shown in Figure 3. It is known from the experiment which mixing mode is realised under given conditions. Let us agree that for diffusion we use the notation in the form of lightened points «o». The mode, where mixing is determined by the convective perturbations, is denoted by the dark symbol «●». A collection of points on the plane (Ra₁, Ra₂) determines the correspondence of the observed mixing modes to the calculated boundary relations. Critical Rayleigh numbers, which determine the stability boundary, have the following values: Ra₁ = 94.4773 and Ra₂ = 61.6623. In a range of pressures of 0.2 to 0.6 MPa, the system under consideration is in the diffusion area, which is in agreement with the experimental data shown in Figure 2. Numerical calculations showed that the transition to the convective area occurs at a pressure of 0.775 MPa (point 4). Based on the presented comparison, it can be concluded that concentration convection in the system under study can occur under conditions in which the density of the mixture decreases with height.

The possibility of the system transition from the area, where diffusion mechanisms operate to the area, where the conditions of mechanical equilibrium are violated is associated with the existence of density inversion in the vertical channel due to a significant difference in the diffusion coefficients of the components.

Density distribution in the diffusion channel plays one of the important roles in creating conditions for the gravitational convection, therefore, it is necessary to analyse the behaviour of the total density of the gas mixture and concentrations of the components. For this, it is necessary to solve the system of equations of stable three-component diffusion for a closed system of two flasks connected by a vertical channel:

$$\begin{gathered} \mathrm{p}=\mathrm{const},\mathrm{t}=\mathrm{const}, \\ {\displaystyle \sum _{\mathrm{i}=1}^3{\mathrm{c}}_{\mathrm{i}}=1;}\mathrm{n}{\displaystyle \sum _{\mathrm{i}=1}^3{\mathrm{c}}_{\mathrm{i}}{\overrightarrow{\mathrm{u}}}_{\mathrm{i}}=0}, \\ \mathrm{div}(\mathrm{n}\cdot {\mathrm{c}}_{\mathrm{i}}\cdot {\overrightarrow{\mathrm{u}}}_{\mathrm{i}})=0,\mathrm{i}=1,2; \\ {\displaystyle \sum _{\mathrm{j}\ne \mathrm{i}}\frac{{\mathrm{c}}_{\mathrm{i}}\cdot {\mathrm{c}}_{\mathrm{j}}}{{\mathrm{D}}_{\mathrm{i}\mathrm{j}}}\cdot ({\overrightarrow{\mathrm{u}}}_{\mathrm{i}}-{\overrightarrow{\mathrm{u}}}_{\mathrm{j}})}=-\mathrm{grad}({\mathrm{c}}_{\mathrm{i}}),\mathrm{i}=1,2;\mathrm{j}=1,2,3. \end{gathered}$$

(7)

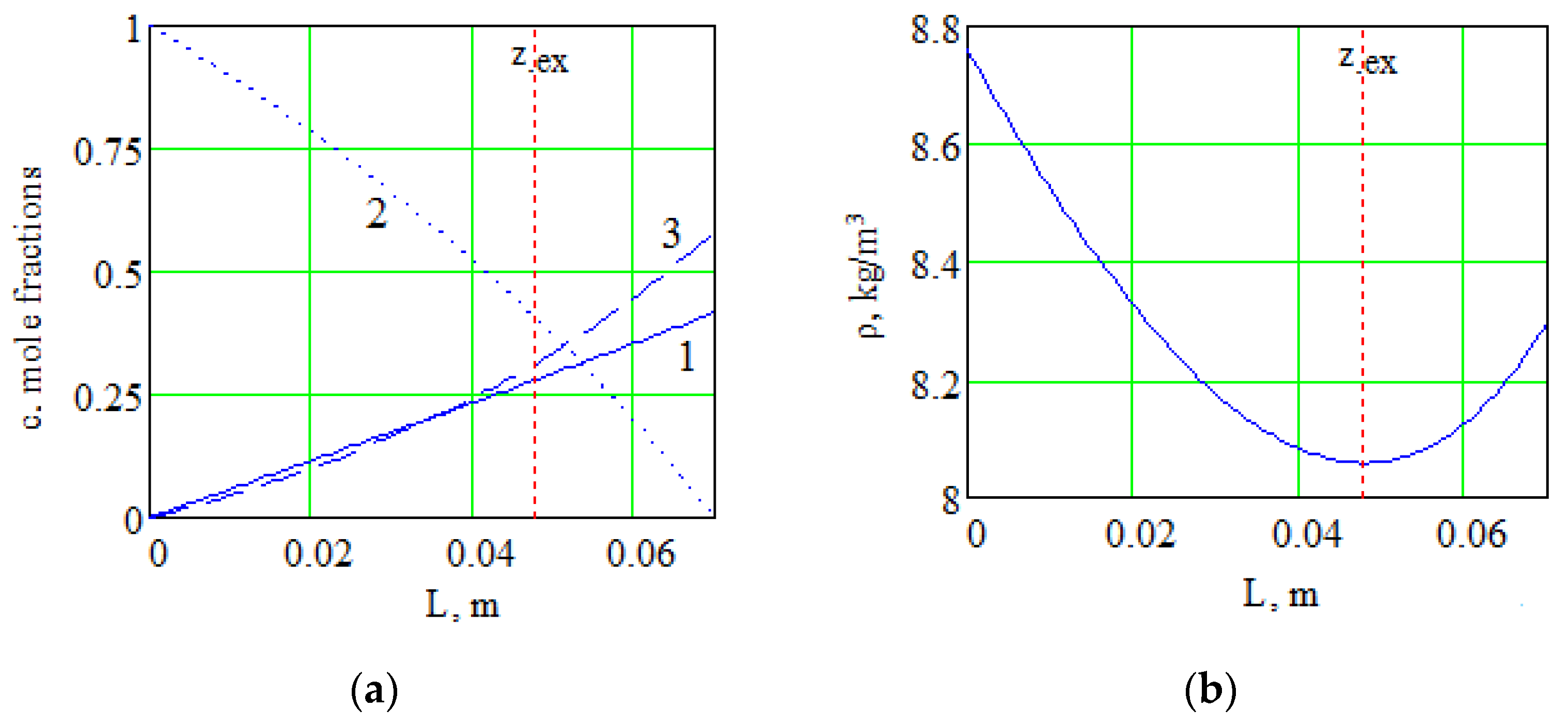
Solution of the system of Equation (7) numerically makes it possible to obtain the distribution of component concentrations along the diffusion channel and the distribution of the mixture density. Figure 4 shows the distribution of the density of the mixture under consideration and the concentration of components along the length of the channel at a pressure of 0.775 MPa, which determines the transition of the system from one kinetic regime to another one. The value of the extremum coordinate in the channel corresponds to z_ex = 0.0478 m.

According to Figure 4a, for the heaviest in density component of the mixture (carbon dioxide), a nonlinear concentration distribution is observed along the diffusion channel. The appearance of nonlinearity in the concentration profile of the heavy component is due to the fact that a significant difference in the interdiffusion coefficients (${\mathrm{D}}_{12},{\mathrm{D}}_{13}\gg {\mathrm{D}}_{23}$) leads to a diffusion “lock” of carbon dioxide. The diffusion “lock” is conditioned by the fact that a more mobile gas (hydrogen) diffusing into the pure component (nitrogen) causes the appearance of a diffusion baroeffect. In this case, the diffusion baroeffect generates a hydrodynamic flow. The intensity of this flow is such that the counter diffusion flow of the heavy component (carbon dioxide) cannot overcome this flow, i.e., a decrease in the flux of the heavy component is observed. This state of the component with the highest molecular weight continues until the concentration of the components in the flasks is redistributed to such values that the magnitude of the baroeffect cannot generate a hydrodynamic flow of the required intensity to keep the heavy component in a locked state. Thus, a significant difference in the interdiffusion coefficients of the components creates conditions for a nonlinear distribution of the concentration of the heaviest component in terms of density. Nonlinearity of the concentration distribution of the component with the highest molecular weight results in the inversion of the density gradient of the gas mixture (Figure 4b), which is the reason for the occurrence of convective flows in the gas mixture under consideration.

4. Conclusions

Experimental data obtained for the system 0.4163H₂ (1) + 0.5837CO₂ (2) − N₂ (3) indicate that in the system under consideration at a pressure of 0.6 MPa, a transition from a stable diffusion process to an unstable one is observed. The increase of pressure in the experiment creates conditions under which the diffusion tendency of the process is disturbed and convection occurs. The behaviour analysis of the dimensionless parameter α on pressure showed that in the pressure range from 0.6 to 1.5 MPa, the largest transfer for the heavy component (carbon dioxide) is observed. This behaviour of the concentration of carbon dioxide on pressure indicates an increase in the intensity of convective currents. The performed stability analysis made it possible to determine the pressure area (p = 0.775 MPa), where the conditions for the occurrence of convective flows and the priority transfer of carbon dioxide are realised. The obtained distributions of component concentrations and the average density of mixture for the system under consideration have shown a significant role of the inversion of density gradient in the occurrence of convective flows. For the mixture under consideration and the given geometry of the diffusion channel, the inversion of the density gradient is observed at the extreme coordinate z_ex = 0.0478 m. The discovered mechanisms of the predominant transfer of carbon dioxide in gas mixtures can be used in the technological processes associated with the removal of greenhouse gases. Further experimental studies will be aimed at establishing the boundaries of the transition from diffusion to convection in non-isothermal conditions, in vertical and inclined channels of various geometries. Theoretical research involves the study of developed convective mixing and the determination of the boundaries of stability of various modes of motion.