Abstract
Simulations of fluid flows at the nanoscale feature massive data production and machine learning (ML) techniques have been developed during recent years to leverage them, presenting unique results. This work facilitates ML tools to provide an insight on properties among molecular dynamics (MD) simulations, covering missing data points and predicting states not previously located by the simulation. Taking the fluid flow of a simple Lennard-Jones liquid in nanoscale slits as a basis, ML regression-based algorithms are exploited to provide an alternative for the calculation of transport properties of fluids, e.g., the diffusion coefficient, shear viscosity and thermal conductivity and the average velocity across the nanochannels. Through appropriate training and testing, ML-predicted values can be extracted for various input variables, such as the geometrical characteristics of the slits, the interaction parameters between particles and the flow driving force. The proposed technique could act in parallel to simulation as a means of enriching the database of material properties, assisting in coupling between scales, and accelerating data-based scientific computations.
1. Introduction
It is a fact that the study of physical phenomena and the extraction of material properties near the atomic scale have matured with aid of the various computational techniques during recent decades, along with experimental efforts that validate fundamental knowledge. Although it remains a challenge to fabricate devices at the nanoscale [1], experimental nanofluidics have suggested the construction of nanodevices for DNA applications [2], charge-sensitive biosensing [3], nanofilters, filtration membranes and desalination [4,5], to name a few. Continuum theory may be sometimes accurate in calculating bulk fluid properties; however, in cases where wall/fluid interaction becomes significant, bulk description of the fluid is not valid, and molecular dynamics (MD) simulations are incorporated to describe the flow behavior [6].
Apart from static properties, such as density, velocity or temperature distribution, the transport properties of fluids, e.g., the diffusion coefficient, shear viscosity and thermal conductivity, that control the rate of mass, momentum and heat transfer, are also affected in confined space [7,8,9]. Simulation of Poiseuille-like flows in nanochannels has been a popular choice among researchers to investigate fluid flows at the nanoscale, along with experiments, where possible [10]. Surface topology, atomic, thermal or geometrical roughness [11] and wall material properties such as particle mass and degree of wettability [12] result in density inhomogeneity near the surface [13]; the overall particle dynamics were found to slow down [14] and slip lengths arise that violate the no-slip assumption from the macroscale [15].
Even though simulations are applicable from nano- to micro-scale, for systems containing some millions of particles, there are cases where the underlying physics would necessitate extreme computational load and effort. In the new computational era, machine learning (ML) has arisen as an efficient alternative technique to classical physical problems. The statistical nature of ML, based on its implementation simplicity, has favored a unique development and made it possible to predict material properties, overcoming long simulation processes. For example, the concept of physics-informed neural networks (PINN) has been introduced as a class of universal function approximators, capable of encoding the underlying physical laws behind a given dataset [16]. For most cases, ML approaches have been exploited to predict and develop force fields for a wide range of solid and liquid materials, with accuracy comparable to first principles [17,18,19,20].
Moving to higher space and time dimensions, it is of importance to create a database of training data so that various ML models can be tested. Artificial neural network (ANN)-based regression models have been found to learn and predict features associated with density profiles of ionic liquids, and the predictions lie in agreement with the results from MD simulations [21]. In [22], MD results are fed into a kernel ridge regression process and the model seems able to reproduce the radial distribution function, pressure and internal energy of a Lennard-Jones (LJ) fluid with increased accuracy. There may be cases where calculation of material properties with empirical relations, such as diffusion coefficients, may require tuning of a number of adjustable parameters that increase the computational complexity, and ML methods could be easier to adopt. In [23], diffusion rates for an LJ fluid are extracted with the use of Random Forest (RF) decision trees and ANNs. The accuracy of the method depends both on the number and the relevance of the samples. Utilization of regression methods has been also incorporated to recreate linear equations from large science and engineering datasets [24].
Inspired by the current trend of embedding ML algorithms in physics-related problems, this work investigates the possibility of predicting useful material properties with the aid of ML techniques. The fluid flow of a simple Lennard-Jones liquid in nanoscale slits of various dimensions and interaction parameters are exploited to create a parametric database to be fed into a regression-based system. The desired outputs include the widely used transport properties of fluids, e.g., the diffusion coefficient, shear viscosity and thermal conductivity, and the average velocity across the slit. It is shown that, even with a relatively small but characteristic set of training points, accurate results are obtained. We believe that providing ML-predicted values for the aforementioned transport properties in various simulation conditions is of paramount importance, since their calculation demands computationally intensive simulations and significant post-processing effort. However, we are still far from replacing methods of physics-based simulations such as classical or ab initio MD, which have been extensively tested during recent decades and have been proven to verify analogous experimental results, leading manufacturing processes at small scales. By combining simulation results and ML-based predictions in cases where missing data among various scales exist, when appropriate, we believe that it is possible to build a material properties database to be used for various physics calculations [25].
2. Materials and Methods
2.1. System Model
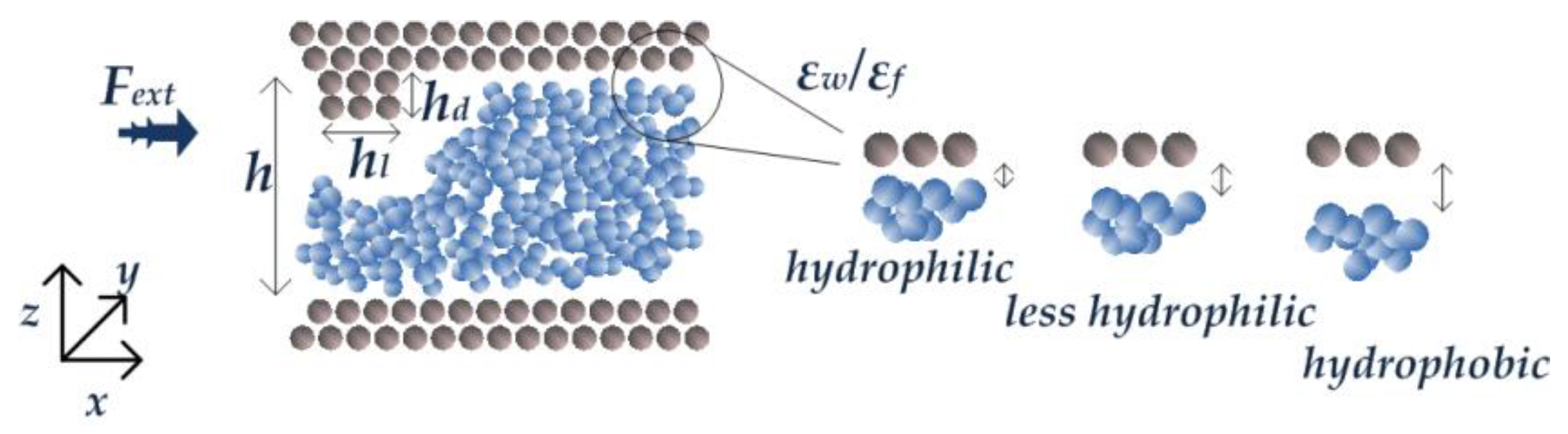
The generation of datasets to be used for training the ML model came both from simulations of our previous works and relative literature datasets. As far as our generic system model is concerned, a Lennard-Jones (LJ) monoatomic liquid is flowing between two infinite solid walls, which can be flat or grooved (Figure 1). Periodic boundary conditions are considered in x- and y-directions. The distance between the two walls in the z-direction is h, while groove height and length are hg and hl, respectively. Fluid/fluid, wall/fluid and wall/wall interactions are described by the Lennard-Jones (LJ) 12-6 potential
with a cut-off radius rc = 2.5σ. The values of the LJ parameters σ and ε and the masses of the particles were chosen to correspond to argon (Ar) in liquid state, i.e., σf = σw = 0.3405 nm (w: wall; f: fluid), and = 39.95 a.u. The system was simulated for different wall/fluid interaction energy ratios, , which is analogous to surface wettability (hydrophobic when and hydrophilic when ; see [26] for details).
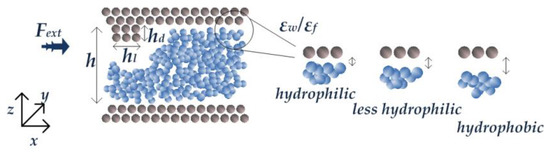
Figure 1.
Channel model, with y-direction normal to the page, where is the driving force applied in x-direction, the channel height is , the length of the grooves is and the height is . The ratio of wall-to-fluid interaction defines how close fluid atoms approach the wall.
A flow originates due to the application of an external force equally applied to all fluid particles, while the system temperature remains constant through the application of Nosé–Hoover thermostats in the NVT ensemble. Depending on the simulation, various time steps have been considered. In most cases, each simulation begins with an NVE equilibration stage; at the second stage, fluid particles attain random velocities and, finally, consecutive NVT simulations are performed to provide simulation outputs, each one for at least 20 ns total time, which are averaged to provide the final parameter value.
To understand the complexity of MD simulations, we have to keep in mind that at each time step, the interactions of all atoms are calculated, and then, the atoms are moved to their next positions by incorporating the resulting forces. By using atom positions and velocities during the simulation, one can obtain several material properties through appropriate relations. The relations used to extract the three transport properties of fluids investigated, i.e., the diffusion coefficient, D, shear viscosity, η, and thermal conductivity, k, are given in Appendix A. There is a strong effect of the walls on fluid flows in small dimensions; however, all properties approach their respective bulk values as the channel width increases (e.g., for the argon case, h > 20σ) [27]. Calculations arise from tracking-down of the microscopic state of the system being simulated and demand time-consuming calculations to achieve satisfying accuracy. Specifically, for the calculation of shear viscosity and thermal conductivity, precise and long simulations are needed in order to obtain statistically significant and convergent values. Thus, having the alternative to predict them with ML techniques would be an asset.
2.2. Machine Learning
Machine learning is a subfield of Artificial Intelligence (AI) that involves the use of statistical methods to investigate and construct algorithms that are trained on data inputs and make predictions for data outputs. The algorithms inferred operate by building a model from example inputs, follow a decision process and provide predictions, which are usually verified by the same input dataset. Estimating an output from an input dataset is called regression, a type of supervised learning in machine learning. Learning corresponds to adjusting the parameters so that the model makes the most accurate predictions on the data [28].
In a simple regression model, if is the predicted variable, is the input variable, is the bias term and is the weight of the variable, then:
For a set of n independent input variables (e.g., the regressor), the multiple linear regression model is:
In the above expression, are a set of unknown parameters, representing the impact of the respective independent inputs on the dependent variable, and and the bias terms which equal the unknown error imposed in the model.
A useful metric for the success of the predicted value over the real value is the root mean square error (RMSE). It is given by:
The mean square error (MSE) is given by:
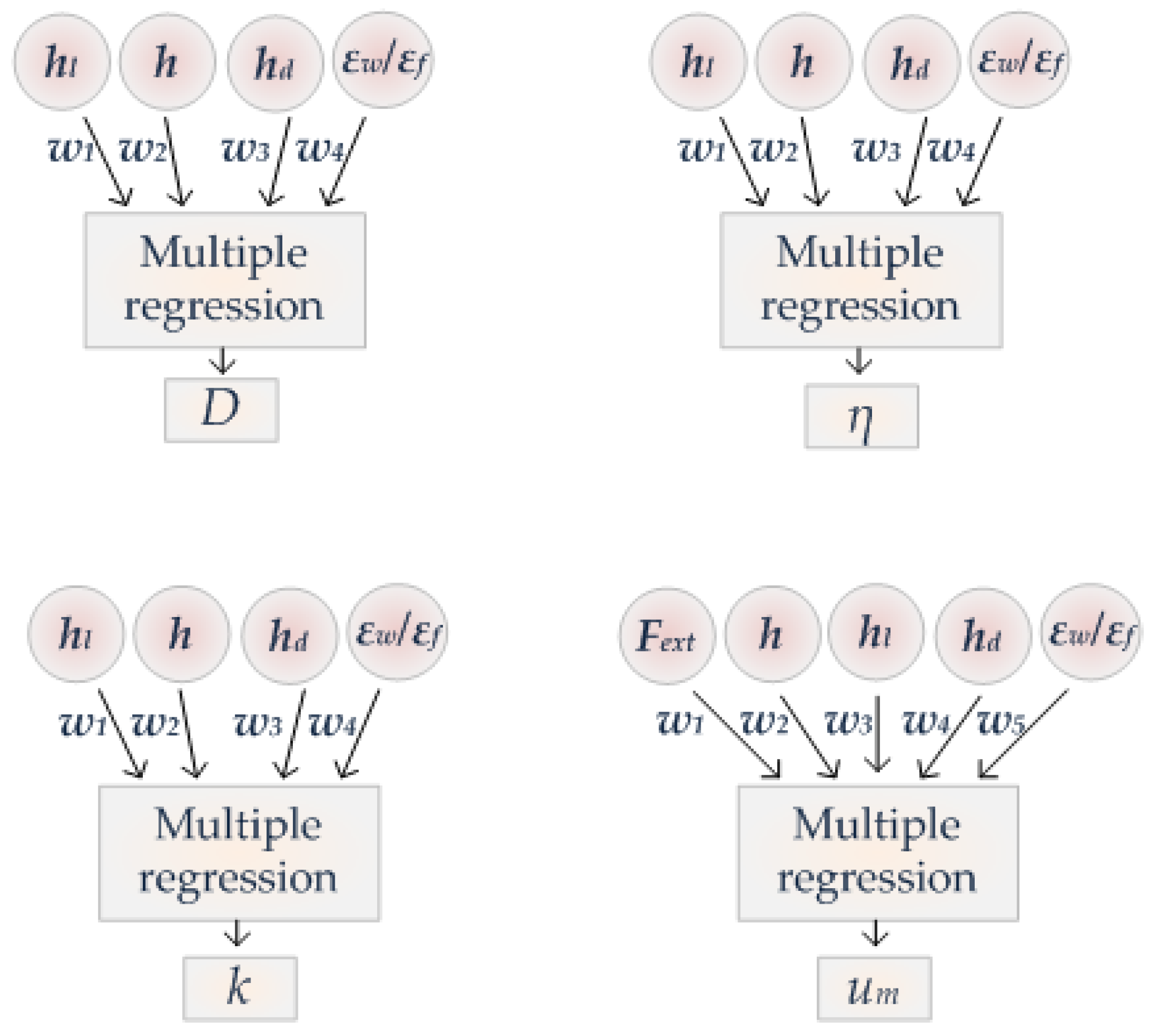
The model investigated in this work is graphically presented in Figure 2. The algorithm was written in Python, with functions employed from the scikit-learn library [29]. There are five inputs fed in the ML algorithm; the external force , the channel height , the length percentage , the height percentage of the grooves (if they exist) and the ratio of wall-to-fluid interaction . The algorithm is expected to estimate the weight of each input and its impact on each one of the four independent outputs, the diffusion coefficient D, the shear viscosity η, the thermal conductivity k and the average channel velocity .
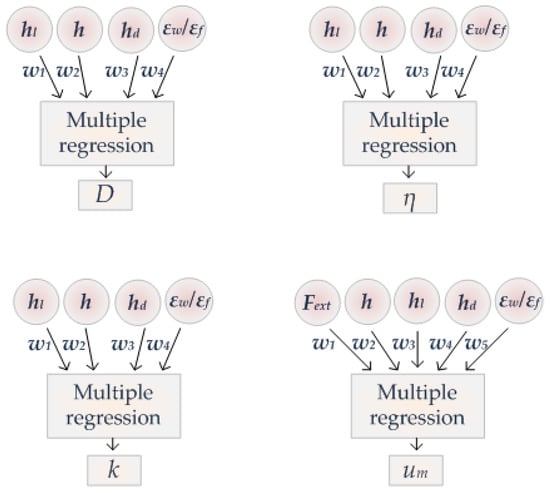
Figure 2.
Machine learning (ML) multi-regression diagram. Outputs are not correlated to each other and are derived from a different ML network.
The choice of these input parameters was made because relevant simulation evidence supports the assumption that they are significant in affecting most flow and transport properties in nanochannels [9,21,30,31]. With , and being the geometrical characteristics of the channels, affecting atomic interactions and being the main factor defining the Reynolds number, we believe that we cover a wide range of simulation cases. The external driving force is considered only for the training and prediction of ; it has no significant effect on the three transport properties D, η, and k [7], at least in the range of forces studied so far. Furthermore, one could also consider the system temperature T, the average fluid density ρ, the LJ parameter σ, the particle mass m or the surface stiffness K as parameters affecting the flow in nanochannels [26,30]. Nevertheless, the simulation complexity would increase and data from the literature would be hard to obtain.
2.3. Dataset Creation
An extensive literature search was performed to employ simulation data to train and test the model, along with our in-house simulation data. This is a non-trivial task since the obtained data should be in accordance with our input data. Therefore, we had to be careful with what values we could use from the vast database of MD papers found in the literature. It must be clarified that although data from our own simulations have been extracted under the same conditions, data from the literature may differ. For example, different types of thermostats may have been used, or different simulation parameters, such as the set temperature or time step, fluid and wall density, the wall spring constant K that keeps wall atoms around their original positions, etc. However, we believe that these differences may only have a small effect on the accuracy of the model, and they can still be incorporated to quantitatively verify our model.
Table 1 presents the literature sources and the types of data incorporated to create the dataset. From each of these sources, only values corresponding to similar simulation conditions were kept. Each number under the output properties denotes the number of points extracted from the respective reference. The dataset may seem small; however, it is regarded as a representative set of parameters that could represent simulation results in a qualitative manner, while more data points are to be added in a future work.

Table 1.
Dataset sources and number of points incorporated.
2.4. Data Preprocessing
During the process of producing output data in our simulation system, each independent input variable (, , , and ) covers a range of values while the four others are kept constant. The range of input values for the simulations is tabulated in Table 2.

Table 2.
Range of input data in reduced Lennard-Jones (LJ) units.
The complete dataset was divided into training points to feed the model and testing points to compare with predicted data, in a percentage of 80/20, respectively. Training points can be selected randomly or from carefully selected data points. For the dataset employed in this work, training points were chosen randomly and cover the entire dataset length.
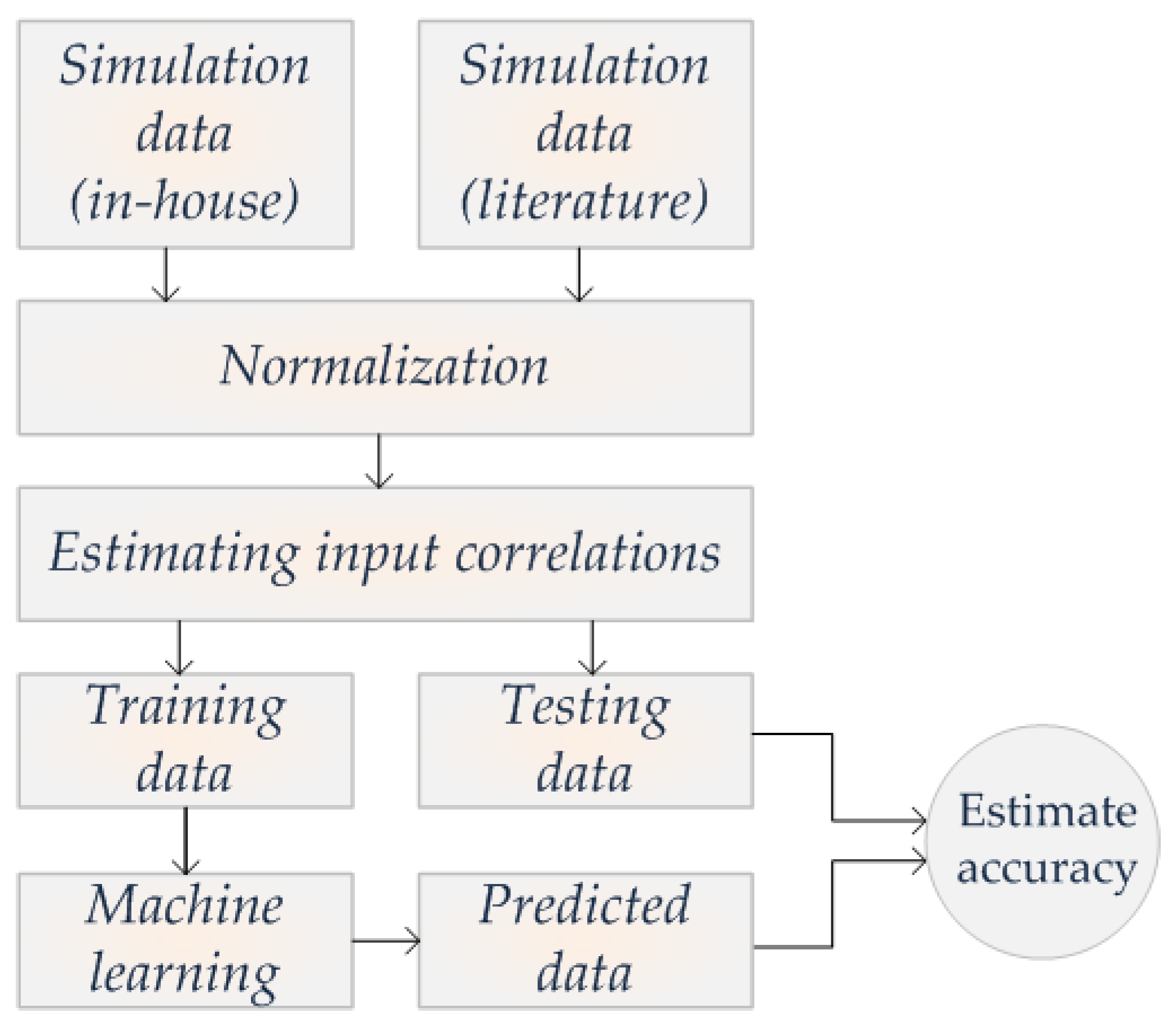
Data inputs/outputs were first pre-processed before being fed to the regression model in Figure 2. The flowchart in Figure 3 demonstrates the complete data flow. After data collection, a normalization stage followed, to restrict the input value range, which transforms to:
Next, a correlation check was performed. There are five independent input variables in the model that define, in a weighted manner, each one of the 4 dependent output variables. It is common practice in statistics to check whether any correlations exist between the independent variables. A popular measure is the Pearson correlation coefficient, rxy. It is employed to quantify a correlation between two inputs, Xi and Yi, of length n, with mean values of and as follows:
The variation inflation factor (VIF) provides an estimate of high multicollinearity between variables and is given by:
where is the coefficient of determination for an independent variable [43]. In general, VIF values greater than 10 denote that the respective input can be omitted.
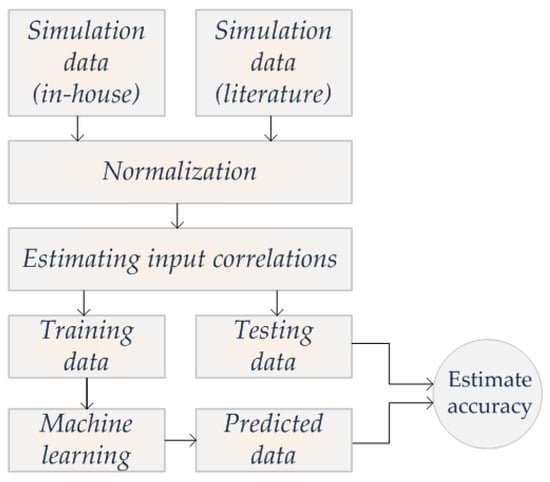
Figure 3.
ML data flow.
Apart from possible input rejection due to collinearity, the regression analysis can spot output points, the so-called “outliers”, that lie far from the regression lines and whose behavior needs further investigation. They could be considered either as “bad” predictions, or, in many cases, they may have resulted from statistical errors, noisy data or some kind of computational inaccuracies during the simulations [44].
A statistical measure used to identify the contribution of a data point to the total regression quality, identifying outliers, is Cook’s distance [45], given by
where yj is the jth output value, yj(i) is the jth output value after the removal of yj, p is the number of regression coefficients and σ is the estimated variance from the fit.
3. Results
3.1. Correlations
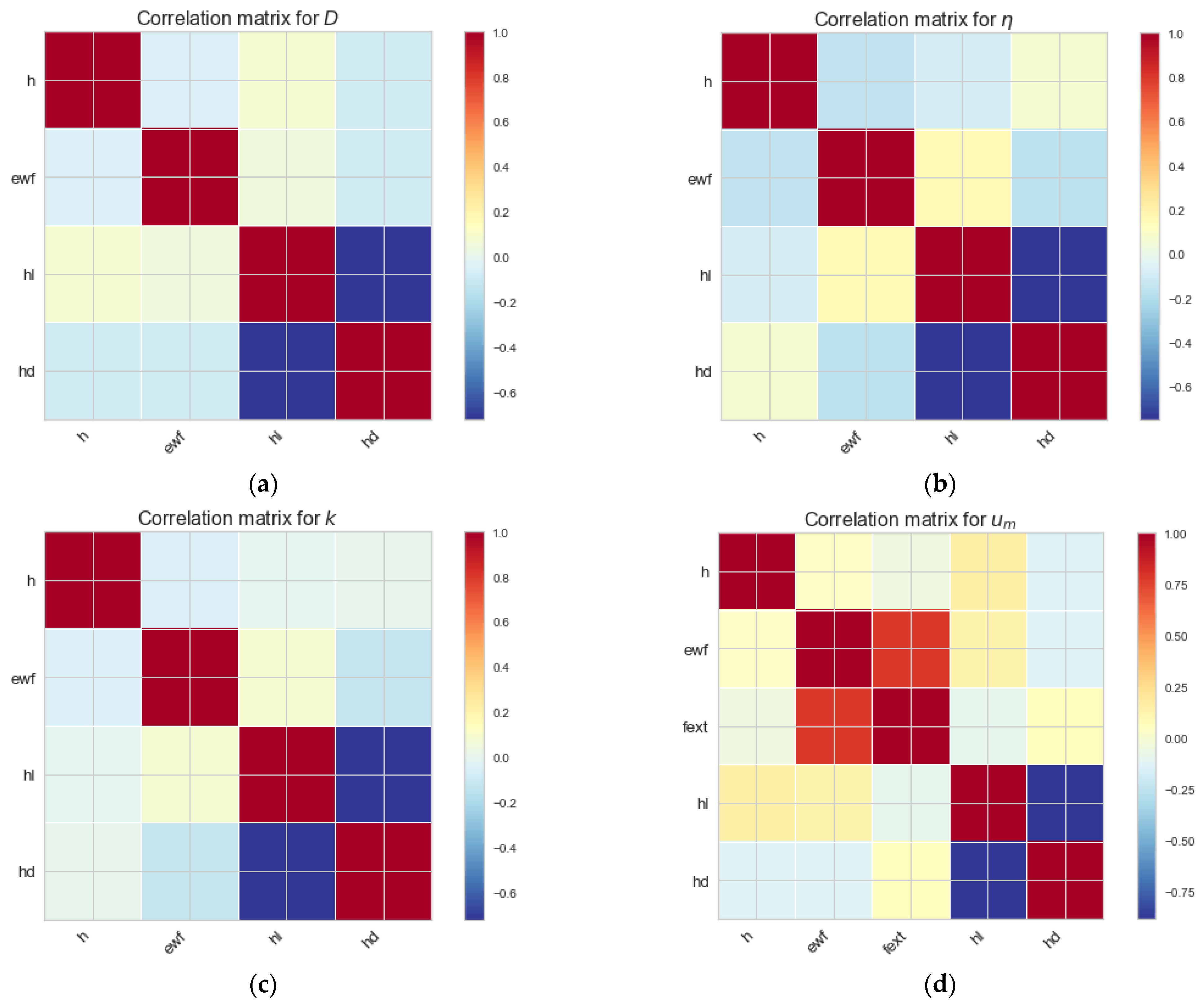
Figure 4 presents the correlation matrices of each one of the three transport properties (dependent variables) and the average channel velocity, um, according to the Pearson coefficient calculation (Equation (7)). In all correlation matrices, it is shown that there is a strong negative correlation between the two geometrical wall characteristics, and . In grooved channels, the simulations have shown that the length of the grooves has an inverse proportional effect to the groove height; for example, when the groove length is large (compared to the channel height), the flow resembles the smooth channel case, while, on the other hand, when the groove height is large, it blocks the flow, affecting all parameters. It is expected that diffusion coefficient values in Figure 4a are affected mainly by the channel width h (large channel–large D).
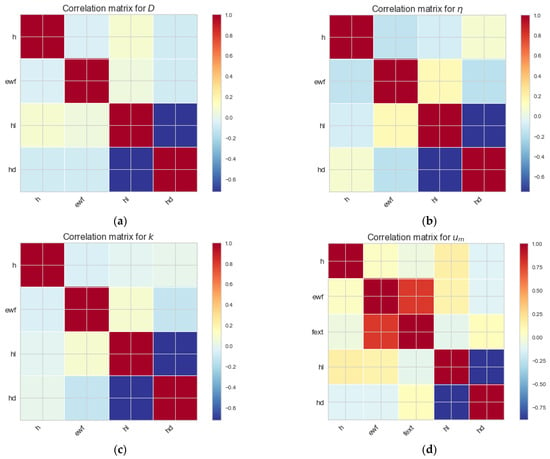
Figure 4.
Correlation matrices for dataset parameters: (a) diffusion coefficient D, (b) shear viscosity η, (c) thermal conductivity k and (d) average channel velocity um.
In Figure 4b, the respective correlation matrix for the shear viscosity η does not locate any correlations between the inputs. MD simulations have revealed the prominent effect of the channel width h to η (large channel–small shear viscosity [7,33]). The correlation matrix for thermal conductivity presents no significant correlation between the inputs (Figure 4c). In contrast to the other dependent variables, the correlation matrix reveals a remarkable behavior for the average velocity um case, shown in Figure 4d. The input parameters and are highly correlated.
This finding indicates possible multicollinearity, and further investigation is to be performed. The VIF (Equation (8)) was calculated for every input and the values are shown in Table 3. All input parameters are only slightly correlated, below the threshold of , and this denotes that the ML procedure is to be executed keeping in mind all input parameters.

Table 3.
Variation inflation factors (VIFs).
3.2. Model Accuracy
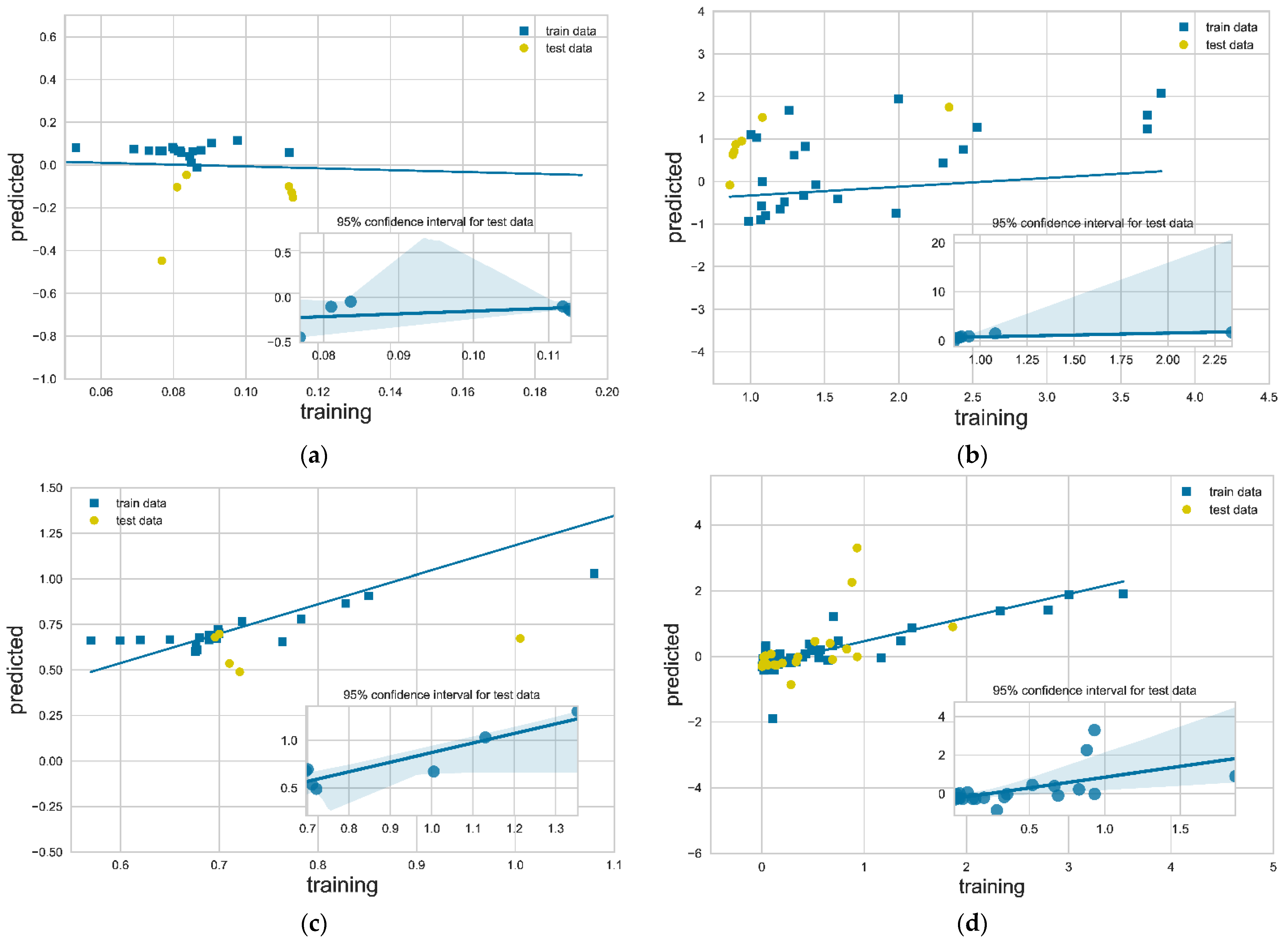
To scrutinize the regression model performance, calculated and predicted values for each output are plotted in Figure 5a–d. Each diagram includes the training (blue squares) and the testing (yellow circles) points. The lines correspond to the linear ML model regression fits. Inset figures include the 95% confidence intervals, i.e., a statistical measure to quantify the uncertainty of predicted values over values used to test the model. The calculated prediction accuracy results (RMSE, MAE and R2), as well as the weights for every input according to Equation (3), are presented in Table 4. The predictions of two of the three transport properties, D and k, show remarkable accuracy between the tested and predicted values, as shown by the high R2 values. In contrast, the model performance on shear viscosity, η, and the average channel velocity, um, is small, albeit acceptable. The data points in Figure 5a–d that do not fit well on the regression line (outliers) may have a significant impact on the model accuracy. The outliers lie far from the middle of the distribution.
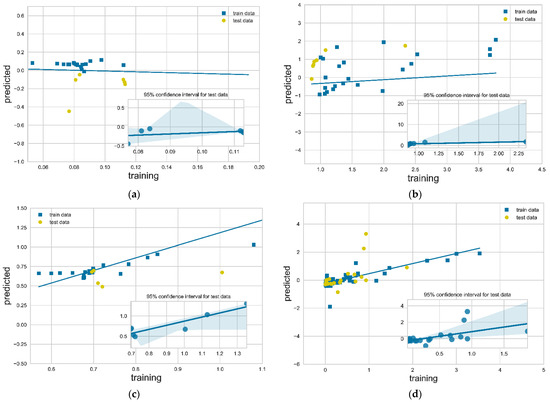
Figure 5.
Error estimation for dataset parameters: (a) D, (b) η, (c) k and (d) . Lines are the respective regression lines from the ML models in Figure 2. Insets display the 95% confidence intervals for the predicted values of each output.

Table 4.
Prediction accuracy and regression coefficients for each output.
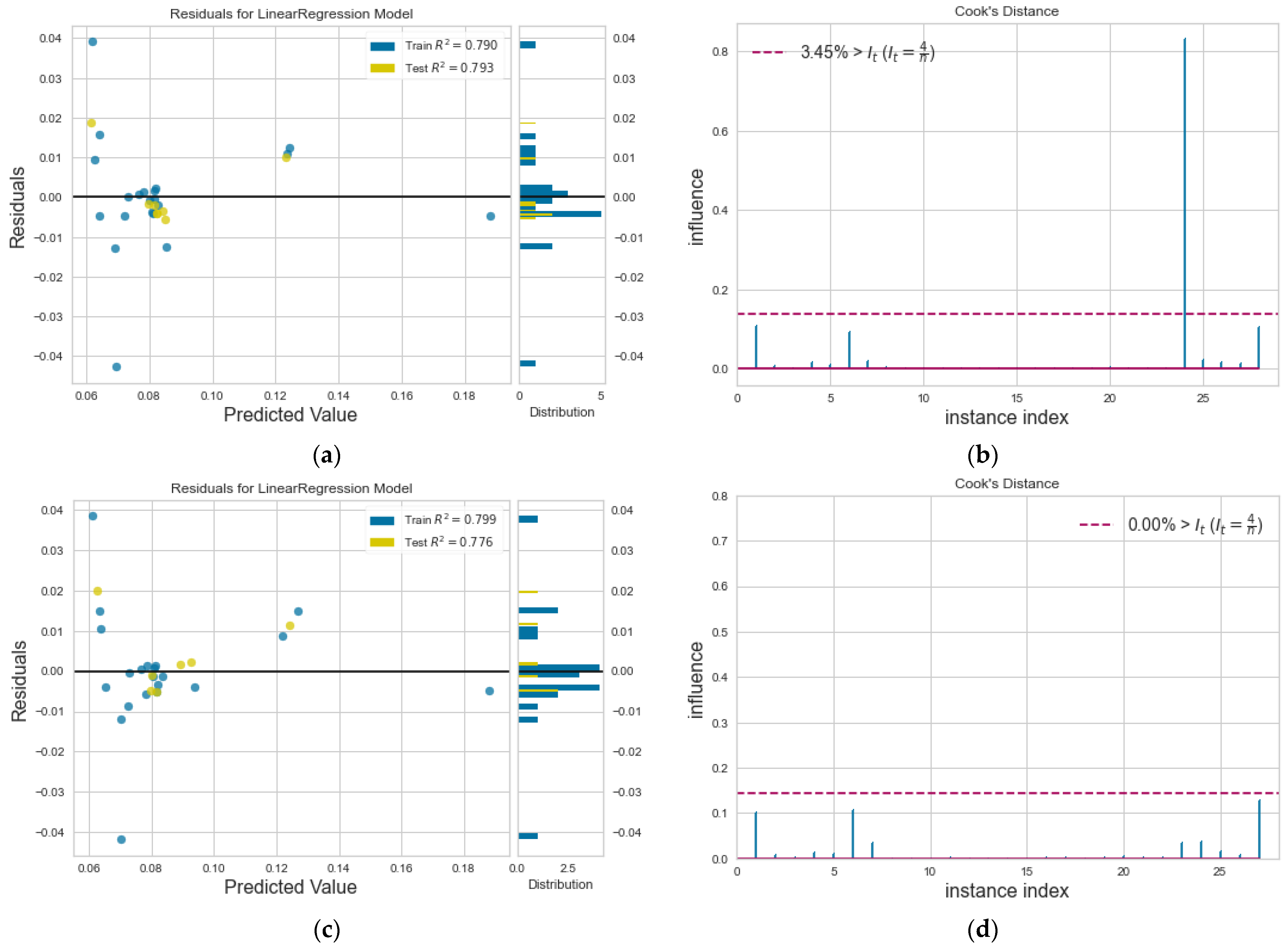
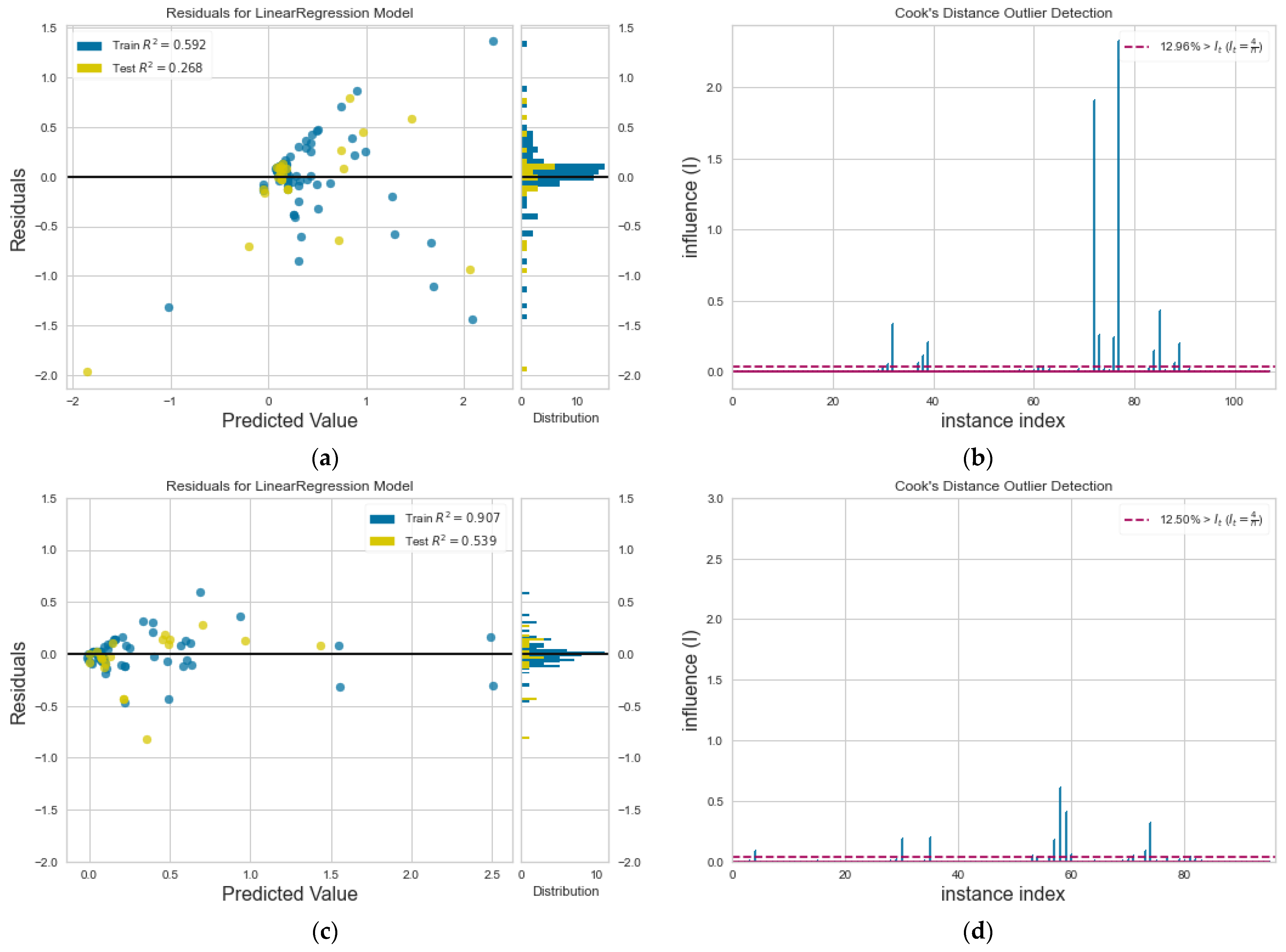
However, further investigation is needed to characterize a data point as outlier or not. Towards this direction, we have employed two of the most widely used statistical tools, the residuals plot and the Cook’s Distance plot. Visualization for these is made possible with the Python Yellowbrick package [46]. The residuals plot presents the calculated difference between the real value and the predicted value, i.e., the prediction error. Figure 6a is a residual plot for D train and test data. Data points are scattered around the horizontal axis. A good regression fit is considered when data are close to the horizontal line. The respective histogram shows that the induced error is distributed around zero. There are data points in the histogram far from zero, nevertheless, the main distribution is around zero. Train and test R2 values shown in the diagram are similar to the average value shown in Table 4.
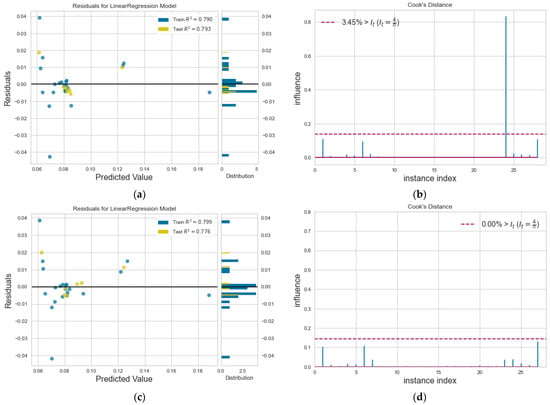
Figure 6.
(a) Residuals plot and (b) Cook’s distance for D, and, after the removal of outliers from the dataset, (c) new residuals plot and (d) new Cook’s distance.
To strengthen our statistical evidence, Figure 6b depicts the calculated Cook’s distance for the diffusion coefficient in our model (Equation (9)), a measure that identifies the influential outliers, providing the index of the data from a stem plot, where a horizontal line is drawn at the 4/n threshold. Stems above this line are possible outliers and their percentage is shown in the Figure legend. For the diffusion coefficient, D, simulation data with index = 24 are considered as outliers. Going back on the dataset incorporated, it is found that this point belongs to a simulation result from a h = 18.5σ nanochannel, taken from our in-house simulations, with the extreme value of wall/fluid interaction = 5.0, which is found to have a decreasing effect on D, as reported in [8].
If we remove this outlier from the dataset, we obtain the respective residuals plot and Cook’s distance in Figure 6c,d. The outlier removal does not seem to affect the accuracy of the regression model, as shown in the residuals plot; only one outlier is not so influential. No other possible influential outliers exist, as all data points are now below the threshold horizontal line (Figure 6d).
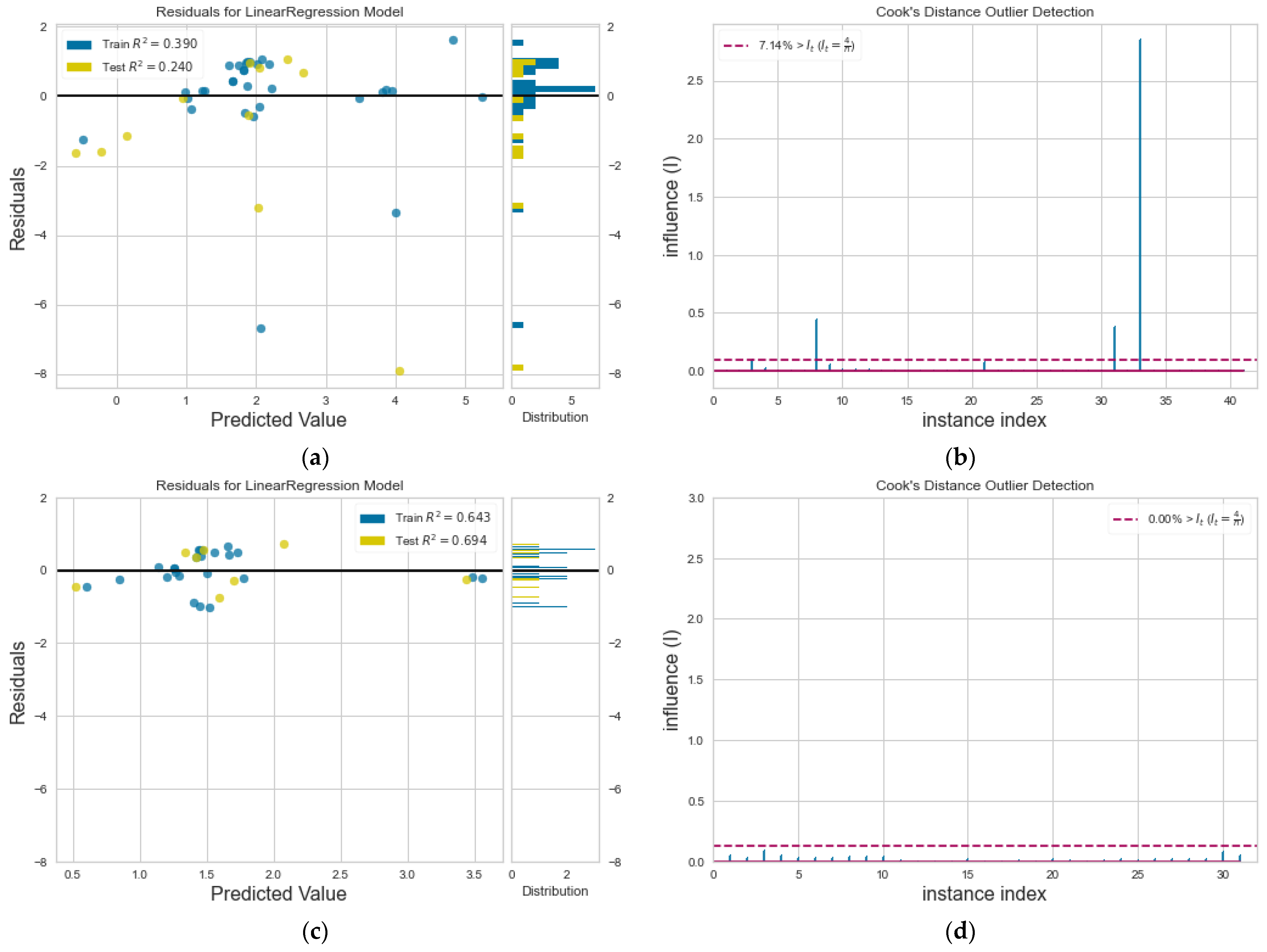
For the shear viscosity, η, a residual plot for train and test data is shown in Figure 7a. Although data is mainly scattered around the horizontal line, yet, there are scarce points that keep the R2 value low. The Cook’s distance (Figure 7b) depicts these outliers, and after their removal, we observe that residuals have significantly improved and data distribution is around zero, as shown from the respective histogram plot in Figure 7c. No other outliers remain in the dataset (Figure 7d). We argue that linear regression has reached its prediction limits for shear viscosity with acceptable accuracy, at least for this dataset range. Previous works have shown that shear viscosity values are high at small nanochannels (from h = 2σ) and reach the bulk value for h > 10 − 12σ [6]. Moreover, η also increases when roughness elements “block” the flow region inside nanochannels, i.e., and when the walls are strongly hydrophilic, i.e., [8]. Therefore, our ML model fails to predict shear viscosity values for small nanochannels, with roughness elements that block the flow, and strongly hydrophilic walls, creating outliers. However, in all other cases, accuracy obtained with multivariant regression is good.
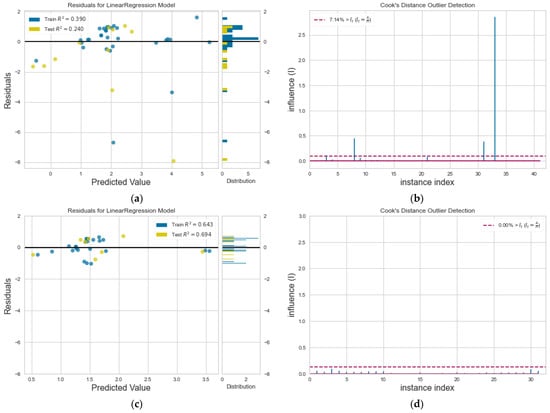
Figure 7.
(a) Residuals plot and (b) Cook’s distance for η, and, after the removal of outliers from the dataset, (c) new residuals plot and (d) new Cook’s distance.
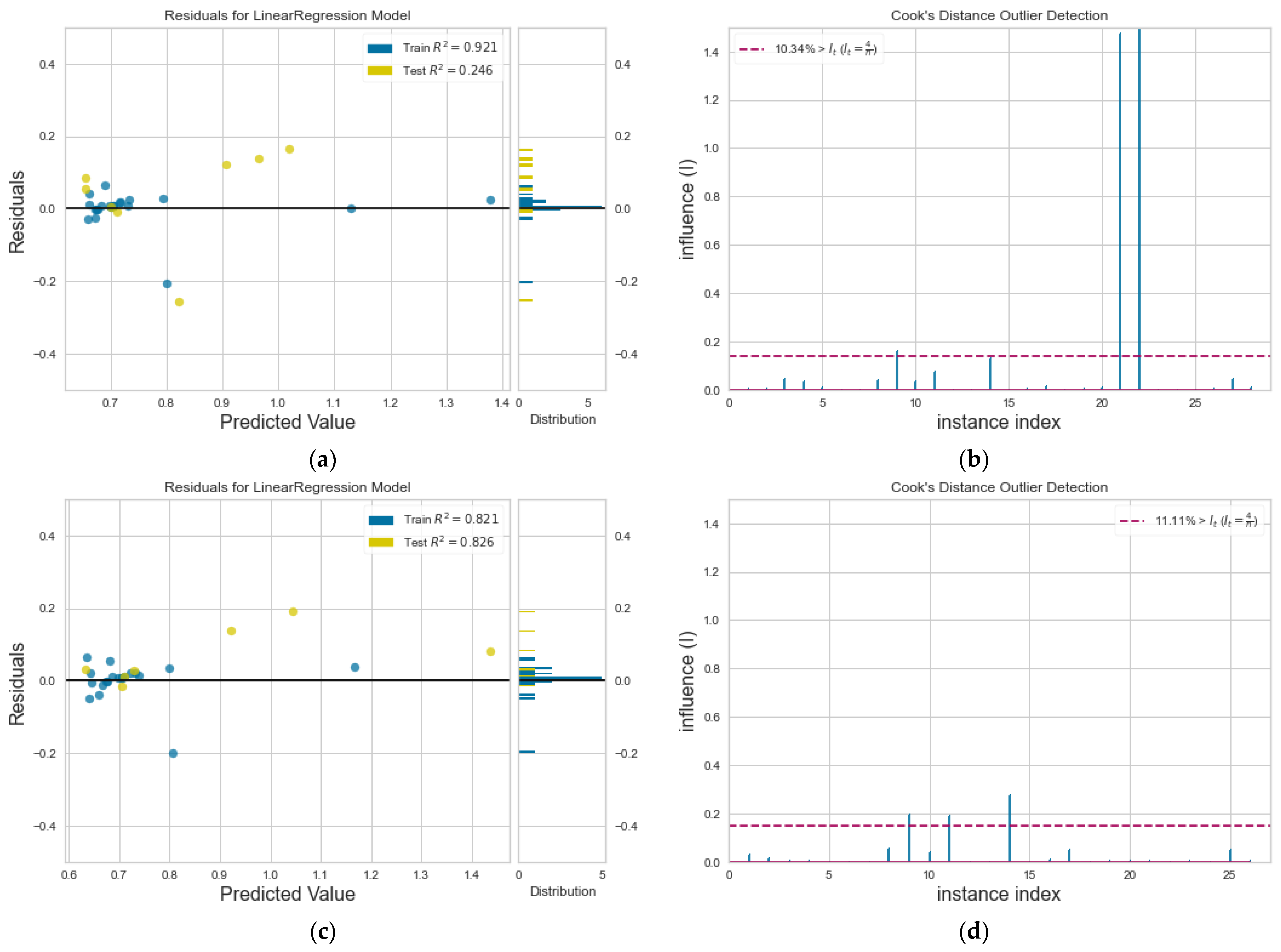
For thermal conductivity, k, the residual plot in Figure 8a shows good accuracy for training data. We must point out that small R2 in test data is circumstantial, since our model selects randomly from the dataset which data to consider as train and test. The Cook’s distance (Figure 8b) depicts two outliers, and after their removal, we observe that R2 is improved for test data. The large ratio (strongly hydrophilic wall) is also responsible for the outliers in thermal conductivity values. We note that thermal conductivity has shown remarkable accuracy to the regression method investigated here.
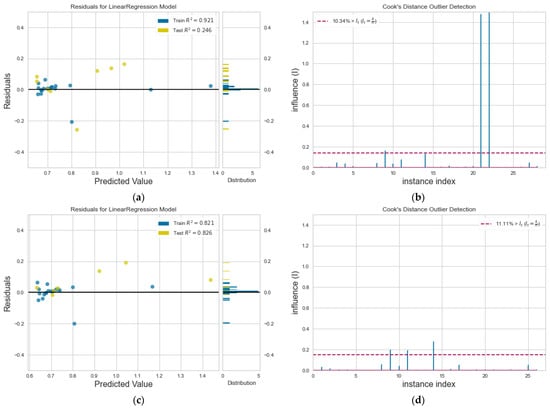
Figure 8.
(a) Residuals plot and (b) Cook’s distance for k, and, after the removal of outliers from the dataset, (c) new residuals plot and (d) new Cook’s distance.
The residuals plot for um in Figure 9a reveals good accuracy to the regression model, while the histogram on the same plot presents normal distribution. This is evidence that linear regression is a choice for predicting average velocity values with ML in systems with similar characteristics. After the outlier removal, the model accuracy is further increased, as shown in Figure 9c. As in previous cases, outliers for um are due to roughness elements height, , and hydrophilic walls.
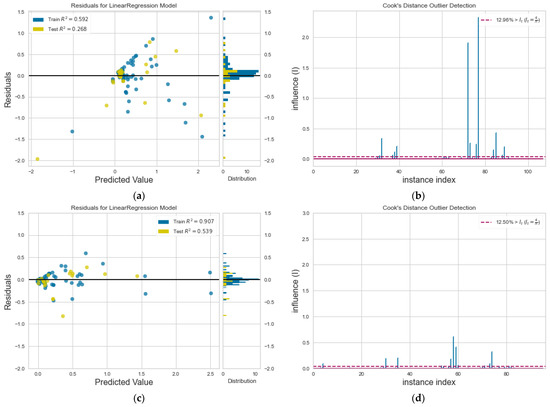
Figure 9.
(a) Residuals plot and (b) Cook’s distance for um, and, after the removal of outliers from the dataset, (c) new residuals plot and (d) new Cook’s distance.
4. Discussion
The ML regression technique incorporated in this work has shown a good performance in predicting the three transport properties of fluids, D, η and k, and the average velocity across the channel, um, a property that is a basic element in many computational fluid mechanics equations, such as the estimation of the Reynolds number [38]. To our knowledge, data from nanoscale simulations have been mainly used for coupling ab initio calculations to MD simulations for the construction of Coarse-Grained systems or for decreasing the order of ordinary and partial differential equations. Nevertheless, as ML is currently a widely investigated field in the condensed matter physics region, it is expected to continuously provide new research results.
Data curation, when obtained from various databases, is an important issue as indicated by early papers in this domain [47], although it seems that there is no commonly accepted protocol or set of procedures for data preprocessing, with data regularization/normalization one of the widely used techniques. Our input data were normalized before being fed to the regression model. A small, though representative, dataset, was chosen which covers a wide range of simulation cases. The quality of the datasets is considered high with respect to the impact of the journals from which they were imported. Checking for outliers and their effects in the resulting model can also act as a control for the quality of the dataset. As regards the number of points to incorporate in such a procedure, there is no clear answer. In the literature, there are cases for successful ML models with datasets containing from less than a hundred [48] to thousands of values [25]. It is generally accepted that for smaller datasets, classical and statistical ML approaches (e.g., regression, support vector machines, k-nearest neighbors and decision trees) are more suitable [49].
Our work focused on fluid flows at the nanoscale. As simulation systems become bigger and multiscale methods have succeeded in coupling flow phenomena among scales, it has to be investigated whether there is a way of replacing some time- and hardware-demanding computations with procedures that are easier to perform. In the previous sections, it was shown that, even with common multivariate regression techniques, ML models can be constructed that are capable of predicting values close to properties extracted from MD simulations found in the literature.
Calculation of the three transport properties, D, η and k, is computationally demanding, especially in nano-confined systems where the impact of the walls is significant and stronger shear stresses exist. Calculating the interactions between all atoms in a system is challenging and many researchers have suggested modified relations from the macroscale that could be applied at the nano- and micro-scale after some modifications [50,51,52]. The equations for the extraction of the three transport properties used in our simulations are presented in Appendix A.
For the ML model exploited here, five inputs are fed in a regression-based ML procedure; the geometrical channel characteristics, such as the channel height, wall groove length and groove height (, and , respectively), the interaction ratio between wall/fluid atoms, , and the external driving force used to drive the flow (taken into consideration only for the um extraction). These independent parameters have been proven to be uncorrelated for the prediction of D, η, k and um.
Predicted values from our model apply well on linear regression fits. Based on the residual plots presented in Section 3.2, it is inferred that multiple linear regression can be a good choice for data prediction, at least at the nanoscale, with accuracy comparable to MD results. Values that influence the model accuracy have been spotted for each output. From the interpretation of the results in Figure 6, Figure 7, Figure 8 and Figure 9, it is inferred that statistical tools such as residuals plots and Cook’s distance can locate data outliers from a database. It is expected that, since one must deal with simulation data, immersed statistical errors or noise would affect the ML model. In contrast, these inaccuracies do not seem to qualitatively affect the procedure in our regression-based ML; nevertheless, values taken from extreme simulation conditions, such as with large ratios or at channels with grooves of large height, seem to affect the efficiency. These points could be removed from our dataset to achieve increased accuracy, yet this would still affect the physical meaning of the ML model. Since intuition plays a key role in selecting which outliers are to be removed [44], we believe that what has to be done is to increase the training samples with more extreme data points so that the model is fully trained and achieves higher accuracy.
Another approach would be the incorporation of other ML algorithms, such as various types of neural networks and deep learning. It is anticipated, though, that this would demand a larger dataset which, in order to comply with our simulation data, must be created from scratch. Training and test data, apart from our simulation database, were also drawn from the literature. We have to note that slight inaccuracies may have occurred during the data extraction from the respective published papers. Moreover, there may be simulation conditions different from our own, with different simulation techniques, time steps, temperatures, etc., that may also induce some inaccuracies.
In a broad sense, this work aimed to couple machine learning and computational condensed matter physics. Overall, our results, despite the approximations necessarily made to permit the inclusion of data coming from different sources, appear to be in qualitative agreement with a number of literature results and achieved satisfying accuracy. Simulation techniques combined with machine learning analysis enable us to use scarce data more effectively [53].
5. Conclusions
It is widely believed that when classical, quantum simulations and ML methods are joined, it could change our efforts towards making predictions in condensed matter physics. In this work, we focused on flow simulations in nanoslits of various dimensions for a range of characteristics affecting the flow, such as the wall structure, the interaction strength between fluid/solid and the external driving forces. Along with data obtained from the literature, a small, albeit indicative, database was created. Transport and flow properties of a simple LJ fluid were predicted after employing the appropriate technique, with multivariate regression showing good accuracy.
We have shown that, in this context, ML can be a valuable predictive tool, especially at the point where missing data among various scales exist. This would increase our ability to replace some simulation points and, in the next step, further facilitate coupling across scales. The key concept towards this direction is the creation of a statistically large database that could be incorporated from a powerful machine learning framework. However, it should be kept in mind that the proposed method should not be viewed as a replacement of current simulation techniques, which have been verified and tested over various conditions throughout the years. Simulations and ML techniques could coexist in order to unlock new, promising possibilities in computational science and engineering problems.
Author Contributions
Writing—original draft preparation, software, methodology and visualization: F.S.; supervision and writing—review and editing: T.E.K. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data may be available from the authors upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The diffusion coefficient is obtained using Einstein’s relation:
where is the position vector of the jth atom and d is the dimensionality of the system (d = 1 for diffusivity calculation in one direction, d = 2 in two directions and d = 3 in three directions). The brackets indicate the time average, while is the number of LJ fluid atoms.
Shear viscosity and thermal conductivity for systems in equilibrium can be calculated using the Green–Kubo formalism. Shear viscosity η for a pure fluid is computed by the relation
where is the off-diagonal component of the microscopic stress tensor:
is the LJ potential of atom i interacting with atom j, is the distance vector between atoms i and j and is the j-component (j = x, y or z) of the velocity of atom i. is the computational domain fluid volume (V = ).
Thermal conductivity k can be calculated by the integration of the time-autocorrelation function of the microscopic heat flow , i.e.,
where the microscopic heat flow is given by
where is the speed velocity magnitude of atom i and is the unitary matrix.
References
- Bohn, P.W. Science and technology of electrochemistry at nano-interfaces: Concluding remarks. Faraday Discuss. 2018, 210, 481–493. [Google Scholar] [CrossRef]
- Heerema, S.J.; Dekker, C. Graphene nanodevices for DNA sequencing. Nat. Nanotech. 2016, 11, 127–136. [Google Scholar] [CrossRef] [PubMed]
- Karnik, R.; Castelino, K.; Fan, R.; Yang, P.; Majumdar, A. Effects of Biological Reactions and Modifications on Conductance of Nanofluidic Channels. Nano Lett. 2005, 5, 1638–1642. [Google Scholar] [CrossRef]
- Prakash, S.; Piruska, A.; Gatimu, E.N.; Bohn, P.W.; Sweedler, J.V.; Shannon, M.A. Nanofluidics: Systems and Applications. IEEE Sens. J. 2008, 8, 441–450. [Google Scholar] [CrossRef]
- Prakash, S.; Shannon, M.A.; Bellman, K. Water desalination: Emerging and existing technologies. In Aqua Nanotechnology; Reisner, D.E., Pradeep, T., Eds.; CRC Press: Boca Raton, FL, USA, 2014; pp. 533–562. [Google Scholar]
- Qiao, R.; Aluru, N.R. Atomistic simulation of KCl transport in charged silicon nanochannels: Interfacial effects. Colloids Surf. Physicochem. Eng. Asp. 2005, 267, 103–109. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.E.; Liakopoulos, A. Transport properties of liquid argon in krypton nanochannels: Anisotropy and non-homogeneity introduced by the solid walls. Int. J. Heat Mass Transf. 2009, 52, 735–743. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.E.; Liakopoulos, A. How wall properties control diffusion in grooved nanochannels: A molecular dynamics study. Heat Mass Transf. 2013, 49, 1081–1088. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.E.; Giannakopoulos, A.E.; Liakopoulos, A. Molecular dynamics simulation on flows in nano-ribbed and nano-grooved channels. Heat Mass Transf. 2016, 52, 153–162. [Google Scholar] [CrossRef]
- Lee, J.; Laoui, T.; Karnik, R. Nanofluidic transport governed by the liquid/vapour interface. Nat. Nanotechnol. 2014, 9, 317–323. [Google Scholar] [CrossRef]
- Priezjev, N.V. Effect of surface roughness on rate-dependent slip in simple fluids. J. Chem. Phys. 2007, 127, 144708. [Google Scholar] [CrossRef] [PubMed]
- Polster, J.W.; Acar, E.T.; Aydin, F.; Zhan, C.; Pham, T.A.; Siwy, Z.S. Gating of hydrophobic nanopores with large anions. ACS Nano 2020, 14, 4306–4315. [Google Scholar] [CrossRef]
- Bhadauria, R.; Aluru, N.R. A quasi-continuum hydrodynamic model for slit shaped nanochannel flow. J. Chem. Phys. 2013, 139, 074109. [Google Scholar] [CrossRef] [PubMed]
- Eral, H.B.; van den Ende, D.; Mugele, F.; Duits, M.H.G. Influence of confinement by smooth and rough walls on particle dynamics in dense hard-sphere suspensions. Phys. Rev. E 2009, 80, 061403. [Google Scholar] [CrossRef]
- Thompson, P.; Troian, S. A general boundary condition for liquid flow at solid surfaces. Nature 1997, 389, 360–362. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Behler, J. Perspective: Machine learning potentials for atomistic simulations. J. Chem. Phys. 2016, 145, 170901. [Google Scholar] [CrossRef]
- Botu, V.; Ramprasad, R. Adaptive machine learning framework to accelerate ab initio molecular dynamics. Int. J. Quantum Chem. 2015, 115, 1074–1083. [Google Scholar] [CrossRef]
- Chan, H.; Narayanan, B.; Cherukara, M.J.; Sen, F.G.; Sasikumar, K.; Gray, S.K.; Chan, M.K.Y.; Sankaranarayanan, S.K.R.S. Machine Learning classical interatomic potentials for Molecular Dynamics from first-principles training data. J. Phys. Chem. C 2019, 123, 6941–6957. [Google Scholar] [CrossRef]
- Scherer, C.; Scheid, R.; Andrienko, D.; Bereau, T. Kernel-Based Machine Learning for Efficient Simulations of Molecular Liquids. J. Chem. Theory Comput. 2020, 16, 3194–3204. [Google Scholar] [CrossRef]
- Kadupitiya, J.C.S.; Sun, F.; Fox, G.; Jadhao, V. Machine learning surrogates for molecular dynamics simulations of soft materials. J. Comput. Sci. 2020, 42, 101107. [Google Scholar] [CrossRef]
- Craven, G.T.; Lubbers, N.; Barros, K.; Tretiak, S. Machine learning approaches for structural and thermodynamic properties of a Lennard-Jones fluid. J. Chem. Phys. 2020, 153, 104502. [Google Scholar] [CrossRef]
- Allers, J.P.; Harvey, J.A.; Garzon, F.H.; Alam, T.M. Machine learning prediction of self-diffusion in Lennard-Jones fluids. J. Chem. Phys. 2020, 153, 034102. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Machine learning of linear differential equations using Gaussian processes. J. Comput. Phys. 2017, 348, 683–693. [Google Scholar] [CrossRef]
- Stephan, S.; Thol, M.; Vrabec, J.; Hasse, H. Thermophysical properties of the Lennard-Jones Fluid: Database and data assessment. J. Chem. Inf. Model. 2019, 59, 4248–4265. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.E.; Liakopoulos, A. Surface wettability effects on flow in rough wall nanochannels. Microfluid. Nanofluidics 2012, 12, 25–31. [Google Scholar] [CrossRef]
- Giannakopoulos, A.E.; Sofos, F.; Karakasidis, T.E.; Liakopoulos, A. A quasi-continuum multi-scale theory for self-diffusion and fluid ordering in nanochannel flows. Microfluid. Nanofluidics 2014, 17, 1011–1023. [Google Scholar] [CrossRef]
- Alpaydin, E. Machine Learning: The New AI; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. JMLR 2011, 12, 2825–2830. [Google Scholar]
- Asproulis, N.; Drikakis, D. Boundary slip dependency on surface stiffness. Phys. Rev. E 2010, 81, 061503. [Google Scholar] [CrossRef]
- Vinogradova, O.; Belyaev, A. Wetting, roughness and hydrodynamic slip. In Nanoscale Liquid Interfaces: Wetting, Patterning and Force Microscopy at the Molecular Scale; Ondarcucu, T., Aime, J.-P., Eds.; Pan Stanford Publishing: Singapore, 2013; pp. 29–82. [Google Scholar]
- Hu, Y.Z.; Wang, H.; Guo, Y. Molecular dynamics simulation of poiseuille flow in ultra-thin film. Tribotest 1995, 1, 301–310. [Google Scholar] [CrossRef]
- Hyżorek, K.; Tretiakov, K.V. Thermal conductivity of liquid argon in nanochannels from molecular dynamics simulations. J. Chem. Phys. 2016, 144, 194507. [Google Scholar] [CrossRef] [PubMed]
- Jabbarzadeh, A.; Atkinson, J.D.; Tarner, R.I. Effect of the wall roughness on slip and rheological properties of hexadecane in molecular dynamics simulation of Couette shear flow between two sinusoidal walls. Phys. Rev. E 2000, 61, 690–699. [Google Scholar] [CrossRef]
- Markesteijn, A.P.; Hartkamp, R.; Luding, S.; Westerweel, J. A comparison of the value of viscosity for several water models using Poiseuille flow in a nano-channel. J. Chem. Phys. 2012, 136, 134104. [Google Scholar] [CrossRef] [PubMed]
- Sofos, F.; Karakasidis, T.E.; Liakopoulos, A. Effects of wall roughness on flow in nanochannels. Phys. Rev. E 2009, 79, 026305. [Google Scholar] [CrossRef] [PubMed]
- Sofos, F.; Karakasidis, T.E.; Liakopoulos, A. Non-Equilibrium Molecular Dynamics investigation of parameters affecting planar nanochannel flows. Contemp. Eng. Sci. 2009, 2, 283–298. [Google Scholar]
- Sofos, F.; Karakasidis, T.E.; Liakopoulos, A. Fluid structure and system dynamics in nanodevices for water desalination. Desalination Water Treat. 2015, 57, 11561–11571. [Google Scholar] [CrossRef]
- Somers, S.A.; Davis, H.T. Microscopic dynamics of fluids confined between smooth and atomically structured solid surfaces. J. Chem. Phys. 1991, 96, 5389–5407. [Google Scholar] [CrossRef]
- Toghraie Semiromi, D.; Azimian, A.R. Nanoscale Poiseuille flow and effects of modified Lennard–Jones potential function. Heat Mass Transf. 2010, 46, 791–801. [Google Scholar] [CrossRef]
- Travis, K.; Todd, B.D.; Evans, D. Departure from Navier-Stokes hydrodynamics in confined liquids. Phys. Rev. E 1997, 55, 4288–4295. [Google Scholar] [CrossRef]
- Yang, S.C. Effects of surface roughness and interface wettability on nanoscale flow in a nanochannel. Microfluid. Nanofluidics 2006, 2, 501–511. [Google Scholar] [CrossRef]
- Swamynathan, M. Mastering Machine Learning with Python in Six Steps; Apress: New York, NY, USA, 2017. [Google Scholar]
- Osborne, J.W.; Overbay, A. The power of outliers (and why researchers should ALWAYS check for them). Pract. Assess. Res. Eval. 2004, 9, 6. [Google Scholar]
- Cook, R.D. Detection of influential observation in linear regression. Technometrics 1977, 19, 15–18. [Google Scholar]
- Bengfort, B.; Bilbro, R. Yellowbrick: Visualizing the Scikit-Learn Model Selection Process. J. Open Source Softw. 2019, 4, 1075. [Google Scholar] [CrossRef]
- Fourches, D.; Muratov, E.; Tropsha, A. Trust, but verify: On the importance of chemical structure curation in cheminformatics and QSAR modeling research. J. Chem. Inf. Model. 2010, 50, 1189–1204. [Google Scholar] [CrossRef]
- Elton, D.C.; Boukouvalas, Z.; Butrico, M.S.; Fuge, M.D.; Chung, P.W. Applying machine learning techniques to predict the properties of energetic materials. Sci. Rep. 2018, 8, 9059. [Google Scholar] [CrossRef]
- Wang, A.Y.-T.; Murdock, R.J.; Kauwe, S.K.; Oliynyk, A.O.; Gurlo, A.; Brgoch, J.; Persson, K.A.; Sparks, T.D. Machine Learning for Materials Scientists: An Introductory guide toward best practices. Chem. Mater. 2020, 32, 4954–4965. [Google Scholar] [CrossRef]
- Hess, B. Determining the shear viscosity of model liquids from molecular dynamics simulations. J. Chem. Phys. 2002, 116, 209–217. [Google Scholar] [CrossRef]
- Hartkamp, R.; Ghosh, A.; Weinhart, T.; Luding, S. A study of the anisotropy of stress in a fluid confined in a nanochannel. J. Chem. Phys. 2012, 137, 044711. [Google Scholar] [CrossRef]
- Frank, M.; Drikakis, D. Thermodynamics at solid-liquid interfaces. Entropy 2018, 20, 362. [Google Scholar] [CrossRef]
- Cao, B.; Adutwum, L.A.; Oliynyk, A.O.; Luber, E.J.; Olsen, B.C.; Mar, A.; Buriak, J.M. How to optimize materials and devices via design of experiments and machine learning: Demonstration using organic photovoltaics. ACS Nano 2018, 12, 7434–7444. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).