Magneto-Bioconvection Flow of Williamson Nanofluid over an Inclined Plate with Gyrotactic Microorganisms and Entropy Generation

Abstract

The fluid flow through inclined plates has several applications in magneto-aerodynamics, materials processing and magnetohydrodynamic propulsion thermo-fluid dynamics. Inspired by these applications, the rate of entropy production in a bio-convective flow of a magnetohydrodynamic Williamson nanoliquid over an inclined convectively heated stretchy plate with the influence of thermal radiation, porous materials and chemical reaction has been deliberated in this paper. The presence of microorganisms aids in stabilizing the suspended nanoparticles through a bioconvection process. Also, the thermal radiation assumed an optically thick limit approximation. With the help of similarity transformations, the coupled partial differential equations are converted to nonlinear ordinary differential equations and the resulting model is numerically tackled using the shooting method. The influences of the determining thermo-physical parameters on the flow field are incorporated and extensively discussed. The major relevant outcomes of the present analysis are that the upsurge in values of Schmidt number decays the mass transfer characteristics, but the converse trend is depicted for boost up values of the thermophoresis parameter. Enhancement in bioconvection Peclet and Schmidt numbers deteriorates the microorganism density characteristics. Further, the upsurge in the Williamson parameter declines the Bejan number and irreversibility ratio.

1. Introduction

The industrial cooling system relies on a standard base fluid, which is not sufficient to meet the requirements of industrial processes. To overcome this issue, a modern phase of nanotechnology is proposed to achieve a higher cooling rate in the performance of industrial processes. Nanofluids can be exploited in cars as cooling and shock absorbers and in improving refrigeration/air-conditioners. Inspired by these applications, several researchers examined the flow of nanoliquids past diverse surfaces [1,2,3,4,5]. The Williamson liquid is an important class of pseudo-plastic liquid model. The study of the boundary layer stream of pseudoplastic liquid is of great interest due to its widespread use in industry such as polymer sheet extraction, emulsion sheets and melting of high-density polymers. Inspired by these, Prasannakumara et al. [6] examined the consequence of chemical reaction in a Williamson nanoliquid stream through an extending sheet. Mabood et al. [7] deliberated on the radiative stream of Williamson liquid past an incessantly moving intense surface. Rasool et al. [8] exemplified the consequences of chemical reactions on a Williamson nanoliquid stream through a widening flat surface with entropy production. Haq et al. [9] deliberated on the behavior of gyrotactic microorganisms on Williamson nanoliquid stream through a stretchy cylinder.

In the last few decades, a number of investigations into energy production in several fluid stream conditions have been carried out by researchers focusing on the generation of entropy. Research studies were motivated by recognizing the significance of entropy production in liquid flow and its importance in some industrial uses such as air conditioners, refrigerators, heat pumps, fire engines and much more. Entropy management efforts were first discussed by Bejan [10]. Later, Yusuf et al. [11] deliberated the entropy production in the magnetohydrodynamic (MHD) Williamson nanoliquid stream past a stretchy sheet with chemical reaction. Azam et al. [12] scrutinized the production of entropy on a Williamson nanoliquid stream. Bhatti et al. [13] explored the entropy production on a Williamson nanoliquid stream. For a better biological process, a better liquid mixture is needed, which is why gyrotactic microorganisms are essential. The main reason for bioconvection refers to the gradient size of gyrotactic microorganisms. This phenomenon has great potential for use. For example, it has been used for bio-microsystems of enzyme biosensors and biomedicine treatment of cancer. Waqas et al. [14] scrutinized the time-dependent MHD stream of Williamson liquid on taking account of motile gyrotactic microorganism with suspended nanoparticles. Khan et al. [15] examined the bioconvective stream of Williamson liquid with the suspension of nanoparticles through stretching sheet with gyrotactic microorganisms. Hayat et al. [16] inspected the influence of radiation effect on an MHD stream of non-Newtonian nanoliquid through a stretching cylinder with gyrotactic microorganisms. Jayadevamurthy et al. [17] explored the performance of a moving rotating disk on stream of hybrid nanoliquid on taking account of gyrotactic microorganisms.

The state of radiation contributes significantly to the formation of high temperatures. Non-linear heat transfer conditions in a stretched surface play a major role in fluid conversion and have many applications in chemical engineering and metallurgy. Over the past decades, several researchers have scrutinized the influence of thermal radiation effect on different fluid flow patterns with the existence of porous medium. Hosseinzadeh et al. [18] scrutinized the influence of chemical reaction and radiation effect on the non-Newtonian liquid stream through a plate on taking account of permeable medium. Dogonchi et al. [19] examined the influence of porous medium and thermal radiation effect on copper-water nanoliquid stream though a cylinder. Yusuf et al. [20] inspected the consequences of the radiation effect on a Darcy-Forchhiemer stream of hybrid nanoliquid through a stretchy sheet with a porous medium. Shehzad et al. [21] examined the impact of radiation effect on a micropolar nanoliquid stream through a stretching sheet on taking account of the porous medium. The diffusion of species on taking account of chemical reaction in the interface layer stream has abundant applications in atmospheric flows, fibrous insulation, water and air pollutions and several chemical engineering issues. Inspired by these applications, several researchers scrutinized the consequences of chemical reactions on different fluid streams on taking account of several influencing factors. Khan et al. [22,23,24] deliberated the influence of chemical reaction on non-Newtonian liquid streams through stretchy surfaces with production of entropy. Alsaadi et al. [25] inspected the impact of chemical reaction on a non-Newtonian nanoliquid stream through a stretching sheet with entropy production. Kotresh et al. [26] examined the impact chemical reaction on a nanofluid stream through a disk.

In view of the above literature survey, it is obvious to the best of the writer’s knowledge, that no efforts have so far been initiated with respect to studying the encouragement of chemical reaction on the Williamson nanoliquid along an aligned semi-infinite plate embedded in a porous medium, which constitutes the novelty of the current study. In this investigation, we scrutinized entropy production on bioconvective flow of Williamson nanofluid along an aligned semi-infinite plate embedded in a porous medium under the influence of thermal radiation and gyrotactic microorganisms.

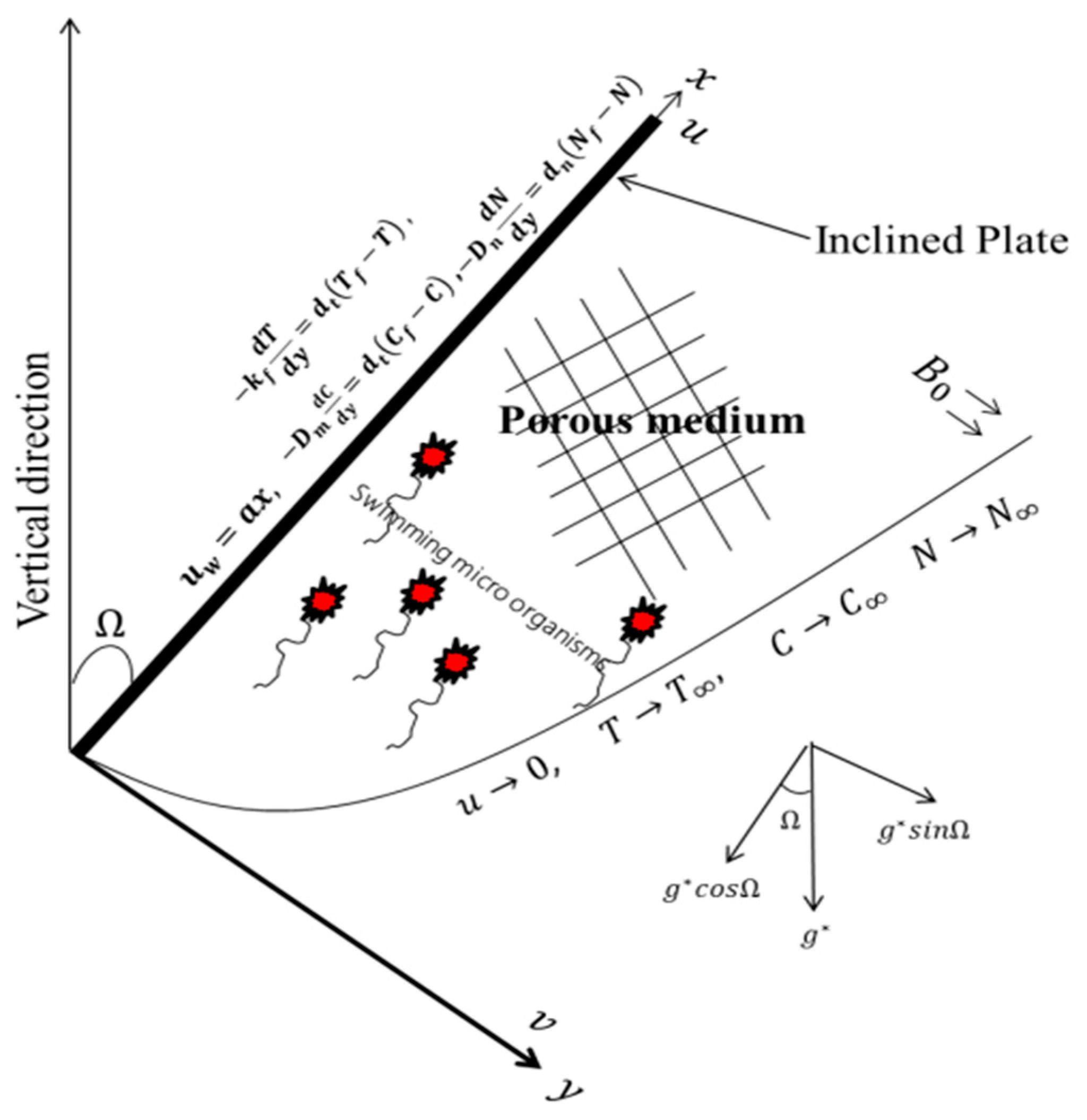
2. Problem Formulation

Mixed convective flow of Williamson nanofluid along an inclined semi-infinite plate embedded in a porous medium under the influence of thermal radiation and gyrotactic microorganisms is examined. The flow configuration is depicted in Figure 1. The considered fluid is conducted in an imposed applied magnetic field of strength $B_0$ parallel to the y-axis. This semi-infinite plate is inclined about the vertical direction making an angle $\mathsf{\Omega }$. The stretchy surface velocity is $u_w=ax$, where $a$ is a positive constant. Here, we assume a two-dimensional steady flow and the fluid is assumed to be an incompressible. Also, the magnetic Reynolds number and the induced electric field are assumed to be small and negligible.

It is adopted that, at the boundary, the temperature, concentration and microorganism concentrations are characterized by a convective heating process and that nanoparticles have no influence on the movement of microorganisms. The influence of thermal radiation along with chemical reaction is accounted for. Williamson fluid is a pseudoplastic type of non-Newtonian fluid for which the stress component of the velocity and the extra shear stress $S_{xy}$ is expressed as (Nadeem et al. [27]) $S_{xy}={\mu }_0\left(1-\mathsf{\Delta }\dot{\gamma }\right)\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)$. Here, ${\mu }_0$ is the viscosity, $\mathsf{\Delta }>0$ is the material constant of the fluid and $\dot{\gamma }$ is defined as $\dot{\gamma }={\left[{\left(\frac{\partial u}{\partial x}\right)}^2+\frac{1}{2}{\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial y}\right)}^2+{\left(\frac{\partial v}{\partial y}\right)}^2\right]}^{\frac{1}{2}}$. We assumed that the fluid properties are invariant. The magnetic Reynolds number, electric field due to polarization of charges, and Hall effects are assumed to be negligible. Under the above assumptions and boundary layer approximations, the governing model can be expressed by exploring the Buongiorno nanofluid model given as follows:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\upsilon \left(\frac{{\partial }^{2}u}{\partial y^2}+\sqrt{2}\mathsf{\Delta }\frac{\partial u}{\partial y}\frac{{\partial }^{2}u}{\partial x^2}\right)-\left(\frac{\sigma B^2}{{\rho }_f}+\frac{\upsilon }{k_p}\right)u+\frac{1}{{\rho }_f} \left\{\begin{array}{l}\left(1-C_{\infty }\right)g{\rho }_f{\Lambda }_1\left(T-T_{\infty }\right)-g\left({\rho }_p-{\rho }_f\right)\\ \left(C-C_{\infty }\right)-\left({\rho }_m-{\rho }_f\right)g{\Lambda }_2\left(N-N_{\infty }\right)\end{array}\right\}\cos \mathsf{\Omega }$$

(2)

$${\left(\rho c\right)}_f\left(u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right)=k_f\frac{{\partial }^{2}T}{{\partial }^{2}y}-\frac{\partial q_r}{\partial y}-\sigma B_0^2{u}^2+\frac{\mu }{k_p}{u}^2+\mu {\left(\frac{\partial u}{\partial y}\right)}^2\left(1+\frac{\mathsf{\Delta }}{\sqrt{2}}\frac{\partial u}{\partial y}\right)+{\left(\rho c\right)}_p\left(D_m\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2\right)$$

(3)

$$u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D_m\frac{{\partial }^{2}C}{\partial y^2}+\frac{D_T}{T_{\infty }}\frac{{\partial }^{2}T}{\partial y^2}-\alpha \left(C-C_{\infty }\right)$$

(4)

$$u\frac{\partial N}{\partial x}+v\frac{\partial N}{\partial y}=\frac{b{W}_c}{C_{\infty }}\left\{\frac{\partial }{\partial y}\left(N\frac{\partial C}{\partial y}\right)\right\}=D_n\left(\frac{{\partial }^{2}N}{\partial y^2}\right).$$

(5)

Subject to the boundary conditions

$$u=u_w=ax, v=0, -k_f\frac{\partial T}{\partial y}=d_t\left(T_f-T\right),-D_m\frac{\partial T}{\partial y}=d_c\left(C_f-C\right),D_n\frac{\partial n}{\partial y}=d_n\left(N_f-N\right)\mathrm{at}y=0$$

(6)

$$u\to 0, T\to T_{\infty }C\to C_{\infty },N\to N_{\infty }\mathrm{as}y\to \infty .$$

(7)

For optically thick media, Rosseland approximation is expressed as

$$q_r=-\frac{4{\sigma }_{*}}{3k_s}\frac{\partial T^4}{\partial y},$$

(8)

where $k_s$ is the Rosseland mean spectral absorption coefficient and the Stefan–Boltzmann radiation is denoted as ${\sigma }_{*}$. Therefore, Taylor series expansion about $T_{\infty }$

$$T^4=T_{\infty }^4+4T_{\infty }^3\left(T-T_{\infty }\right)+6T_{\infty }^2{\left(T-T_{\infty }\right)}^2+\dots$$

(9)

Neglecting the higher order term of $\left(T-T_{\infty }\right)$ to get

$$T^4\cong 4T_{\infty }^{3}T-3T_{\infty }^4.$$

(10)

Combining Equations (8) and (10) yield

$$q_r=-\frac{16{\sigma }_1}{3k_s}{T}_{\infty }^3\frac{\partial T}{\partial y}.$$

(11)

Also in view of Equation (11), Equation (3) therefore becomes

$$\begin{array}{l}u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k_f}{{\left(\rho c\right)}_f}\frac{{\partial }^{2}T}{{\partial }^{2}y}+\frac{1}{{\left(\rho c\right)}_f}\frac{16{\sigma }_1}{3k_s}{T}_{\infty }^3\frac{{\partial }^{2}T}{{\partial }^{2}y} -\frac{\sigma B_0^2{u}^2}{{\left(\rho c\right)}_f}+\frac{\mu }{{\left(\rho c\right)}_f}{\left(\frac{\partial u}{\partial y}\right)}^2\left(1+\frac{\mathsf{\Delta }}{\sqrt{2}}\frac{\partial u}{\partial y}\right)+\\ \tau \left(D_m\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2\right)+\frac{\mu }{{\left(\rho c\right)}_f{k}_p}{u}^2\end{array}$$

(12)

Now the following similarity variables are introduced

$$\begin{array}{l}u=ax{f}^{\prime }\left(\eta \right),v=\sqrt{av}xf\left(\eta \right),\eta =\sqrt{\frac{a}{\nu }}y,\theta \left(\eta \right)=\frac{\left(T-T_{\infty }\right)}{\left(T_f-T_{\infty }\right)},\\ \varphi \left(\eta \right)=\frac{\left(C-C_{\infty }\right)}{\left(C_f-C_{\infty }\right)},\psi \left(\eta \right)=\frac{\left(N-N_{\infty }\right)}{\left(N_f-N_{\infty }\right)}.\end{array}$$

(13)

Equation (1) is satisfied trivially and the dimensionless model are

$$f^{‴}+f{f}^{″}-{f^{\prime }}^2+\beta f^{″}{f}^{‴}-\left(M^2+K\right)f^{\prime } +\lambda \left(\theta -A\varphi -Rb\psi \right)\cos \mathsf{\Omega }=0$$

(14)

$$\left(1+Rd\right){\theta }^{″}+Prf{\theta }^{\prime }+EcPr\left[\left(M^2+K\right){f^{\prime }}^2+{f^{″}}^2\left(1+\frac{\beta }{2}{f}^{\prime }\right)\right] +Pr\left(N_b\theta \prime \varphi \prime +N_t\theta {\prime }^2\right)=0$$

(15)

$${\varphi }^{″}+S{c}_1\left(f{\varphi }^{\prime }-\delta \varphi \right)+\frac{N_t}{N_b}{\theta }^{″}=0$$

(16)

$${\psi }^{″}+S{c}_{2}f{\psi }^{\prime }-Pe\left\{{\psi }^{\prime }{\varphi }^{\prime }+\left(\psi +1\right){\varphi }^{″}\right\}=0.$$

(17)

And the boundary conditions

$$\{\begin{array}{l}f\left(\eta \right)=0,f^{\prime }\left(\eta \right)=1,{\theta }^{\prime }\left(\eta \right)=-B_1\left(1-\theta \left(\eta \right)\right),{\varphi }^{\prime }\left(\eta \right)=-B_2\left(1-\varphi \left(\eta \right)\right),\psi \prime \left(\eta \right)=-B_3\left(1-\psi \left(\eta \right)\right)\mathrm{at}\eta =0\\ f^{\prime }\left(\eta \right)\to 0,\theta \left(y\right)\to 0,\varphi \left(\eta \right)\to 0,\varphi \left(\eta \right)\to 0,\psi \left(\eta \right)\to 0\mathrm{at}\eta \to \infty \end{array}\},$$

(18)

where prime represents the differentiation w.r.t $\left(\eta \right)$ only, and $\beta =\mathsf{\Delta }x\sqrt{\frac{2a^3}{v}}$, $M^2=\sqrt{\frac{2\sigma B_0{}^2}{a{\rho }_f\left(n+1\right)}}$, $Pr=\frac{{\left(\rho c\right)}_{f}v}{k}$, $Sc=\frac{v}{D_m}$, $\lambda =\frac{Gr}{R{e}_x^2}$, $Ec=\frac{u_w{}^2}{c_f\left(T_f-T_{\infty }\right)}$, $Rd=\frac{16{\sigma }_{*}{T}_{\infty }^3}{3k_s{k}_f}$, $N_b=\frac{{\left(\rho c\right)}_p{D}_B\left(C_f-C_{\infty }\right)}{\alpha {\left(\rho c\right)}_f}$, $N_t=\frac{{\left(\rho c\right)}_p{D}_T\left(T_f-T_{\infty }\right)}{\alpha {\left(\rho c\right)}_f{T}_{\infty }}$, $\delta =\frac{\alpha }{a}$ $K=\frac{v}{a{k}_p}$ $Gr=\frac{g{\Lambda }_1\left(1-C_{\infty }\right){\rho }_f\beta T_{\infty }{x}^3}{{\upsilon }^2}$, $A=\frac{Gr}{Gm}=\frac{\left({\rho }_p-{\rho }_f\right)C_{\infty }}{\left(1-C_{\infty }\right){\rho }_f\beta T_{\infty }}$, $B_1=d_t\sqrt{\frac{v}{a}}$, $B_2=d_c\sqrt{\frac{v}{a}}$ and $B_3=d_n\sqrt{\frac{v}{a}}$, $S{c}_1=\frac{v}{D_m}$, $S{c}_2=\frac{v}{D_n}$, $Rb=\frac{\left({\rho }_m-{\rho }_f\right)\gamma N_{\infty }}{\left(1-C_{\infty }\right){\rho }_f\beta T_{\infty }}$, $Pe=\frac{b{W}_c}{D_n}$.

3. Entropy Generation

The effective expression in the entropy generation $E_G$ is characterized by entropy generation via heat transfer with thermal radiation, Joule dissipation, porous medium, fluid friction and diffusion effect. This is expressed as:

$$\begin{array}{l}{E}_G=\frac{k}{T_{\infty }^2}\left(1+\left(\frac{16{\sigma }_1}{3k_s{k}^{*}}{T}_{\infty }^3\right)\frac{\partial T}{\partial y}\right)+\left(\frac{\sigma B_0{}^2}{T_{\infty }}+\frac{\mu }{T_{\infty }{k}_p}\right)u^2 +\frac{\mu }{T_{\infty }}{\left(\frac{\partial u}{\partial y}\right)}^2\left(1+\frac{\mathsf{\Delta }}{\sqrt{2}}\frac{\partial u}{\partial y}\right)+\frac{R{D}_m}{C_{\infty }}{\left(\frac{\partial C}{\partial y}\right)}^2+\\ \frac{R{D}_m}{T_{\infty }}\left(\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}\right)+\frac{R{D}_m}{N_{\infty }}{\left(\frac{\partial N}{\partial y}\right)}^2+\frac{R{D}_m}{T_{\infty }}\left(\frac{\partial N}{\partial y}\frac{\partial T}{\partial y}\right)\end{array}$$

(19)

The non-dimensional entropy generation number is given by

$$\begin{array}{l}Ns=\frac{E_G}{E_0}=\left(Re\left(1+Rd\right)\theta \prime {\left(\eta \right)}^2\right)+\frac{ReBr}{\mathsf{\zeta }}\left(\left(H^2+K\right)f{\prime }^2+f\prime {\prime }^2\left(1+\frac{\beta }{2}f\prime \right)\right) +Re{\left(\frac{\mathsf{\Pi }}{\mathsf{\zeta }}\right)}^2\varphi \prime {\left(\eta \right)}^2+\\ Re{\mathsf{\Phi }}_C\left(\frac{\mathsf{\Pi }}{\mathsf{\zeta }}\right)\theta \prime \left(\eta \right)\varphi \prime \left(\eta \right) +Re{\left(\frac{\mathsf{\xi }}{\mathsf{\zeta }}\right)}^2\psi \prime {\left(\eta \right)}^2+Re{\mathsf{\Phi }}_N\left(\frac{\mathsf{\xi }}{\mathsf{\zeta }}\right)\theta \prime \left(\eta \right)\psi \prime \left(\eta \right)\end{array}$$

(20)

The Bejan number is defined as the fraction part involving the entropy generation via heat transfer and diffusion and total entropy and is given as

$$Be=\frac{\left(1+Rd\right)\theta \prime {\left(\eta \right)}^2+{\left(\frac{\mathsf{\Pi }}{\mathsf{\zeta }}\right)}^2\varphi \prime {\left(\eta \right)}^2+{\mathsf{\Phi }}_C\left(\frac{\mathsf{\Pi }}{\mathsf{\zeta }}\right)\theta \prime \left(\eta \right)\varphi \prime \left(\eta \right) +{\left(\frac{\mathsf{\xi }}{\mathsf{\zeta }}\right)}^2\psi \prime {\left(\eta \right)}^2+{\mathsf{\Phi }}_N\left(\frac{\mathsf{\xi }}{\mathsf{\zeta }}\right)\theta \prime \left(\eta \right)\psi \prime \left(\eta \right)}{\begin{array}{l}\left(1+Rd\right)\theta \prime {\left(\eta \right)}^2+\frac{Br}{\mathsf{\zeta }}\left(\left(M^2+K\right)f{\prime }^2+f\prime {\prime }^2\left(1+\frac{\beta }{2}f\prime \right)\right) +{\left(\frac{\mathsf{\Pi }}{\mathsf{\zeta }}\right)}^2\varphi \prime {\left(\eta \right)}^2+{\mathsf{\Phi }}_C\left(\frac{\mathsf{\Pi }}{\mathsf{\zeta }}\right)\theta \prime \left(\eta \right)\varphi \prime \left(\eta \right) \\ +{\left(\frac{\mathsf{\xi }}{\mathsf{\zeta }}\right)}^2\psi \prime {\left(\eta \right)}^2+{\mathsf{\Phi }}_N\left(\frac{\mathsf{\xi }}{\mathsf{\zeta }}\right)\theta \prime \left(\eta \right)\psi \prime \left(\eta \right)\end{array}}$$

(21)

The irreversibility ratio is also given as

$$\Phi =\frac{\frac{Br}{\mathsf{\zeta }}\left(\left(H^2+K\right)f{\prime }^2+f\prime {\prime }^2\left(1+\frac{\beta }{2}f\prime \right)\right)}{\left(1+Rd\right)\theta \prime {\left(\eta \right)}^2},$$

where $E_0=\frac{k{\left(T_f-T_{\infty }\right)}^{2}a}{T_f{}^2\upsilon }$, $\mathsf{\zeta }=\frac{T_f-T_{\infty }}{T_{\infty }}$, $\mathsf{\Pi }=\frac{\left(C_f-C_{\infty }\right)}{C_{\infty }}$, $\mathsf{\xi }=\frac{\left(N_f-N_{\infty }\right)}{N_{\infty }}$, ${\mathsf{\Phi }}_C=\frac{R{D}_m{C}_{\infty }}{k}$, ${\mathsf{\Phi }}_N=\frac{R{D}_m{N}_{\infty }}{k}$, $Br=PrEc$ and $R{e}_L=\frac{a{L}^2}{\upsilon }$.

Interesting quantities portraying the skin friction $C_f$ and the Nusselt number $Nu$, Sherwood number $Sh$ and the nanoparticle Sherwood number $N_n$ at the vertical walls are expressed below

$$C_f=\frac{p_w}{\rho u^2{}_w}, Nu=\frac{q_w}{k_f\left(T_f-T_{\infty }\right)},Sh=\frac{j_w}{D_m\left({\mathrm{C}}_f-{\mathrm{C}}_{\infty }\right)}\mathrm{and}{N}_n=\frac{j_n}{D_n\left(N_f-N_{\infty }\right)},$$

(22)

where $p_w,$$q_w$, $j_w$ and $j_n$ are defined as:

$$p_w={\mu \left(\frac{\partial u}{\partial y}+\frac{\mathsf{\Delta }}{\sqrt{2}}{\left(\frac{\partial u}{\partial y}\right)}^2\right)|}_{y=0},q_w=\left(1+\frac{16{\sigma }_1}{3k_1{k}_f}{T}_{\infty }^3\right){\frac{\partial T}{\partial y}|}_{y=0},j_w=D_m{\frac{\partial C}{\partial y}|}_{y=0}\mathrm{and}{j}_n=D_n{\frac{\partial N}{\partial y}|}_{y=0}.$$

(23)

The dimensionless forms are

$$\begin{array}{l}{\mathrm{Re}}_r{}^{0.5}{C}_f=f^{″}\left(0\right)+\frac{\beta }{2}{\left(f^{″}\left(0\right)\right)}^2,{\mathrm{Re}}_r{}^{-0.5}Nu=-\left(1+Rd\right){\theta }^{\prime }\left(0\right),\\ {\mathrm{Re}}_r{}^{-0.5}Sh=-{\varphi }^{\prime }\left(0\right),{\mathrm{Re}}_r{}^{-0.5}Nn=-{\psi }^{\prime }\left(0\right)\end{array}\}.$$

(24)

4. Numerical Solution

In the present investigation, an effective numerical scheme, Runge-Kutta-4 with a shooting method, has been explored to examine the stream model Equations (14)–(17) in conjunction with boundary constraints (18) for varying values of governing parameters. The choice of step size and convergence criteria is carefully made to be 0.001 and 10⁻⁶ respectively. In the absence of Williamson and mixed convection parameters for the special case of the model, the current results are in accordance with those conveyed by [28], as depicted in

Table 1. Comparison of the skin friction coefficient for several values of the magnetic parameter when $\beta =\lambda =K=0$.

${\mathit{M}}^2$	0	1	5	10	50	100	500
Mabood & Das [28]	1.000008	−1.4142135	−2.4494897	−3.3166247	−7.1414284	−10.049875	−22.383029
Present results	1.00000	−1.4142136	−2.4494897	−3.3166247	−7.1414284	−10.049876	−22.383029

, and this serves as a benchmark for the accuracy of our numerical procedure.

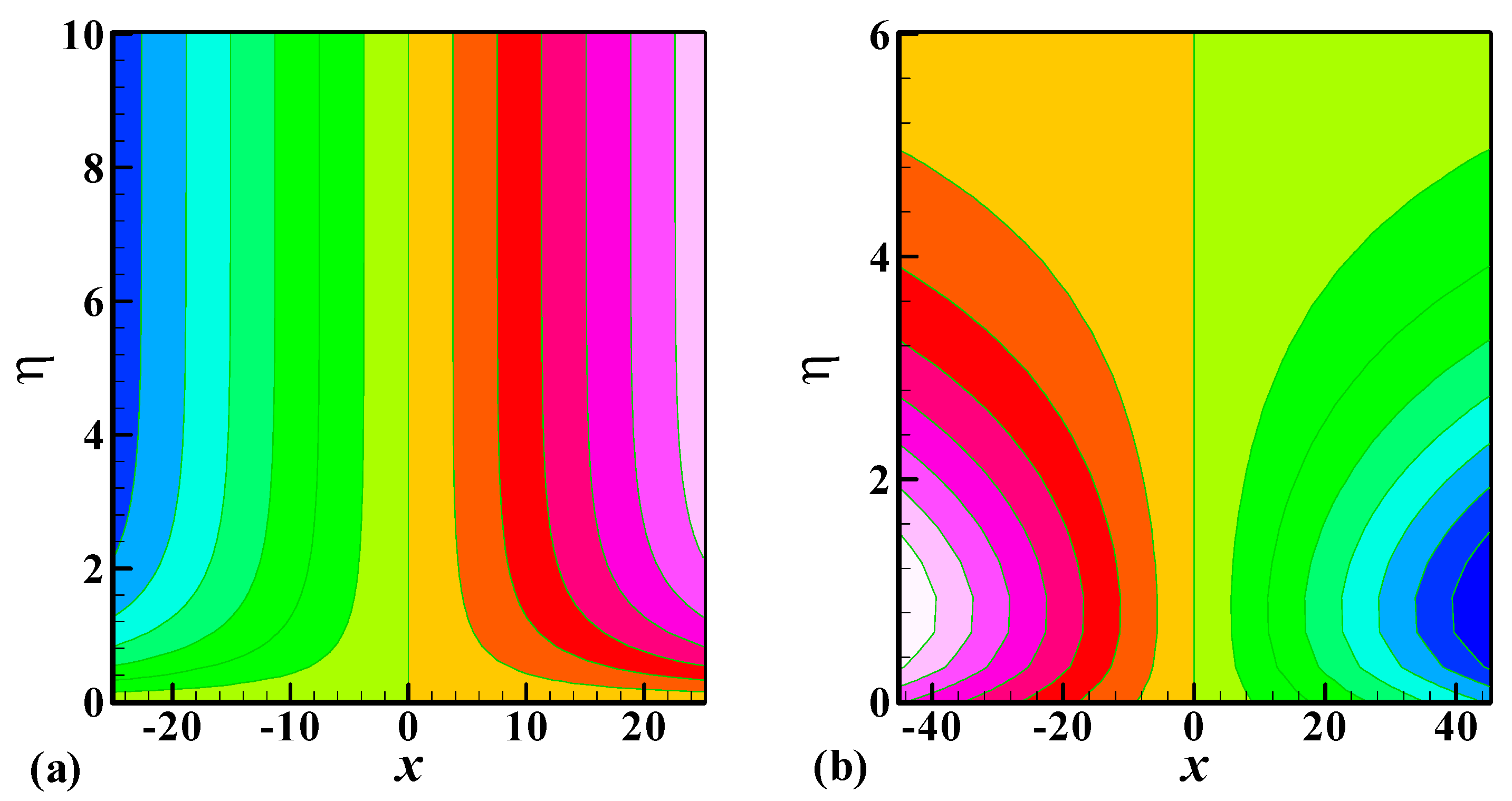
5. Results and Discussion

The main aspect of this section is to scrutinize the entropy production in a mixed convective stream of Williamson nanofluid along an inclined semi-infinite plate embedded in a porous medium, taking account of gyrotactic microorganisms and thermal radiation. The described flow pattern is expressed in terms of PDEs. The framed PDEs are reduced to ODEs by opting suitable similarity variables. To understand this, the ODE’s with the boundary constraints, they are solved by applying an efficient numerical scheme Runge-Kutta-4 with shooting technique. In this section, the behavior of the magnetic field parameter $\left(M\right)$, Williamson parameter $\left(\beta \right)$, porosity parameter $\left(K\right)$, buoyancy forces ratios $\left(A\right)$, angle inclination parameter $\left(\mathsf{\Omega }\right)$ mixed convection parameter $\left(\lambda \right)$, Biot numbers due to heat transfer $(B_2)$, thermal radiation $(Rd)$, bioconvection Schmidt number $(S{c}_2)$, the Biot numbers due to mass transfer $\left(B_3\right)$ and the bioconvection Peclet number $\left(Pe\right)$ on the dimensionless velocity, thermal, concentration, microorganism, mass transfer rate $\left(Sh\right)$, heat transfer rate $\left(Nu\right)$, skin friction ..coefficient, and motile microorganisms transfer rate $\left(Nn\right)$, on entropy generation rate via friction variation $(N_{Gf})$, entropy generation rate via heat variation $(N_{Gh})$, the irreversibility ratio $(\Phi )$, the total entropy generation rate $\left(N_G\right)$ and the Bejan number $\left(Be\right)$ are revealed in Figures [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17].

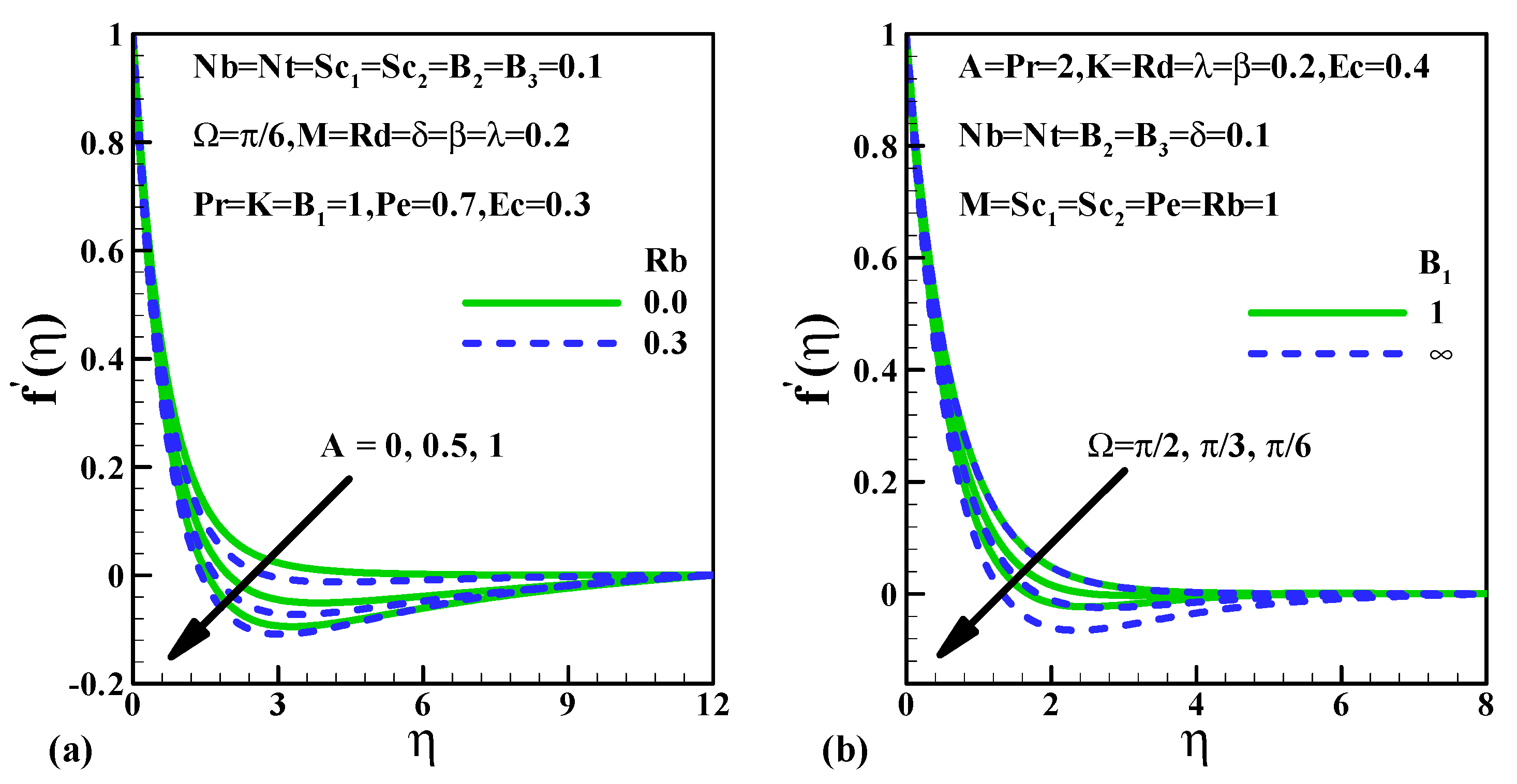
5.1. Flow Characteristics

Figure 2a portrays the influence of $M$ on velocity gradient for dual values of porosity parameter. Here, the escalation in values of $M$ decays the velocity gradient. Physically, inclination in M creates a resistive force to the fluid motion which automatically declines the velocity gradient. Further, the rate of declination in the velocity gradient is faster in the presence of a porous medium when compared to the absence of a porous medium. Physically, the presence of a porous medium creates the resistance to the fluid motion due to which fluid velocity decreases. The sway of mixed convection parameter on the velocity gradient in the presence and absence of Williamson parameter is displayed in Figure 2b. It is seen from the plotted figure that boost up values of $\lambda$ escalate the velocity gradient. Materially, upsurge in $\lambda$ produces a higher thermal buoyancy force, which is the reason for the inclination in the velocity of the liquid. Further, rate of inclination is slightly faster for the case $\beta =0$ when compared to $\beta =0.2$. Figure 3a displays the sway of buoyancy forces ratios on velocity gradient in the presence and absence of thermal radiation parameter. One can notice from the plotted figure that, boost up values of $A$ declines the velocity of the fluid motion. Further, the rate of declination in the velocity gradient is faster in the presence of thermal radiation parameter. Figure 3b portrays the impact of angle inclination parameter on velocity gradient for the case $B_1=0$ and $B_1=\infty$. The result reveals that declination in angle inclination parameter declines the velocity of the fluid motion. Further, the rate of declination in the velocity gradient is little bit faster for the case $B_1=\infty$ when compared to $B_1=0$.

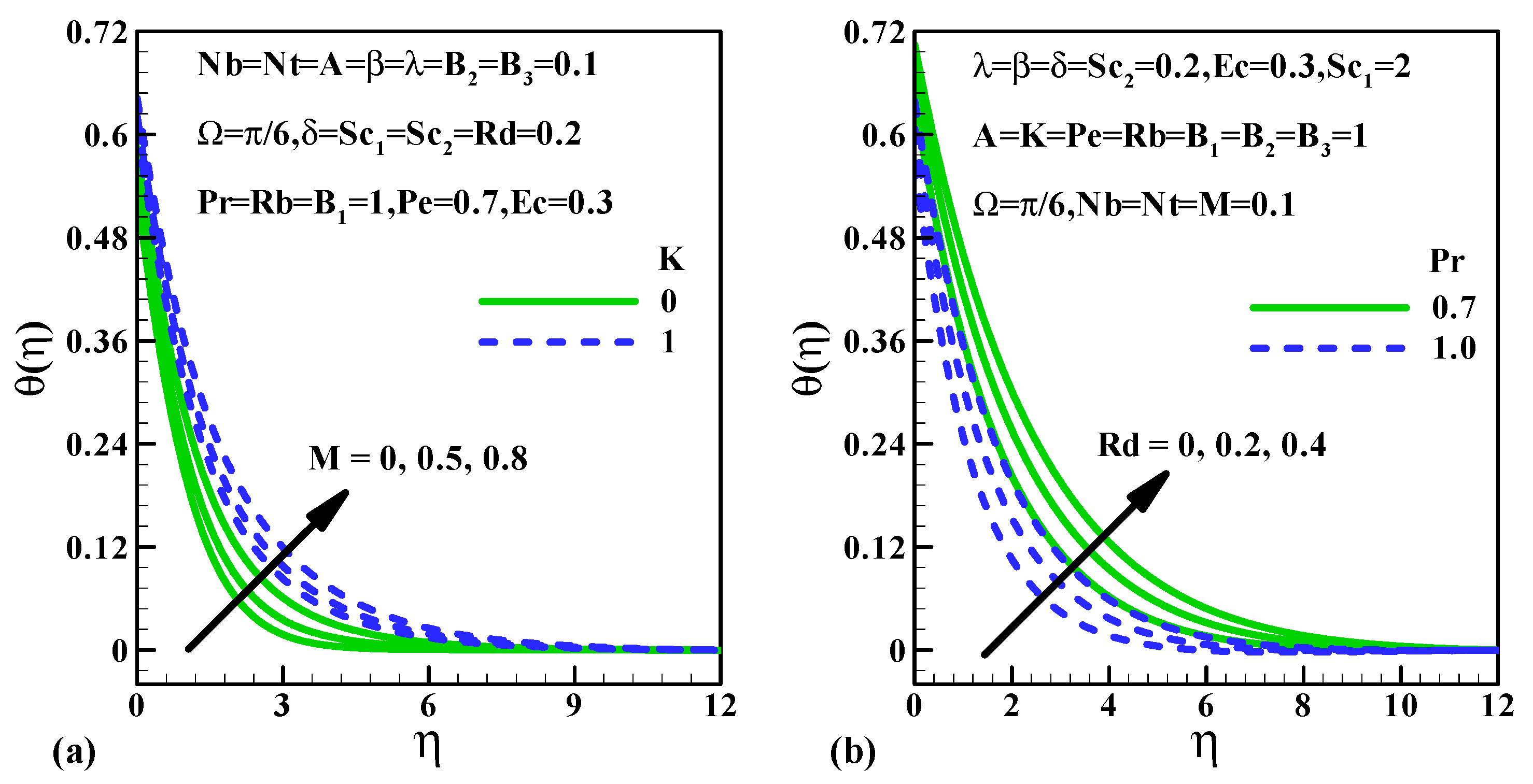
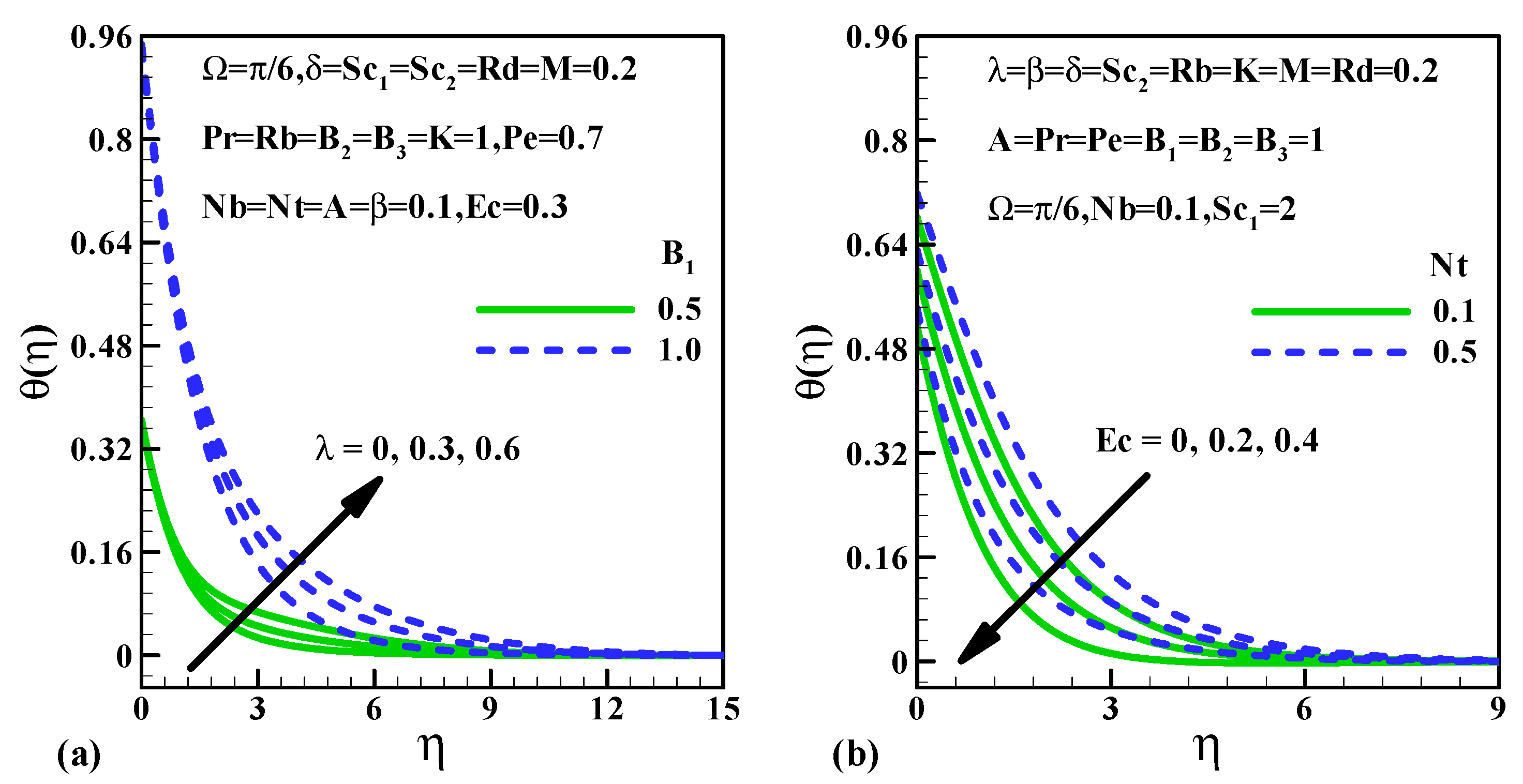
5.2. Heat Transfer Characteristics

Figure 4a reveals the sway of +$M$ on the thermal gradient for dual values of porosity parameter. It is observed from the figure that escalation in the values of $M$ improves the thermal gradient. Further, the rate of inclination in the thermal gradient is faster in the presence of a porosity meter. Physically, the presence of a porous medium with inclination in magnetic parameter produces resistance to the fluid motion, which automatically upsurges the thermal gradient. The sway of the thermal radiation parameter on the thermal gradient for the case $Pr=0$ and $Pr=1$ is illustrated in Figure 4b. Here, the heightening of $Rd$ heightens the thermal gradient. Physically, inclined values of $Rd$ produce inner heat, which is the reason for the inclination of the thermal gradient. Here, the rate of inclination in the thermal gradient of the fluid is faster for a lower $Pr$ value case when compared to a higher $Pr$ value case. The sway of $\lambda$ on the thermal gradient for the cases $B_1=0.5$ and $B_1=1$ is displayed in Figure 5a. It is detected from the plotted graph that the rise in values of $\lambda$ improves the thermal gradient. Further, the rate of inclination is faster for case $B_1=1$ when compared to $B_1=0.5$. Figure 5b portrays the dual solutions for the impact of $Ec$ on the thermal gradient. It is noticed in the plotted figure that escalating values of $Ec$ decline the thermal gradient. Moreover, the rate of declination in heat transfer is faster for the case $N_t=0.1$ when compared to $N_t=0.5$.

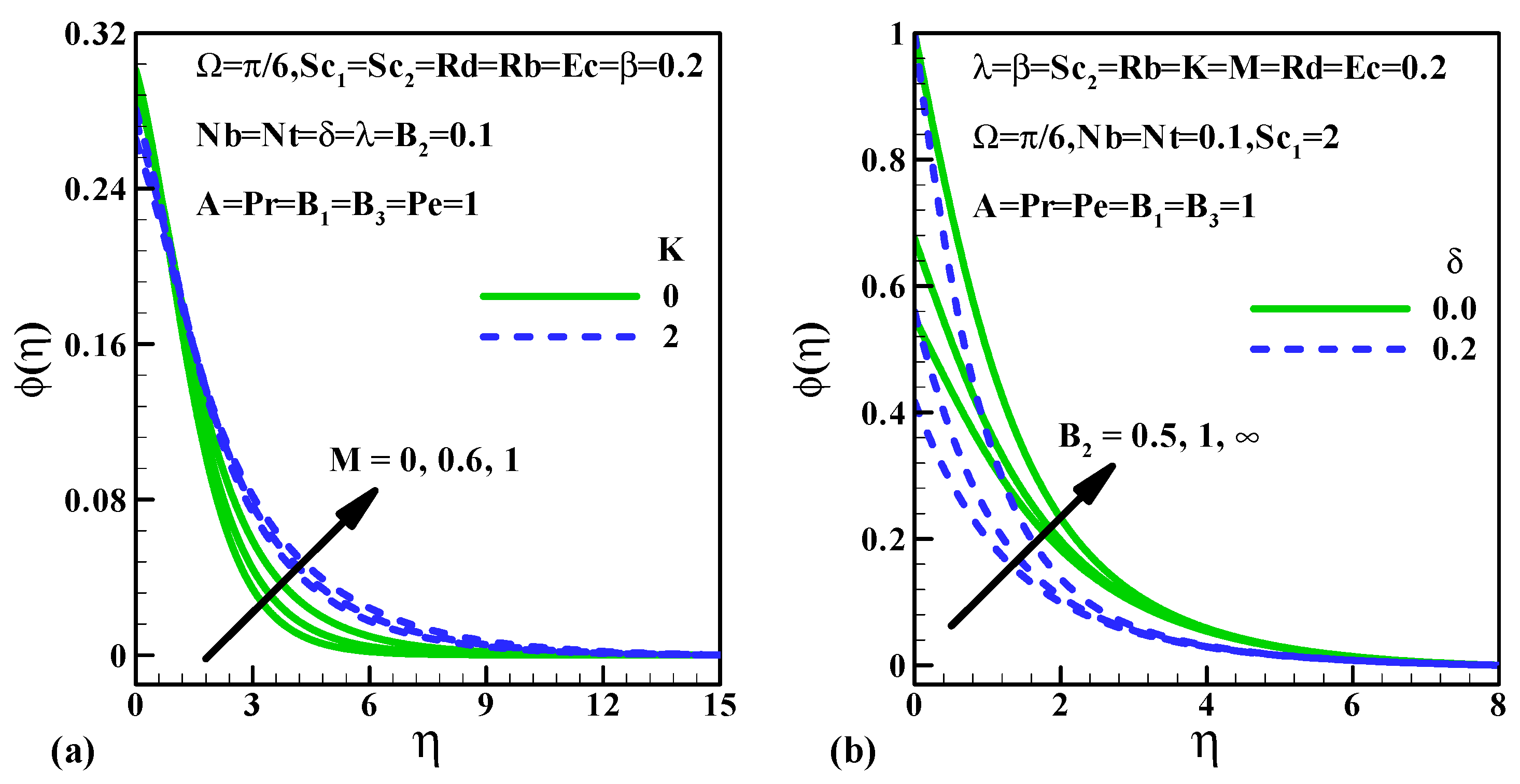
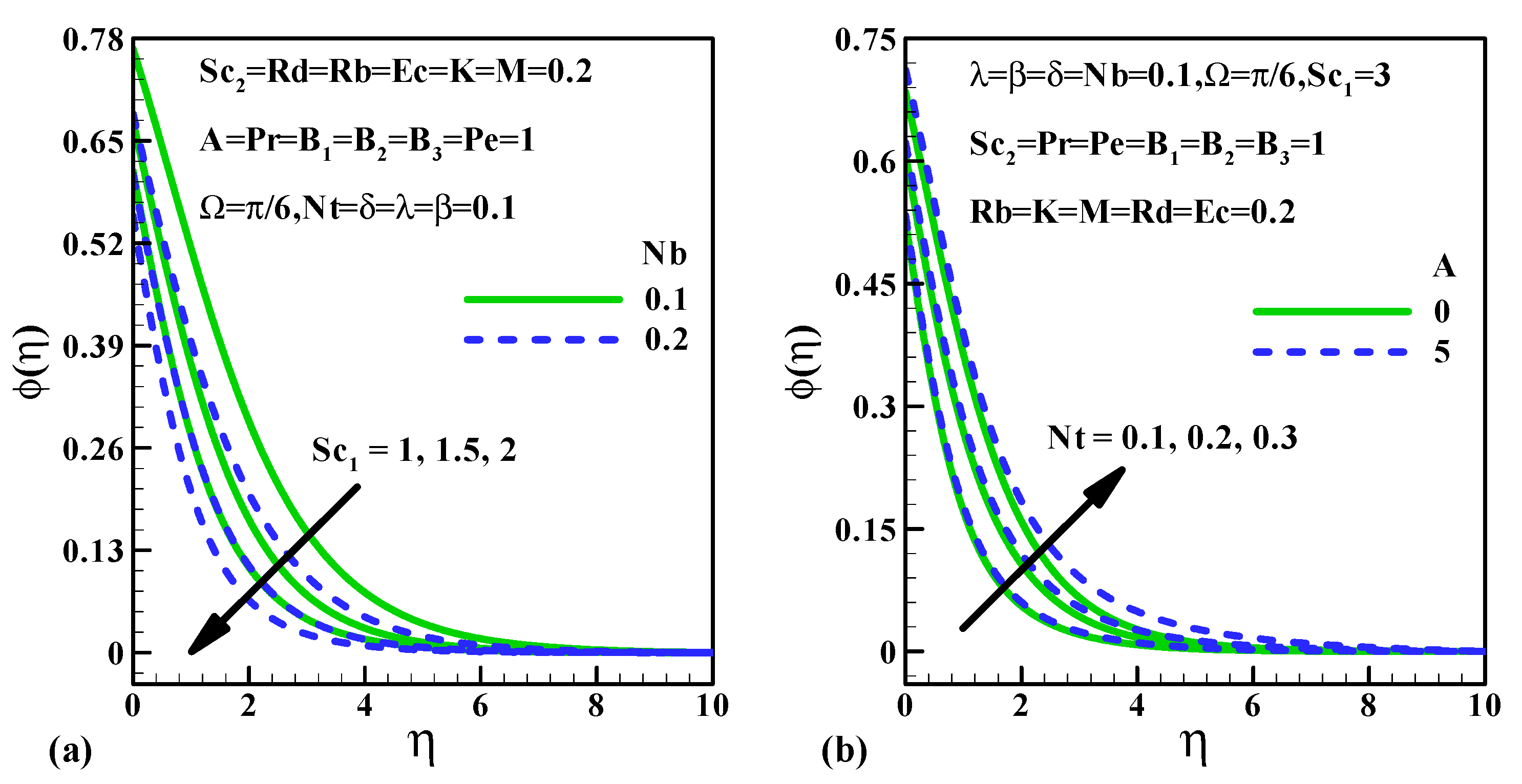
5.3. Mass Transfer Characteristics

Figure 6a portrays the multiple solution for the influence of $M$on mass transfer. One can notice from the plotted figure that escalation in $M$ escalates the concentration gradient. Further, the rate of inclination is faster in the presence of a porous medium. The sway of $B_2$ on the concentration gradient for dual cases of $\delta$ is depicted in Figure 6b. It is detected from graph that a rise in the values of $B_2$ improves the mass transfer. The further rate of inclination is slower in the presence of the chemical reaction rate parameter. The multiple solutions for the fluctuation in the concentration gradient for diverse values of Schmidt number are depicted in Figure 7a. Here, a rise in the values of the Schmidt number declines the mass transfer characteristics. In the physical fact of sight, an increase in the Sc lessens the molecular diffusivity and it results in the declination of the concentration gradient. Further, the rate of declination in mass transfer is faster for case $N_b=0.2$ when compared to $N_b=0.1$. Figure 7b portrays the impact of $N_t$ on the concentration gradient in both the presence and absence of $A$. One can notice from the graph that the upsurge in $N_t$ improves the mass transfer. Further, the rate of inclination in the concentration gradient is faster in the presence of $A$ when compared to the absence of $A$.

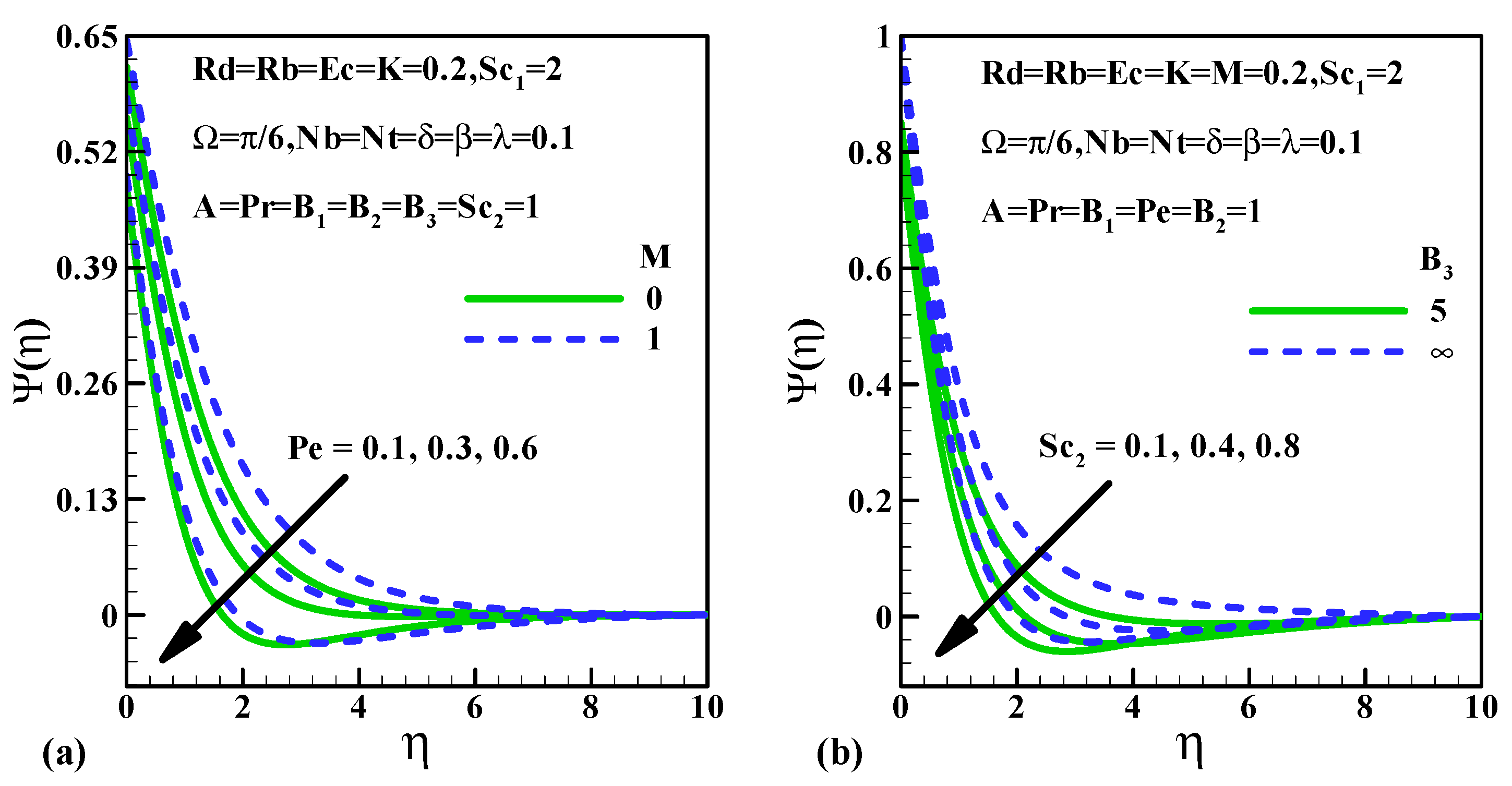
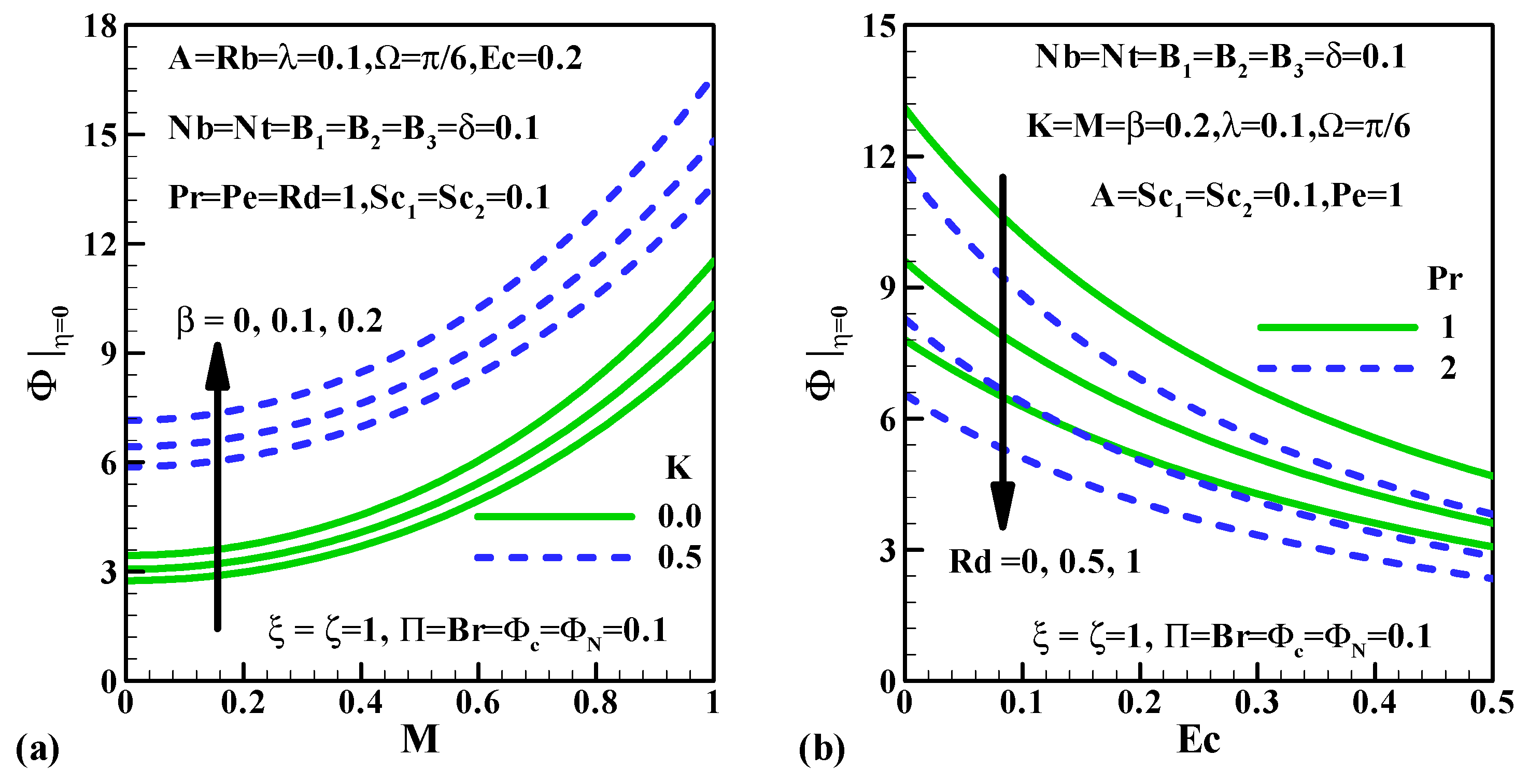
5.4. Microorganism Density Characteristics

The sway of the bioconvection Peclet number on the microorganism profile in the absence and the presence of magnetic parameter is portrayed in Figure 8a. Here, a rise in the values of $Pe$ declines the Microorganism density characteristics. The rate of declination in the microorganism profile is faster in the absence of the magnetic parameter when compared to the presence of $M$. The influence of bioconvection Schmidt number on microorganism profile for the cases $B_3=5$ and $B_3=\infty$ is illustrated in Figure 8b. Here, the inclined values of the bioconvection Schmidt number declines the microorganism profile. The rate of declination in the microorganism profile is faster for case $B_3=5$ when compared to $B_3=\infty$.

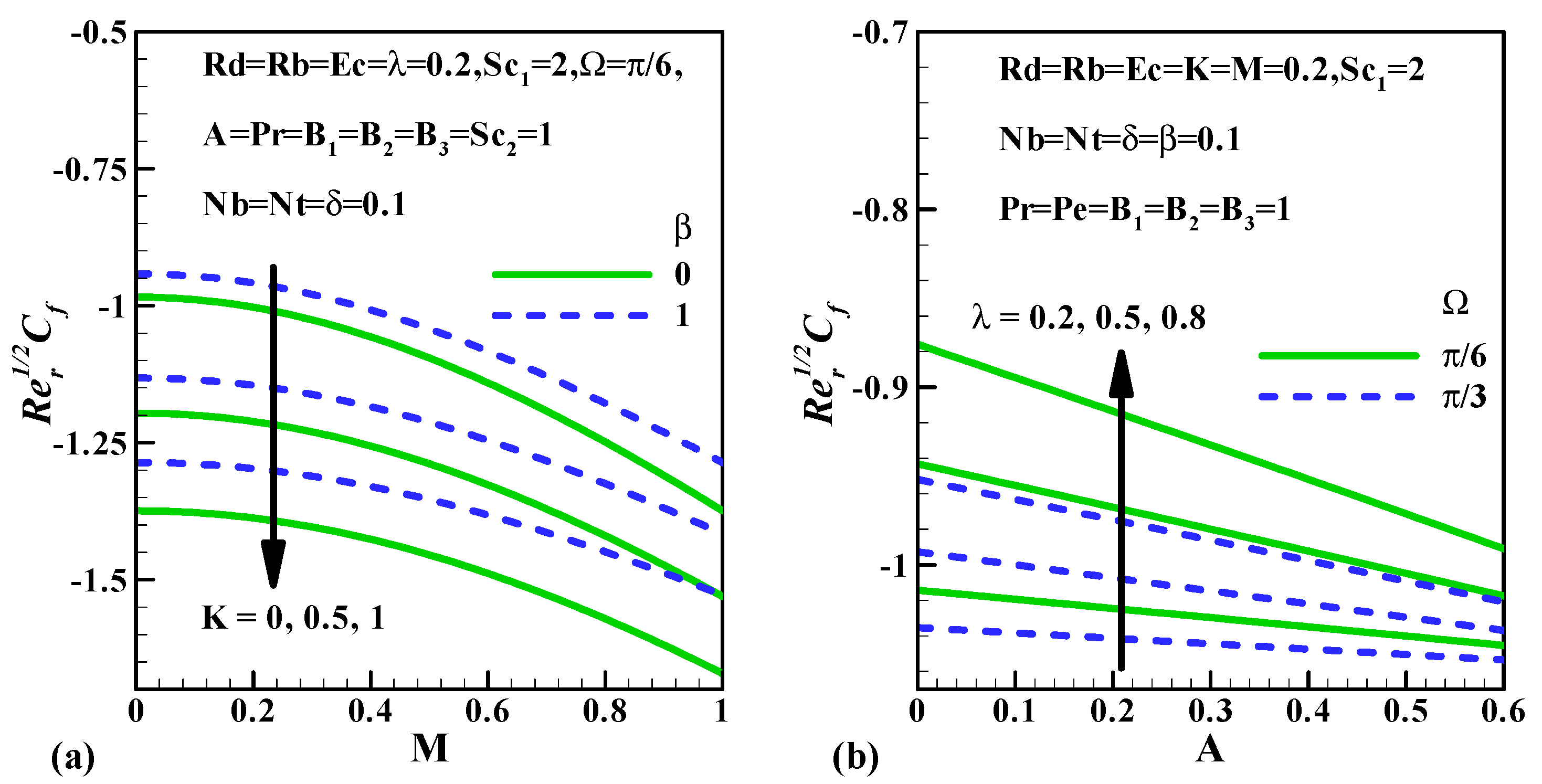
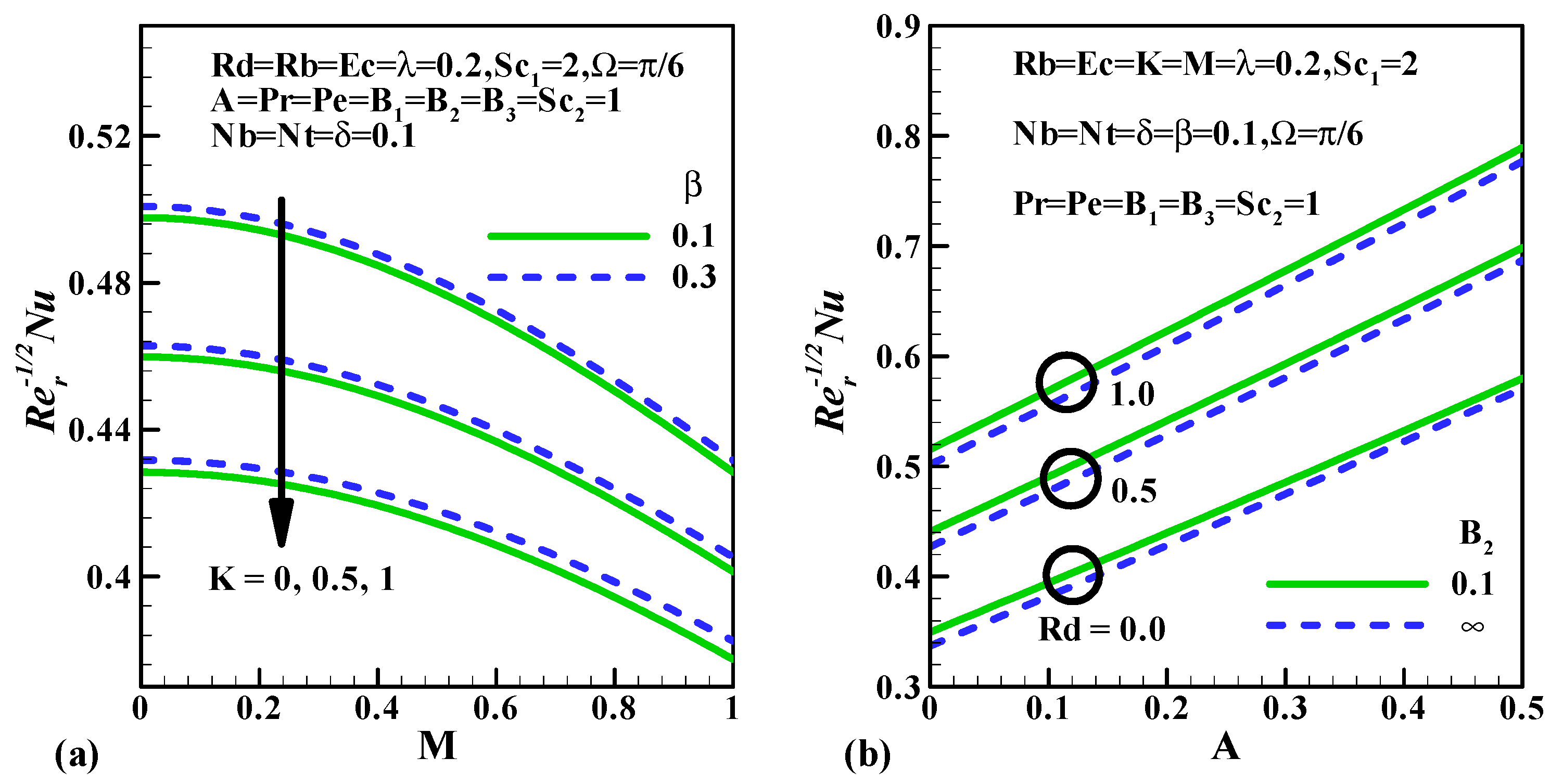
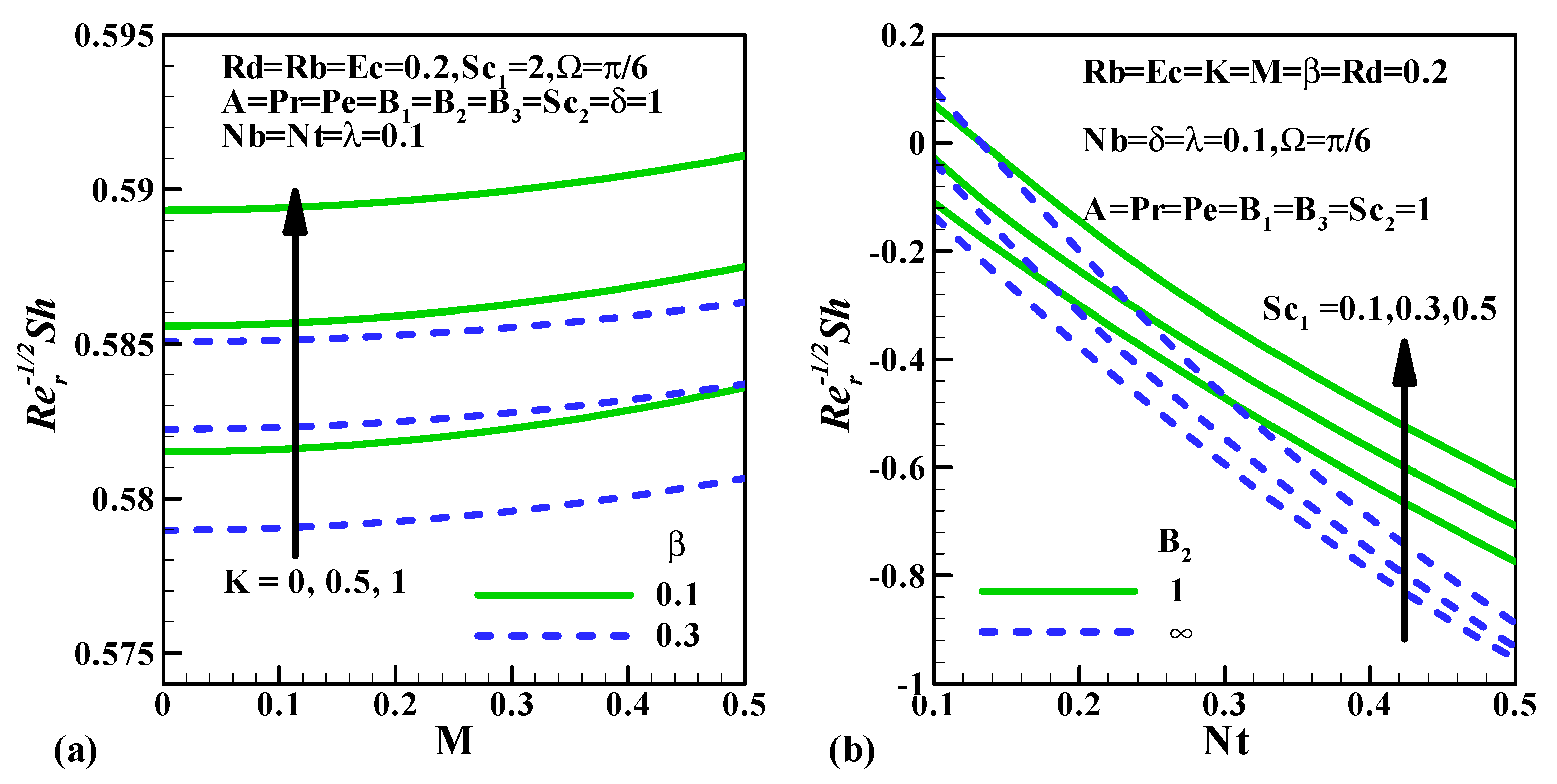
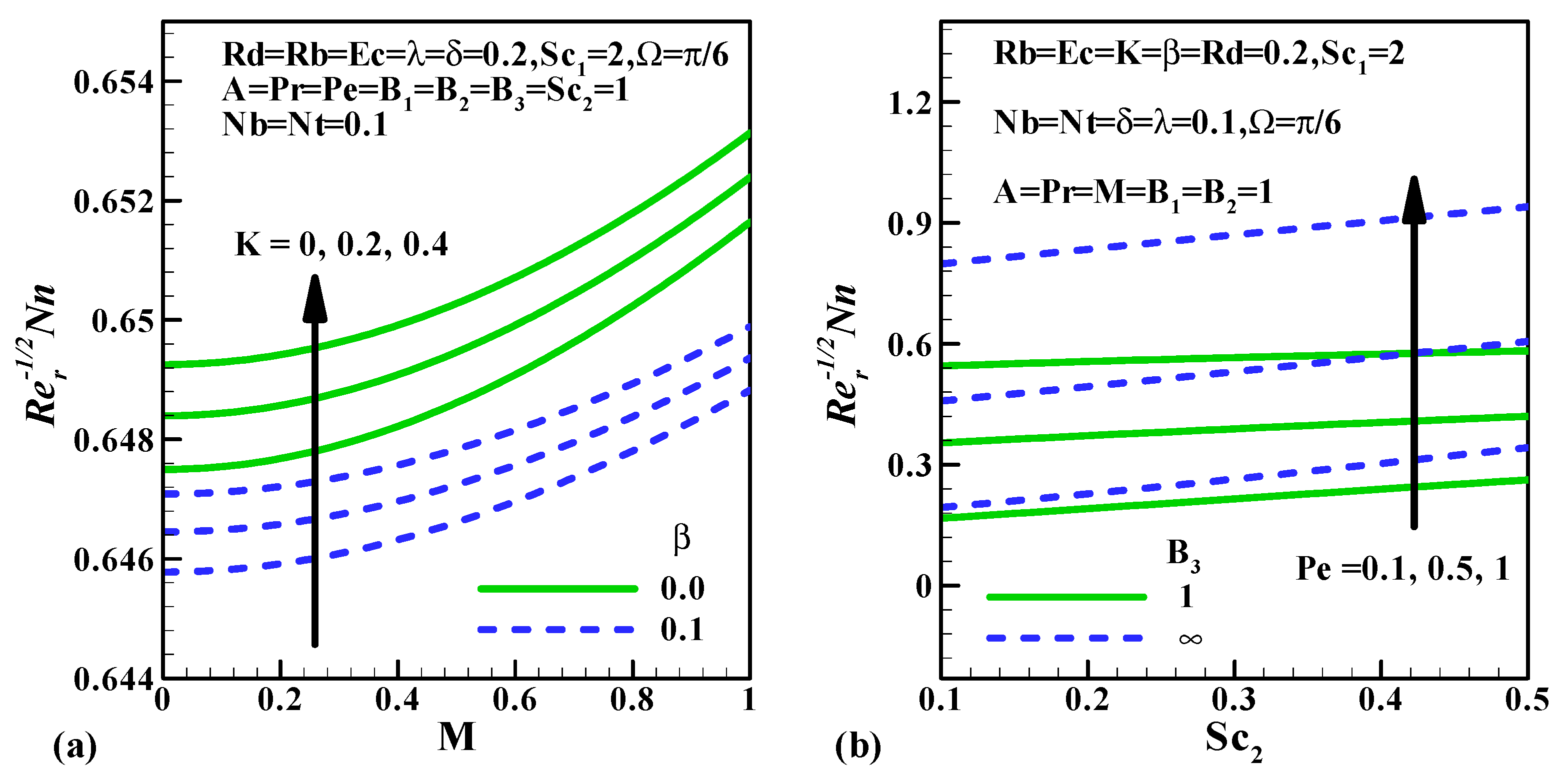
5.5. Skin Friction Coefficient, Nusselt Number, Sherwood Number and the Density Number of the Motile Microorganisms

The influence of $K$ on $R{e}_r{}^{1/2}{C}_f$ versus $M$ in the presence and absence of the Williamson parameter is represented in Figure 9a. Here, the heightening of $K$ decays the friction factor. Moreover, the rate of declination in skin friction is faster in the absence of $\beta$ and skin friction acts as a decreasing function of the magnetic parameter. The sway of $\lambda$ on $R{e}_r{}^{1/2}{C}_f$ versus $A$ for dual values of $\mathsf{\Omega }$ is illustrated in Figure 9b. Here, the inclined values of $\lambda$ improve the skin friction coefficient. Further, the rate of inclination in the friction factor is faster for case $\mathsf{\Omega }=\mathsf{\pi }/6$ when compared to $\mathsf{\Omega }=\mathsf{\pi }/3$ and the friction factor acts as a decreasing function of $A$. The dual solutions for the influence of K on $R{e}_r{}^{-1/2}Nu$ versus $M$ are portrayed in Figure 10a. One can notice from plotted figure that an upsurge in $K$ declines the rate of heat transfer. The rate of declination in the Nusselt number is faster for case $\beta =0.1$ when compared to $\beta =0.3$ and the Nusselt number acts as a decreasing function of the magnetic parameter. The sway of $Rd$ on $R{e}_r{}^{-1/2}Nu$ versus $A$ for cases $B_2=0.1$ and $B_2=\infty$ is portrayed in Figure 10b. It can be detected from the plotted figure that a rise in values of $Rd$ improves the rate of heat transfer.

Furthermore, the rate of inclination in the heat transfer rate is faster for case $B_2=0.1$ when compared to $B_2=\infty$. The twin solutions for the influence of K on $R{e}_r{}^{-1/2}Sh$ versus $M$ are portrayed in Figure 11a. Here, an escalation in $K$ increases the mass transfer rate. Further, the rate of inclination in the mass transfer rate is faster for lower values of the Williamson parameter and also the Sherwood number acts as a growing function of $M$. Figure 11b displays the sway of the Schmidt number on the rate of mass transfer versus $N_t$ for cases $B_2=1$ and $B_2=\infty$. Here, the boost up values of the Schmidt number decline the mass transfer rate. Furthermore, the rate of declination in the mass transfer rate is faster for case $B_2=\infty$ when compared to $B_2=1$ and the Sherwood number acts as a decreasing function of $A$. The sway of the porosity parameter on the microorganisms transfer rate versus the magnetic parameter in the presence and absence of the Williamson parameter is displayed in Figure 12a. Here, an inclination in $K$ improves the rate of the microorganism’s transfer. Further, the rate of inclination in the microorganism’s transfer rate is faster in the absence of $\beta$ and the microorganism transfer rate acts as a growing function of $M$. The sway of $Pe$ on the microorganism transfer rate versus $S{c}_2$ for cases $B_3=1$ and $B_3=\infty$ is depicted in Figure 12b. One can notice from the plotted graph that a rise in the values of $Pe$ improves the microorganism transfer rate and the rate of inclination in the microorganism transfer rate is faster for case $B_3=\infty$ when compared to $B_3=1$. Further, the microorganism transfer rate acts as an increasing function of $S{c}_2$.

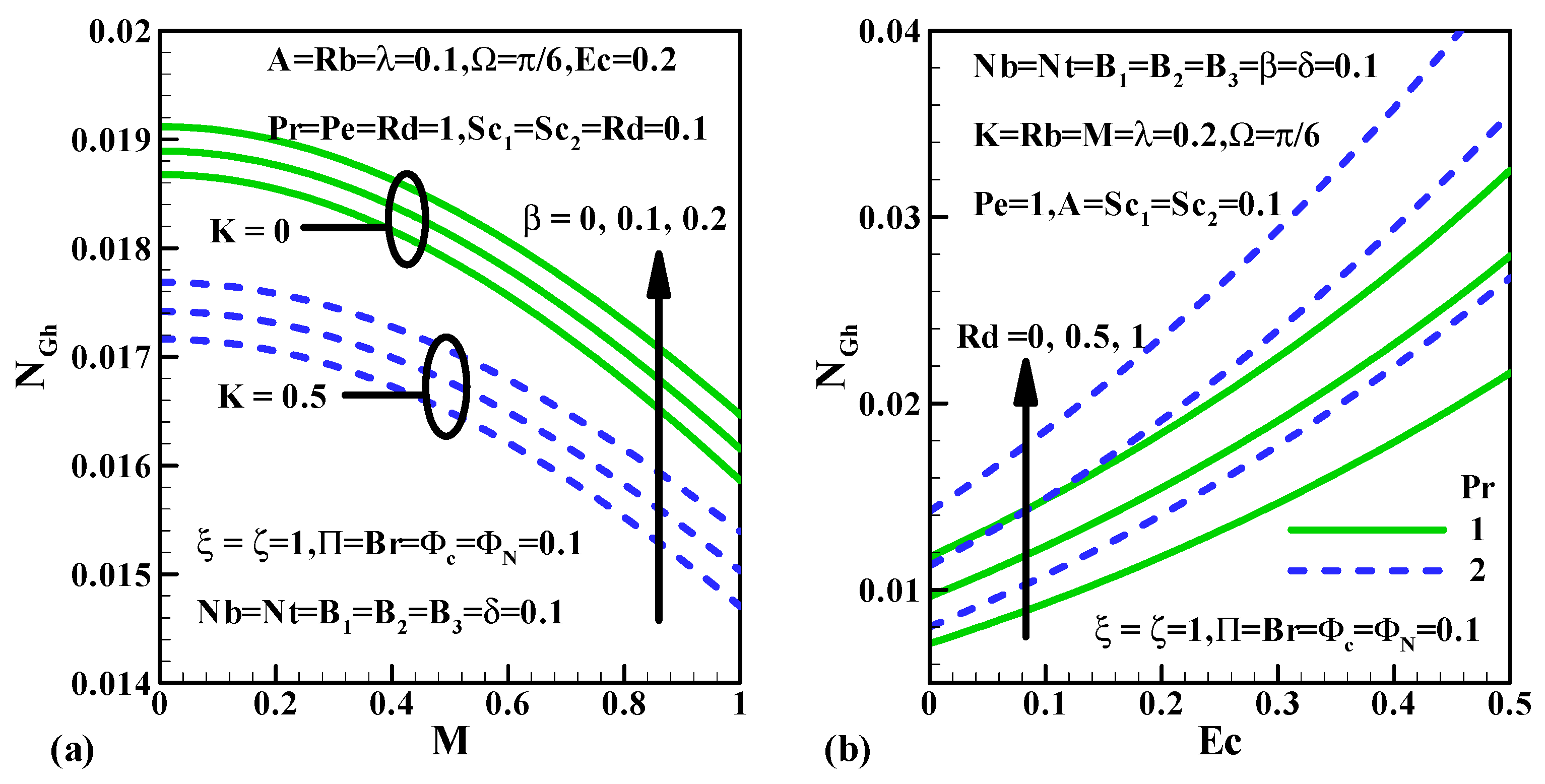
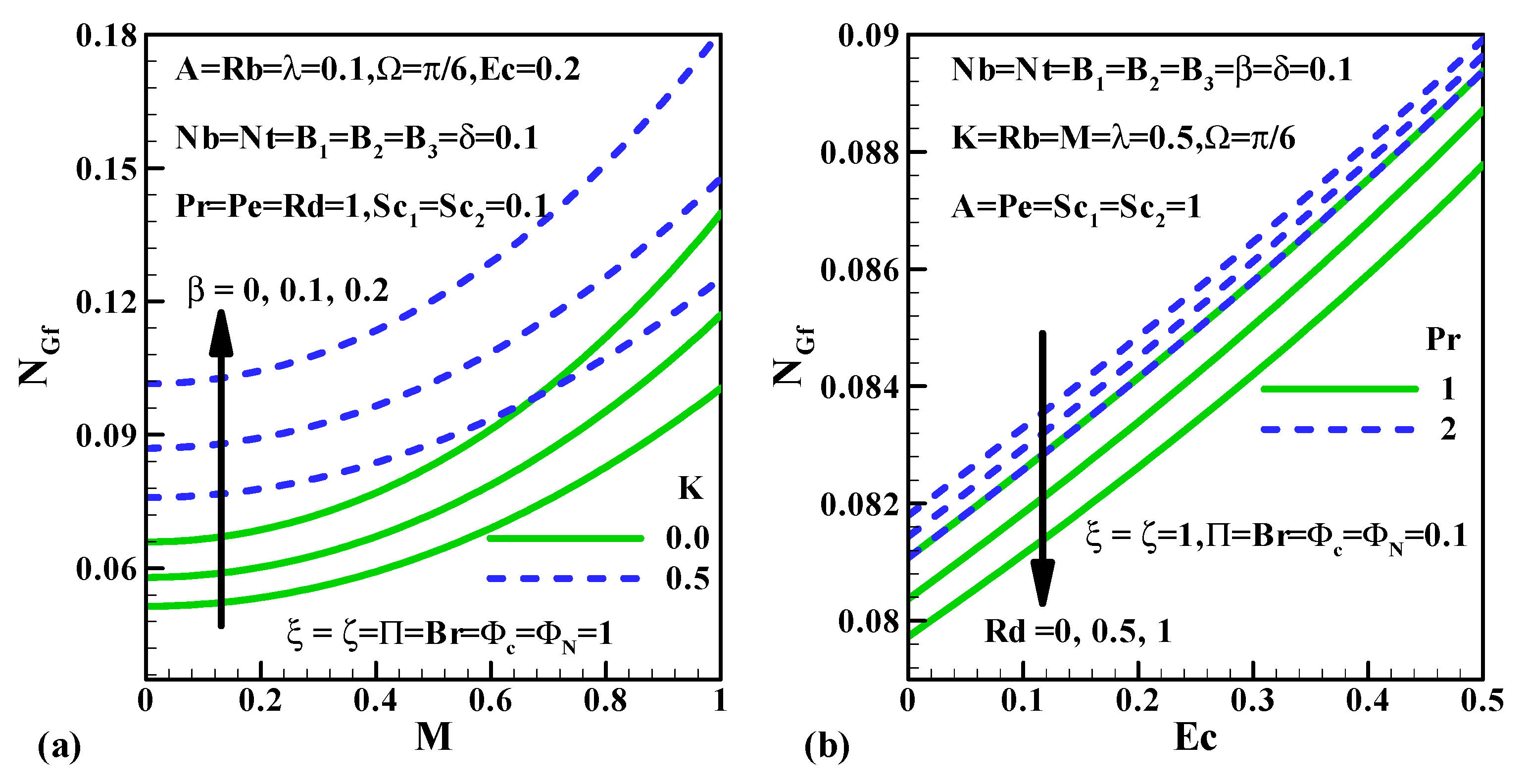
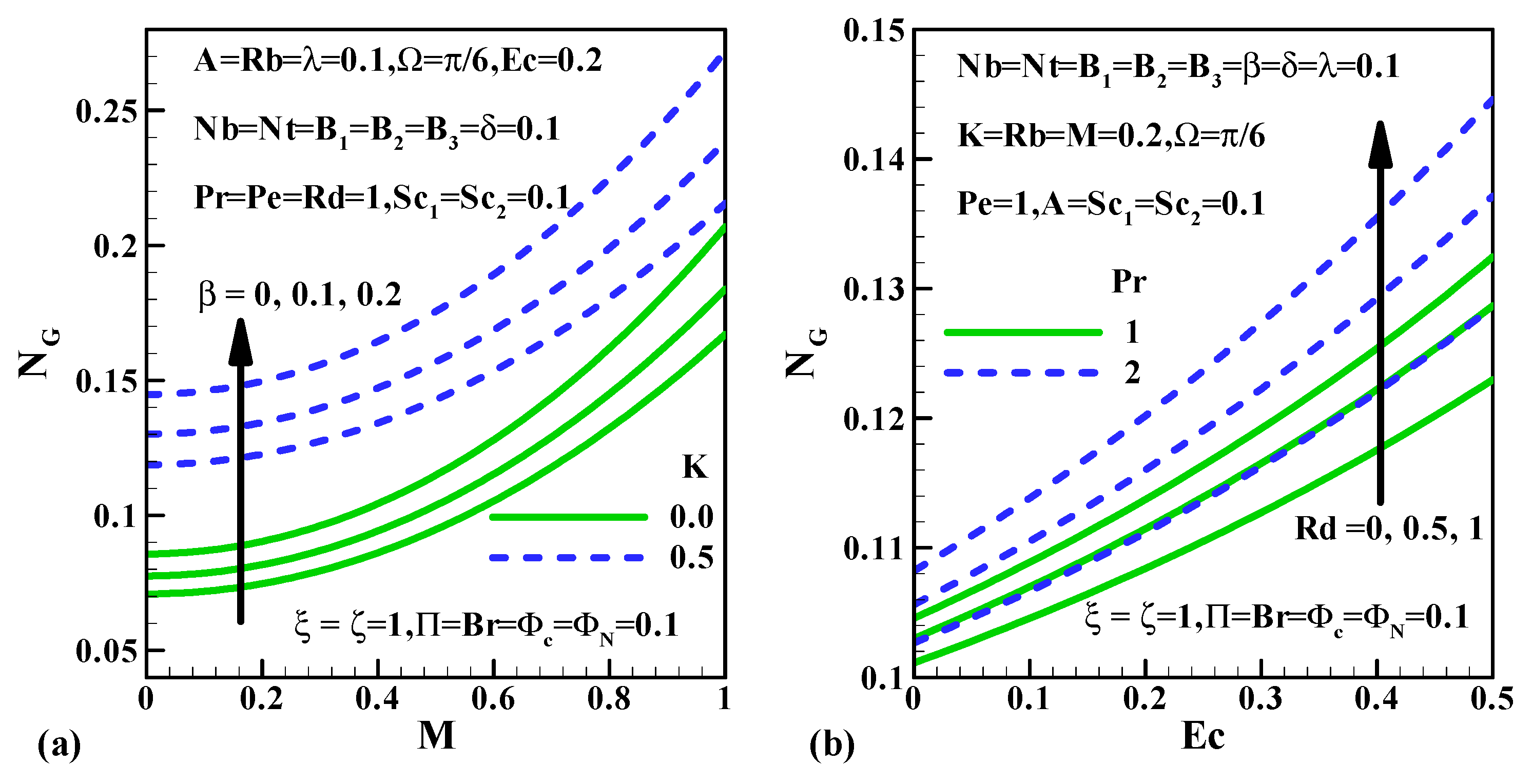
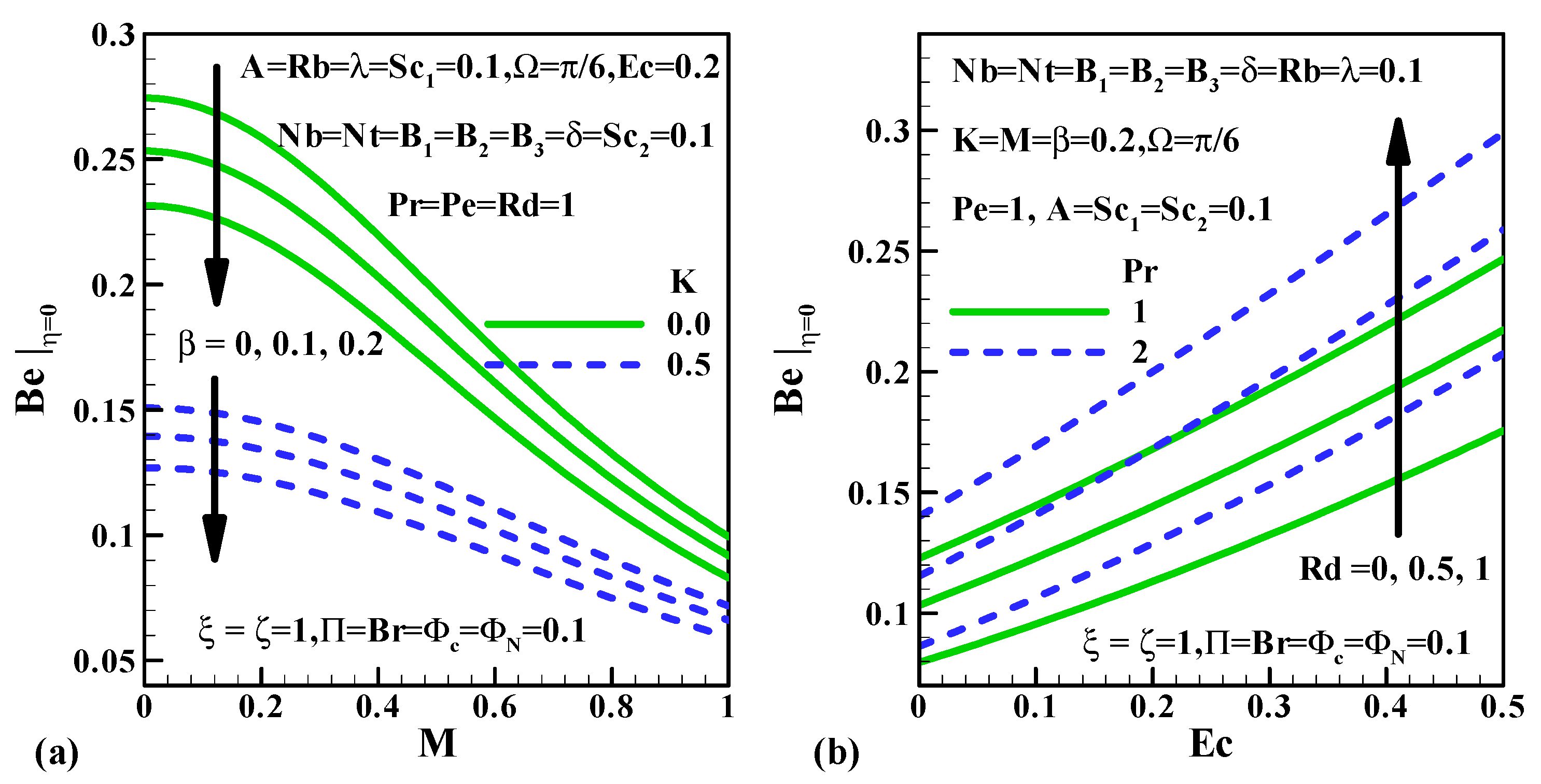
5.6. Entropy Generation, Bejan Number and Irreversibility Ratio

The influence of $\beta$ on the entropy generation rate due to heat variation versus $M$ in the presence and absence of the porosity parameter is portrayed in Figure 13a. It is seen from the figure that the upsurge in $\beta$ improves the $N_{Gh}$. Further, the rate of inclination in $N_{Gh}$ is faster in the absence of $K,$ and $N_{Gh}$ acts as a decreasing function of $M$. The sway of $Rd$ on the entropy generation rate due to heat variation versus $Ec$ for the cases $Pr=1$ and $Pr=2$ is portrayed in Figure 13b. It is observed from the plotted graph that the boost up values of $Rd$ improve the $N_{Gh}$. Further, the rate of inclination in $N_{Gh}$ is faster for higher $Pr$ values. Here, $N_{Gh}$ acts as a growing function of $Ec$. The influence of $\beta$ on the entropy generation rate due to friction action versus $M$ in the presence and absence of porosity parameter is portrayed in Figure 14a. It is seen from the figure that an upsurge in $\beta$ improves the $N_{Gf}$. Further, the rate of inclination in $N_{Gf}$ is faster in the presence of $K$ and $N_{Gf}$acts as an increasing function of $M$. The sway of $Rd$ on the entropy generation rate due to friction action versus $Ec$ for cases $Pr=1$ and $Pr=2$ is portrayed in Figure 14b. It is observed from the plotted graph that the boost up values of $Rd$ declines the $N_{Gf}$. Further, the rate of declination in $N_{Gf}$ is slower for higher $Pr$ values. Here, $N_{Gh}$ acts as a growing function of $Ec$. The sway of $\beta$ on the entropy generation profile in the presence and absence of $K$ is portrayed in Figure 15a. Here, inclination in $\beta$ escalates the entropy generation rate. The rate of inclination in the entropy generation rate is faster in the presence of $K$ and $N_G$acts as an increasing function of $M$. The control of $Rd$ on the entropy generation rate versus $Ec$ for cases $Pr=1$ and $Pr=2$ is portrayed in Figure 15b. It is observed from the plotted graph that the boost up values of $Rd$ improve the $N_G$. Moreover, the rate of inclination in $N_G$ is faster for higher $Pr$ values and $N_G$ acts as a growing function of $Ec$.

The influence of $\beta$ on $Be$versus $M$ in the presence and absence of the porosity parameter is portrayed in Figure 16a. it is seen from the figure that an upsurge in $\beta$ declines the Bejan number. Further, the rate of declination in $Be$ is faster in the presence of $K$ and $Be$acts as a decreasing function of $M$. The power of $Rd$ on the Bejan number versus $Ec$ for cases $Pr=1$ and $Pr=2$ is portrayed in Figure 16b. It is observed from the plotted graph that the boost up values of $Rd$ improve the $Be$. Further, the rate of inclination in $Be$ is faster for higher $Pr$ values and $N_G$ acts as a growing function of $Ec$. The sway of $\beta$ on the irreversibility ratio in the presence and absence of $K$ is portrayed in Figure 17a. Here, the inclination in $\beta$ escalates the irreversibility ratio. Further, the rate of inclination in the irreversibility ratio rate is faster in the presence of $K$ and $\mathsf{\Phi }$acts as a cumulative function of $M$. The sway of $Rd$ on the irreversibility ratio versus $Ec$ for the cases $Pr=1$ and $Pr=2$ is portrayed in Figure 17b. It is observed from the plotted graph that the boost up values of $Rd$ declines the $\mathsf{\Phi }$. Further, the rate of declination in $\mathsf{\Phi }$ is faster for higher $Pr$ values. Here, $\mathsf{\Phi }$ acts as a decreasing function of $Ec$. Figure 18a portrays the streamlines pattern. Generally, streamlines are the path of imaginary particles suspended in the liquid and carried along with it. Figure 18b portrays the isotherms pattern. Physically, an isotherm is the relationship between the fluid and concentrations of a solid particle, used to describe states of no change in the sorption process.

6. Conclusions

In this article, a numerical simulation for an incompressible, two-dimensional, steady, mixed convective flow of Williamson nanofluid along an inclined semi-infinite plate embedded in a porous medium under the influence of gyrotactic microorganisms and thermal radiation is examined. Applications of this scrutiny are comprised of magnetohydrodynamic propulsion thermo-fluid dynamics materials processing and laminar magneto-aerodynamics. The characteristics of velocity, thermal, concentration, entropy generation and microorganisms’ profiles have been deliberated under the influence of involved flow controlling physical parameters. The main outcomes of the present investigation are as follows:

➢

The escalation in values of $M$ declines the velocity gradient and improves the thermal and concentration gradients.

➢

The inclination in radiation parameter improves the thermal gradient.

➢

The rise in values of the Schmidt number declines the mass transfer characteristics but the converse trend is depicted for the boost up values of $N_t$.

➢

The escalating values of $Ec$ decline the thermal gradient.

➢

The rise in values of $Pe$ and $S{c}_2$ declines the microorganism density characteristics.

➢

The inclination in $\beta$ and $Rd$ escalates the entropy generation rate.

➢

The upsurge in $\beta$ declines the Bejan number and the irreversibility ratio but the converse trend is depicted in both the profiles for inclined values of $Rd$.

➢

The upsurge in $K$ declines the rate of heat transfer but the converse trend is depicted for inclined values of $Rd$.

➢

The escalation in $K$ increases the mass transfer rate but the converse trend is depicted for inclined values of $S{c}_1$.

➢

The inclination in $K$ and $Pe$ improves the rate of a microorganism’s transfer.