Effect of Varying Bottom Topography on the Radiation of Water Waves by a Floating Rectangular Buoy
Abstract
1. Introduction
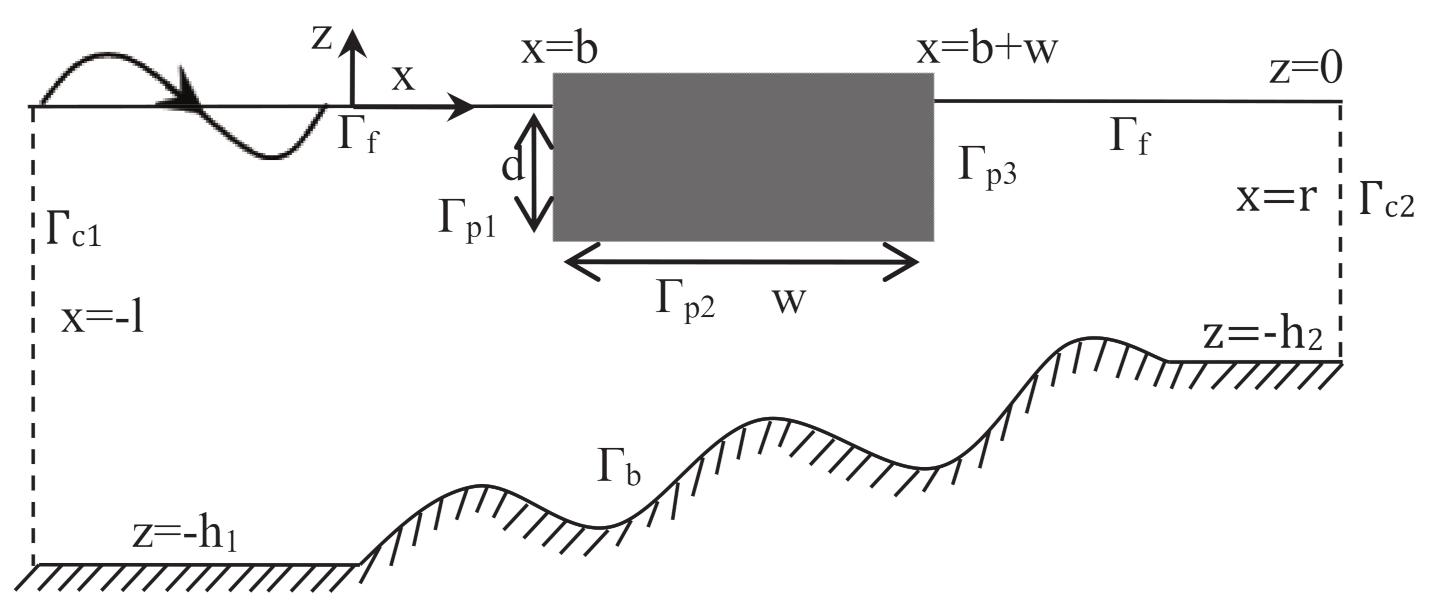
2. Mathematical Formulation
3. Numerical Solutions Based on BEM
4. Results & Discussion
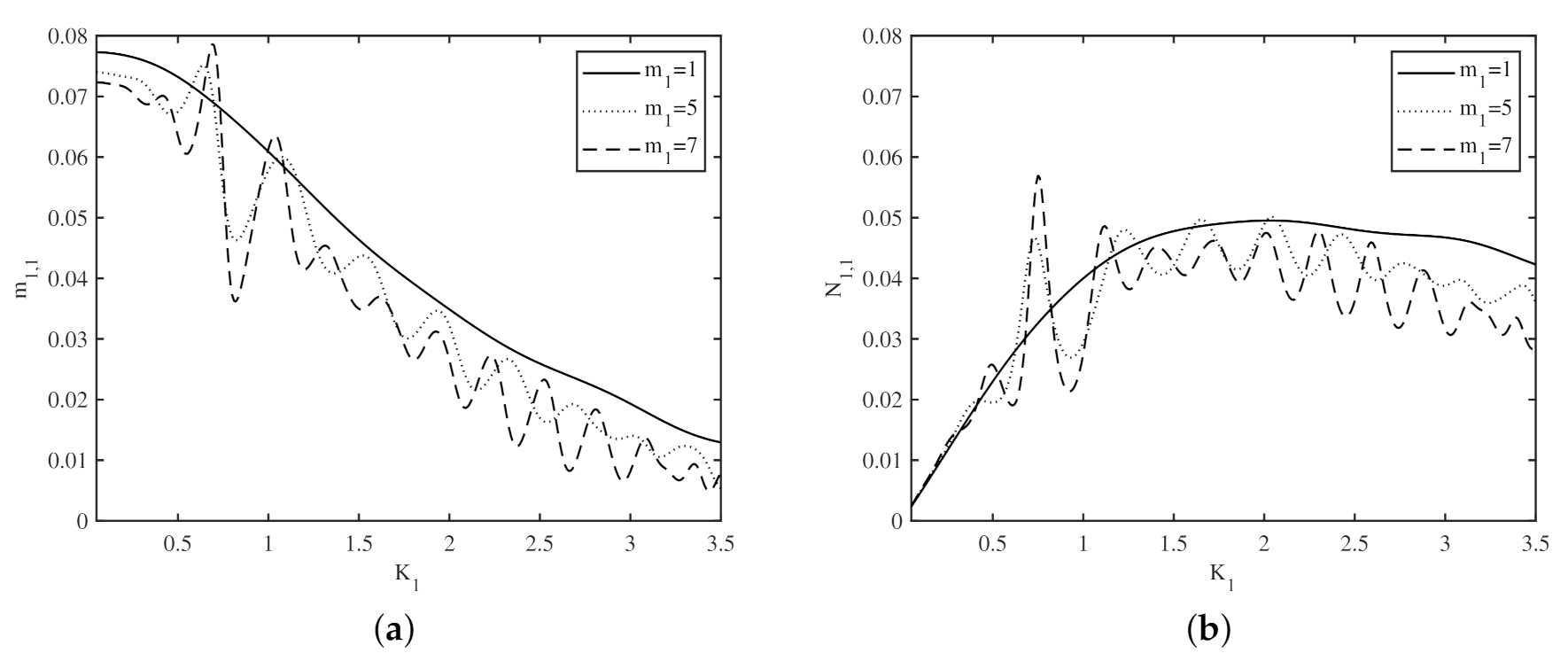
4.1. Numerical Convergence in BEM
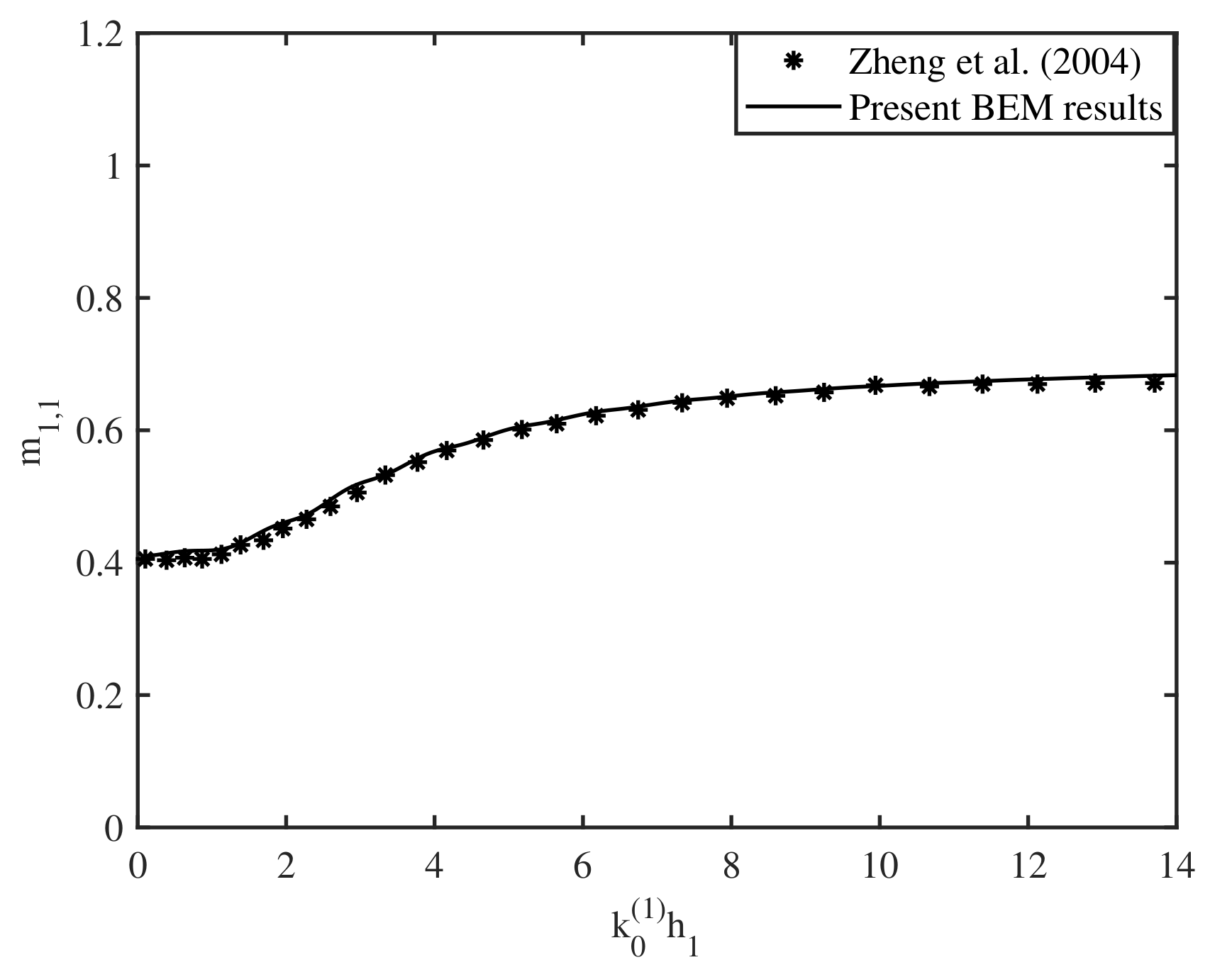
4.2. Comparison with Existing Results
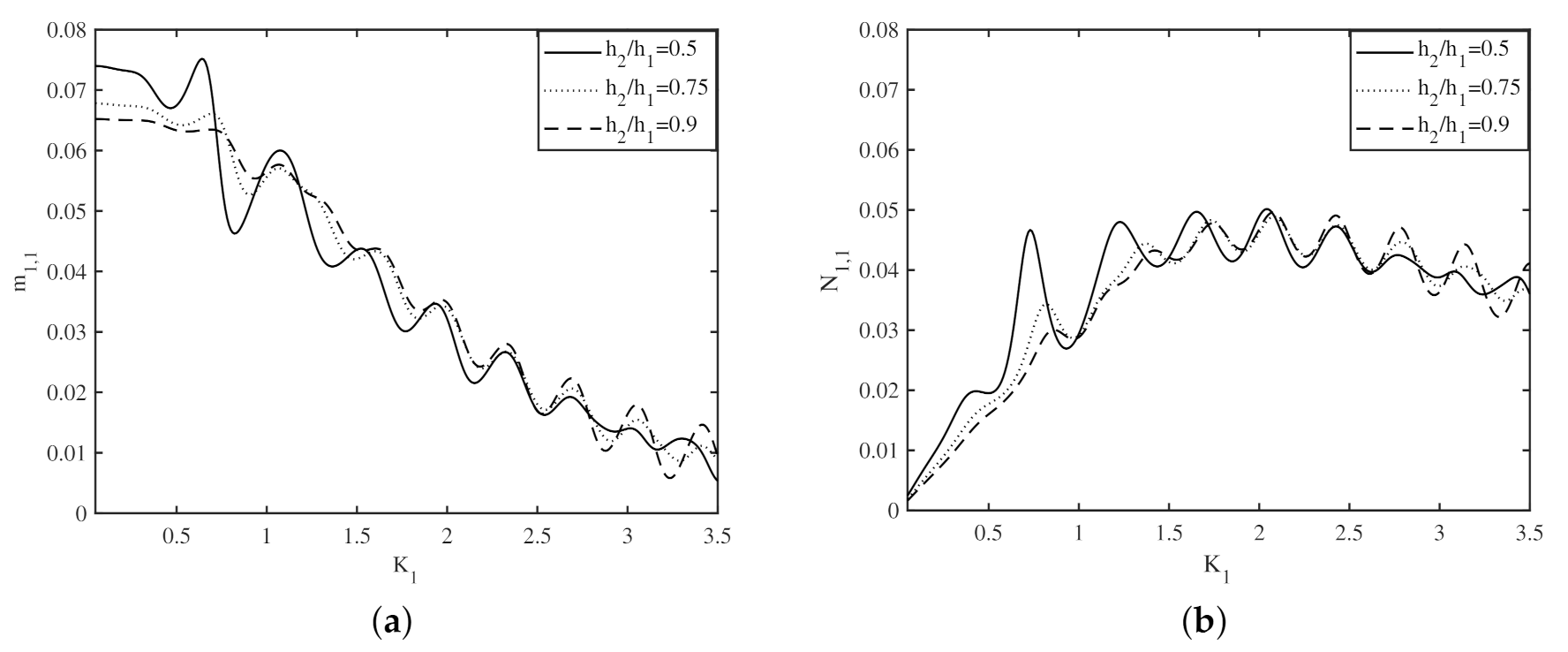
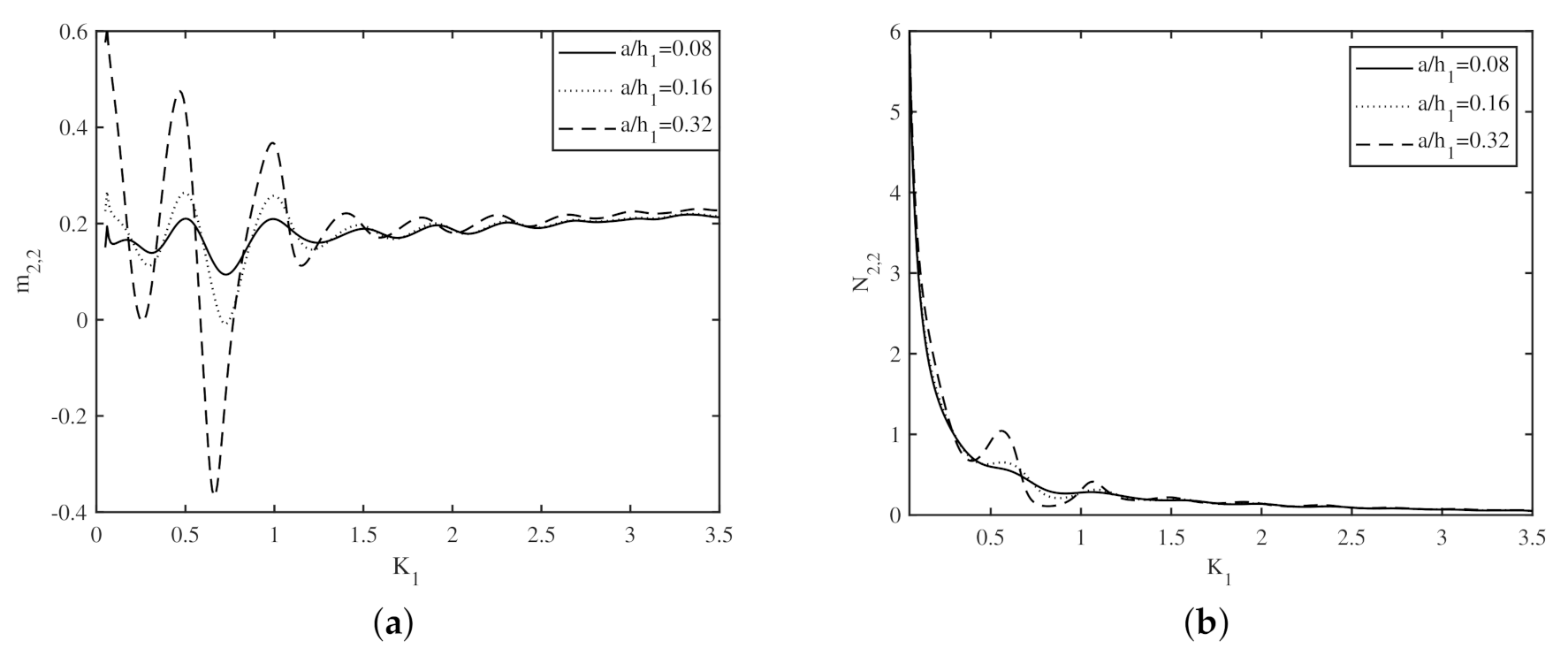
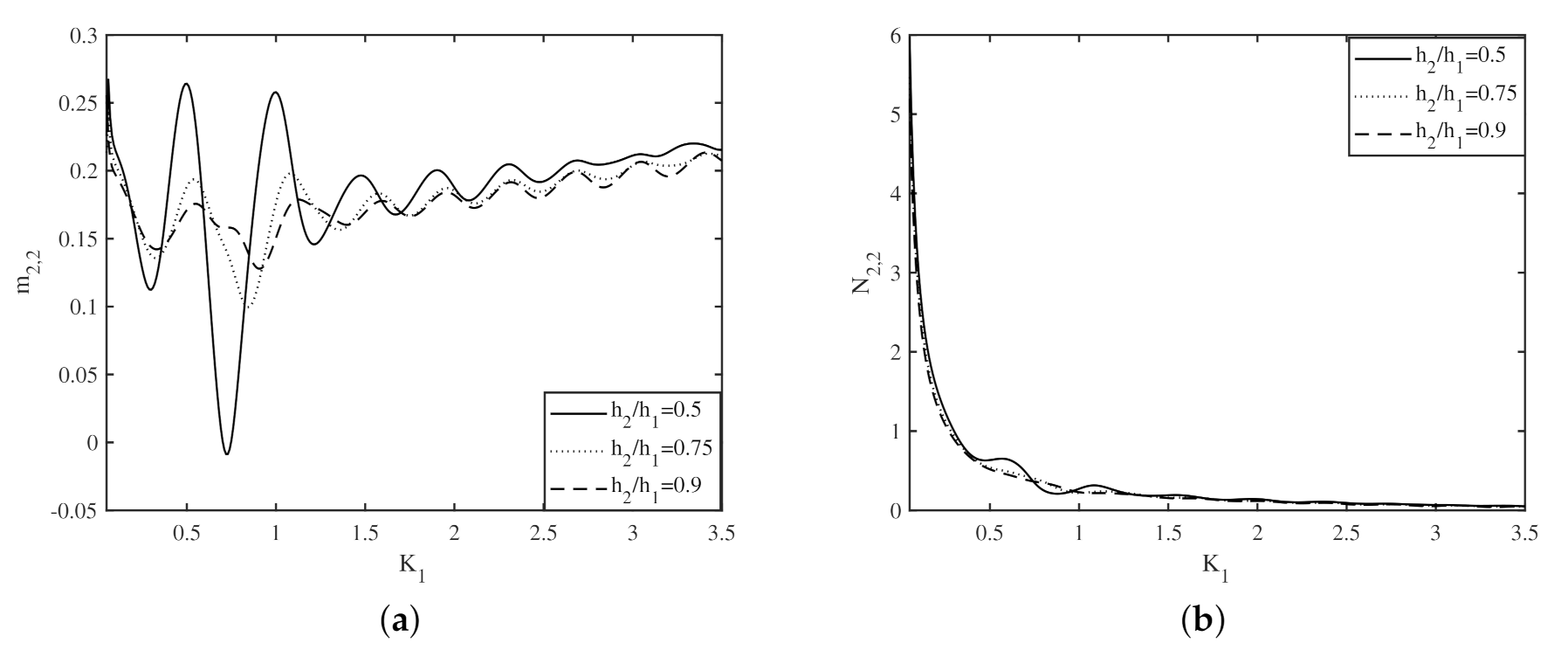
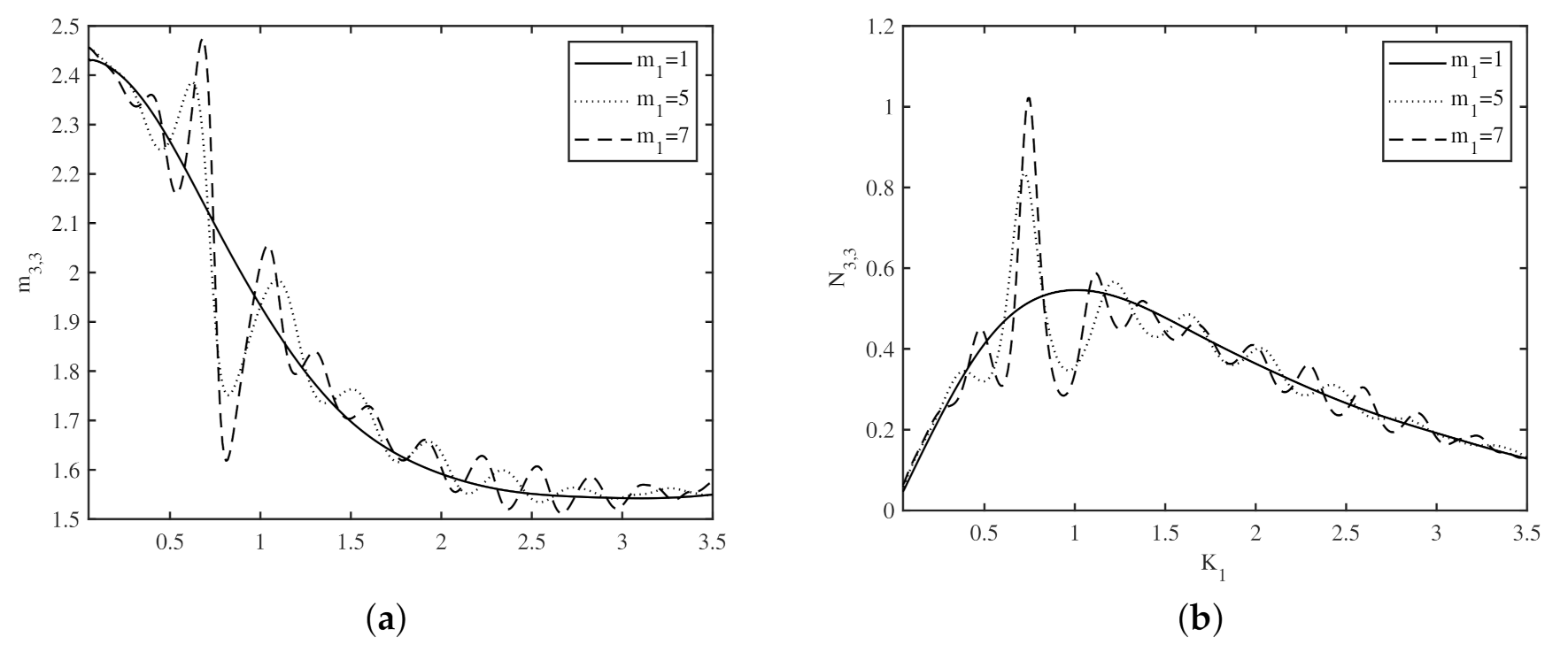
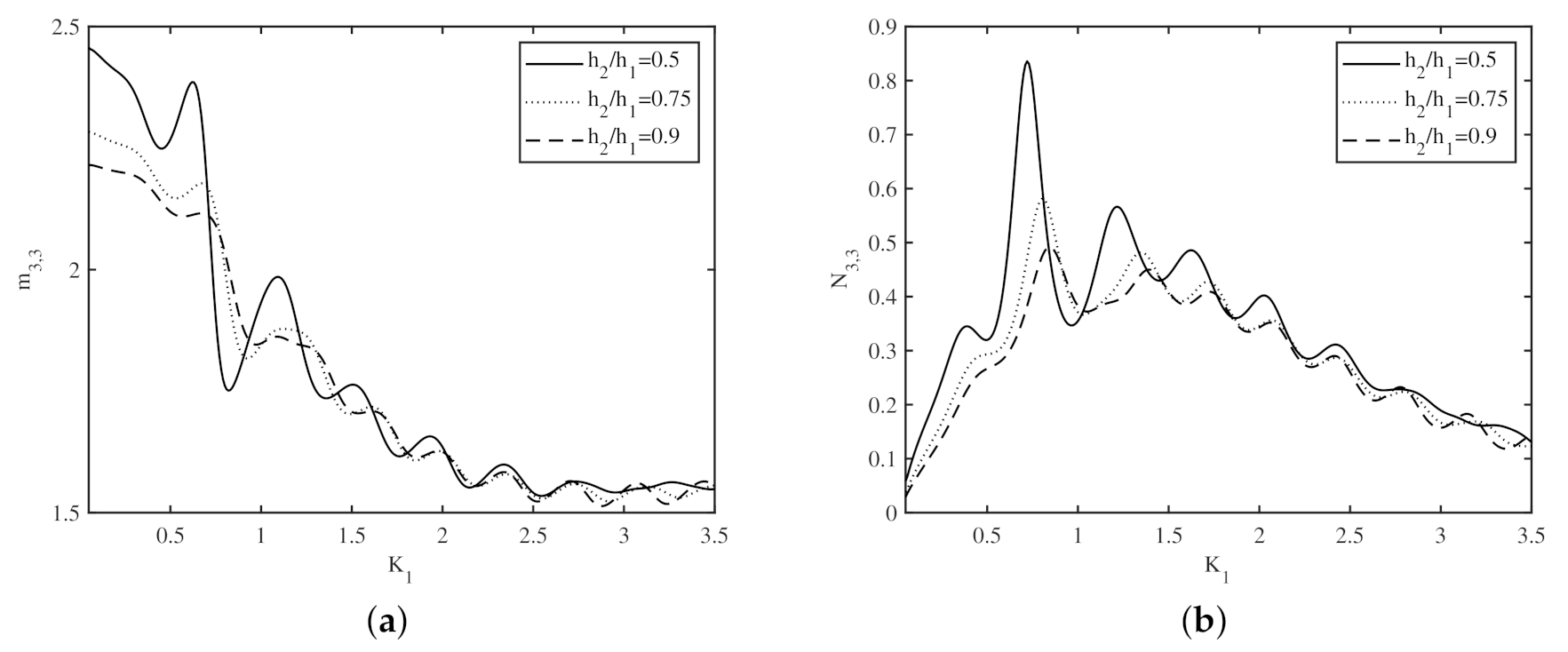
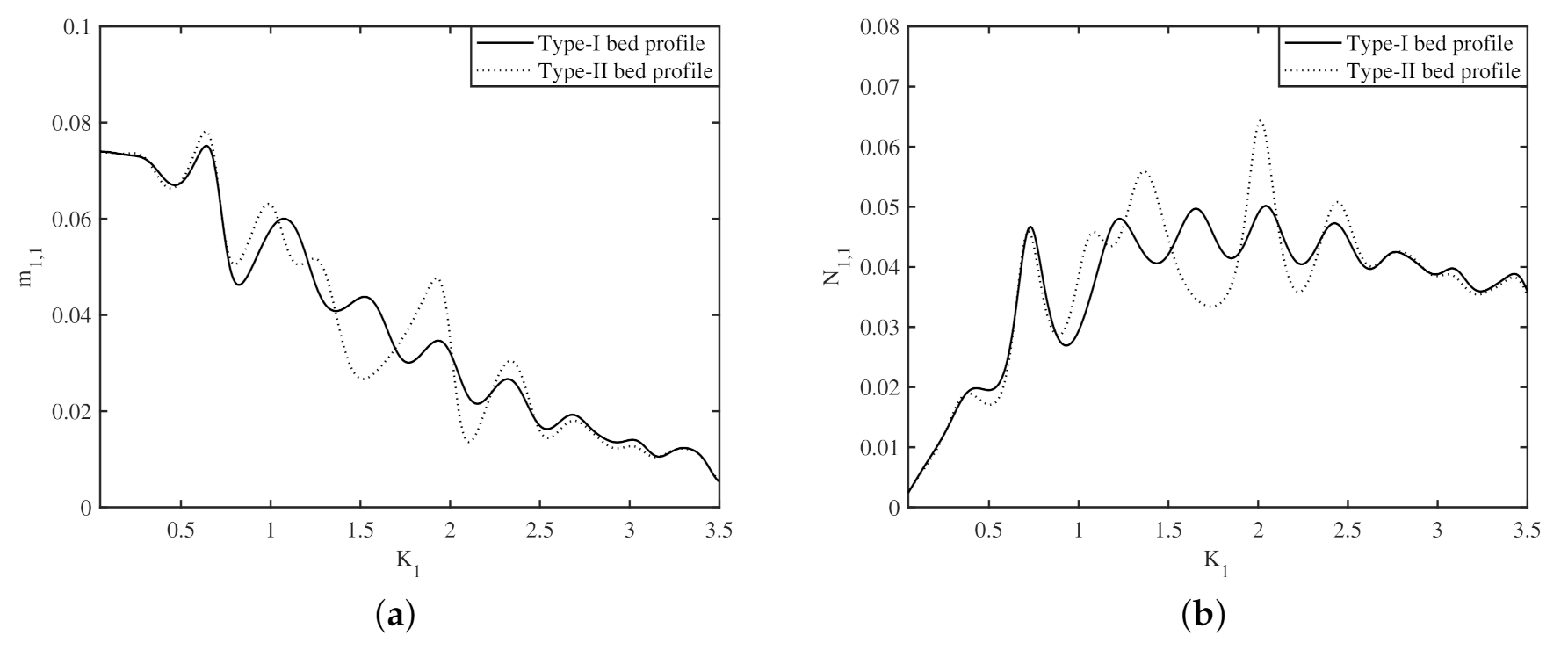
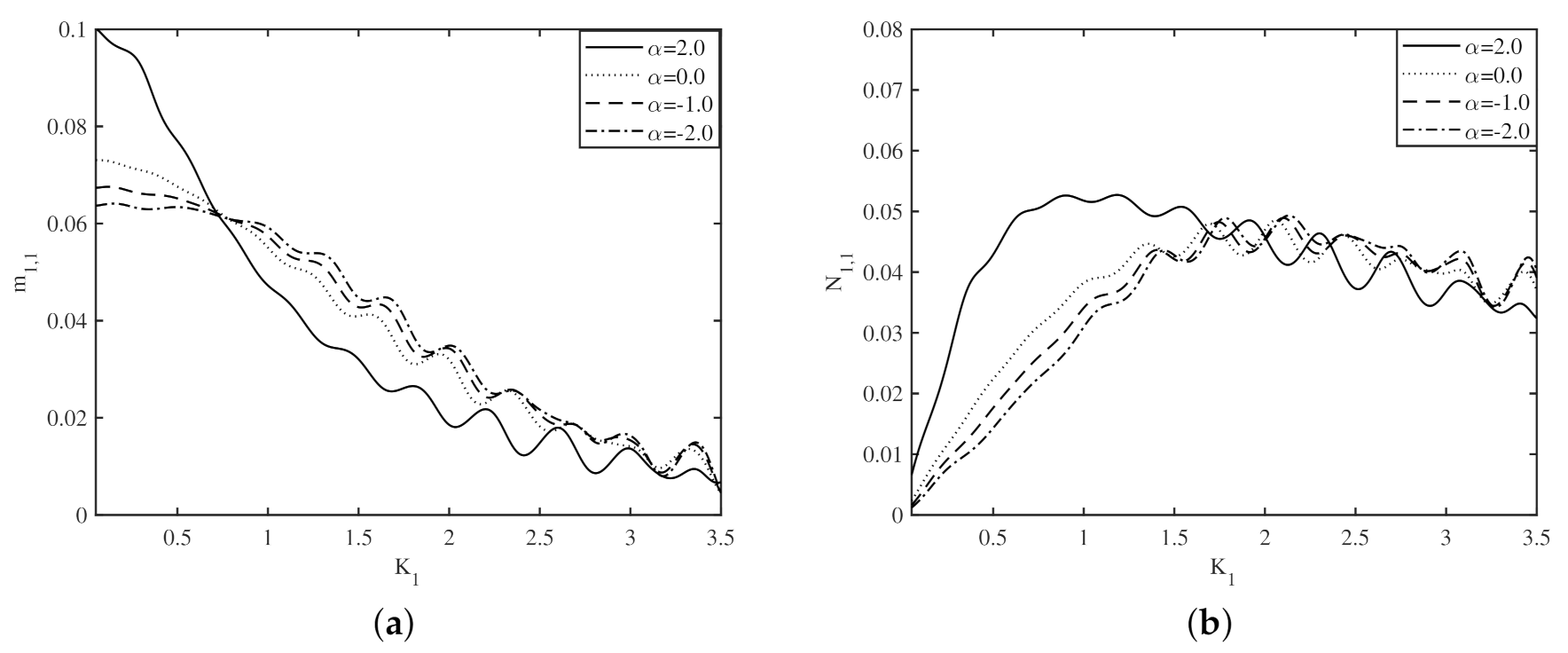
4.3. Effect of Bottom Undulations on the Added Mass and Radiation Damping
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lee, J.F. On the heave radiation of a rectangular structure. Ocean Eng. 1995, 22, 19–34. [Google Scholar] [CrossRef]
- Newman, J.N. Marine hydrodynamics; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Zheng, Y.H.; You, Y.G.; Shen, Y.M. On the radiation and diffraction of water waves by a rectangular buoy. Ocean Eng. 2004, 31, 1063–1082. [Google Scholar] [CrossRef]
- Drobyshevski, Y. Hydrodynamic coefficients of a floating, truncated vertical cylinder in shallow water. Ocean Eng. 2004, 31, 269–304. [Google Scholar] [CrossRef]
- Wu, B.J.; Zheng, Y.H.; You, Y.G.; Sun, X.Y.; Chen, Y. On diffraction and radiation problem for a cylinder over a caisson in water of finite depth. Int. J. Eng. Sci. 2004, 42, 1193–1213. [Google Scholar] [CrossRef]
- Shen, Y.M.; Zheng, Y.H.; You, Y.G. On the radiation and diffraction of linear water waves by a rectangular structure over a sill. Part I. Infinite domain of finite water depth. Ocean Eng. 2005, 32, 1073–1097. [Google Scholar] [CrossRef]
- Bhatta, D.D. Computation of added mass and damping coefficients due to a heaving cylinder. J. Appl. Math. Comput. 2007, 23, 127–140. [Google Scholar] [CrossRef]
- Siddorn, P.; Taylor, R.E. Diffraction and independent radiation by an array of floating cylinders. Ocean Eng. 2008, 35, 1289–1303. [Google Scholar] [CrossRef]
- Belibassakis, K.A. A boundary element method for the hydrodynamic analysis of floating bodies in variable bathymetry regions. Eng. Anal. Bound. Elem. 2008, 32, 796–810. [Google Scholar] [CrossRef]
- Finnegan, W.; Meere, M.; Goggins, J. The wave excitation forces on a truncated vertical cylinder in water of infinite depth. J. Fluids Struct. 2013, 40, 201–213. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, Y. Wave radiation from a truncated cylinder in front of a vertical wall. Ocean Eng. 2016, 111, 602–614. [Google Scholar] [CrossRef]
- Yu, H.; Zheng, S.; Zhang, Y.; Iglesias, G. Wave radiation from a truncated cylinder of arbitrary cross section. Ocean Eng. 2019, 173, 519–530. [Google Scholar] [CrossRef]
- Li, Y.; Xu, B.; Zhang, D.; Shen, X.; Zhang, W. Numerical Analysis of Combined Wave Radiation and Diffraction on a Floating Barge. Water 2020, 12, 205. [Google Scholar] [CrossRef]
- Liu, X.; Wang, X.; Xu, S.; Ding, A. Influences of a varying sill at the seabed on two-dimensional radiation of linear water waves by a rectangular buoy. J. Offshore Mech. Arct. Eng. 2020, 142, 041202. [Google Scholar] [CrossRef]
- Belibassakis, K.A.; Athanassoulis, G.A. A coupled-mode model for the hydroelastic analysis of large floating bodies over variable bathymetry regions. J. Fluid Mech. 2005, 531, 221–249. [Google Scholar] [CrossRef]
- Bennetts, L.G.; Biggs, N.R.T.; Porter, D.A. Multi-mode approximation to wave scattering by ice sheets of varying thickness. J. Fluid Mech. 2007, 579, 413–443. [Google Scholar] [CrossRef]
- Manam, S.R.; Kaligatla, R.B. A mild-slope model for membrane-coupled gravity waves. J. Fluids Struct. 2012, 30, 173–187. [Google Scholar] [CrossRef]
- Koley, S.; Sarkar, A.; Sahoo, T. Interaction of gravity waves with bottom-standing submerged structures having perforated outer-layer placed on a sloping bed. Appl. Ocean Res. 2015, 52, 245–260. [Google Scholar] [CrossRef]
- Koley, S.; Trivedi, K. Mathematical modeling of oscillating water column wave energy converter devices over the undulated sea bed. Eng. Anal. Bound. Elem. 2020, 117, 26–40. [Google Scholar] [CrossRef]
- Koley, S. Water wave scattering by floating flexible porous plate over variable bathymetry regions. Ocean Eng. 2020, 214, 107686. [Google Scholar] [CrossRef]
- Katsikadelis, J.T. The Boundary Element Method for Engineers and Scientists: Theory and Applications; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Mei, C.C.; Stiassnie, M.A.; Yue, D.K. Theory and Applications of Ocean Surface Waves; World Scientific Publishing Company: Singapore, 2018; Volume 42. [Google Scholar]
- Koley, S. Integral Equation and Allied Methods for Wave Interaction with Porous and Flexible Structures. Ph.D. Thesis, IIT Kharagpur, Kharagpur, India, 2016. [Google Scholar]



| 5 | 0.05898 | 0.03657 | 0.21986 | 0.26502 | 1.95023 | 0.43259 | |
| 0.05860 | 0.02653 | 0.27811 | 0.29653 | 1.96290 | 0.36134 | ||
| 0.06985 | 0.02780 | 0.35897 | 0.31237 | 2.11002 | 0.28153 | ||
| 15 | 0.05601 | 0.03310 | 0.21001 | 0.27670 | 1.92010 | 0.43001 | |
| 0.05782 | 0.02898 | 0.25840 | 0.27279 | 1.93306 | 0.36017 | ||
| 0.06904 | 0.02710 | 0.36751 | 0.30834 | 2.05607 | 0.28001 | ||
| 25 | 0.05549 | 0.03325 | 0.20930 | 0.27170 | 1.92100 | 0.42930 | |
| 0.05777 | 0.02938 | 0.25780 | 0.27160 | 1.93200 | 0.35480 | ||
| 0.06858 | 0.02607 | 0.36570 | 0.30730 | 2.06100 | 0.27100 | ||
| 30 | 0.05549 | 0.03320 | 0.20932 | 0.27171 | 1.92101 | 0.42928 | |
| 0.05778 | 0.02937 | 0.25781 | 0.27162 | 1.93202 | 0.35481 | ||
| 0.06859 | 0.02610 | 0.36572 | 0.30731 | 2.06103 | 0.27105 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trivedi, K.; Koley, S. Effect of Varying Bottom Topography on the Radiation of Water Waves by a Floating Rectangular Buoy. Fluids 2021, 6, 59. https://doi.org/10.3390/fluids6020059
Trivedi K, Koley S. Effect of Varying Bottom Topography on the Radiation of Water Waves by a Floating Rectangular Buoy. Fluids. 2021; 6(2):59. https://doi.org/10.3390/fluids6020059
Chicago/Turabian StyleTrivedi, Kshma, and Santanu Koley. 2021. "Effect of Varying Bottom Topography on the Radiation of Water Waves by a Floating Rectangular Buoy" Fluids 6, no. 2: 59. https://doi.org/10.3390/fluids6020059
APA StyleTrivedi, K., & Koley, S. (2021). Effect of Varying Bottom Topography on the Radiation of Water Waves by a Floating Rectangular Buoy. Fluids, 6(2), 59. https://doi.org/10.3390/fluids6020059







