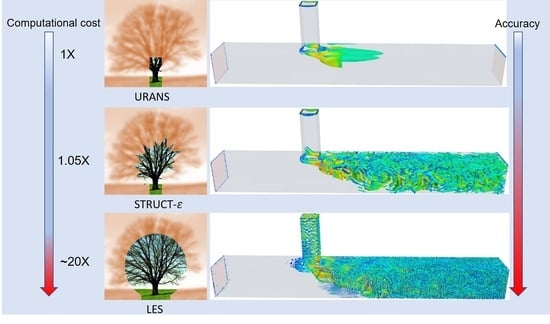
Assessing the Applicability of the Structure-Based Turbulence Resolution Approach to Nuclear Safety-Related Issues
Abstract
1. Introduction
2. Turbulence Models Description
2.1. Realizable k- Model
2.2. STRUCT- Model
2.3. Large Eddy Simulation Model
3. Model Assessment
3.1. Flow over Periodic Hills
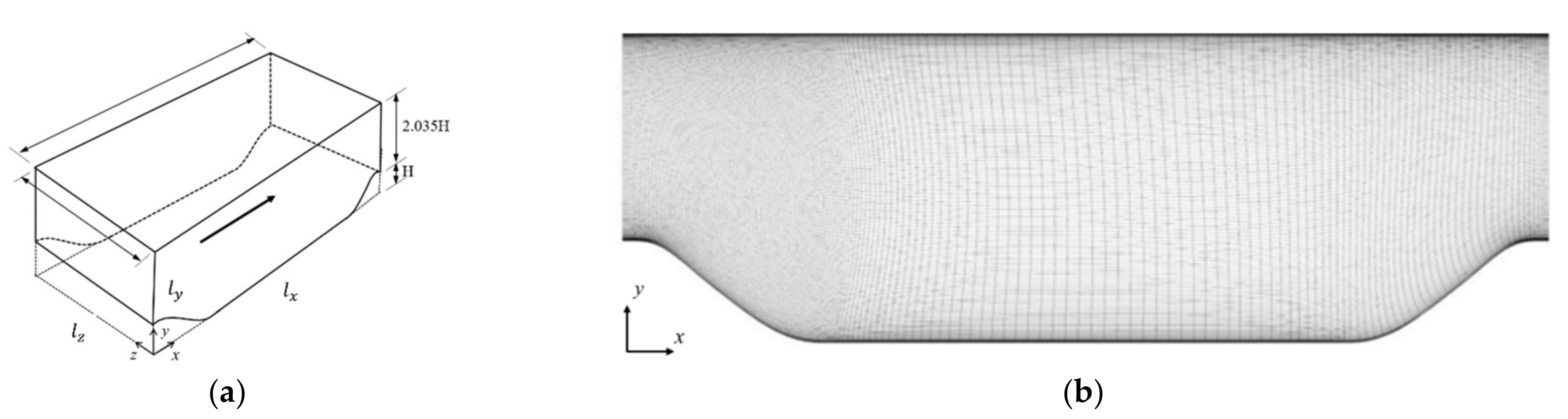
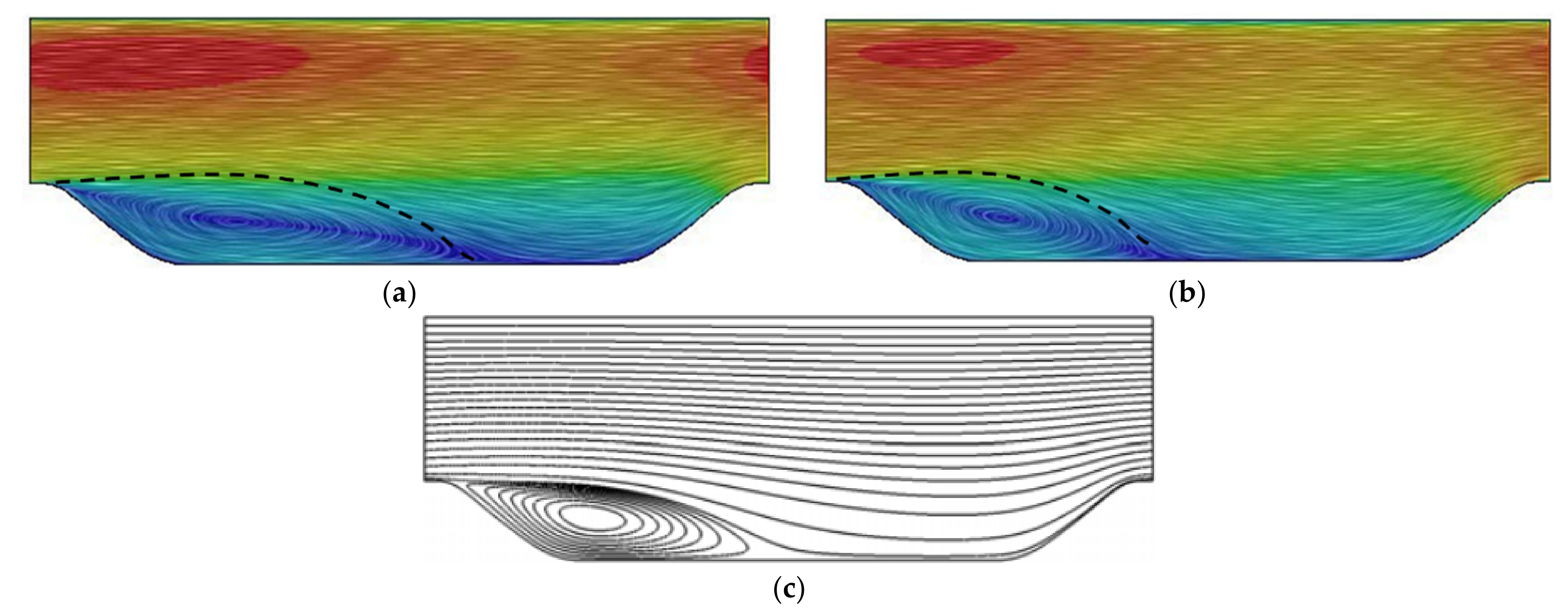
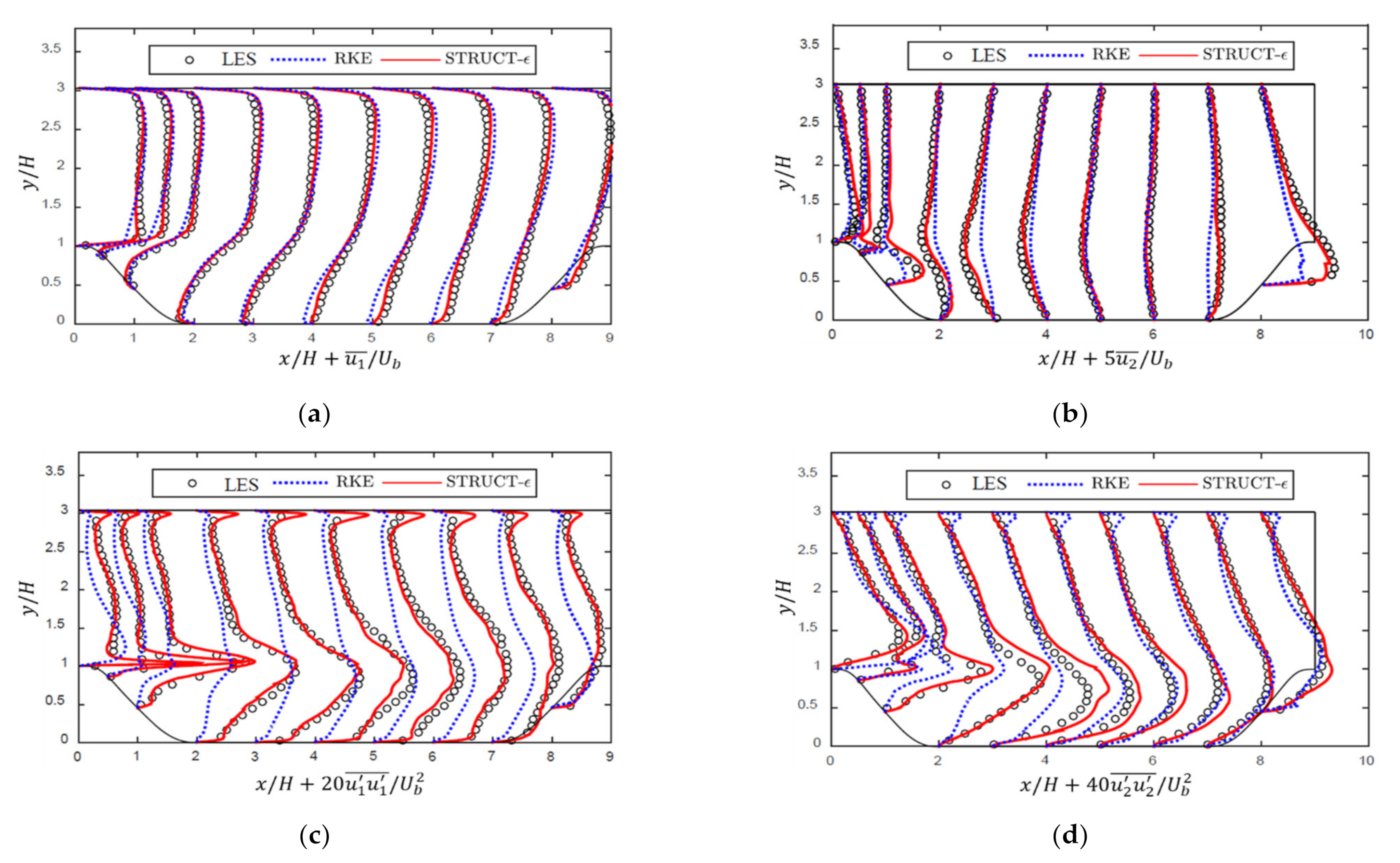
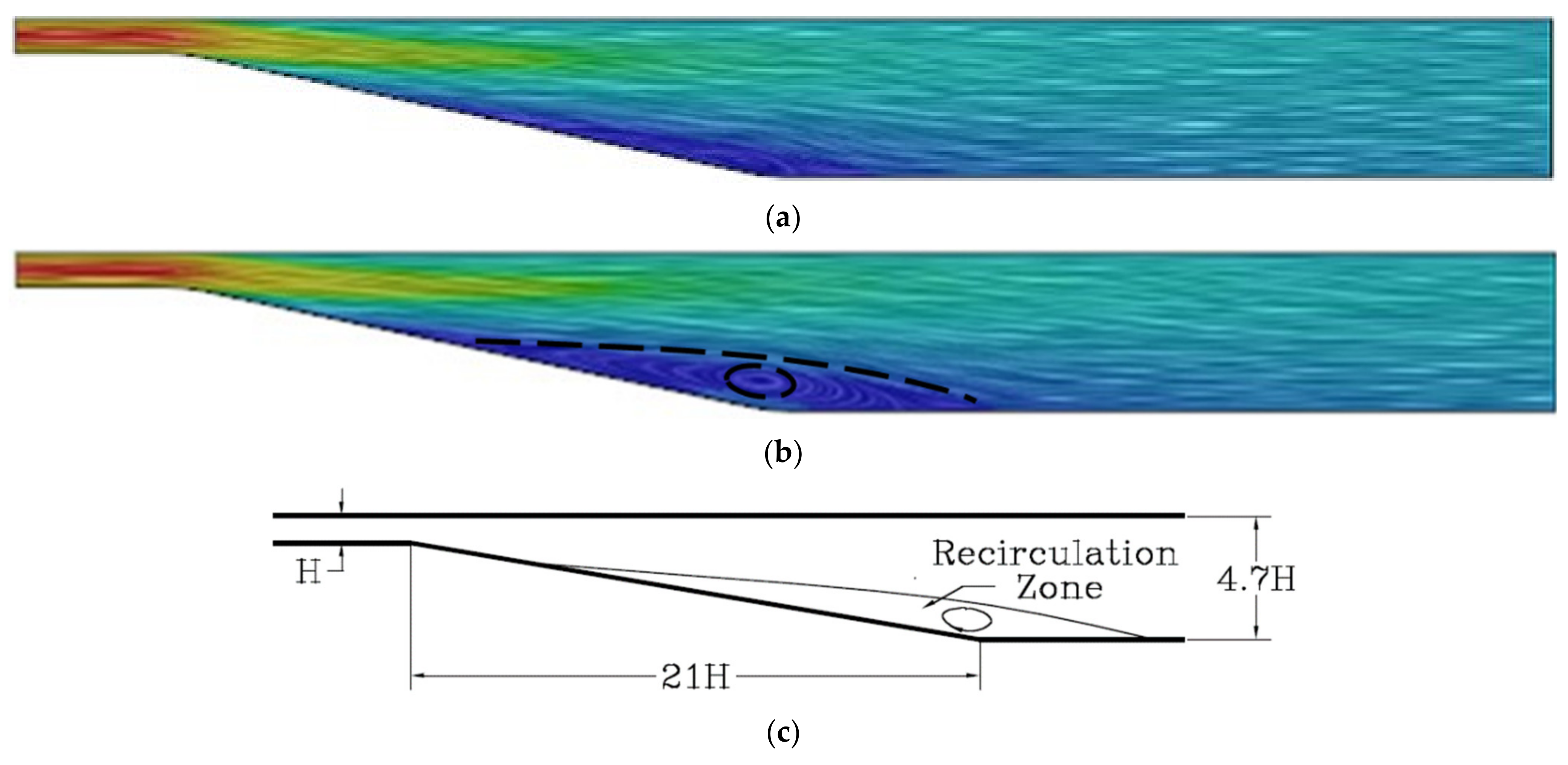
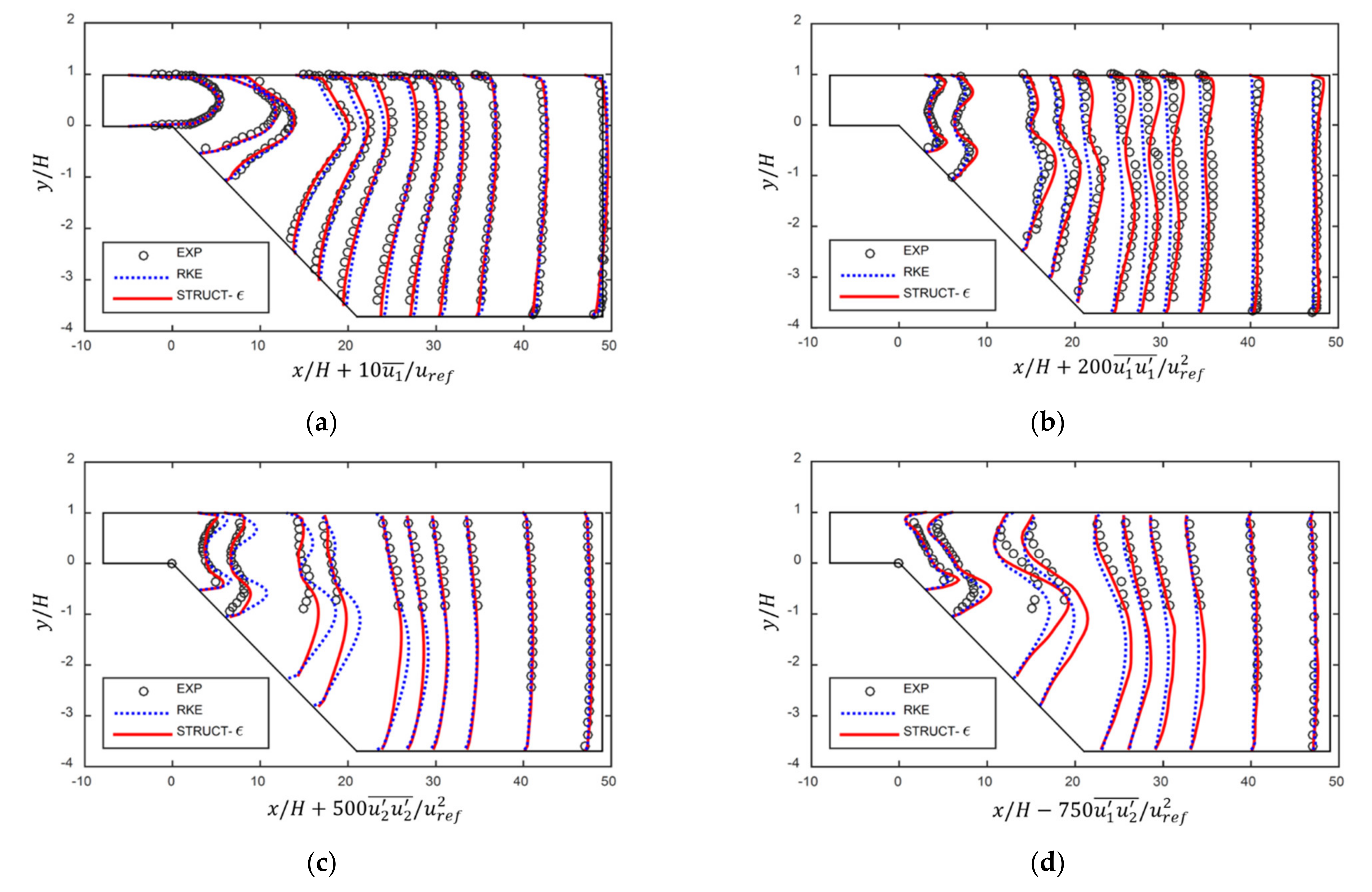
3.2. Flow in an Asymmetric Diffuser
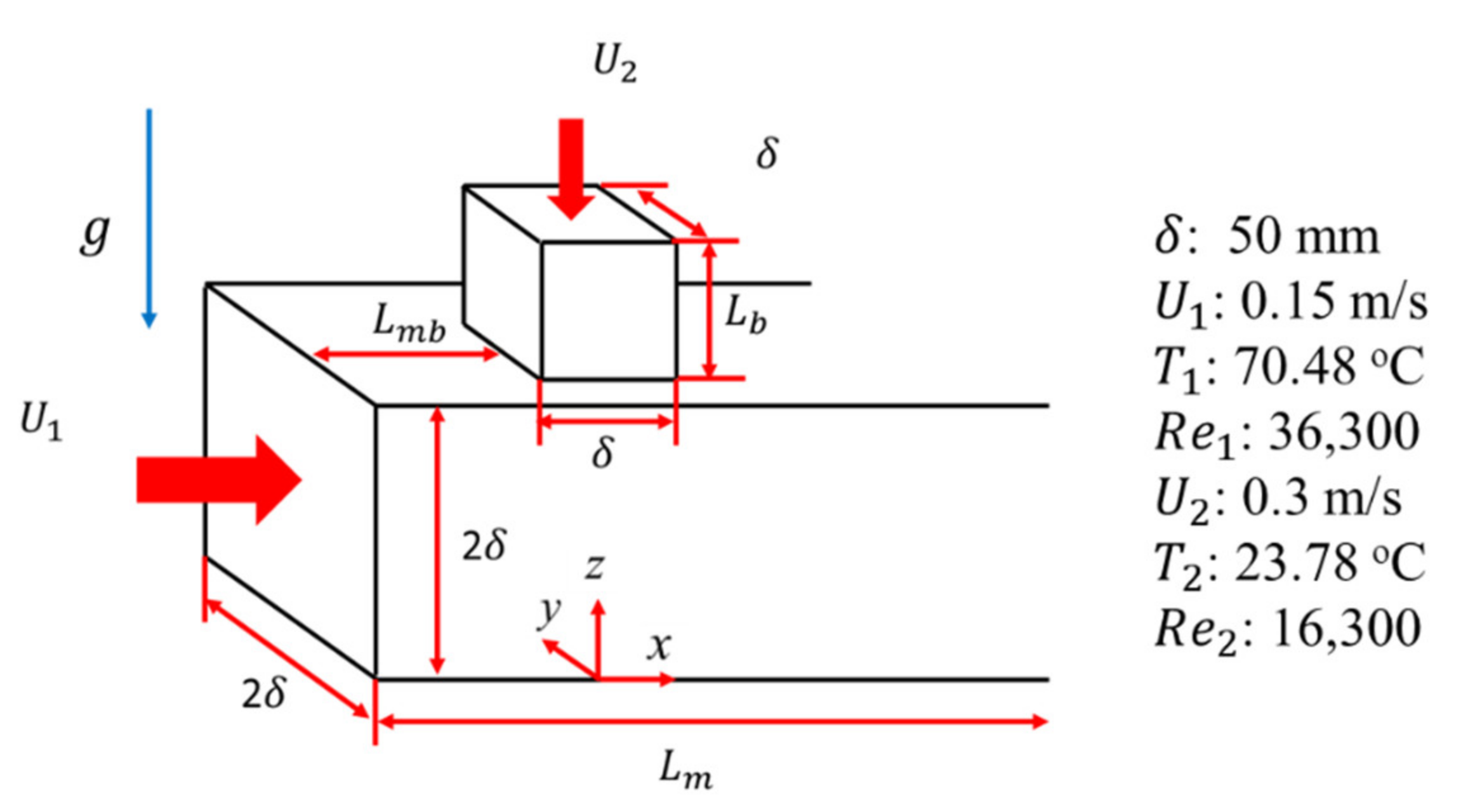
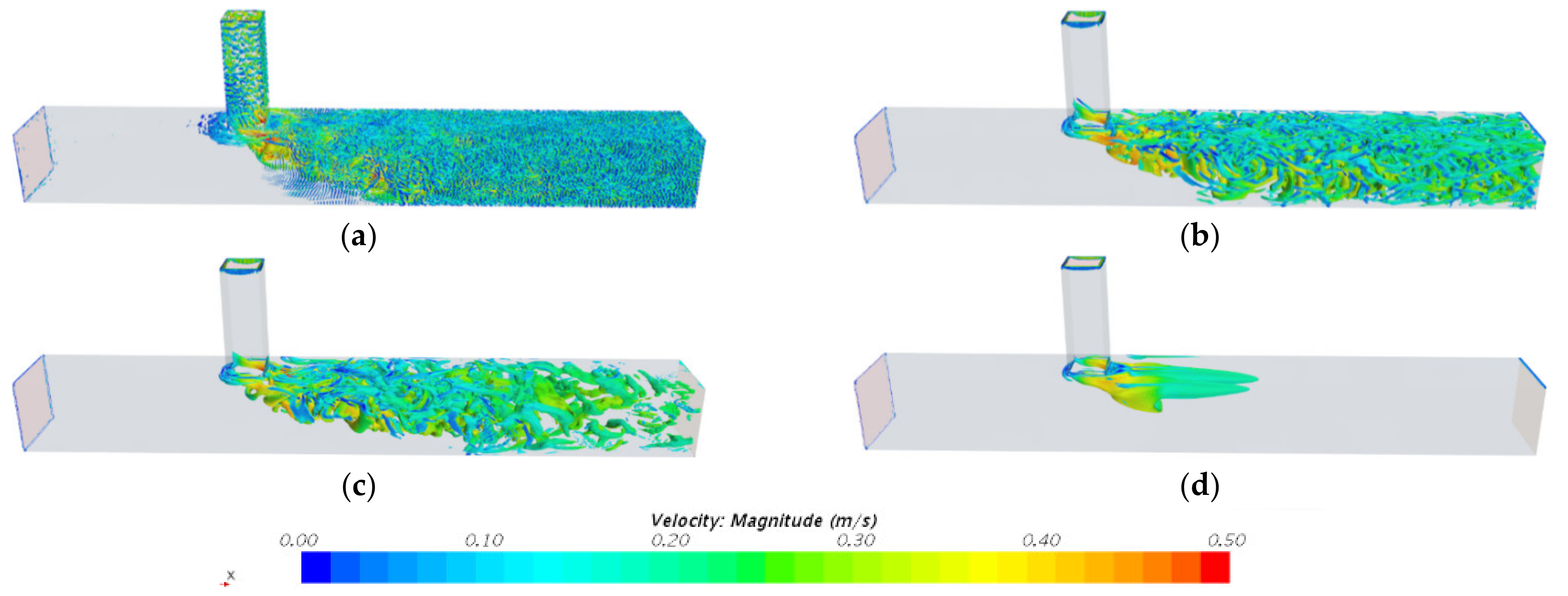
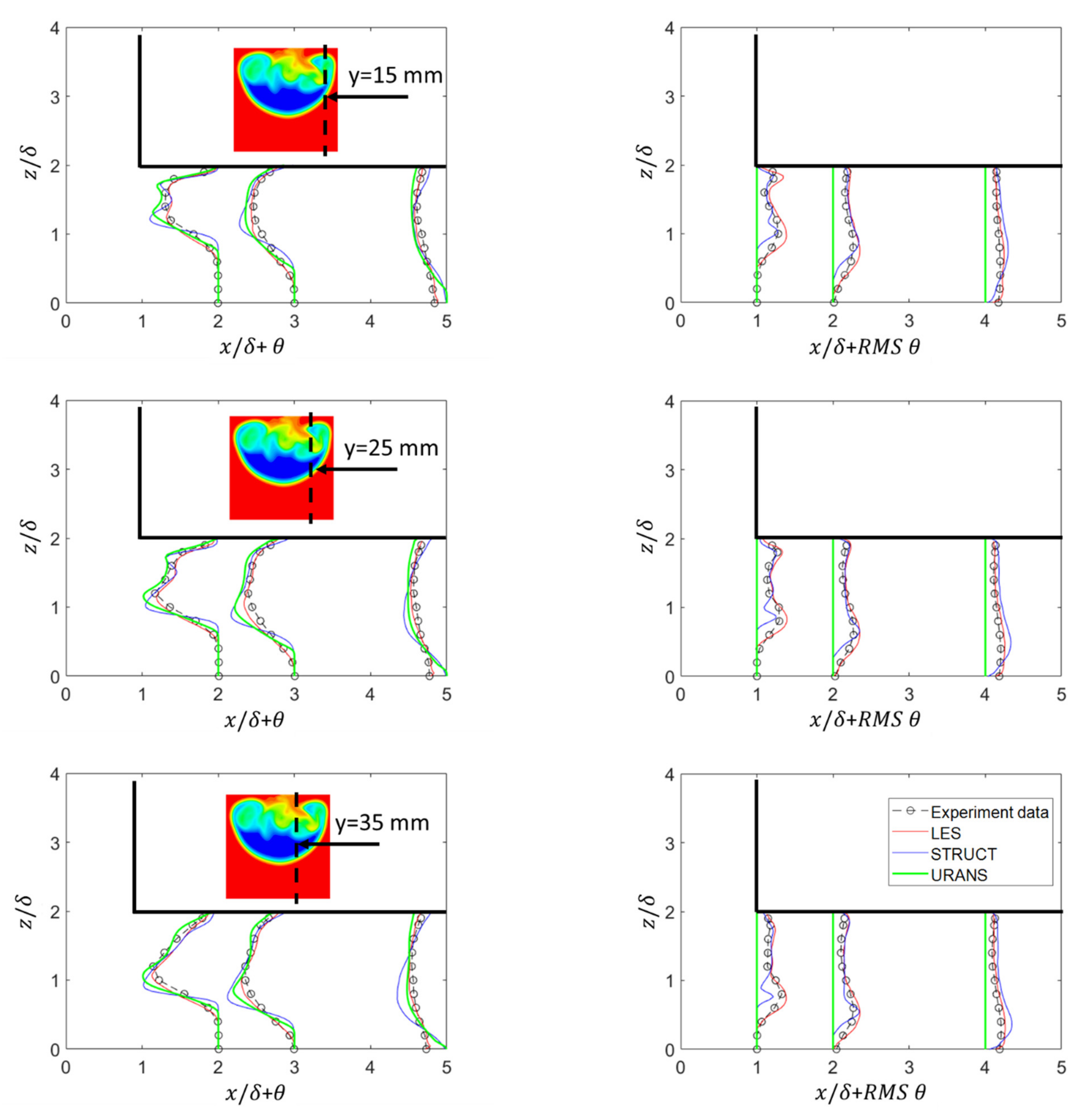
3.3. Thermal Mixing in T-Junction
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Atomic Energy Agency. Use of Computational Fluid Dynamics Codes for Safety Analysis of Nuclear Reactor Systems, IAEA TECDOC-1379; IAEA: Vienna, Austria, 2003. [Google Scholar]
- Smith, B.L.; Mahaffy, J.H.; Angele, K. A CFD benchmarking exercise based on flow mixing in a T-junction. Nucl. Eng. Des. 2013, 264, 80–88. [Google Scholar] [CrossRef]
- Fröhlich, J.; von Terzi, D. Hybrid LES/RANS methods for the simulation of turbulent flows. Prog. Aerosp. Sci. 2008, 44, 349–377. [Google Scholar] [CrossRef]
- Speziale, C.G. Computing non-equilibrium turbulent flows with time-dependent RANS and VLES. In Fifteenth International Conference on Numerical Methods in Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1997; pp. 123–129. [Google Scholar]
- Spalart, P.R. Detached-eddy simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Girimaji, S. Partially-averaged Navier-Stokes model of turbulence: A Reynolds-averaged Navier-Storkes to direct numerical simulation bridging method. J. Appl. Mech. 2006, 73, 413–421. [Google Scholar] [CrossRef]
- Menter, F.; Kuntz, M.; Bender, R. A scale-adaptive simulation model for turbulent flow predictions. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 6–9 January 2003; ARC: Reno, NV, USA, 2003; Volume 767, pp. 1–12. [Google Scholar]
- Menter, F.R.; Egorov, Y. A scale-adaptive simulation model using two-equation models. In Proceedings of the 43rd Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 10–13 January 2005; ARC: Reno, NV, USA, 2005; Volume 1095, pp. 1–13. [Google Scholar]
- Lenci, G. A Methodology Based on Local Resolution of Turbulent Structures for Effective Modeling of Unsteady Flows. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2016. [Google Scholar]
- Feng, J.; Baglietto, E.; Tanimoto, K.; Kondo, Y. Demonstration of the STRUCT turbulence model for mesh consistent resolution of unsteady thermal mixing in a T-junction. Nucl. Eng. Des. 2020, 361, 110572. [Google Scholar] [CrossRef]
- Feng, J.; Frahi, T.; Baglietto, E. STRUCTure-based URANS simulations of thermal mixing in T-junctions. Nucl. Eng. Des. 2018, 340, 275–299. [Google Scholar] [CrossRef]
- Acton, M.J.; Lenci, G.; Baglietto, E. Structure-Based Resolution of Turbulence for Sodium Fast Reactor Thermal Striping Applications. In Proceeding of the International Topical Meeting on Nuclear Reactor Thermal Hydraulics, Chicago, IL, USA, 30 August–4 September 2015. [Google Scholar]
- Xu, L. A Second Generation URANS Approach for Application to Aerodynamic Design and Optimization in the Automotive Industry. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2020. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Rehm, M.; Hatman, A.; Farges, B. Framatome’s unified single-phase CFD methodology for fuel design and analysis. In Proceedings of the CFD4NRS-8, Virtual Conference. 25–27 November 2020. [Google Scholar]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-epsilon eddy viscosity model for high Reynolds number turbulent flows: Model development and validation. NASA Sti Recon Tech. Rep. N 1994, 95, 1442. [Google Scholar]
- Baglietto, E.; Ninokata, H. Anisotropic eddy viscosity modeling for application to industrial engineering internal flows. Int. J. Transp. Phenom. 2006, 8, 109. [Google Scholar]
- Baglietto, E.; Ninokata, H. A turbulence model study for simulating flow inside tight lattice rod bundles. Nucl. Eng. Des. 2005, 235, 773–784. [Google Scholar] [CrossRef]
- Feng, J.; Baglietto, E. Thermal Mixing Test for Struct Benchmark; Mitsubishi Heavy Industry, LTD: Tokyo, Japan, 2018. [Google Scholar]
- Feng, J.; Acton, M.; Baglietto, E.; Kraus, A.R.; Merzari, E. On the relevance of turbulent structures resolution for cross-flow in a helical-coil tube bundle. Ann. Nucl. Energy 2020, 140, 107298. [Google Scholar] [CrossRef]
- Launder, E.B.; Spaulding, B.D. Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- STAR-CCM+, Version 13.06; Siemens: Lebanon, NH, USA, 2018.
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Taylor & Francis: Abingdon, UK, 1980. [Google Scholar]
- Rhie, C.M.; Chow, W.L. Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Venkatakrishnan, V. Convergence to Steady State Solutions of the Euler Equations on Unstructured Grids with Limiters. J. Comput. Phys. 1995, 118, 120–130. [Google Scholar] [CrossRef]
- Temmerman, M.; Leschziner, L. Large eddy simulation of separated flow in a channel with corrugated wall. In Proceedings of the Conference on Turbulence and Shear Flow, Stockholm, Sweden, 25–27 June 2001. [Google Scholar]
- Fröhlich, J.; Mellen, C.P.; Rodi, W.; Temmerman, L.; Leschziner, M.A. Highly resolved large-eddy simulation of separated flow in a channel with streamwise periodic constrictions. J. Fluid Mech. 2005, 526, 19–66. [Google Scholar] [CrossRef]
- ERCOFTAC Database. Univ. Manch. 2019. Available online: www.ercoftac.org (accessed on 29 August 2020).
- Mellen, C.P.; Fröhlich, J. Large eddy simulation of the flow over periodic hills. In Proceedings of the 16th IMACS World Congress, Lausanne, Switzerland, 21–25 August 2000. [Google Scholar]
- Davidson, L. Evaluation of the SST-SAS model: Channel flow, asymmetric diffuser and axi-symmetric hill. In Proceedings of the European Conference on Computational Fluid Dynamics, TU Delft, The Netherlands, 5–8 September 2006. [Google Scholar]
- Buice, C.U.; Eaton, J.K. Experimental Investigation of Flow through an Asymmetric Plane Diffuser. CTR Annu. Res. Briefs 1997, 1996, 243–248. [Google Scholar] [CrossRef][Green Version]
- Lawn, C.J. The attenuation of temperature oscillations by liquid metal boundary l layers. Nucl. Eng. Des. 1977, 42, 209–222. [Google Scholar] [CrossRef]
- International Atomic Energy Agency. Validation of fast reactor thermomechanical and thermohydraulic codes. In IAEA Tecdoc-1318; International Atomic Energy Agency: Wien, Austria, 2002. [Google Scholar]
- Jungclaus, D.; Voswinkel, A.; Negri, P. Common IPSN/GRS safety assessment of primary coolant un-isolable leak incidents caused by stress cycling. In NEA-CSNI-R—1998-8; Nuclear Energy Agency: Paris, France, 1998. [Google Scholar]
- Fukushima, N.; Fukagata, K.; Kasagi, N.; Noguchi, H.; Tanimoto, K. Numerical and experimental study on turbulent thermal mixing in a T-junction flow. In Proceedings of the 6th ASME-JSME Thermal Engineering Joint Conference, Hawaii Island, HI, USA, 16–20 March 2003; pp. 16–20. [Google Scholar]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, J.; Xu, L.; Baglietto, E. Assessing the Applicability of the Structure-Based Turbulence Resolution Approach to Nuclear Safety-Related Issues. Fluids 2021, 6, 61. https://doi.org/10.3390/fluids6020061
Feng J, Xu L, Baglietto E. Assessing the Applicability of the Structure-Based Turbulence Resolution Approach to Nuclear Safety-Related Issues. Fluids. 2021; 6(2):61. https://doi.org/10.3390/fluids6020061
Chicago/Turabian StyleFeng, Jinyong, Liangyu Xu, and Emilio Baglietto. 2021. "Assessing the Applicability of the Structure-Based Turbulence Resolution Approach to Nuclear Safety-Related Issues" Fluids 6, no. 2: 61. https://doi.org/10.3390/fluids6020061
APA StyleFeng, J., Xu, L., & Baglietto, E. (2021). Assessing the Applicability of the Structure-Based Turbulence Resolution Approach to Nuclear Safety-Related Issues. Fluids, 6(2), 61. https://doi.org/10.3390/fluids6020061