Turbulent Premixed Flame Modeling Using the Algebraic Flame Surface Wrinkling Model: A Comparative Study between OpenFOAM and Ansys Fluent
Abstract
:1. Introduction
2. Theoretical Background
2.1. Premixed Combustion Model
2.2. Energy Equation Treatment
2.3. Thermophysical and Transport Properties
3. Solver Implementation in OpenFOAM






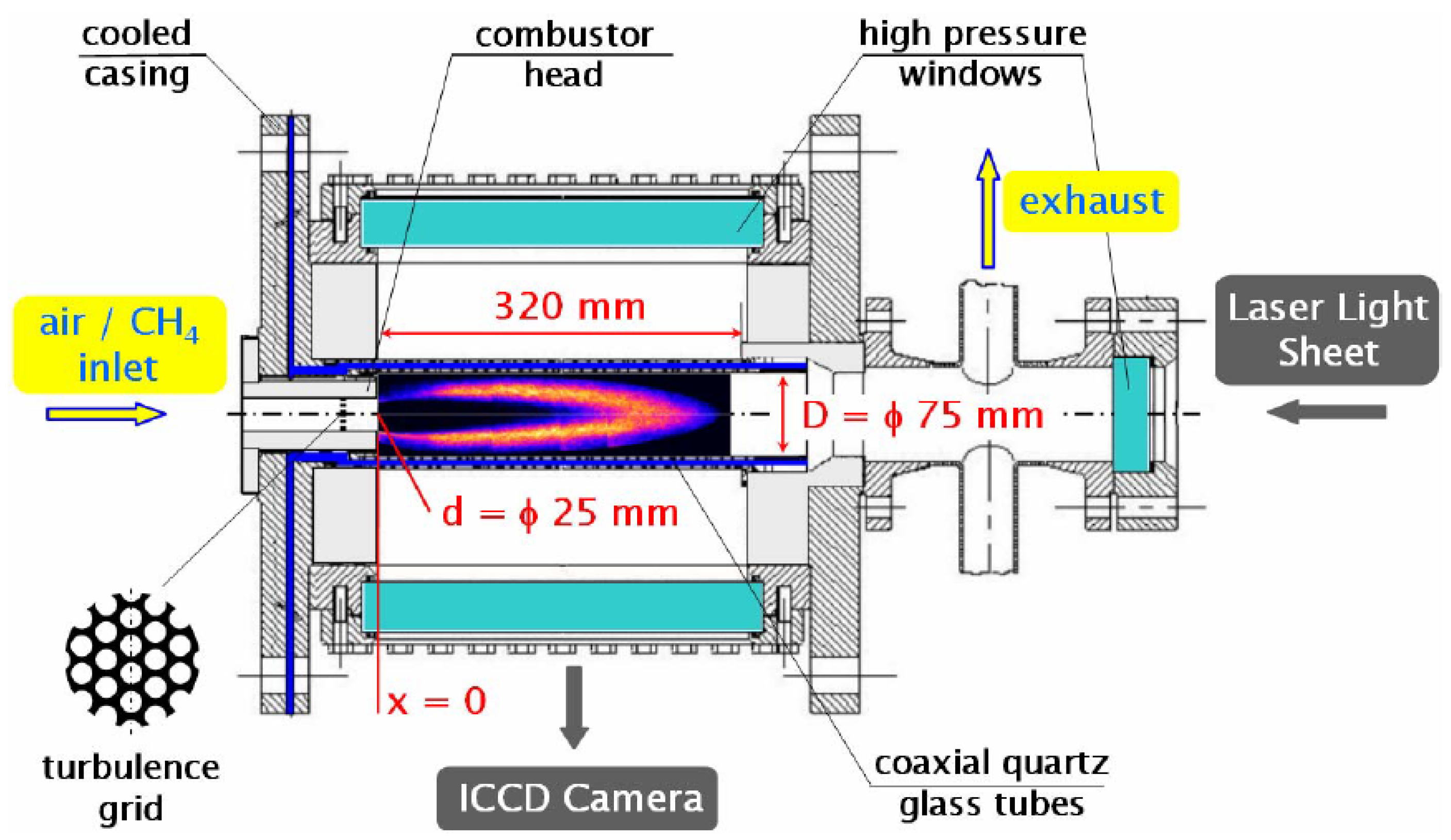
4. Experimental Setup and Data
5. Numerical Background
5.1. Computational Domain and Mesh
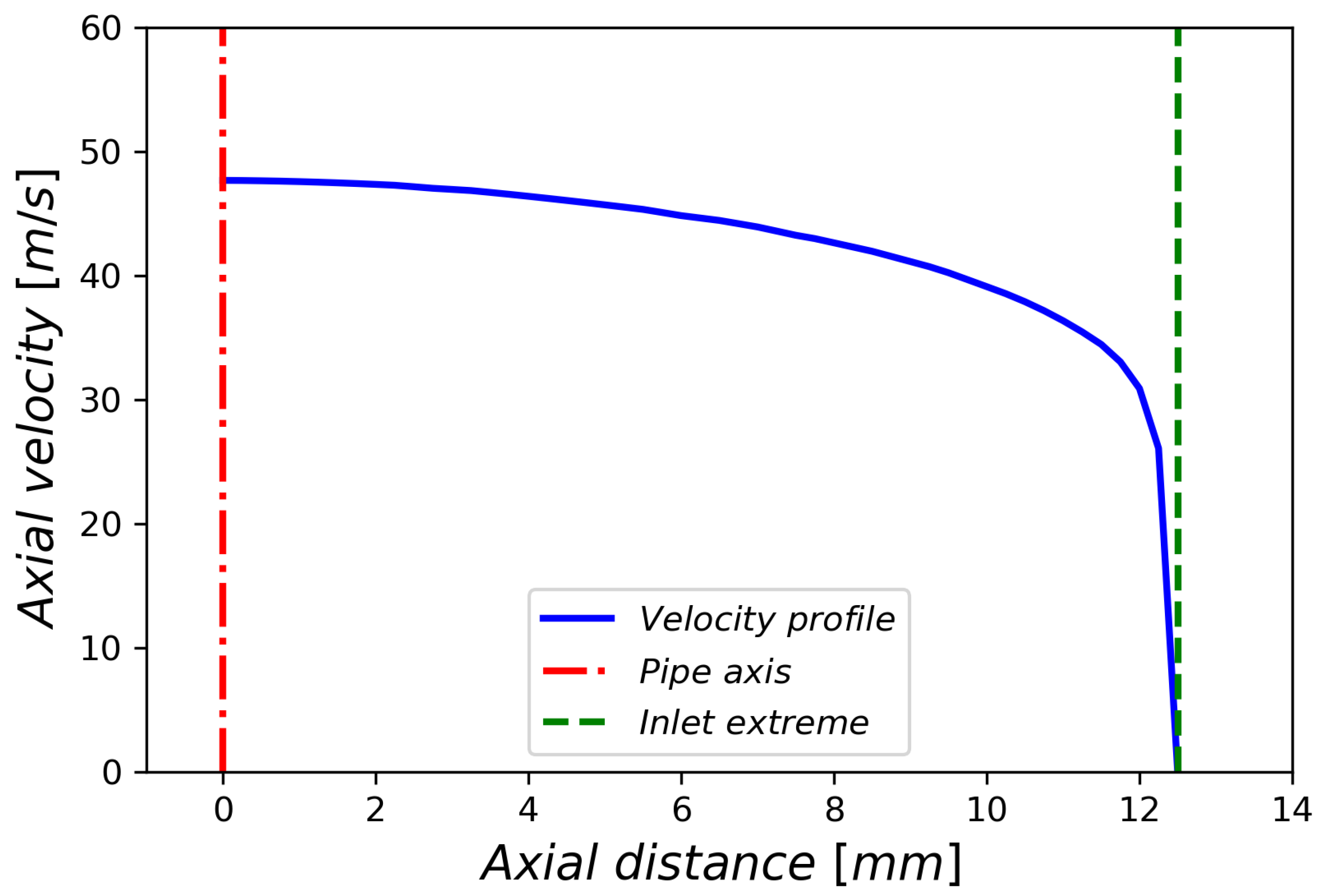
5.2. Boundary and Initial Conditions
5.3. Numerical Setup and Discretization Schemes
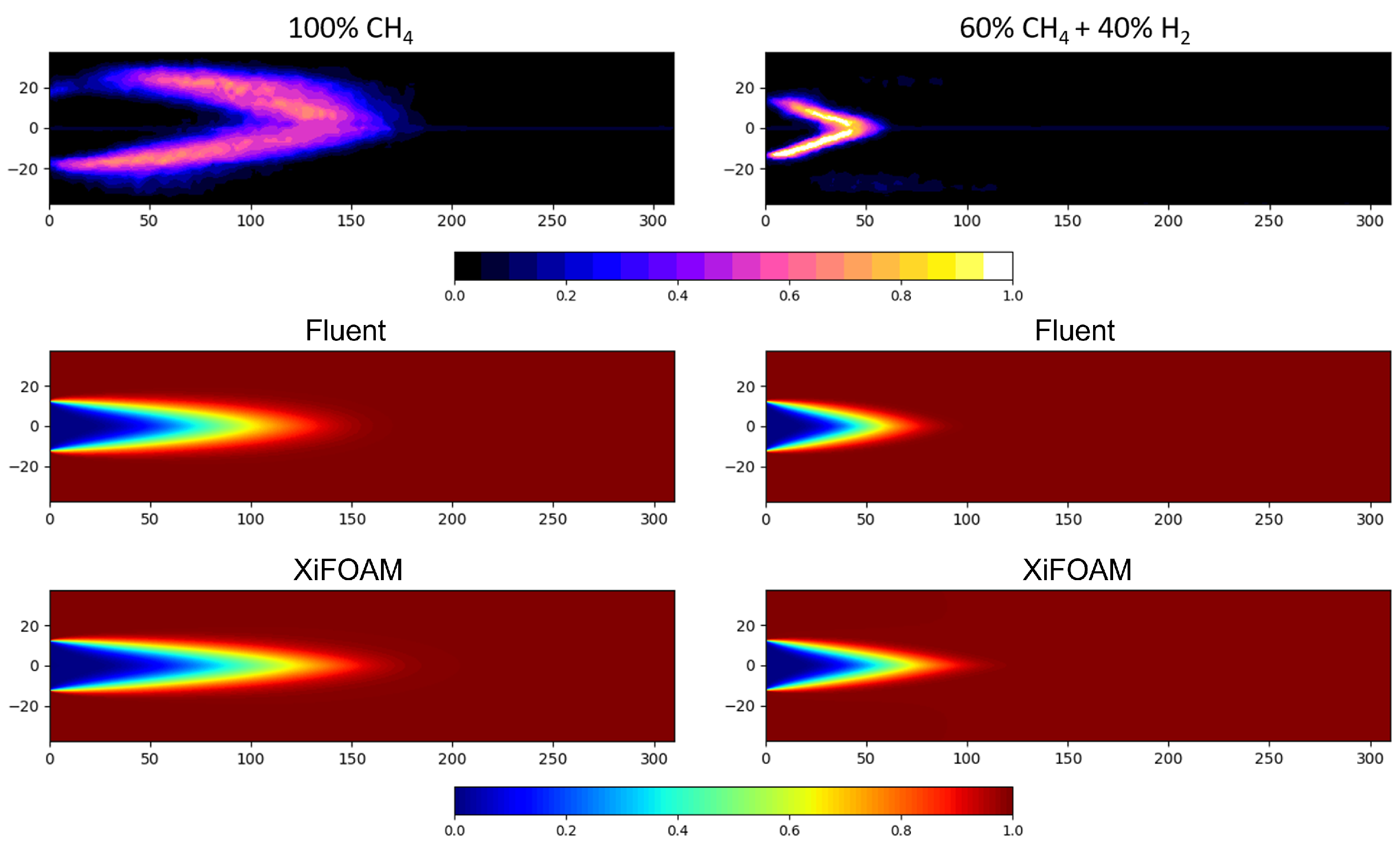
6. Results and Discussion
7. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Reynolds average. | |
| Favre average. | |
| Thermal diffusivity (molecular), measured in . | |
| Lower heating value of combustion, measured in . | |
| Turbulence dissipation rate, measured in . | |
| Thermal conductivity, measured in . | |
| Dynamic viscosity, measured in . | |
| ∇ | Gradient operator. |
| Kinematic viscosity, . | |
| Reaction rate source term, measured in . | |
| in the regress variable b equation, measured in . |
| in the progress variable c equation, measured in . | |
| Equivalence ratio, non-dimensional. | |
| Density, measured in . | |
| Heat release factor, non-dimensional. | |
| a | JANAF table coefficient, non-dimensional. |
| Sutherland model coefficient, measured in . | |
| Air-to-fuel ratio, non-dimensional. | |
| Specific heat, measured in . | |
| Standard state specific heat, measured in . | |
| Methane species. | |
| D | Binary mass diffusivity, measured in . |
| h | Enthalpy, measured in . |
| Standard state enthalpy, measured in . | |
| Hydrogen species. | |
| K | Specific kinetic energy, measured in . |
| Turbulence length scale, measured in . | |
| m | Mass, measured in . |
| n | Mole number, measured in . |
| Nitrogen Oxide. | |
| Nitrogen species. | |
| Oxygen species. | |
| R | Universal gas constant, measured in . |
| Standard state entropy, measured in . | |
| Turbulent flame speed, measured in . | |
| Unstrained adiabatic laminar flame speed, measured in . | |
| T | Temperature, measured in . |
| Sutherland model coefficient, measured in . | |
| Standard state temperature, measured in . | |
| Turbulent fluctuating velocity, measured in . | |
| X | Molar ratio, non-dimensional. |
| Fuel mixture mass fraction, non-dimensional. | |
| b | Regress variable, non-dimensional. |
| c | Progress variable, non-dimensional. |
| k | Turbulent kinetic energy, measured in . |
| Lewis number, non-dimensional. | |
| P | Absolute pressure, measured in . |
| Prandtl number, non-dimensional. | |
| Reynolds number, non-dimensional. | |
| Schmidt number, non-dimensional. | |
| t | Time, measured in . |
| u | Velocity, measured in . |
| x | Spatial coordinates, measured in . |
| Sub-indices | |
| Adiabatic conditions. | |
| Mix of and species. | |
| Absolute. | |
| Burnt mixture property. | |
| Chemical. | |
| Methane species. | |
| Effective. | |
| Fuel. | |
| or . | |
| Hydrogen species. | |
| Index of the spatial dimension, where . |
| Property temperature at which the maximum heat is released. | |
| species. | |
| Stoichiometric condition. | |
| Sensible. | |
| Turbulent property. | |
| Unburnt mixture property. | |
| Acronyms | |
| AFSW | Algebraic Flame Surface Wrinkling. |
| CFD | Computational Fluid Dynamics. |
| JANAF | Joint Army, Navy, and Air Force. |
| Probability Density Function. | |
| PSI | Paul Scherrer Institute |
| RANS | Reynolds-Averaged Navier–Stokes. |
| RHS | Right-Hand Side. |
| SIMPLE | Semi-Implicit Method for Pressure Linked Equations. |
| Standard turbulence model. | |
| UDF | User-Defined Function. |
| URANS | Unsteady Reynolds-Averaged Navier–Stokes. |
References
- Spalding, D.B. Development of the eddy-break-up model of turbulent combustion. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1977; Volume 16, pp. 1657–1663. [Google Scholar] [CrossRef]
- Zimont, V.; Polifke, W.; Bettelini, M.; Weisenstein, W. An efficient computational model for premixed turbulent combustion at high reynolds numbers based on a turbulent flame speed closure. J. Eng. Gas Turbines Power 1998, 120, 526–532. [Google Scholar] [CrossRef]
- Magnussen, B.; Hjertager, B. On mathematical modeling of turbulent combustion with special emphasis on soot formation and combustion. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1977; Volume 16, pp. 719–729. [Google Scholar] [CrossRef]
- Poinsot, T.; Veynante, D.; Candel, S. Diagrams of premixed turbulent combustion based on direct simulation. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1991; Volume 23, pp. 613–619. [Google Scholar] [CrossRef]
- Colin, O.; Benkenida, A.; Angelberger, C. 3d Modeling of Mixing, Ignition and Combustion Phenomena in Highly Stratified Gasoline Engines. Oil Gas Sci. Technol.-Rev. IFP 2003, 58, 47–62. [Google Scholar] [CrossRef] [Green Version]
- Peters, N. A spectral closure for premixed turbulent combustion in the flamelet regime. J. Fluid Mech. 1992, 242, 611–629. [Google Scholar] [CrossRef]
- Peters, N. Turbulent Combustion; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Muppala, S.; Aluri, N.; Dinkelacker, F.; Leipertz, A. Development of an algebraic reaction rate closure for the numerical calculation of turbulent premixed methane, ethylene, and propane/air flames for pressures up to 1.0 MPa. Combust. Flame 2005, 140, 257–266. [Google Scholar] [CrossRef]
- Griebel, P.; Boschek, E.; Janson, P. Lean blowout limits and NOx emissions of turbulent, lean premixed, hydrogen-enriched methane/air flames at high pressure. J. Eng. Gas Turbines Power 2007, 129, 404–410. [Google Scholar] [CrossRef]
- Siewert, P. Flame Front Characteristics of Turbulent Lean Premixed Methane/Air Flames at High-Pressure. Ph.D. Thesis, Swiss Federal Institute of Technology Zurich (ETH Zurich), Zürich, Switzerland, 2006. [Google Scholar] [CrossRef]
- Dinkelacker, F.; Manickam, B.; Muppala, S. Modelling and simulation of lean premixed turbulent methane/hydrogen/air flames with an effective Lewis number approach. Combust. Flame 2011, 158, 1742–1749. [Google Scholar] [CrossRef]
- Kobayashi, H.; Tamura, T.; Maruta, K.; Niioka, T.; Williams, F. Burning velocity of turbulent premixed flames in a high-pressure environment. Proc. Combust. Inst. 1996, 26, 389–396. [Google Scholar] [CrossRef]
- Aluri, N.; Muppala, S.; Dinkelacker, F. Large-Eddy simulation of lean premixed turbulent flames of three different combustion configurations using a novel reaction closure. Flow Turbul. Combust. 2008, 80, 207–224. [Google Scholar] [CrossRef]
- Manickam, B.; Franke, J.; Muppala, S.; Dinkelacker, F. Large-eddy Simulation of Triangular-stabilized Lean Premixed Turbulent Flames: Quality and Error Assessment. Flow Turbul. Combust. 2012, 88, 1573–1987. [Google Scholar] [CrossRef]
- The OpenFOAM Foundation. Available online: http://www.openfoam.org (accessed on 1 December 2021).
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Ansys Fluent Academic Research, Release 19, Help System, Ansys Fluent Theory Guide; Ansys, Inc.
- Launder, B.; Spalding, D. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Hanjalic, K. Two-Dimensional Asymmetric Turbulent Flow in Ducts. Ph.D. Thesis, Faculty of Engineering, University of London, London, UK, 1970. Available online: http://hdl.handle.net/10044/1/8036 (accessed on 1 December 2021).
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion, 3rd ed.; Institut de Mécanique des Fluides de Toulouse: Toulouse, France, 2012; Available online: http://elearning.cerfacs.fr/combustion/onlinePoinsotBook/buythirdedition/index.php (accessed on 1 December 2021).
- Libby, P.A.; Williams, F.A. Turbulent Reacting Flows; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar] [CrossRef]
- Lipatnikov, A. Fundamentals of Premixed Turbulent Combustion, 1st ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar] [CrossRef]
- Kuo, K.K.; Acharya, R. Fundamentals of Turbulent and Multiphase Combustion, 1st ed.; Wiley: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Weller, H.; Tabor, G.; Gosman, A.; Fureby, C. Application of a flame-wrinkling LES combustion model to a turbulent mixing layer. Proc. Combust. Inst. 1998, 27, 899–907. [Google Scholar] [CrossRef]
- Yeung, P.K. Lagrangian investigations of turbulence. Annu. Rev. Fluid Mech. 2002, 34, 115–142. [Google Scholar] [CrossRef]
- Iurashev, D. Numerical and Analytical Study of Combustion Instabilities in Industrial Gas Turbines. Ph.D. Thesis, University of Genoa, Genoa, Italy, 2012. [Google Scholar]
- Goodwin, D.G.; Speth, R.L.; Moffat, H.K.; Weber, B.W. Cantera: An Object-oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes. Version 2.5.1. Available online: https://www.cantera.org (accessed on 1 December 2021). [CrossRef]
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, W.C.; et al. GRI-Mech 3.0. Available online: http://combustion.berkeley.edu/gri-mech/version30/text30.html (accessed on 1 December 2021).
- Donohoe, N.; Heufer, A.; Metcalfe, W.K.; Curran, H.J.; Davis, M.L.; Mathieu, O.; Plichta, D.; Morones, A.; Petersen, E.L.; Guthe, F. Ignition delay times, laminar flame speeds, and mechanism validation for natural gas/hydrogen blends at elevated pressures. Combust. Flame 2014, 161, 1432–1443. [Google Scholar] [CrossRef] [Green Version]
- Ji, C.; Wang, D.; Yang, J.; Wang, S. A comprehensive study of light hydrocarbon mechanisms performance in predicting methane/hydrogen/air laminar burning velocities. Int. J. Hydrog. Energy 2017, 42, 17260–17274. [Google Scholar] [CrossRef]
- Kutkan, H.; Amato, A.; Campa, G.; Ghirardo, G.; Hilares, L.T.W.C.; Asoy, E. Modelling of Turbulent Premixed CH4/H2/Air Flames Including the Influence of Stretch and Heat Losses. J. Eng. Gas Turbines Power 2021. [Google Scholar] [CrossRef]
- Gordon, S.; McBride, B. Computer Program for Calculation of Complex Chemical Equilibrium Compositions and Applications. NASA Reference Publication 1311. 1994. Available online: https://shepherd.caltech.edu/EDL/PublicResources/sdt/refs/NASA-RP-1311-1.pdf (accessed on 1 December 2021).
- LII, W.S. The viscosity of gases and molecular force. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1893, 36, 507–531. [Google Scholar] [CrossRef] [Green Version]
- Guerrero, J.; Kutkan, H. Case repository-Turbulent Premixed Flame Modeling using The Algebraic Flame Surface Wrinkling (AFSW) Model. A Comparative Study Between OpenFOAM and Ansys Fluent. figshare. Software. Available online: https://figshare.com/articles/software/Case_repository_-_Turbulent_Premixed_Flame_Modeling_using_The_Algebraic_Flame_Surface_Wrinkling_AFSW_Model_A_Comparative_Study_Between_OpenFOAM_and_Ansys_Fluent_/16778914 (accessed on 1 December 2021). [CrossRef]
- Rhie, C.M.; Chow, W.L. Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Kim, S.; Makarov, B.; Caraeni, D. A Multidimensional Linear Reconstruction Scheme for Arbitrary Unstructured Grid. In Proceedings of the AIAA 16th Computational Fluid Dynamics Conference, Orlando, FL, USA, 23–26 June 2003. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretized fluid flow equations by operator-splitting. J. Comput. Phys. 1985, 62, 40–65. [Google Scholar] [CrossRef]
- Lipatnikov, A.; Chomiak, J. Turbulent flame speed and thickness: Phenomenology, evaluation, and application in multi-dimensional simulations. Prog. Energy Combust. Sci. 2002, 28, 1–74. [Google Scholar] [CrossRef]
- Guerrero, J.; Mantelli, L.; Naqvi, S.B. Cloud-Based CAD Parametrization for Design Space Exploration and Design Optimization in Numerical Simulations. Fluids 2020, 5, 36. [Google Scholar] [CrossRef] [Green Version]






| P | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.0 | 0.0 | 0.5 | 673 | 5 | 2.52 | 3.25 × | 7.93 × | 2.60 × | 7.56 × | 0.232 | 1606 | 1777 |
| 0.6 | 0.4 | 0.5 | 673 | 5 | 2.46 | 3.25 × | 7.79 × | 2.55 × | 8.05 × | 0.334 | 1589 | 1803 |
| Species Volumetric Ratio | ||
|---|---|---|
| Fuel mixture—Case 1 | 100% | 0% |
| Fuel mixture—Case 2 | 60% | 40% |
| Boundary Condition | Initial Conditions | |||
|---|---|---|---|---|
| Variable | Inlet | Outlet | Wall | Initialization Type |
| k | FV | ZG | KWF | uniform |
| FV | ZG | EWF | uniform | |
| C | ZG | NKWF | uniform | |
| U | UDP | ZG | NS | uniform |
| p | ZG | FV | ZG | uniform |
| T | FV | ZG | ZG | uniform |
| b | FV | ZG | ZG | uniform |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kutkan, H.; Guerrero, J. Turbulent Premixed Flame Modeling Using the Algebraic Flame Surface Wrinkling Model: A Comparative Study between OpenFOAM and Ansys Fluent. Fluids 2021, 6, 462. https://doi.org/10.3390/fluids6120462
Kutkan H, Guerrero J. Turbulent Premixed Flame Modeling Using the Algebraic Flame Surface Wrinkling Model: A Comparative Study between OpenFOAM and Ansys Fluent. Fluids. 2021; 6(12):462. https://doi.org/10.3390/fluids6120462
Chicago/Turabian StyleKutkan, Halit, and Joel Guerrero. 2021. "Turbulent Premixed Flame Modeling Using the Algebraic Flame Surface Wrinkling Model: A Comparative Study between OpenFOAM and Ansys Fluent" Fluids 6, no. 12: 462. https://doi.org/10.3390/fluids6120462
APA StyleKutkan, H., & Guerrero, J. (2021). Turbulent Premixed Flame Modeling Using the Algebraic Flame Surface Wrinkling Model: A Comparative Study between OpenFOAM and Ansys Fluent. Fluids, 6(12), 462. https://doi.org/10.3390/fluids6120462






