Topographically Controlled Marangoni-Rayleigh-Bénard Convection in Liquid Metals
Abstract
1. Introduction
2. Mathematical Model
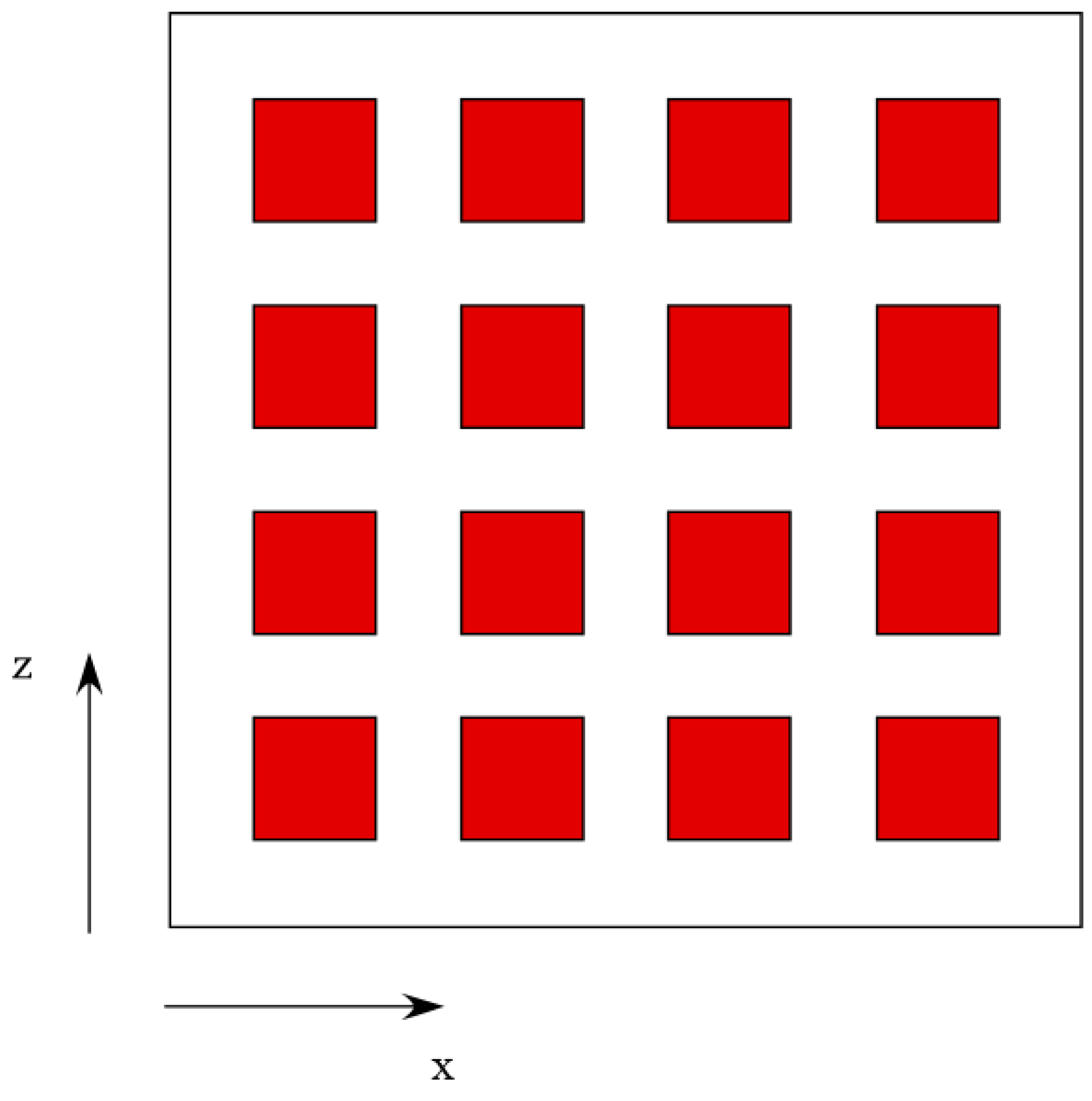
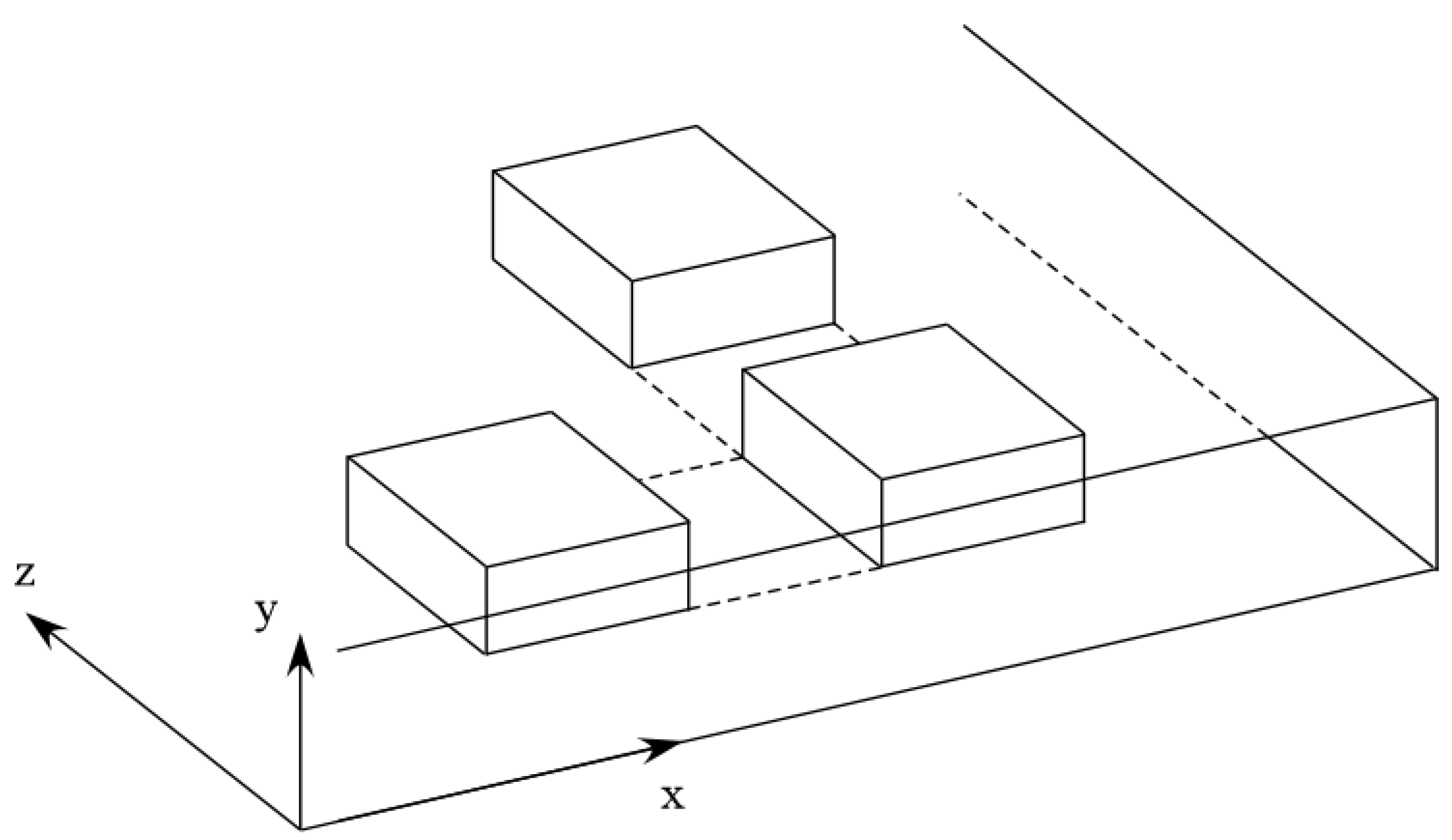
2.1. The Geometry
2.2. The Governing Equations
3. Numerical Method
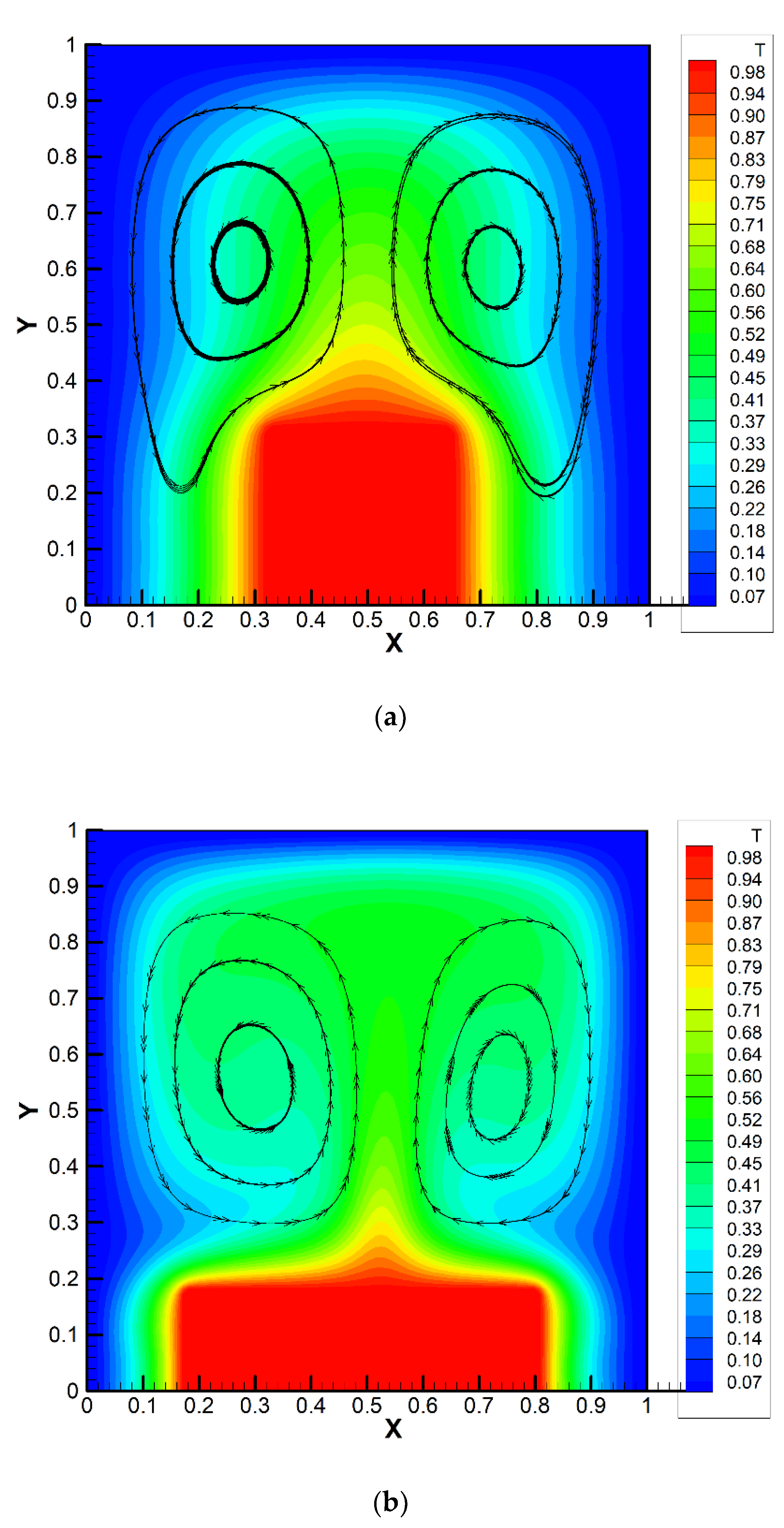
3.1. Validation
3.2. Grid Refinement Study
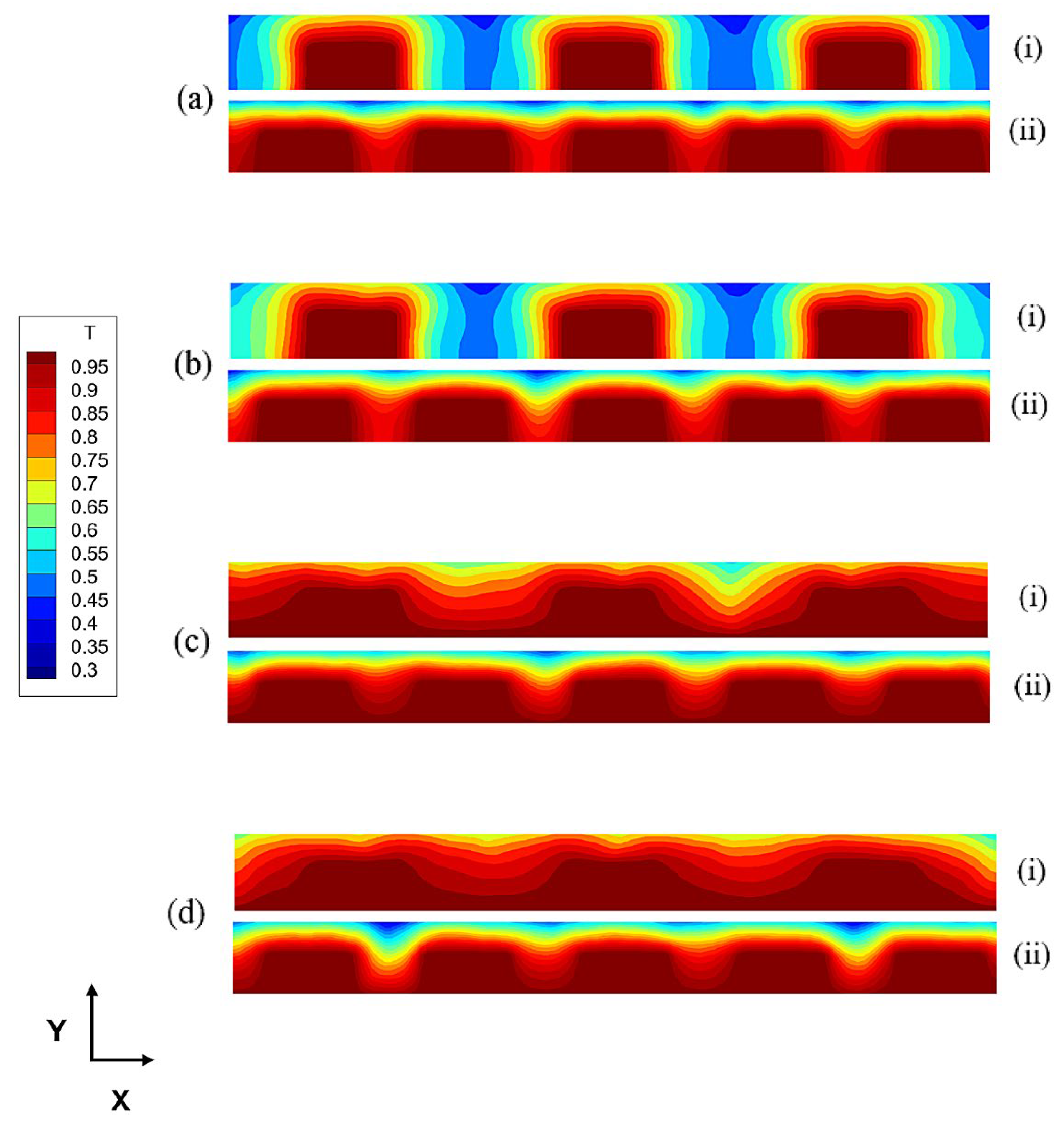
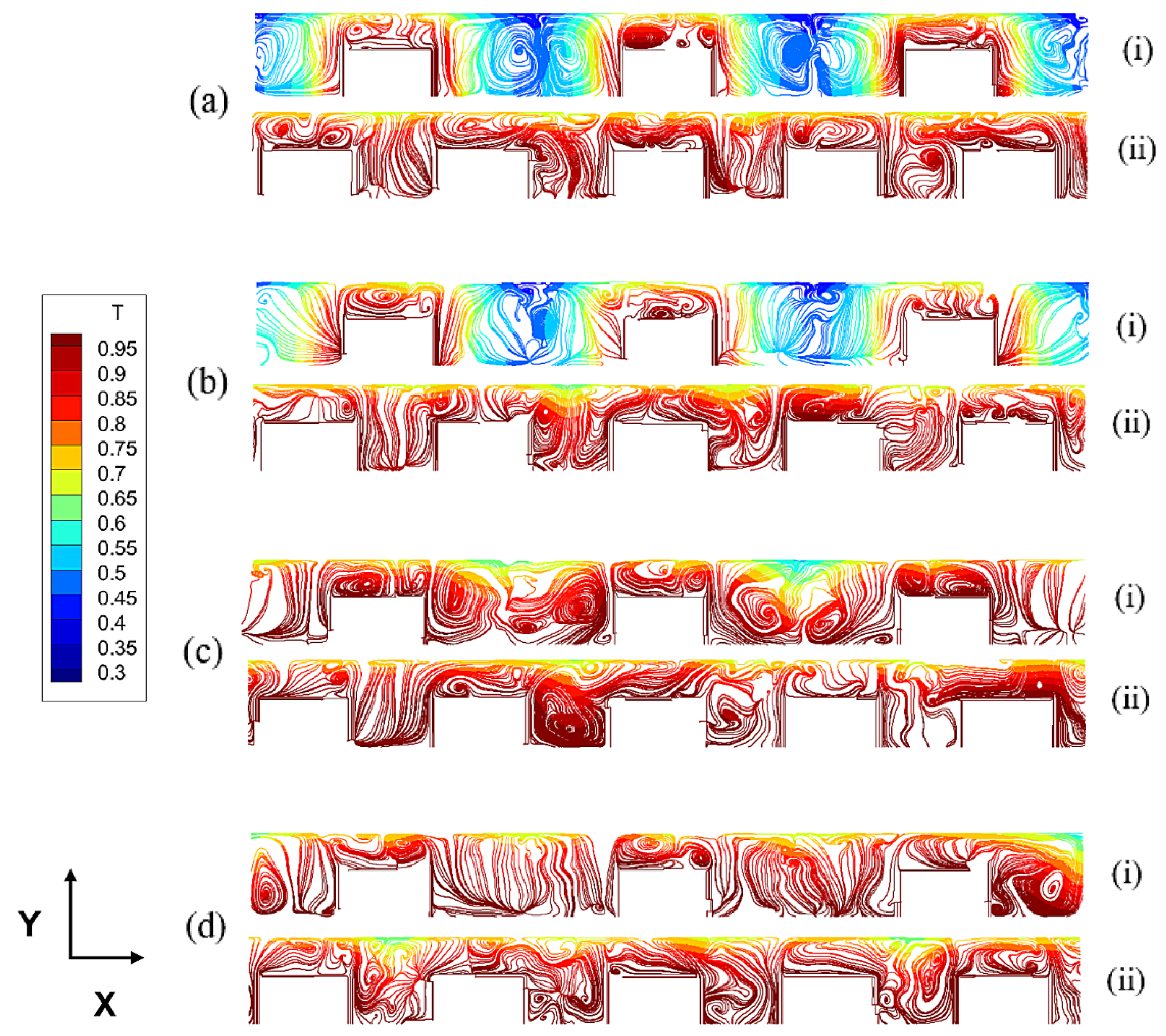
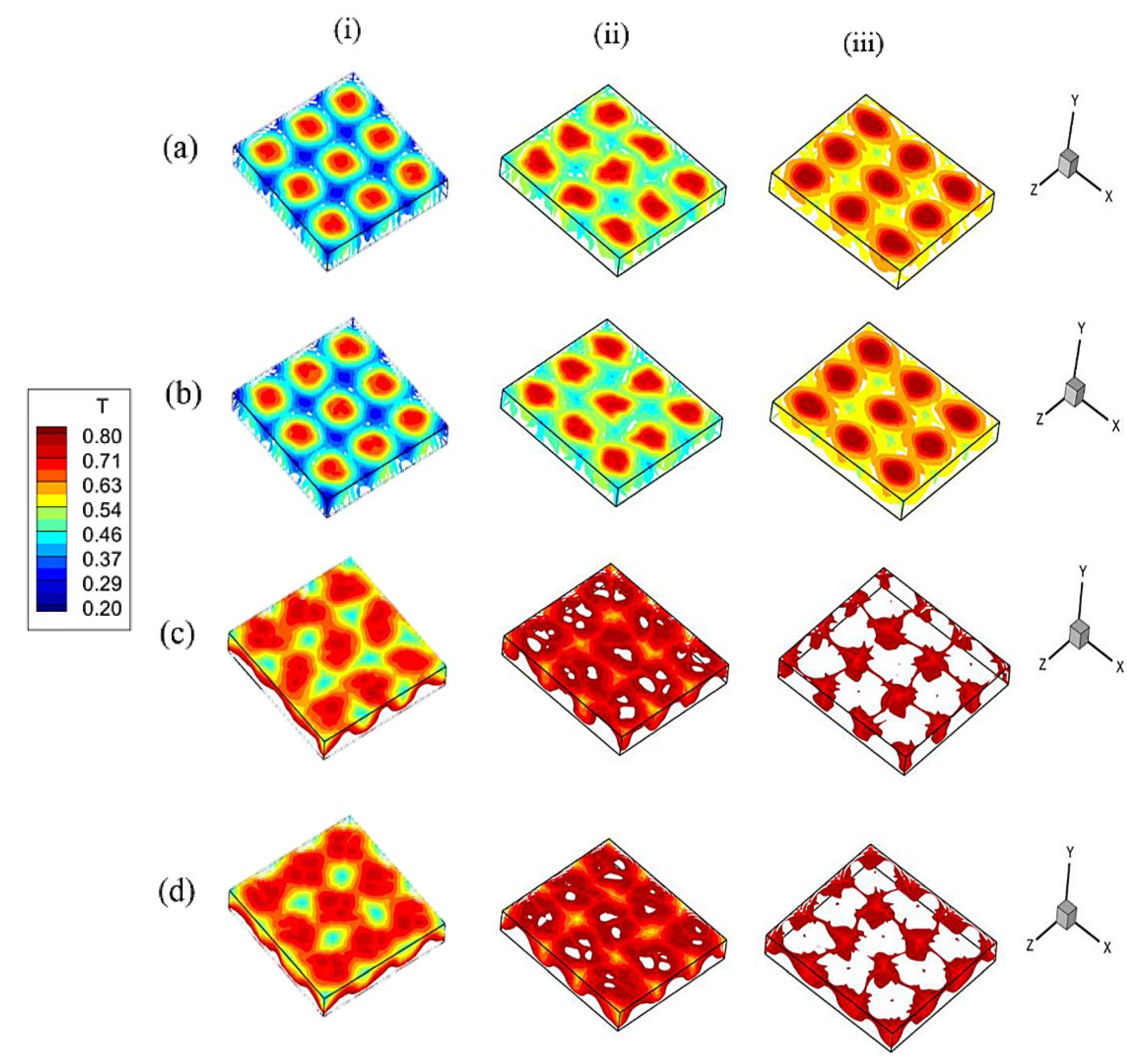
4. Results
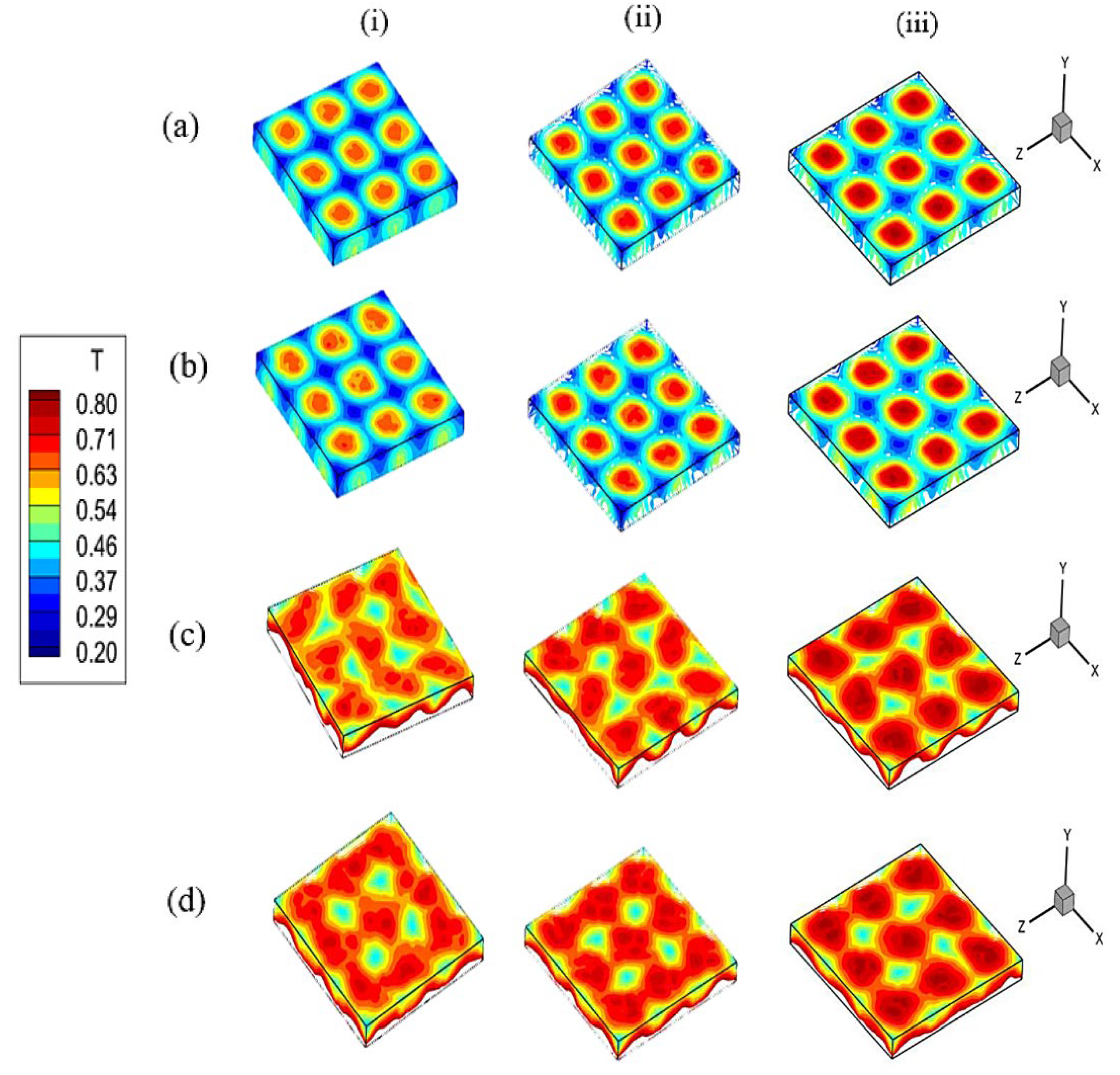
4.1. Silicon Melt with Variable Block Height
4.2. Silicon Melt with Variable Number of Blocks
4.3. Effect of the Prandtl Number
4.4. Time-Dependence and Related Effects
4.5. Heat Exchange Effects
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kaddeche, S.; Henry, D.; Putelat, T.; Ben Hadid, H. Instabilities in liquid metals controlled by constant magnetic field, Part I: Vertical magnetic field. J. Cryst. Growth 2002, 242, 491–500. [Google Scholar] [CrossRef]
- Busse, F.H.; Clever, R.M. An asymptotic model of two-dimensional convection in the limit of low Prandtl number. J. Fluid Mech. 1981, 102, 75–83. [Google Scholar] [CrossRef]
- Clever, R.M.; Busse, F.H. Low Prandtl number convection in a layer heated from below. J. Fluid Mech. 1981, 102, 61–74. [Google Scholar] [CrossRef]
- Clever, R.M.; Busse, F.H. Nonlinear oscillatory convection. J. Fluid Mech. 1987, 176, 403–417. [Google Scholar] [CrossRef]
- Clever, R.M.; Busse, F.H. Convection at very low Prandtl numbers. Phys. Fluids A 1990, 2, 334–339. [Google Scholar] [CrossRef]
- McLaughlin, J.B.; Orszag, S.A. Transition from periodic to chaotic thermal convection. J. Fluid Mech. 1982, 122, 123–142. [Google Scholar] [CrossRef]
- Meneguzzi, M.; Sulem, C.; Sulem, P.L.; Thual, O. Three-Dimensional numerical simulation of convection in low-Prandtl-number fluids. J. Fluid Mech. 1987, 182, 169–191. [Google Scholar] [CrossRef]
- Thual, O. Zero-Prandtl-Number convection. J. Fluid Mech. 1992, 240, 229–258. [Google Scholar] [CrossRef]
- Lappa, M. On the nature and structure of possible three-dimensional steady flows in closed and open parallelepipedic and cubical containers under different heating conditions and driving forces. Fluid Dyn. Mater. Process. 2005, 1, 1–19. [Google Scholar]
- Lappa, M. Thermal convection and related instabilities in models of crystal growth from the melt on earth and in microgravity: Past history and current status. Cryst. Res. Technol. 2005, 40, 531–549. [Google Scholar] [CrossRef]
- Thess, A.; Bestehorn, M. Planform selection in Bénard-Marangoni convection: L hexagons versus g hexagons. Phys. Rev. E 1995, 52, 6358–6367. [Google Scholar] [CrossRef]
- Parmentier, P.M.; Regnier, V.C.; Lebon, G. Nonlinear analysis of coupled gravitational and capillary thermoconvention in thin fluid layers. Phys. Rev. E 1996, 54, 411–423. [Google Scholar] [CrossRef]
- Boeck, T.; Thess, A. Bénard–Marangoni convection at low Prandtl number. J. Fluid Mech. 1999, 399, 251–275. [Google Scholar] [CrossRef]
- Lappa, M. Thermal Convection: Patterns, Evolution and Stability; John Wiley & Sons, Ltd.: Chichester, UK, 2009. [Google Scholar]
- Lappa, M. Rotating Thermal Flows in Natural and Industrial Processes; John Wiley & Sons, Ltd.: Chichester, UK, 2012. [Google Scholar]
- Lappa, M. A mathematical and numerical framework for the simulation of oscillatory buoyancy and Marangoni convection in rectangular cavities with variable cross section, Chapter 12. In Computational Modeling of Bifurcations and Instabilities in Fluid Mechanics; Alexander, G., Ed.; (Springer Mathematical Series, 2018, Part of the Computational Methods in Applied Sciences book series—COMPUTMETHODS); Springer International Publishing: Cham, Switzerland, 2019; Volume 50, pp. 419–458. ISBN 978-3-319-91493-0. [Google Scholar] [CrossRef]
- Lappa, M. On the gravitational suppression of hydrothermal modes in liquid layers with a blockage on the bottom wall. Int. J. Therm. Sci. 2019, 145, 19. [Google Scholar] [CrossRef]
- Lappa, M. On the Highly Unsteady Dynamics of Multiple Thermal Buoyant Jets in Cross Flows. Phys. Fluids 2019, 31, 27. [Google Scholar] [CrossRef]
- Lappa, M.; Boaro, A. Rayleigh–Bénard convection in viscoelastic liquid bridges. J. Fluid Mech. 2020, 904, A2. [Google Scholar] [CrossRef]
- Gresho, P.M. Incompressible fluid dynamics: Some fundamental formulation issues. Ann. Rev. Fluid Mech. 1991, 23, 413–453. [Google Scholar] [CrossRef]
- Guermond, J.-L.; Quartapelle, L. On stability and convergence of projection methods based on pressure Poisson equation. Int. J. Numer. Meth. Fluids 1998, 26, 1039–1053. [Google Scholar] [CrossRef]
- Guermond, J.-L. Some practical implementations of projection methods for Navier–Stokes equations. Model. Math. Anal. Num. 1996, 30, 637–667. [Google Scholar] [CrossRef]
- Guermond, J.-L.; Minev, P.; Shen, J. An Overview of Projection Methods for Incompressible Flows. Comput. Methods Comput. Methods Appl. Mech. Eng. 2006, 195, 6011–6045. [Google Scholar] [CrossRef]
- Petersson, N.A. Stability of Pressure Boundary Conditions for Stokes and Navier–Stokes Equations. J. Comput. Phys. 2001, 172, 40–70. [Google Scholar] [CrossRef]
- Strikwerda, J.C.; Lee, Y.S. The accuracy of the fractional step method. SIAM J. Numer. Anal. 1999, 37, 37–47. [Google Scholar] [CrossRef]
- Biswas, N.; Mahapatra, P.S.; Manna, N.K.; Roy, P.C. Influence of Heater Aspect Ratio on Natural Convection in a Rectangular Enclosure. Heat Transf. Eng. 2016, 37, 125–139. [Google Scholar] [CrossRef]
- Pearson, J.R.A. On convection cells induced by surface tension. J. Fluid Mech. 1958, 4, 489–500. [Google Scholar] [CrossRef]
- Colinet, P.; Legros, J.C.; Velarde, M.G. Nonlinear Dynamics of Surface-Tension-Driven Instabilities; John Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- De, A.K.; Eswaran, V.; Mishra, P.K. Scalings of heat transport and energy spectra of turbulent Rayleigh-Bénard convection in a large-aspect-ratio box. Int. J. Heat Fluid Flow 2017, 67, 111–124. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluids at very large Reynolds numbers. Dokl. Akad. Nauk. SSSR 1941, 30, 299–303, Reprinted in Proc. R. Soc. Lond. A 1991, 434, 9–13. [Google Scholar]
- Kolmogorov, A.N. On the degeneration of isotropic turbulence in an incompressible viscous fluids. Dokl. Akad. Nauk. SSSR 1941, 31, 538–541. [Google Scholar]
- Kolmogorov, A.N. Dissipation of energy in isotropic turbulence. Dokl. Akad. Nauk. SSSR 1941, 32, 19–21. [Google Scholar]
- Kolmogorov, A.N. Equations of turbulent motion in an incompressible fluid. Izv. Akad. Nauk. SSSR Ser. Fiz. 1942, 6, 56–58. [Google Scholar]
- Incropera, F.P. Convection heat transfer in electronic equipment cooling. J. Heat Transf. 1988, 110, 1097–1111. [Google Scholar] [CrossRef]
- Liu, Y.; Phan-Thien, N. An Optimum Spacing Problem for Three Chips Mounted on a Vertical Substrate in an Enclosure. Numer. Heat Transf. Part A 2000, 37, 613–630. [Google Scholar]
- Chuang, S.H.; Chiang, J.S.; Kuo, Y.M. Numerical Simulation of Heat Transfer in a Three-Dimensional Enclosure with Three Chips in Various Position Arrangements. Heat Transf. Eng. 2003, 24, 42–59. [Google Scholar] [CrossRef]
- Rahman, M.M.; Alim, M.A.; Saha, S.; Chowdhury, M.K. Numerical study of mixed convection in a square cavity with a heat conducting square cylinder at different locations. J. Mech. Eng. 2008, 39, 78–85. [Google Scholar] [CrossRef][Green Version]
- Venkatachalapathy, S.; Udayakumar, M. Numerical investigation of natural convection heat transfer from multiple heat sources in a square enclosure. J. Eng. Appl. Sci. 2010, 5, 56–63. [Google Scholar]
- Tyacke, J.; Tucker, P. LES of heat transfer in electronics. Appl. Math. Model. 2012, 36, 3112–3133. [Google Scholar] [CrossRef][Green Version]
- Nakayama, H.; Takemi, T.; Nagai, H. LES analysis of the aerodynamic surface properties for turbulent flows over building arrays with various geometries. J. Appl. Meteorol. Climatol. 2011, 50, 1692–1712. [Google Scholar] [CrossRef]
- Nakayama, H.; Jurcakova, K.; Nagai, H. Development of local-scale high resolution atmospheric dispersion model using large-eddy simulation. Part 3: Turbulent flow and plume dispersion in building arrays. J. Nucl. Sci. Technol. 2013, 50, 503–519. [Google Scholar] [CrossRef][Green Version]
- Meinders, E.; Hanjalic, K. Vortex structure and heat transfer in turbulent flow over a wall-mounted matrix of cubes. Int. J. Heat Fluid Flow 1999, 20, 255–267. [Google Scholar] [CrossRef]
- Yaghoubi, M.; Velayati, E. Undeveloped convective heat transfer from an array of cubes in cross-stream direction. Int. J. Therm. Sci. 2005, 44, 756–765. [Google Scholar] [CrossRef]
- Coceal, O.; Dobre, A.; Thomas, T.G.; Belcher, S.E. Structure of turbulent flow over regular arrays of cubical roughness. J. Fluid Mech. 2007, 589, 375–409. [Google Scholar] [CrossRef]
- Leonardi, S.; Castro, I.P. Channel flow over large cube roughness: A direct numerical simulation study. J. Fluid Mech. 2010, 651, 519–539. [Google Scholar] [CrossRef]
- Lee, J.H.; Sung, H.J.; Krogstad, P.A. Direct numerical simulation of the turbulent boundary layer over a cube-roughened wall. J. Fluid Mech. 2011, 669, 397–431. [Google Scholar] [CrossRef]
- Basara, B. Fluid flow conjugate heat transfer in a matrix of surface-mounted cubes: A PANS study. Int. J. Heat Fluid Flow 2015, 51, 166–174. [Google Scholar] [CrossRef]
- Saeedi, M.; Wang, B.-C. Large-Eddy simulation of turbulent flow and dispersion over a matrix of wall-mounted cubes. Phys. Fluids 2015, 27, 115104. [Google Scholar] [CrossRef]
- Blackman, K.; Perret, L. Non-Linear interactions in a boundary layer developing over an array of cubes using stochastic estimation. Phys. Fluids 2016, 28, 095108. [Google Scholar] [CrossRef]
- Khan, B.A.; Saha, A.K. Direct numerical simulation of turbulent flow and heat transfer over a heated cube placed in a matrix of unheated cubes. Int. J. Heat Mass Transf. 2021, 171, 121052. [Google Scholar] [CrossRef]
- Da Vià, R.; Giovacchini, V.; Manservisi, S. A Logarithmic Turbulent Heat Transfer Model in Applications with Liquid Metals for Pr = 0.01–0.025. Appl. Sci. 2020, 10, 4337. [Google Scholar] [CrossRef]
- Da Vià, R.; Manservisi, S.; Menghini, F. A k-Ω-kθ-Ωθ four parameter logarithmic turbulence model for liquid metals. Int. J. Heat Mass Transf. 2016, 101, 1030–1041. [Google Scholar] [CrossRef]
- Da Vià, R.; Manservisi, S. Numerical simulation of forced and mixed convection turbulent liquid sodium flow over a vertical backward facing step with a four parameter turbulence model. Int. J. Heat Mass Transf. 2019, 135, 591–603. [Google Scholar] [CrossRef]



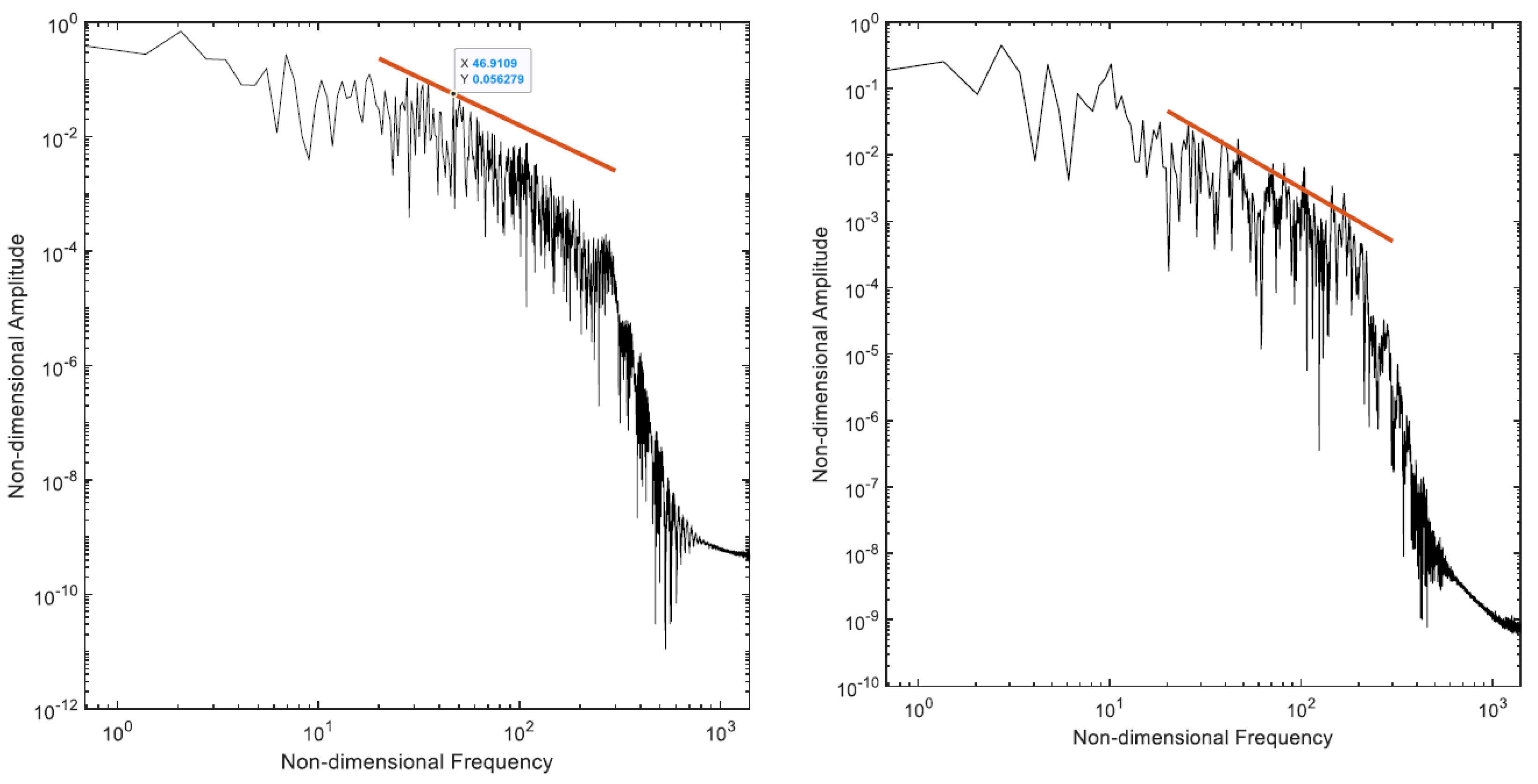
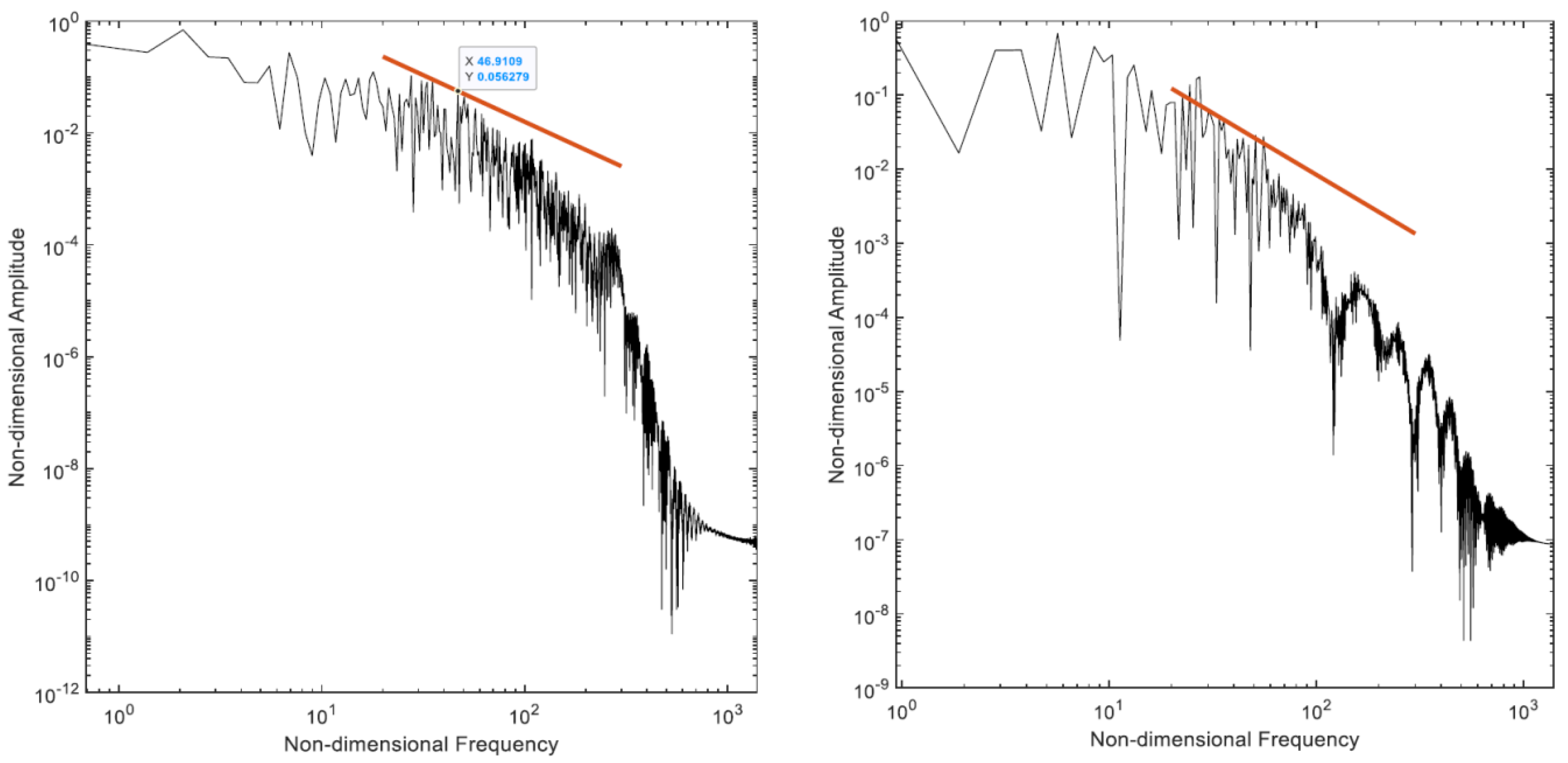
| Ma | Disturbance Growth Rate |
|---|---|
| 145 | 1.535 |
| 140 | 1.3791 |
| 135 | 1.15125 |
| 130 | 0.8528 |
| 125 | 0.4899 |
| 119.3 (extrapolated) | 0 |
| δhoriz | Ra | (Present) | (Present) | (Present) | Biswas et al. [26] | |
|---|---|---|---|---|---|---|
| 0.64 | 0.3 | 104 | 5.56593 | 4.2414 | 4.8381 | ≅4.8 |
| 0.33 | 1.0 | 104 | 4.8209 | 3.8613 | 4.5010 | ≅4.5 |
| 0.64 | 0.3 | 105 | 10.0709 | 7.7318 | 8.6032 | ≅8.65 |
| 0.33 | 1.0 | 105 | 10.5065 | 6.0701 | 9.0277 | ≅9.1 |
| Grid Size | 135 × 135 × 32 | 130 × 130 × 30 | 100 × 100 × 24 | 85 × 85 × 21 | 60 × 60 × 15 |
|---|---|---|---|---|---|
| 1.74 | 1.74 | 1.75 | 1.82 | 1.79 | |
| 1.42 | 1.42 | 1.41 | 1.74 | 1.75 | |
| 1.66 | 1.66 | 1.65 | 1.80 | 1.81 |
| Pr | N | δvert | Adiabatic Floor, Lateral PBC | Adiabatic Floor, Lateral SW | Hot Floor, Lateral PBC | Hot Floor, Lateral SW |
|---|---|---|---|---|---|---|
| 0.01 | 3 | 0.5 | 1.9812 | 2.0203 | 0.3864 | 0.2839 |
| 0.01 | 3 | 0.6 | 1.7447 | 1.7915 | 0.3351 | 0.2613 |
| 0.01 | 3 | 0.7 | 1.6406 | 1.6601 | 0.3313 | 0.3038 |
| 0.01 | 5 | 0.6 | 0.6150 | 0.6175 | 0.3691 | 0.3662 |
| 0.1 | 3 | 0.6 | 2.2188 | 2.1873 | 0.2822 | 0.2850 |
| 1.0 | 3 | 0.6 | 2.4194 | 2.4497 | 0.3880 | 0.4203 |
| Pr | N | δvert | Adiabatic Floor, Lateral PBC | Adiabatic Floor, Lateral SW | Hot Floor, Lateral PBC | Hot Floor, Lateral SW |
|---|---|---|---|---|---|---|
| 0.01 | 3 | 0.5 | 1.5137 | 1.5138 | 1.0898 | 0.9938 |
| 0.01 | 3 | 0.6 | 1.5025 | 1.4941 | 1.1511 | 1.1057 |
| 0.01 | 3 | 0.7 | 1.4867 | 1.4908 | 1.2336 | 1.2357 |
| 0.01 | 5 | 0.6 | 1.2531 | 1.2374 | 1.2176 | 1.2283 |
| 0.1 | 3 | 0.6 | 1.3962 | 1.4032 | 1.0314 | 1.0317 |
| 1.0 | 3 | 0.6 | 1.5760 | 1.5952 | 0.8291 | 0.9107 |
| Pr | N | δvert | Adiabatic Floor, Lateral PBC | Adiabatic Floor, Lateral SW | Hot Floor, Lateral PBC | Hot Floor, Lateral SW |
|---|---|---|---|---|---|---|
| 0.01 | 3 | 0.5 | 1.8254 | 1.8514 | 0.62085 | 0.5205 |
| 0.01 | 3 | 0.6 | 1.6735 | 1.7041 | 0.5751 | 0.5096 |
| 0.01 | 3 | 0.7 | 1.6001 | 1.6155 | 0.5688 | 0.5491 |
| 0.01 | 5 | 0.6 | 0.8027 | 0.800 | 0.6187 | 0.6198 |
| 0.1 | 3 | 0.6 | 1.9768 | 1.9567 | 0.5026 | 0.5046 |
| 1.0 | 3 | 0.6 | 2.1714 | 2.1984 | 0.5178 | 0.5645 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lappa, M.; Sayar, A.; Waris, W. Topographically Controlled Marangoni-Rayleigh-Bénard Convection in Liquid Metals. Fluids 2021, 6, 447. https://doi.org/10.3390/fluids6120447
Lappa M, Sayar A, Waris W. Topographically Controlled Marangoni-Rayleigh-Bénard Convection in Liquid Metals. Fluids. 2021; 6(12):447. https://doi.org/10.3390/fluids6120447
Chicago/Turabian StyleLappa, Marcello, Aydin Sayar, and Wasim Waris. 2021. "Topographically Controlled Marangoni-Rayleigh-Bénard Convection in Liquid Metals" Fluids 6, no. 12: 447. https://doi.org/10.3390/fluids6120447
APA StyleLappa, M., Sayar, A., & Waris, W. (2021). Topographically Controlled Marangoni-Rayleigh-Bénard Convection in Liquid Metals. Fluids, 6(12), 447. https://doi.org/10.3390/fluids6120447






