Abstract
Heat convection is one of the main mechanisms of heat transfer, and it involves both heat conduction and heat transportation by fluid flow; as a result, it usually requires numerical simulation for solving heat convection problems. Although the derivation of governing equations is not difficult, the solution process can be complicated and usually requires numerical discretization and iteration of differential equations. In this paper, based on neural networks, we developed a data-driven model for an extremely fast prediction of steady-state heat convection of a hot object with an arbitrary complex geometry in a two-dimensional space. According to the governing equations, the steady-state heat convection is dominated by convection and thermal diffusion terms; thus the distribution of the physical fields would exhibit stronger correlations between adjacent points. Therefore, the proposed neural network model uses convolutional neural network (CNN) layers as the encoder and deconvolutional neural network (DCNN) layers as the decoder. Compared with a fully connected (FC) network model, the CNN-based model is good for capturing and reconstructing the spatial relationships of low-rank feature spaces, such as edge intersections, parallelism, and symmetry. Furthermore, we applied the signed distance function (SDF) as the network input for representing the problem geometry, which contains more information compared with a binary image. For displaying the strong learning and generalization ability of the proposed network model, the training dataset only contains hot objects with simple geometries: triangles, quadrilaterals, pentagons, hexagons, and dodecagons, while the testing cases use arbitrary and complex geometries. According to the study, the trained network model can accurately predict the velocity and temperature field of the problems with complex geometries, which has never been seen by the network model during the model training; and the prediction speed is two orders faster than the CFD. The ability of accurate and extremely fast prediction of the network model suggests the potential of applying reduced-order network models to the applications of real-time control and fast optimization in the future.
1. Introduction
There are many applications of forced convection in daily life and in the industry. Attributed to the fast development of computational technique and computational ability, numerical simulations have been one of the main methods for solving complex convective heat transfer problems. It is well known that numerically solving differential equations of heat convection is time-consuming, which may become prohibitive for optimization problems involving a large number of design parameters. While during the early stage of design/optimization it usually does not require high-fidelity simulation results, what is favored is that the numerical prediction should be fast for quick iteration. A popular strategy is to use the framework of reduced order modeling (ROM) to enable a fast fluid flow and heat transfer predictions [1,2,3].
In general, a ROM attempts to convert and represent the high-dimension dynamic system into the linear subspace domain by choosing an appropriate transforming coordinate system [4,5]. An important feature of this transformed space is that it allows for decoupling of spatial and temporal modes effectively [6]. The most common choice for the construction of these spatial transformation bases is the method of proper orthogonal decomposition (POD). The POD method has provided powerful tools for building ROM for fluid flow and heat transfer problems [7,8,9]. Indeed, the low computational expense and small memory requirement of this method make it particularly suitable for optimization and aftertreatment analysis. However, the POD method is also limited because it is a linear combination of eigenvectors and eigenvalues and does not explicitly account for the nonlinear interactions of the highly nonlinear dynamic system. That is to say that the POD method is significantly effective for quasi-steady-state, time-periodic problems, but might be challenging for highly nonstationary and nonlinear problems [10].
In recent years, machine learning (ML)- and deep learning (DL)-based techniques/methods have been showing power on building a surrogate/reduced-order model for highly nonlinear dynamic problems, including applications of aerodynamics, heat transfer, and fluid flow. The big difference between DL-enabled and POD-based ROM is that DL can be used to directly set up a nonlinear relationship between abundance of inputs and outputs of a target system. This process of fitting to available data, known as model training, generates a low-dimensional subspace, which records the mean behavior of the underlying phenomena of flows; and this training process allows for the representation of complex relationships/features, which cannot be expressed explicitly in a functional form [11]. In practice, the DL-enabled ROM has been demonstrated to be able to accurately capture the spatial and temporal nonlinear features of fluid flow. Wang et al. [12] presented a model identification of reduced-order fluid dynamic systems by using deep learning, and proved that the framework is capable of capturing the features of complex fluid dynamics with less computational cost. Fukami et al. [13] used machine learning to perform super-resolution analysis of grossly under-resolved turbulent flow data and reconstructed the high-resolution flow field; that is, their model successfully builds a nonlinear mapping between a low-resolution and high-resolution turbulent field. Alternatively, an approach known as DL-based closure modeling has been used to improve the performance of the traditional ROM methods [14,15,16].
The deep learning (DL)-based reduced-order modeling method has started to catch the attention of the thermal engineering community, although there are only a few publications available. San and Maulik [6] applied the machine learning method for developing a data-driven closure modeling for stabilizing projection-based reduced-order models for the Boussinesq equations, that is, improving the performance of the traditional ROM by DL. Gao et al. [17] proposed a physics-constrained CNN architecture to learn solutions of parametric PDEs on irregular domains, where the PDEs include a heat transfer equation and Navier–Stokes equations. Their results demonstrate the effectiveness of the proposed DL approach in predicting the temperature field and velocity field.
In the current study, we apply CNN to build a reduced-order, geometry-adaptive, and steady-state heat convection model, since CNN has demonstrated strong feasibility in geometry representation and per-pixel prediction in two-dimensional fields [18,19,20]. In Section 2, we introduce the network architecture of the reduced-order model, the preparation of the datasets, and the training algorithm. In Section 3 and Section 4, we present and discuss the outstanding performance of the network model.
2. Methods
In this paper, we propose that a CNN-based ROM directly builds a mapping between physical fields and signed distance function (SDF), which represents the problem geometry. The networks and its training are implemented using Tensorflow. The “ground truth” (training dataset) is generated through CFD simulation using OpenFOAM.
2.1. Design of the CNNs-ROM Framework
2.1.1. Framework Workflow
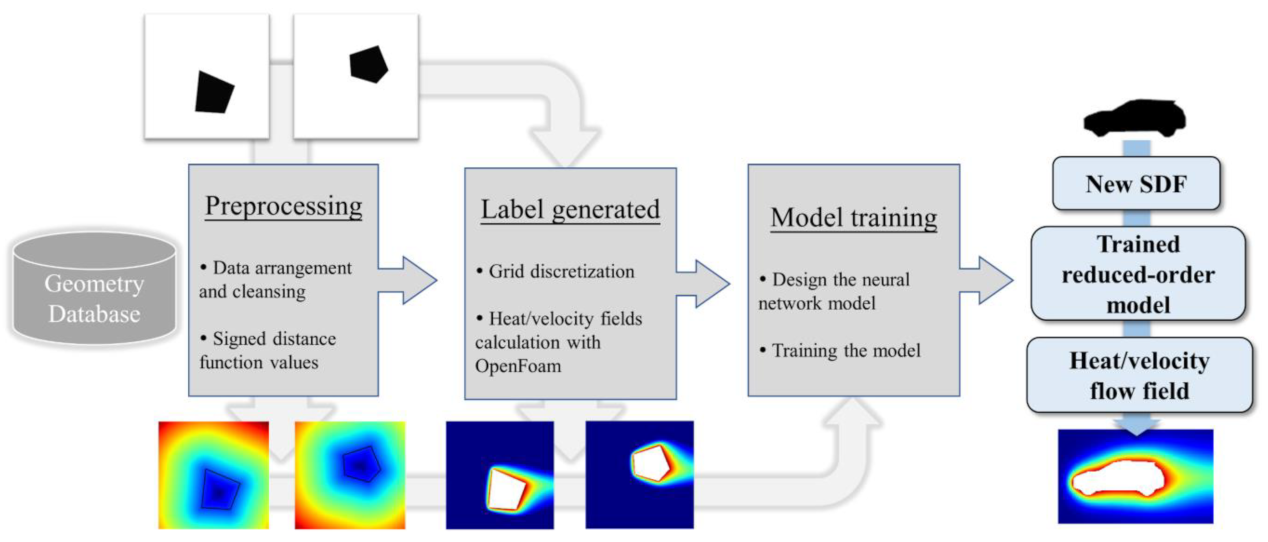
Figure 1 depicts the schematic of the proposed reduced-order model, which shows the learning/training strategy and the method of a new prediction using the network model. For the model training, we use the signed distance function (SDF), which carries physical information of the geometry as the network input and the results (temperature/velocity) of numerical simulations as the learning target (output/label) of the CNNs. After training with the proper amount of dataset, the trained CNNs can predict the temperature/velocity fields based on the new SDF values.
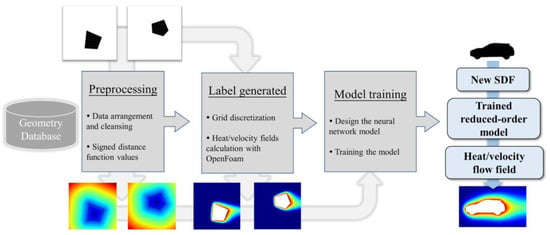
Figure 1.
Schematic of the CNNs-ROM framework.
2.1.2. Signed Distance Function
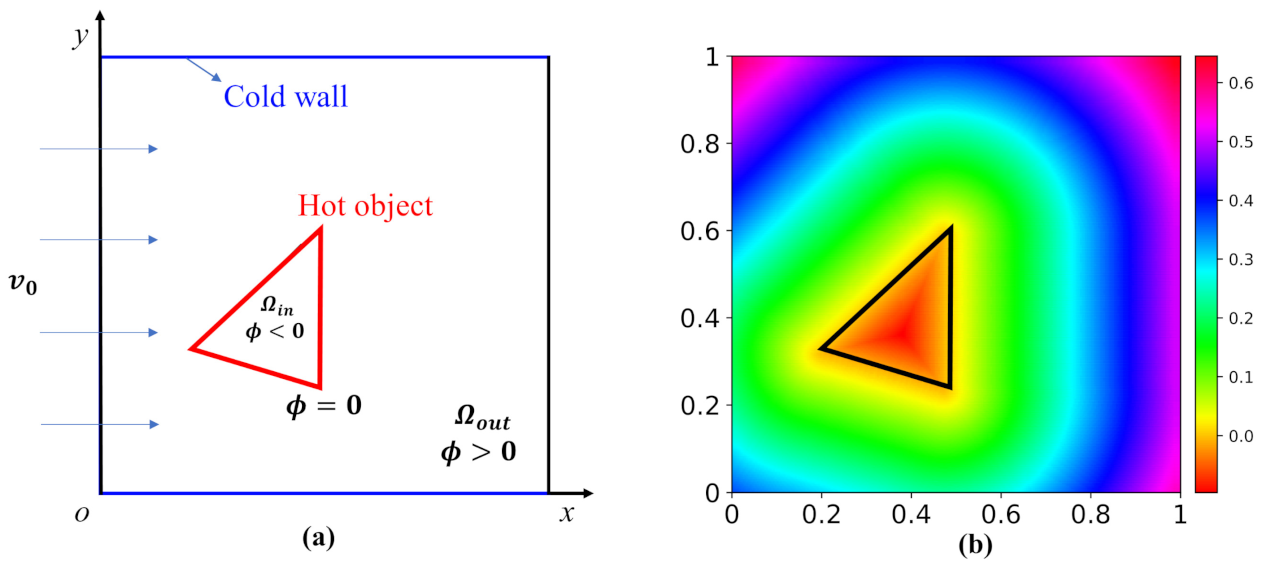
The signed distance function (SDF) is proposed as the geometry representation at the network input. Using the SDF, the geometry of the object is represented as a level-set function defined over the simulated space in which the object is embedded [21,22]. Compared with the boundaries and geometric parameters representation, the SDF provides more physical and mathematical information for CNNs. In the SDF representation method, the zero-level set is created to represent the location of the boundary of the object. That is, the boundary of the object, , is represented as the zero-level set of a continuous level-set function “” defined in a domain , and stands for a 2D bounded domain; that is,
The level-set function is defined everywhere in the domain , and if and only if is on the object boundary, such as the edge of the polygon shown in Figure 2a. The SDF associated with the level-set function is defined as
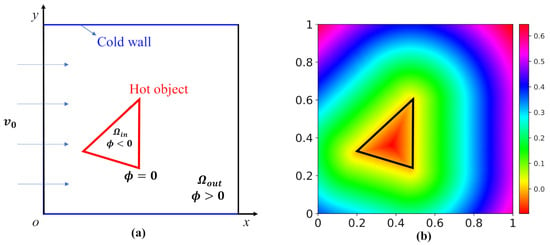
Figure 2.
(a) Schematic of the object and the studied domain; (b) distribution of the SDF representation of a triangle, where the boundary of the triangle is in black, and the magnitude of the SDF values equals the minimal distance of the space point to the triangle boundary.
is an oriented distance function, X2 is a point on the boundary of the object, and the sign function “” is defined as:
By using the above level-set function, one can represent an arbitrary shape in the fixed design domain, [23]. Figure 2b gives the distribution of the SDF representation of a training dataset.
2.1.3. Architecture of CNNs
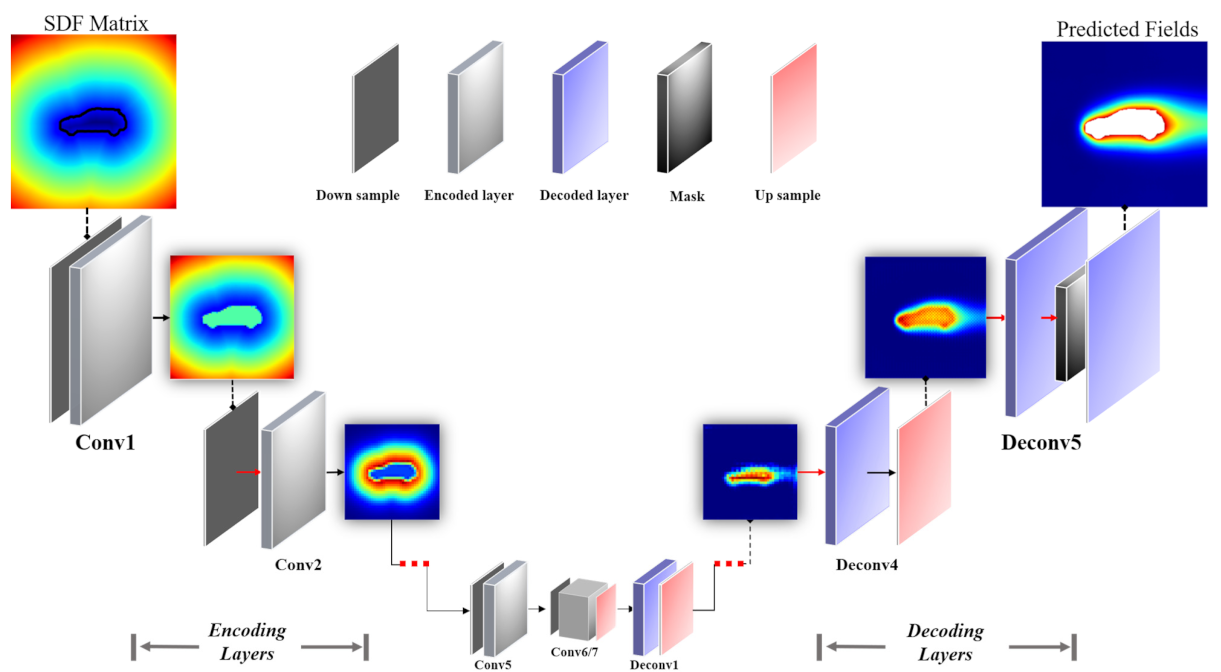
The proposed network architecture consists of convolution layers and transposed convolution (also called deconvolution) layers. To ensure the high nonlinearity of the proposed reduced-order model, we use a multilayer deep structure for our neural network [24]. In the model, multiple convolutional layers are applied to extract a highly encoded [25] geometry representation from the SDF (input matrix of the network), and the encoded geometry representation is decoded by multiple deconvolutional layers [26] to predict the physical fields. The choice of the network structure is highly dependent on the problem, the data quality, and even the dataset size [27]. For example, it would be necessary to build deep convolutional neural networks in our problem due to the big size and complexity of the training dataset. Figure 3 shows the structure and components of the CNN model, and Table 1 displays the parameters of each layer of the network model. We will describe each part of the network in the following subsection.
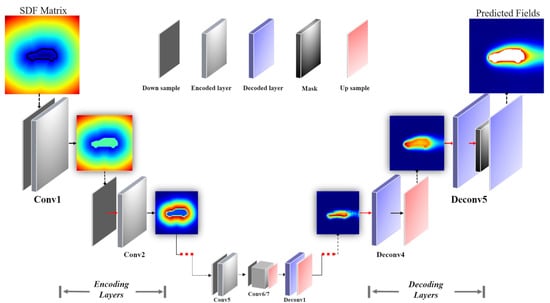
Figure 3.
Architecture of the CNN-based reduced-order model. “Conv” denotes the convolutional layer; “Deconv” denotes the deconvolution layer.

Table 1.
Parameters of the neural network model of each layer, where
denotes the size of the convolution kernel (F), denotes the number of F, and is the size of the lth layer after operation.
2.1.4. Encoding Part
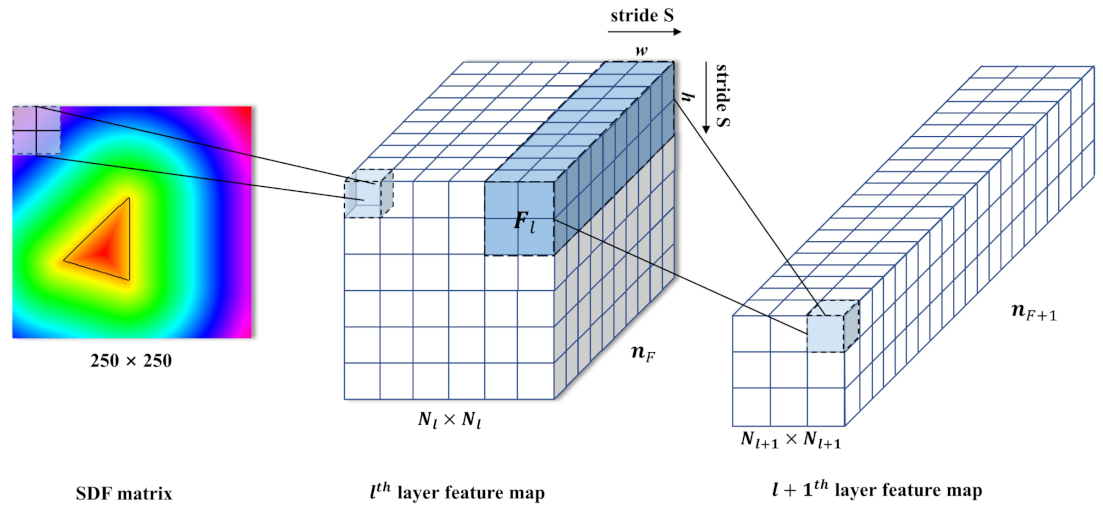
The encoding part aims to reduce the dimension of the input data and extract the potential spatial features between neighboring points of the SDF matrix and convolution layers. According to the governing equations, the steady-state heat convection is dominated by convection and thermal diffusion terms; thus the distribution of the physical fields would exhibit stronger correlations between adjacent points. As the CNNs are very powerful for handing two dimensional data with a locality structure [28,29], in the current approach, the data-driven model is developed using the CNNs. Figure 4 shows the schematic of the convolution (down sample) operation by the network.
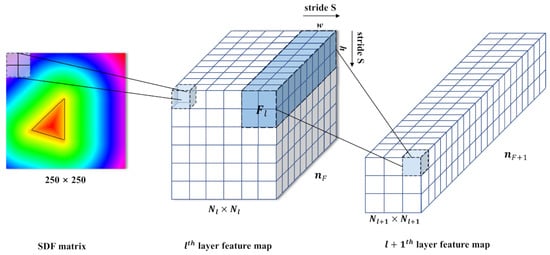
Figure 4.
Schematic of the convolution operation. The light blue matrix denotes a 2 × 2 convolutional kernel, and the white matrix represents the feature map.
In Figure 4, the light blue matrix denotes the convolutional kernel, the white matrix is the feature map matrix (also called the next layer’s input matrix), and the blue translucent matrix represents the output of the convolution operation. Besides the size of the kernel, (), the convolutional output is also influenced by the kernel stride, ; the size of the channels, ; and the padding size, . The padding operation adds zeros around the border of the input matrix, and the kernel stride controls the sliding step size of the kernel. The size of the output matrix after the convolutional operation can be calculated as:
where is the size of feature map at the layer (l = 0 represents the layer of the input matrix of the network model). In the current work, zero padding size (P = 0) is used. From the above equation, it can be seen that after several convolutional operations, the size of the original input can be reduced significantly, and the features of the original input are also highly encoded; thus the memory space required by the CNN training was reduced.
To increase the nonlinear capability of CNNs, each convolution or deconvolution layer involves the nonlinear activation operations. Mathematically, the nonlinear activation operation can be expressed as:
where is the weights or convolutional kernel of the current layer; denotes the nonlinear activation function; and are the input and the output of the layer, respectively; is the convolutional operator; and is the bias term. The introduction of is crucial for neural networks to possess nonlinearity. In this paper, we apply the rectified linear unit (RELU) activation function:
The advantages of RELU are that its computation cost is cheap as the function has no complicated math, and it converges fast; thus the model takes less time to train or run. It should be noticed that, because the final prediction of the network model needs to be a continuous regression, there is no activation function between the output layer and the “Deconv5” layer.
2.1.5. Decoding Part
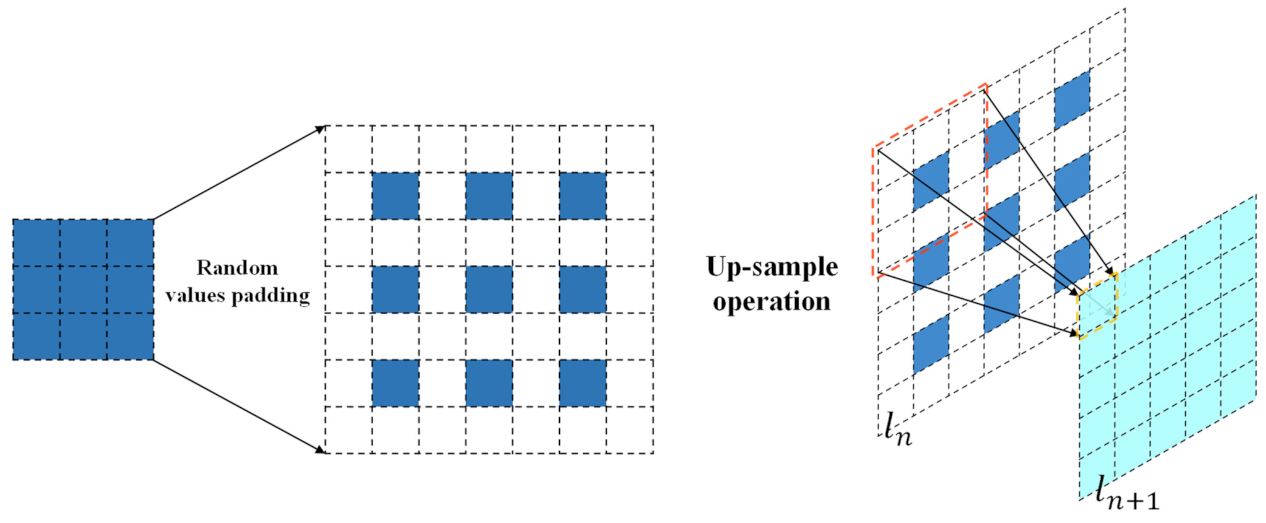
The decoding part is designed to analyze the highly encoded features and decode them to be a recognizable velocity and temperature fields. The decoding part is composed by multiple deconvolutional layers, and these up-sample operations (deconvolution) unravel the high-level features encoded by the encoding part. Figure 5 shows the schematic of the deconvolution operation of one channel.
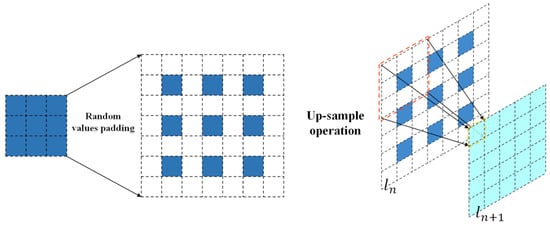
Figure 5.
Schematic of the deconvolutional layer: the dark blue block represents the feature map at the
layer, the white block illustrates the padding location of the layer’s feature map, and the pool blue block represents the feature map at the next layer ().
The deconvolution operation needs appropriate basis functions to learn invariant subspaces of the feature map, and then compensates the minutia information to predict the physical fields by multilayer iterative optimization. For instance, as shown in Figure 5, for adjusting the width and height of the output feature map (pool blue block), random values (optimized by the algorithm) will be padded at the white block around the block (dark blue block) of the input feature map. Therefore, highly encoded information is recovered by applying the deconvolutional decoder. Meanwhile, the CNNs learn/train their ability to predict physical fields based on the SDF through this process.
2.2. Model Training
The model training is an iterative process that continuously minimizes the loss between the outputs of the network predicted () and the ground truth () for obtaining the optimal model parameters, . Further, we need to condition our ROM prediction based on the SDF, as the flow field within the geometry should be ignored and must not affect the loss function. The SDF-based conditioning operation is defined as follows:
where (x, y) is the index of the space point and is the index of the case number, is the size of the (batch) dataset, indicates the result by the numerical simulation, is the result predicted by the network model, denotes all the weight of the network layers, is the regularization coefficient, and is the L2 regularization term for preventing model overfitting. Such a conditioning operation eases the training process and improves the prediction accuracy [30].
During the training process, the SDF (shape: 250 × 250) and velocity/temperature field (shape: 250 × 250) are the input and the output of the CNN model. Specifically, the velocity/temperature field is regarded as the ground truth (label) of the network model, while the SDF is treated as the input matrix of the CNNs. After the model training, the network extracts the features from the input matrix and builds a proper mapping between the SDF and the physical fields. Obviously, the training process of the CNNs is to reduce the deviation of Equation (7).
To train the model efficiently, a minibatch-based learning strategy is used. Small batch training has been shown to provide improved generalization performance and reduces the memory cost significantly [31]. The loss function is computed using a randomly selected subset (i.e., the batch size), and the whole optimization process forms an iteration way. Moreover, the adaptive moment estimation (Adam) method is implemented as the optimization algorithm for the model training; the Adam method has been proved to be robust and well suited for large datasets and/or optimization problems of high-dimensional parameter spaces [32]. The hyperparameters of the optimization algorithm for the network training are shown in Table 2.

Table 2.
Hyperparameters of the optimization algorithm. Regularization coefficient () and learning rate ().
2.3. Preparation of Dataset
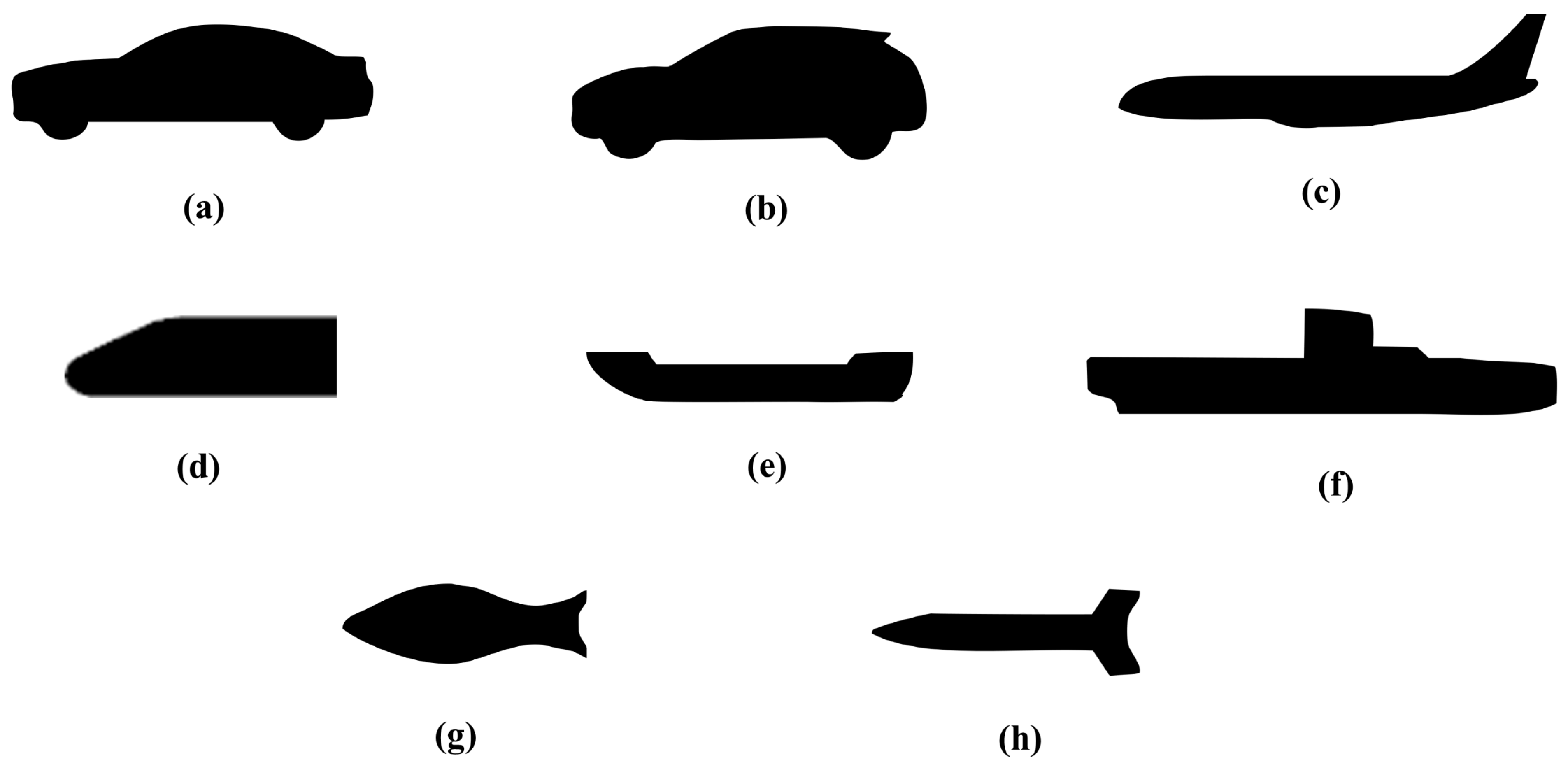
The simulation domain of the studied heat convection problem is shown in Figure 2a, where the geometry of the hot object is changeable. The flow direction is flow left to right. The up and bottom boundaries are a cold wall, whose temperature is same to that of the inlet flow. Such a configuration is chosen as it is a typical forced convection problem and can be seen in many engineering applications [33,34]. The training and test datasets consist of 5 types of 2D simple hot objects in a square simulated domain (see Figure 2 as an example): triangles, quadrilaterals, pentagons, hexagons, and dodecagons. With the simulated domain kept unchanged, each set of the hot objects is randomly different in size, shape, orientation, and location. In general, it is more often that the object locates near the center of the studied domain; therefore, the location of the object is generated following a normal distribution in the function of x- and y- coordinates and using the center of the domain as the mean. Each 2D simple object is preprocessed into a 250 × 250 pixel matrix based on the SDF. The training and testing datasets contain a total of 10,000 samples (2000 random samples for each type of object), where the testing dataset contains 1000 samples (random separated from the whole training and testing dataset). The simulated domain is discretized using an unstructured mesh tool, SnappyHexMesh [35,36], and the numerical simulation is performed using OpenFOAM (openfoam.org), where the SIMPLE algorithm is used. Regarding the validation dataset, which is dedicated to validating and indicating the generalization ability of our CNN model, more complex geometries of the hot objects are chosen (see Figure 6). Those samples have never been seen by the network model during the training process. All the processes of the mesh generation and numerical simulation for generating the validation dataset are similar to that for the training dataset.
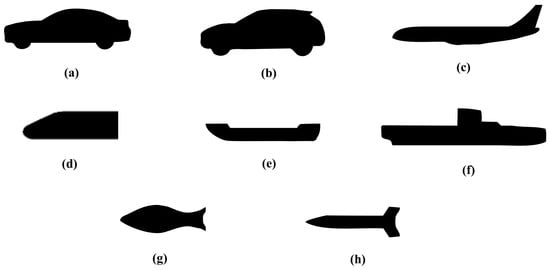
Figure 6.
Geometry of the objects of the validation dataset: (a) Car, (b) Car2, (c) Airplane, (d) Locomotive, (e) Ship, (f) Submarine, (g) Bionic Fish, (h) Missile.
The physics or governing equations of the steady-state heat convection can be given as:
where is the velocity vector, is the pressure, is the temperature, is the divergence operator, and is the gradient operator; and are the momentum and thermal diffusivity. It should be noticed that the viscous dissipation has been ignored. Based on the following parameters:
The governing equations can be normalized as follows:
where is the reference length, is the temperature of the cold wall and is the temperature of the hot object, is the inlet mean velocity, is the Reynolds number, and is the Lewis number, which is the ratio of thermal diffusivity to convective mass transport. Notice that the asterisks have been ignored for simplicity. In the following study, we keep the Reynolds number and the Lewis number at 10 and 15, respectively. The differential equation is solved based on the SIMPLE algorithm. The boundary conditions used here are listed in Table 3. Moreover, the grid independency study is carried out to determine the appropriate meshes to use. We only show the results for the case of a complex geometry (Car), as shown in Table 4. To speed up the data generation, grid-one (approximate value) is chosen for further studies.

Table 3.
Boundary conditions of the numerical model.

Table 4.
Average temperature at the outlet (Ot) with different meshes.
3. Results
We use the average, mean, and maximum relative error to measure the prediction accuracy of the network model. For a studied case, the relative error for velocity and temperature is calculated as:
The maximum point relative error is defined as:
The mean relative error is defined as:
For evaluating the performance of the network model over several different cases, we also define the average relative error as:
where is the index of the studied cases. Furthermore, from Equation (15), it should be noticed that when calculating the error, we only consider the domain outside the hot object.
3.1. Feasibility of the CNN-Based Model
In this section, we verify the feasibility of the proposed framework on three aspects: (1) the outstanding performance of the CNN model in predicting the velocity and temperature fields, (2) the advantage of the SDF representation, and (3) the optimization process of the CNN model structure.
3.1.1. Performance of the Temperature Field Prediction
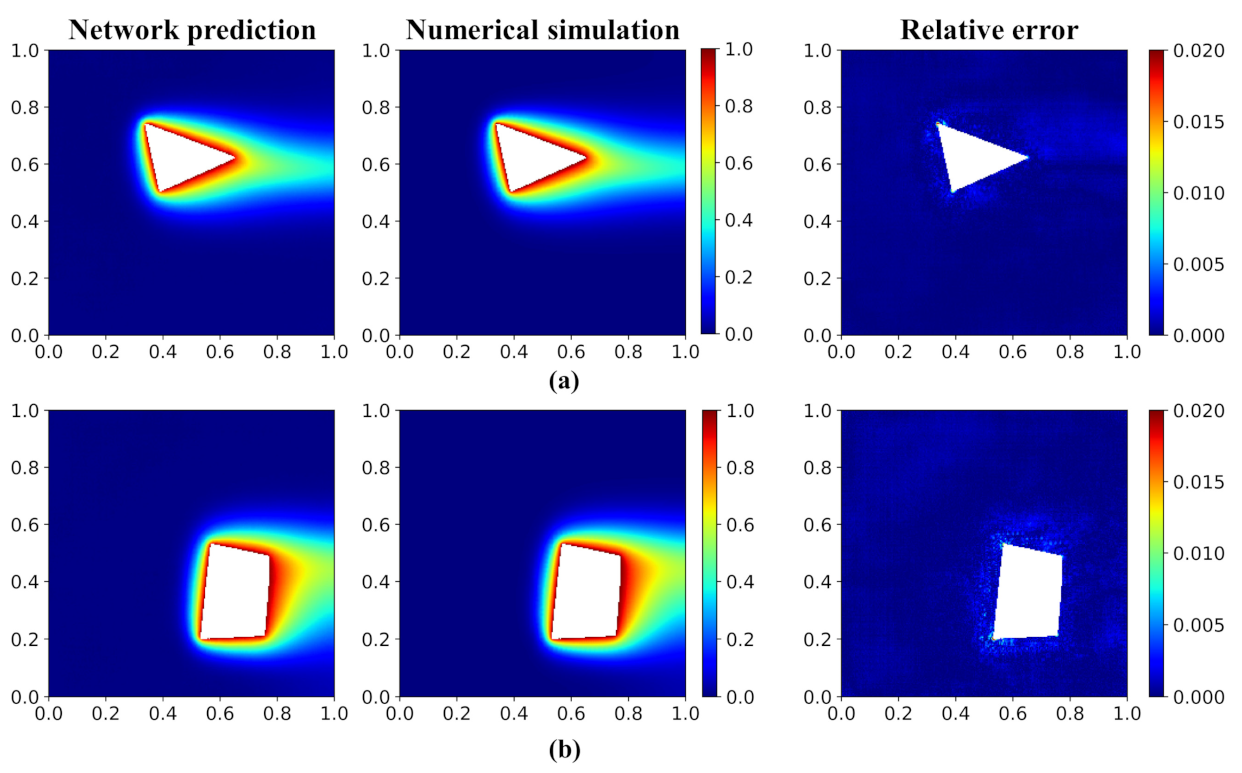
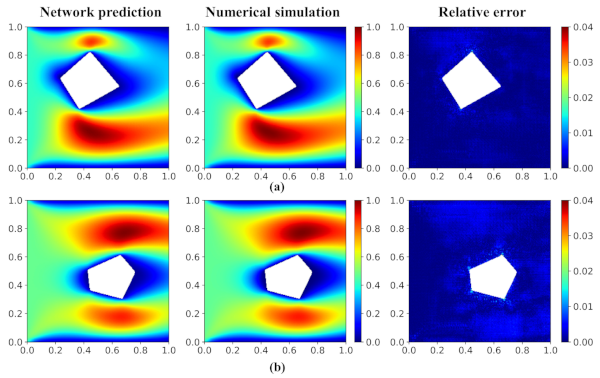
We first evaluate the prediction performance of the temperature field of the network model. After proper model training, the prediction accuracy of the testing dataset is higher than 98.75%. Figure 7 visualizes two typical temperature fields of the test dataset predicted by the network model and numerical simulation (OpenFOAM) and the corresponding relative error distribution (see Figure 7). We can see that the network model has given a satisfied accurate prediction on the temperature field. Furthermore, the figure of the relative error distribution indicates that the large error mainly locates in the region with a large temperature gradient.
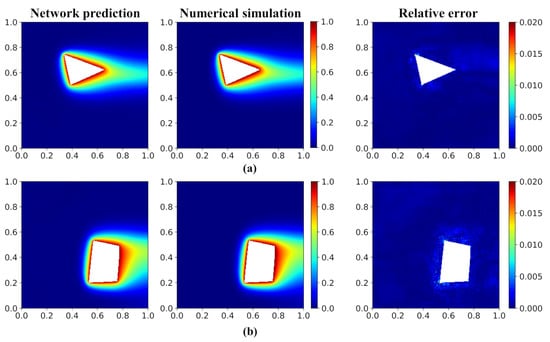
Figure 7.
Temperature field and error distribution of validation cases. (a) Triangle and (b) quadrangle. The first and second columns show the temperature field predicted by the network model and the numerical simulation (OpenFOAM). The third column shows the relative error distribution.
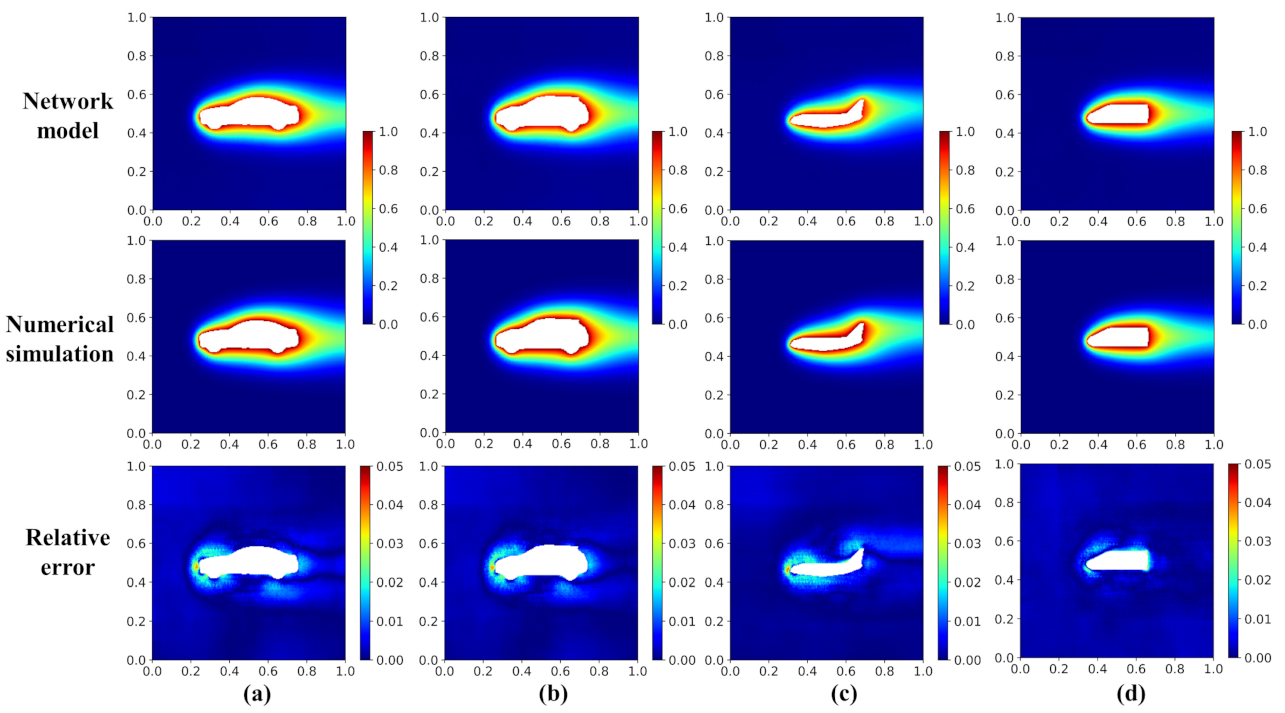
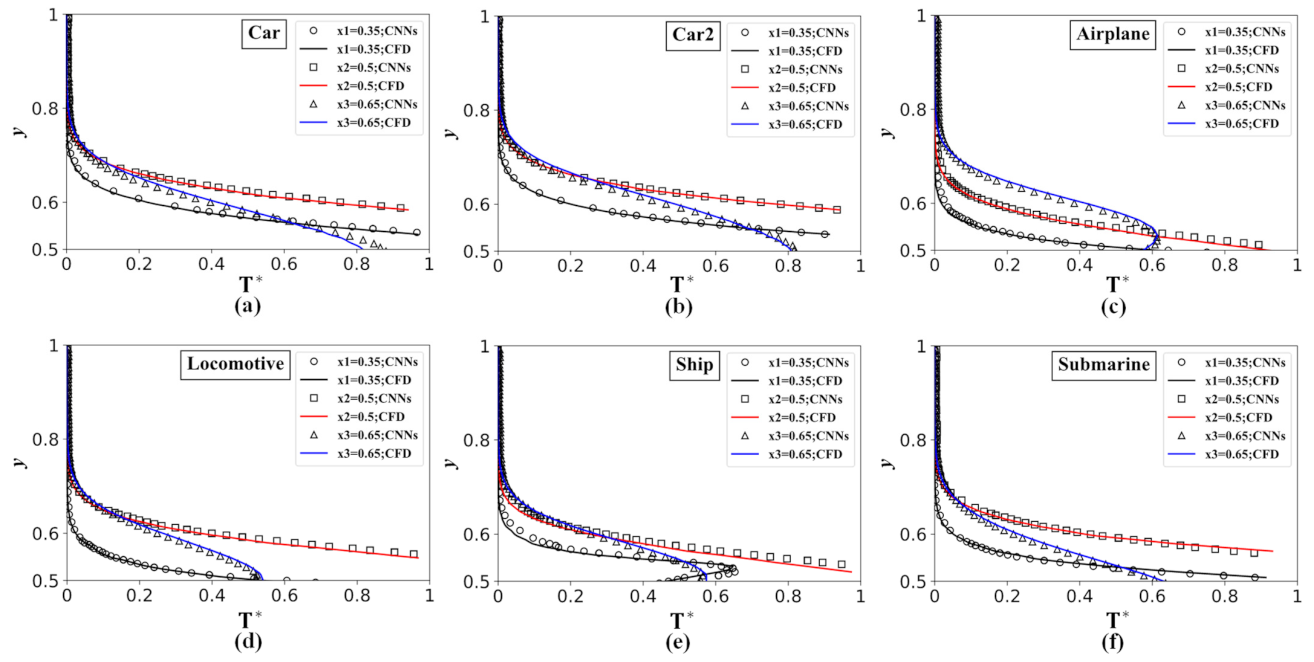
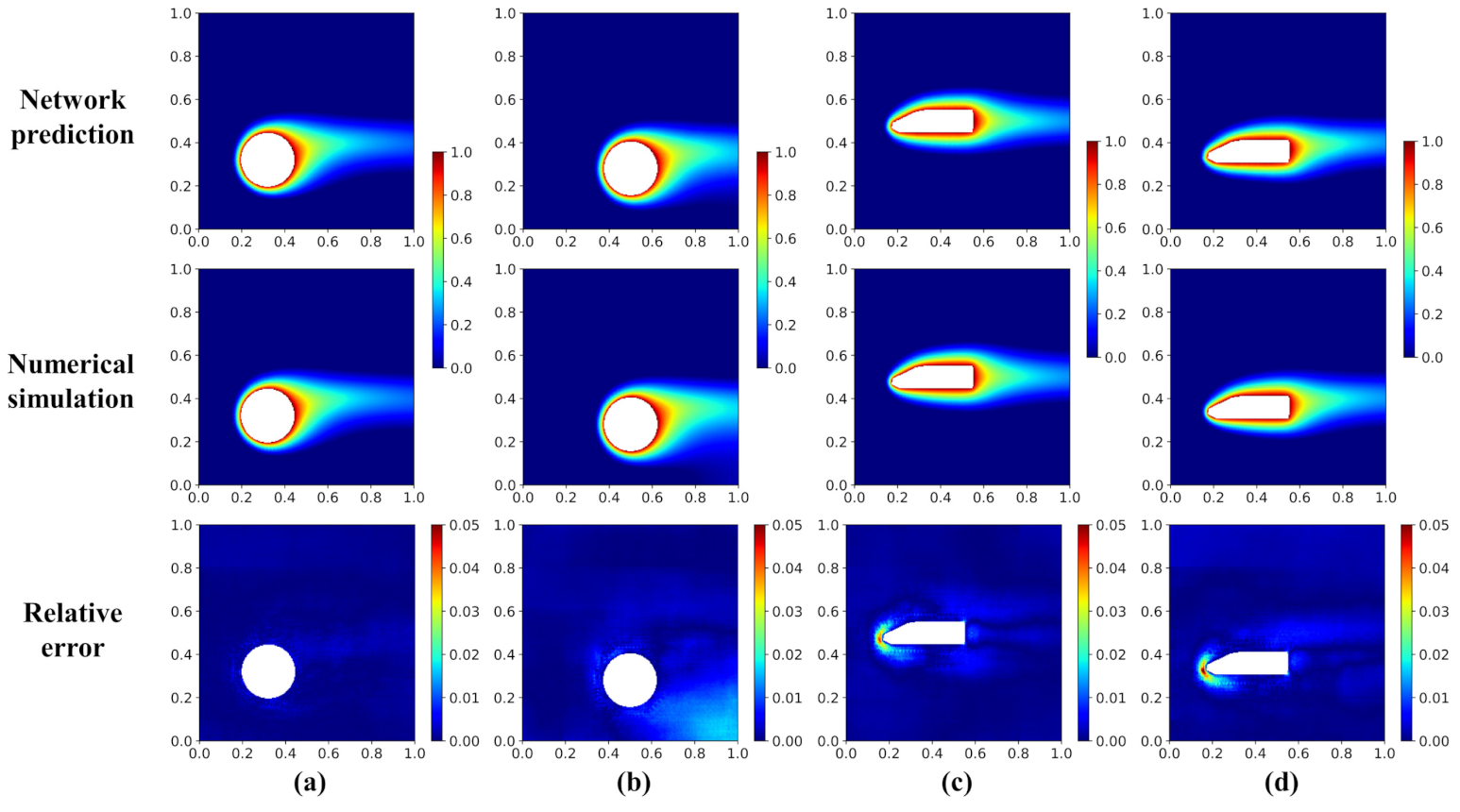
Figure 8 shows the temperature fields of the validation cases by the network model and the numerical simulation. The displayed validation cases include: Car, Car2, Airplane, and Locomotive. For the cases shown in Figure 8, the maximum relative error () is lower than 5.2%; the large error happens more frequently near the hot objects, especially at the boundary with large curvature. Figure 9 shows the temperature profile distribution along the y-direction at a different x-position by the network model (symbols) and numerical simulation (lines). The good coincident of the symbols and lines quantitatively affirms the accuracy of the network model. From the results, a comparatively poor prediction performance appears in the wake (x = 0.65, blue line), but the error is still within the acceptable range.
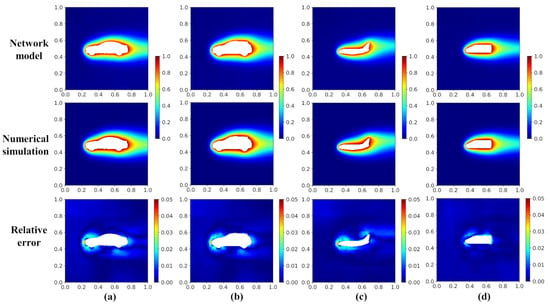
Figure 8.
Temperature field and relative error distribution of the validation cases with the geometries of (a) Car, (b) Car2, (c) Airplane, and (d) Locomotive.
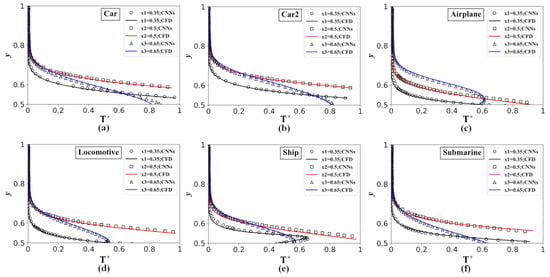
Figure 9.
Dimensionless temperature profiles of the validation case distribution along the y-direction at
= 0.35, = 0.5, and = 0.65 by the network model (symbols) and numerical simulation (lines): (a) Car, (b) Car2, (c) Airplane, (d) Locomotive, (e) Ship, (f) Submarine.
Overall, considering that the network model has only “seen” triangles, quadrilaterals, pentagons, hexagons, and dodecagons during the training process, such a high-prediction accuracy on the validation cases with much complex geometries indicates that the network model has an outstanding ability of generalization and extensionality.
Furthermore, we study the computational cost of the field prediction by the network model and CFD. Table 5 quantitatively compares the time consumption for predicting the steady-state temperature field by the network model and the numerical simulation. Overall, the network model can speed up the prediction for two orders; and as the geometry of the problem becomes more complex (that is, it requires a finer mesh for the CFD to converge the simulation), the prediction speedup by the network model becomes more outstanding. In addition, we compare the prediction time costs by the network model using different GPUs, 2080ti and 1660s (see Table 6). From the table, we can see that the performances of these two equipment have no big difference.

Table 5.
Time consumption for predicting the steady-state temperature field by the network model (GPU, 2080ti) and the numerical simulation (CPU, Ryzen 7 3700X, OpenFOAM).

Table 6.
Time consumption for predicting the steady-state temperature field by the network model on GPU 1660s and GPU 2080ti.
3.1.2. Performance of the Velocity Field Prediction
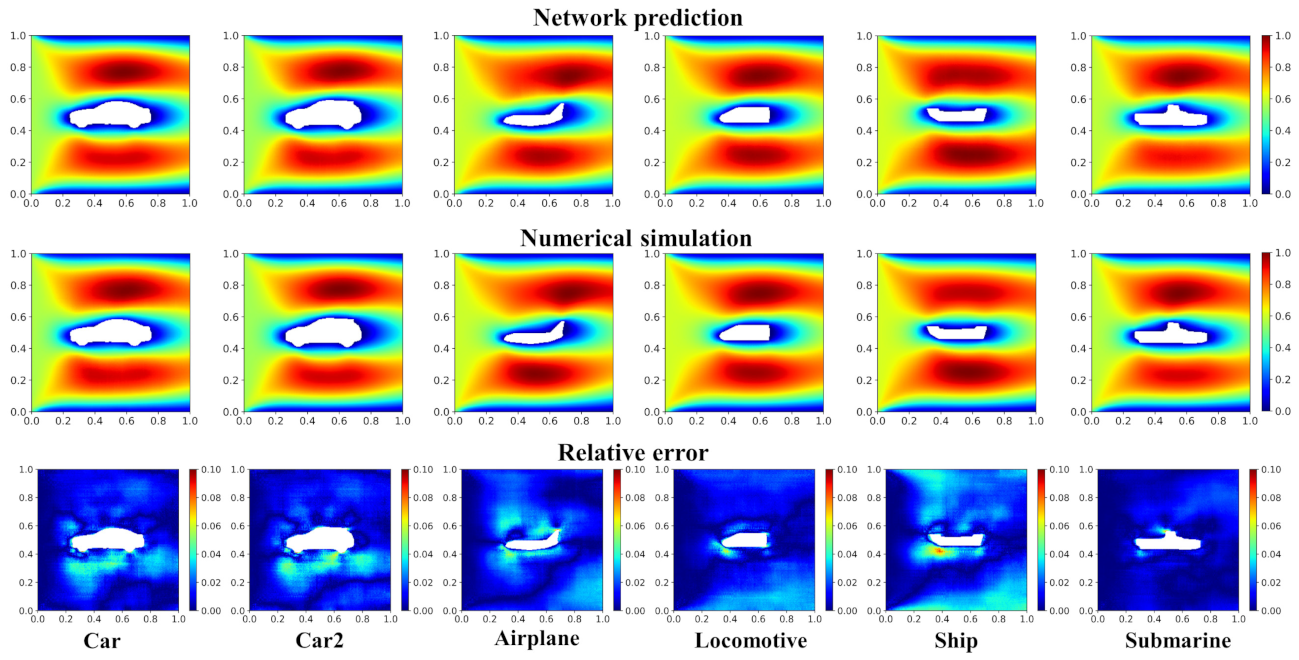
The steady-state velocity fields of the validation cases predicted by the network model and numerical simulation are shown in Figure 10. From the results, it can be observed that the velocity field by the network model shows good agreement with the CFD simulation. The right column in Figure 10 shows the distributions of the relative error: we can see that the maximum error happens frequently on the edge of the objects, because the flow field there is usually accompanied by a large velocity gradient.
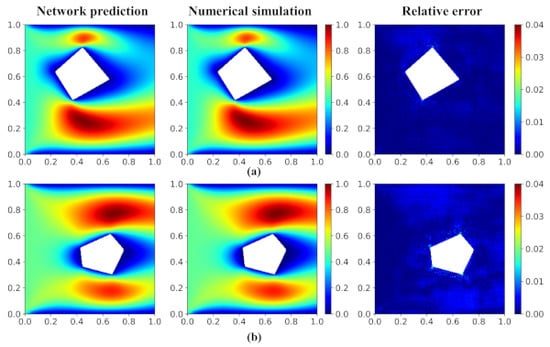
Figure 10.
Velocity field and error distribution of the testing cases. (a) Quadrangle and (b) Pentagon. The first and second columns are the fields predicted by the network model and the numerical simulation (OpenFOAM), respectively. The third column shows the relative error distribution.
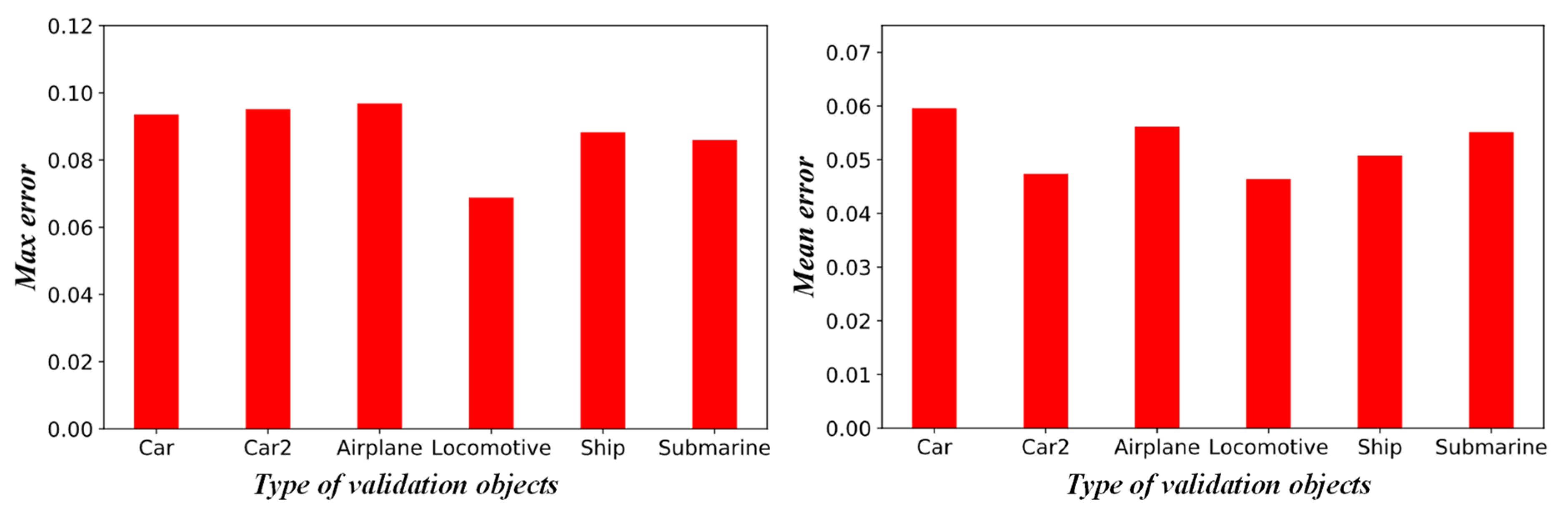
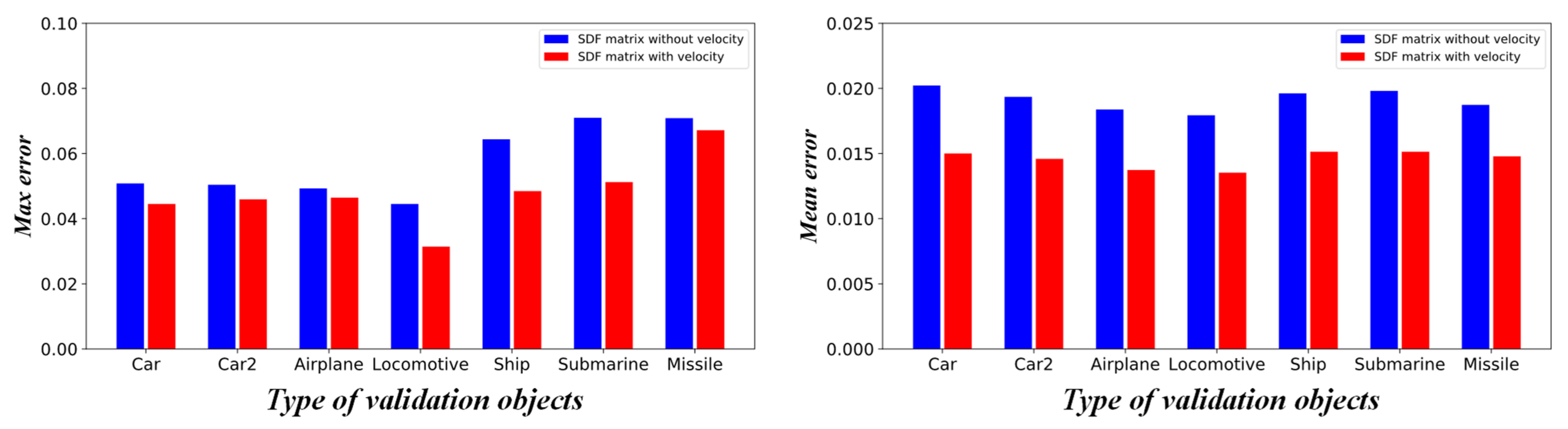
We further verify the ability of generalization and extensionality of the network model with validation datasets (see Figure 6). The velocity fields of the validation dataset predicted by the network model and numerical simulation (OpenFOAM) and the corresponding relative error distribution are shown in Figure 11. For the six cases shown in the figure, the maximum mean relative error () is less than 6%, and the maximum point relative error is less than 10%. In Figure 12, we quantitatively compare the max () and mean relative error of the studied validation cases. Compared with the testing cases, since the complexity of the geometric objects increases, the prediction error of the network model becomes larger. Furthermore, as the predicted shape gradually deviates from the polygon (e.g., Ship, Submarine), the prediction error increases. Overall, the low mean error suggests that the network model is able to provide an accurate prediction on cases with arbitrary complex geometries.
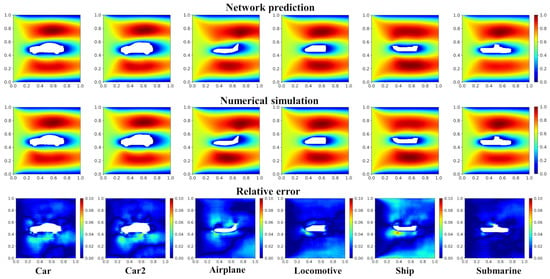
Figure 11.
Velocity field and relative error distribution of the validation cases with the geometries of Car, Car2, Airplane, Locomotive, Ship, and Submarine.
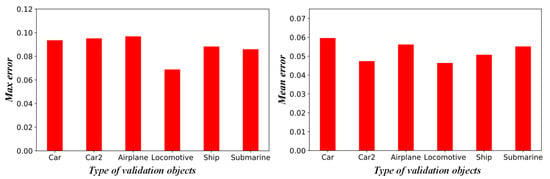
Figure 12.
Max (
) and mean () relative prediction error on the velocity field by the network model for various validation objects.
3.1.3. Advantages of the SDF Representation
In previous subsections, we showed the outstanding performance of the proposed network model, where the SDF is used as the geometry representation and the neural network inputs, while according to the literature review, in most previous works a binary image is used as the input of the CNNs [37,38]. The binary image represents the geometry as follows: its element is 0 if and only if the position is on the object boundary or inside the object. To indicate the effectiveness of the SDF, we trained a model using a binary image as the geometric representation with the exact same network architecture. The average relative error () by two different network models on the testing and validation datasets is summarized in Table 7.

Table 7.
Average relative error () on the prediction of the testing and validation datasets by the network models using the SDF and binary image representation.
Table 7 indicates that the SDF representation is much more effective than the binary representation. Regarding the validation dataset, the error of using the SDF representation is significantly smaller than the model using the binary representation. This can be attributed to the reason that each value in the SDF matrix carries a certain level of global information, while for a binary image, only the values on the boundary of the object carry useful information. Therefore, the SDF representation achieves a much better performance than the binary representation. In the following investigation, only the SDF representation is used as the model input.
3.1.4. Influence of the CNN Model Structure
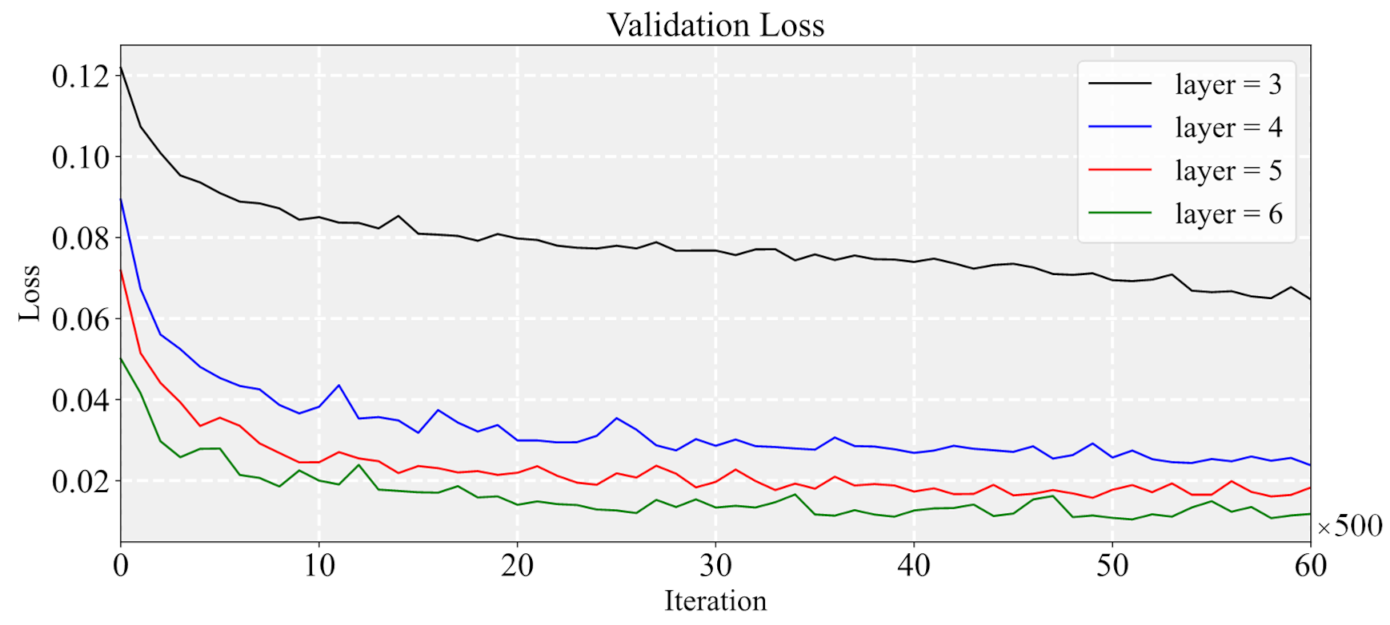
The outstanding performance of the prediction results is sufficient to illustrate the feasibility of the current network structure. To further gain insight into the performance and the characteristic of the network model, we study the optimization process of the network structure. To avoid showing the tedious trial and error, the results presentation will be simplified, and we will only study the performance of the network model with different numbers of the layers, which represents the depth of the network. Four types of network depth, L = {3, 4, 5, 6}, are studied, where each layer is accompanied by a symmetric decoding layer. All cases are trained in the same iterations.
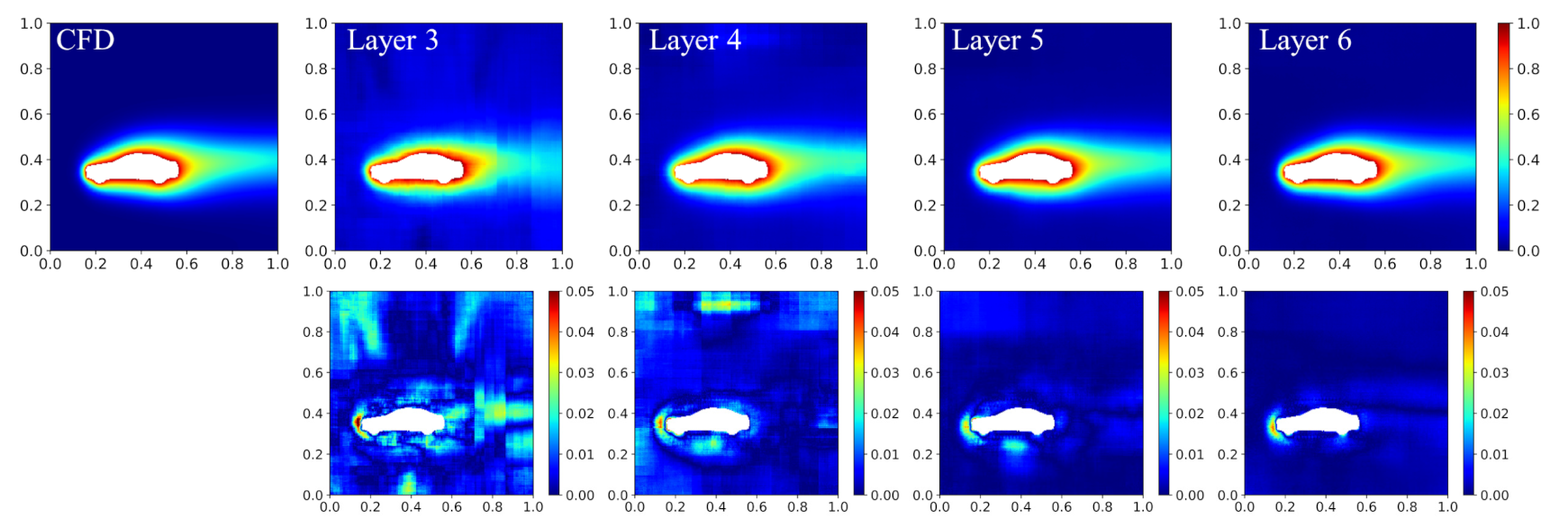
Figure 13 shows that, as the number of the network layer increases, the validation loss decreases obviously, especially when the layer number changes from 3 to 4. Figure 14 shows the prediction of the temperature fields of each network model and proves the above observation. The studied geometry is a car placed on the lower left of the calculation domain, and the network with six layers has the smallest error. In addition, in terms of error distribution, the result of a six-layer network is more reasonable than the result of a three-layer model, which implies that a deeper neural network model has stronger learning capabilities than a shallow one. On the other hand, it should also be noticed that the parameters of the network, the training time, and the prediction time rise accordingly (see Table 8). It can be found that when the number of the layers increases from five to six, there is no significant improvement in the validation loss, but the prediction time cost increases significantly. Hence, when optimizing the structure of the neural network, the prediction accuracy and the time cost need to be balanced according to the demand. In this paper, the main aim is to improve the performance of the network model; therefore, the current network structure has been designed to have six layers.
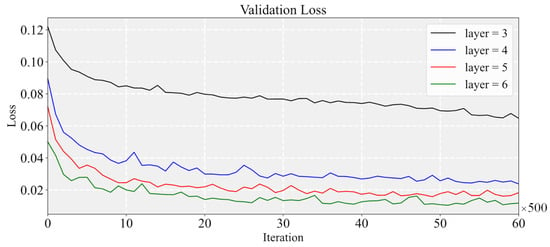
Figure 13.
Convergence history of the network models with different structures of the network.
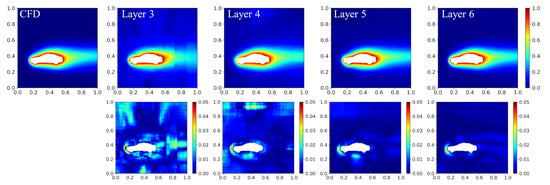
Figure 14.
Predicted temperature field obtained using different network structures. The top row is the predicted field by the network model and the CFD; the second row is the corresponding error distribution.

Table 8.
Parameters memory, training time, and prediction time costs for the network model with different numbers of layers.
3.2. Influence of the Space Distribution of the Hot Object
In this part, first, we investigate the effect of the space distribution of the hot object on the performance of the network model. Although the network model has shown good prediction accuracy on the validation dataset, the predicted objects above are fixed at the center of the entire field. As mentioned in the section of data preparation, the location of the object is generated following a normal distribution in the function of x- and y-coordinates and using the center of the domain as the mean. Hence, in this section, we study the effect of the distance between the center of the hot object and the center of the studied domain. Figure 15 shows the prediction results by the network model and numerical simulation (OpenFOAM) and the corresponding relative error. The result shows that the maximum error is less than 6%, which illustrates that the network model is robust to the randomness of the space distribution of the hot object in the entire flow field.
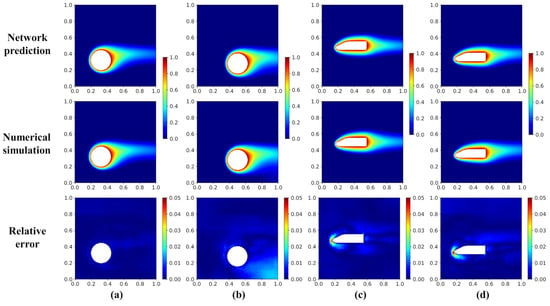
Figure 15.
Temperature distribution predicted by the network model and numerical simulation with different positions of the hot objects and the corresponding relative error: (a) left circle, (b) down circle, (c) left locomotive, (d) lower left locomotive.
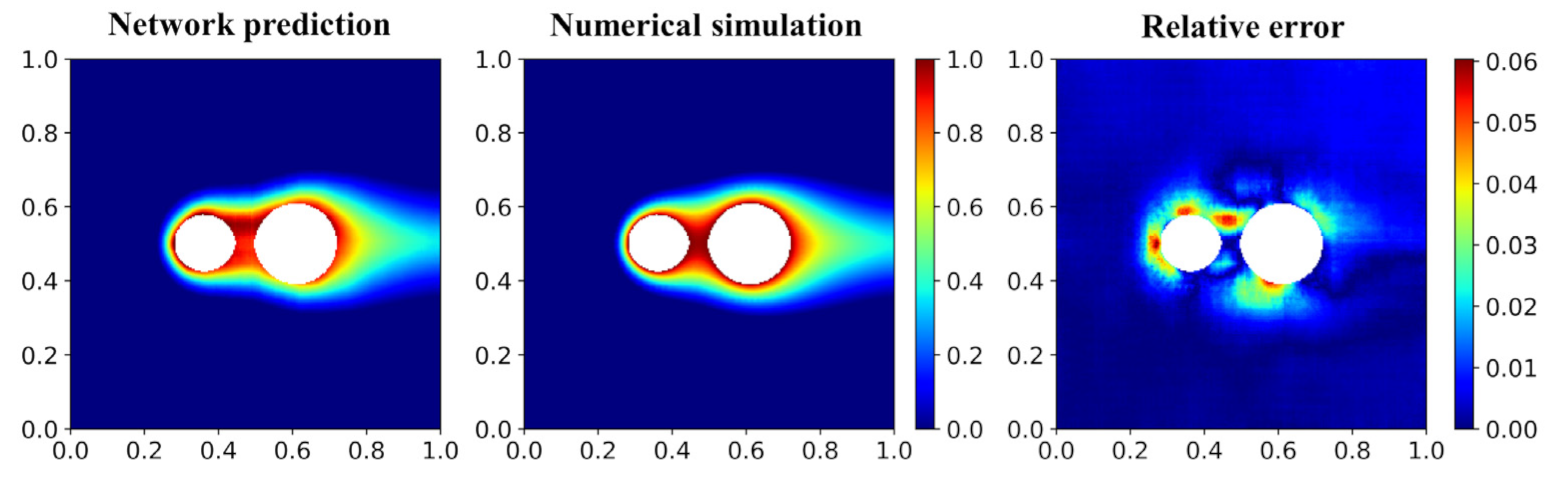
Second, since all the training cases only contain a single hot object, here we also investigate the performance of the network model in predicting the problems with multiple hot objects. Compared with studying the spatial distribution of the hot object, the problem with multiple hot objects is providing a huger challenge to the network model. Figure 16 shows the temperature fields of the case with two circles predicted by the network model and numerical simulation and the corresponding relative error. It can be observed that the network model can still give a less accurate but still reasonable prediction. Using more training datasets to train the network model is an effective solution to further improve the prediction accuracy of the cases with multiple hot objects.
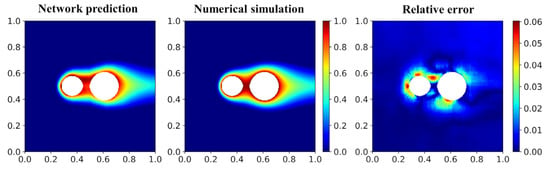
Figure 16.
Temperature fields of the case with two circles predicted by the network model and numerical simulation and the corresponding relative error.
3.3. Influence of Incorporating Velocity into Input Matrices
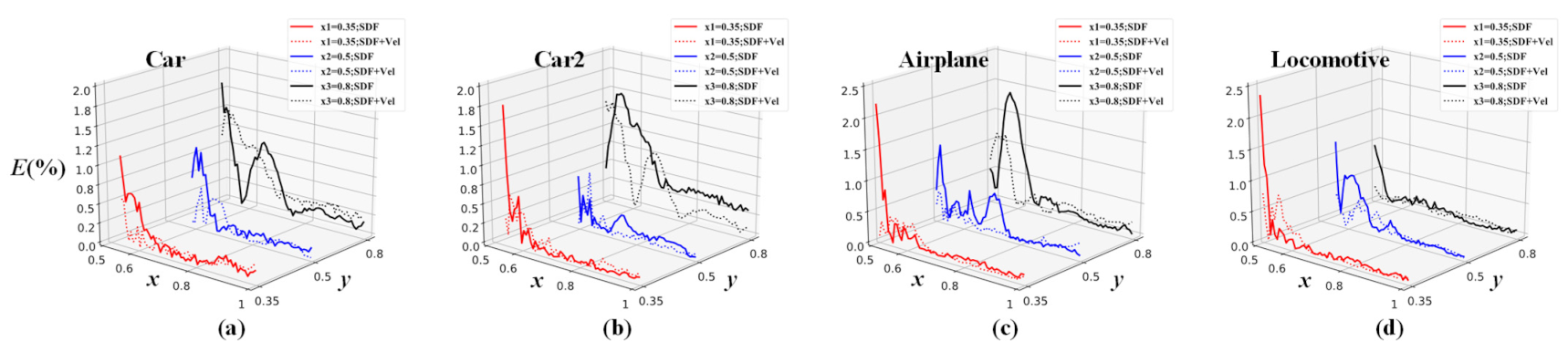
For most thermal applications, people are more interested in the temperature than the velocity field. In this section, we study the effect of additionally incorporating the velocity field as a portion of the input matrices. The prepared cases have the same hyper-parameters and network architecture. Figure 17 shows the mean () and maximum () relative prediction error on the temperature field by the network models with and without incorporating the velocity field as the portion of the input matrices. Figure 18 plots the relative prediction error of the two studied situations along the y-direction at different x-positions. The relative error () is calculated by Equation (15). From Figure 17 and Figure 18, it can be observed that the overall prediction accuracy increases as the network model further incorporates velocity information, while the improvement is moderate. Therefore, for current problems, incorporating velocity information is not economic.
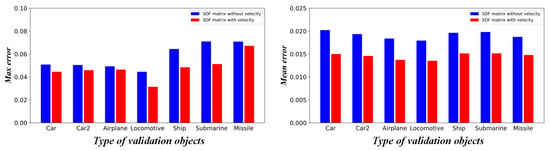
Figure 17.
Max () and mean () relative prediction error on the temperature field by the network models with and without incorporating the velocity field as part of the input matrices. The blue bar denotes the cases without velocity information, and the red bar denotes the cases with velocity information.
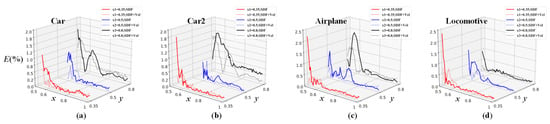
Figure 18.
Relative error profile along the y-direction at
= 0.35, = 0.5, and = 0.8. The studied validation cases are (a) Car, (b) Car2, (c) Airplane, and (d) Locomotive.
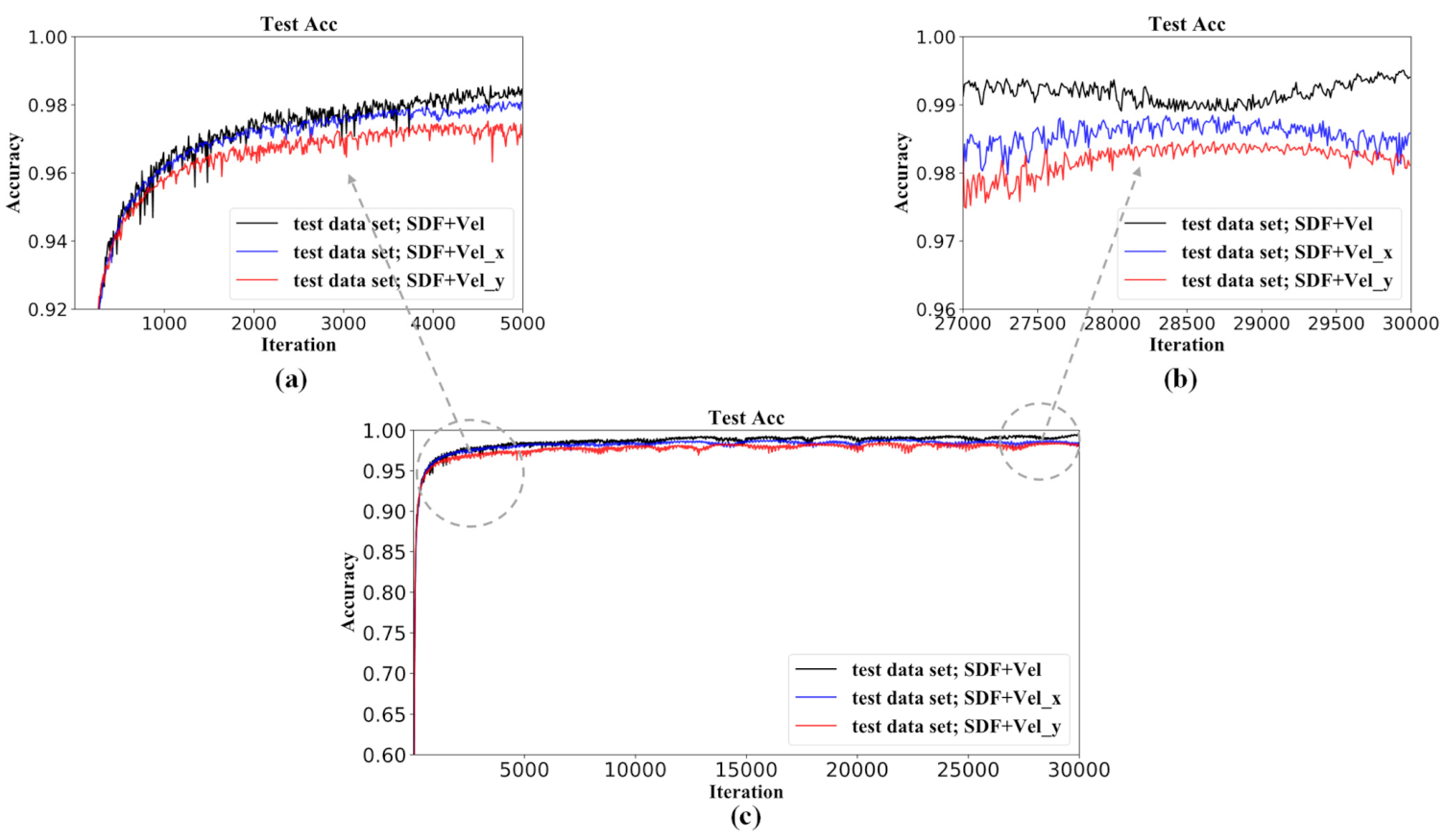
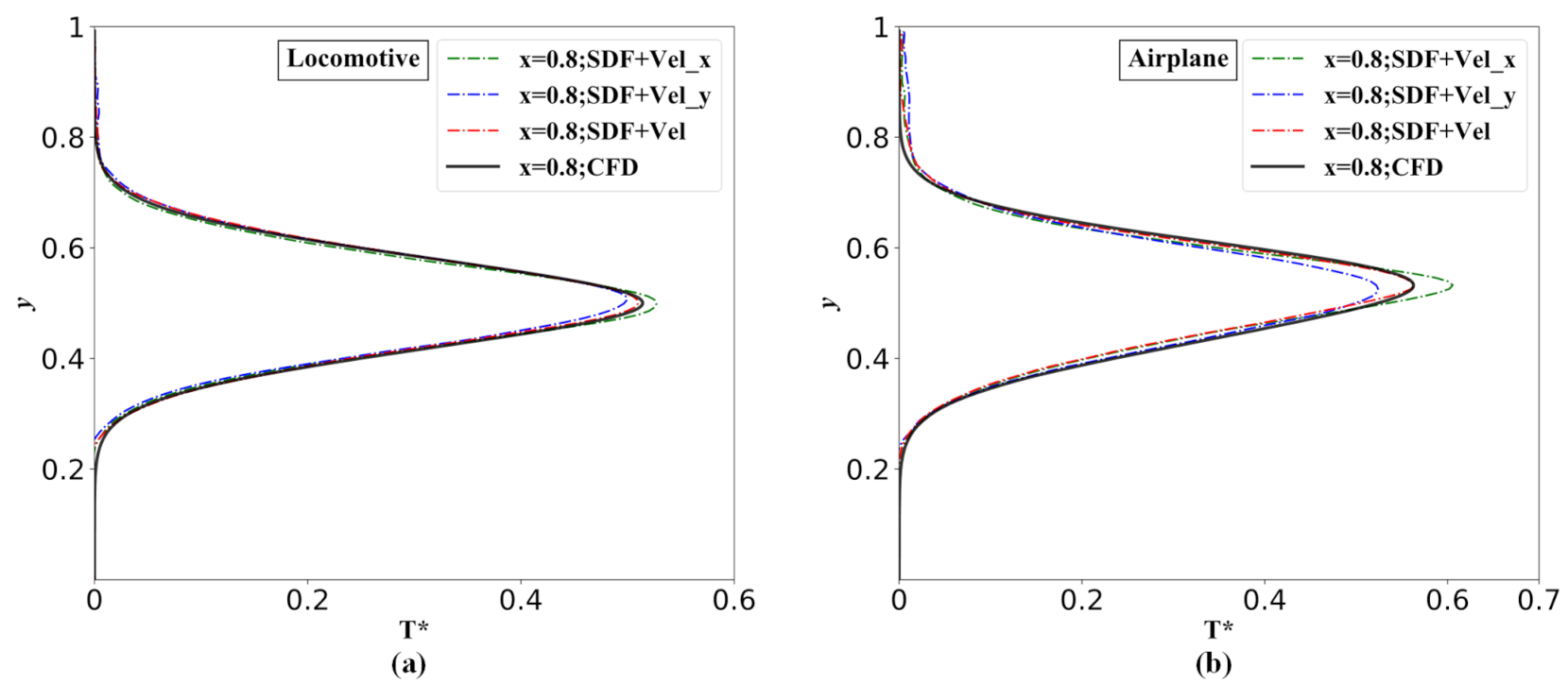
It can be concluded from the above results that additionally incorporating the velocity field as the portion of the input matrices can enhance the accuracy of the temperature prediction of the neural network. Here, we further investigate the impact of the type of the embedded velocity field on the performance of the neural network model. In the above portion, the input matrix of the SDF combined with the velocity magnitude is studied; then, we investigate another two types of input matrix: SDF-combined x-velocity, SDF-combined y-velocity. Figure 19 shows the training history of the model with different input matrices. Figure 20 shows the temperature profile distribution along the y-direction at the dimensionless x-position of 0.8, predicted by the network model with different input matrices and numerical simulations. It can be seen from Figure 19 and Figure 20 that the case of the SDF-combined velocity shows the fastest convergence speed and the highest accuracy, as it contains the most physical information.
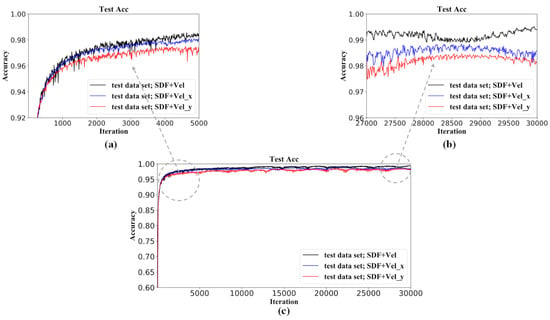
Figure 19.
Training/convergence history of the network models: (a) local magnification in iteration from 0 to 5000; (b) local magnification in iteration from 27,000 to 30,000.
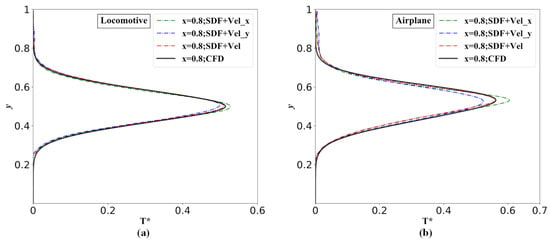
Figure 20.
Dimensionless temperature profiles of the validation case distribution along the y-direction at
= 0.8 by the network model with different input matrices and numerical simulations: (a) Locomotive and (b) Airplane.
4. Discussion
Reduced-order modelling is a data-driven method, and it provides a way of fast predicting physical fields without solving partial differential equations (PDEs) iteratively and numerically. An efficient reduced-order prediction model is useful for production design and optimization and real-time simulation/prediction in some control scenarios. The results discussed in the last section indicate that the proposed CNN-based reduced-order model achieves high accuracy and robustness, even though the geometry of the problem is much more complex than that of the training dataset. The strong ability of generalization and extensionality is one of the major advantages of the CNNs. Furthermore, compared with the CFD, the time consumption for the field prediction by the network model can be negligible.
Although the proposed model has shown outstanding extensionality, the prediction accuracy is still affected obviously as the physical conditions (geometric in the current paper) gradually deviate from the training dataset; and of course, this also applies to the traditional data-driven method, such as POD and DMD [39,40]. Certainly, for relieving this problem, a CNN-based ROM should be trained using as exhaustive a dataset as possible, while it is time-consuming to retrain the network model once we get new/additional data. One solution to this problem is to make full use of the trained reduced-order model for fast reconstruction/retraining of the model.
This is a preliminary attempt to develop the reduced-order model predicting the heat convection fields with arbitrary geometries based on the CNNs. As the beginning of the exploration, the studied problem is kept two-dimensional and laminar, and the performance of the network model is satiated and exciting, while the problems of engineering optimization and design in real applications are usually three-dimensional and turbulent, which are greatly challenging for the network model. Therefore, paying more attention to machine-learning-based reduced-order modeling and making it able to better serve the physics or engineering community is warranted.
5. Conclusions
In this paper, based on the deep convolutional neural networks (CNNs), we proposed a data-driven model for predicting the steady-state heat convection of a hot object with an arbitrary complex geometry in a two-dimensional space, and the signed distance function (SDF) is applied to represent the geometry of the problem. The training and validation datasets only contain the hot objects with simple geometries, including triangles, quadrilaterals, pentagons, hexagons, and dodecagons. According to the results, the velocity and temperature fields of the problems with complex geometries predicted by the network model agree well with the CFD simulation. As the location and the number of hot objects vary, the network model is still able to give a satisfied prediction. In addition, further incorporating velocity information into the input matrix will moderately improve the performance of the network model in the temperature field prediction. Although the training process takes about 42 min in the current work, the time cost of the CNNs to predict the heat convection fields is negligible compared with the CFD simulation; specifically, the prediction speed of the network model is two orders faster. Therefore, it is potentially possible that this approach can provide some enlightenment for fast optimization, real-time simulation, and control.
Author Contributions
J.-Z.P. performed the numerical simulations and results preparation. W.-T.W. developed the structure of the paper. X.L., Z.-D.X., N.A., Z.C. and W.-T.W. supervised the work and revised the manuscript. All authors contributed to the manuscript preparation. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Natural Science Foundation of China, No. 11802135, and the Fundamental Research Funds for the Central Universities, No. 30919011401.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ravindran, S.S. A reduced-order approach for optimal control of fluids using proper orthogonal decomposition. Int. J. Numer. Methods Fluids 2000, 34, 425–448. [Google Scholar] [CrossRef]
- Burkardt, J.; Gunzburger, M.; Lee, H.-C. POD and CVT-based reduced-order modeling of Navier–Stokes flows. Comput. Methods Appl. Mech. Eng. 2006, 196, 337–355. [Google Scholar] [CrossRef]
- Lucia, D.J.; King, P.I.; Beran, P.S. Reduced order modeling of a two-dimensional flow with moving shocks. Comput. Fluids 2003, 32, 917–938. [Google Scholar] [CrossRef]
- Lucia, D.J.; Beran, P.S.; Silva, W.A. Reduced-order modeling: New approaches for computational physics. Prog. Aerosp. Sci. 2004, 40, 51–117. [Google Scholar] [CrossRef] [Green Version]
- Taira, K.; Hemati, M.S.; Brunton, S.L.; Sun, Y.; Duraisamy, K.; Bagheri, S.; Dawson, S.T.; Yeh, C.A. Modal analysis of fluid flows: Applications and outlook. AIAA J. 2020, 58, 998–1022. [Google Scholar] [CrossRef]
- San, O.; Maulik, R. Machine learning closures for model order reduction of thermal fluids. Appl. Math. Model. 2018, 60, 681–710. [Google Scholar] [CrossRef]
- Li, T.; Gao, Y.; Han, D.; Yang, F.; Yu, B. A novel POD reduced-order model based on EDFM for steady-state and transient heat transfer in fractured geothermal reservoir. Int. J. Heat Mass Transf. 2020, 146, 118783. [Google Scholar] [CrossRef]
- Mahapatra, P.S.; Chatterjee, S.; Mukhopadhyay, A.; Manna, N.K.; Ghosh, K. Proper orthogonal decomposition of thermally-induced flow structure in an enclosure with alternately active localized heat sources. Int. J. Heat Mass Transf. 2016, 94, 373–379. [Google Scholar] [CrossRef]
- Williams, M.O.; Kevrekidis, I.G.; Rowley, C.W. A Data–Driven Approximation of the Koopman Operator: Extending Dynamic Mode Decomposition. J. Nonlinear Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef] [Green Version]
- El Majd, B.A.; Cordier, L. New Regularization Method for Calibrated POD Reduced-Order Models. Math. Model. Anal. 2016, 21, 47–62. [Google Scholar] [CrossRef] [Green Version]
- Demuth, H.B.; Beale, M.H.; de Jess, O.; Hagan, M.T. Neural Network Design; Hagan, M.T., Ed.; PWS Publishing Co: Cambridge, MA, USA, 2014. [Google Scholar]
- Wang, Z.; Xiao, D.; Fang, F.; Govindan, R.; Pain, C.C.; Guo, Y. Model identification of reduced order fluid dynamics systems using deep learning. Int. J. Numer. Methods Fluids 2018, 86, 255–268. [Google Scholar] [CrossRef] [Green Version]
- Fukami, K.; Fukagata, K.; Taira, K. Super-resolution reconstruction of turbulent flows with machine learning. J. Fluid Mech. 2019, 870, 106–120. [Google Scholar] [CrossRef] [Green Version]
- Lui, H.F.S.; Wolf, W.R. Construction of reduced-order models for fluid flows using deep feedforward neural networks. J. Fluid Mech. 2019, 872, 963–994. [Google Scholar] [CrossRef] [Green Version]
- Kani, J.N.; Elsheikh, A.H. Reduced-order modeling of subsurface multi-phase flow models using deep residual recurrent neural networks. Transp. Porous Media 2019, 126, 713–741. [Google Scholar] [CrossRef] [Green Version]
- Nair, N.J.; Goza, A. Leveraging reduced-order models for state estimation using deep learning. J. Fluid Mech. 2020, 897, R1. [Google Scholar] [CrossRef]
- Gao, H.; Sun, L.; Wang, J.-X. PhyGeoNet: Physics-Informed Geometry-Adaptive Convolutional Neural Networks for Solving Parametric PDEs on Irregular Domain. arXiv 2020, arXiv:2004.13145. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Fischer, P.; Ilg, E.; Hausser, P.; Hazirbas, C.; Golkov, V.; Van Der Smagt, P.; Cremers, D.; Brox, T. Flownet: Learning optical flow with convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2758–2766. [Google Scholar]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. Adv. Neural Inf. Process. Syst. 2014, 3, 2366–2374. [Google Scholar]
- Gupta, S.; Girshick, R.; Arbeláez, P.; Malik, J. Learning rich features from RGB-D images for object detection and segmentation. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 345–360. [Google Scholar]
- Park, J.J.; Florence, P.; Straub, J.; Newcombe, R.; Lovegrove, S. Deepsdf: Learning continuous signed distance functions for shape representation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 165–174. [Google Scholar]
- Li, C.; Xu, C.; Gui, C.; Fox, M.D. Distance regularized level set evolution and its application to image segmentation. IEEE Trans. Image Process. 2010, 19, 3243–3254. [Google Scholar] [CrossRef] [PubMed]
- Yamasaki, S.; Nomura, T.; Kawamoto, A.; Sato, K.; Izui, K.; Nishiwaki, S. A level set based topology optimization method using the discretized signed distance function as the design variables. Struct. Multidiscip. Optim. 2010, 41, 685–698. [Google Scholar] [CrossRef]
- Yeung, E.; Kundu, S.; Hodas, N. Learning deep neural network representations for Koopman operators of nonlinear dynamical systems. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 4832–4839. [Google Scholar]
- Lawrence, S.; Giles, C.L.; Tsoi, A.C.; Back, A.D. Face recognition: A convolutional neural-network approach. IEEE Trans. Neural Netw. 1997, 8, 98–113. [Google Scholar] [CrossRef] [Green Version]
- Mohan, R. Deep deconvolutional networks for scene parsing. arXiv 2014, arXiv:1411.4101. [Google Scholar]
- Zolotukhin, A.B.; Gayubov, A.T. Machine learning in reservoir permeability prediction and modelling of fluid flow in porous media. IOP Conf. Ser. Mater. Sci. Eng. 2019, 700, 012023. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Y.; Qi, D. Deep spatio-temporal residual networks for citywide crowd flows prediction. In Proceedings of the 31 AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 1655–1661. [Google Scholar]
- Zhang, J.; Zheng, Y.; Qi, D.; Li, R.; Yi, X. DNN-Based Prediction Model for Spatio-Temporal Data. In Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Francisco, CA, USA, 31 October–3 November 2016. [Google Scholar]
- Guo, X.; Li, W.; Iorio, F. Convolutional neural networks for steady flow approximation. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 481–490. [Google Scholar]
- Masters, D.; Luschi, C. Revisiting Small Batch Training for Deep Neural Networks. arXiv 2018, arXiv:1804.07612. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Turki, S.; Abbassi, H.; Nasrallah, S.B. Two-dimensional laminar fluid flow and heat transfer in a channel with a built-in heated square cylinder. Int. J. Therm. Sci. 2003, 42, 1105–1113. [Google Scholar] [CrossRef]
- Baranyi, L. Computation of unsteady momentum and heat transfer from a fixed circular cylinder in laminar flow. J. Comput. Appl. Mech. 2003, 4, 13–25. [Google Scholar]
- Gisen, D. Generation of a 3D mesh using snappyHexMesh featuring anisotropic refinement and near-wall layers. In Proceedings of the 11th International Conference on Hydroscience & Engineering (ICHE), Hamburg, Germany, 29 September–2 October 2014; pp. 983–990. [Google Scholar]
- Lucchini, T.; della Torre, A.; D’Errico, G.; Montenegro, G.; Fiocco, M.; Maghbouli, A. Automatic Mesh Generation for CFD Simulations of Direct-Injection Engines. SAE Tech. Pap. 2015. [Google Scholar] [CrossRef]
- Zhang, Y.; Sung, W.J.; Mavris, D. Application of convolutional neural network to predict airfoil lift coefficient. In Proceedings of the 2018 AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Kissimmee, FL, USA, 8–12 January 2018; pp. 1–9, No. 210049. [Google Scholar] [CrossRef] [Green Version]
- Sekar, V.; Jiang, Q.; Shu, C.; Khoo, B.C. Fast flow field prediction over airfoils using deep learning approach. Phys. Fluids 2019, 31, 57103. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Pan, S.J.; Kwok, J.T.; Yang, Q. Transfer learning via dimensionality reduction. AAAI 2008, 8, 677–682. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).