Flow Structure and Deformation of Two Bubbles Rising Side by Side in a Quiescent Liquid
Abstract
:1. Introduction
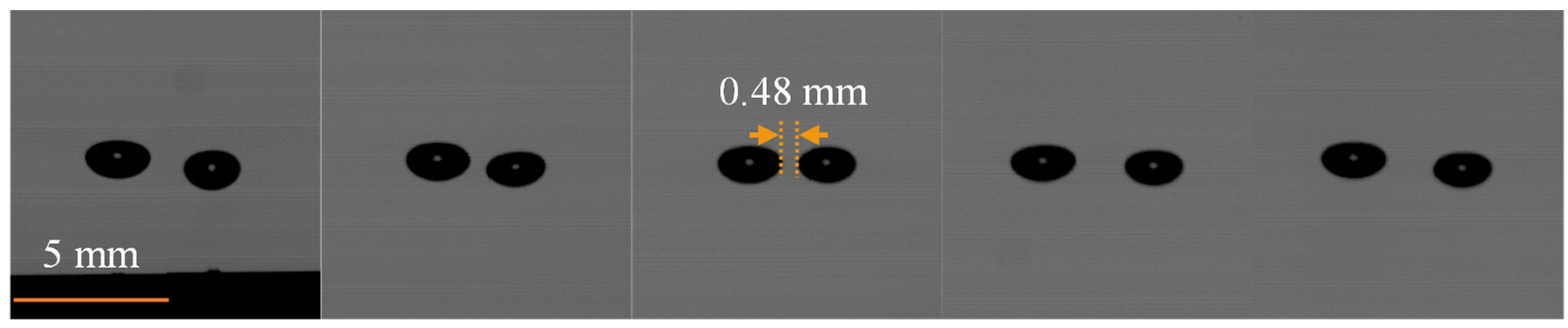
2. Experimental Methods
3. Experimental Results and Discussion
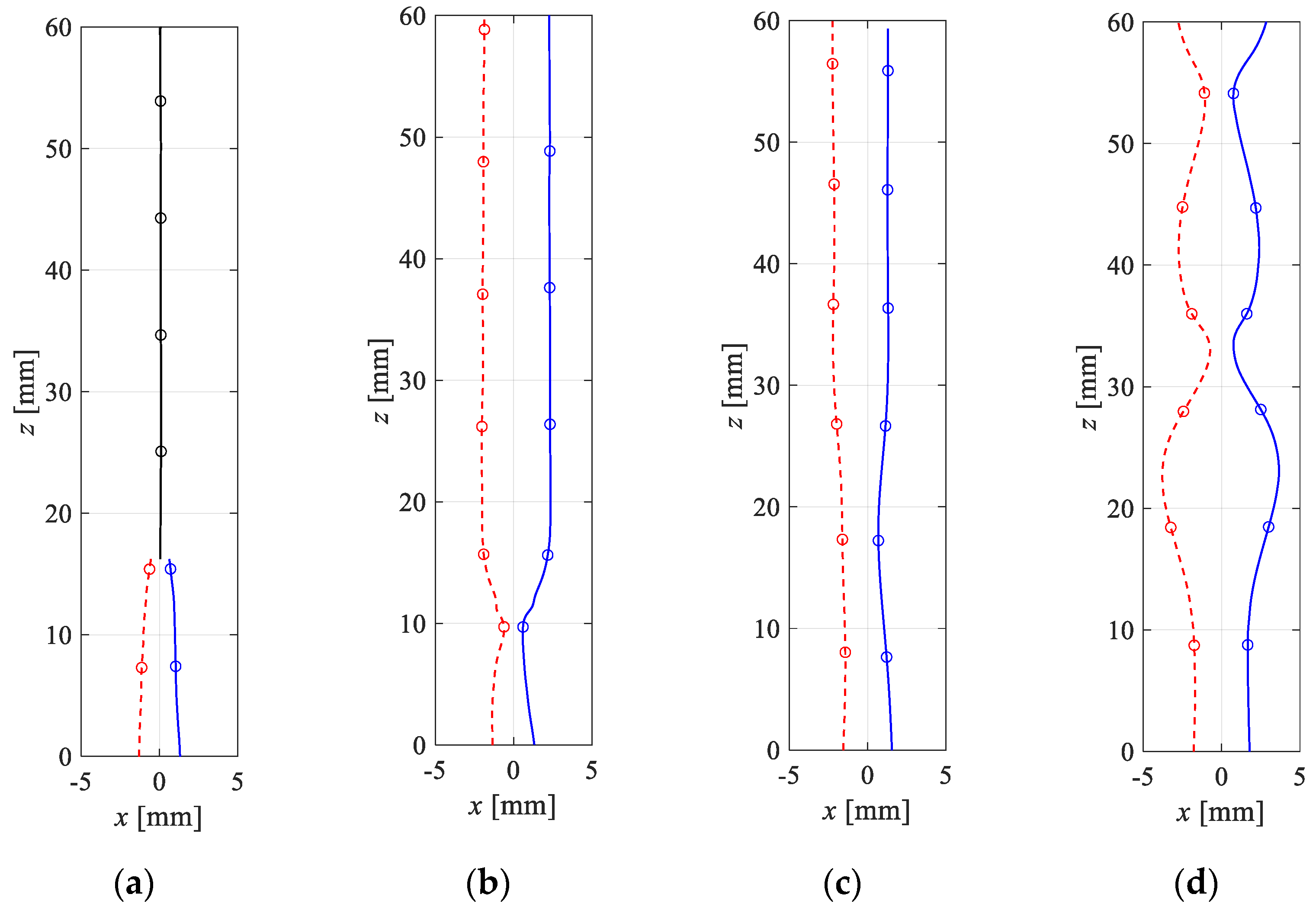
3.1. Trajectories of a Pair of Bubbles
3.2. Shape of a Pair of Bubbles with Nonkissing Repulsion
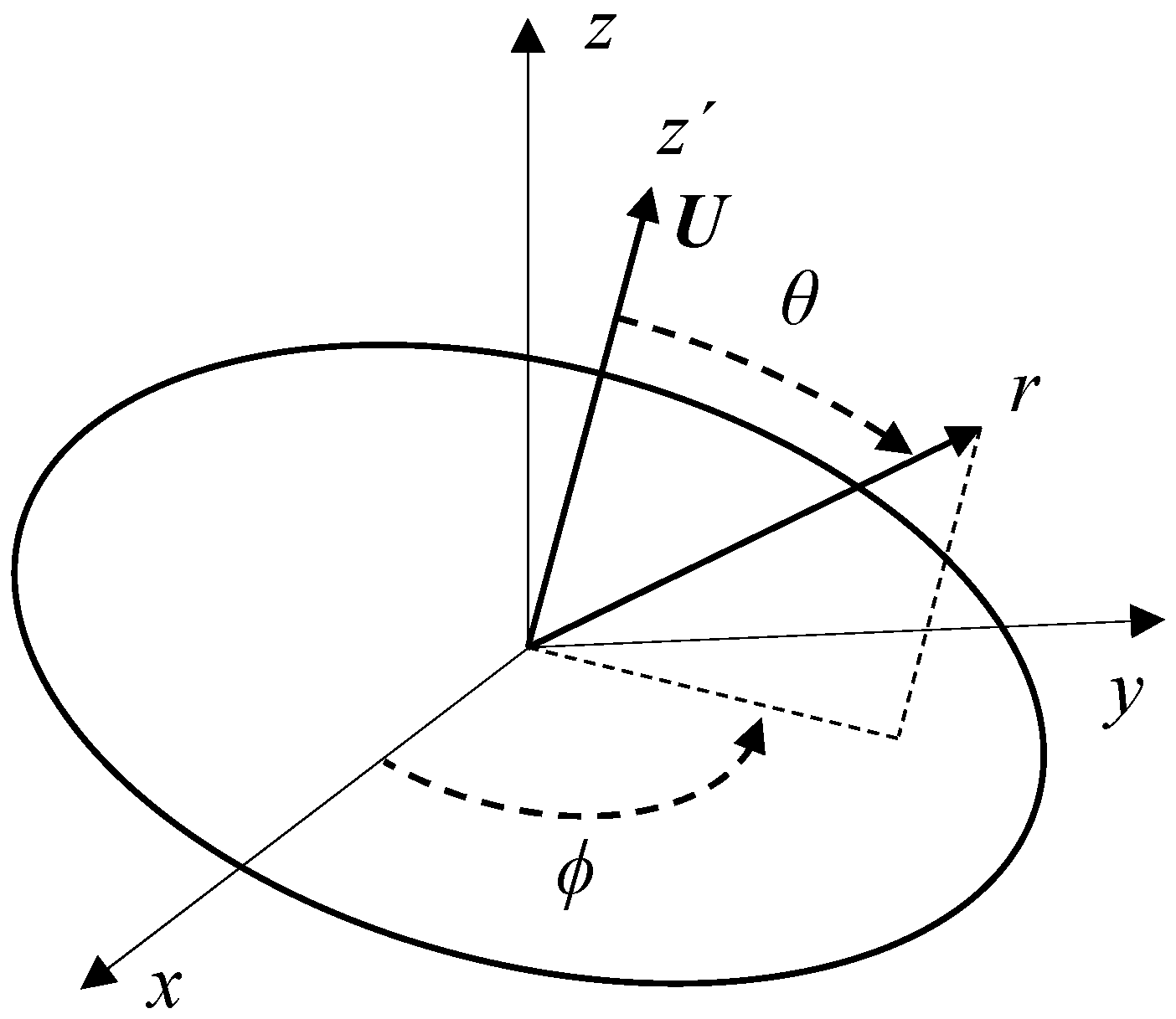
4. Numerical Methods
5. Numerical Results and Discussion
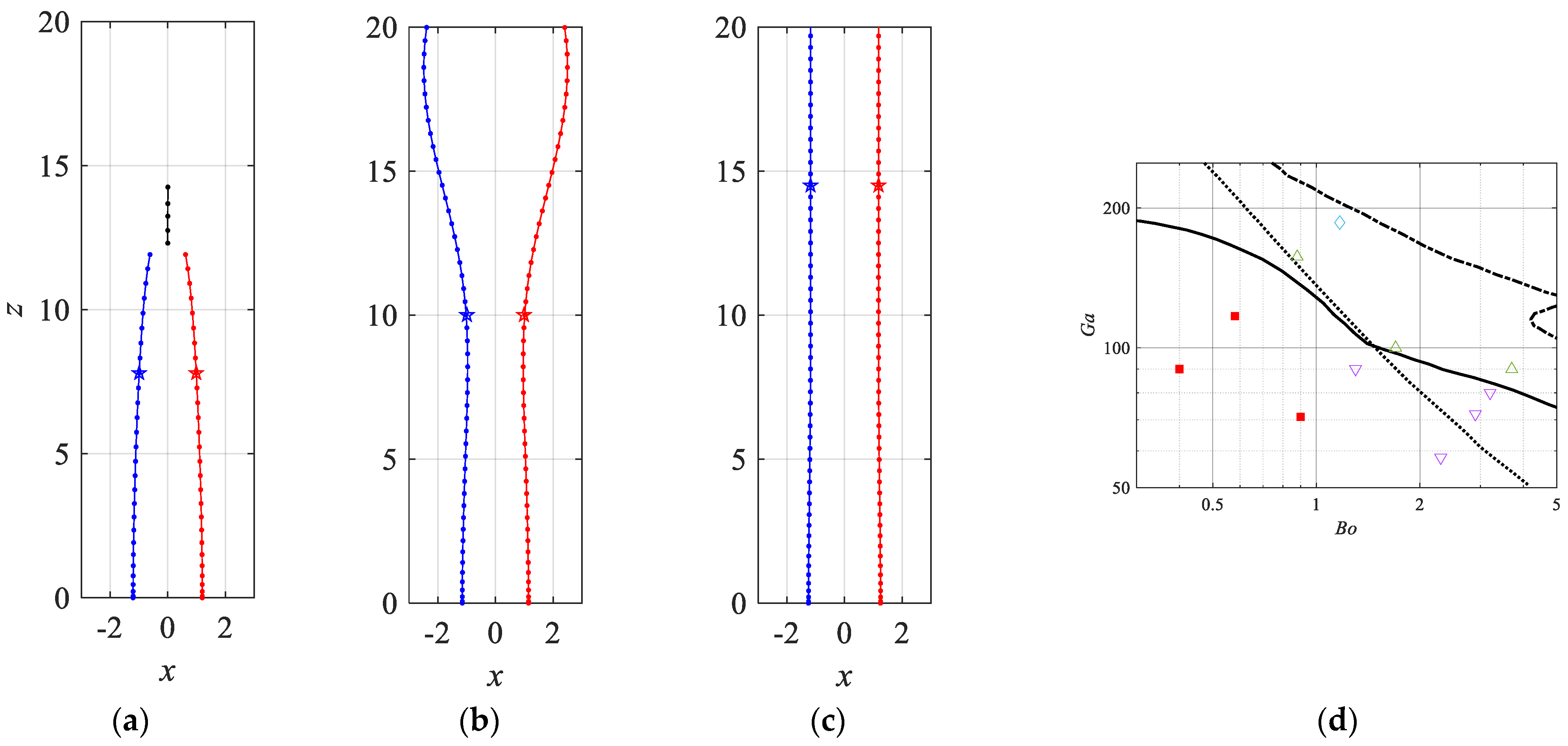
5.1. Overview of the Numerical Simulations
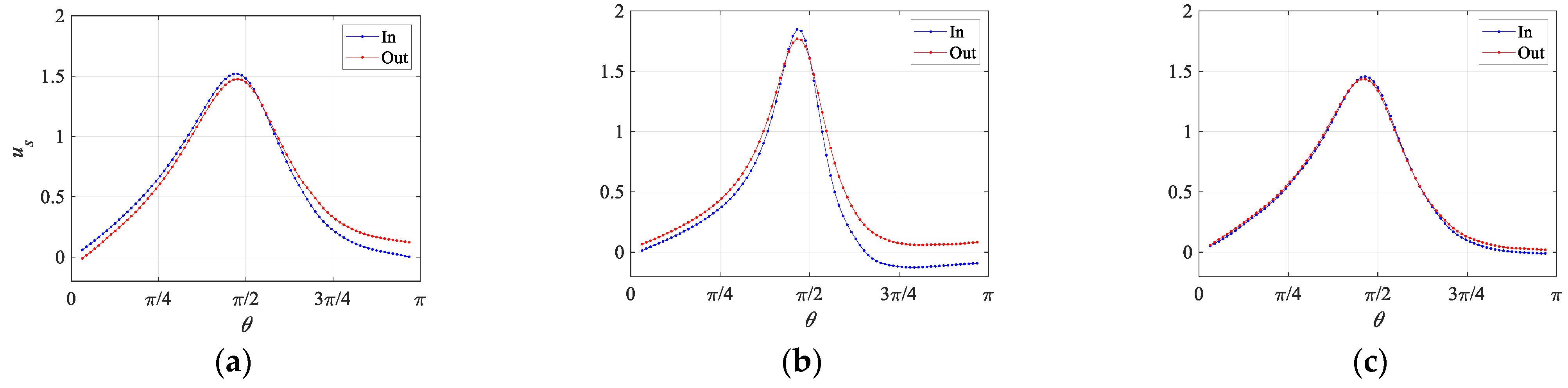
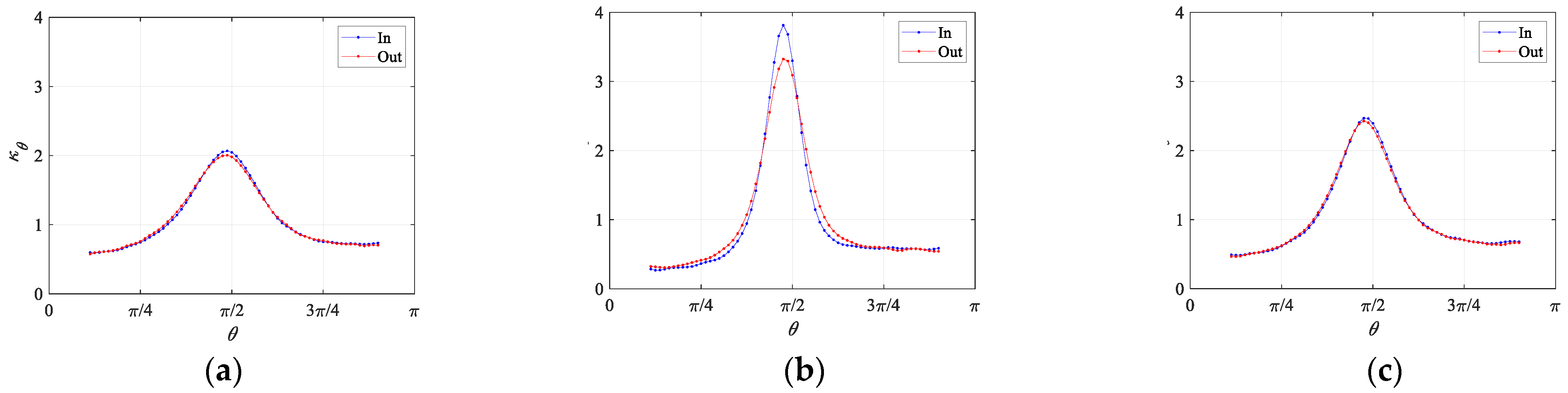
5.2. Velocity, Curvature and Spanwise Vorticity
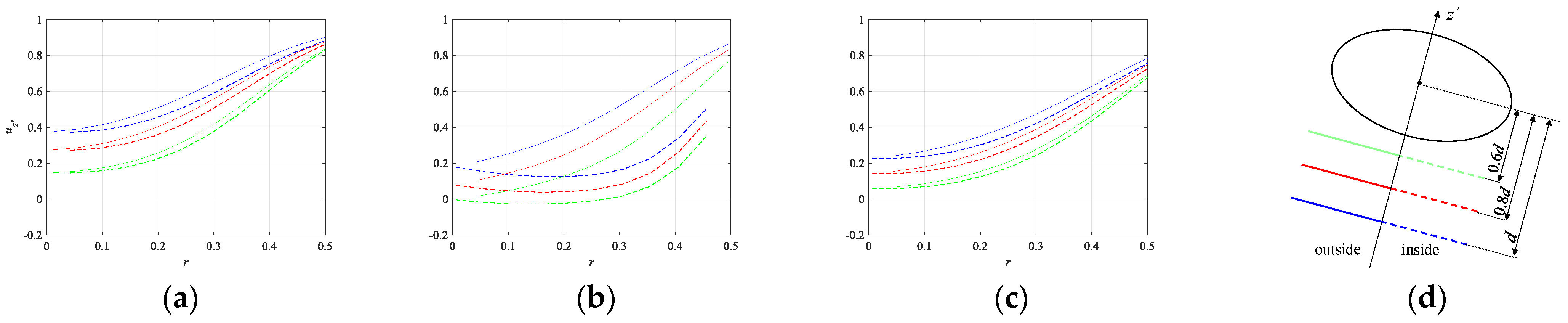
5.3. Streamwise Vorticity behind the Bubbles
- (i)
- We previously obtained the spanwise vorticity at the bubble surface (Figure 10), and the vorticity sign is the same except in the rear part; however, in the rear part, it is approximately zero. The vorticity sign is the same at any azimuthal angle except in the recirculate region.
- (ii)
- We previously obtained the velocity at the bubble surface (Figure 8); the velocity of the equatorial plane inside the gap is larger, whereas that behind the inside of the gap is smaller. Figure 12 shows the streamwise velocity profile behind the bubble where the condition is the same as that in Figure 8. Figure 12a–c shows that the streamwise velocity inside the gap behind the bubble is smaller in attracting, repelling, and holding. These velocity profiles are significant in determining the vorticity pair because ∂uz/∂ϕ is nonzero.
- (iii)
5.4. Streamline on x-z Plane and Lift
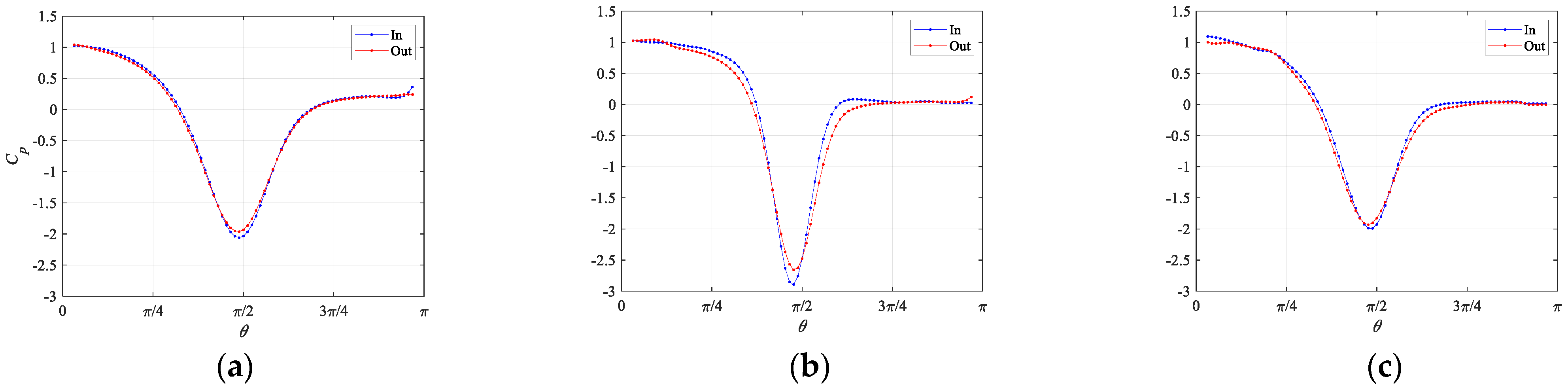
5.5. Pressure at the Bubble Surface
6. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haas, T.; Schubert, C.; Eickhoff, M.; Pfeifer, H. A Review of Bubble Dynamics in Liquid Metals. Metals 2021, 11, 664. [Google Scholar] [CrossRef]
- Takagi, S.; Matsumoto, Y. Surfactant effects on bubble motion and bubbly flows. Annu. Rev. Fluid Mech. 2011, 43, 615–636. [Google Scholar] [CrossRef]
- Legendre, D.; Magnaudet, J.; Mougin, G. Hydrodynamic interactions between two spherical bubbles rising side by side in a viscous liquid. J. Fluid Mech. 2003, 497, 133–166. [Google Scholar] [CrossRef]
- Duineveld, P.C. Bouncing and coalescence of bubble pairs rising at high Reynolds number in pure water or aqueous surfactant solutions. In Fascination of Fluid Dynamics; Springer: Dordrecht, The Netherlands, 1998; pp. 409–439. [Google Scholar]
- Sanada, T.; Sato, A.; Shirota, M.; Watanabe, M. Motion and coalescence of a pair of bubbles rising side by side. Chem. Eng. Sci. 2009, 64, 2659–2671. [Google Scholar] [CrossRef] [Green Version]
- Yamaguchi, E.; Sanada, T. Bouncing of a pair of clean bubbles rising side by side. In Proceedings of the Ninth JSME-KSME Thermal and Fluids Engineering Conference, Ginowan City, Japan, 27–30 October 2017. [Google Scholar]
- Tripathi, M.K.; Premlata, A.R.; Sahu, K.C.; Govindarajan, R. Two initially spherical bubbles rising in quiescent liquid. Phys. Rev. Fluids 2017, 2, 073601. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Chen, L.; Ni, M.J. Vortex interactions between a pair of bubbles rising side by side in ordinary viscous liquids. Phys. Rev. Fluids 2019, 4, 043604. [Google Scholar] [CrossRef]
- Shirota, M.; Sanada, T.; Sato, A.; Watanabe, M. Formation of a submillimeter bubble from an orifice using pulsed acoustic pressure waves in gas phase. Phys. Fluids 2008, 20, 043301. [Google Scholar] [CrossRef]
- Kong, G.; Mirsandi, H.; Buist, K.A.; Peters, E.A.J.F.; Baltussen, M.W.; Kuipers, J.A.M. Hydrodynamic interaction of bubbles rising side-by-side in viscous liquids. Exp. Fluids 2019, 60, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Chesters, A.K.; Hofman, G. Bubble coalescence in pure liquids. In Mechanics and Physics of Bubbles in Liquids; Springer: Dordrecht, The Netherlands, 1982; pp. 353–361. [Google Scholar]
- Cano-Lozano, J.C.; Martinez-Bazan, C.; Magnaudet, J.; Tchoufag, J. Paths and wakes of deformable nearly spheroidal rising bubbles close to the transition to path instability. Phys. Rev. Fluids 2016, 1, 053604. [Google Scholar] [CrossRef] [Green Version]
- Magnaudet, J.; Mougin, G. Wake instability of a fixed spheroidal bubble. J. Fluid Mech. 2007, 572, 311–337. [Google Scholar] [CrossRef]
- Zhang, J.; Ni, M.J. What happens to the vortex structures when the rising bubble transits from zigzag to spiral? J. Fluid Mech. 2017, 828, 353–373. [Google Scholar] [CrossRef]
- Popinet, S. Basilisk. Available online: https://basilisk.fr (accessed on 7 September 2021).
- Blanco, A.; Magnaudet, J. The structure of the axisymmetric high-Reynolds number flow around an ellipsoidal bubble of fixed shape. Phys. Fluids 1995, 7, 1265–1274. [Google Scholar] [CrossRef]
- Kusuno, H.; Sanada, T. Velocity distribution in the boundary layer of a bubble rising with a rectilinear motion. Trans. JSME 2020, 86, 19-00453. [Google Scholar] [CrossRef]
- Shew, W.L.; Poncet, S.; Pinton, J.F. Force measurements on rising bubbles. J. Fluid Mech. 2006, 569, 51–60. [Google Scholar] [CrossRef] [Green Version]
- Harper, J.F. Bubbles rising in line: Champagne, lager, cider. In Bubbles in Food 2; AACC International Press: Washington, DC, USA, 2008; pp. 147–152. [Google Scholar]
- Adoua, R.; Legendre, D.; Magnaudet, J. Reversal of the lift force on an oblate bubble in a weakly viscous linear shear flow. J. Fluid Mech. 2009, 628, 23–41. [Google Scholar] [CrossRef] [Green Version]







| Liquid | μ [mPa⋅s] | ρ [kg/m3] | σ [mN/m] | Mo |
|---|---|---|---|---|
| K1 | 0.8 | 818 | 16.9 | 1.1 × 10−9 |
| K2 | 1.7 | 873 | 18.3 | 1.7 × 10−8 |
| Case | Ga | Bo | Mo | Trajectory | Single Trajectory | Trajectory after Repulsion |
|---|---|---|---|---|---|---|
| 1E | 71 | 0.9 | 1.7 × 10−8 | M1 | rectilinear | - |
| 2E | 117 | 0.6 | 1.1 × 10−9 | M2 | rectilinear | rectilinear |
| 3E | 90 | 1.3 | 1.7 × 10−8 | M3 | rectilinear | rectilinear |
| 4E | 186 | 1.1 | 1.1 × 10−9 | M4 | zigzag | repeated bounce |
| Fluid | μ [mPas] | ρ [kg/m3] | σ [mN/m] | Mo |
|---|---|---|---|---|
| K1 | 0.8 | 818 | 16.9 | 1.1 × 10−9 |
| K2 | 1.7 | 873 | 18.3 | 1.7 × 10−8 |
| K5 | 4.6 | 915 | 19.7 | 6.1 × 10−7 |
| Air | 0.018 | 1.2 | - | - |
| Case | Ga | Bo | Mo | Trajectory | Single Trajectory | Trajectory after Repulsion |
|---|---|---|---|---|---|---|
| 1N | 90 | 0.4 | 1.1 × 10−9 | M1/M2 | rectilinear | - |
| 2N | 117 | 0.6 | 1.1 × 10−9 | M1/M2 | rectilinear | - |
| 3N | 157 | 0.9 | 1.1 × 10−9 | M3 | zigzag | zigzag |
| 4N | 186 | 1.1 | 1.1 × 10−9 | M4 | zigzag | zigzag |
| 5N | 71 | 0.9 | 1.7 × 10−8 | M1/M2 | rectilinear | - |
| 6N | 90 | 1.3 | 1.7 × 10−8 | M5 | rectilinear | - |
| 7N | 100 | 1.7 | 1.7 × 10−8 | M3 | zigzag | zigzag |
| 8N | 58 | 2.2 | 6.1 × 10−7 | M5 | rectilinear | - |
| 9N | 72 | 3.0 | 6.1 × 10−7 | M5 | rectilinear | - |
| 10N | 80 | 3.4 | 6.1 × 10−7 | M5 | rectilinear | - |
| 11N | 90 | 3.7 | 6.1 × 10−7 | M3 | zigzag | zigzag |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kusuno, H.; Sanada, T. Flow Structure and Deformation of Two Bubbles Rising Side by Side in a Quiescent Liquid. Fluids 2021, 6, 390. https://doi.org/10.3390/fluids6110390
Kusuno H, Sanada T. Flow Structure and Deformation of Two Bubbles Rising Side by Side in a Quiescent Liquid. Fluids. 2021; 6(11):390. https://doi.org/10.3390/fluids6110390
Chicago/Turabian StyleKusuno, Hiroaki, and Toshiyuki Sanada. 2021. "Flow Structure and Deformation of Two Bubbles Rising Side by Side in a Quiescent Liquid" Fluids 6, no. 11: 390. https://doi.org/10.3390/fluids6110390
APA StyleKusuno, H., & Sanada, T. (2021). Flow Structure and Deformation of Two Bubbles Rising Side by Side in a Quiescent Liquid. Fluids, 6(11), 390. https://doi.org/10.3390/fluids6110390






