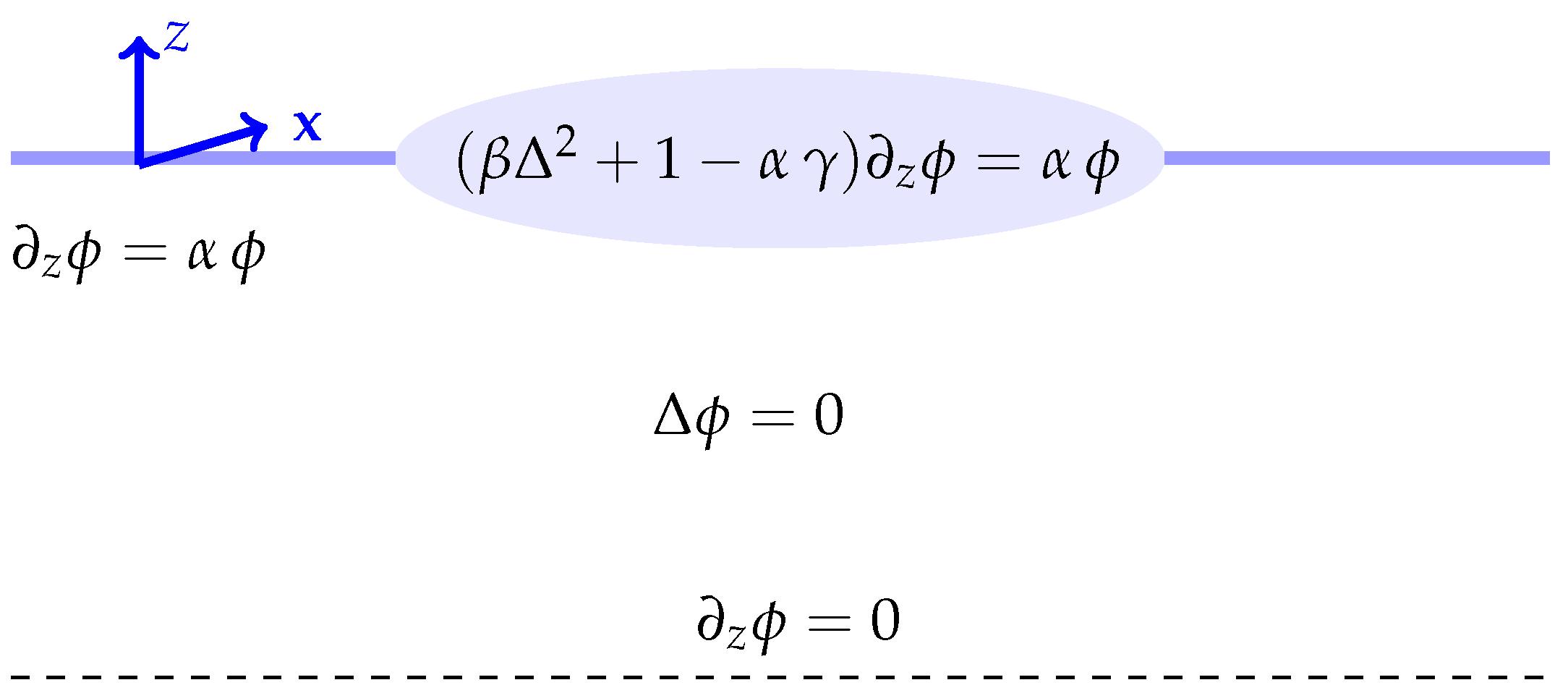Time-Dependent Motion of a Floating Circular Elastic Plate

Abstract

The motion of a circular elastic plate floating on the surface is investigated in the time-domain. The solution is found from the single frequency solutions, and the method to solve for the circular plate is given using the eigenfunction matching method. Simple plane incident waves with a Gaussian profile in wavenumber space are considered, and a more complex focused wave group is considered. Results are given for a range of plate and incident wave parameters. Code is provided to show how to simulate the complex motion.

1. Introduction

The single frequency solution for the linear water wave problem is extensively used to model the hydroelastic response of very large floating structures, container ships, or an ice floe [1,2,3,4]. The simplest example problem in hydroelasticity is the floating elastic plate, which has been the subject of extensive research. Many different methods of solution have been developed, including Green function methods [5,6], eigenfunction matching [7,8,9], multi-mode methods [10] and the Wiener–Hopf method [11,12].

The problem becomes more complicated if we consider the time-dependent problem. If the floating plate is assumed to be of infinite extent, the problem becomes simpler and a spatial Fourier transform gives the solution [13,14,15,16,17,18,19]. The forced vibration of a finite floating elastic plate was solved by [20] using a variational formulation and the Rayleigh–Ritz method. The problem was analyzed in shallow water by [21,22,23] and in finite depth by [24]. The solution for incident waves in two-dimensions was given in finite depth by [25,26,27] and in shallow water in two by [21,22] and three–dimensions by [23]. A comparison for the time–dependent motion in two-dimensions for an initial condition was given in [28]. The solution for finite water depth in three–dimensions was found by [29,30,31,32] and was experimentally investigated by [33]. The solution due to a transient incident wave forcing was given in [34]. Recently, there has been extensive work on nonlinear simulations using computational fluid dynamics to investigate nonlinear phenomena [35,36,37,38]. However, even for the case of high amplitude waves, the linear wave problem remains valid for a floating plate [39], and this model continues to the basis of offshore engineering and scattering by an ice floe.

The eigenfunction matching method has been applied to many floating elastic plate problems. It has proved to give the most uncomplicated solutions, provided that the geometry is sufficiently simple that it can be applied. The solution method was first described in [7] and this is where the solution of the special dispersion equation for a floating elastic plate was introduced. This method was extended to circular [9], multiple [40,41,42], and submerged elastic plates [43,44].

We present here a solution to the time-dependent problem of a floating circular plate subject to incident wave forcing. In part, the purpose of this work is to show how simply the complex time-domain motion of such systems can easily be computed using the frequency-domain solution. We also extend the formulation to a focused incident wavepacket. The outline is as follows. In Section 2, we derive the equations of motion in the time and frequency domain. In Section 3, we show how the solution can be found using eigenfunction matching in the frequency domain. In Section 4, we illustrate how the solution in the time domain can be found straightforwardly from the frequency domain solutions.

We acknowledge that much of the material presented here has appeared in various previous works. In particular, the eigenfunction matching for a circular plate which underlies the calculations presented here. However, the present work aims to show how the time-domain solution can be found straightforwardly from the frequency domain solution. In some sense, the floating elastic plate is just a beautiful example to illustrate this method. We have given sufficient details of the solution method to understand the code that accompanies the paper. We also note that the code which accompanies this work is an essential part of it, and this has not been made available previously.

2. Equations of Motion

We consider here a floating elastic plate of uniform thickness and negligible draft. The plate is assumed to be circular with radius a. The fluid is of constant depth H with the z axis pointing vertically up and the free surface at $z=0$. Such a plate has been the subject of extensive research. The displacement of the plate is denoted by w and the spatial velocity potential for the fluid by $\varphi$. The equation The plate has a uniform thickness h. This uniform thickness floating plate model has been the validated by laboratory experiments [45,46]. It reduces to that of a rigid body in the case of long waves.

We begin by stating the governing equations for the plate–water system, which was discussed in detail in [47], assuming that the equation of linear water waves governs the problem. The kinematic condition is

$${\partial }_{t}w={\partial }_z\mathsf{\Phi },z=0;$$

(1)

where w is the displacement of the fluid surface (which is also the plate displacement for $r<a$) and $\mathsf{\Phi }$ is the velocity potential of the fluid. The dynamic condition is

$$\rho gw+\rho {\partial }_t\mathsf{\Phi }=\left\{\begin{array}{c}\frac{E{h}^3}{12(1-{\nu }^2)}{\partial }_x^{4}w+{\rho }_{i}h{\partial }_t^{2}w,r<a,\\ 0,r>a\end{array}\right.z=0;$$

(2)

where $\rho$ is the water density, g is the gravitational acceleration, E is the Young’s modulus of the plate, $\nu$ is its Poisson’s ratio, and ${\rho }_i$ is its density. Laplace’s equation applies throughout the fluid

$$\mathsf{\Delta }\mathsf{\Phi }=0,-H<z<0$$

(3)

and the usual non-flow condition at the bottom surface

$${\partial }_z\mathsf{\Phi }=0,z=-H.$$

(4)

Assuming that all motions are time harmonic with radian frequency $\omega$, the velocity potential of the water, $\mathsf{\Phi }$, can be expressed as

$$\mathsf{\Phi }(\mathbf{x},z,t)=\mathrm{Re}\left\{\varphi (\mathbf{x},z){\mathrm{e}}^{-\mathrm{i}\omega t}\right\}\mathrm{and}w(\mathbf{x},t)=\mathrm{Re}\left\{\eta \left(\mathbf{x}\right){\mathrm{e}}^{-\mathrm{i}\omega t}\right\},$$

(5)

where the reduced velocity potential $\varphi$ is complex-valued, and $\mathbf{x}=(x,y)$ is the horizontal spatial variable.

The frequency-domain potential satisfies the boundary value problem

$$\mathsf{\Delta }\varphi =0,-H<z<0,$$

(6a)

$${\partial }_z\varphi =0,z=-H,$$

(6b)

$${\partial }_z\varphi =\alpha \varphi ,z=0,r>a,$$

(6c)

$$(\beta {\overline{\mathsf{\Delta }}}^2+1-\alpha \gamma ){\partial }_z\varphi =\alpha \varphi ,z=0,r<a,$$

(6d)

where $\overline{\mathsf{\Delta }}$ is the Laplacian operator in the horizontal plane. The constant $\alpha ={\omega }^2/g$ and $\beta$ and $\gamma$ are

$$\beta =\frac{E{h}^3}{12(1-{\nu }^2)\rho g}\mathrm{and}\gamma =\frac{{\rho }_{i}h}{\rho },$$

(7)

The free plate boundary conditions and the radiation condition need to be applied. Figure 1 gives a schematic diagram of the problem.

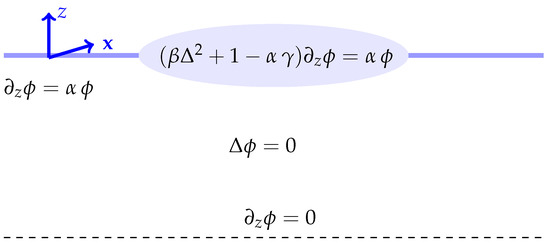
Figure 1. Frequency-domain equations for a floating circular plate.

3. Eigenfunction Matching

We derive the solution by the eigenfunction matching method here. The solution in two-dimensions first appeared in [7] and the three–dimensional solution was given in [9]. We begin by separating variables and writing

$$\varphi (\mathbf{x},z)=\zeta \left(z\right)X\left(\mathbf{x}\right).$$

(8)

Applying Laplace’s equation, we obtain

$${\zeta }_{zz}+{\mu }^2\zeta =0,$$

(9)

so that

$$\zeta =cos\mu (z+H),$$

(10)

where the separation constant ${\mu }^2$ must satisfy the standard dispersion equations

$$ktan\left(kH\right)=-\alpha ,\mathbf{x}\notin \mathsf{\Omega },$$

(11)

$$\kappa tan\left(\kappa H\right)=\frac{-\alpha }{\beta {\kappa }^4+1-\alpha \gamma },\mathbf{x}\in \mathsf{\Omega }.$$

(12)

Note that we have set $\mu =k$ under the free surface and $\mu =\kappa$ under the plate. The dispersion equations are discussed in detail in [7]. We denote the negative imaginary solution of (11) by $k_0$ and the positive real by $k_m$, $m\ge 1$. The solutions of (12) are denoted by ${\kappa }_m$, $m\ge -2$. The fully complex with positive real part are ${\kappa }_{-2}$ and ${\kappa }_{-1}$ (where ${\kappa }_{-1}=\overline{{\kappa }_{-2}}$), the negative imaginary is ${\kappa }_0$ and the positive real are ${\kappa }_m$, $m\ge 1$. We define

$${\varphi }_m\left(z\right)={\displaystyle \frac{cos{k}_m(z+H)}{cos{k}_{m}H}},m\ge 0,$$

(13)

as the vertical eigenfunction of the potential in the open water region and

$${\psi }_m\left(z\right)={\displaystyle \frac{cos{\kappa }_m(z+H)}{cos{\kappa }_{m}H}},m\ge -2,$$

(14)

as the vertical eigenfunction of the potential in the plate covered region.

We now use circular symmetry to write

$$X\left(\mathbf{x}\right)={\rho }_n\left(r\right){\mathrm{e}}^{\mathrm{i}n\theta }$$

(15)

where $(r,\theta )$ are the polar coordinates in the $\mathbf{x}$ direction. We now solve for the function ${\rho }_n\left(r\right)$. Using Laplace’s equation in polar coordinates, we obtain

$${\displaystyle \frac{{\mathrm{d}}^2{\rho }_n}{\mathrm{d}{r}^2}}+\frac{1}{r}{\displaystyle \frac{\mathrm{d}{\rho }_n}{\mathrm{d}r}}-\left(\frac{n^2}{r^2}+{\mu }^2\right){\rho }_n=0,$$

(16)

where $\mu$ is $k_m$ or ${\kappa }_m,$ depending on whether r is greater or less than a. We can convert this equation to the standard form by substituting $y=\mu r$ to obtain

$$y^2{\displaystyle \frac{{\mathrm{d}}^2{\rho }_n}{\mathrm{d}{y}^2}}+y{\displaystyle \frac{\mathrm{d}{\rho }_n}{\mathrm{d}y}}-(n^2+y^2){\rho }_n=0.$$

(17)

The solution of this equation is a linear combination of the modified Bessel functions of order n, $I_n\left(y\right)$ and $K_n\left(y\right)$. Since the solution must be bounded, we know that under the plate it will be a linear combination of $I_n\left(y\right)$ while outside the plate will be a linear combination of $K_n\left(y\right)$. Therefore, the potential can be expanded as

$$\varphi (r,\theta ,z)=\sum _{n=-\infty }^{\infty }\sum _{m=0}^{\infty }{a}_{mn}{K}_n\left(k_{m}r\right){\mathrm{e}}^{\mathrm{i}n\theta }{\varphi }_m\left(z\right),r>a,$$

(18)

$$\varphi (r,\theta ,z)=\sum _{n=-\infty }^{\infty }\sum _{m=-2}^{\infty }{b}_{mn}{I}_n\left({\kappa }_{m}r\right){\mathrm{e}}^{\mathrm{i}n\theta }{\psi }_m\left(z\right),r<a,$$

(19)

where $a_{mn}$ and $b_{mn}$ are the coefficients in the open water and the plate covered region, respectively.

The incident potential is a wave of amplitude A in displacement travelling in the positive x-direction. Following [8], it can be written as

$$\begin{array}{cc}\hfill {\varphi }^{\mathrm{I}}& ={\displaystyle \frac{A}{\mathrm{i}\sqrt{\alpha }}}{e}^{k_{0}x}{\varphi }_0\left(z\right)=\sum _{n=-\infty }^{\infty }{e}_n{I}_n\left(k_{0}r\right){\varphi }_0\left(z\right){\mathrm{e}}^{\mathrm{i}n\theta }\hfill \end{array}$$

(20)

where $e_n=A/\left(\mathrm{i}\sqrt{\alpha }\right)$.

The boundary conditions for the plate also have to be considered. The vertical force and bending moment must vanish, which can be written as

$$\left[\overline{\mathsf{\Delta }}-\frac{1-\nu }{r}\left(\frac{\partial }{\partial r}+\frac{1}{r}\frac{{\partial }^2}{\partial {\theta }^2}\right)\right]\eta =0,$$

(21)

and

$$\left[\frac{\partial }{\partial r}\overline{\mathsf{\Delta }}-\frac{1-\nu }{r^2}\left(\frac{\partial }{\partial r}+\frac{1}{r}\right)\frac{{\partial }^2}{\partial {\theta }^2}\right]\eta =0,$$

(22)

where w is the time-independent surface displacement, $\nu$ is Poisson’s ratio, and $\overline{\mathsf{\Delta }}$ is the in polar coordinates is

$$\overline{\mathsf{\Delta }}=\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{{\partial }^2}{\partial {\theta }^2}$$

(23)

The surface displacement and the velocity potential at the water surface are linked through the kinematic boundary condition

$${\varphi }_z=-\mathrm{i}\sqrt{\alpha }\eta ,z=0$$

(24)

The relationship between the potential and the surface displacement is

$$\eta =\mathrm{i}\sqrt{\alpha }\varphi ,r>a$$

(25)

$$(\beta {\overline{\mathsf{\Delta }}}^2+1-\alpha \gamma )\eta =\mathrm{i}\sqrt{\alpha }\varphi ,r<a.$$

(26)

The surface displacement can also be expanded in eigenfunctions as

$$\eta (r,\theta )=\sum _{n=-\infty }^{\infty }\sum _{m=0}^{\infty }\mathrm{i}\sqrt{\alpha }{a}_{mn}{K}_n\left(k_{m}r\right){\mathrm{e}}^{\mathrm{i}n\theta },r>a,$$

(27)

$$\eta (r,\theta )=\sum _{n=-\infty }^{\infty }\sum _{m=-2}^{\infty }\mathrm{i}\sqrt{\alpha }{(\beta {\kappa }_m^4+1-\alpha \gamma )}^{-1}{b}_{mn}{I}_n\left({\kappa }_{m}r\right){\mathrm{e}}^{\mathrm{i}n\theta },r<a,$$

using the fact that

$$\overline{\mathsf{\Delta }}\left(I_n\left({\kappa }_{m}r\right){\mathrm{e}}^{\mathrm{i}n\theta }\right)={\kappa }_m^2{I}_n\left({\kappa }_{m}r\right){\mathrm{e}}^{\mathrm{i}n\theta }.$$

(28)

The boundary conditions (21) and (22) can be expressed in terms of the potential using (28). Since the angular modes are uncoupled, the conditions apply to each, giving

$$\begin{array}{cc}\hfill & \sum _{m=-2}^{\infty }{(\beta {\kappa }_m^4+1-\alpha \gamma )}^{-1}{b}_{mn}\times \hfill \\ \hfill & \left({\kappa }_m^2{I}_n\left({\kappa }_{m}a\right)-\frac{1-\nu }{a}\left({\kappa }_m{I}_n^{\prime }\left({\kappa }_{m}a\right)-\frac{n^2}{a}{I}_n\left({\kappa }_{m}a\right)\right)\right)=0,\hfill \end{array}$$

(29)

and

$$\begin{array}{cc}\hfill & \sum _{m=-2}^{\infty }{(\beta {\kappa }_m^4+1-\alpha \gamma )}^{-1}{b}_{mn}\times \hfill \\ \hfill & \left({\kappa }_m^3{I}_n^{\prime }\left({\kappa }_{m}a\right)+n^2\frac{1-\nu }{a^2}\left({\kappa }_m{I}_n^{\prime }\left({\kappa }_{m}a\right)+\frac{1}{a}{I}_n\left({\kappa }_{m}a\right)\right)\right)=0.\hfill \end{array}$$

(30)

The potential and its derivative must be continuous across the transition from open water to the plate-covered region. Therefore, at $r=a$ they have to be equal. Again we know that this must be true for each angle and we obtain

$$\begin{array}{cc}\hfill e_n{I}_n\left(k_{0}a\right){\varphi }_0\left(z\right)+\sum _{m=0}^{\infty }{a}_{mn}& K_n\left(k_{m}a\right){\varphi }_m\left(z\right)\hfill \\ \hfill & =\sum _{m=-2}^{\infty }{b}_{mn}{I}_n\left({\kappa }_{m}a\right){\psi }_m\left(z\right),\hfill \end{array}$$

(31)

and

$$\begin{array}{cc}\hfill e_n{k}_0{I}_n^{\prime }\left(k_{0}a\right){\varphi }_0\left(z\right)+\sum _{m=0}^{\infty }& a_{mn}{k}_m{K}_n^{\prime }\left(k_{m}a\right){\varphi }_m\left(z\right)\hfill \\ \hfill & =\sum _{m=-2}^{\infty }{b}_{mn}{\kappa }_m{I}_n^{\prime }\left({\kappa }_{m}a\right){\psi }_m\left(z\right),\hfill \end{array}$$

(32)

for each n. We solve these equations by multiplying both by ${\varphi }_l\left(z\right)$ and integrating from $-H$ to 0 to obtain

$$\begin{array}{c}\hfill e_n{I}_n\left(k_{0}a\right)A_0{\delta }_{0l}+a_{ln}{K}_n\left(k_{l}a\right)A_l=\sum _{m=-2}^{\infty }{b}_{mn}{I}_n\left({\kappa }_{m}a\right)B_{ml}\end{array}$$

(33)

$$\begin{array}{cc}\hfill e_n{k}_0{I}_n^{\prime }\left(k_{0}a\right)A_0{\delta }_{0l}+a_{ln}{k}_l{K}_n^{\prime }& \left(k_{l}a\right)A_l\hfill \\ \hfill & =\sum _{m=-2}^{\infty }{b}_{mn}{\kappa }_m{I}_n^{\prime }\left({\kappa }_{m}a\right)B_{ml},\hfill \end{array}$$

(34)

where

$${\int }_{-H}^0{\varphi }_m\left(z\right){\varphi }_n\left(z\right)\mathrm{d}z=A_m{\delta }_{mn},$$

(35)

where

$$A_m=\frac{1}{2}\left(\frac{cos{k}_{m}Hsin{k}_{m}H+k_{m}H}{k_m{cos}^2{k}_{m}H}\right),$$

(36)

and

$${\int }_{-H}^0{\varphi }_n\left(z\right){\psi }_m\left(z\right)\mathrm{d}z=B_{mn},$$

(37)

where

$$B_{mn}={\displaystyle \frac{k_{n}sin{k}_{n}Hcos{\kappa }_{m}H-{\kappa }_{m}cos{k}_{n}Hsin{\kappa }_{m}H}{\left(cos{k}_{n}Hcos{\kappa }_{m}H\right)\left(k_n^2-{\kappa }_m^2\right).}}$$

(38)

Equation (33) can be solved for the open water coefficients $a_{mn}$

$$a_{ln}=-e_n{\displaystyle \frac{I_n\left(k_{0}a\right)}{K_n\left(k_{0}a\right)}}{\delta }_{0l}+\sum _{m=-2}^{\infty }{b}_{mn}{\displaystyle \frac{I_n\left({\kappa }_{m}a\right)B_{ml}}{K_n\left(k_{l}a\right)A_l}},$$

(39)

which can then be substituted into Equation (34) to give us

$$\begin{array}{cc}\hfill & \left(k_0{I}_n^{\prime }\left(k_{0}a\right)-k_0{\displaystyle \frac{K_n^{\prime }\left(k_{0}a\right)}{K_n\left(k_{0}a\right)}}{I}_n\left(k_{0}a\right)\right)e_n{A}_0{\delta }_{0l}\hfill \\ \hfill & =\sum _{m=-2}^{\infty }\left({\kappa }_m{I}_n^{\prime }\left({\kappa }_{m}a\right)-k_l{\displaystyle \frac{K_n^{\prime }\left(k_{l}a\right)}{K_n\left(k_{l}a\right)}}{I}_n\left({\kappa }_{m}a\right)\right)B_{ml}{b}_{mn},\hfill \end{array}$$

(40)

for each n. Together with (29) and (30), (40) gives the required equations to solve for the coefficients of the water velocity potential in the plate covered region. For the numerical solution, we truncate the sum at N, and then we have $N+1$ equations from matching through the depth and two extra equations from the boundary conditions.

It should be noted that the solutions for positive and negative n are complex conjugates so that they do not both need to be calculated. There are some minor simplifications which are a consequence of this and are discussed in more detail in [8].

4. Time-Dependent Forcing and Numerical Results

We have denoted the surface displacement in the frequency domain is given by $\eta \left(\mathbf{x}\right)$. However, the surface displacement is a function of $\omega$ and $\omega$ is a function of wavenumber k. We have also only considered waves incident from the positive x direction ($\theta =0)$. This choice of direction makes sense given the circular symmetry, but we can consider waves incident from other angles (found by rotation of the solution by the angle). Therefore, we denote the complex frequency domain surface displacement by $\eta \left(\right(x),\theta ,k)$.

4.1. Plane Incident Wave Forcing

The simplest time-dependent problem is to consider a place incident wave from the positive x direction. We assume that the incident wave is a Gaussian at $t=0$. Therefore, the time–dependent displacement is then given by the following Fourier integral

$$w(\mathbf{x},t)=\mathrm{Re}\left\{{\int }_0^{\infty }\widehat{f}\left(k\right)\eta (\mathbf{x},0,k){\mathrm{e}}^{\mathrm{i}\omega t}\mathrm{d}k\right\},$$

(41)

where $\widehat{f}\left(k\right)$ is

$$\widehat{f}\left(k\right)=\sqrt{\frac{\sigma }{\pi }}exp\left(\sigma {(k-k_0)}^2\right).$$

(42)

where $\sigma$ is a scale factor and we set $\sigma -0.1$ and $k_0$ is the central wavenumber, we set $k_0=3$.

4.2. Focused Wave Group

It is more interesting to consider two-dimensional incident waves. A simple focused wave group can be constructed as from the following formula

$$w(\mathbf{x},t)=\mathrm{Re}\left\{{\int }_{-\pi /2}^{\pi /2}{\int }_0^{\infty }\widehat{f}\left(k\right){\mathrm{e}}^{-{\theta }_{\sigma }{k}^2{sin}^2\left(\theta \right)}\eta (\mathbf{x},\theta ,k){\mathrm{e}}^{\mathrm{i}\omega t}\mathrm{d}k\mathrm{d}\theta \right\},$$

(43)

where ${\theta }_{\sigma }$ is another scaling parameters which we set to be ${\theta }_{\sigma }=0.1$

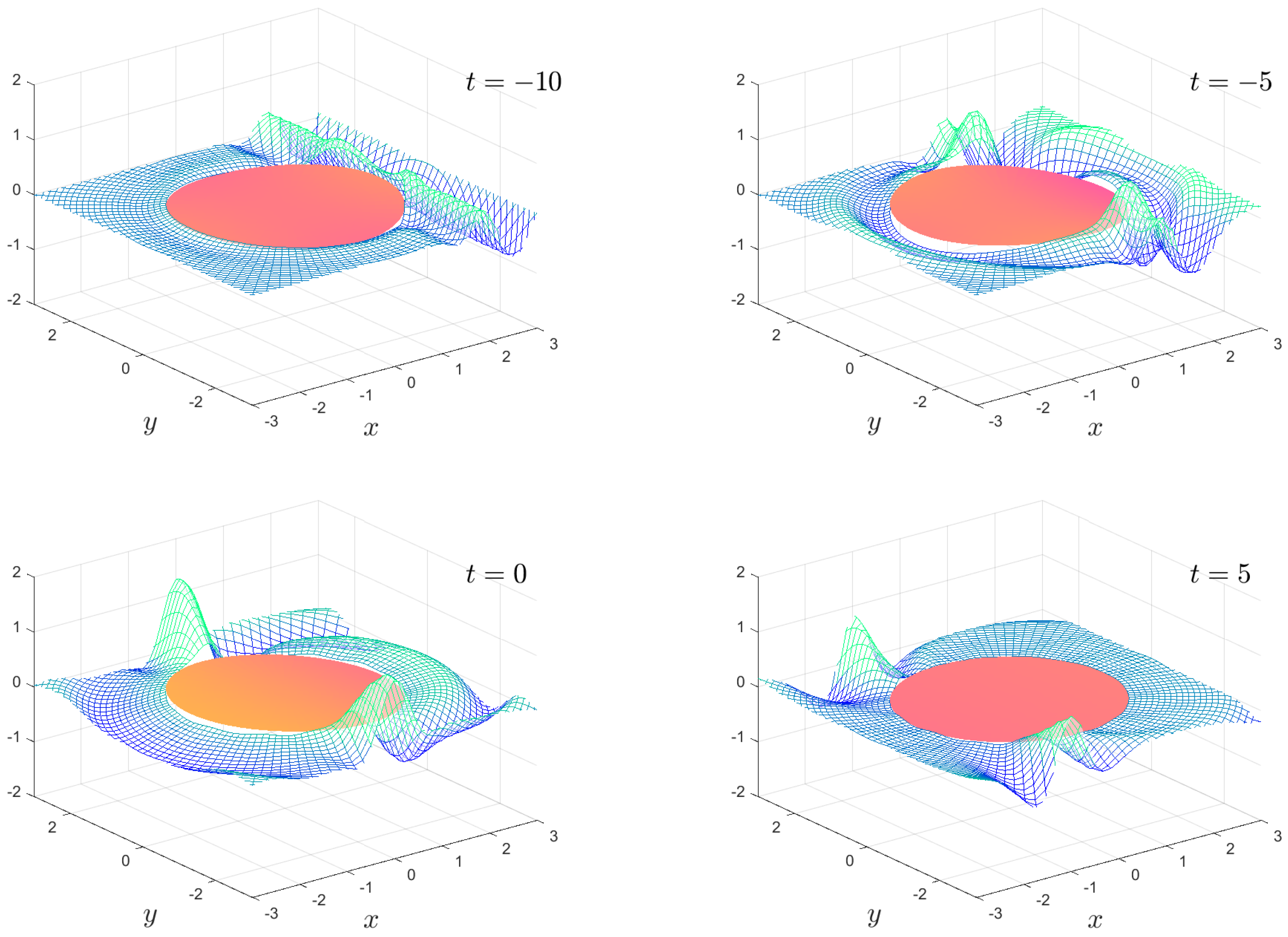
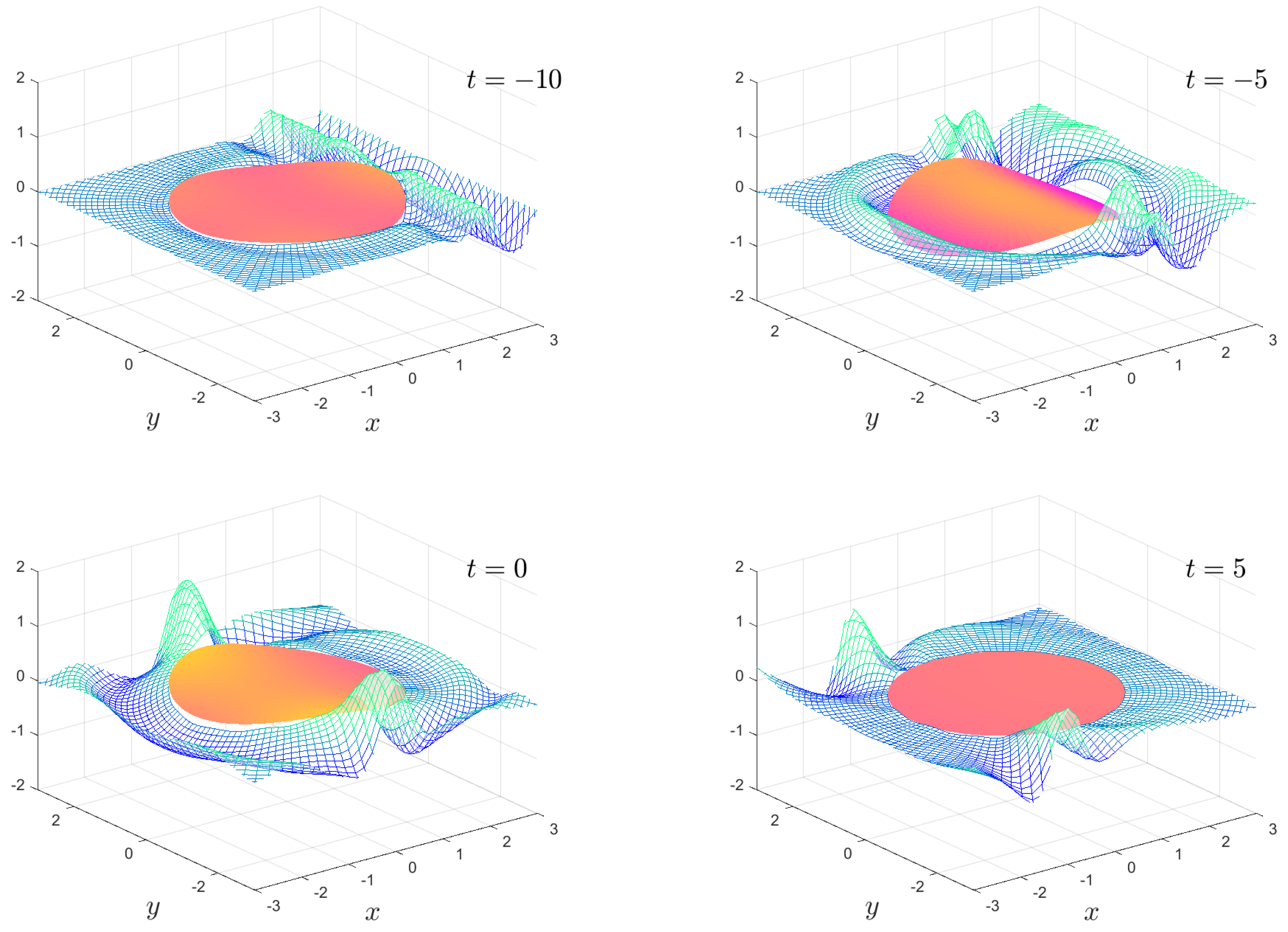
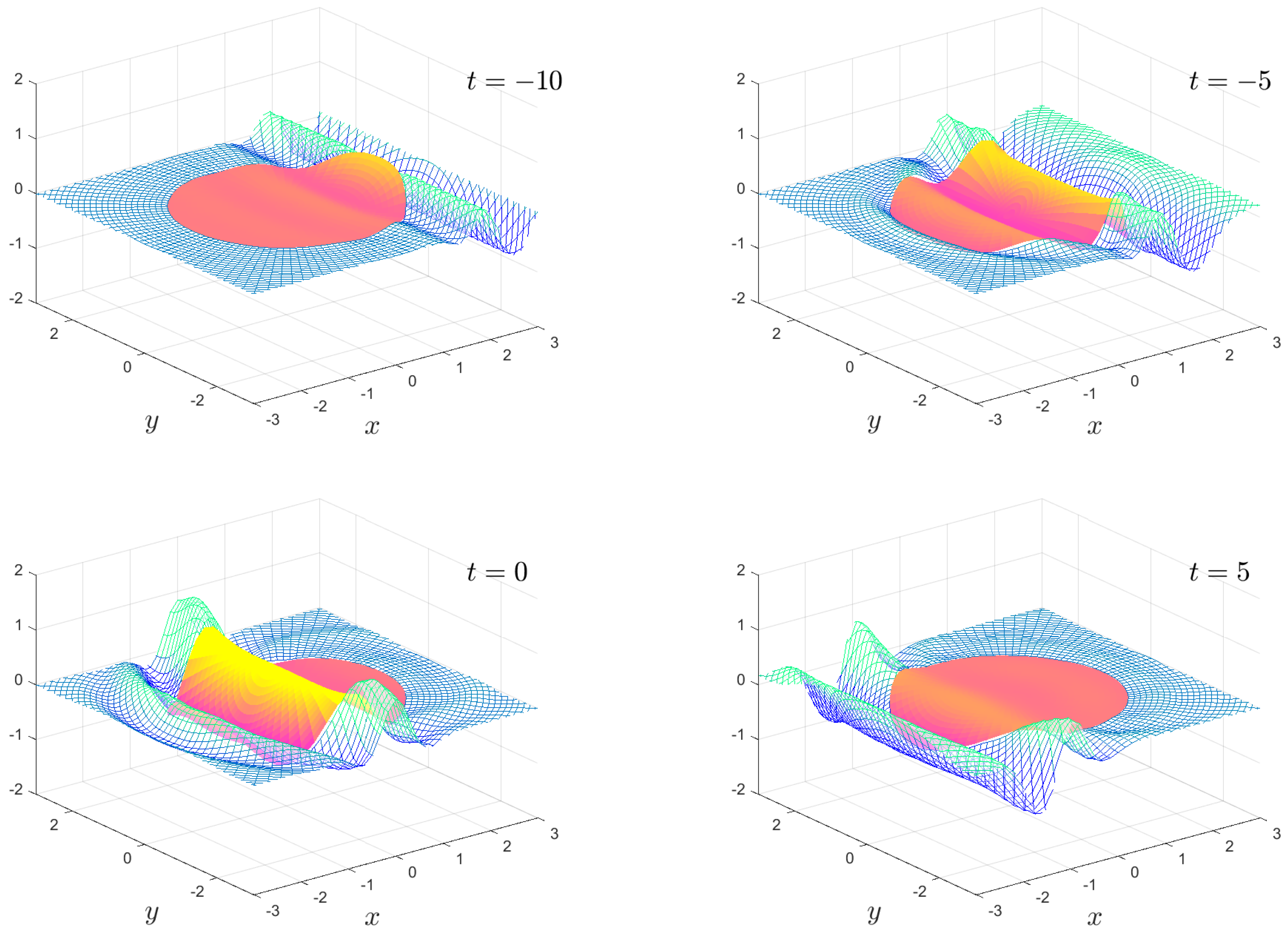
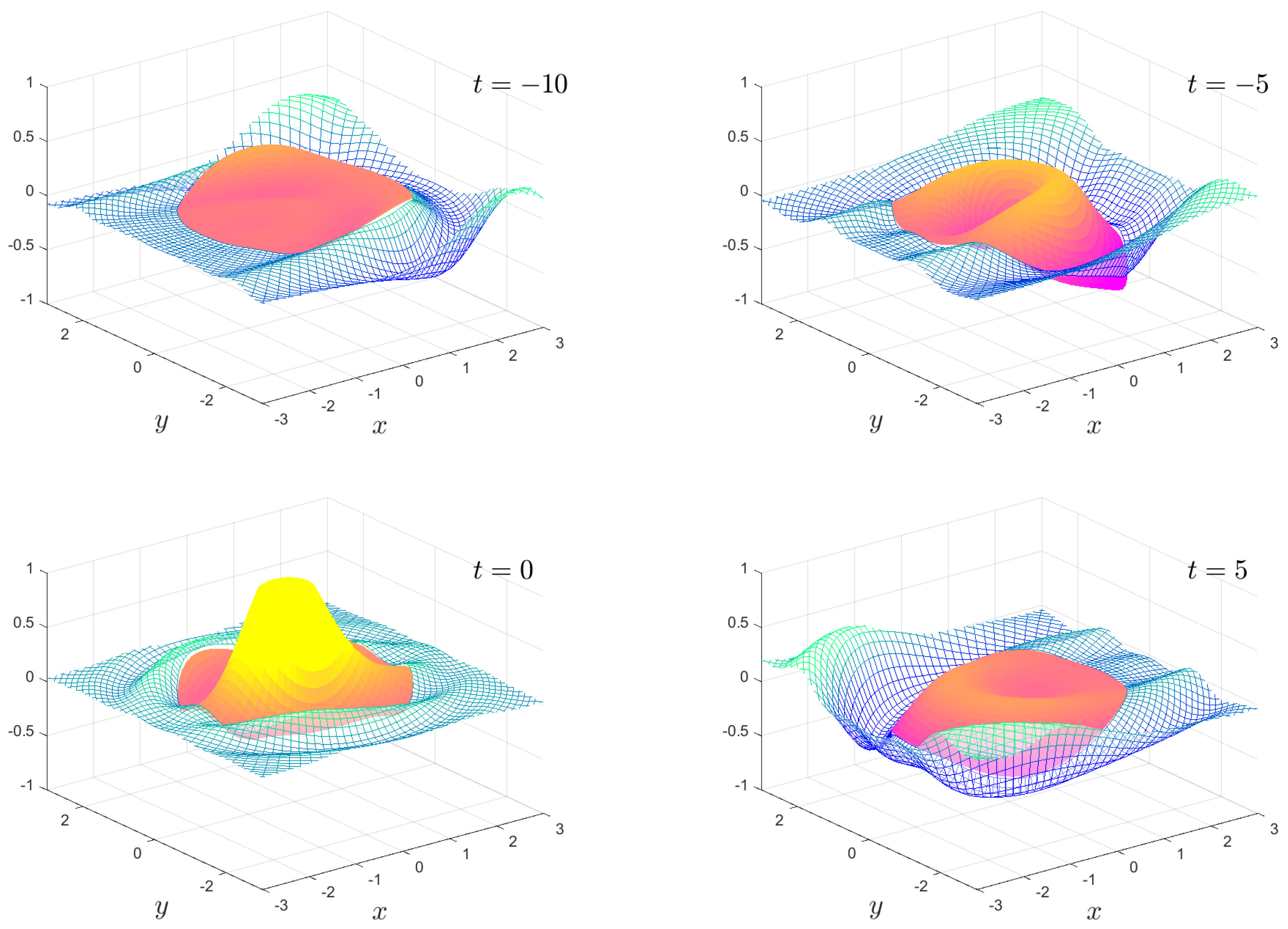
The numerical results we present are a subset of the possible motions which are possible. We fix the mass $\gamma =0$, the water depth $h=1$ and the floe radius $a=2$ for all calculations. The solution is shown as an animation in movies 1 to 8, which are given as Supplementary Material. Figure 2, Figure 3, Figure 4 and Figure 5 show snapshots from movies 1 to 4, respectively, for the times $t=-5,0,5,10$. We change the stiffness from $\beta =1\times {10}^{-1}$ in Figure 2 to $\beta =1\times {10}^{-4}$ in Figure 5. The plate goes from being virtually stiff to highly flexible. The complex motion of the plate and fluid systems can be seen, especially in the movies in the Supplementary Material.

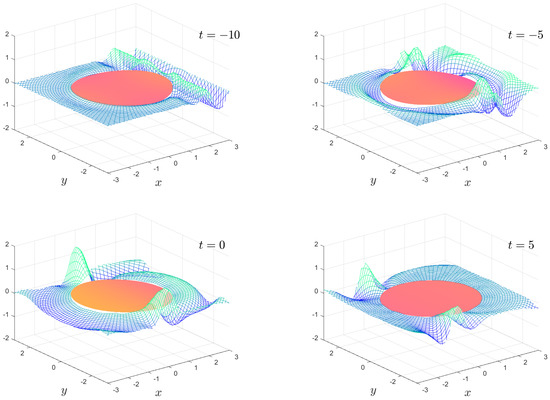
Figure 2. The time-dependent motion $\beta =1\times {10}^{-1}$, $\gamma =0$, $h=1$ and $a=2$ for the times shown. The full animation can be found in movie 1.

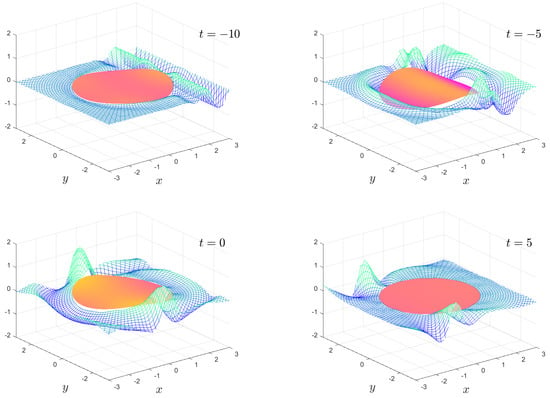
Figure 3. As in Figure 2, except $\beta =1\times {10}^{-2}$. The full animation can be found in movie 2.

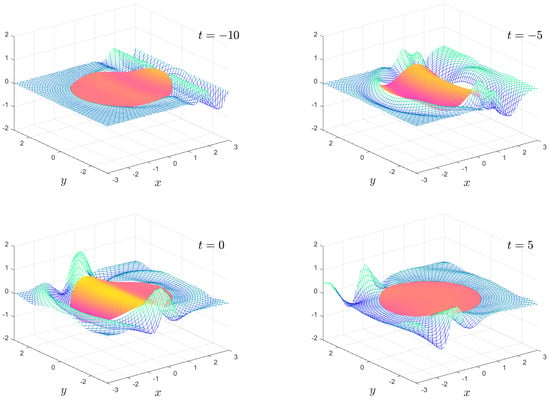
Figure 4. As in Figure 2, except $\beta =1\times {10}^{-3}$. The full animation can be found in movie 3.

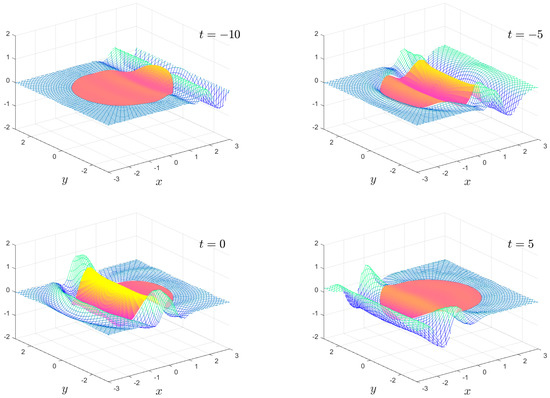
Figure 5. As in Figure 2, except $\beta =1\times {10}^{-4}$. The full animation can be found in movie 4.

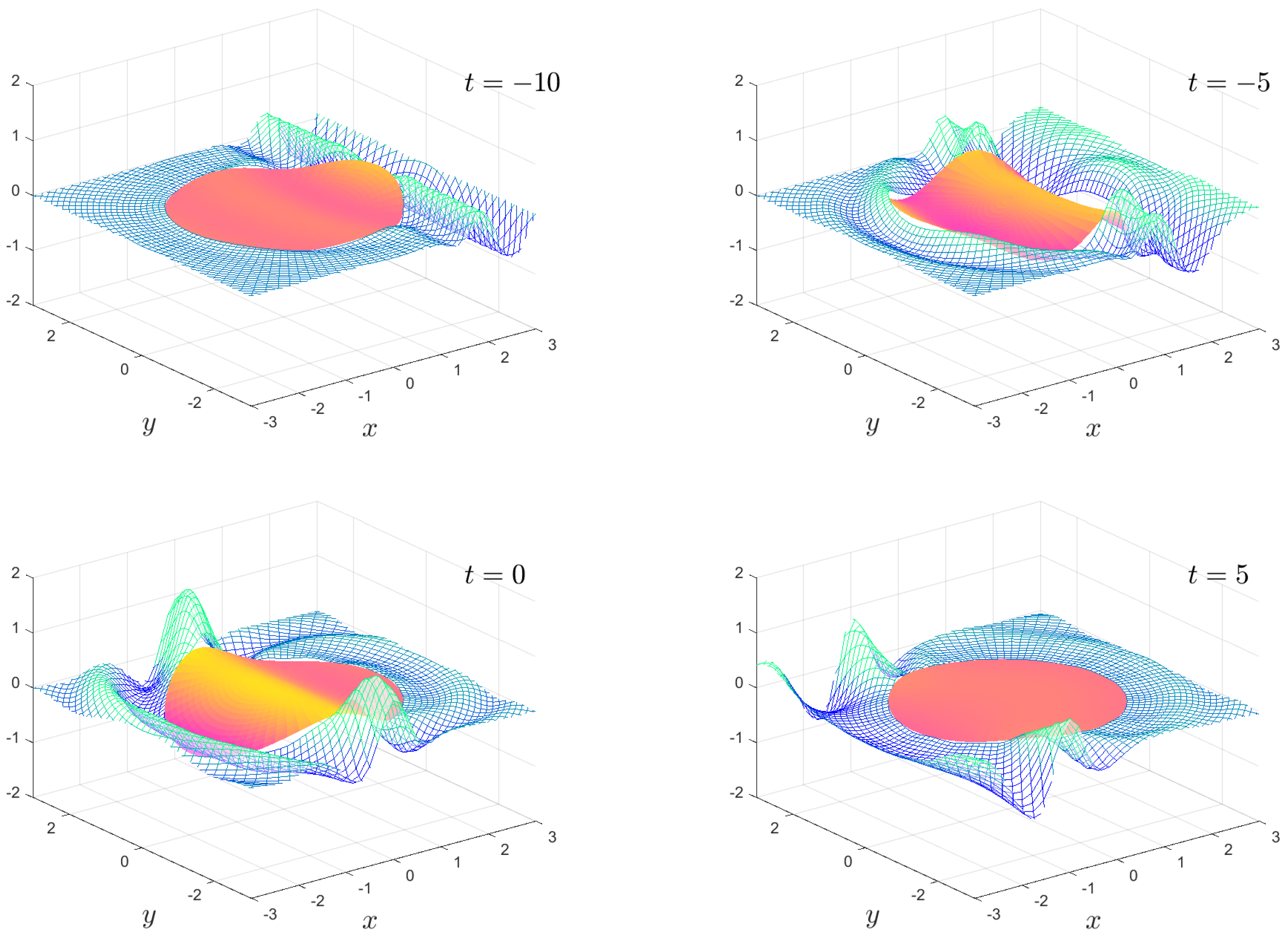
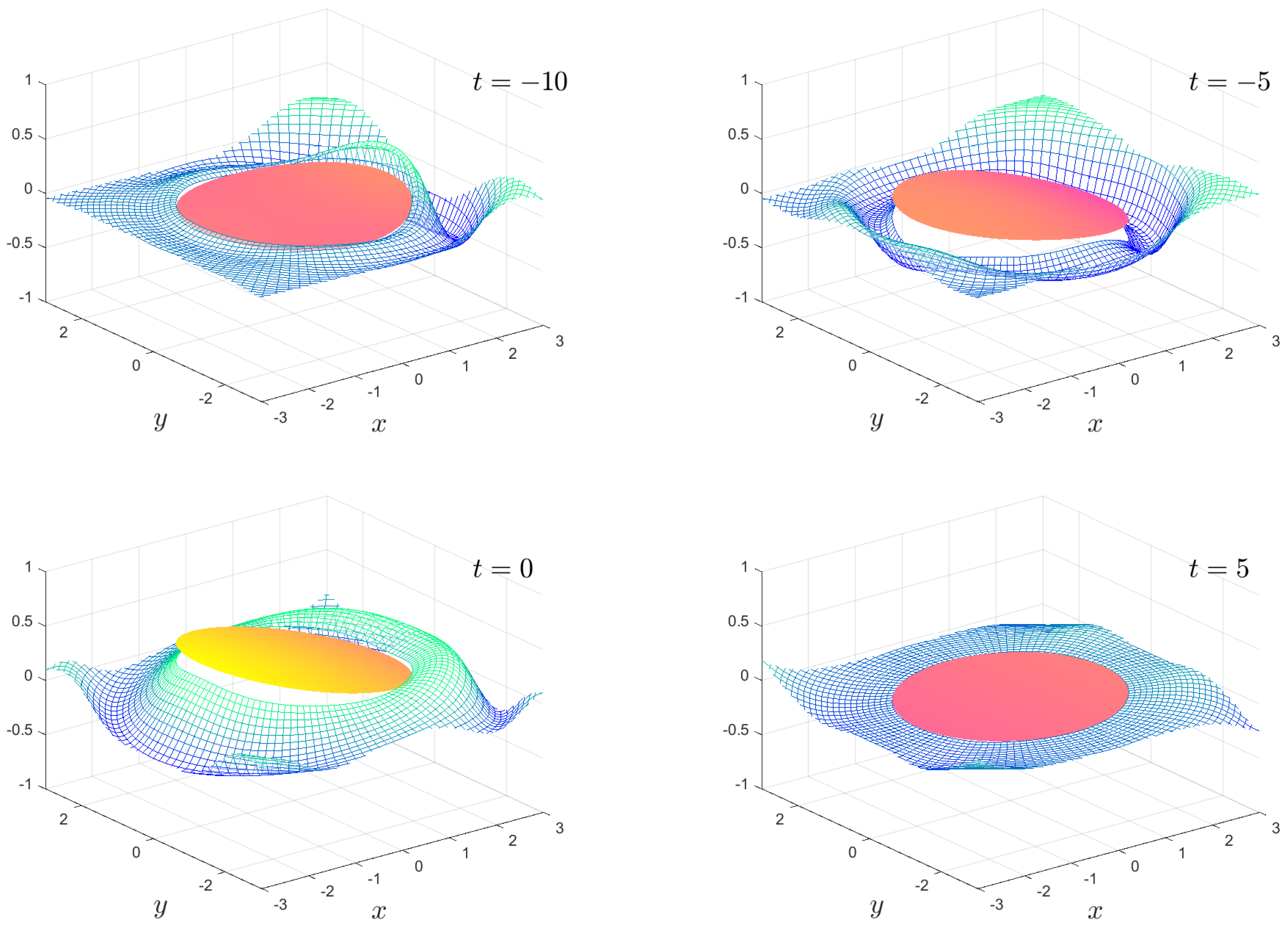
Figure 6, Figure 7, Figure 8 and Figure 9 show the solution for the more complicated and interesting case of an incident wave packet. The complex and resonant behaviour of the plate and fluid system is clearly visible. In particular, the transition from the wave diffracting around the plate to the wave travelling under the plate as the stiffness transitions from high to low is visible. Moreover, we have an intermediate region where resonances exist, and the plate motion becomes highly complicated. The ability to visualise this motion offers insights which are not so easily obtained from the frequency domain solution.

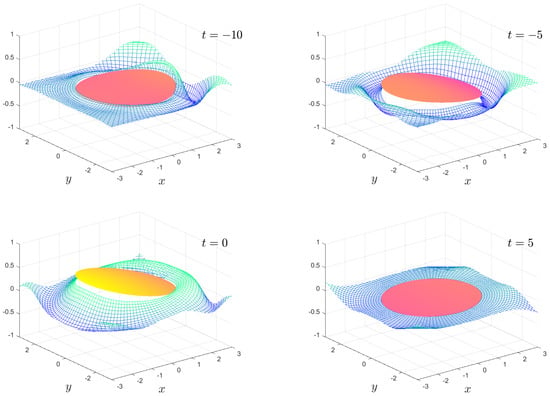
Figure 6. The time-dependent motion $\beta =1\times {10}^{-1}$, $\gamma =0$, $h=1$ and $a=2$ for the times shown. The full animation can be found in movie 5.

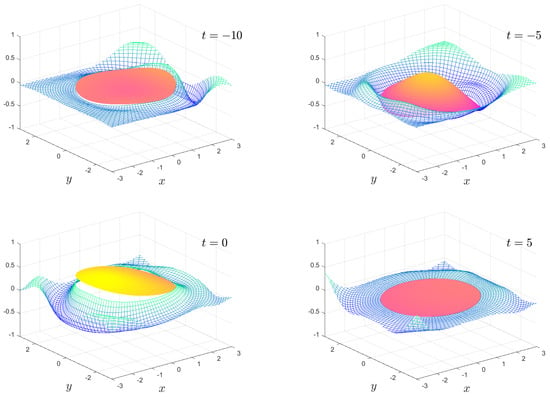
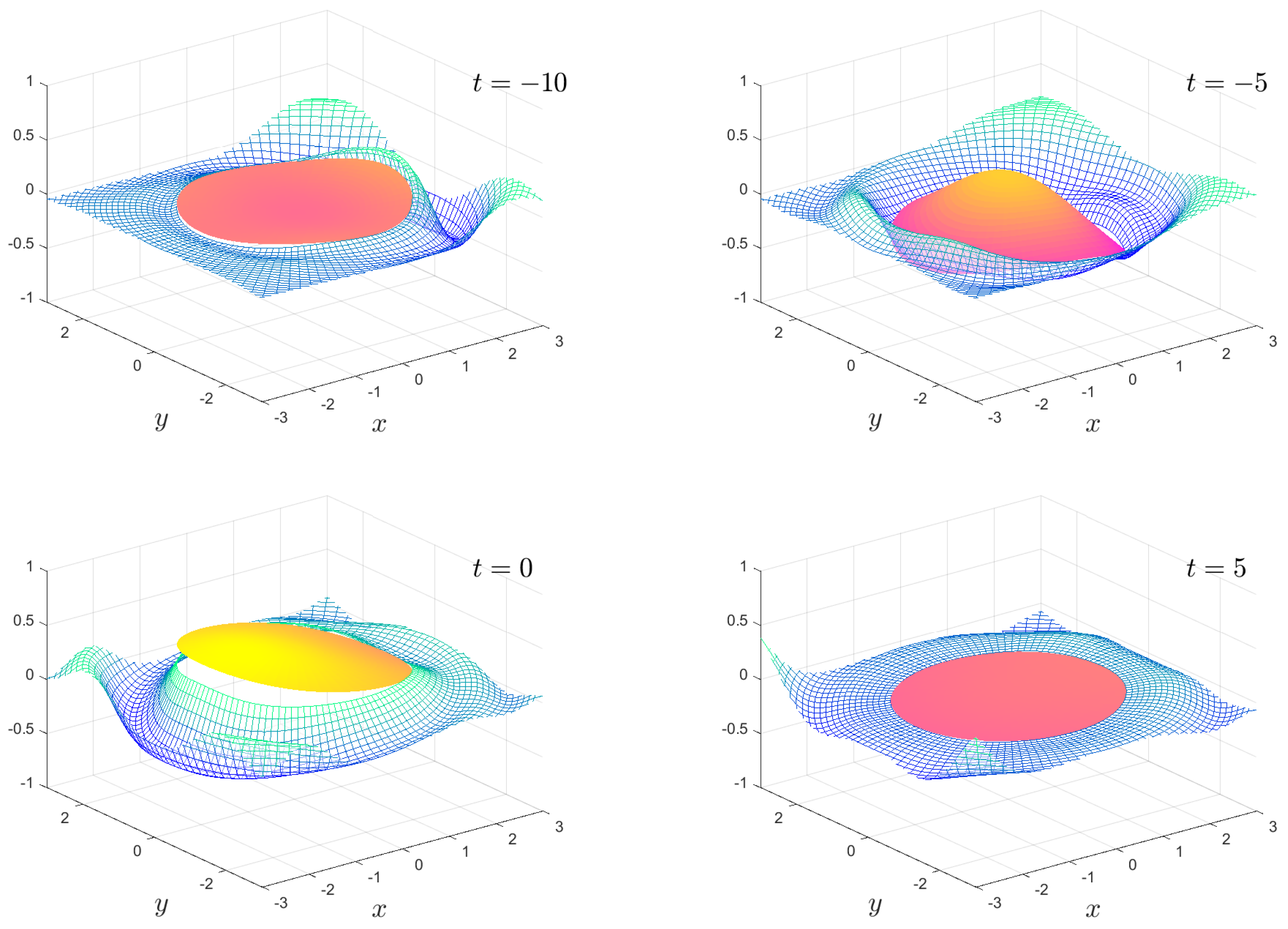
Figure 7. As in Figure 6, except $\beta =1\times {10}^{-3}$. The full animation can be found in movie 6.

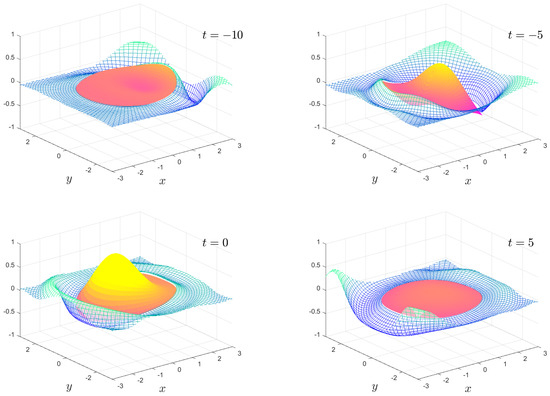
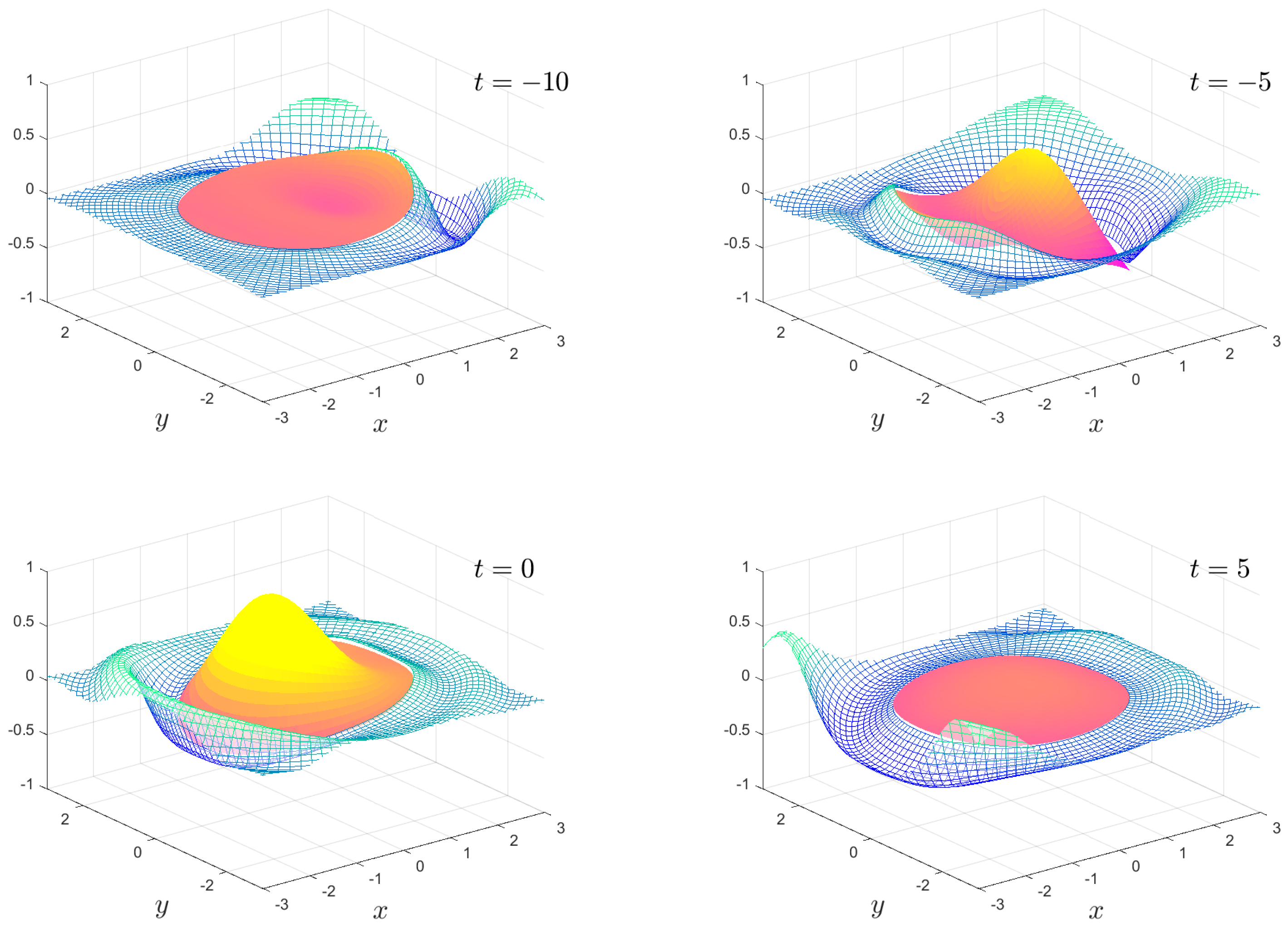
Figure 8. As in Figure 6, except $\beta =1\times {10}^{-4}$. The full animation can be found in movie 7.

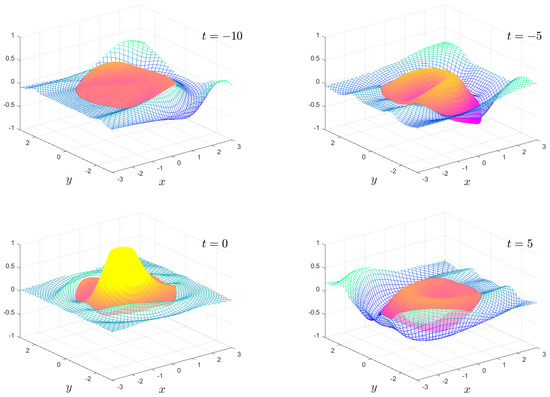
Figure 9. As in Figure 6, except $\beta =1\times {10}^{-2}$. The full animation can be found in movie 8.

5. Conclusions

The purpose of this work is to show how we can easily visualise the complex time-domain behaviour of complex wave scattering problems such as those which arise from the scattering by a flexible plate. While the frequency–domain solution is central to our calculations, the scattering results from the frequency domain solution are often challenging to interpret in the context of incident wave packets. By the simple visualisation using the suitable superposition of incident waves, we can bring the complex motion to life. The author hopes that these results, and the accompanying computer code, will encourage others to also investigate such visualisations for their complex water wave scattering problem.