A Momentum-Conserving Scheme for Flow Simulation in 1D Channel with Obstacle and Contraction
Abstract
1. Introduction
2. Mathematical Model—The Saint-Venant Equations
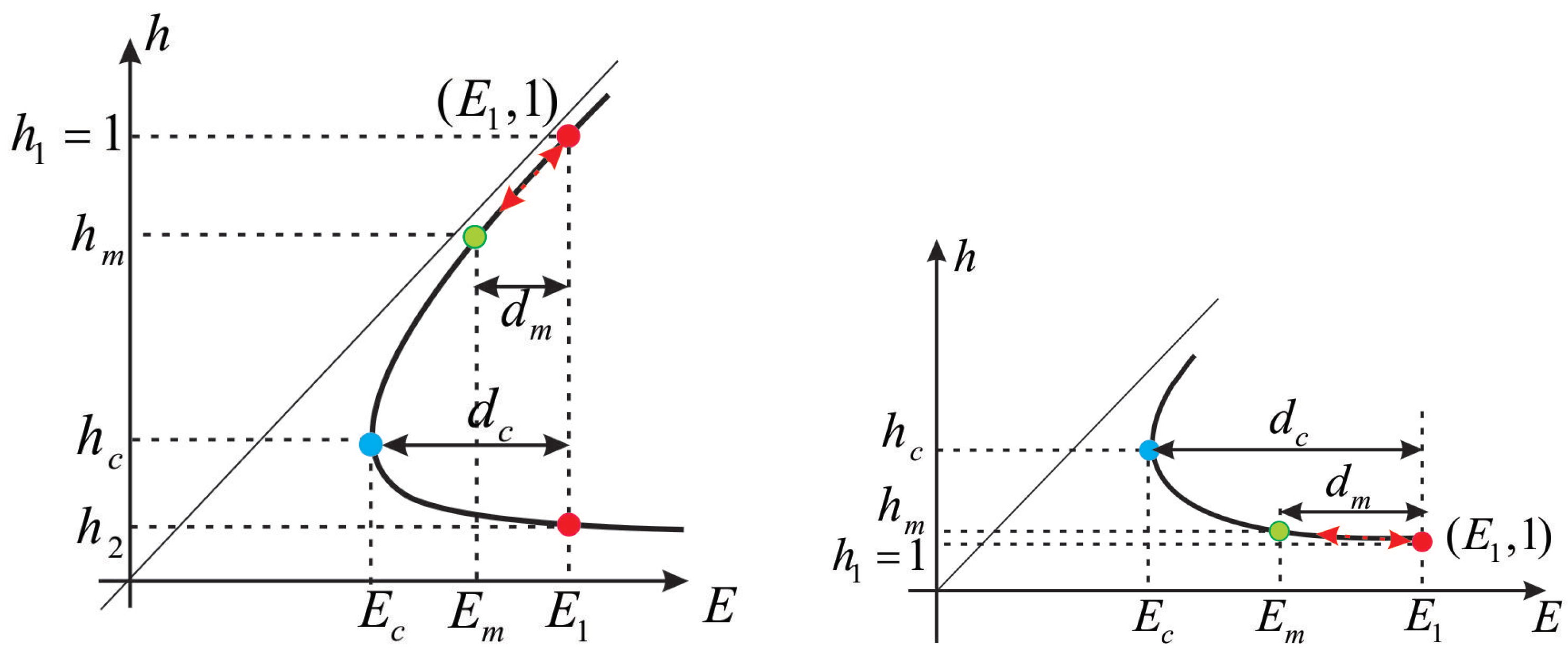
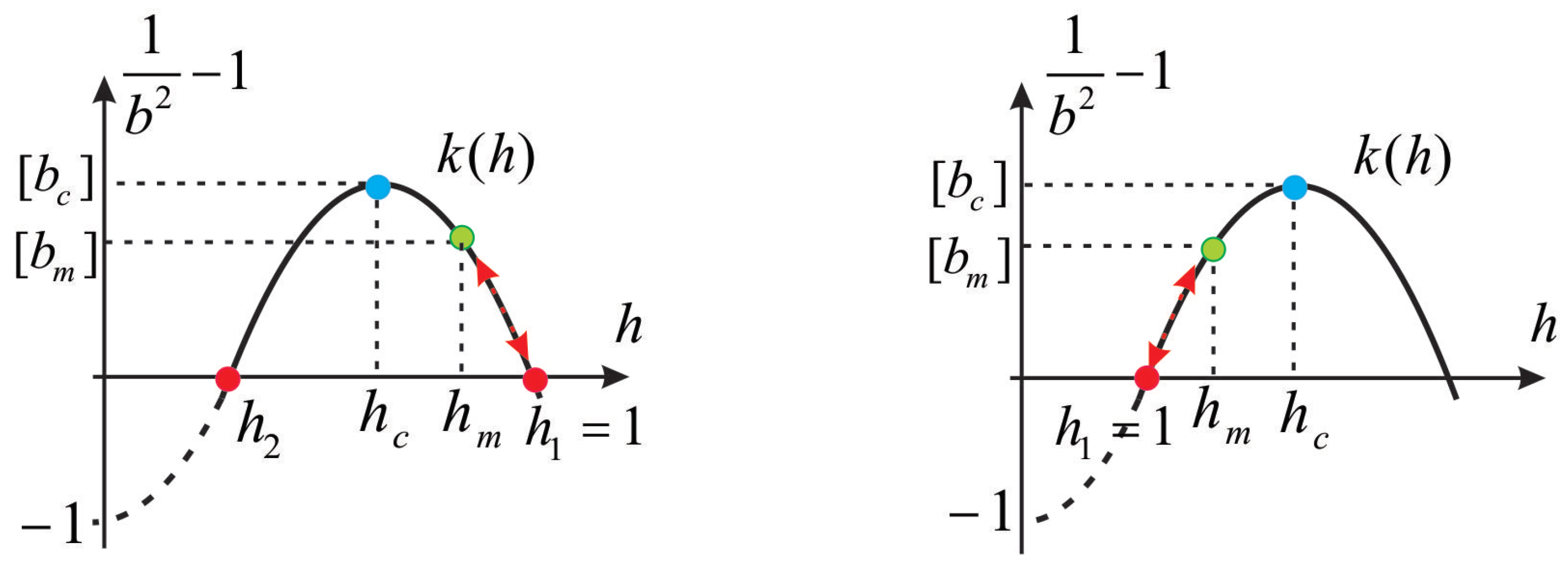
2.1. Flow over a Bump
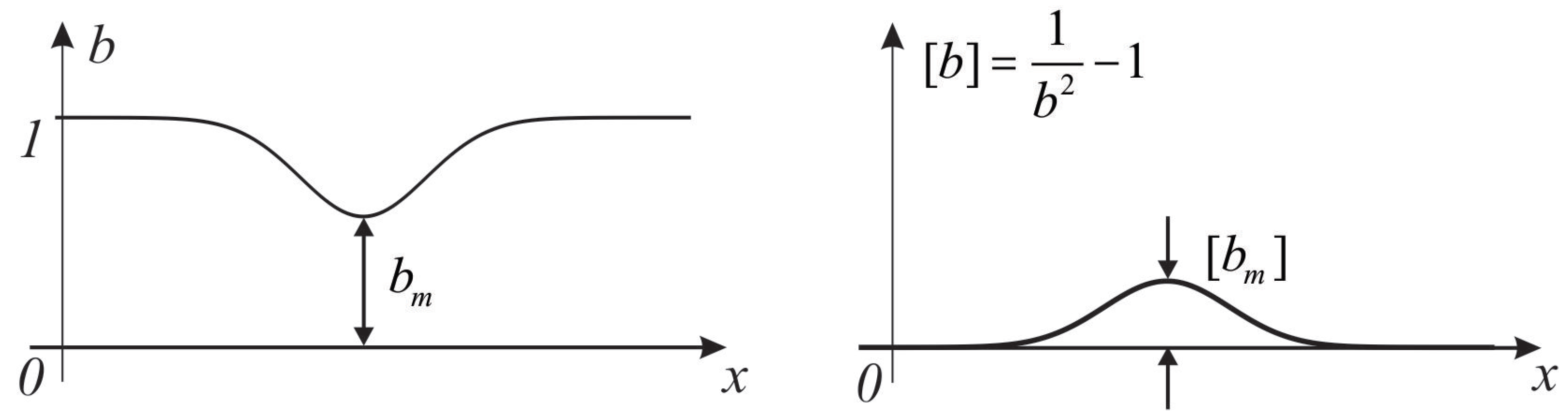
2.2. Flow through a Contraction
3. Numerical Model and Flow Simulations
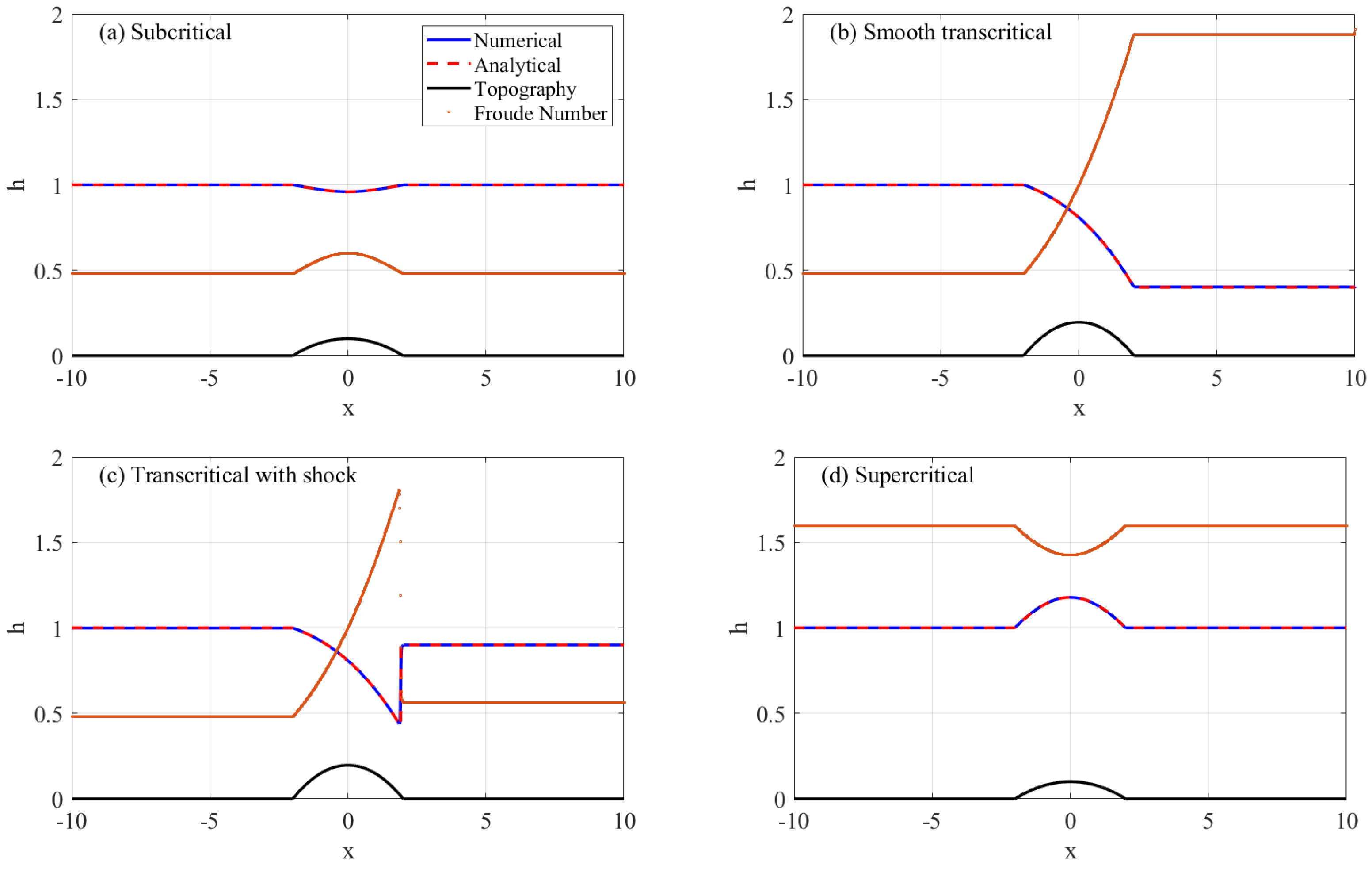
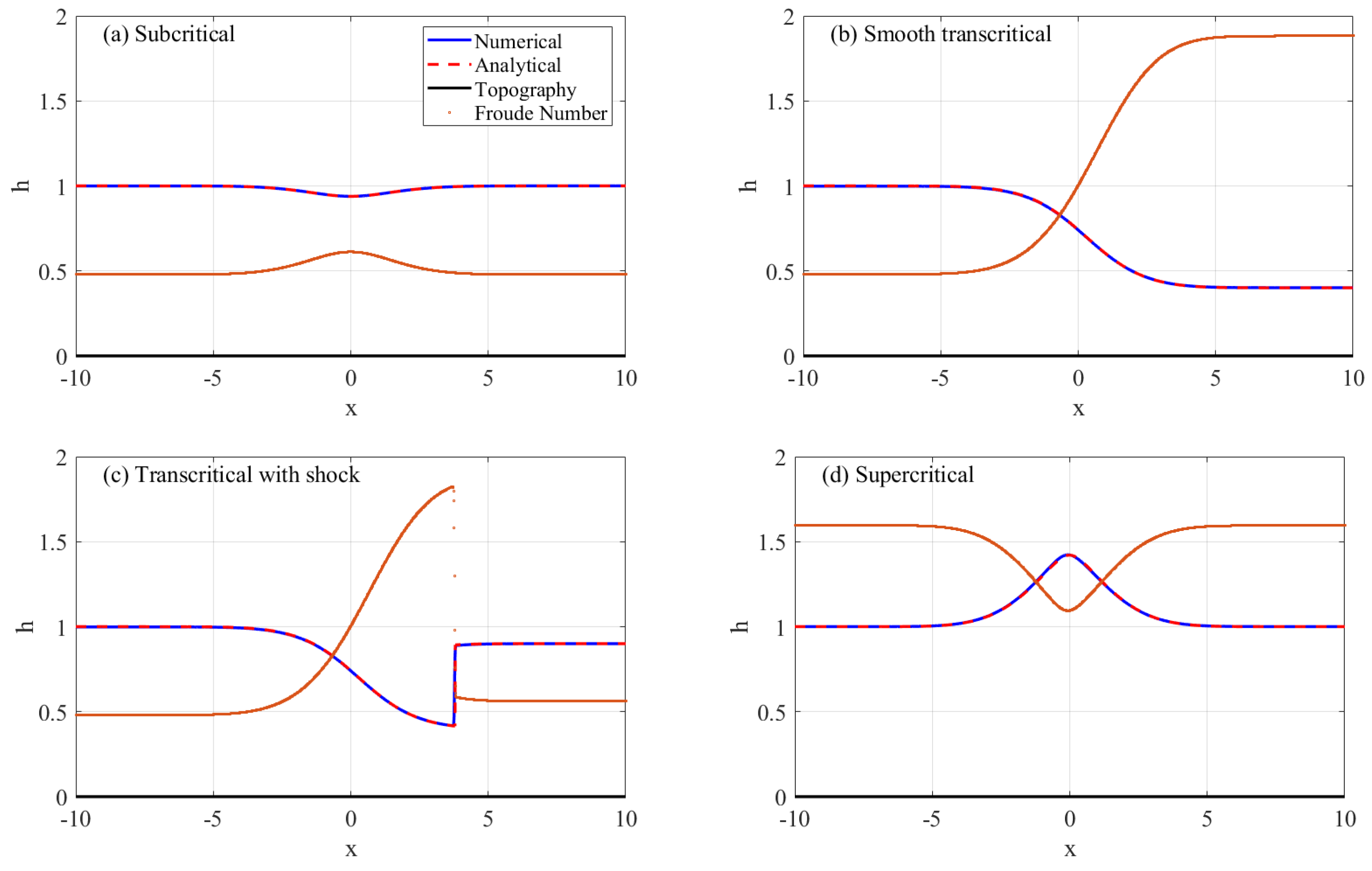
3.1. Simulation of Flow over a Bump
3.1.1. Example 1: Subcritical Steady Flow
3.1.2. Example 2: Smooth Transcritical Steady Flow
3.1.3. Example 3: Transcritical Steady Flow with a Shock
3.1.4. Example 4: Supercritical Steady Flow
3.2. Simulation of Flow through a Contraction
3.2.1. Example 1: Subcritical Steady Flow
3.2.2. Example 2: Smooth Transcritical Steady Flow
3.2.3. Example 3: Transcritical Steady Flow with a Shock
3.2.4. Example 4: Supercritical Steady Flow
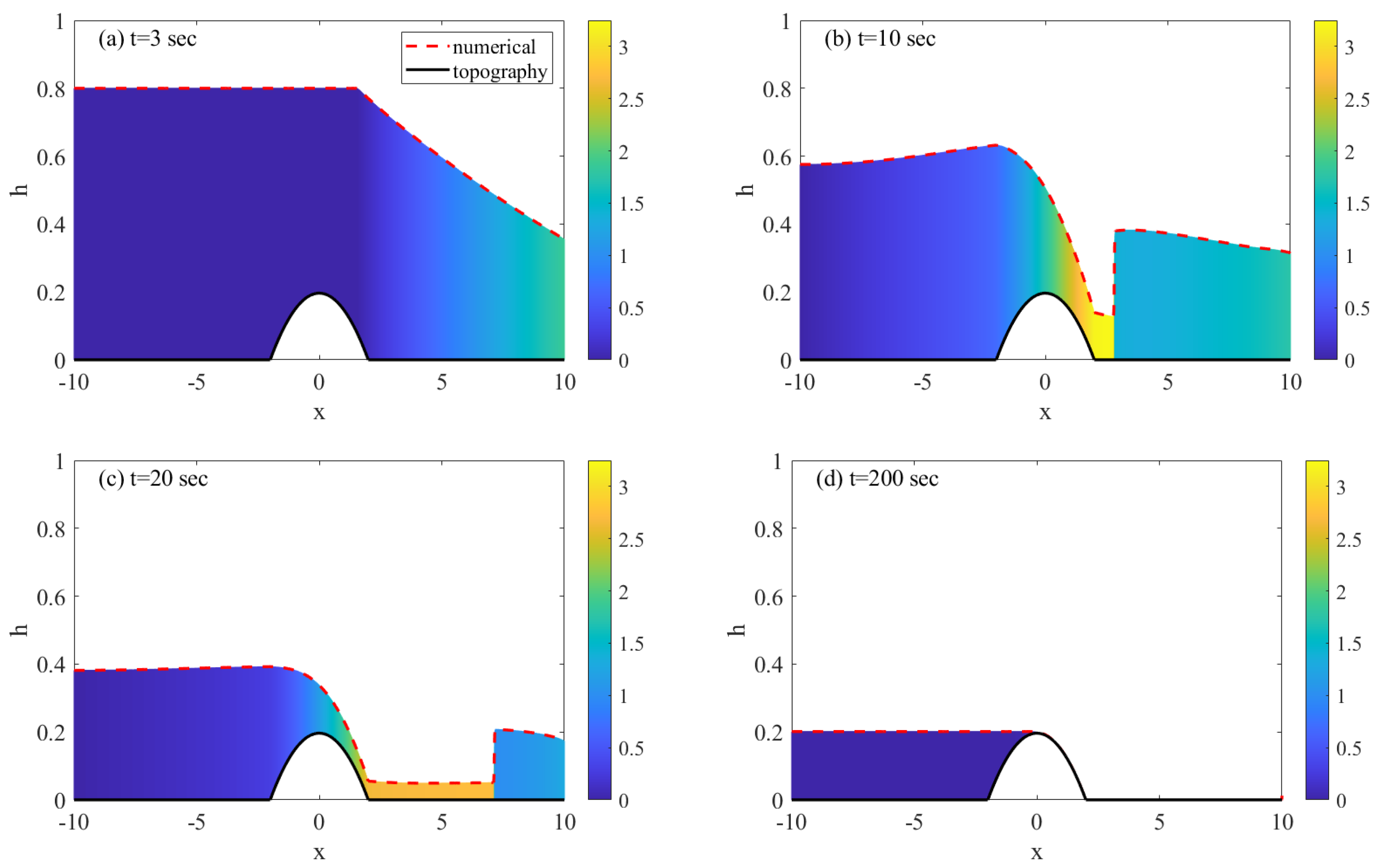
3.3. Simulation of Flow over a Bump and through a Contraction
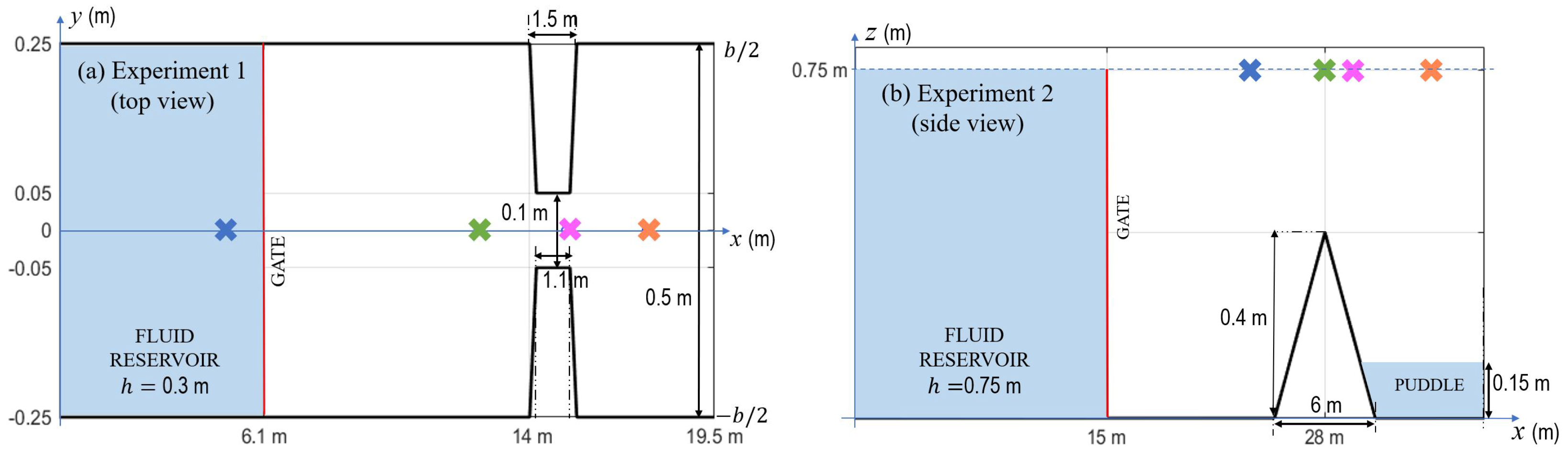
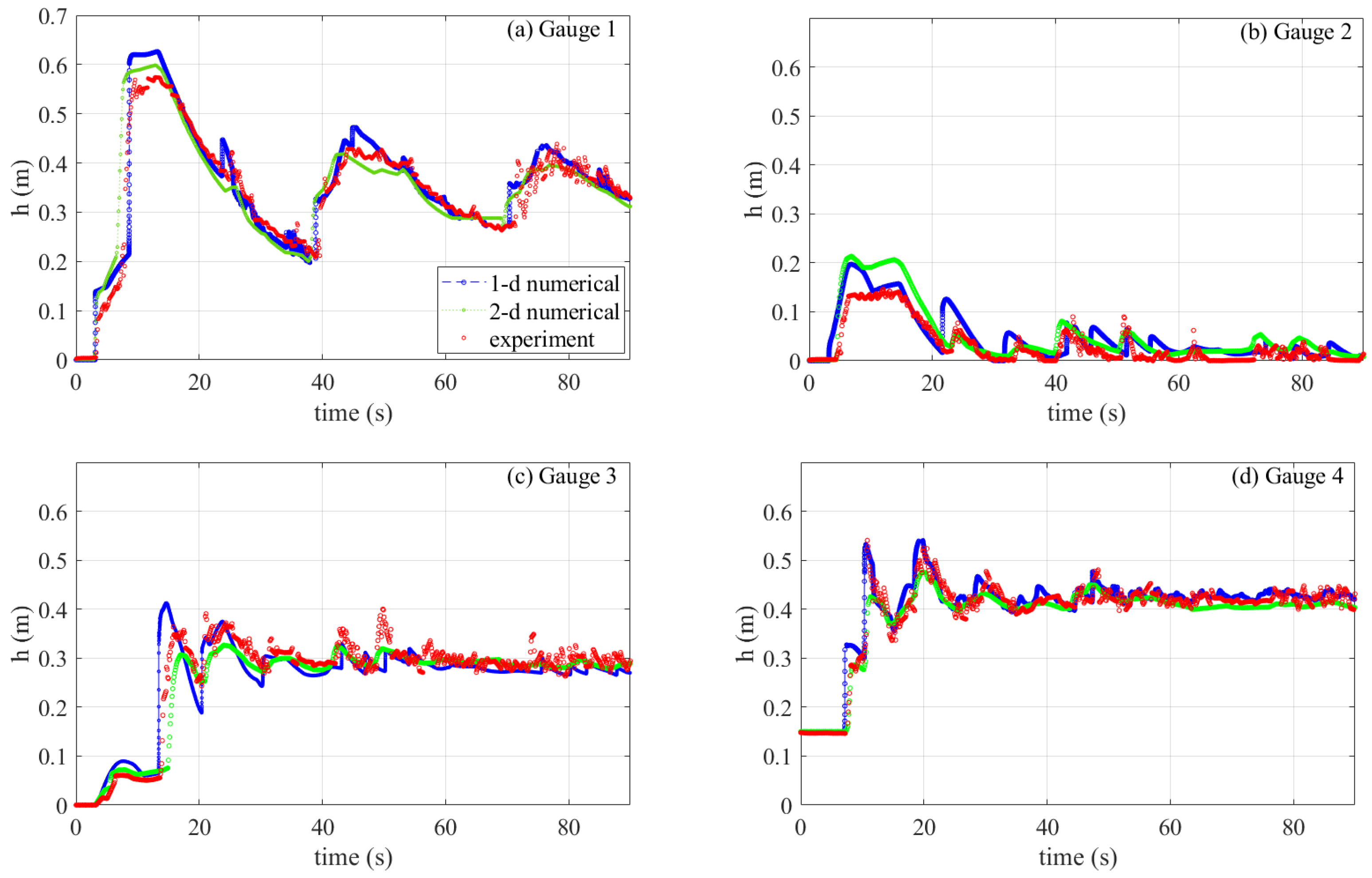
4. Experimental Validation
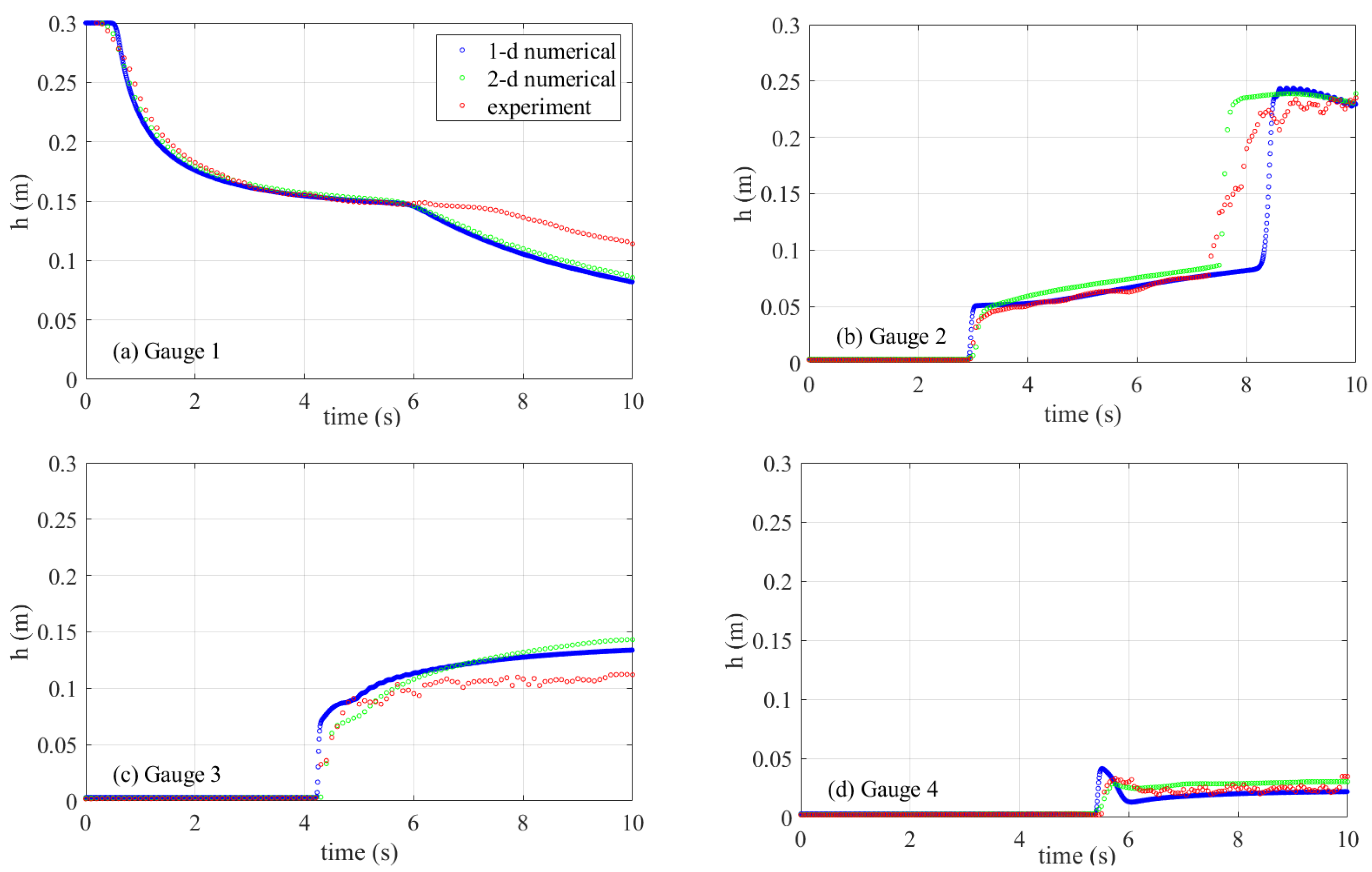
4.1. Dam Break Flow in a Channel with a Contraction
4.2. Dam Break Flow in a Channel with a Triangular Obstacle
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MCS | Momentum-conserving staggered grid |
References
- Eymard, R.; Gallouët, T.; Herbin, R. Finite volume methods. Handb. Numer. Anal. 2000, 7, 713–1018. [Google Scholar]
- LeVeque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002; Volume 31. [Google Scholar]
- Alias, N.A.; Liang, Q.; Kesserwani, G. A Godunov-type scheme for modelling 1D channel flow with varying width and topography. Comput. Fluids 2011, 46, 88–93. [Google Scholar] [CrossRef]
- Gouta, N.; Maurel, F. A finite volume solver for 1D shallow-water equations applied to an actual river. Int. J. Numer. Methods Fluids 2002, 38, 1–19. [Google Scholar] [CrossRef]
- Wang, G.T.; Chen, S.; Boll, J. A semianalytical solution of the Saint-Venant equations for channel flood routing. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Moussa, R.; Bocquillon, C. Approximation zones of the Saint-Venant equations f flood routing with overbank flow. Hydrol. Earth Syst. Sci. 2000, 4, 251–260. [Google Scholar] [CrossRef]
- Liu, H.; Wang, H.; Liu, S.; Hu, C.; Ding, Y.; Zhang, J. Lattice Boltzmann method for the Saint–Venant equations. J. Hydrol. 2015, 524, 411–416. [Google Scholar] [CrossRef]
- Hernández-Dueñas, G.; Karni, S. Shallow Water Flows in Channels. J. Sci. Comput. 2011, 48, 190–208. [Google Scholar] [CrossRef]
- Akbari, G.; Firoozi, B. Implicit and explicit numerical solution of Saint-Venant equations for simulating flood wave in natural rivers. In Proceedings of the 5th National Congress on Civil Engineering, Mashhad, Iran, 4–6 May 2010; p. 7. [Google Scholar]
- Catella, M.; Paris, E.; Solari, L. Conservative scheme for numerical modeling of flow in natural geometry. J. Hydraul. Eng. 2008, 134, 736–748. [Google Scholar] [CrossRef]
- Ying, X.; Khan, A.A.; Wang, S.S. Upwind conservative scheme for the Saint Venant equations. J. Hydraul. Eng. 2004, 130, 977–987. [Google Scholar] [CrossRef]
- Sanders, B.F. High-resolution and non-oscillatory solution of the St. Venant equations in non-rectangular and non-prismatic channels. J. Hydraul. Res. 2001, 39, 321–330. [Google Scholar] [CrossRef]
- Liu, X. A steady-state-preserving scheme for shallow water flows in channels. J. Comput. Phys. 2020, 423, 109803. [Google Scholar] [CrossRef]
- Pudjaprasetya, S.; Magdalena, I. Momentum conservative scheme for dam break and wave run up simulations. East Asian J. Appl. Math. 2014, 4, 152–165. [Google Scholar] [CrossRef]
- Erwina, N.; Adytia, D.; Pudjaprasetya, R.; Nuryaman, T. Staggered Conservative Scheme for 2-Dimensional Shallow Water Flows. Fluids 2020, 5, 149. [Google Scholar] [CrossRef]
- Stelling, G.S.; Duinmeijer, S.A. A staggered conservative scheme for every Froude number in rapidly varied shallow water flows. Int. J. Numer. Methods Fluids 2003, 43, 1329–1354. [Google Scholar] [CrossRef]
- Liang, Q. Flood simulation using a well-balanced shallow flow model. J. Hydraul. Eng. 2010, 136, 669–675. [Google Scholar] [CrossRef]

| Case | Flow Type | RMSE-Error |
|---|---|---|
| Flow | Subcritical | 0.00016 |
| over | Supercritical | 0.00034 |
| a bump | Smooth transcritcal | 0.00111 |
| Transcritical with shock | 0.00641 | |
| Flow | Subcritical | 0.00008 |
| through | Supercritical | 0.00209 |
| a contraction | Smooth transcritical | 0.00114 |
| Transcritical with shock | 0.01211 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swastika, P.V.; Pudjaprasetya, S.R.; Wiryanto, L.H.; Hadiarti, R.N. A Momentum-Conserving Scheme for Flow Simulation in 1D Channel with Obstacle and Contraction. Fluids 2021, 6, 26. https://doi.org/10.3390/fluids6010026
Swastika PV, Pudjaprasetya SR, Wiryanto LH, Hadiarti RN. A Momentum-Conserving Scheme for Flow Simulation in 1D Channel with Obstacle and Contraction. Fluids. 2021; 6(1):26. https://doi.org/10.3390/fluids6010026
Chicago/Turabian StyleSwastika, Putu Veri, Sri Redjeki Pudjaprasetya, Leo Hari Wiryanto, and Revi Nurfathhiyah Hadiarti. 2021. "A Momentum-Conserving Scheme for Flow Simulation in 1D Channel with Obstacle and Contraction" Fluids 6, no. 1: 26. https://doi.org/10.3390/fluids6010026
APA StyleSwastika, P. V., Pudjaprasetya, S. R., Wiryanto, L. H., & Hadiarti, R. N. (2021). A Momentum-Conserving Scheme for Flow Simulation in 1D Channel with Obstacle and Contraction. Fluids, 6(1), 26. https://doi.org/10.3390/fluids6010026





