On the Optimal Control of Stationary Fluid–Structure Interaction Systems
Abstract
1. Introduction
2. Mathematical Model
Optimality System
- On we have andwith ;
- On we have which implies or .
3. Numerical Implementation and Results
| Algorithm 1 Description of the Steepest Descent algorithm. | |
| 1. Set a state satisfying (16) and (17) | ▹ Setup of the state - Reference case |
| 2. Compute the functional in (20) | |
| 3. Set | |
| fordo | |
| 4. Solve the system (46) and (47) to obtain the adjoint state | |
| 5. Compute the control update with (42)–(44) | |
| 6. Set | |
| while do | ▹ Line search |
| 7. Set | |
| 8. Solve (16) and (17) for the state with | |
| if then | |
| Line search not successful | ▹ End of the algorithm |
| end if | |
| end while | |
| end for | |
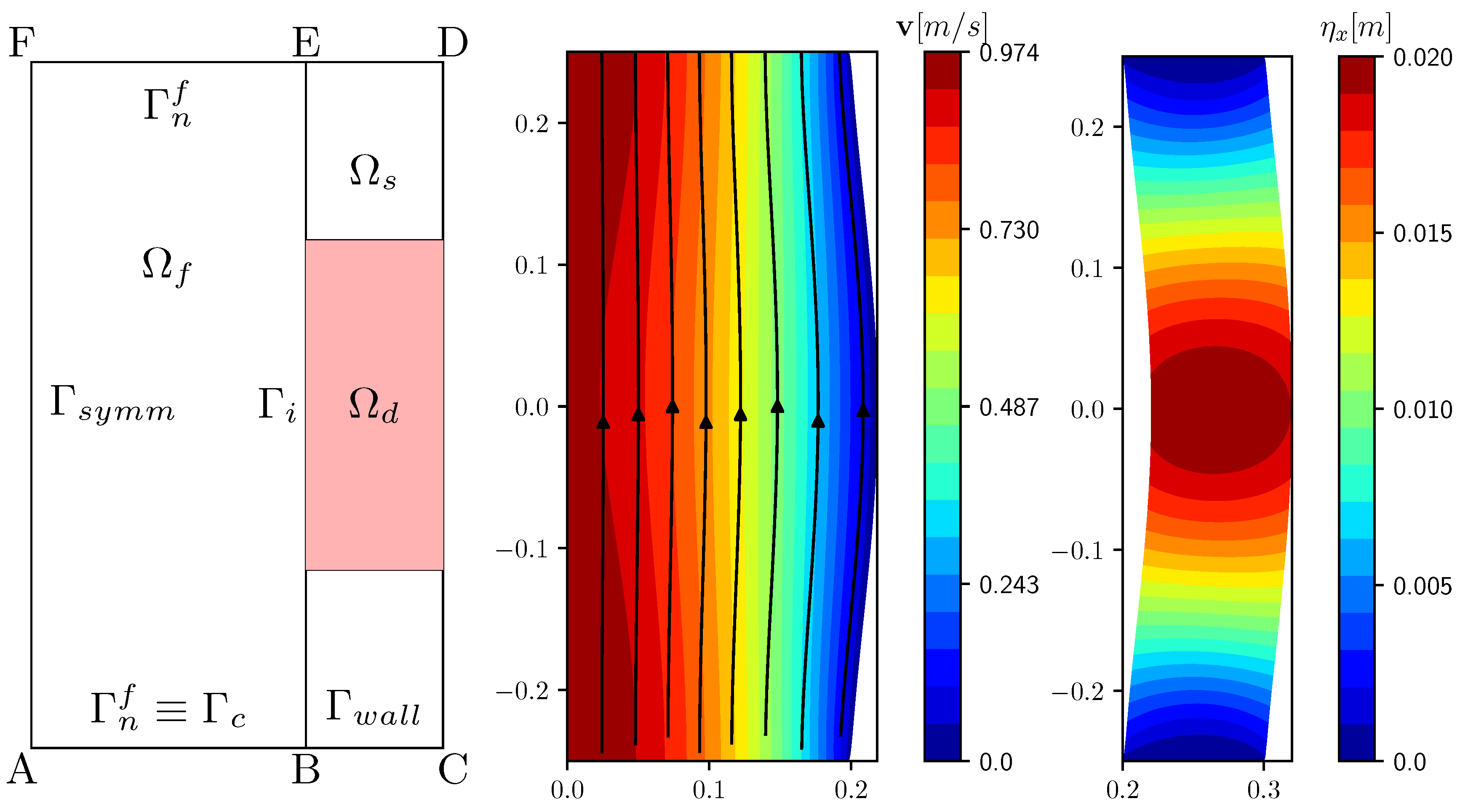
3.1. Test Case Configuration
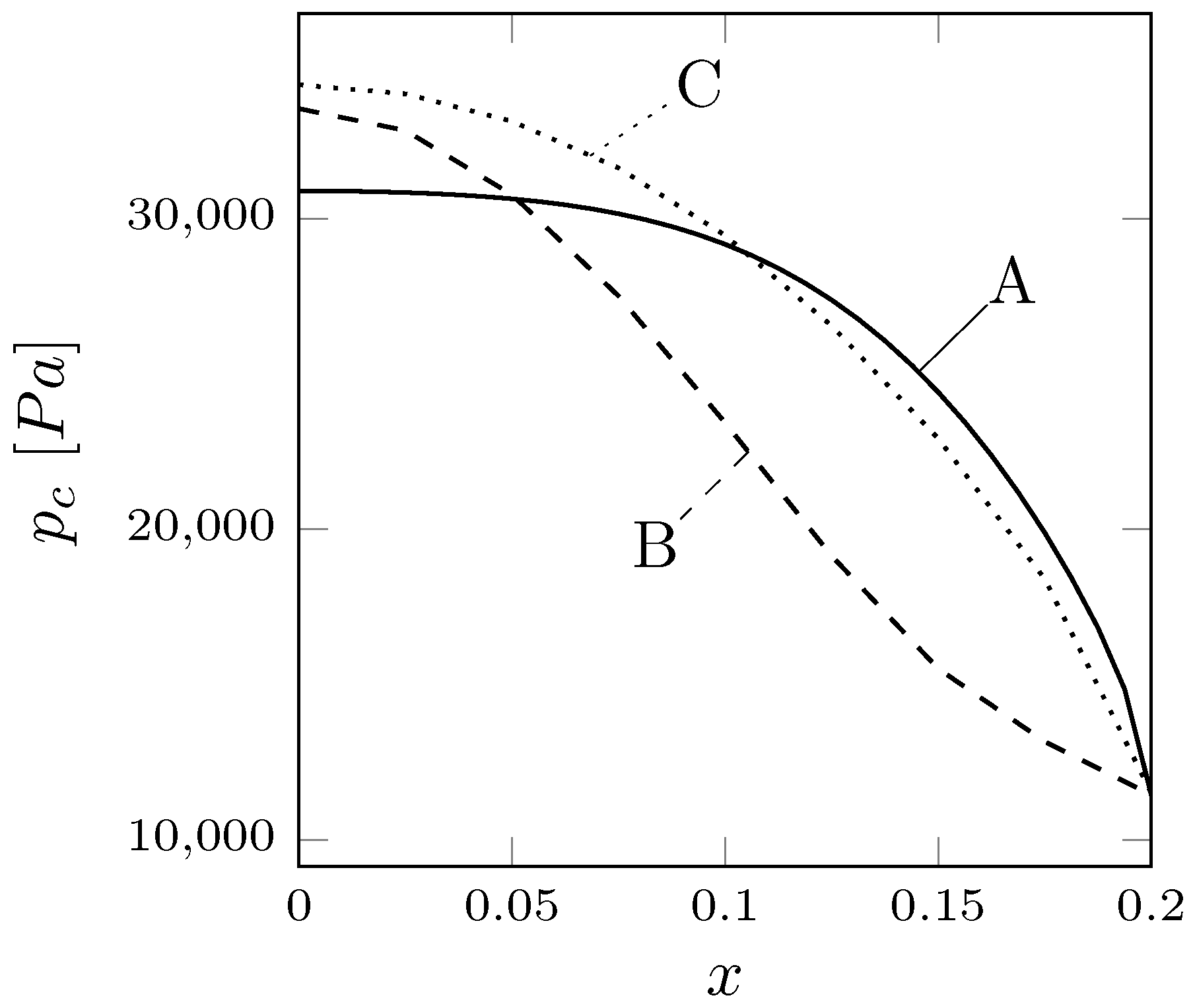
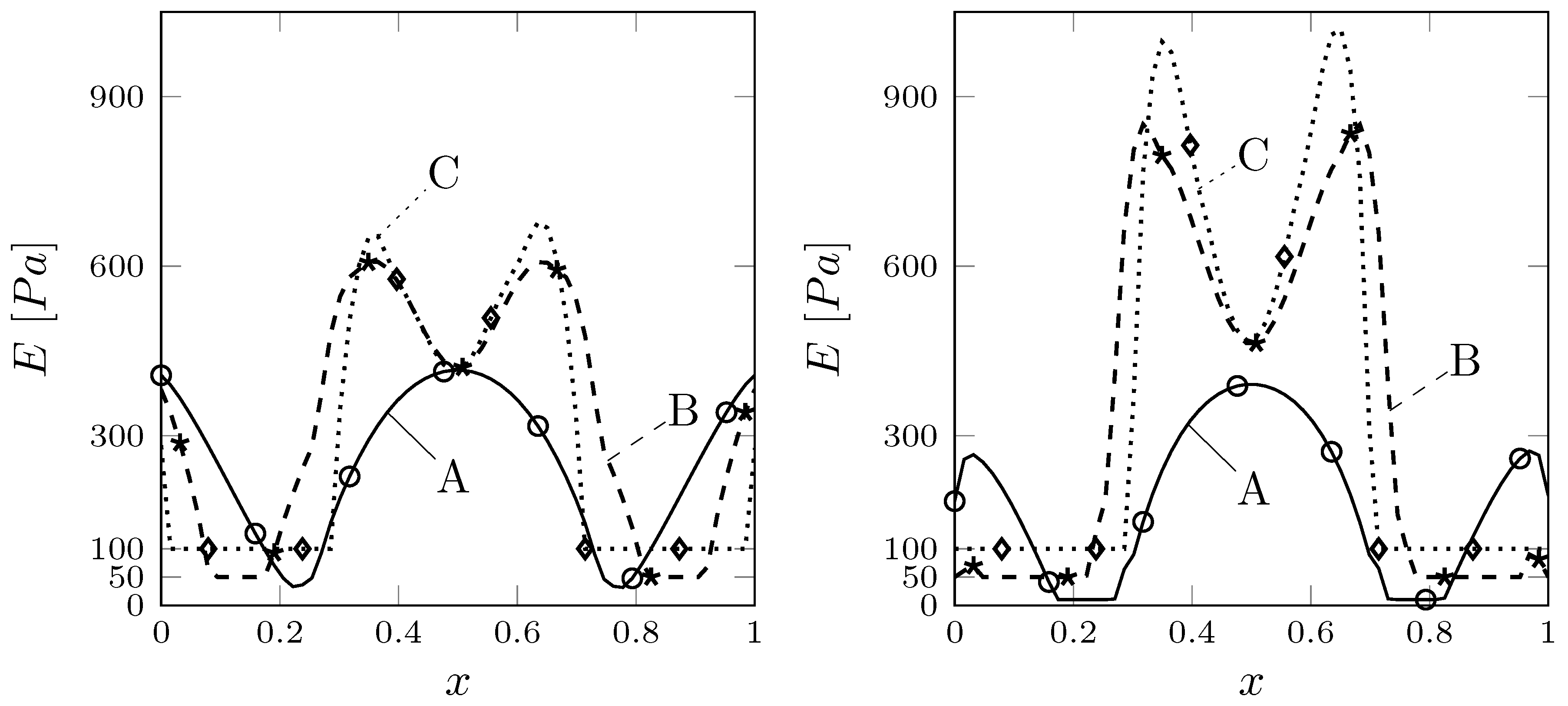
3.2. Pressure Boundary Control
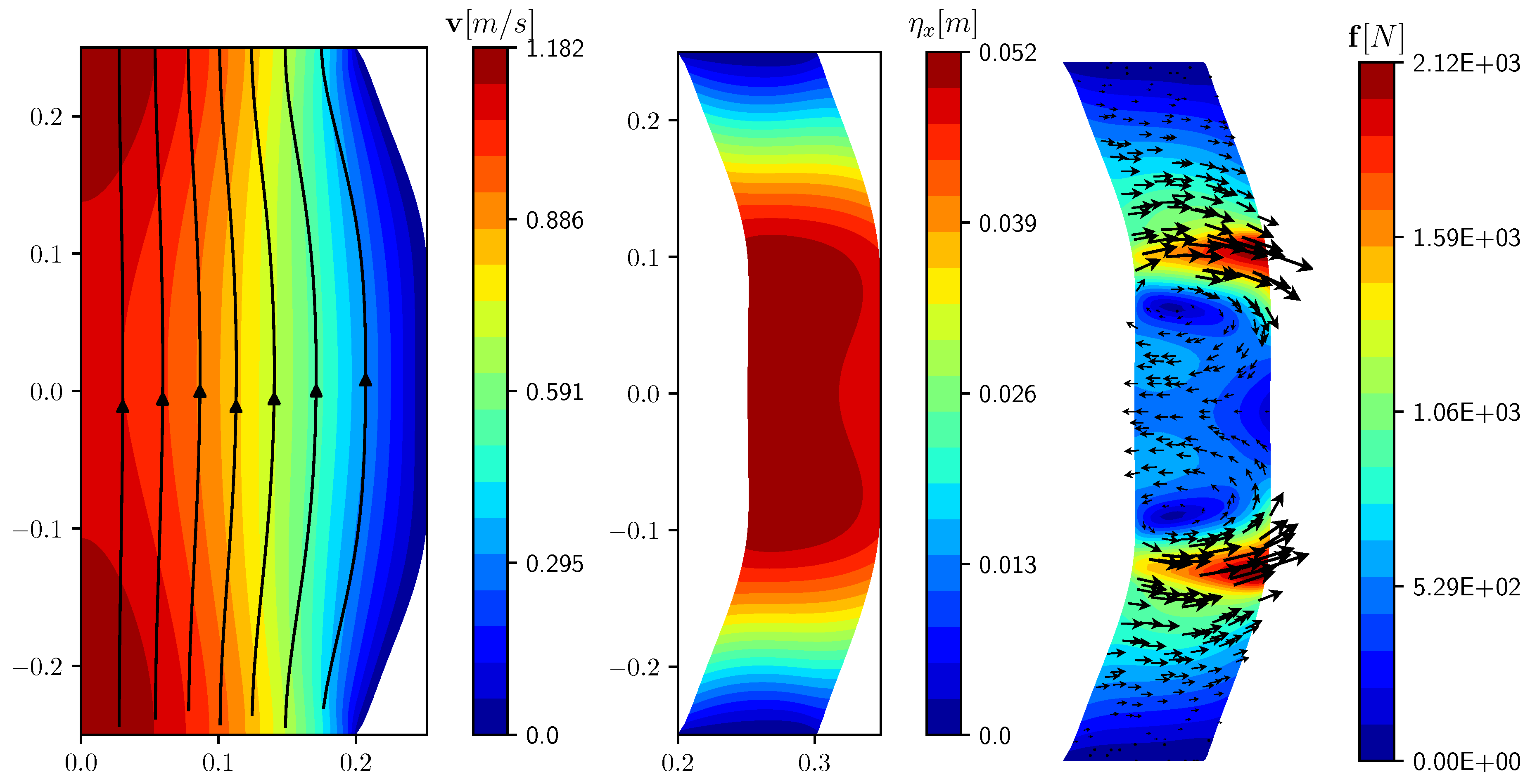
3.3. Distributed Control
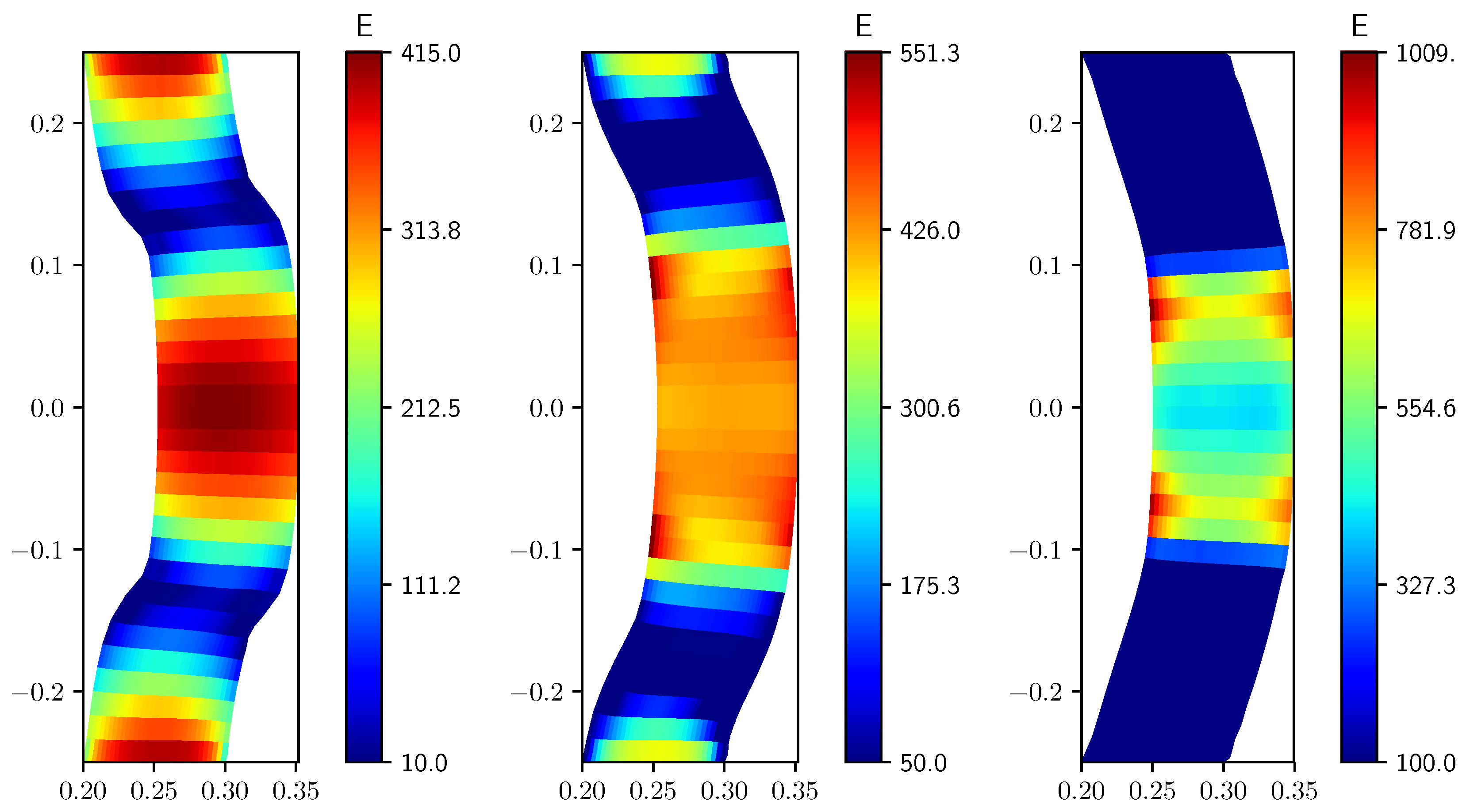
3.4. Parameter Estimation Problem
Control with Gradient Regularization
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gunzburger, M.D. Perspectives in Flow Control and Optimization; Siam: Philadelphia, PA, USA, 2003; Volume 5. [Google Scholar]
- Maute, K.; Nikbay, M.; Farhat, C. Sensitivity analysis and design optimization of three-dimensional non-linear aeroelastic systems by the adjoint method. Int. J. Numer. Methods. Eng. 2003, 56, 911–933. [Google Scholar] [CrossRef]
- Lund, E.; Møller, H.; Jakobsen, L.A. Shape design optimization of stationary fluid–structure interaction problems with large displacements and turbulence. Struct. Multidiscipl. Optim. 2003, 25, 383–392. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Takizawa, K.; Tezduyar, T. Computational Fluid-Structure Interaction; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Bungartz, H.J.; Schäfer, M. Fluid-Structure Interaction: Modelling, Simulation, Optimisation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 53. [Google Scholar]
- Bodnár, T.; Galdi, G.P.; Nečasová, Š. Fluid-Structure Interaction and Biomedical Applications; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Formaggia, L.; Quarteroni, A.; Veneziani, A. Cardiovascular Mathematics: Modeling and Simulation of the Circulatory System; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; Volume 1. [Google Scholar]
- Degroote, J.; Bathe, K.J.; Vierendeels, J. Performance of a new partitioned procedure versus a monolithic procedure in fluid—Structure interaction. Comput. Struct. 2009, 87, 793–801. [Google Scholar] [CrossRef]
- Habchi, C.; Russeil, S.; Bougeard, D.; Harion, J.L.; Lemenand, T.; Ghanem, A.; Della Valle, D.; Peerhossaini, H. Partitioned solver for strongly coupled fluid–structure interaction. Comput. Fluids 2013, 71, 306–319. [Google Scholar] [CrossRef]
- Nobile, F.; Vergara, C. Partitioned algorithms for fluid–structure interaction problems in haemodynamics. Milan J. Math. 2012, 80, 443–467. [Google Scholar] [CrossRef]
- Causin, P.; Gerbeau, J.F.; Nobile, F. Added-mass effect in the design of partitioned algorithms for fluid–structure problems. Comput. Methods Appl. Mech. Eng. 2005, 194, 4506–4527. [Google Scholar] [CrossRef]
- Brenner, S.; Scott, R. The Mathematical Theory of Finite Element Methods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; Volume 15. [Google Scholar]
- Bramble, J.H. Multigrid Methods; CRC Press: Boca Raton, FL, USA, 1993; Volume 294. [Google Scholar]
- Turek, S.; Hron, J.; Madlik, M.; Razzaq, M.; Wobker, H.; Acker, J.F. Numerical simulation and benchmarking of a monolithic multigrid solver for fluid–structure interaction problems with application to hemodynamics. In Fluid Structure Interaction II; Springer: Berlin/Heidelberg, Germany, 2011; pp. 193–220. [Google Scholar]
- Richter, T. A monolithic multigrid solver for 3d fluid–structure interaction problems. Siam J. 2011. [Google Scholar] [CrossRef]
- Aulisa, E.; Bnà, S.; Bornia, G. A monolithic ALE Newton–Krylov solver with multigrid-Richardson–Schwarz preconditioning for incompressible fluid–structure interaction. Comput. Fluids 2018, 174, 213–228. [Google Scholar] [CrossRef]
- Failer, L.; Richter, T. A parallel Newton multigrid framework for monolithic fluid–structure interactions. J. Sci. Comput. 2020, 82, 28. [Google Scholar] [CrossRef]
- Failer, L.; Meidner, D.; Vexler, B. Optimal Control of a Linear Unsteady Fluid–Structure Interaction Problem. J. Optim. Theory Appl. 2016, 170, 1–27. [Google Scholar] [CrossRef]
- Perego, M.; Veneziani, A.; Vergara, C. A variational approach for estimating the compliance of the cardiovascular tissue: An inverse fluid–structure interaction problem. SIAM J. Sci. Comput. 2011, 33, 1181–1211. [Google Scholar] [CrossRef]
- Wick, T.; Wollner, W. Optimization with nonstationary, nonlinear monolithic fluid–structure interaction. Int. J. Numer. Methods Eng. 2020. [Google Scholar] [CrossRef]
- Chirco, L.; Manservisi, S. An adjoint based pressure boundary optimal control approach for fluid–structure interaction problems. Comput. Fluids 2019, 182, 118–127. [Google Scholar] [CrossRef]
- Richter, T.; Wick, T. Optimal control and parameter estimation for stationary fluid–structure interaction problems. SIAM J. Sci. Comput. 2013, 35, B1085–B1104. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Hsu, M.C.; Bement, M. Adjoint-based control of fluid–structure interaction for computational steering applications. Procedia Comput. Sci. 2013, 18, 1989–1998. [Google Scholar] [CrossRef]
- Hron, J.; Turek, S. A monolithic FEM/multigrid solver for an ALE formulation of fluid–structure interaction with applications in biomechanics. In Fluid-Structure Interaction; Springer: Berlin/Heidelberg, Germany, 2006; pp. 146–170. [Google Scholar]
- Chirco, L.; Da Vià, R.; Manservisi, S. An optimal control method for fluid structure interaction systems via adjoint boundary pressure. J. Phys. Conf. Ser. 2017, 923, 012026. [Google Scholar] [CrossRef]
- Anzengruber, S.W.; Ramlau, R. Morozov’s discrepancy principle for Tikhonov-type functionals with nonlinear operators. Inverse Probl. 2009, 26, 025001. [Google Scholar] [CrossRef]
- Manservisi, S. An optimal control approach to an inverse nonlinear elastic shell problem applied to car windscreen design. Comput. Meth. Appl. Mech. Eng. 2000, 189, 463–480. [Google Scholar] [CrossRef]
- Manservisi, S.; Gunzburger, M. Variational inequality formulation of an inverse elasticity problem. Appl. Numer. Math. 2000, 34, 99–126. [Google Scholar] [CrossRef]
- Sokolowski, J.; Zolesio, J.P. Introduction to shape optimization. In Introduction to Shape Optimization; Springer: Berlin/Heidelberg, Germany, 1992; pp. 5–12. [Google Scholar]
- Armijo, L. Minimization of functions having Lipschitz continuous first partial derivatives. Pacific J. Math. 1966, 16, 1–3. [Google Scholar] [CrossRef]
- FEMuS—Multigrid Finite Element Code. Available online: https://github.com/FemusPlatform/femus (accessed on 5 August 2020).
- Aulisa, E.; Manservisi, S.; Seshaiyer, P. A computational multilevel approach for solving 2D Navier–Stokes equations over non-matching grids. Comput. Meth. Appl. Mech. Eng. 2006, 195, 4604–4616. [Google Scholar] [CrossRef]
- Cerroni, D.; Manservisi, S.; Menghini, F. An improved monolithic multigrid Fluid- Structure Interaction solver with a new moving mesh technique. Int. J. Math. Model. Meth. Appl. Sci. 2015, 9, 227–234. [Google Scholar]
- Girault, V.; Raviart, P.A. Finite Element Methods for Navier-Stokes Equations: Theory and Algorithms; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 5. [Google Scholar]



| ∞ | 0.0180 | |
| 0.0202 | ||
| 0.0469 | ||
| 0.0497 |
| ∞ | ||||
|---|---|---|---|---|
| 1292.4 | 25.854 | 5.8864 | 2.3875 | |
| 0.0180 | 0.0494 | 0.0498 | 0.0499 |
| Level | 10 | 50 | 100 | 200 | NC |
|---|---|---|---|---|---|
| 2 | 1.63 | 2.08 | 1.82 | 2.73 | 1.23 |
| 3 | 1.41 | 1.12 | 1.53 | 2.58 | 1.23 |
| 4 | 1.23 | 1.62 | 1.18 | 2.58 | 1.23 |
| 5 | 1.19 | 9.17 | 1.16 | 2.52 | 1.23 |
| 10 | 50 | 100 | 200 | NC | |
|---|---|---|---|---|---|
| 3.29 | 3.29 | 3.51 | 2.68 | 1.23 | |
| 9.79 | 9.20 | 3.22 | 2.68 | 1.23 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chirco, L.; Manservisi, S. On the Optimal Control of Stationary Fluid–Structure Interaction Systems. Fluids 2020, 5, 144. https://doi.org/10.3390/fluids5030144
Chirco L, Manservisi S. On the Optimal Control of Stationary Fluid–Structure Interaction Systems. Fluids. 2020; 5(3):144. https://doi.org/10.3390/fluids5030144
Chicago/Turabian StyleChirco, Leonardo, and Sandro Manservisi. 2020. "On the Optimal Control of Stationary Fluid–Structure Interaction Systems" Fluids 5, no. 3: 144. https://doi.org/10.3390/fluids5030144
APA StyleChirco, L., & Manservisi, S. (2020). On the Optimal Control of Stationary Fluid–Structure Interaction Systems. Fluids, 5(3), 144. https://doi.org/10.3390/fluids5030144






