Altimetry-Based Diagnosis of Deep-Reaching Sub-Mesoscale Ocean Fronts
Abstract
1. Introduction
2. Materials and Methods
2.1. LLC4320 Numerical Simulation
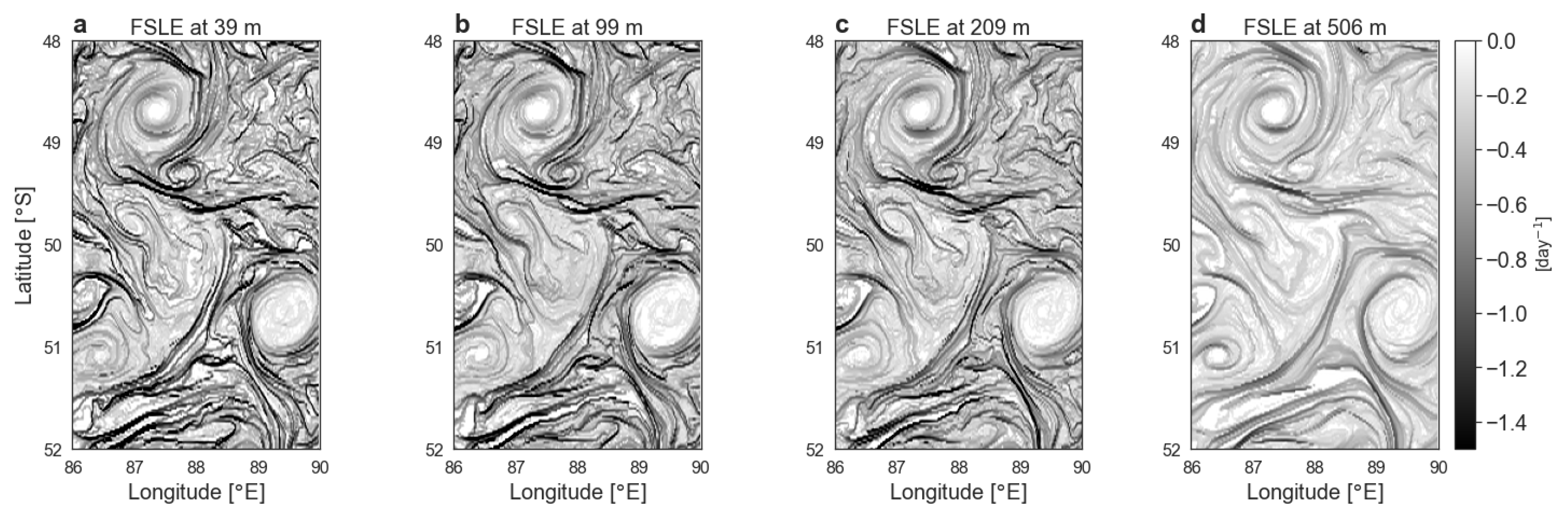
Finite-Size Lyapunov Exponent
2.2. Altimetry Data
2.3. Southern Elephant Seal Dataset
2.3.1. Buoyancy
2.3.2. Vertical Velocities
3. Numerical Results
3.1. Physical Context
3.2. Frontal Dynamics
3.3. Recovering Frontal Dynamics at Depth from Finite-Size Lyapunov Exponent at the Surface
4. Application to In Situ Data
5. Discussion
- A1.
- We recover the orientation of sampled lateral buoyancy gradients, and subsequently their correct magnitude through a normalization scheme. This normalization takes into account the angle between the sampling platform and the front’s orientation deduced from the FSLE’s eigenvector.
- A2.
- We diagnose vertical velocities from the normalized lateral buoyancy gradients using a 2-D QG version of the omega equation.
- B1.
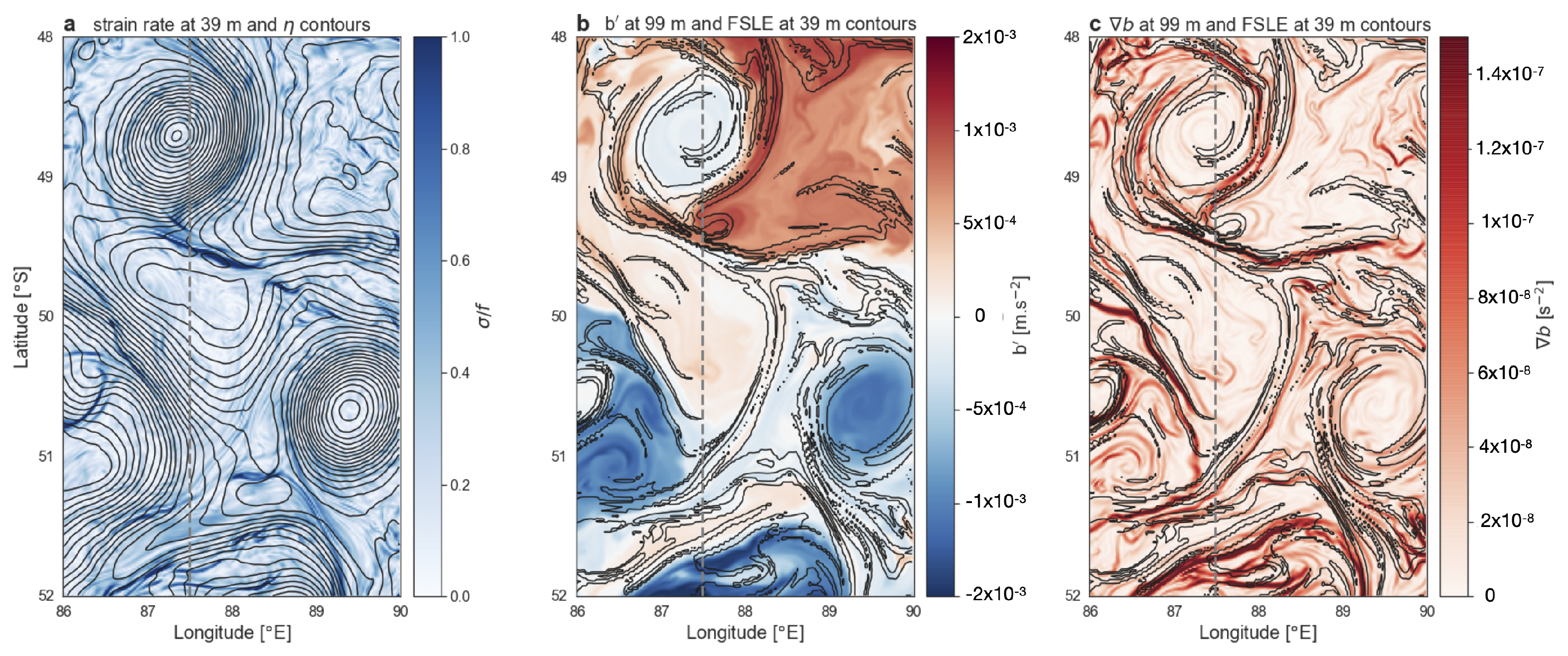
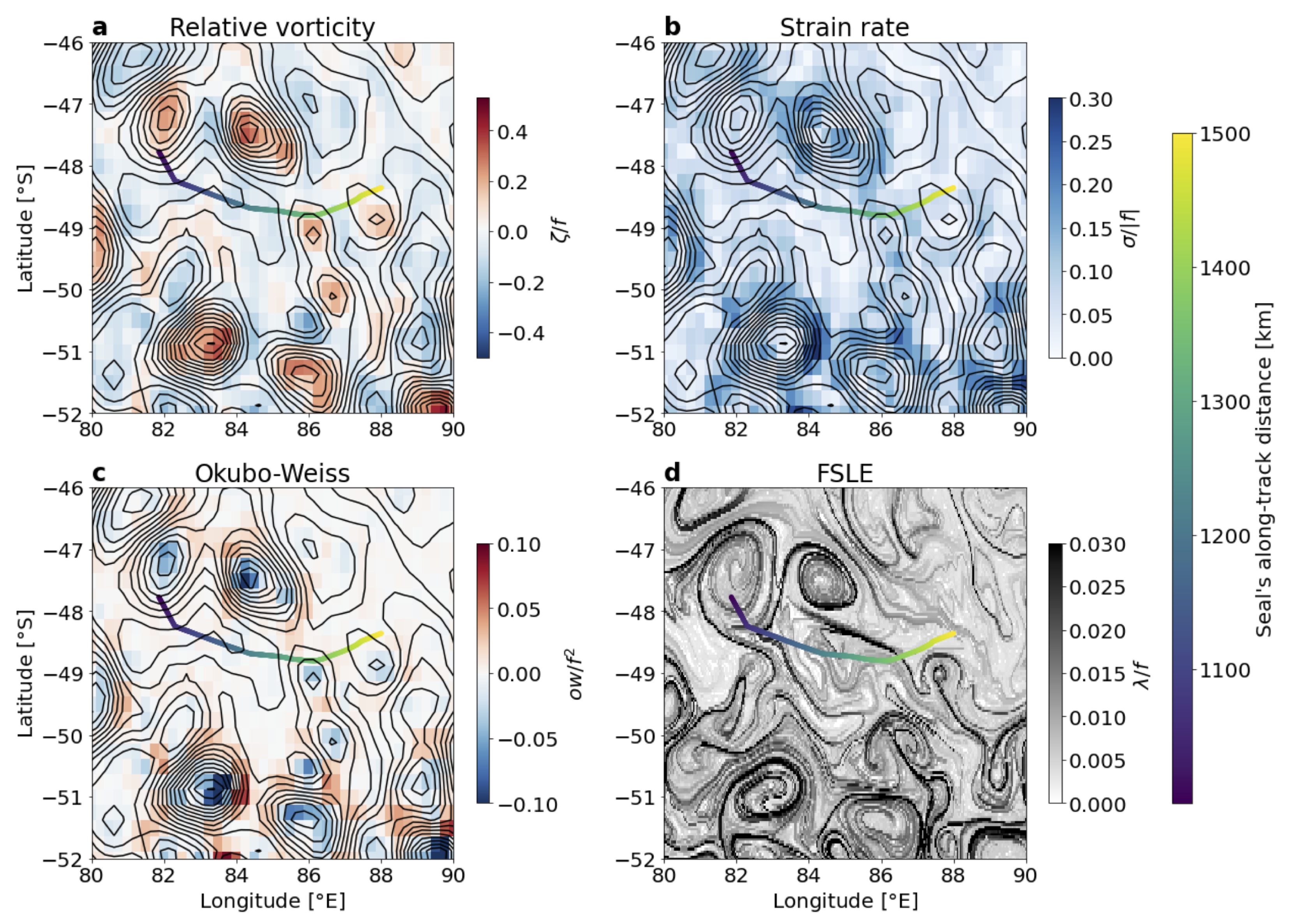
- Identify areas of strong background strain from near-real time satellite observations of geostrophic currents (i.e., when the Okubo-Weiss quantity is positive, Figure 11c).
- B2.
- Use near-real time AVISO-FSLE products to identify the location and orientation of FSLE filaments (Figure 11d).
- B3.
- Pilot the ship/robot perpendicular to this orientation. One should then perpendicularly cross sub-mesoscale fronts embedded in the background flow.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
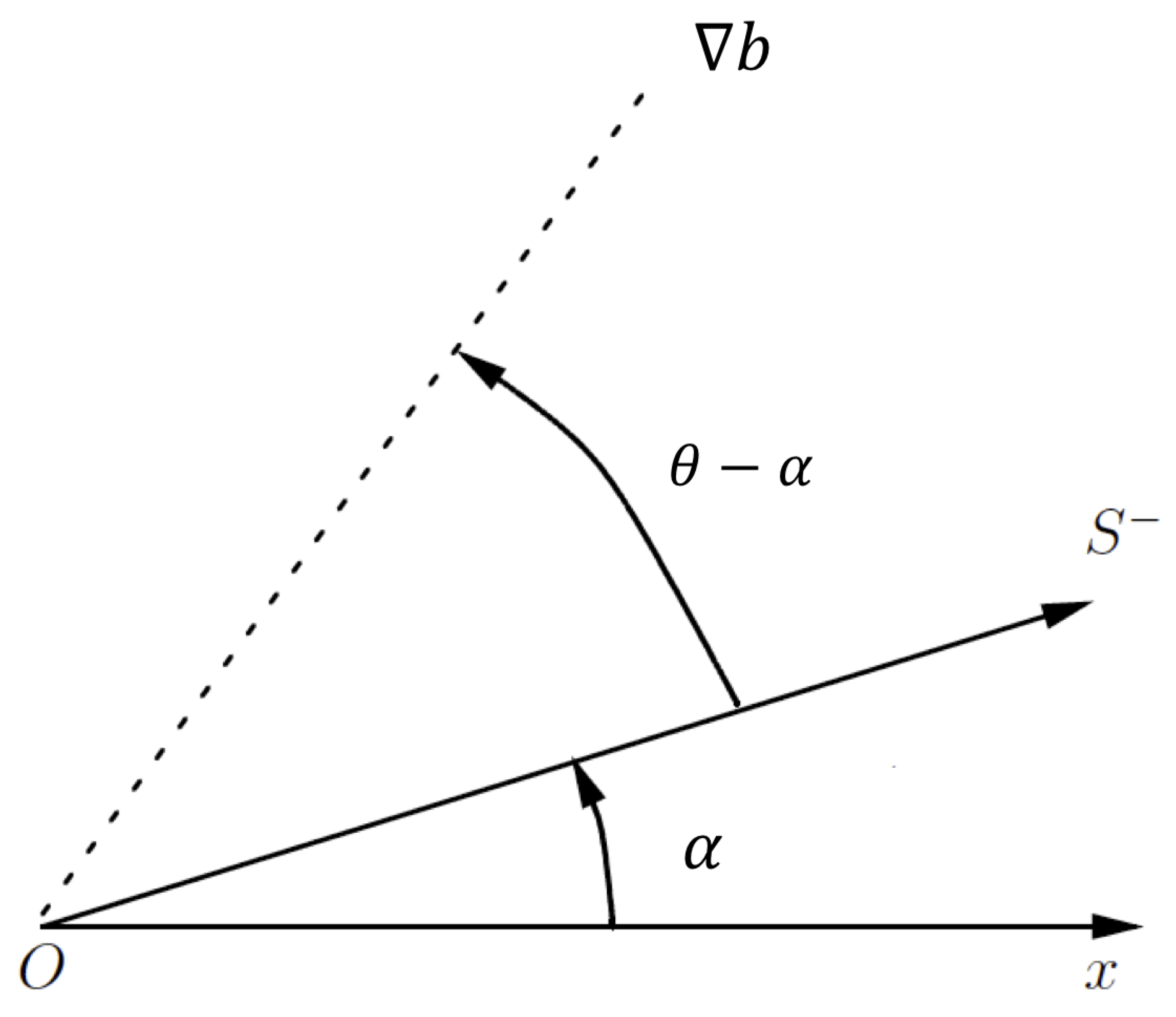
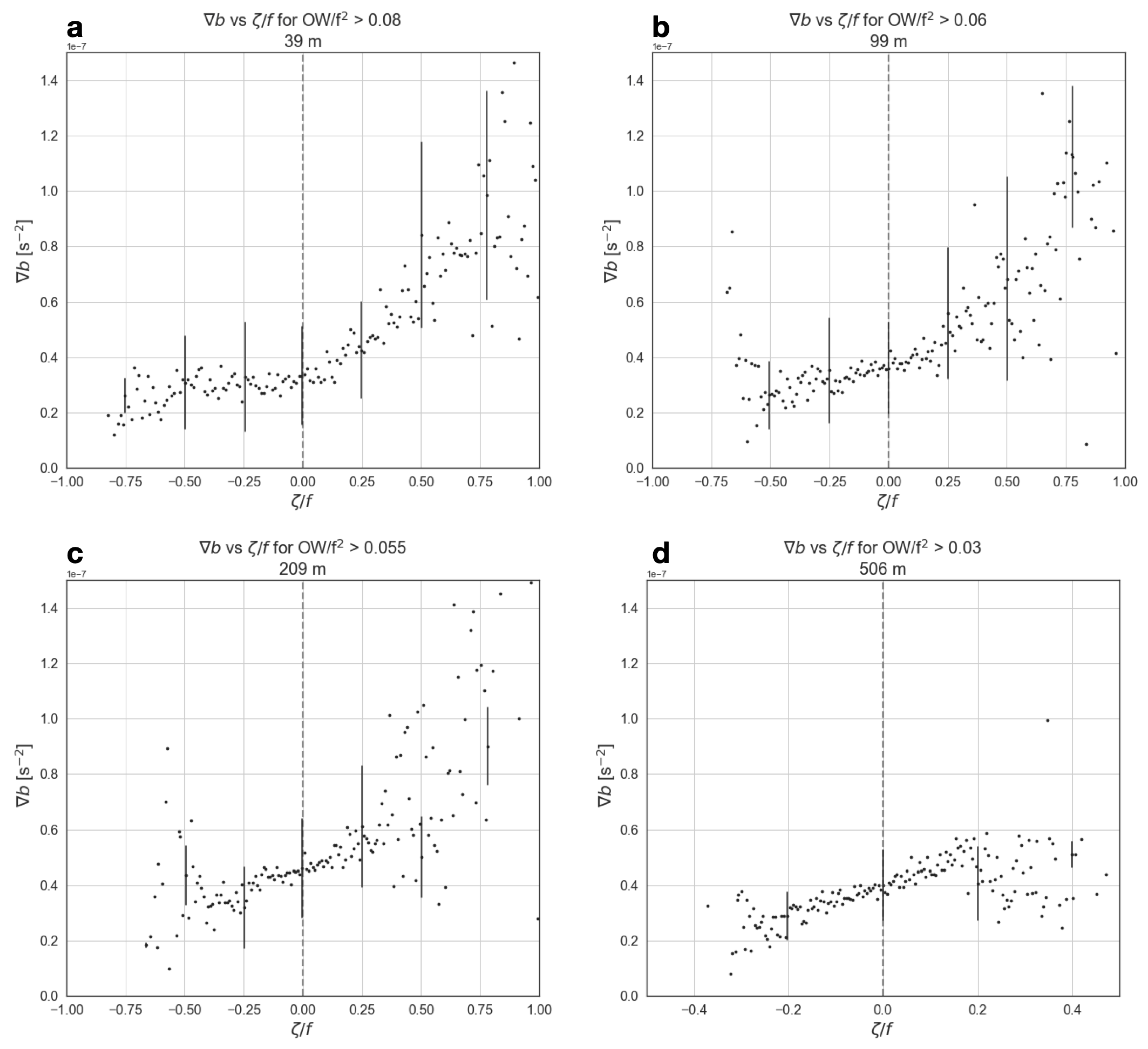
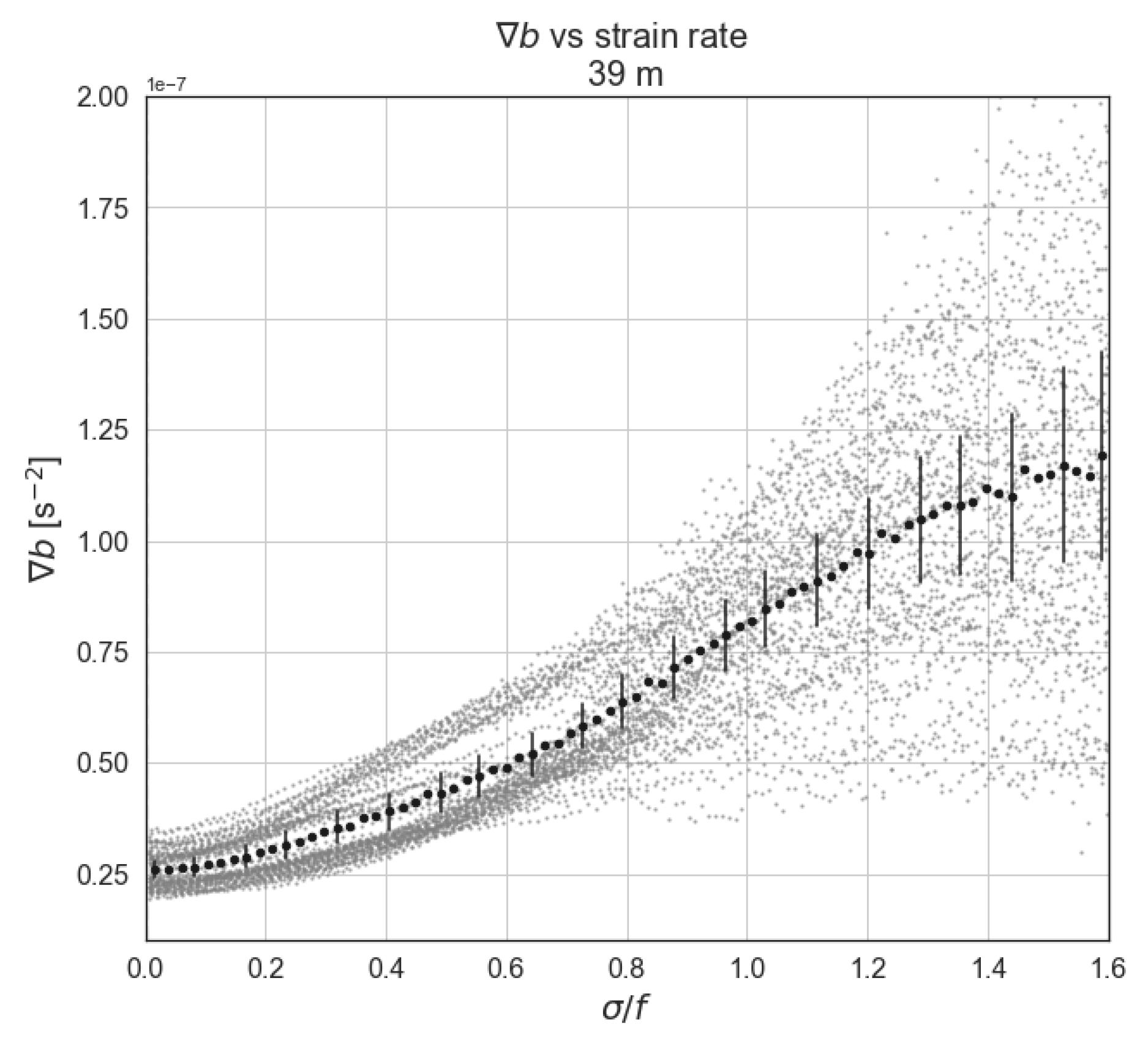
Appendix A. On the Growth Rate and Orientation of Buoyancy Gradient
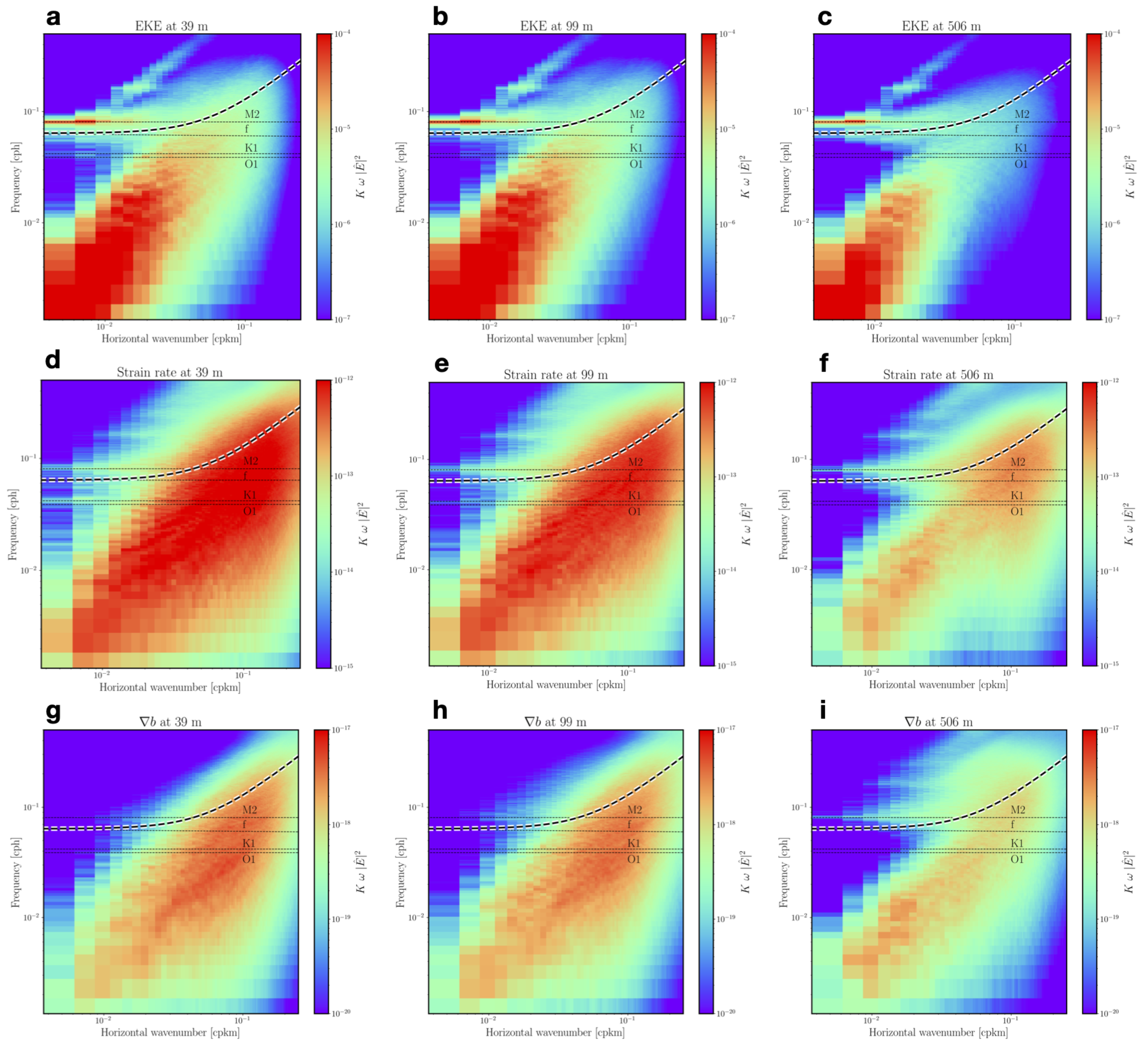
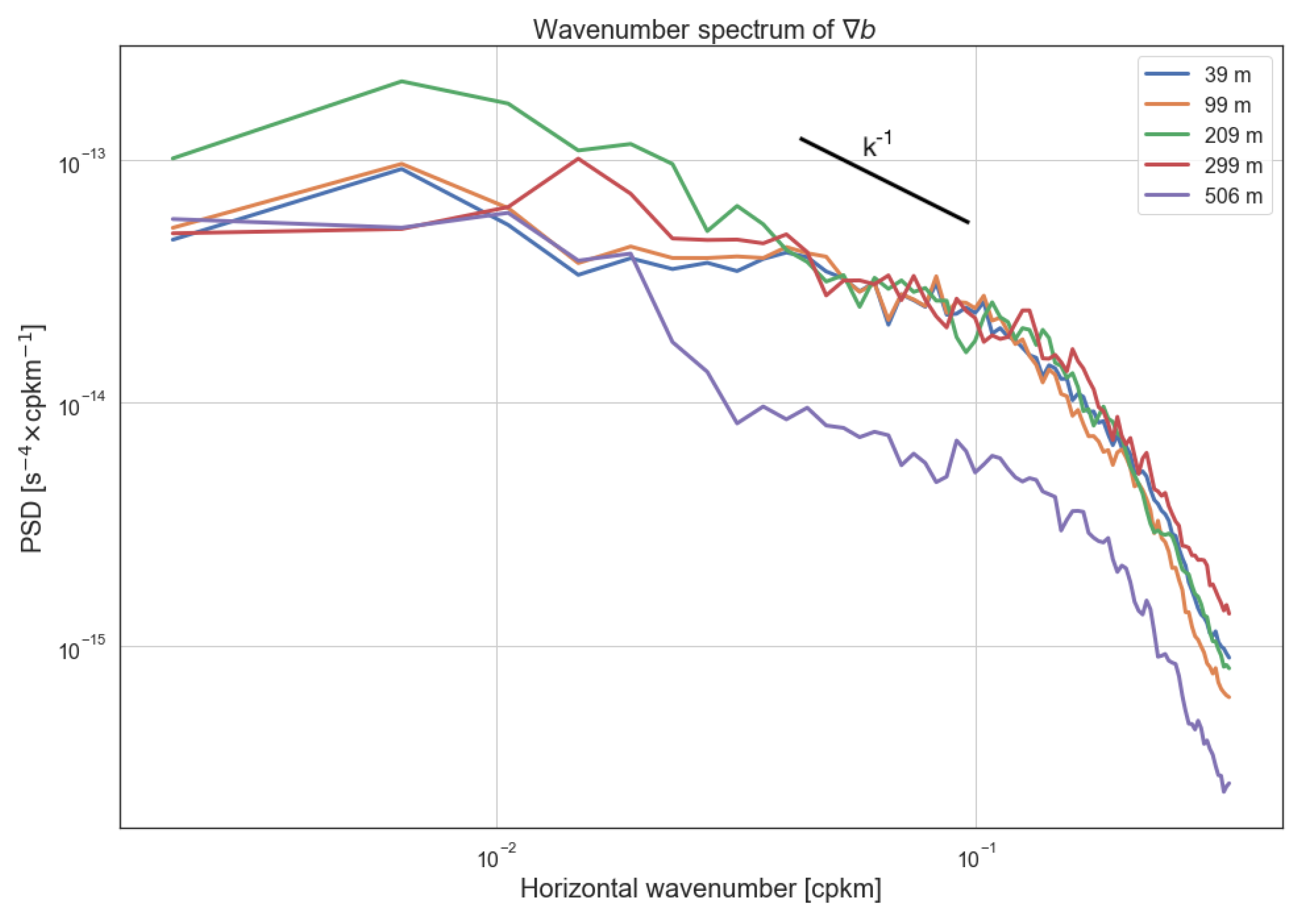
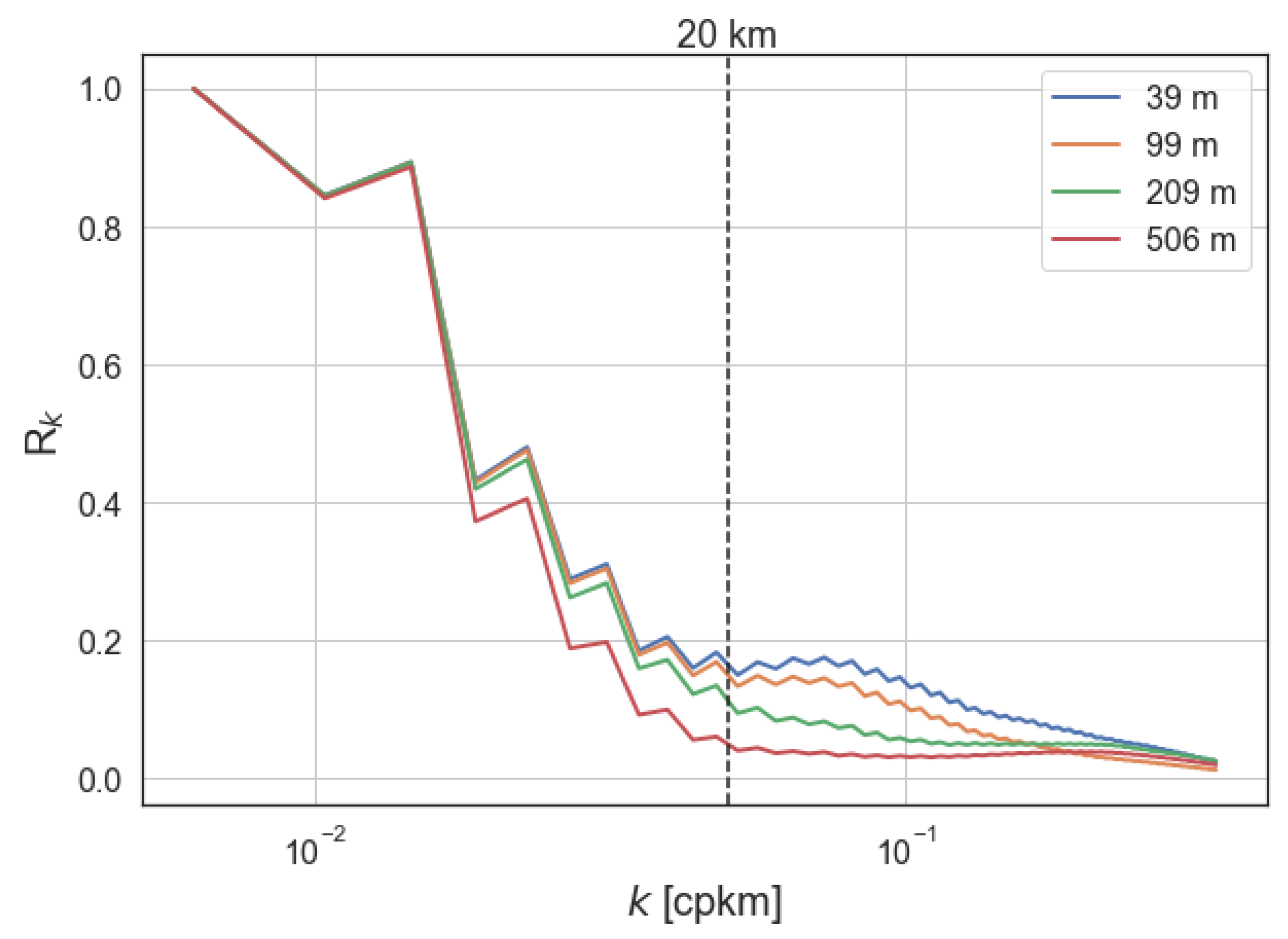
Appendix B. Frequency-Wavenumber Spectrum
Appendix C. Filter Cutoff Wavelength
References
- Thompson, A.F.; Lazar, A.; Buckingham, C.; Naveira Garabato, A.C.; Damerell, G.M.; Heywood, K.J. Open-ocean submesoscale motions: A full seasonal cycle of mixed layer instabilities from gliders. J. Phys. Oceanogr. 2016, 46, 1285–1307. [Google Scholar] [CrossRef]
- Yu, X.; Naveira Garabato, A.C.; Martin, A.P.; Buckingham, C.E.; Brannigan, L.; Su, Z. An annual cycle of submesoscale vertical flow and restratification in the upper ocean. J. Phys. Oceanogr. 2019, 49, 1439–1461. [Google Scholar] [CrossRef]
- Siegelman, L.; Klein, P.; Rivière, P.; Thompson, A.F.; Torres, H.S.; Flexas, M.; Menemenlis, D. Enhanced upward heat transport at deep submesoscale ocean fronts. Nat. Geosci. 2020, 13, 50–55. [Google Scholar] [CrossRef]
- Siegelman, L. Energetic submesoscale dynamics in the ocean interior. J. Phys. Oceanogr. 2020, 50, 727–749. [Google Scholar] [CrossRef]
- Thomas, L.N.; Tandon, A.; Mahadevan, A. Submesoscale processes and dynamics. Ocean. Model. Eddying Regime 2008, 177, 17–38. [Google Scholar]
- Su, Z.; Wang, J.; Klein, P.; Thompson, A.F.; Menemenlis, D. Ocean submesoscales as a key component of the global heat budget. Nat. Commun. 2018, 9, 775. [Google Scholar] [CrossRef]
- Marshall, J.; Adcroft, A.; Hill, C.; Perelman, L.; Heisey, C. A finite-volume, incompressible Navier Stokes model for studies of the ocean on parallel computers. J. Geophys. Res. Ocean. 1997, 102, 5753–5766. [Google Scholar] [CrossRef]
- Hill, C.; Menemenlis, D.; Ciotti, B.; Henze, C. Investigating solution convergence in a global ocean model using a 2048-processor cluster of distributed shared memory machines. Sci. Program. 2007, 15, 107–115. [Google Scholar] [CrossRef]
- Torres, H.S.; Klein, P.; Menemenlis, D.; Qiu, B.; Su, Z.; Wang, J.; Chen, S.; Fu, L.L. Partitioning ocean motions into balanced motions and internal gravity waves: A modeling study in anticipation of future space missions. J. Geophys. Res. Ocean. 2018, 123, 8084–8105. [Google Scholar] [CrossRef]
- d’Ovidio, F.; Fernández, V.; Hernández-García, E.; López, C. Mixing structures in the Mediterranean Sea from finite-size Lyapunov exponents. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Lapeyre, G. Characterization of finite-time Lyapunov exponents and vectors in two-dimensional turbulence. Chaos Interdiscip. J. Nonlinear Sci. 2002, 12, 688–698. [Google Scholar] [CrossRef] [PubMed]
- Keating, S.R.; Smith, K.S.; Kramer, P.R. Diagnosing lateral mixing in the upper ocean with virtual tracers: Spatial and temporal resolution dependence. J. Phys. Oceanogr. 2011, 41, 1512–1534. [Google Scholar] [CrossRef]
- Waugh, D.W.; Abraham, E.R. Stirring in the global surface ocean. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Siegelman, L.; Roquet, F.; Mensah, V.; Rivière, P.; Pauthenet, E.; Picard, B.; Guinet, C. Correction and accuracy of high-and low-resolution ctd data from animal-borne instruments. J. Atmos. Ocean. Technol. 2019, 36, 745–760. [Google Scholar] [CrossRef]
- Intergovernmental-Oceanographic-Commission. The International Thermodynamic Equation of Seawater—2010: Calculation and Use of Thermodynamic Properties. [Includes Corrections Up to 31st October 2015]; UNESCO: Paris, France, 2010. [Google Scholar]
- Hoskins, B.J.; Draghici, I.; Davies, H.C. A new look at the ω-equation. Q. J. R. Meteorol. Soc. 1978, 104, 31–38. [Google Scholar] [CrossRef]
- Giordani, H.; Prieur, L.; Caniaux, G. Advanced insights into sources of vertical velocity in the ocean. Ocean. Dyn. 2006, 56, 513–524. [Google Scholar] [CrossRef]
- Burns, K.J.; Vasil, G.M.; Oishi, J.S.; Lecoanet, D.; Brown, B. Dedalus: Dedalus: A flexible framework for numerical simulations with spectral methods. Phys. Rev. Res. 2020, 2, 023068. [Google Scholar] [CrossRef]
- Thompson, A.F.; Naveira Garabato, A.C. Equilibration of the Antarctic Circumpolar Current by standing meanders. J. Phys. Oceanogr. 2014, 44, 1811–1828. [Google Scholar] [CrossRef]
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Haynes, P.; Anglade, J. The vertical-scale cascade in atmospheric tracers due to large-scale differential advection. J. Atmos. Sci. 1997, 54, 1121–1136. [Google Scholar] [CrossRef]
- Klein, P.; Treguier, A.M.; Hua, B.L. Three-dimensional stirring of thermohaline fronts. J. Mar. Res. 1998, 56, 589–612. [Google Scholar] [CrossRef]
- Meunier, T.; Ménesguen, C.; Schopp, R.; Le Gentil, S. Tracer stirring around a meddy: The formation of layering. J. Phys. Oceanogr. 2015, 45, 407–423. [Google Scholar] [CrossRef]
- Hua, B.L.; Haidvogel, D.B. Numerical simulations of the vertical structure of quasi-geostrophic turbulence. J. Atmos. Sci. 1986, 43, 2923–2936. [Google Scholar] [CrossRef]
- Smith, K.S.; Ferrari, R. The production and dissipation of compensated thermohaline variance by mesoscale stirring. J. Phys. Oceanogr. 2009, 39, 2477–2501. [Google Scholar] [CrossRef]
- Molemaker, M.J.; McWilliams, J.C.; Capet, X. Balanced and unbalanced routes to dissipation in an equilibrated Eady flow. J. Fluid Mech. 2010, 654, 35–63. [Google Scholar] [CrossRef]
- Roullet, G.; Klein, P. Cyclone-anticyclone asymmetry in geophysical turbulence. Phys. Rev. Lett. 2010, 104, 218501. [Google Scholar] [CrossRef] [PubMed]
- Klein, P.; Lapeyre, G.; Siegelman, L.; Qiu, B.; Fu, L.L.; Torres, H.; Su, Z.; Menemenlis, D.; Le Gentil, S. Ocean-Scale Interactions From Space. Earth Space Sci. 2019, 6, 795–817. [Google Scholar] [CrossRef]
- Lapeyre, G.; Klein, P.; Hua, B.L. Oceanic Restratification Forced by Surface Frontogenesis. J. Phys. Oceanogr. 2006, 36, 1577–1590. [Google Scholar] [CrossRef]
- Okubo, A. Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences. Deep. Sea Res. Oceanogr. Abstr. 1970, 17, 445–454. [Google Scholar] [CrossRef]
- Hua, B.L.; Klein, P. An exact criterion for the stirring properties of nearly two-dimensional turbulence. Phys. D Nonlinear Phenom. 1998, 113, 98–110. [Google Scholar] [CrossRef]
- Lapeyre, G.; Klein, P.; Hua, B.L. Does the tracer gradient vector align with the strain eigenvectors in 2D turbulence? Phys. Fluids 1999, 11, 3729–3737. [Google Scholar] [CrossRef]
- Smith, K.S.; Vallis, G.K. The scales and equilibration of midocean eddies: Freely evolving flow. J. Phys. Oceanogr. 2001, 31, 554–571. [Google Scholar] [CrossRef]
- Lapeyre, G. What vertical mode does the altimeter reflect? On the decomposition in baroclinic modes and on a surface-trapped mode. J. Phys. Oceanogr. 2009, 39, 2857–2874. [Google Scholar] [CrossRef]
- Foussard, A.; Berti, S.; Perrot, X.; Lapeyre, G. Relative dispersion in generalized two-dimensional turbulence. J. Fluid Mech. 2017, 821, 358–383. [Google Scholar] [CrossRef]
- Scott, R. Local and nonlocal advection of a passive scalar. Phys. Fluids 2006, 18, 116601. [Google Scholar] [CrossRef]
- Lapeyre, G.; Hua, B.L.; Klein, P. Dynamics of the orientation of active and passive scalars in two-dimensional turbulence. Phys. Fluids 2001, 13, 251–264. [Google Scholar] [CrossRef][Green Version]
- Ballarotta, M.; Ubelmann, C.; Pujol, M.I.; Taburet, G.; Fournier, F.; Legeais, J.F.; Faugère, Y.; Delepoulle, A.; Chelton, D.; Dibarboure, G.; et al. On the resolutions of ocean altimetry maps. Ocean. Sci. 2019, 15, 1091–1109. [Google Scholar] [CrossRef]
- McGillicuddy, D.J., Jr. Mechanisms of physical-biological-biogeochemical interaction at the oceanic mesoscale. Annu. Rev. Mar. Sci. 2016, 8, 125–159. [Google Scholar] [CrossRef]
- Kunze, E. Near-inertial wave propagation in geostrophic shear. J. Phys. Oceanogr. 1985, 15, 544–565. [Google Scholar] [CrossRef]
- Hakim, G.; Keyser, D. Canonical frontal circulation patterns in terms of Green’s functions for the Sawyer-Eliassen equation. Q. J. R. Meteorol. Soc. 2001, 127, 1795–1814. [Google Scholar] [CrossRef]
- Viúdez, Á.; Tintoré, J.; Haney, R.L. About the nature of the generalized omega equation. J. Atmos. Sci. 1996, 53, 787–795. [Google Scholar] [CrossRef][Green Version]
- Qiu, B.; Chen, S.; Klein, P.; Torres, H.; Wang, J.; Fu, L.L.; Menemenlis, D. Reconstructing Upper-Ocean Vertical Velocity Field from Sea Surface Height in the Presence of Unbalanced Motion. J. Phys. Oceanogr. 2020, 50, 55–79. [Google Scholar] [CrossRef]
- Sasaki, H.; Klein, P.; Qiu, B.; Sasai, Y. Impact of oceanic-scale interactions on the seasonal modulation of ocean dynamics by the atmosphere. Nat. Commun. 2014, 5, 6636. [Google Scholar] [CrossRef] [PubMed]
- Legal, C.; Klein, P.; Tréguier, A.M.; Paillet, J. Diagnosis of the vertical motions in a mesoscale stirring region. J. Phys. Oceanogr. 2007, 37, 1413–1424. [Google Scholar] [CrossRef]
- Weiss, J. The dynamics of enstrophy transfer in two-dimensional hydrodynamics. Phys. D Nonlinear Phenom. 1991, 48, 273–294. [Google Scholar] [CrossRef]
- Weiss, J. Report LJI-TN-81-121; La Jolla Inst.: San Diego, CA, USA, 1981. [Google Scholar]
- Gent, P.R.; McWilliams, J.C. Consistent balanced models in bounded and periodic domains. Dyn. Atmos. Ocean. 1983, 7, 67–93. [Google Scholar] [CrossRef]
- Basdevant, C.; Philipovitch, T. On the validity of the “Weiss criterion” in two-dimensional turbulence. Phys. D Nonlinear Phenom. 1994, 73, 17–30. [Google Scholar] [CrossRef]
- Hua, B.L.; McWilliams, J.C.; Klein, P. Lagrangian accelerations in geostrophic turbulence. J. Fluid Mech. 1998, 366, 87–108. [Google Scholar] [CrossRef]
- Muraki, D.J.; Snyder, C.; Rotunno, R. The next-order corrections to quasigeostrophic theory. J. Atmos. Sci. 1999, 56, 1547–1560. [Google Scholar] [CrossRef]
- Klein, P.; Hua, B.L.; Lapeyre, G. Alignment of tracer gradient vectors in 2D turbulence. Phys. D Nonlinear Phenom. 2000, 146, 246–260. [Google Scholar] [CrossRef][Green Version]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; Farrar, J.T.; Molemaker, M.J.; McWilliams, J.C.; Gula, J. Prospects for future satellite estimation of small-scale variability of ocean surface velocity and vorticity. Prog. Oceanogr. 2019, 173, 256–350. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siegelman, L.; Klein, P.; Thompson, A.F.; Torres, H.S.; Menemenlis, D. Altimetry-Based Diagnosis of Deep-Reaching Sub-Mesoscale Ocean Fronts. Fluids 2020, 5, 145. https://doi.org/10.3390/fluids5030145
Siegelman L, Klein P, Thompson AF, Torres HS, Menemenlis D. Altimetry-Based Diagnosis of Deep-Reaching Sub-Mesoscale Ocean Fronts. Fluids. 2020; 5(3):145. https://doi.org/10.3390/fluids5030145
Chicago/Turabian StyleSiegelman, Lia, Patrice Klein, Andrew F. Thompson, Hector S. Torres, and Dimitris Menemenlis. 2020. "Altimetry-Based Diagnosis of Deep-Reaching Sub-Mesoscale Ocean Fronts" Fluids 5, no. 3: 145. https://doi.org/10.3390/fluids5030145
APA StyleSiegelman, L., Klein, P., Thompson, A. F., Torres, H. S., & Menemenlis, D. (2020). Altimetry-Based Diagnosis of Deep-Reaching Sub-Mesoscale Ocean Fronts. Fluids, 5(3), 145. https://doi.org/10.3390/fluids5030145




