Geophysical Equatorial Edge Wave with Underlying Currents in the f-Plane Approximation

Abstract

I present an exact and explicit solution to the nonlinear governing equations in the equatorial f-plane, describing geophysical edge waves propagating over a plane-sloping beach, in the presence of underlying uniform currents. I also derive the analytical expressions of geophysical edge wave dynamics and the mass transport velocity.

1. Introduction

Edge waves propagating along a sloping beach are trapped near the shoreline, with their amplitude maximal at the shoreline and decaying rapidly offshore. These three-dimensional waves play an important role in the dynamics of coastal zone and in beach erosion processes [1,2]. The edge wave phenomenon has been extensively studied and discussed within the framework of linear and nonlinear theory in the Eulerian coordinates [3,4,5,6,7,8,9,10].

Some exact solutions describing nonlinear edge waves in the Lagrangian framework were obtained by Ref. [11,12]. They found that the deep-water wave solution discovered by Ref. [13] can be adapted to construct edge waves propagating along a plane-sloping beach. However, this treatment of the edge wave problem provides only an implicit form for the free water surface. Recently, Gerstner-type solutions have been derived and adapted to model a number of different physical and geophysical fluid dynamics [14,15,16]. These solutions were shown to incorporate constant underlying currents [17,18,19,20,21], with an analysis of the effects of the mathematical modification on the resulting physical flow properties. Constantin [22] presented an explicit edge wave solution. This flow has been a starting point for some interesting studies within the class of geophysical edge waves [23,24,25].

An explicit solution in Lagrangian variables for the geophysical edge wave problem over a plane sloping beach with the shoreline parallel to the equator (an example being the Bolaanguki beach of the Molucca Sea in Indonesia) was recently obtained in the f-plane setting [23]. Our aim is to show that one can accommodate an underlying uniform current in the longshore direction. While the inclusion of longshore currents for linear edge waves is well-understood (see, e.g., the discussion in Ref. [26]), the fact that it is possible to do this within the framework of exact solutions to the governing equations in the equatorial f-plane is far from obvious. Our solution yields an exact solution to the governing equations for gravity edge waves propagating over a flat bed, in the presence of an underlying uniform current. In the absence of a current, this wave flow particularizes to the only known explicit three-dimensional solution to the governing equations for gravity water waves with a non-flat free surface [22]. The fact that it is possible to specify explicitly the particle trajectories for our solution is due to the inspiring role played by Gerstner’s wave [13]—the only known explicit solution for deep-water gravity waves with a non-flat surface, cf. the discussion in Ref. [27,28].

In Section 2 I discuss the equatorial f-plane setting for geophysical edge waves and in Section 3 I present the explicit solution. Section 4 is devoted to a discussion of various aspects of the flow.

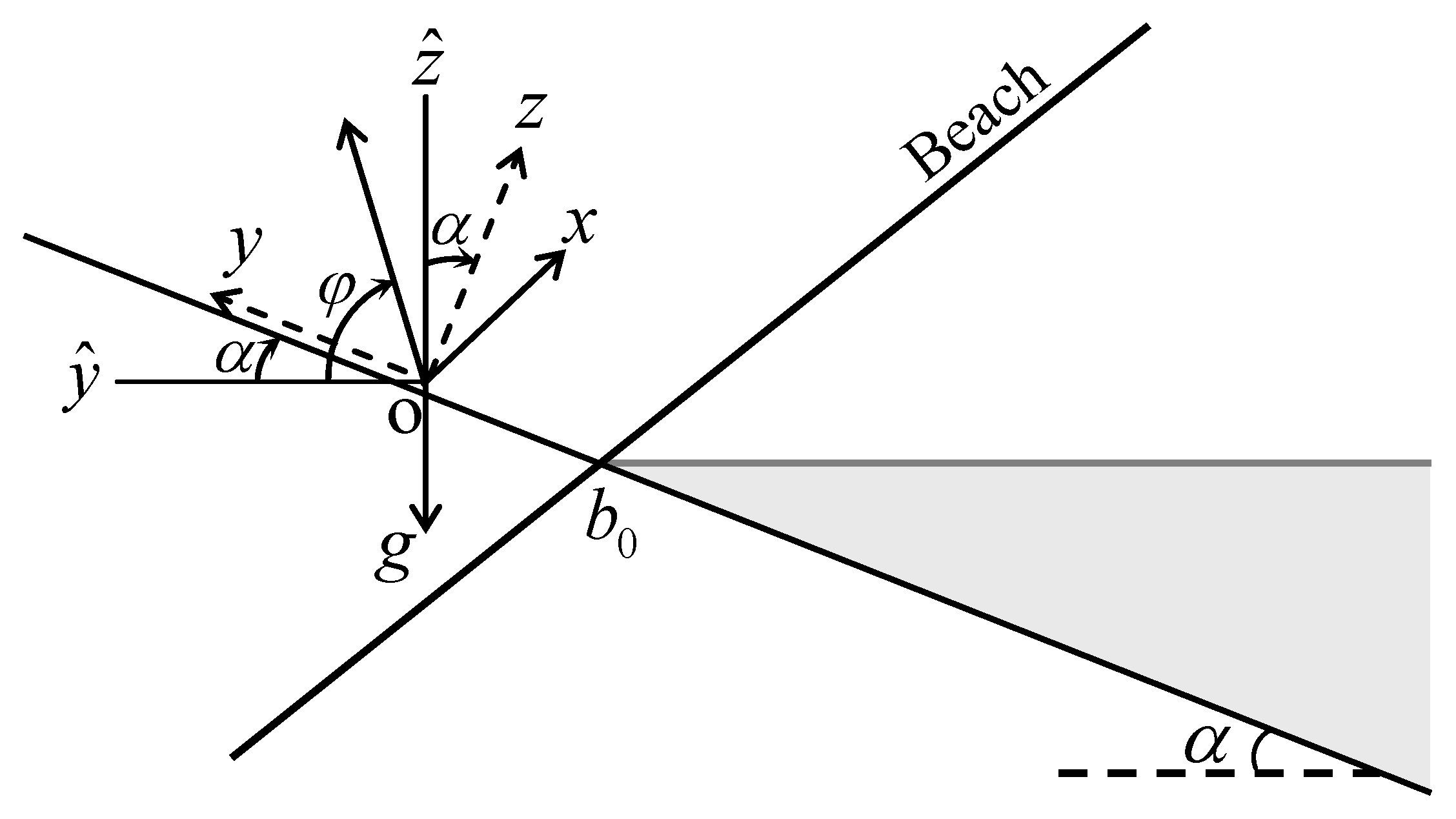
2. Governing Equations

I consider a rotating frame with the origin at the point O on Earth’s surface. Let $\overrightarrow{u}=(u,v,w)$ be the velocity of fluid, P be the pressure, while t is time. In this paper, I consider a sloping beach and adopt a coordinate system as shown in Figure 1, the shoreline being the x-axis and with the still sea in the region

$$R=\{(x,y,z):x\in ℝ, y\le b_0, 0\le z\le (b_0-y)\tan \alpha \}$$

for some $b_0\le 0$; here $\alpha \in (0,\pi /2)$ defines the uniform slope. The xy-plane is taken to be parallel to the sloping bed, with the z-axis normal to it. Moreover, the x-axis is tangent to the equator, pointing eastwards, while the y-axis and the earth’s rotation vector $\overrightarrow{\mathsf{\Omega }}$ form an angle equal to $\alpha$. In the coordinate system Oxyz, the rotation and the gravity vector have the following representation:

$$\overrightarrow{\mathsf{\Omega }}=(0,\mathsf{\Omega }\cos \alpha ,-\mathsf{\Omega }\sin \alpha ), \mathrm{and} \overrightarrow{g}=(0,-g\sin \alpha ,g\cos \alpha ),$$

with $\mathsf{\Omega }\hspace{0.17em}= 73\times {10}^{-6}\mathrm{rad}\hspace{0.17em}{\mathrm{s}}^{-1}$ denoting the rotational speed of the Earth, g = 9.81 $\mathrm{m}\hspace{0.17em}{\mathrm{s}}^{-2}$ being the (constant) gravitational acceleration at the Earth’s surface. The governing equations for geophysical ocean waves [29] are given by

$$\{\begin{array}{l}{u}_t+u{u}_x+v{u}_y+w{u}_z+2\mathsf{\Omega }[w\cos (\phi -\alpha )-v\sin (\phi -\alpha ))]=-\frac{1}{\rho }{P}_x,\\ v_t+u{v}_x+v{v}_y+w{v}_z+2\mathsf{\Omega }u\sin (\phi -\alpha )=-\frac{1}{\rho }{P}_y-g\sin \alpha ,\\ w_t+u{w}_x+v{w}_y+w{w}_z-2\mathsf{\Omega }u\cos (\phi -\alpha )=-\frac{1}{\rho }{P}_z-g\cos \alpha ,\end{array}$$

(1)

The subscripts x, y, z mean the partial derivative of x, y, z. By restricting our attention to a symmetric band of width of about 250 km on each side of the equator, we may neglect viscous term, the variations of the Coriolis parameter (2$\mathsf{\Omega }\cos \phi$, 2$\mathsf{\Omega }\sin \phi$, $\phi$ is latitude) and use the $f$-plane approximation, cf. the discussion in Ref. [30]. In this setting the governing equations for the geophysical ocean waves could be reduced to the following form:

$$\{\begin{array}{l}{u}_t+u{u}_x+v{u}_y+w{u}_z+2\mathsf{\Omega }(w\cos \alpha +v\sin \alpha )=-\frac{1}{\rho }{P}_x,\\ v_t+u{v}_x+v{v}_y+w{v}_z-2\mathsf{\Omega }u\sin \alpha =-\frac{1}{\rho }{P}_y-g\sin \alpha ,\\ w_t+u{w}_x+v{w}_y+w{w}_z-2\mathsf{\Omega }u\cos \alpha =-\frac{1}{\rho }{P}_z-g\cos \alpha ,\end{array}$$

(2)

coupled with the incompressibility constraint

$$u_x+v_y+w_z=0,$$

(3)

under the assumption of constant density $\rho$.

The kinematic and dynamic boundary conditions for the fluid on the free surface are given by

$$w={\eta }_t+u{\eta }_x+v{\eta }_y,$$

(4)

$$P=P_0, \mathrm{on} z=\eta (x,y,t).$$

(5)

where $P_0$ is the constant atmosphere pressure, decoupled the motion of the air from that of the water. The kinematic boundary condition at the free surface, expressing the fact that the same particle is always from the free water surface. The bottom is assumed impermeable, so that the normal velocity component at the sloping bed is zero.

$$w=0, \mathrm{on} z=0.$$

(6)

The general description of the propagation of a geophysical edge wave is provided by Equations (2) and (3), with the boundary conditions Equations (4)–(6). Special features confer to these solutions the character of an edge wave: The direction of propagation is along the shore, and the wave amplitude decays offshore. These features will be obtained as a by-product of our explicit specification of the flow beneath the waves.

3. An Exact Solution in the Lagrangian Description

In this section, I will describe an exact solution of the geophysical edge wave problem. The solution represents geophysical edge waves travelling parallel to the shoreline, with constant propagation speed $c_0$, in the presence of a constant underlying current of strength U. Throughout this paper, the Lagrangian positions (x, y, z) of the fluid particles are supposed as functions of labeling variables $(a,b,c)$ and time t by generalizing the solution presented in Ref. [22] to the geophysical water waves with a constant underlying current.

$$\{\begin{array}{l}x=a-Ut-\frac{1}{k}{e}^{k(b-c)}\sin [k(a+c_{0}t)],\\ y=b-c+\frac{1}{k}{e}^{k(b-c)}\cos [k(a+c_{0}t)]+\frac{2\mathsf{\Omega }{c}_0\cot \alpha }{\tilde{g}}z(c),\\ z=\frac{\tilde{g}}{\tilde{g}+2\mathsf{\Omega }{c}_0}[c+c\tan \alpha -\frac{\tan \alpha }{2k}{e}^{2k{b}_0}(1-e^{-2kc(1+\cot \alpha )})].\end{array}$$

(7)

where k > 0 is a fixed wave number, and $\tilde{g}=g+2\mathsf{\Omega }U$. The quantities a, b, c are labeling variables for the identification of individual particles. Our aim is to prove that the motion (7) is dynamically possible and that we can associate to it an expression for the hydrodynamical pressure P such that the governing equations and boundary conditions are all satisfied. The resulting free surface of the water at $c=(b_0-b)\tan \alpha$ is the geophysical edge wave we are looking for.

The map (7) is a diffeomorphism from the still water region R to the water region bounded below by the rigid bed z = 0 and above by the free water surface, which is parameterized by

$$\{\begin{array}{l}x=a-Ut-\frac{1}{k}{e}^{kb(1+\tan \alpha )-k{b}_0\tan \alpha }\sin [k(a+c_{0}t)],\\ y=b(1+\tan \alpha )-k{b}_0\tan \alpha +\frac{1}{k}{e}^{kb(1+\tan \alpha )-k{b}_0\tan \alpha }\cos [k(a+c_{0}t)]+\frac{2\mathsf{\Omega }{c}_0\cot \alpha }{\tilde{g}}z((b_0-b)\tan \alpha ),\\ z=\frac{\tilde{g}}{\tilde{g}+2\mathsf{\Omega }{c}_0}[(b-b_0)(1+\tan \alpha )\tan \alpha -\frac{\tan \alpha }{2k}{e}^{2k{b}_0}(1-e^{2k(b-b_0)(1+\tan \alpha )})],\end{array}$$

(8)

with $a\in ℝ$, $b\le b_0$ and $t\ge 0$. Indeed, observing that $(a,b,c)\mapsto (a,b-c,c)$ defines a diffeomorphism of ${ℝ}^3$, it suffices to show that the mapping

$$\left(\begin{array}{l}a\\ b^{\prime }\\ c\end{array}\right)\mapsto \{\begin{array}{l}a-Ut-\frac{1}{k}{e}^{k{b}^{\prime }}\sin [k(a+c_{0}t)],\\ b^{\prime }+\frac{1}{k}{e}^{k{b}^{\prime }}\cos [k(a+c_{0}t)],\\ \frac{\tilde{g}}{\tilde{g}+2\mathsf{\Omega }{c}_0}[c+c\tan \alpha -\frac{\tan \alpha }{2k}{e}^{2k{b}_0}(1-e^{-2kc(1+\cot \alpha )})],\end{array}$$

(9)

with $a\in ℝ$, $b^{\prime }\le b_0-c(1+\cot \alpha )$ and $t\ge 0$, is a diffeomorphism. For this, see Constantin [22].

For notational convenience, denote

$$\xi =k(b-c), \theta =k(a+c_{0}t).$$

We can easily check that the determinant of the Jacobian of the transformation (7) is equal to $(1-e^{2\xi })z^{\prime }(c)$, which is time independent. Due to the time-independence of the determinant, the fluid flow is volume-preserving, so that the Lagrangian form of the equation of continuity (3) is fulfilled. From (7) we compute the velocity and acceleration of a particle as

$$\{\begin{array}{l}u=\frac{Dx}{Dt}=-U-c_0{e}^{\xi }\cos \theta ,\hfill \\ v=\frac{Dy}{Dt}=-c_0{e}^{\xi }\sin \theta ,\hfill \\ w=\frac{Dz}{Dt}=0,\hfill \end{array},\{\begin{array}{l}\frac{Du}{Dt}=k{c}_0^2{e}^{\xi }\sin \theta ,\hfill \\ \frac{Dv}{Dt}=-k{c}_0^2{e}^{\xi }\cos \theta ,\hfill \\ \frac{Dw}{Dt}=0.\hfill \end{array}$$

(10)

At every instant t, (7) is a global diffeomorphism from the label domain R to the fluid domain. It can be shown by direct calculation that the motion prescribed by (7) satisfies (2) when the pressure function is given by

$$P=P_0+\frac{\rho \tilde{g}\sin \alpha }{2k}{e}^{2\xi }-\rho \tilde{g}(c\cos \alpha +(b-b_0)\sin \alpha )-\frac{\rho \tilde{g}\sin \alpha }{2k}{e}^{2k{b}_0}{e}^{-2kc(1+\cot \alpha )}.$$

(11)

and the dispersion relation can be obtained as

$$k{c}_0^2-2\mathsf{\Omega }{c}_0\sin \alpha -\tilde{g}\sin \alpha =0.$$

(12)

Therefore, the flow determined by Equation (7) satisfies the governing Equations (2) and (3). At the free surface $c=(b_0-b)\tan \alpha$, we have $P=P_0$ so that the dynamic free surface boundary condition (5) is satisfied. The kinematic free surface boundary condition (4) at the free surface is also satisfied as at any instance the free surface (8) is the image of the still water surface $c=(b_0-b)\tan \alpha$ under (7) for all $t\ge 0$. Since the velocity of field is given by (7), the fluid velocity has no normal component to the beach when z = 0, which proves (6). The proof that (7) is an explicit solution to the governing equations for water waves with a uniform current on a sloping beach is thus completed.

Note that if there is no underlying current, then all particles move on closed circles, as it is the case in the geophysical edge wave solution from Ref. [23], in the gravity edge wave solution from Ref. [22], and in Gerstner’s solution Ref. [13]. This situation contrasts to the case of irrotational gravity water flows, whether in finite or infinite depth, setting in which the particle paths are known to be not closed paths but open loops, cf. the discussion in Ref. [31,32]. On the other hand, for our solution the presence of an underlying uniform current has the effect that the particle trajectories are no longer circles but open orbits, due to the effect of the longshore current. These orbits lie in planes parallel to the sloped bottom. The particle trajectories move clockwise for the waves travelling from west to east and counterclockwise for the waves travelling westward. The fact that an underlying uniform current distorts considerably the particle paths is not surprising—something similar occurs in irrotational gravity water waves [33].

4. Discussion

4.1. Wave Phase Celerity

The phase velocity $c_0$ of the geophysical edge wave is given by the dispersion relation

$$c_{0+/-}=\frac{\mathsf{\Omega }\sin \alpha \pm \sqrt{{\mathsf{\Omega }}^2{\sin }^2\alpha +\tilde{g}k\sin \alpha }}{k}.$$

(13)

There are two choices: If $c_0=c_{0+}$, then the wave propagates along the equator from west to east, and if $c_0=c_{0-}$ it travels from east to west. Note that the Coriolis force as well as the underlying uniform current influence the propagation speed. Neglecting the longshore current, that is, setting U = 0, (13) reduces to the solution derived in Ref. [23]. Neglecting also the Coriolis effect, that is, setting U = 0 as well as $\mathsf{\Omega }$ = 0, our solution particularizes to the gravity edge wave solution obtained in Ref. [22].

4.2. Vorticity

In this section we will compute the vorticity of the flow (3). The fact that Gerstner’s solution has non-constant vorticity suggests that we will also encounter a similar feature. From (7) we get

$$\left(\begin{array}{ccc}\frac{\partial a}{\partial x}& \frac{\partial b}{\partial x}& \frac{\partial c}{\partial x}\\ \frac{\partial a}{\partial y}& \frac{\partial b}{\partial y}& \frac{\partial c}{\partial y}\\ \frac{\partial a}{\partial z}& \frac{\partial b}{\partial z}& \frac{\partial c}{\partial z}\end{array}\right)=\frac{1}{1-e^{2\xi }}\left(\begin{array}{ccc}1+e^{\xi }\cos \theta & e^{\xi }\sin \theta & 0\\ e^{\xi }\sin \theta & 1-e^{\xi }\cos \theta & 0\\ -\frac{2\mathsf{\Omega }{c}_0\cot \alpha }{\tilde{g}}{e}^{\xi }\sin \theta & \frac{1-e^{2\xi }}{z^{\prime }(c)}-\frac{2\mathsf{\Omega }{c}_0\cot \alpha }{\tilde{g}}(1-e^{\xi }\cos \theta )& \frac{1-e^{2\xi }}{z^{\prime }(c)}\end{array}\right).$$

(14)

Thus, the vorticity $\omega$ can be straightforward calculated as

$$\omega =(w_y-v_z,u_z-w_x,v_x-u_y)=\left(-\frac{\lambda k{c}_0{e}^{\xi }\sin \theta }{1-e^{2\xi }}\begin{array}{ccc},& \frac{\lambda k{c}_0{e}^{\xi }\cos \theta -\lambda k{c}_0{e}^{2\xi }}{1-e^{2\xi }},& -\frac{2k{c}_0{e}^{2\xi }}{1-e^{2\xi }}\end{array}\right).$$

(15)

where $\lambda =\frac{2\mathsf{\Omega }{c}_0\cot \alpha }{\tilde{g}}$. Equation (15) shows that the vorticity of our three-dimensional geophysical wave is time-dependent and decreases exponentially fast away from the shore. We note that since the underlying longshore current is constant, it does not impact on the vorticity of the flow, and the prescription of the vorticity matches that in Ref. [23]. However, in Ref. [23] there are some typographical errors in the Equation (4.2).

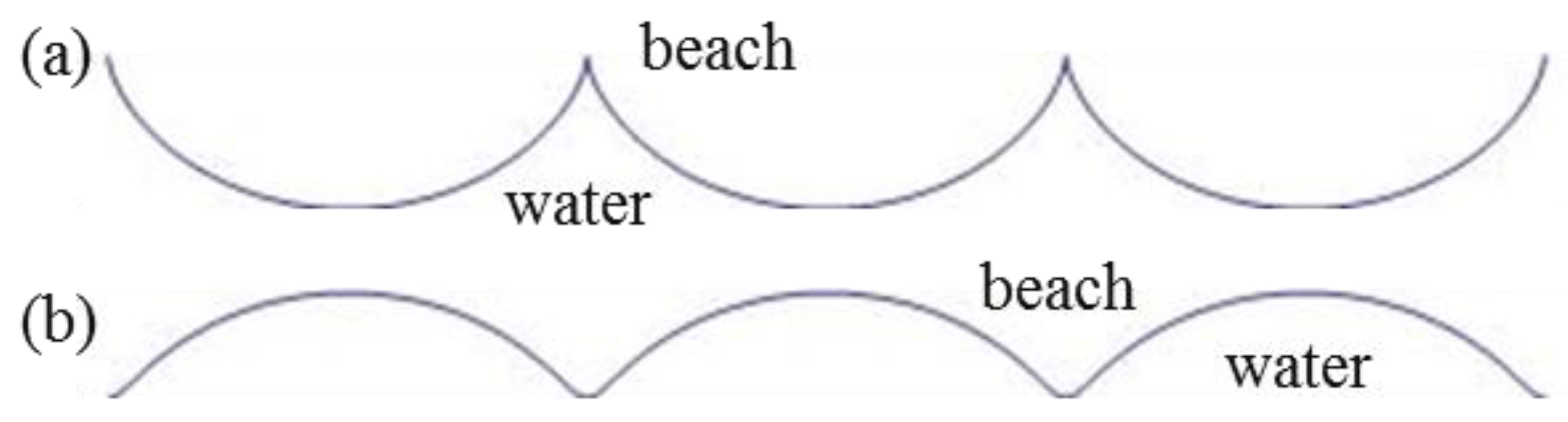
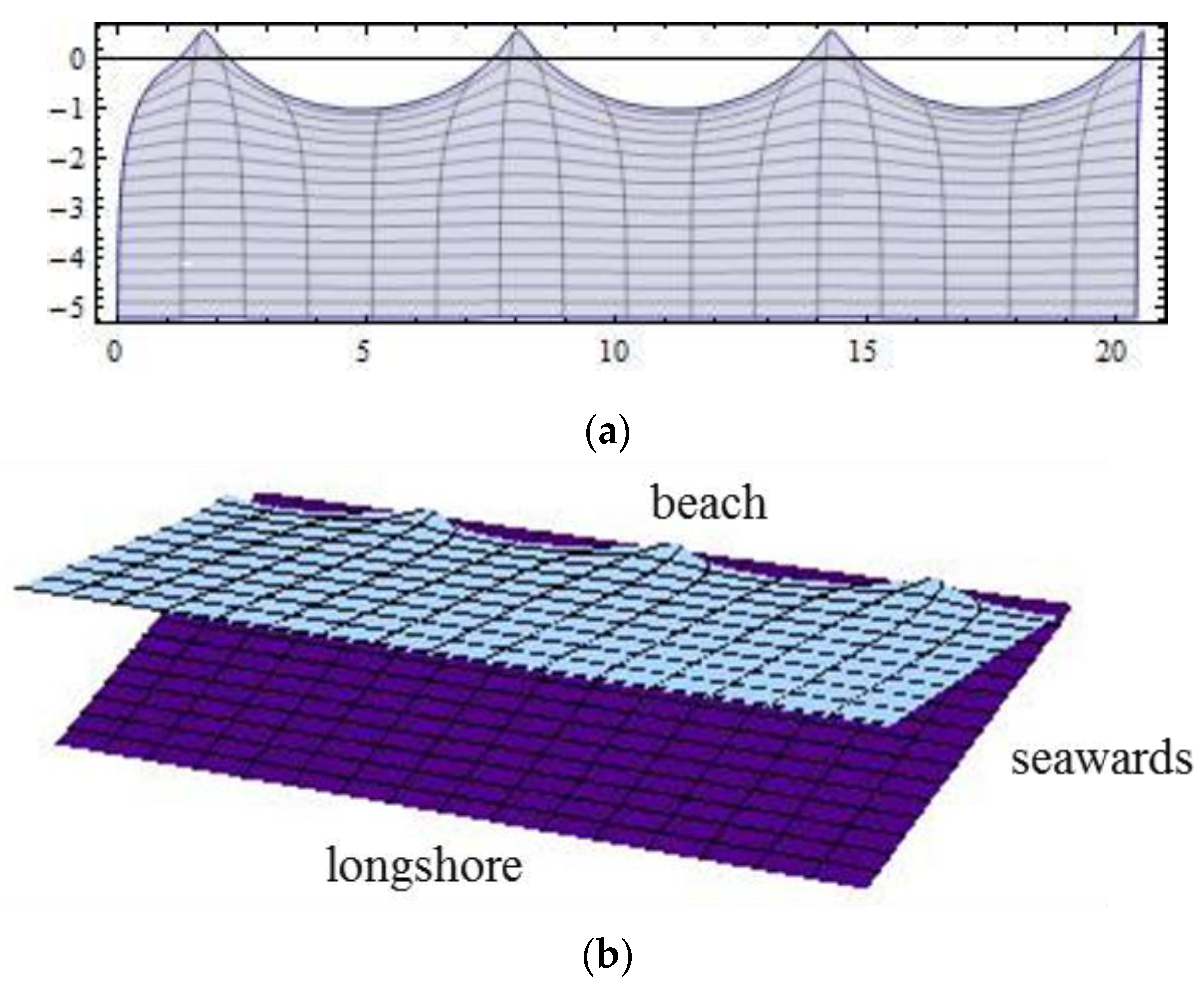
4.3. Run-Up Pattern

The run-up pattern is obtained by setting z = 0 in (7), so that it can be described parametrically by

$$\{\begin{array}{l}x=a-Ut-\frac{1}{k}{e}^{k{b}_0}\sin [k(a+c_{0}t)],\\ y=b_0+\frac{1}{k}{e}^{k{b}_0}\cos [k(a+c_{0}t)],\\ z=0.\end{array}$$

(16)

with $a\in ℝ$. The run-up patterns can be found from the above Formula (16), which represent the parametrization of a cycloid with upward cusps for $b_0=0$ or a smooth trochoid for $b_0<0$ shown in Figure 2. These two different shapes of the run-up pattern are observed in the coastal zone. As indicated by Ref. [34], it can be divided into two different types of cusps: Swash cusps (cycloid with upward cusps) and surf cusps (trochoid pattern) according to the coastal process.

4.4. Amplitude of the Equatorial Edge Wave with Longshore Currents

To determine the elevation with respect to the reference half-plane

$$\left\{z=-\frac{\tan \alpha }{2k}{e}^{2k{b}_0}+(b_0-y)\tan \alpha ;y\le b_0\right\}$$

(17)

we can compute the distance of a point $(x,y,z)$ lying on the free surface (5) to this plane,

$$d=z\cos \alpha +(y-b_0)\tan \alpha +\frac{\tan \alpha }{2k}{e}^{2k{b}_0}.$$

(18)

Setting $c=(b_0-b)\tan \alpha$ in (18) and understanding that positive/negative values on the right-hand side of (18) mean that the point lies above /below the plane, we could obtain that the amplitude of the edge wave is

$$kd=\frac{\sin \alpha }{2}\left(e^{2kb(1+\tan \alpha )-2k{b}_0\tan \alpha }+2e^{kb(1+\tan \alpha )-k{b}_0\tan \alpha }\cos (k(a+c_{0}t))\right).$$

(19)

Note that the amplitude of the geophysical edge wave (19) is exactly that in Ref. [22,23]. We see that the amplitude of the edge wave decays exponentially away the shoreline (as $b\to -\infty$). From (19), we can infer that the crests and troughs correspond to the maximal/minimal values of $\cos (k(a+c_{0}t))$. At a fixed time $t\ge 0$, we obtain the crest curves ($m\in ℝ$ and $b\le b_0$)

$$\{\begin{array}{l}x=\frac{2m\pi }{k}-(\frac{c_0}{k}+U)t,\\ y=b(1+\tan \alpha )-b_0\tan \alpha +\frac{1}{k}{e}^{kb(1+\tan \alpha )-k{b}_0\tan \alpha }+\frac{2\mathsf{\Omega }{c}_0\cot \alpha }{\tilde{g}}z((b_0-b)\tan \alpha ),\\ z=\frac{\tilde{g}}{\tilde{g}+2\mathsf{\Omega }{c}_0}[(b-b_0)(1+\tan \alpha )\tan \alpha -\frac{\tan \alpha }{2k}{e}^{2k{b}_0}(1-e^{2k(b-b_0)(1+\tan \alpha )})].\end{array}$$

(20)

while the troughs are

$$\{\begin{array}{l}x=\frac{(2m+1)\pi }{k}-(\frac{c_0}{k}+U)t,\\ y=b(1+\tan \alpha )-b_0\tan \alpha -\frac{1}{k}{e}^{kb(1+\tan \alpha )-k{b}_0\tan \alpha }+\frac{2\mathsf{\Omega }{c}_0\cot \alpha }{\tilde{g}}z((b_0-b)\tan \alpha ),\\ z=\frac{\tilde{g}}{\tilde{g}+2\mathsf{\Omega }{c}_0}[(b-b_0)(1+\tan \alpha )\tan \alpha -\frac{\tan \alpha }{2k}{e}^{2k{b}_0}(1-e^{2k(b-b_0)(1+\tan \alpha )})].\end{array}$$

(21)

From (20) and (21), we understand that the crest (and the troughs) lines are orthogonal to the shoreline and parallel each other. We can also see that the crest and the trough lines are monotonic curves. It is also important to mention that the amplitude has the same form with the cases of $\mathsf{\Omega }=0$ or U = 0, and the y-component is larger in the geophysical flow ($\mathsf{\Omega }>0$) if $c_0=c_{0+}$ and smaller if $c_0=c_{0-}$. An example of a typical solution for the three-dimensional geophysical edge wave is depicted in Figure 3.

4.5. Mass Transport Velocity

The flow (7) also presents a nonzero horizontal component of the wave-induced relative vorticity, in addition to the planetary vorticity. Since the geophysical edge waves propagate along a sloping bottom, we consider the depth-averaged mass transport velocity. Taking the depth-averaged velocities in the longshore and cross-shore directions are

$$\overline{u}={\displaystyle {\int }_0^{(b_0-b)\tan \alpha }u(a,b,c)\hspace{0.17em}}\mathrm{d}c=-U(b_0-b)\tan \alpha +\frac{c_0}{k}{e}^{kb}\left[e^{k(b-b_0)\tan \alpha }-1\right]\cos (k(a+c_{0}t)),$$

$$\overline{v}={\displaystyle {\int }_0^{(b_0-b)\tan \alpha }v(a,b,c)\hspace{0.17em}}\mathrm{d}c=\frac{c_0}{k}{e}^{kb}\left[e^{k(b-b_0)\tan \alpha }-1\right]\sin (k(a+c_{0}t)),$$

The Lagrangian mean velocities which are known as the mass transport velocity could be obtained by taking the time averaged over a wave period of the depth-averaged velocities in the longshore and cross-shore directions

$${\langle \overline{u}\rangle }_L=\frac{1}{T}{\displaystyle {\int }_0^T\overline{u}}(a,b,c,t)\mathrm{d}t=-U(b_0-b)\tan \alpha .$$

(22)

$${\langle \overline{v}\rangle }_L=\frac{1}{T}{\displaystyle {\int }_0^T\overline{v}}(a,b,c,t)\mathrm{d}t=0.$$

(23)

From Equations (22) and (23) we can find that the Lagrangian velocity can be westward or eastward depending on the sign of underlying currents. As U = 0, the Lagrangian mean velocity is equal to zero.

Therefore, the Eulerian mean velocity in the longshore and cross-shore directions can be expressed by mean of the depth-averaged velocities in the longshore and cross-shore directions

$$\begin{array}{cc}\hfill {\langle \overline{u}\rangle }_E& =\frac{1}{L}{\displaystyle {\int }_0^L[\overline{u}(x,y,z)]\mathrm{d}t}\hfill \\ & =\frac{1}{L}{\displaystyle {\int }_0^L\overline{u}(a,b,c)\frac{\partial x}{\partial a}\mathrm{d}a}\hfill \\ & =\frac{1}{L}{\displaystyle {\int }_0^L\{-U(b_0-b)\tan \alpha +\frac{c_0}{k}{e}^{kb}\left[e^{k(b-b_0)\tan \alpha }-1\right]\cos (k(a+c_{0}t))\}}\times (1-e^{\xi }\cos \theta )\mathrm{d}a\hfill \\ & =-U(b_0-b)\tan \alpha -\frac{c_0}{2k}{e}^{2k(b-c)}\left[e^{k(b-b_0)\tan \alpha }-1\right],\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill {\langle \overline{v}\rangle }_E& =\frac{1}{L}{\displaystyle {\int }_0^L[\overline{v}(x,y,z)]\mathrm{d}t}\hfill \\ & =\frac{1}{L}{\displaystyle {\int }_0^L\overline{v}(a,b,c)\frac{\partial y}{\partial a}\mathrm{d}a}\hfill \\ & =\frac{c_0}{k}{e}^{kb}\left[e^{k(b-b_0)\tan \alpha }-1\right]\sin \theta (-e^{\xi }\sin \theta )\mathrm{d}a\hfill \\ & =-\frac{c_0}{2k}{e}^{k(2b-c)}\left[e^{k(b-b_0)\tan \alpha }-1\right],\hfill \end{array}$$

(25)

so that the Eulerian mean flow in the longshore direction is westward along the equator and is to the offshore in the cross-shore direction as $c_0=c_{0+}$ and vice versa as $c_0=c_{0-}$. Therefore, the Stokes drifts in the longshore and cross-shore directions, defined as the difference between the Lagrangian and the Eulerian mean velocities, are

$$\begin{array}{cc}\hfill {\langle \overline{u}\rangle }_s& ={\langle \overline{u}\rangle }_L-{\langle \overline{u}\rangle }_E\hfill \\ & =\frac{c_0}{2k}{e}^{2k(b-c)}\left[e^{k(b-b_0)\tan \alpha }-1\right],\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill {\langle \overline{v}\rangle }_S& ={\langle \overline{v}\rangle }_L-{\langle \overline{v}\rangle }_E\hfill \\ & =\frac{c_0}{2k}{e}^{k(2b-c)}\left[e^{k(b-b_0)\tan \alpha }-1\right],\hfill \end{array}$$

(27)

These are eastward in the longshore direction along the equator and is to the onshore in the cross-shore direction as $c_0=c_{0+}$ and vice versa as $c_0=c_{0-}$.

5. Conclusions

In this paper, I showed an exact, explicit solution to the governing equations for the three-dimensional nonlinear geophysical water waves with underlying uniform currents. In the absence of current and the Coriolis effect, the solution particularizes to the gravity edge wave solution described in Ref. [22]. The closed form of the solution in the Lagrangian framework permits us to provide clear illustrations of the structure of these geophysical waves. For this solution, the presence of an underlying uniform current has the effect that the particle trajectories are no longer circles but open orbits, due to the effect of the longshore current. These orbits lie in planes parallel to the sloped bottom. Taking the plus sign in (13), the wave propagates along the equator from east to west. On the other hand, taking the minus, it travels from east to west. The Coriolis force as well as the underlying uniform current influence the propagation speed. I also provide an analysis of the mean flow velocities and the related mass transport. Finally, it is possible to extend this solution to the variable underlying currents since the longshore current is not constant.