Abstract
The influence of a strong and gusty wind field on ocean waves is investigated. How the random wind affects solitary waves is analyzed in order to obtain insights about wave generation by randomly time varying wind forcing. Using the Euler equations of fluid dynamics and the method of multiple scales, a random nonlinear Schrödinger equation and a random modified nonlinear Schrödinger equation are obtained for randomly wind forced nonlinear deep water waves. Miles theory is used for modeling the pressure variation at the wave surface resulting from the wind velocity field. The nonlinear Schrödinger equation and the modified nonlinear Schrödinger equation are computed using a relaxation pseudo spectral scheme. The results show that the influence of gusty wind on solitary waves leads to a randomly increasing ocean wave envelope. However, in a laboratory setup with much smaller wave amplitudes and higher wave frequencies, the influence of water viscosity is much higher. This leads to fluctuating solutions, which are sensitive to wind forcing.
1. Introduction
The formation of water waves under the influence of wind is an important physical process, which can result in the emergence of rogue waves. Such waves have been measured in the oceans [1] and can endanger the life of offshore workers, crews, passengers of ships, and can cause major damage to offshore structures and vessels. The accurate modeling of sea states is based on random fields known as random seas, since influences such as wind, swell and currents can in general be quantified only statistically. The nonlinear modeling of random seas allows for the analysis of waves with a significantly greater wave slope than is possible with linear wave theory. In this work, the role of randomness in the forcing of nonlinear waves was studied. In this case it was of interest whether gusty wind leads to the development of large waves or whether it prevents the occurence of such waves. It is sufficient for solving many problems in offshore engineering to use the Euler equations, instead of considering the Navier-Stokes equations. Then, it can be further shown that weakly nonlinear solutions of the Euler equations can be reduced to solutions described by a complex envelope, which satisfies the nonlinear Schrödinger equation (NLS) in the case of one spatial dimension or in general to the Benny-Roskes equations in the case of two spatial dimensions and arbitrary depth, see Reference [2]. Later, the Davey-Stewartson equations were derived in Reference [3], which are a specific case of the Benny-Roskes equations. Such reductions can be achieved by the method of multiple scales, cf. Reference [4]. Higher order approximation of the nonlinear water wave envelope leads to Dysthe equations [5], for which fluid viscosity has been included in Reference [6]. The Dysthe equation is also known as the modified nonlinear Schrödinger equation (MNLS) in one spatial dimension. For the deterministic NLS, a variety of solutions have been presented in References [7,8,9]. In an experimental study, Peregrine breathers were recently observed in random sea states [10]. Thus, it makes sense to study the NLS, as well as the MNLS under perturbations due to random wind, in order to obtain basic results about the behavior of nonlinear random waves and nonlinear stochastic sea states.
The main source of energy for the growth of gravity waves is wind. In a series of papers, Miles described the growth of surface waves by wind quantitatively, For example, References [11,12]. Although Miles used a quasi-laminar approximation leading to a stream function which satisfies the Rayleigh equation, the practical relevance of this theory has been confirmed in field experiments for long waves [13]. Using the method of multiple scales, Leblanc [14] derived a forced NLS for the case of deterministic wind forcing for weakly nonlinear surface gravity waves. The evolution of solutions of the NLS under the influence of deterministic forcing is described in the book by Fabrikant and Stepanyants [15]. Later, deterministic wind forcing and viscous dissipation for weakly nonlinear surface gravity waves by means of a forced and damped NLS was considered by Kharif et al. [16]. For the Dysthe equations [5] fluid viscosity has been included in Reference [6]. Experimental studies on the effect of wind forcing on water waves have also been conducted. For example, Chabchoub et al. [17] presented results on the modulation instability and the Peregrine breather in the presence of wind forcing. Theoretical results concerning the effect of strong wind on modulation instability were obtained in References [18,19]. Moreover, the spectral up- and downshifting of Akhmediev breathers under wind forcing has been shown recently numerically and experimentally [20] using the MNLS and Miles mechanism [11].
Combining the NLS and MNLS with a random wind forcing leads to a stochastic partial differential equation (SPDE). For the stochastic NLS in optics and Bose-Einstein condensation, finite difference schemes were derived by Debussche, de Bouard and Di Menza in References [21,22,23,24] in order to obtain numerical solutions.
This work is organized as follows: after the introduction, a forced modified nonlinear Schrödinger equation for time and space variant wind-induced pressure is stated in Section 2; then the numerical solution method for the evolution equations from Section 2 is presented in Section 3, followed by a description of the modeling and generation of a random wind velocity field in Section 4; in Section 5, the obtained results are presented and discussed; followed by the conclusions in the last Section.
2. Formulation
An essential part of the presented research is the consideration of a time variant wind field. It can be shown that the unforced Euler equations can be reduced to the MNLS in the case of deep water, see Reference [25]. Such a reduction can be achieved by the method of multiple scales up to order in wave steepness , cf. Reference [4]. Considering expansions up to the fourth order and a time variant forcing term , the multiple scales expansion leads to the following evolution equation of the wave envelope for the case of deep water ()
Thereby, is the wave envelope, is the scaled time, is a spatial coordinate moving with the deep water group velocity , amd is the wave steepness, is the viscosity of water, k is the wave number and is the frequency of a carrier wave. Moreover, is the Hilbert transform of the function f, which is connected with the Fourier transform by
The forcing term is obtained from the well-known Miles mechanism [11], which has proven to be a simple and versatile model for wind-induced wave growth [13]. Following Reference [16], can be stated as
where is the wave surface elevation, is the friction velocity, is the von Karman constant, is the density of air, and was obtained by Miles in Reference [12,26]. In this study, the friction velocity is time-variant in expression (3), leading to a time-variant . The relation between wind velocity at height z and friction velocity for a logarithmic wind profile is given by
where the roughness length is given by , with the Charnock constant . For the values of , which are a function of , the results of Conte and Miles [27] for the logarithmic wind profile (4) are used. Thereby, the dimensionless roughness length is chosen for numerical calculations. In order to compute the time and space dependent friction velocity from the velocity field at height z from (4), a fix point iteration has to be used.
The corresponding MNLS for constant was obtained previously in Reference [20]. Neglecting terms, which are multiplied by in the MNLS (1), the nonlinear Schrödinger equation (NLS) is obtained
which has been previously derived for constant in References [14,16,28]. Results on deterministic soliton solutions of the unforced NLS (5) with are well known and a closed-form expression is available for the undisturbed case. For the unperturbed NLS a soliton solution is given by
with the free background amplitude parameter , and . The corresponding soliton solution is shown in Figure 1.
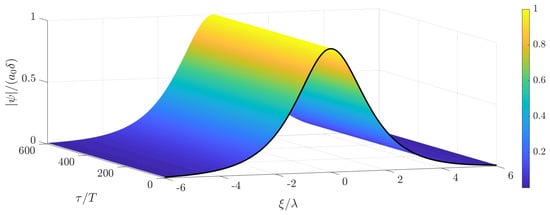
Figure 1.
Temporal evolution of a soliton solution of the unforced nonlinear Schrödinger equation (NLS) (5) with .
In the case of constant forcing in the NLS (5), a closed-form expression of a slowly varying solitary wave is determined by Grimshaw [28] based on the theory in Reference [29]. Such a slowly varying solitary wave is shown in Figure 2 and is given by
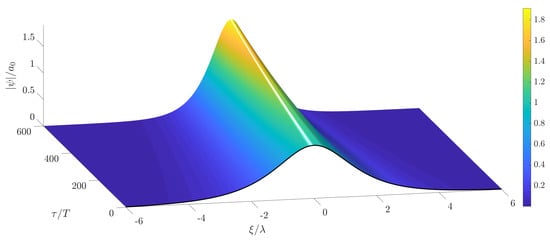
Figure 2.
Temporal evolution of a solitary wave solution of the constantly forced NLS (5).
3. Numerical Solution Method for the NLS
For the calculation of solutions of nonlinear water wave surface elevation excited by a random wind process, stochastic partial differential equations have to be solved numerically.
In order to obtain numerical solutions for the NLS (5) and the MNLS (1) in the deterministic, as well as in the stochastic case, a relaxation finite difference scheme is used. The relaxation scheme has been introduced by Besse [30] for the NLS as an extension to schemes of Crank-Nicolson type. In contrast to Crank-Nicolson type schemes, the used pseudo spectral relaxation scheme does not need to fulfill a Courant-Friedrichs-Lewy (CFL) condition, which links the discretization in time to the discretization in space and can make the numerical computation infeasible. Details of the relaxation scheme are shown in Appendix A. For the numerical solution of the NLS (5) and MNLS (1), periodic boundary conditions on a large enough domain are considered, as well as an initial condition at time .
In the following, the soliton solution of the NLS as given in Equation (6) is used as the initial condition .
Random Excitation by White Noise
Before analyzing a random excitation of the NLS (5) resulting from a random wind velocity process, a Gaussian white noise process in time is considered. This process has the properties and , , where is the Dirac function.
With this, sample results for the stochastic NLS (5) under white noise excitation are calculated. The random excitation due to such a white noise process reveals fundamental random dynamics of the stochastic NLS (5). A sample solution to Equation (5) under excitation by white noise in time starting at a soliton solution from Equation (6) as initial condition with m and rad/s is shown in Figure 3. Thereby, the variance of the white noise excitation has been set to . In this case the random forcing is very severe, which means that it is of more then one order of magnitude stronger then typical random forcing due to extreme wind conditions. This leads to a large deviation of the solution compared to the initial solitary wave.
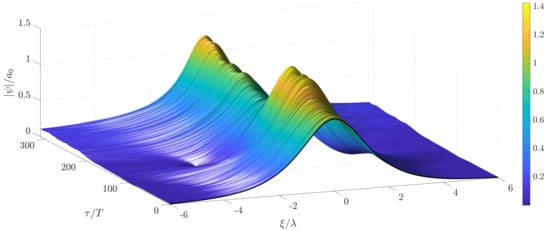
Figure 3.
Temporal evolution of a solution of the stochastic NLS with white noise excitation in time and a soliton solution as initial condition. Strong random forcing with a variance .
4. Random Excitation by Wind
An important question is how the characteristic behavior of special solutions of the NLS, such as the soliton solution (6), is changed in an environment with random forcing due to wind.
In the following, the necessary theory for the generation of a stochastic process for the wind velocity is presented. Real gusty wind has been measured by Van der Hoven in [31]. Such wind velocity processes can be described by the von Karman model, which is characterized by the power spectral density [32]
For the von Karman spectrum the coefficients and are given by
and depend on the mean wind speed , the correlation length , and the standard deviation of the wind speed fluctuation.
A CARMA process as given in Reference [33] is used in order to generate a non white wind velocity process, which takes random wind gusts into account. A second-order rational transfer function approximation for the von Karman spectrum is chosen, which has been obtained in Reference [34]
From this, a CARMA(2,1) process is generated, which is given by the following stochastic differential equation
where is the increment of a standard Wiener process and
This CARMA(2,1) process has the spectral density
which is an accurate approximation of the von Karman spectrum in Equation (8), as can be seen in Figure 4. A continuous time wind velocity process in the surface boundary layer can now be generated using the CARMA(2,1) process from Equation (11). An example of such a process is shown in Figure 5.
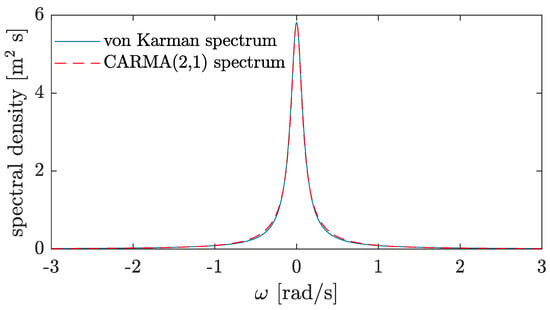
Figure 4.
Von Karman spectrum and its CARMA(2,1) approximation for mean wind speed m/s, correlation length , and .
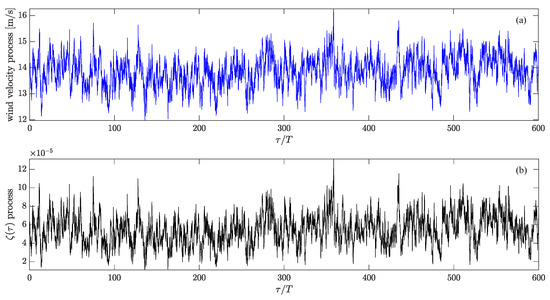
Figure 5.
Wind velocity process and corresponding time dependent random forcing process for m/s and m/s.
5. Results for Water Waves Forced by Random Wind
In this section, results for the randomly forced MNLS and NLS are presented. Thereby, the effect of physically realistic turbulent wind on solutions initialized by soliton solutions (6) of the NLS is analyzed.
The NLS (5) and the MNLS (1) are forced by a time varying random wind velocity process at height z. The wind velocity field is generated by a CARMA(2,1) process from Equation (11), with the von Karman spectrum given by Equation (8) at height m. A logarithmic wind profile according to Equation (4) is assumed. From the randomly time varying wind velocity process the friction velocity is calculated by means of a fix point iteration using Equation (4). The resulting random friction velocity defines the process according to Equation (3), which is a stochastic process. Then this process is used as the excitation in the NLS (5) and the MNLS (1).
In the following numerical calculations, the coordinate moving with the deep water group velocity is considered. First, results for the NLS are shown, followed by results for the MNLS. A randomly time dependent wind forced soliton is calculated using the soliton solution from Equation (6) as initial condition and parameter values from Equations (12) and Table 1, as well as wave parameters m and rad/s, which correspond to real ocean waves. In Figure 6, Figure 7 and Figure 8 the evolution of the wave envelope of the NLS (5) forced by a wind process with mean velocity m/s at the height and different standard deviations m/s, m/s, and m/s is shown. The results in Figure 6 and Figure 7 could also be accurately approximated using a constant forcing as described for example in References [28,35]. As can be seen in the comparative plots in Figure 9 the analytical solution using the theory in Reference [28] as given in Equation (7) leads to accurate approximations of the stochastic NLS solutions for the cases with and .

Table 1.
Parameter specifications.
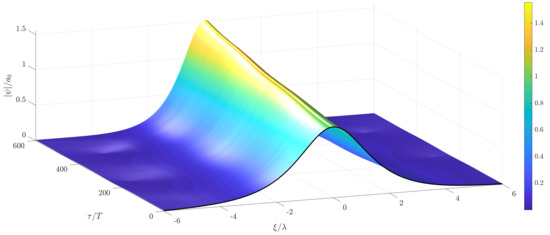
Figure 6.
Temporal evolution of a soliton solution of the stochastic NLS with non-white noise excitation in time, mean wind velocity m/s and m/s.
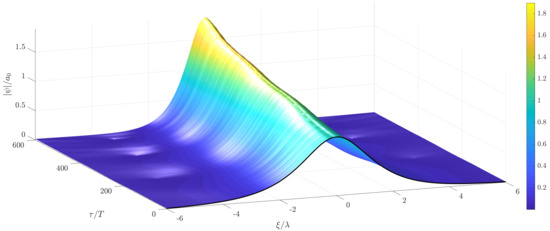
Figure 7.
Temporal evolution of a soliton solution of the stochastic NLS with non-white noise excitation in time, mean wind velocity m/s and m/s.
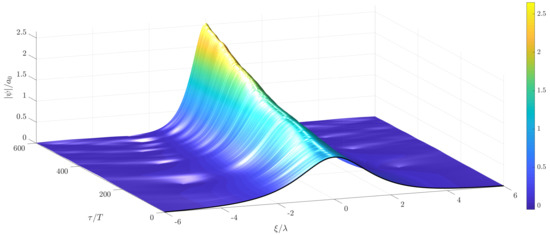
Figure 8.
Temporal evolution of a soliton solution of the stochastic NLS with non-white noise excitation in time, mean wind velocity m/s and m/s.
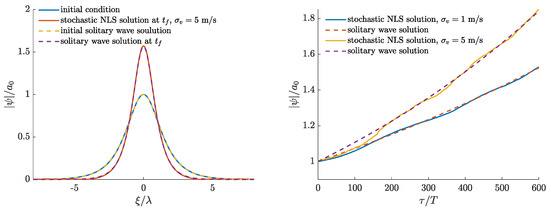
Increasing the wind velocity standard deviation leads to increasing fluctuations of the wind velocity. The corresponding wind velocity processes, as well as the resulting random forcing
are shown in Figure 5, Figure 10 and Figure 11. As can be observed in Figure 6, Figure 7 and Figure 8, the zero water level gets disturbed as well during the evolution of the randomly wind forced soliton. In contrast to the soliton solution in Figure 1, a time varying growth in the envelope amplitude and a symmetric behavior in space of the resulting random solution is observed in these figures. Corresponding results of the MNLS were also computed using the same random forcing from Figure 5, Figure 10 and Figure 11. These results can be seen in Figure 12, Figure 13 and Figure 14. The randomly increasing behavior of the wave envelope is the same, as in the case of the corresponding solutions of the NLS; however, the solutions are not symmetric anymore and a slight drift to the right can be observed. This drift can be attributed to the terms with first and third order of derivatives which appear in the MNLS additional terms, cf. (1). In order to show this behavior more clearly, the long-term evolution of the wave envelope is shown in Figure 15 for the wind velocity standard deviation m/s. The drift and the non-symmetric behavior can be clearly seen in Figure 16. This figure shows a comparison between solutions of the NLS and the MNLS at the initial time, as well as at the final time of the computations.
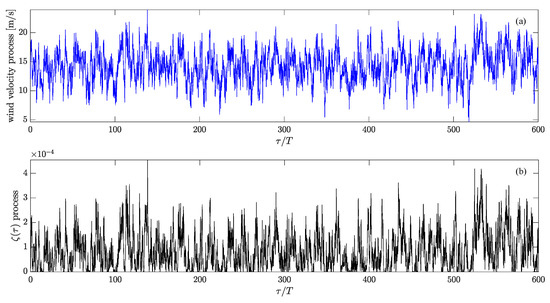
Figure 10.
Wind velocity process and corresponding time dependent random forcing process for m/s and m/s.
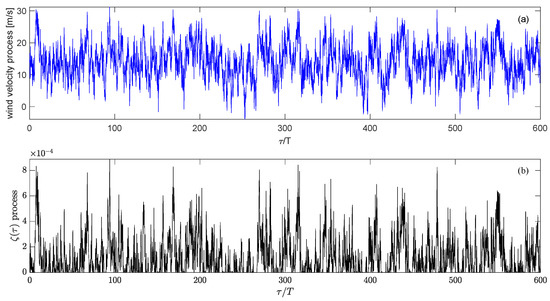
Figure 11.
Wind velocity process and corresponding time dependent random forcing process for m/s and m/s.
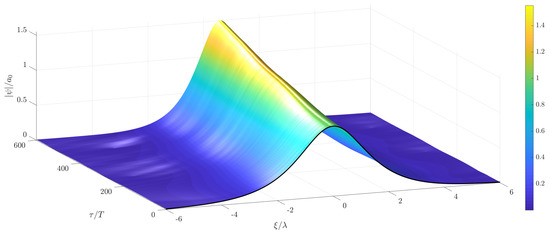
Figure 12.
Temporal evolution of a soliton solution of the stochastic modified Schrödinger equation (MNLS) with non-white noise excitation in time, mean wind velocity m/s and m/s.
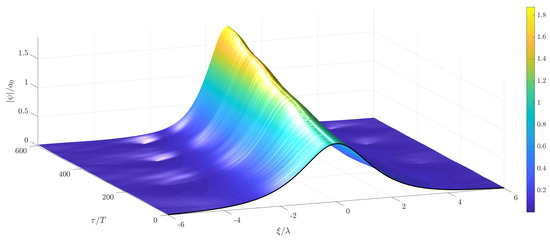
Figure 13.
Temporal evolution of a soliton solution of the stochastic MNLS with non-white noise excitation in time, mean wind velocity m/s and m/s.
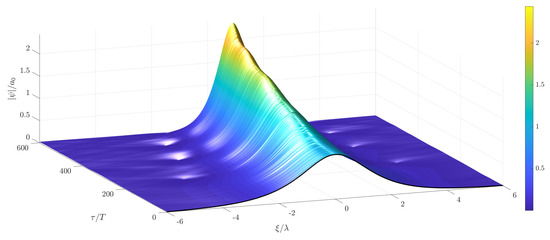
Figure 14.
Temporal evolution of a soliton solution of the stochastic MNLS with non-white noise excitation in time, mean wind velocity m/s and m/s.
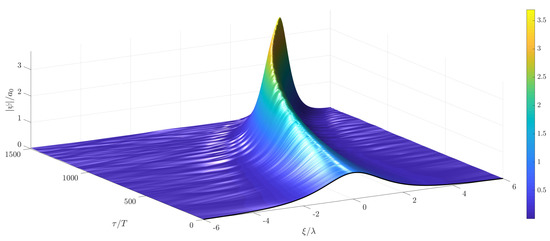
Figure 15.
Long-term evolution of a solitary wave solution of the stochastic MNLS with random wind forcing in time. Mean wind velocity m/s and m/s.
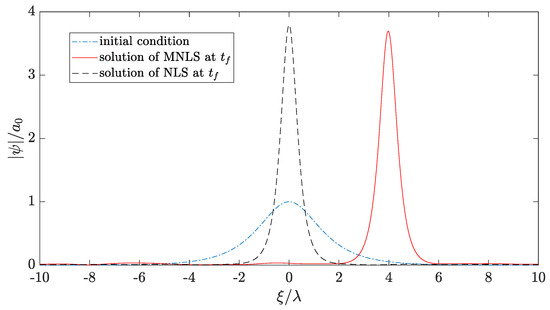
Figure 16.
Temporal evolution of a soliton solution of the stochastic MNLS with non-white noise excitation in time, mean wind velocity m/s and m/s.
An important observation from these results is that random fluctuations in the wind excitation do not destroy the solitary wave appearance of the solutions.
As a next case, solutions with the laboratory scale parameter values cm, rad/s, 1/m, m/s and m/s are calculated. These parameter values correspond to the experimental setup from Reference [17], where Peregrine breather solutions were studied under the influence of wind in a wind-wave flume. With the wind velocity process from Figure 17, the wave envelope evolves according to Figure 18 for the NLS and Figure 19 for the MNLS in the laboratory scale setup. The difference between the solution of the NLS and the MNLS is shown in Figure 20, where the non-symmetricity of the MNLS solution, as well as the right shift can be seen.
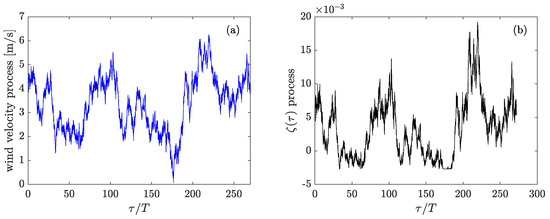
Figure 17.
(a) Wind velocity process and (b) corresponding time dependent random forcing process for the lab parameters m/s, m/s, carrier wave frequency rad/s and wave number .
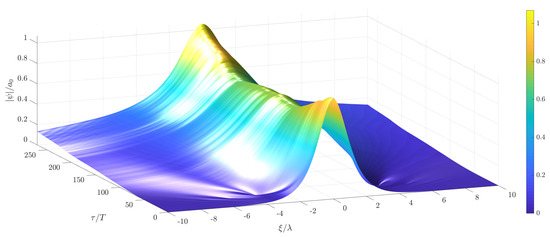
Figure 18.
Temporal evolution of a soliton solution of the stochastic NLS with non-white noise excitation in time using laboratory scale parameters cm, rad/s, 1/m, mean wind velocity m/s and m/s.
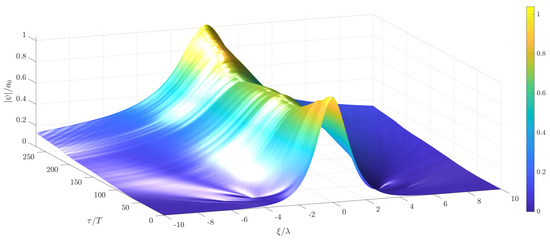
Figure 19.
Temporal evolution of a soliton solution of the stochastic MNLS with non-white noise excitation in time using laboratory scale parameters cm, rad/s, 1/m, mean wind velocity m/s and m/s.
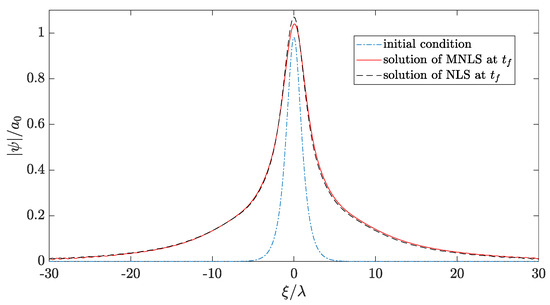
Figure 20.
Comparison between the soliton solutions of the stochastic MNLS and the stochastic NLS with non-white noise excitation in time using the lab parameters and mean wind velocity m/s and m/s.
By comparing the random processes in Figure 17 with for the real scale case in Figure 5, Figure 10 and Figure 11, it can be seen that the viscosity has a much greater influence at the experimental scale, since there is a significantly greater amount of time at which the process is negative. Moreover, in comparison to the case in Figure 5, Figure 10 and Figure 11, the random forcing process is stronger. Hence, the resulting forced solution deviates more from the soliton solution (6) than in the real scale case.
In this laboratory parameter setup, solutions with higher amplitude peaks appeared as well, as can be seen in Figure 21. In this figure, a different realization of the wind velocity process was used, having the same statistical parameters as the process in Figure 17. This shows that larger waves can also emerge from an initial soliton solution under the action of wind. However, such solutions were not observed in the real ocean parameter setup. Further investigations will be carried out in the future in order to find out whether larger waves emerging from soliton solutions, as in the laboratory parameter case, can also occur in real ocean waves.
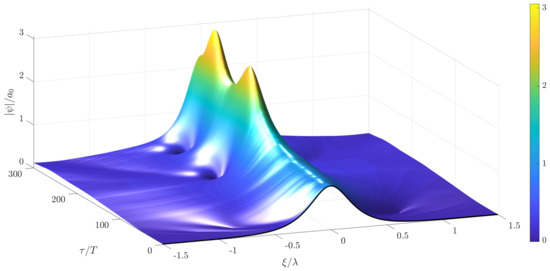
Figure 21.
Different realization of the temporal evolution of a soliton solution of the stochastic MNLS with non-white noise excitation in time using the same parameters as in Figure 19. This solution shows the appearance of higher amplitude waves.
6. Conclusions
Solutions of the randomly wind excited nonlinear Schrödinger equation (NLS) and the modified nonlinear Schrödinger equation (MNLS) have been calculated starting at the soliton solutions of the unperturbed NLS. Thereby, the deviation from the soliton solution of the wave envelope is analyzed. The influence of different wind forcing cases in these solutions was shown. It was found that no rogue waves coming out of nowhere appeared during the computations for parameter values related to ocean waves and moderate wind with mean velocity of 14 m/s and peak velocity up to 28 m/s. However, using laboratory scale parameter sets, the solutions of the wind forced NLS amd MNLS showed a higher sensitivity to the water viscosity and wind forcing with a mean velocity of 3 m/s and a peak velocity of about 6 m/s. During the laboratory scale simulations, higher solution peaks also appeared. The obtained results indicate that solitary waves are not considerably disturbed in the oceans under moderate random wind forcing.
Funding
This research received no external funding.
Acknowledgments
The relaxation scheme of the MNLS was implemented by Marten Hollm, which is gratefully acknowledged.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Numerical Schemes for the MNLS
A numerical scheme based on the relaxation scheme of Antoine and Duboscq [36] is introduced for the modified nonlinear Schrödinger equation of the form
Thereby, and are constant coefficients and are time dependent real functions. The resulting relaxation scheme for the MNLS (A1) is obtained as
In this numerical scheme, the space can be discretized by a pseudo-spectral approximation. The Hilbert transform can be computed by (2) using the Fourier transform. Neglecting the terms multiplied by in (A1), a numerical scheme for the NLS is obtained.
In these schemes, the stochastic processes and are generated using the CARMA process (11) with the same step size .
References
- Kharif, C.; Pelinovsky, E.; Slunyaev, A. Rogue Waves in the Ocean; Springer: New York, NY, USA, 2009. [Google Scholar]
- Benney, D.; Roskes, G. Wave instabilities. Stud. Appl. Math. 1969, 48, 377–385. [Google Scholar] [CrossRef]
- Davey, A.; Stewartson, K. On three-dimensional packets of surface waves. Proc. R. Soc. Lond. A 1974, 338, 101–110. [Google Scholar] [CrossRef]
- Mei, C.C. The Applied Dynamics of Ocean Surface Waves; Wiley-Interscience: New York, NY, USA, 1983. [Google Scholar]
- Dysthe, K.B. Note on a Modification to the Nonlinear Schrödinger Equation for Application to Deep Water Waves. Proc. R. Soc. A 1979, 369, 105–114. [Google Scholar] [CrossRef]
- Carter, J.D.; Govan, A. Frequency downshift in a viscous fluid. Eur. J. Mech. B/Fluids 2016, 59, 177–185. [Google Scholar] [CrossRef]
- Kuznetsov, E. Solitons in a parametrically unstable plasma. Akademiia Nauk SSSR Doklady 1977, 236, 575–577. [Google Scholar]
- Akhmediev, N.; Eleonskii, V.; Kulagin, N. Generation of periodic trains of picosecond pulses in an optical fiber: Exact solutions. Sov. Phys. JETP 1985, 62, 894–899. [Google Scholar]
- Peregrine, D. Water waves, nonlinear Schrödinger equations and their solutions. ANZIAM J. 1983, 25, 16–43. [Google Scholar] [CrossRef]
- Chabchoub, A. Tracking breather dynamics in irregular sea state conditions. Phys. Rev. Lett. 2016, 117, 144103. [Google Scholar] [CrossRef]
- Miles, J.W. On the generation of surface waves by shear flows. J. Fluid Mech. 1957, 3, 185–204. [Google Scholar] [CrossRef]
- Miles, J.W. On the generation of surface waves by shear flows. Part 2. J. Fluid Mech. 1959, 6, 568–582. [Google Scholar] [CrossRef]
- Hristov, T.; Miller, S.; Friehe, C. Dynamical coupling of wind and ocean waves through wave-induced air flow. Nature 2003, 422, 55–58. [Google Scholar] [CrossRef] [PubMed]
- Leblanc, S. Amplification of nonlinear surface waves by wind. Phys. Fluids 2007, 19, 101705. [Google Scholar] [CrossRef]
- Fabrikant, A.L.; Stepanyants, Y.A. Propagation of Waves in Shear Flows; World Scientific: Singapore, 1998; Volume 18. [Google Scholar]
- Kharif, C.; Kraenkel, R.; Manna, M.; Thomas, R. The modulational instability in deep water under the action of wind and dissipation. J. Fluid Mech. 2010, 664, 138–149. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.; Branger, H.; Kharif, C.; Akhmediev, N. Experiments on wind-perturbed rogue wave hydrodynamics using the Peregrine breather model. Phys. Fluids 2013, 25, 101704. [Google Scholar] [CrossRef]
- Brunetti, M.; Marchiando, N.; Berti, N.; Kasparian, J. Nonlinear fast growth of water waves under wind forcing. Phys. Lett. A 2014, 378, 1025–1030. [Google Scholar] [CrossRef]
- Brunetti, M.; Kasparian, J. Modulational instability in wind-forced waves. Phys. Lett. A 2014, 378, 3626–3630. [Google Scholar] [CrossRef]
- Eeltink, D.; Lemoine, A.; Branger, H.; Kimmoun, O.; Kharif, C.; Carter, J.; Chabchoub, A.; Brunetti, M.; Kasparian, J. Spectral up-and downshifting of Akhmediev breathers under wind forcing. Phys. Fluids 2017, 29, 107103. [Google Scholar] [CrossRef]
- de Bouard, A.; Debussche, A. A Stochastic Nonlinear Schrödinger Equation With Multiplicative Noise. Commun. Math. Phys. 1999, 205, 161–181. [Google Scholar] [CrossRef]
- de Bouard, A.; Debussche, A.; Di Menza, L. Theoretical and numerical aspects of stochastic nonlinear Schrödinger equations. Monte Carlo Methods Appl. 2001, 7, 55–63. [Google Scholar] [CrossRef]
- Debussche, A.; Di Menza, L. Numerical simulation of focusing stochastic nonlinear Schrödinger equations. Phys. D: Nonlinear Phenomena 2002, 162, 131–154. [Google Scholar] [CrossRef]
- de Bouard, A.; Debussche, A. Weak and strong order of convergence of a semidiscrete scheme for the stochastic nonlinear Schrödinger equation. Appl. Math. Optim. 2006, 54, 369–399. [Google Scholar] [CrossRef]
- Trulsen, K.; Dysthe, K.B. A modified nonlinear Schrödinger equation for broader bandwidth gravity waves on deep water. Wave Motion 1996, 24, 281–289. [Google Scholar] [CrossRef]
- Miles, J.W. Surface-wave generation: A viscoelastic model. J. Fluid Mech. 1996, 322, 131–145. [Google Scholar] [CrossRef]
- Conte, S.; Miles, J. On the numerical integration of the Orr-Sommerfeld equation. J. Soc. Ind. Appl. Math. 1959, 7, 361–366. [Google Scholar] [CrossRef]
- Grimshaw, R. Generation of Wave Groups by Shear Layer Instability. Fluids 2019, 4, 39. [Google Scholar] [CrossRef]
- Grimshaw, R. Slowly varying solitary waves. II. Nonlinear Schrödinger equation. Proc. R. Soc. Lond. A Math. Phys. Sci. 1979, 368, 377–388. [Google Scholar] [CrossRef]
- Besse, C. A relaxation scheme for the nonlinear Schrödinger equation. SIAM J. Numer. Anal. 2004, 42, 934–952. [Google Scholar] [CrossRef]
- Van der Hoven, I. Power spectrum of horizontal wind speed in the frequency range from 0.0007 to 900 cycles per hour. J. Meteorol. 1957, 14, 160–164. [Google Scholar] [CrossRef]
- Leithead, W.; De la Salle, S.; Reardon, D. Role and objectives of control for wind turbines. IEE Proc. C-Gen. Transm. Distrib. IET 1991, 138, 135–148. [Google Scholar] [CrossRef]
- Dostal, L.; Kreuzer, E. Probabilistic approach to large amplitude ship rolling in random seas. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2011, 225, 2464–2476. [Google Scholar] [CrossRef]
- Nichita, C.; Luca, D.; Dakyo, B.; Ceanga, E. Large band simulation of the wind speed for real time wind turbine simulators. IEEE Trans. Energy Convers. 2002, 17, 523–529. [Google Scholar] [CrossRef]
- Slunyaev, A.; Sergeeva, A.; Pelinovsky, E. Wave amplification in the framework of forced nonlinear Schrödinger equation: The rogue wave context. Phys. D Nonlinear Phenomena 2015, 303, 18–27. [Google Scholar] [CrossRef]
- Antoine, X.; Duboscq, R. Modeling and computation of Bose-Einstein condensates: Stationary states, nucleation, dynamics, stochasticity. In Nonlinear Optical and Atomic Systems; Springer: New York, NY, USA, 2015; pp. 49–145. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).