1. Introduction
The research field of hydrodynamic stability has the objective of elucidating how the structures of some specific temporal frequency and spatial scale are selected and emerge, owing to the amplification of small-magnitude perturbations. The comprehension of these effects is of huge relevance, since many flows of practical interest are dominated by genuine instability mechanisms that can be either enhanced or alleviated to improve performances. Typical expected benefits consist of the reduction of the operational cost of vehicles by decreasing skin friction or aerodynamic drag, or the extension of the operating conditions of turbomachinery by increasing the surface heat flux. The investigation is based on structural sensitivity [
1,
2], a theoretical concept stemming from the framework of stability analysis in laminar flows. This allows one to identify, beforehand, which regions of a given flow are most sensitive to a prescribed actuation, without the need for calculating the actual controlled flow and of resorting systematically to a trial-and-error procedure, which would represent an insurmountable bottleneck. Here, we apply this concept to determine where and how to control efficiently the turbulent-flow separation occurring at the rear-end of a ground vehicle. Such an approach can, thus, be used to obtain valuable information about the most sensitive regions for open-loop control, based on the underlying physics.
Separated flows often arise in industrial applications, resulting from an adverse pressure gradient stemming from either operating conditions or geometrical constraints (airfoil at high angles of attack, rear-end of a blunt body). They are usually associated with a loss of performance. For a ground vehicle, the flow separation taking place at its rear-end contributes to a huge increase in the drag force and, thus, also in the fuel consumption and pollutant emissions. For instance, a drag increase by 10% is expected to augment the fuel consumption by 5% at highway speeds. Moreover, flow separation causes low-frequency instabilities, which can trigger the excitation of aeroacoustic noise (sunroof cavities, side mirrors). The implementation of efficient control strategies, aimed at preventing separation itself or—when this is prohibitively costly or inevitable—at alleviating its detrimental consequences, is, therefore, a great environmental and economical issue. The dynamics are triggered by complex interactions between small-scale structures inside the shear layer, huge flow separations, and trailing vortices expanding far in the wake.
Many complex phenomena are investigated by means of linear perturbation dynamics, aimed at describing the fate of infinitesimal disturbances superimposed on a steady basic flow, and providing a rigorous mathematical foundation to investigate the control of fluid systems. Various perspectives have emerged, depending on whether the disturbance growth is characterized over large or short time intervals: on one hand, the archetype of disturbance energy amplified over asymptotically large times is the occurrence of vortex-shedding in wake flows, a behaviour called a modal instability [
1]; on the other hand, the transient amplification over finite times is typically observed in channel flows, and is referred to as a non-modal instability [
3,
4,
5].
For boundary-layer-like flows exhibiting a marginal separation, as occurs at the rear-end of a vehicle with small slant angle, a non-modal theoretical analysis can identify flow regions where the transient amplification of streamwise streaks (by the lift-up effect) is most sensitive to steady spanwise periodic disturbances [
6]. In the experiments, such disturbances can result from either steady jets or roughness elements positioned upstream of the separation location, reproducing a parietal or a volumic forcing, respectively. Indeed, it is very well known that the global dynamics of complex flows can be modified by imposing local disturbances. Typical examples are the use of surface rugosities to delay the transition to turbulence in boundary layers, or the injection of fluid into the wake of a bluff body to alleviate unsteadiness [
7]. We remind that the lift-up effect is related to the vertical mixing of large-speed fluid from higher layers to lower ones, and vice versa for small-speed fluid. A streamwise vorticity perturbation arises, and evolves into a set of streamwise stripes characterized by relevant variations of the streamwise velocity, possibly with a periodic structure in the spanwise direction: the streaks.
In practice, one can use the adjoint-state method to calculate the gradient of some objective function (energy gain over a specified time horizon, growth rate of unstable disturbances) with respect to each actuation parameter, thus making it possible to cover large parameter spaces with a limited number of computations. This capability is useful as an aid to guide the design of efficient, tractable control strategies. In the past, it has mainly been applied to related problems of vortex shedding in compressible or incompressible laminar wakes, and the agreement between the experimental results and the theoretical predictions is excellent, near the threshold of instability. Its application to flow separation for ground vehicles of practical importance constitutes a major issue, since substantial developments are necessary in order to encompass the complexity of turbulent-flow regimes, where large intervals of temporal and spatial scales strongly interact.
The paper is organized as follows. In
Section 2, we describe our numerical approach and its validation. In
Section 3, we specify the geometry under consideration and the main equations in play. In
Section 4, we introduce the base flow we have adopted. In
Section 5, we perform the linear-stability analysis and focus on the direct and adjoint perturbations. In
Section 6, we analyze the control mechanisms and the associated kinetic-energy gain. Conclusions and perspectives follow, in
Section 7. The
Appendix A is devoted to showing some further details about boundary conditions and adjoint equations.
2. Description and Validation of Numerical Tools
We have made use of the FreeFEM++ software [
8] to build a Finite-Element Method code. This tool solves the continuity and Navier–Stokes equations in their variational formulation, with prescribed boundary conditions (Dirichlet, Neumann, or mixed). We have implemented a P1 scheme for the pressure field, and a P1b scheme for the velocity field (for which we have also tested a P2 scheme, without any appreciable change in the results) [
9].
We have performed two main validation tests. In both cases, the quantitative validation makes use of a software which, by scanning printed figures from scientific articles, gives the numerical values of plotted points or lines with sufficient precision.
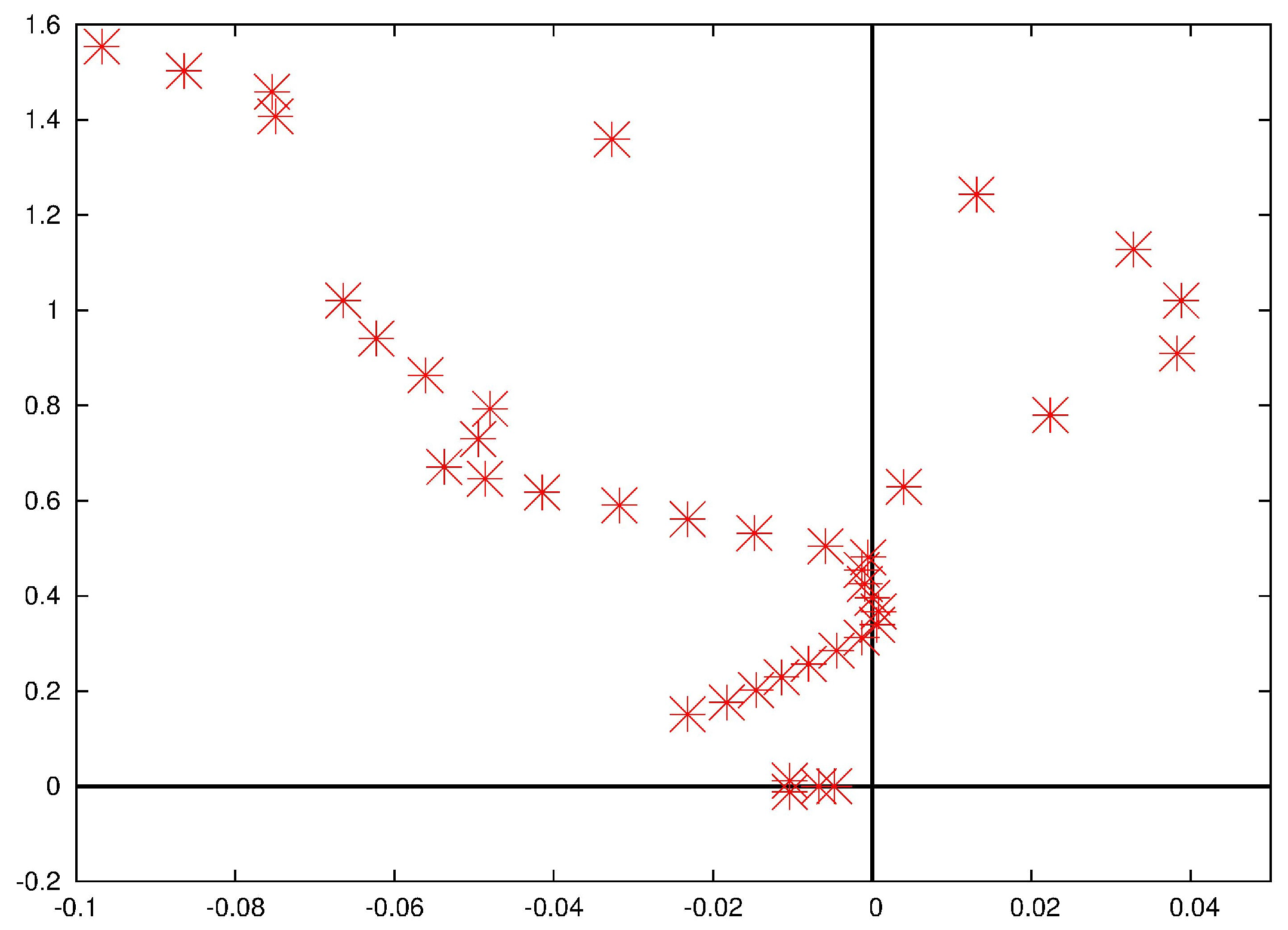
First, we have considered the 2D open cavity from [
10]. We have implemented the same exact geometry and mesh from their Figure 7, consisting of a long flat floor interrupted by a unit square excavated below it. We have performed a qualitative validation against their Figures 8c,d, and 10, for the direct and adjoint perturbations and the eigenvalues. More importantly, we have focused on their Figure 9b, reporting the generalized displacement thickness (to be defined more precisely by Equation (
4)), and have found a good quantitative agreement, as shown in our
Figure 1. (Note that the prefactor
reported in the caption of their Figure 9b in [
10] was wrong, the correct coefficient from the theory and in the plot is actually
[
11].)
Second, we have considered the 3D backward-facing step (inclined at
) from [
12]. We have implemented the same exact geometry from their Figure 1, and (because of the different numerical scheme) an approximate mesh from their Figure 2. We have performed a qualitative validation against their Figures 3, 4, and 7 for the base flow, the skin friction, and the eigenvalues. More importantly, we have focused on their Figure 5, reporting the separation/reattachment points, and have found a good quantitative agreement, as shown in our
Figure 2.
3. Geometry and Equations
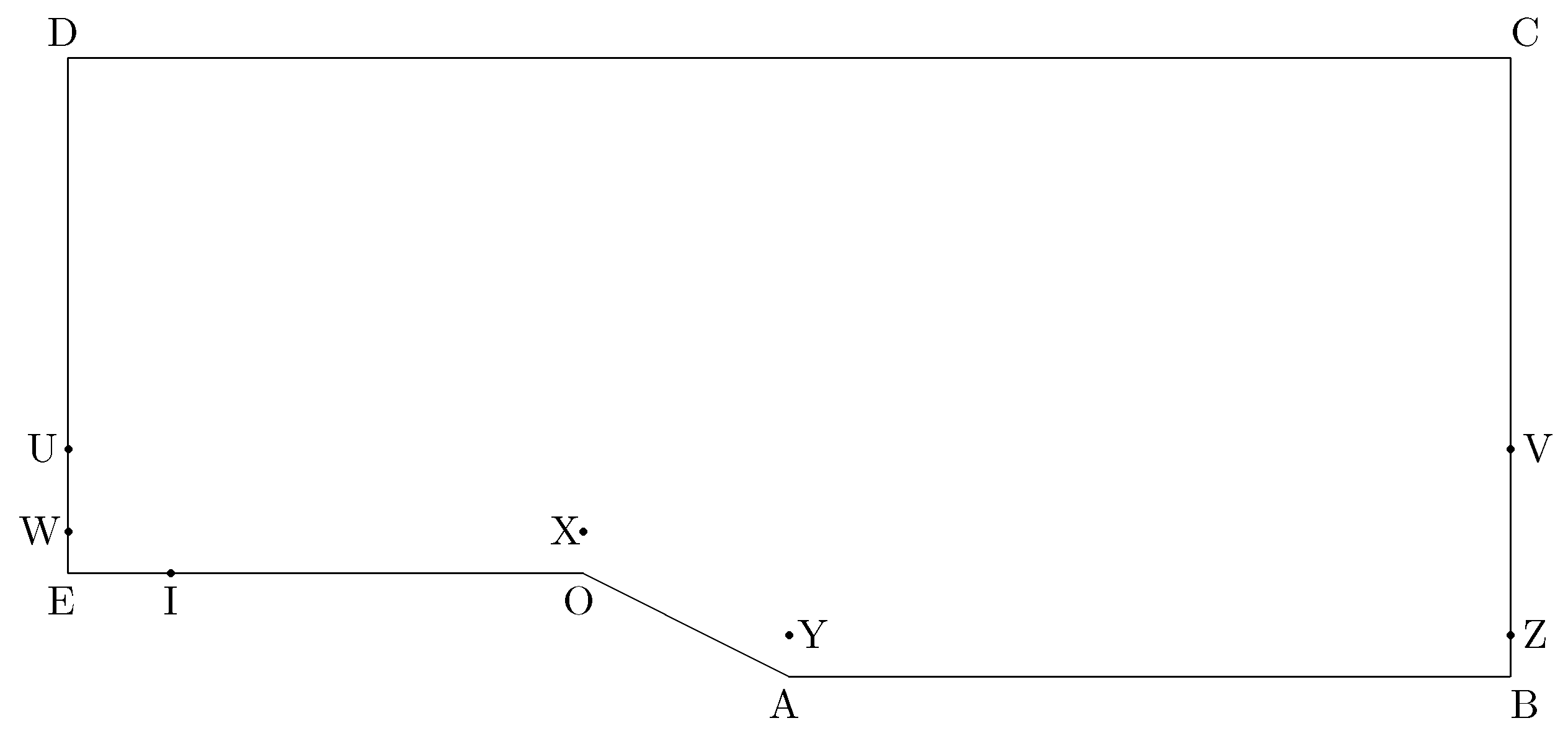
We have focused on a geometry issued from a standard ERCOFTAC benchmark, namely a backward-slanted step with a slope of
with respect to the horizontal surface. This configuration, plotted in
Figure 3, represents a simplification of the rear end of a car and of a portion of Ahmed’s body [
13]. The
x and
y axes correspond to the streamwise and wall-normal components, respectively, with the origin placed at the leftmost/uppermost point of the sloping zone. This picture is assumed to be invariant in the spanwise
z direction, which implies that the base flow is assumed to be two-dimensional, while the perturbations can present a three-dimensional character. (Different geometries investigated through this scheme can be found in, e.g., [
14,
15,
16]).
The linear density of meshing points for the automatic triangulation process has been assumed to be 4 on segments UD, DC, and CV; 14 on segments WU, UV, and VZ; and 24 on segments EW, WX, XY, YZ, ZB, BA, AO, OI, and IE—a finer grid is obviously required close to the lower physical boundary. The resulting number of triangular elements employed in the numerical simulations is about .
To non-dimensionalize, we have assumed as reference units the vertical projection of the step and the uniform inlet speed. As the two quantities have unitary values, the non-dimensionalized kinetic viscosity equals the inverse of the Reynolds number, based on the step height.
We have imposed standard inlet and outlet conditions on the left and right boundaries, respectively, and a free-slip condition on the upper boundary. At the lower boundary (a physical wall) we have imposed the no-slip condition, except for the beginning part, EI, where a free-slip condition has been used, in order to allow for the evolution of a boundary-layer profile [
17]. (See also
Appendix A).
Tests have also been made, in which we have varied the streamwise length of the domain (both upstream and downstream), its normal height, and the length of the segment EI for the imposition of the boundary condition. The chosen reference geometry falls in a range where convergence has already taken place. The case in which the upper boundary is a physical wall has also been briefly investigated, both in the case of the standard segment DC, and in a modified domain where the latter has a curved S-shaped profile to simulate a streamline and to study the influence of confinement [
18,
19]. The effect of the resolution has been tested as well, by implementing a discretization of up to almost
triangles, without appreciable changes.
The full incompressible flow
, comprising both the velocity and the pressure fields, satisfies the Navier–Stokes and continuity equations,
(For an interesting discussion of the role of compressibility—not considered here—see, e.g., [
20,
21].) In what follows, we decompose the flow into a 2D steady solution plus a 3D small perturbation:
for
and
.
4. Base Flow
We have assumed as our base flow,
, a steady solution of the Navier–Stokes and continuity equations,
satisfying the same boundary conditions as the full flow. We have obtained this flow, numerically, by means of Newton’s iterative method [
22]. (The relevance of small modifications in the base flow was studied in, e.g., [
23,
24].)
Notice that, because of mass conservation, this type of base flow presents a speed overshoot (i.e., for some range of
y the horizontal velocity exceeds unity). The vertical profile is not monotonic, as in a standard boundary layer, so it is not appropriate to define a typical width as the height at which the velocity reaches a definite percentage of the far-field value. It is, therefore, more convenient to quantify the boundary layer by means of the so-called “generalized displacement thickness” [
10]:
where
is the vorticity of the base flow (a scalar quantity, i.e., the
z component—the only non-zero—of the vector given by the curl of the base velocity). When this profile reaches the step, we find
, depending on the Reynolds number.
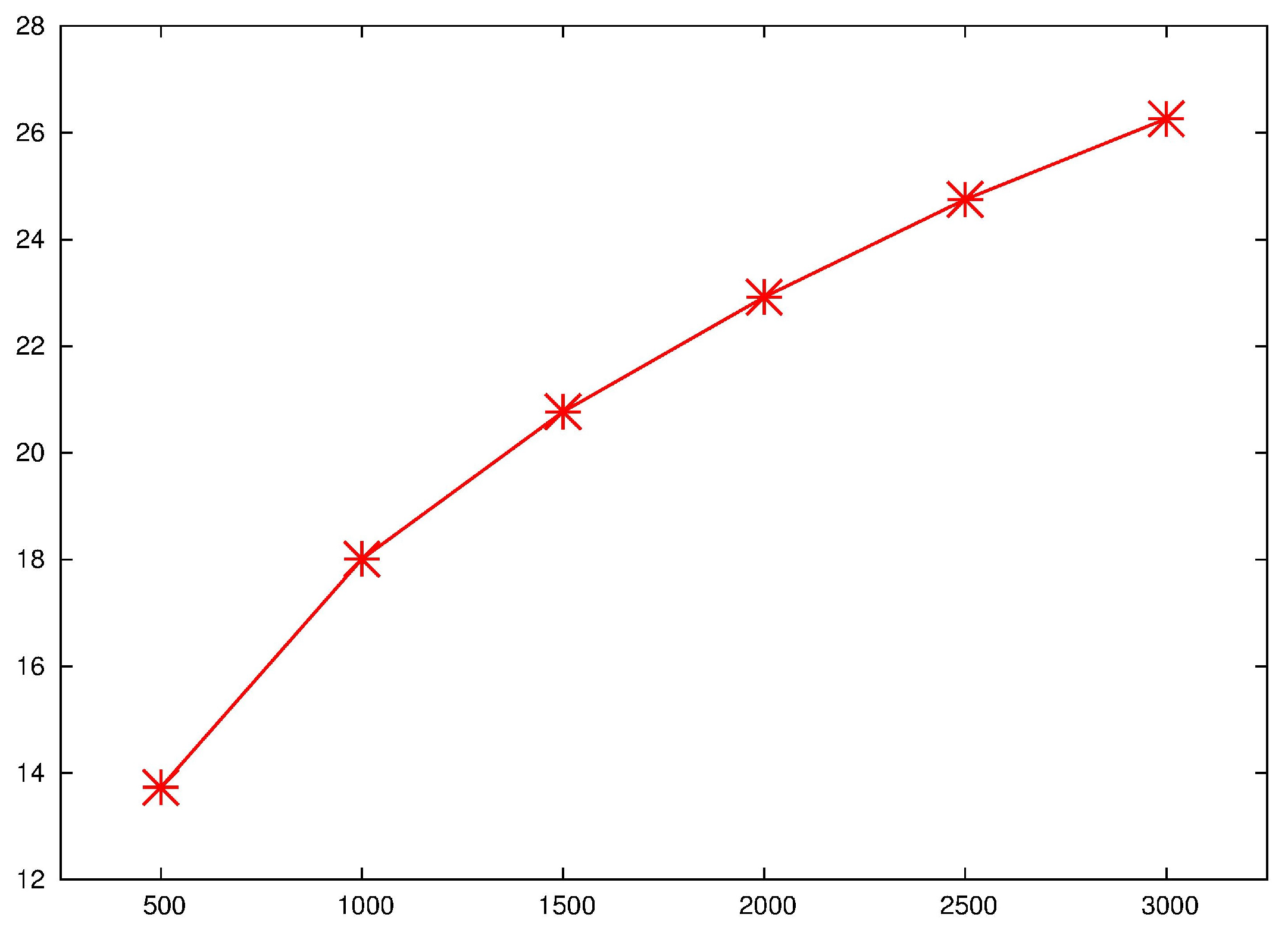
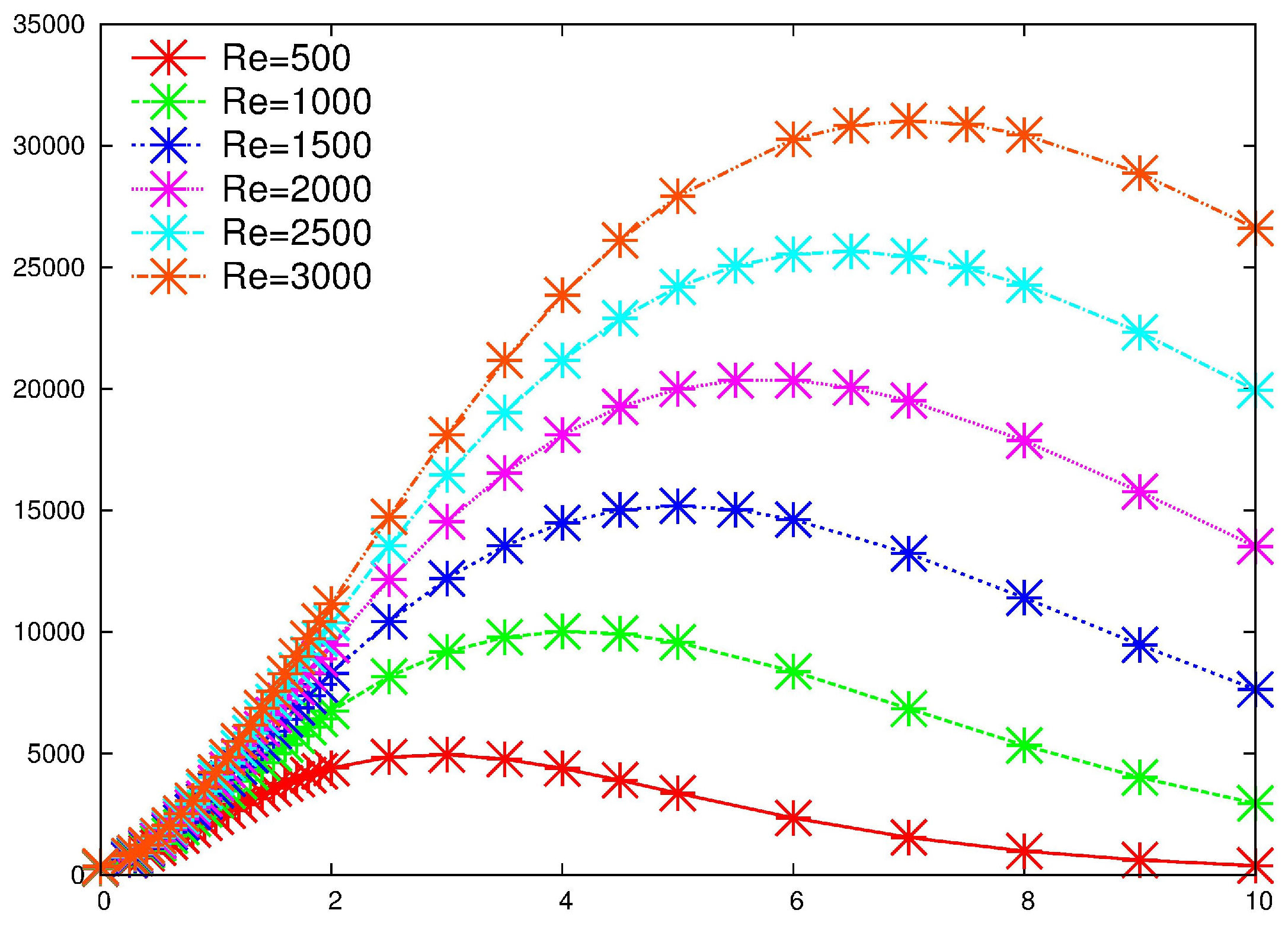
We have taken into consideration Reynolds numbers ranging from 500 to 3000, with increments of 500. The flow separates from the bottom boundary at the step and, with growing Reynolds number, a larger and larger recirculation bubble develops in the wake, until reattachment takes place.
Figure 4 displays the dependence of the reattachment point (i.e., the abscissa after the beginning of the step, at which the vertical derivative of the horizontal velocity at the lower wall turns from negative to positive) as a function of
. A sketch of the base flow for
is shown in
Figure 5.
5. Linear Stability Analysis
Upon fixing our base flow, we have performed a linear stability analysis (see e.g., [
25,
26]). Owing to the steadiness of the base flow and to its invariance in the spanwise direction, we consider the perturbation introduced in Equation (
2) in the form of a Fourier mode in
z, exponentially evolving in time:
The resulting linearized equation for the (direct) perturbation is:
We then seek those complex values of
such that Equation (
6) has nontrivial solutions
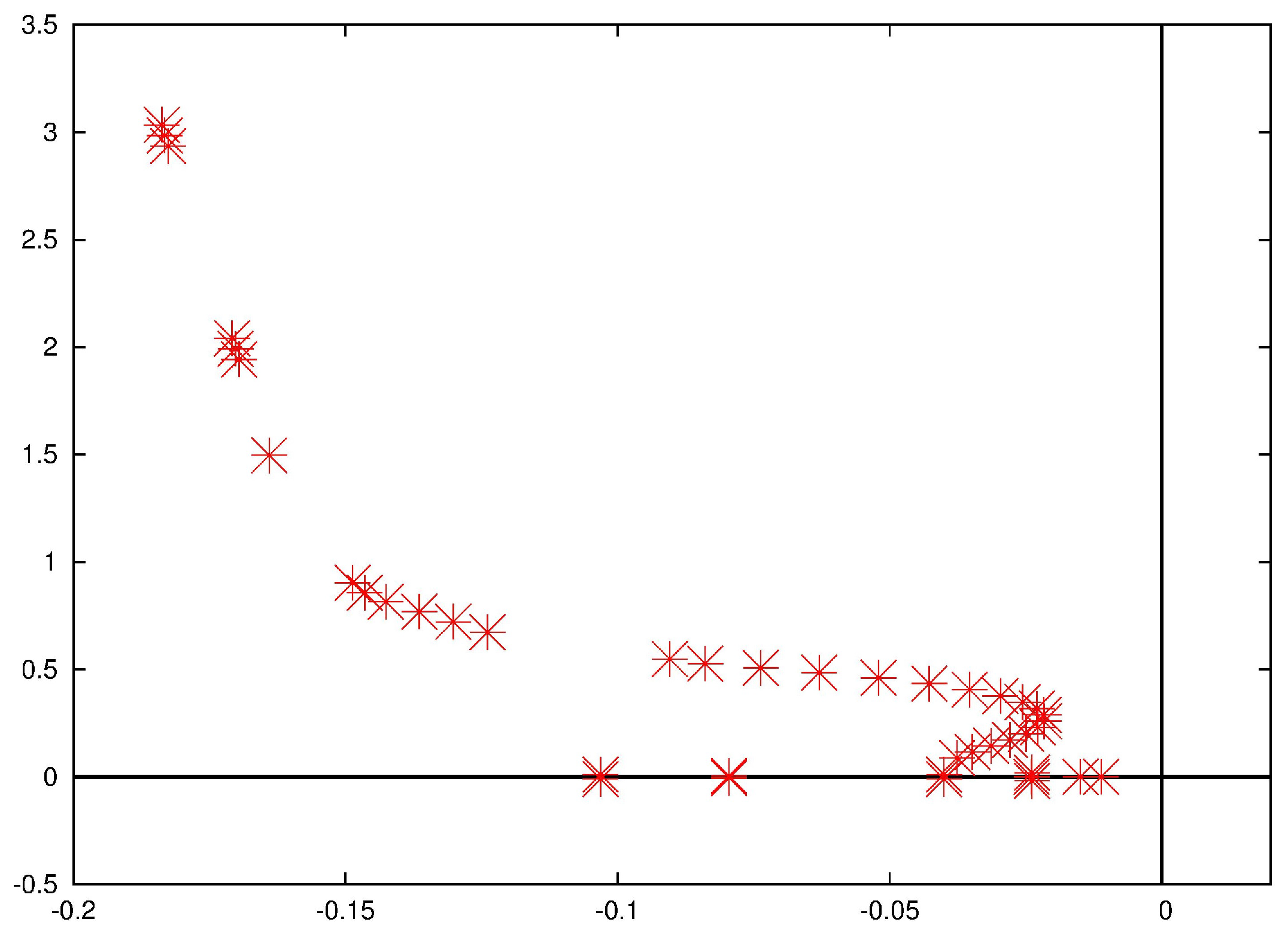
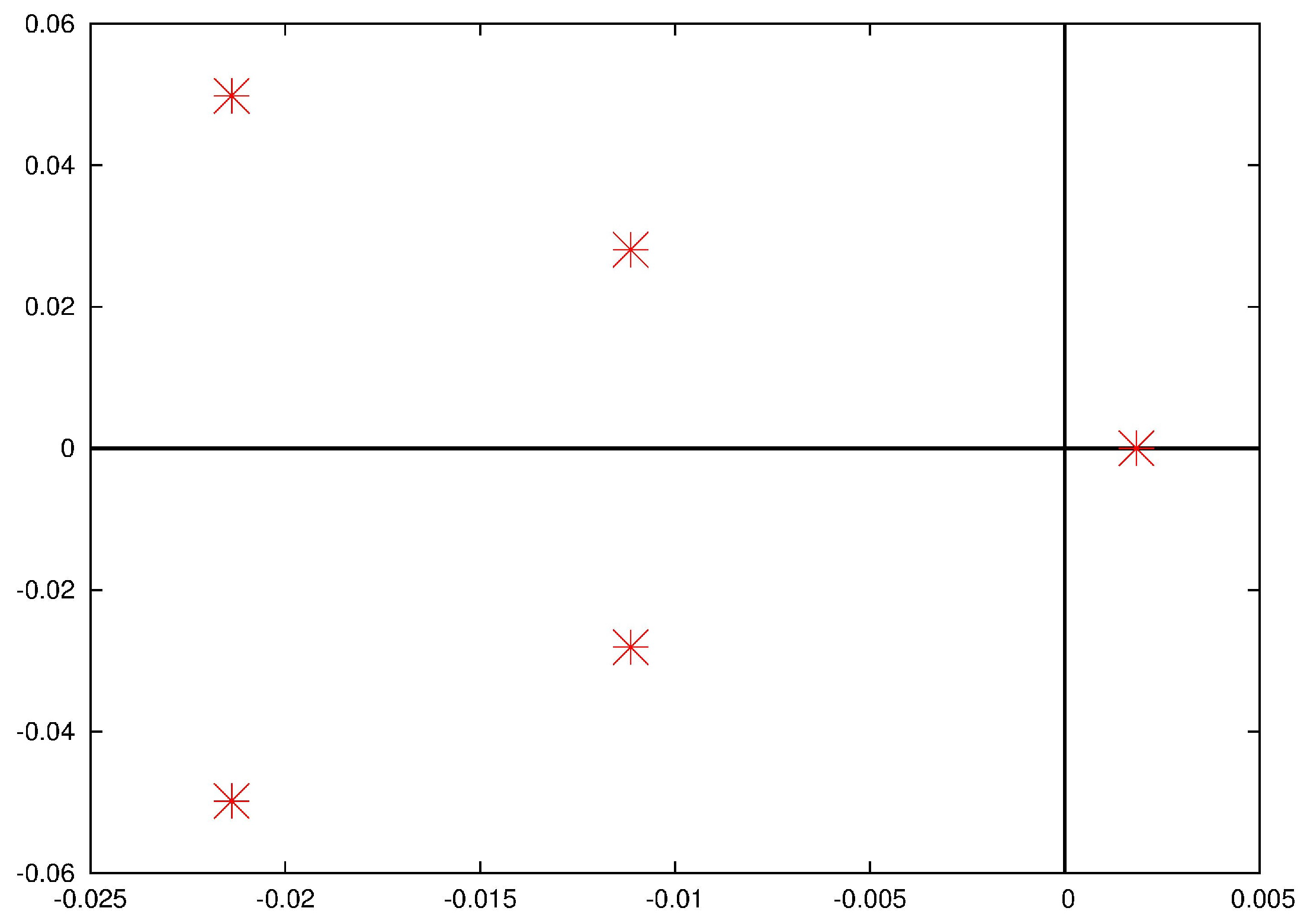
, which can accordingly be defined as (direct) eigenfunctions. The baseline case,
and
(i.e., no spanwise dependence) is stable, as all the eigenvalues have negative real part, as plotted in
Figure 6. Instability can be reached in two ways: either by modifying the spanwise wavenumber (e.g.,
in
Figure 7), or by augmenting the Reynolds number (e.g.,
in
Figure 8). It is worth noticing that the former operation induces stationary instabilities—as the imaginary part of the rightmost eigenvalue still vanishes—while the latter introduces unstationary ones (
for those points where
, and the picture is, of course, symmetric with respect to the horizontal axis). The critical Reynolds number, for which the flow develops its first linear instability at some value of
, is approximately 750.
A sketch of the perturbation (for the largest-real-part eigenvalue, depicted in
Figure 7), at
and
, is presented in
Figure 9. It is evident that this eigenvector is a physically meaningful one, because it is concentrated in the recirculation bubble, which is the zone where instability develops.
6. Control and Gain
In this section, we follow [
27,
28] by introducing a forcing on the right-hand side of the Navier–Stokes equation, which we assume as steady and volumic:
![Fluids 04 00033 i001 Fluids 04 00033 i001]()
. A key point is that this allows us not only to leave the boundary conditions unchanged with respect to Equation (
6), but, more importantly, to confine ourselves to steady solutions
. Indeed, we have already analyzed and found the temporal evolution of the general unforced solutions (eigenvalues and eigenfunctions) in the previous section, and what we are looking for here is just a particular solution to a steady forcing, which can, thus, be assumed as time-independent.
Therefore, we focus on the equations:
We define as gain the quantity
and as optimal gain:
The procedure to find the optimal forcing consists in an iterative algorithm making use of the adjoint variables
satisfying
coupled with the suitable outlet boundary conditions (see, e.g., [
29]) specified in
Appendix A.
6.1. Standard (Non-Penalized) Case
In our reference case (standard geometry with
and
), the magnitudes of what we have obtained numerically as optimal response and corresponding optimal forcing are sketched in
Figure 10.
A clear problem arises here: even if, on one hand, the optimal response develops streamwise for the whole length, on the other hand, the optimal forcing is localized in the vicinity of the step and of the sloping portion of the wall. This is not what one would expect for physical realizability, as, on the contrary, a localization on the horizontal upstream part would be suitable. Indeed, our aim is to take advantage of the formation of counter-rotating longitudinal vortices (i.e., the streak lift-up; see, e.g., [
6,
30,
31]), and to let these interact with the recirculation bubble, in an interesting example of interaction between the Kelvin–Helmholtz and the wake instabilities. In [
7,
32,
33], the formation of streaks was implemented experimentally by placing a series of small cylinders, acting as rugosity elements. (The modified flow that one would obtain after physically placing the roughness elements is clearly not the same as the one in their absence. What is meant here is that this discrepancy must be small for our theory to work—which clearly poses severe restrictions on the applicable elements—so that the modified flow should be obtainable as the sum of the original basic flow plus the weak perturbations currently analyzed.) Notice that the spanwise periodicity of this array of cylinders can be described effectively through our periodic expansion in
z (i.e., by means of the wavenumber
which should equal
divided by the array spacing). In principle, one could introduce step functions in the integrals defining the gain, and we have briefly explored this option preliminarily. However, in the next subsection, we are going to study this problem by means of a penalization method (see, e.g., [
34,
35]).
6.2. Penalized Case
For the present section, let us introduce an effective viscosity
, defined to be equal to
upstream and until the beginning of the step, and to a value some orders of magnitude larger for abscissae downstream of it. We, then, focus on:
In this way, we obtain the optimal response and forcing sketched in
Figure 11, which should more precisely be defined as sub-optimal, because of the penalization scheme. We expect the forcing with such a shape to be physically realizable, due to its localization on the upstream portion of the wall, but the same cannot be said about the velocity response, due to its concentrated character; very different in look from the envisaged streaks appearing in the previous subsection.
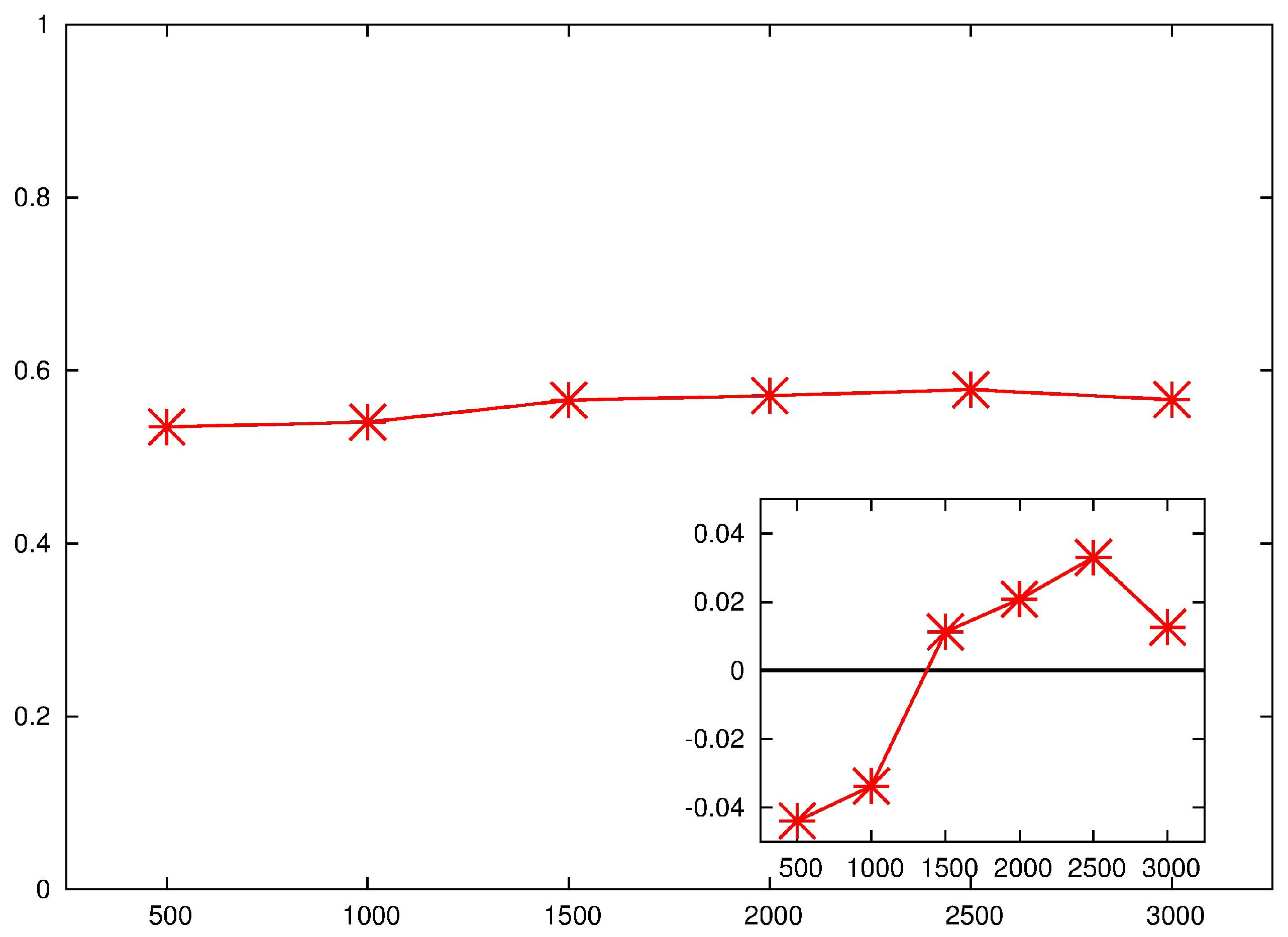
In
Figure 12, we plot the optimal gain
G as a function of
at different
. The maximum of the curve not only obviously grows at larger and larger with
, but also shifts to the right. As, on the contrary, the boundary-layer thickness shrinks when increasing the Reynolds number, we focus on the product between the generalized displacement computed at the step,
, and the optimal wavenumber
. This is shown in
Figure 13, and proves that the ratio between the thickness and the optimal spanwise wavelength is almost independent of
.
6.3. Penalized Control with Non-Penalized Response
The way to circumvent the paradox, presented in the previous subsection, is very simple. One can indeed find the optimal control through the penalized scheme, but, of course, once this forcing has been found, its real action on the physical velocity must be computed with the actual (space-independent) viscosity
. We then implement what one could call a “non-penalized response to penalized-optimal control”:
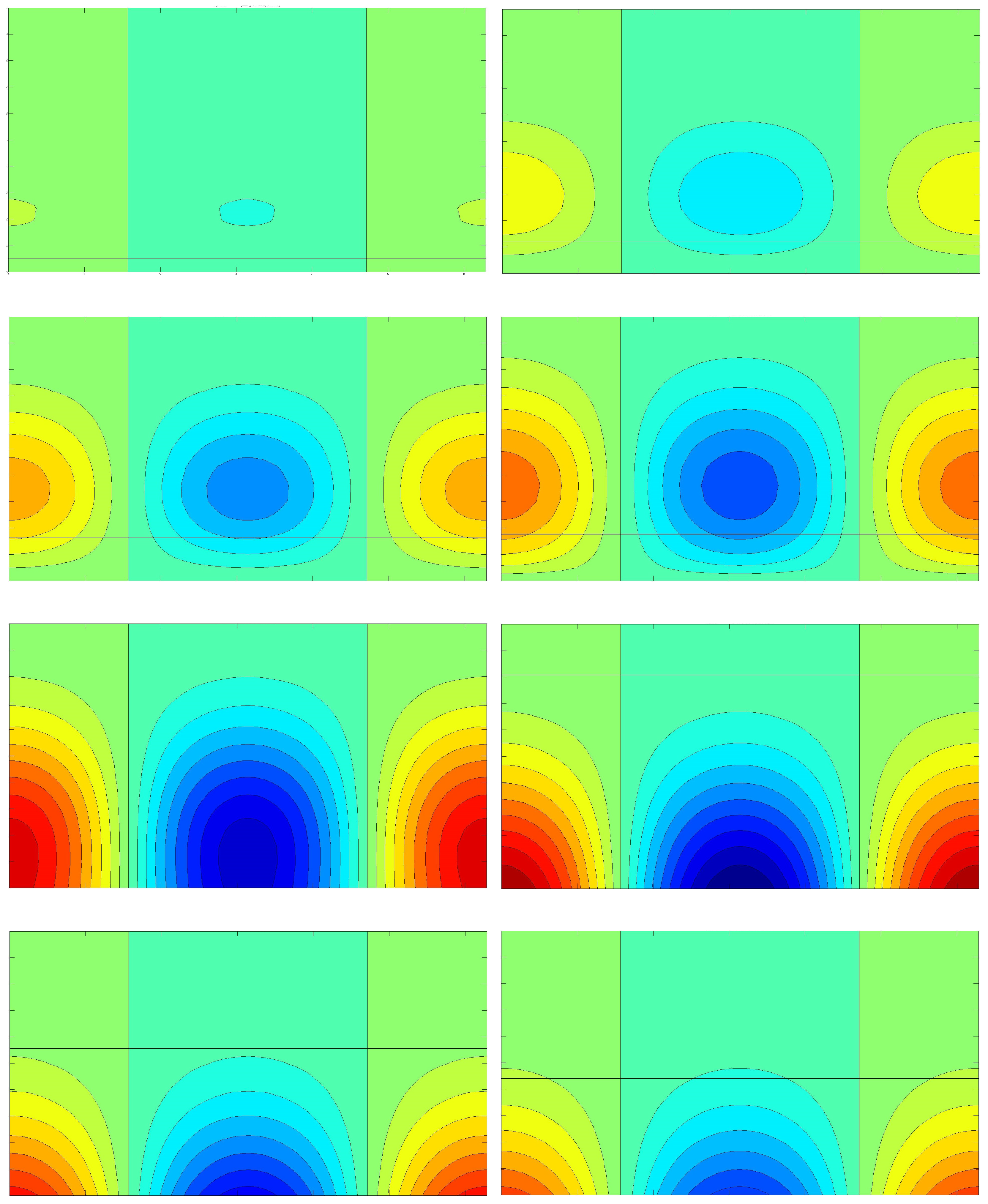
This way we obtain the response sketched in
Figure 14, together with the aforementioned penalized-optimal forcing field. The fact that streaks are actually generated is confirmed by
Figure 15, which represents vertical cuts of the domain
at eight different streamwise locations.
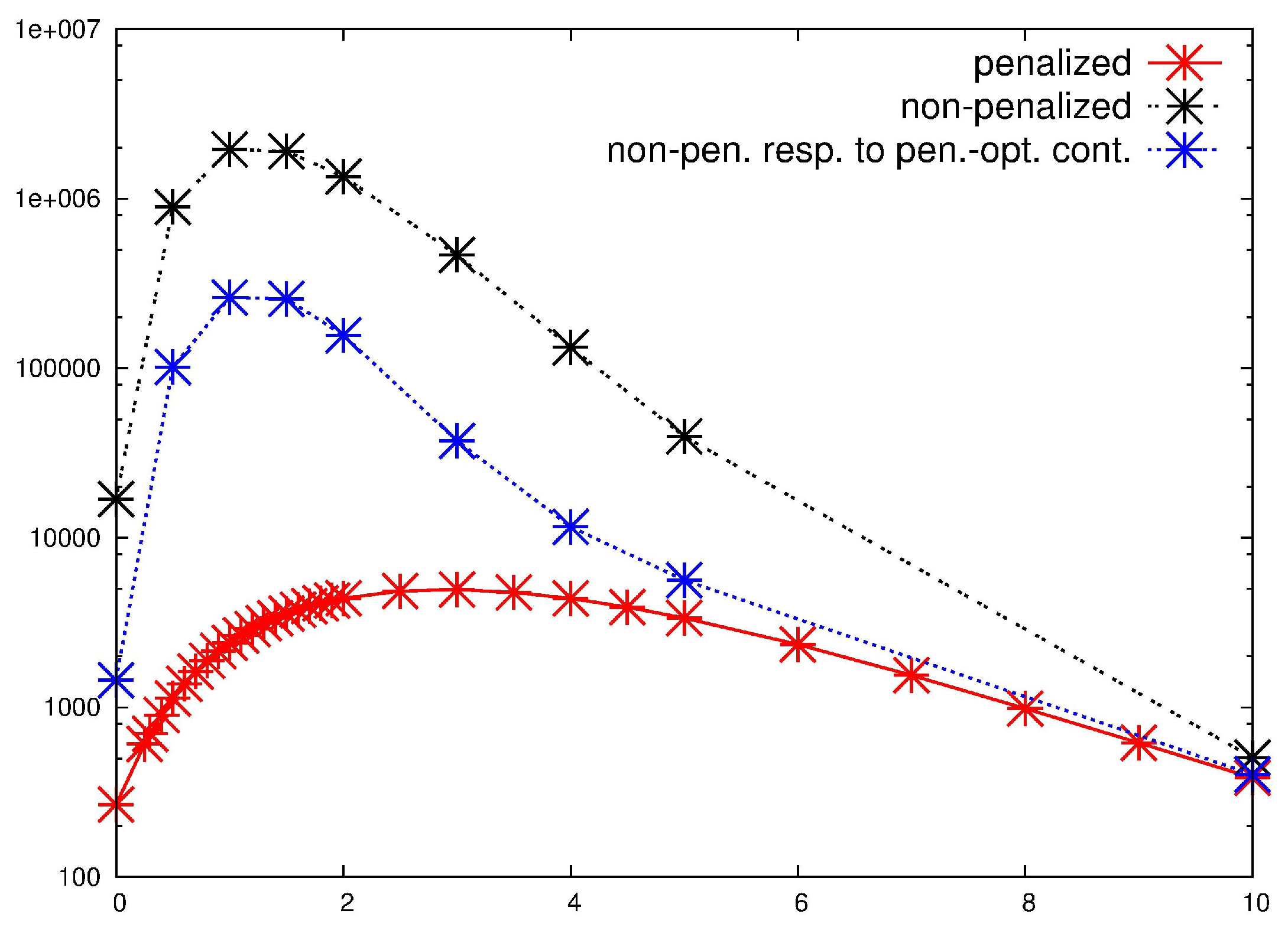
In
Figure 16, we plot a comparison for the optimal
G as a function of
at
, according to the three aforementioned schemes. In this completely-stable situation, one can see that—moving from the initial non-penalized scheme (black) to the final scheme, proposed in this subsection (blue)—the loss in the optimal gain is on less than one order of magnitude, but with the advantage of delivering an optimal forcing definitely feasible, in terms of physical realizability.
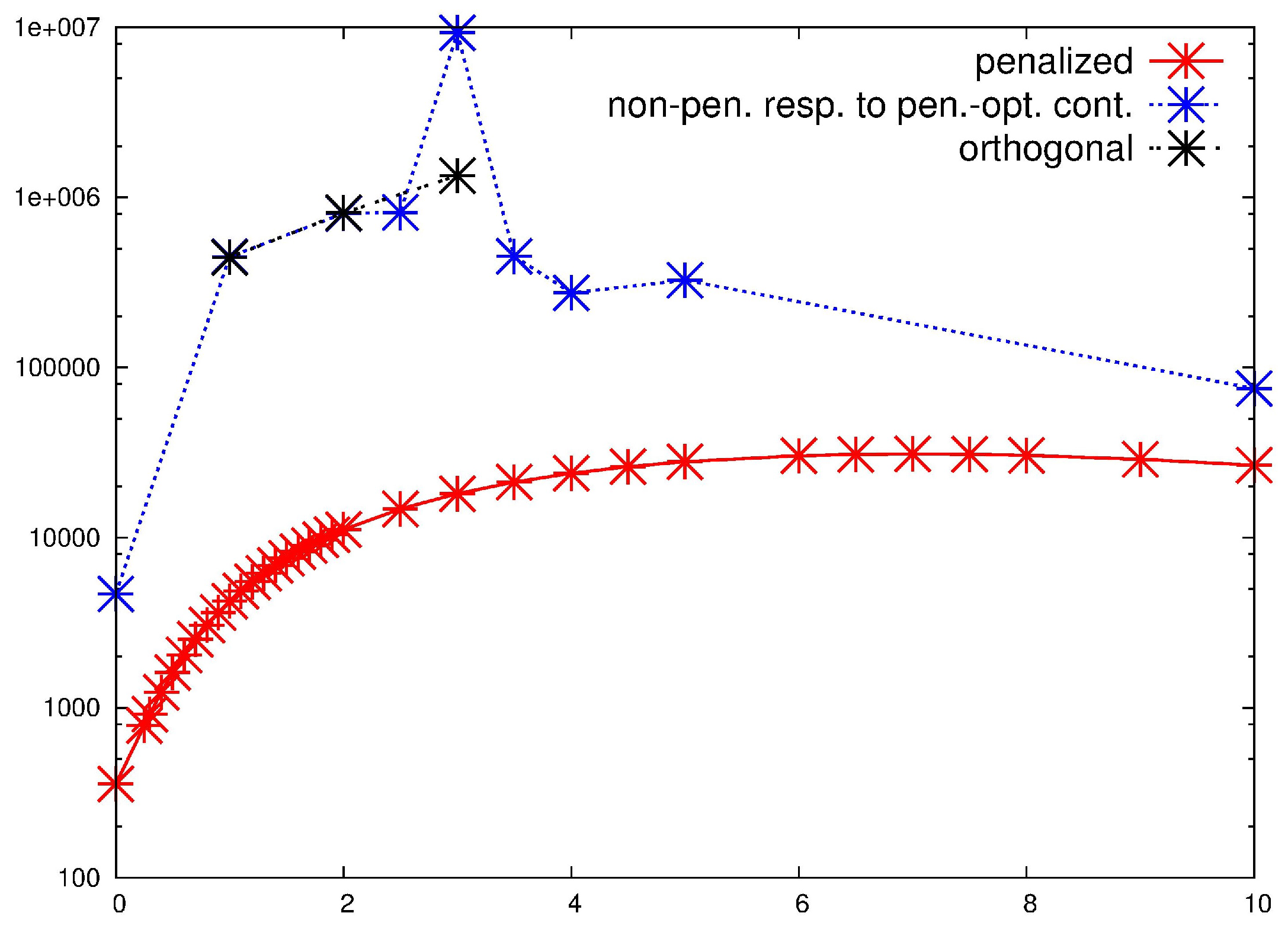
The comparison between (
11) and (
12) is also plotted in
Figure 17 at
. Notice that (
7) cannot be enforced here, because the Reynolds number is larger than the critical value. Moreover, since this configuration is unstable for some perturbations, we also plot (in black) the gain corresponding to a non-modal response field, which is computed through an orthogonalization procedure in order to exclude spurious peaks related to the modal amplification (which we are not interested in).
7. Conclusions and Perspectives
We have studied the transient growth of perturbations in a separated boundary layer, namely in the wake of a backward-slanted step at . We have shown that, by means of a suitable penalization method, unstable cases are also tractable in our formalism. We have been able to find situations where the optimal control is spanwise-periodic and localized on the horizontal upstream portion of the wall (which can be experimentally reproduced by an array of rugosity elements), and the corresponding response is represented by streaks.
Among future perspectives, the following questions are of interest.
First, one could change the nature of the forcing term, from volumic to parietal. This would represent an external blowing or suction on the lower wall upstream of the step, implemented by imposing, on this piece of boundary, a condition on the velocity, which should keep the zero tangential component but have a prescribed nonzero normal component (a function of x). We have already made a preliminary test for this situation, but a more profound investigation is definitely required.
Second, it would be interesting to relax the assumption of steady forcing and to investigate the problem also in the temporal domain. One should, then, fix a finite time horizon for the optimization, and perform back-and-forth temporal loops until convergence [
36]. This is due to the fact that, if one keeps the time dependence in the equations, the evolution of the adjoint field corresponds to a well-known backward-in-time integration, with “final” conditions imposed on the final time horizon. Of course, the evolution of the direct field is forward-in-time, and one has to perform an optimization on the initial conditions.
Also, the incompressibility of the flow is a key ingredient for the results shown here. It might be worth investigating how they change if a compressible flow is considered, instead. We expect the theoretical analysis to be much more difficult, in view of the necessity of introducing a state equation.
Moreover, the present study is a linear one—rigorously speaking, valid only for infinitesimal perturbations. If the perturbations are small but finite, we expect our framework to be still in excellent agreement with the real picture. However, it is evident that this check can be done only numerically, by performing simulations of the full problem, in order to understand whether the nonlinear coupling in the Navier–Stokes advection term induces significant modifications [
37]. This issue could be investigated, for example, by means of appropriate Large-Eddy Simulations and provide the basis for a more direct comparison with experiments [
38].
Last, but definitely not least, a relevant question arises about the stability of the considered steady flows to perturbations involving large spatial scales. Further weakly-nonlinear analysis (as in [
39] for hydrodynamic flows, and in [
40] for MHD flows) may reveal the complex dynamics of large-scale perturbations affecting the performance of the vehicle.
Author Contributions
The authors contributed equally to this work, except for writing—original draft preparation, review, and editing—performed by M.M.A.
Funding
This research was supported by: LabEx “Mécanique et Complexité” (AMU, France); CMUP (UID/MAT/00144/2019), funded by FCT with national (MCTES) and European structural funds through the programs FEDER under the partnership agreement PT2020; Project STRIDE-NORTE-01-0145-FEDER-000033, funded by ERDF-NORTE 2020; and Project MAGIC-POCI-01-0145-FEDER-032485, funded by FEDER via COMPETE 2020-POCI and by FCT/MCTES via PIDDAC.
Acknowledgments
We thank Michel Pognant and Dominique Fougère for technical assistance.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A. Detailed Description of Boundary Conditions and Adjoint Equations
The boundary conditions for the full velocity field are as follows:
Inlet on segment ED: , ;
Outlet on segment BC: ;
Free slip on segments EI and DC: , ;
No slip on segments IO, OA and AB: .
The base flow inherits the same exact conditions. On the contrary, the perturbation must satisfy fully-homogeneous boundary conditions, so that all the formulae above hold also for the quantities with a prime, except for the very first one, which becomes (at inlet ED) .
Equation (
6) can be rewritten, in terms of the field
, as:
(where
).
The derivation of the adjoint equations involves calculating the scalar product of Equations (
6) (regarded as a 4D vector) with the adjoint field
, and in integrating by parts on the whole domain, benefitting from our boundary conditions. In particular, the ones for the adjoint variables are the same as for the direct counterpart, except for the outlet condition which is (on segment BC):
.
However, when a forcing is also present in the direct equations (as in Equation (
7)), the procedure is more complex, as it involves the whole formalism of Lagrange multipliers and functional derivatives [
27,
28]. We do not report it here, and we simply remind the reader of the final result (
10).
References
- Giannetti, F.; Luchini, P. Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 2007, 581, 167–197. [Google Scholar] [CrossRef]
- Marquet, O.; Sipp, D.; Jacquin, L. Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 2008, 615, 221–252. [Google Scholar] [CrossRef]
- Schmid, P.J. Nonmodal stability theory. Ann. Rev. Fluid Mech. 2007, 39, 129–162. [Google Scholar] [CrossRef]
- Åkervik, E.; Ehrenstein, U.; Gallaire, F.; Henningson, D.S. Global two-dimensional stability measures of the flat plate boundary-layer flow. Eur. J. Mech. B Fluids 2008, 27, 501–513. [Google Scholar] [CrossRef]
- Sipp, D.; Marquet, O.; Meliga, P.; Barbagallo, A. Dynamics and control of global instabilities in open flows: A linearized approach. Appl. Mech. Rev. 2010, 63, 030801. [Google Scholar] [CrossRef]
- Cossu, C.; Pujals, G.; Depardon, S. Optimal transient growth and very large-scale structures in turbulent boundary layers. J. Fluid Mech. 2009, 619, 79–94. [Google Scholar] [CrossRef]
- Pujals, G.; Cossu, C.; Depardon, S. Forcing large-scale coherent streaks in a zero-pressure-gradient turbulent boundary layer. J. Turb. 2010, 11, 25. [Google Scholar] [CrossRef]
- Hecht, F. New development in FreeFem++. J. Numer. Math. 2012, 20, 251–265. [Google Scholar] [CrossRef]
- Meliga, P.; Gallaire, F. Control of axisymmetric vortex breakdown in a constricted pipe: Nonlinear steady states and weakly nonlinear asymptotic expansions. Phys. Fluids 2011, 23, 084102. [Google Scholar] [CrossRef]
- Sipp, D.; Lebedev, A. Global stability of base and mean flows: A general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 2007, 593, 333–358. [Google Scholar] [CrossRef]
- Ehrenstein, U.; Gallaire, F. On two-dimensional temporal modes in spatially evolving open flows: The flat-plate boundary layer. J. Fluid Mech. 2005, 536, 209–218. [Google Scholar] [CrossRef]
- Barkley, D.; Gomes, M.G.M.; Henderson, R.D. Three-dimensional instability in flow over a backward-facing step. J. Fluid Mech. 2002, 473, 167–190. [Google Scholar] [CrossRef]
- Ahmed, S.; Ramm, G.; Faltin, G. Some salient features of the time-averaged ground vehicle wake. SAE Transactions 1984, 473–503. [Google Scholar] [CrossRef]
- Sipp, D.; Jacquin, L. Three-dimensional centrifugal-type instabilities of two-dimensional flows in rotating systems. Phys. Fluids 2000, 12, 1740–1748. [Google Scholar] [CrossRef]
- Gallaire, F.; Marquillie, M.; Ehrenstein, U. Three-dimensional transverse instabilities in detached boundary layers. J. Fluid Mech. 2007, 571, 221–233. [Google Scholar] [CrossRef]
- Meliga, P.; Chomaz, J.-M. Global modes in a confined impinging jet: Application to heat transfer and control. Theor. Comput. Fluid Dyn. 2011, 25, 179–193. [Google Scholar] [CrossRef]
- Biancofiore, L.; Gallaire, F.; Pasquetti, R. Influence of confinement on a two-dimensional wake. J. Fluid Mech. 2007, 688, 297–320. [Google Scholar] [CrossRef]
- Marquet, O.; Sipp, D.; Chomaz, J.-M.; Jacquin, L. Amplifier and resonator dynamics of a low-Reynolds-number recirculation bubble in a global framework. J. Fluid Mech. 2008, 605, 429–443. [Google Scholar] [CrossRef]
- Marquet, O.; Lombardi, M.; Chomaz, J.-M.; Sipp, D.; Jacquin, L. Direct and adjoint global modes of a recirculation bubble: Lift-up and convective non-normalities. J. Fluid Mech. 2009, 622, 1–21. [Google Scholar] [CrossRef]
- Meliga, P.; Sipp, D.; Chomaz, J.-M. Effect of compressibility on the global stability of axisymmetric wake flows. J. Fluid Mech. 2010, 660, 499–526. [Google Scholar] [CrossRef]
- Meliga, P.; Sipp, D.; Chomaz, J.-M. Open-loop control of compressible afterbody flows using adjoint methods. Phys. Fluids 2010, 22, 054109:1–054109:18. [Google Scholar] [CrossRef]
- Fornberg, B. Steady viscous flow past a circular cylinder up to Reynolds number 600. J. Comput. Phys. 1985, 61, 297–320. [Google Scholar] [CrossRef]
- Bottaro, A.; Corbett, P.; Luchini, P. The effect of base flow variation on flow stability. J. Fluid Mech. 2003, 476, 293–302. [Google Scholar] [CrossRef]
- Brandt, L.; Sipp, D.; Pralits, J.O.; Marquet, O. Effect of base-flow variation in noise amplifiers: The flat-plate boundary layer. J. Fluid Mech. 2011, 687, 503–528. [Google Scholar] [CrossRef]
- Meliga, P.; Pujals, G.; Serre, E. Sensitivity of 2-D turbulent flow past a D-shaped cylinder using global stability. Phys. Fluids 2012, 24, 061701. [Google Scholar] [CrossRef]
- Vozella, L. Transizione Alla Turbolenza Per Moti in Condotti. Ph.D. Thesis, Università di Genova, Genova, Italy, 2007. [Google Scholar]
- Pujals, G. Perturbations Optimales Dans les écoulements de Paroi Turbulents et Application au Contrôle de Décollement. Ph.D. Thesis, LadHyx, Palaiseau, France, 2009. [Google Scholar]
- Marquet, O. Stabilité Globale et Contrôle D’écoulements de Recirculation. Ph.D. Thesis, Université de Poitiers, Poitiers, France, 2007. [Google Scholar]
- Meliga, P.; Boujo, E.; Pujals, G.; Gallaire, F. Sensitivity of aerodynamic forces in laminar and turbulent flow past a square cylinder. Phys. Fluids 2014, 26, 104101. [Google Scholar] [CrossRef]
- Del Guercio, G.; Cossu, C.; Pujals, G. Stabilizing effect of optimally amplified streaks in parallel wakes. J. Fluid Mech. 2014, 739, 37–56. [Google Scholar] [CrossRef]
- Del Guercio, G.; Cossu, C.; Pujals, G. Optimal streaks in the circular cylinder wake and suppression of the global instability. J. Fluid Mech. 2014, 752, 572–588. [Google Scholar] [CrossRef]
- Pujals, G.; Depardon, S.; Cossu, C. Drag reduction of a 3D bluff body using coherent streamwise streaks. Exp. Fluids 2010, 49, 1085–1094. [Google Scholar] [CrossRef]
- Pujals, G.; Depardon, S.; Cossu, C. Transient growth of coherent streaks for control of turbulent flow separation. Int. J. Aerodyn. 2011, 1, 318–336. [Google Scholar] [CrossRef]
- Minguez, M.; Pasquetti, R.; Serre, E. High-order large-eddy simulation of flow over the Ahmed body car model. Phys. Fluids 2008, 20, 095101:1–095101:17. [Google Scholar] [CrossRef]
- Minguez, M.; Brun, C.; Pasquetti, R.; Serre, E. Experimental and high-order LES analysis of the flow in near-wall region of a square cylinder. Int. J. Heat Fluid Flow 2011, 32, 558–566. [Google Scholar] [CrossRef]
- Turek, S.; Rivkind, L.; Hron, J.; Glowinski, R. Numerical study of a modified time-stepping θ-scheme for incompressible flow simulations. J. Sci. Comput. 2006, 28, 533–547. [Google Scholar] [CrossRef]
- Del Guercio, G.; Cossu, C.; Pujals, G. Optimal perturbations of non-parallel wakes and their stabilizing effect on the global instability. Phys. Fluids 2014, 26, 024110. [Google Scholar] [CrossRef]
- Meliga, P.; Sipp, D.; Chomaz, J.-M. Elephant modes and low frequency unsteadiness in a high Reynolds number, transonic afterbody wake. Phys. Fluids 2009, 21, 054105. [Google Scholar] [CrossRef]
- Gama, S.; Vergassola, M.; Frisch, U. Negative eddy viscosity in isotropically forced two-dimensional flow: Linear and nonlinear dynamics. J. Fluid Mech. 1994, 260, 95–126. [Google Scholar] [CrossRef]
- Chertovskih, R.; Zheligovsky, V. Large-scale weakly nonlinear perturbations of convective magnetic dynamos in a rotating layer. Physica D 2015, 313, 99–116. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
 . A key point is that this allows us not only to leave the boundary conditions unchanged with respect to Equation (6), but, more importantly, to confine ourselves to steady solutions . Indeed, we have already analyzed and found the temporal evolution of the general unforced solutions (eigenvalues and eigenfunctions) in the previous section, and what we are looking for here is just a particular solution to a steady forcing, which can, thus, be assumed as time-independent.
. A key point is that this allows us not only to leave the boundary conditions unchanged with respect to Equation (6), but, more importantly, to confine ourselves to steady solutions . Indeed, we have already analyzed and found the temporal evolution of the general unforced solutions (eigenvalues and eigenfunctions) in the previous section, and what we are looking for here is just a particular solution to a steady forcing, which can, thus, be assumed as time-independent.