Ionic Fracture Fluid Leak-Off

Abstract

The study is motivated by monitoring the space orientation of a hydrolic fracture used in oil production. Streaming potential arises due to the leakage of ionic fracking fluid under the rock elastic forces which make the fracture disclosure disappear after pumping stops. The vector of electric field correlates with the fracture space orientation since the fluid leakage is directed normally to the fracture surfaces. We develop a mathematical model for the numerical evaluation of the streaming potential magnitude. To this end, we perform an asymptotic analysis taking advantage of scale separation between the fracture disclosure and its length. The contrast between the virgin rock fluid and the fluid invading from the fracture is proved to be crucial in a build up of a net charge at the invasion front. Calculations reveal that an increase of the viscosity and resistivity contrast parameters results in an increase of the streaming potential magnitude. Such a conclusion agrees with laboratory experiments.

1. Introduction

In applying hydraulic fracturing treatment of rocks, one should prepare for execting the size of a fracture and its space orientation. One of the reasons is to avoid hydraulic connectivity of a production well with an injection one, since during water-flood of an initially oil-filled reservoir, encroaching water spoils hydrocarbon recovery. Directional fracturing is also of importance in petrothermal power production while designing geothermal circulation systems within the dry rocks [1]. Typical circulation systems consist of two wells connected by a fracture. By injecting water into the hot, deep, crystalline rocks, a huge amount of heat can be harnessed [2].

The pressure transient data during the injection fall-off test provide a way to determine the dimensions of an induced fracture but not its direction [3]. Microseismic measurements allow us to find the direction of the fracture [4]. However, the reliability of such measurements is not evident due to the extremely low energy of microseismic events and a high level of acoustic noise. Therefore, alternative approaches are of interest.

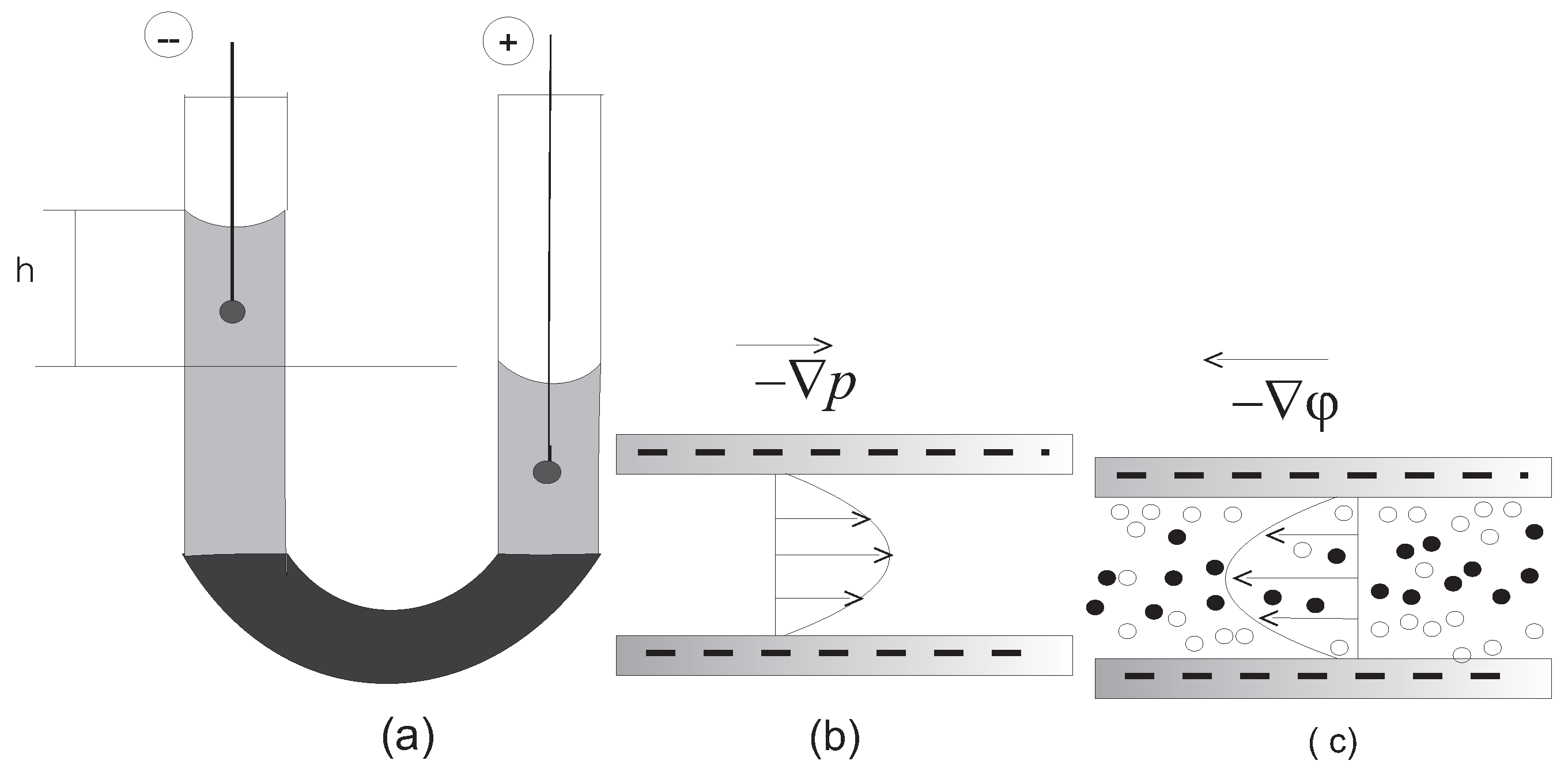
In this study, we estimate the electric field induced near the hydrofracture by leakage of a contrast fluid from the fracture under elastic forces in the rock which make the fracture disclosure disappear after pumping stops. The electric potential, known as the streaming potential, arises due to electrokinetic phenomena when ionic fluid moves through a porous rock [5]. The vector of the induced electric field is directed normally to the fracture surfaces, while the electric potential at the fracture surfaces strongly depends on the location of the invasion front of the fracture fluid. Polarization occurs due to charge concentration at the invasion front. The charge density can be evaluated via the resistivity jump across the front.

Streaming potential measurement is based on response (DC voltage) associated with the excess of electrical charge that is transported by flow of conductive fluids through porous media under a pressure gradient or an electrical conductivity change. Such a method presents a key electrokinetic mechanism to study fluid flows in porous media. An electrical double layer (EDL) forms at the rock–fluid interfaces. The onset of fluid flow perturbs the distribution of the ions present in that layer and induces a current, which is the source of the streaming potential. This electrokinetic mechanism has been tested and employed in the laboratory to monitor the evolution of an oil–water encroachment front over time during hydrocarbon recovery Earlier, the streaming potential dynamics were studied near the production well during water-flood of an initially oil-filled [6,7]. Calculations reveal [8] that encroaching water causes changes in the streaming potential at the production well which could be resolved above background electrical noise; water approaching the well could be detected at several 10s to 100s of meters away. The magnitude of the measured potential depends upon the production rate, the coupling between fluid and streaming potentials, and the nature of the front between the displaced oil and the displacing water. Similar results were obtained via simulation for the streaming potential near the injection borehole during drilling [9].

The fact that the induced electric field is orthogonal to the fracture surfaces allows one to tell the fracture direction starting from the electric field testing. If such a field can be strong enough, one can pass to the next step trying to invent a method of measuring the electric field close to the fracture. In this study, we do not address measurements.

In our mathematical approach, we take advantage of the scale difference between fracture disclosure and its length. With fracture disclosure being small, one can reduce fracture–rock interaction onto the central plane between the fracture surfaces. To evaluate the electric field near the fracture, we apply an asymptotic technique assuming that the contrast between the invasion zone and the virgin rock is small. Agreement with laboratory experiments on correlations between the variations of the streaming potential and fluid flow in the core-sample is provided [10]; it follows from our calculations that electric field in the core-sample can be increased in two ways: when the viscosity of the invading fluid decreases or when the electric conductivity of the invading fluid decreases. Thus, the proposed mathematical model explains the laboratory experiments [10] and set theoretical tools for the streaming potential method applied both in the tracking the water front during production operations and the hydro-fracture development.

2. Basic Equations

We treat the fluid-saturated rock as a Bio’s poroelastic medium enjoying quasi-static deformations and incompressible flows which are explained within mathematical models developed in [3,11]. According to this model, the fluid mass balance and the momentum law of the poroelastic medium are given by the equations

$$\frac{\partial \left({\rho }_f\varphi \right)}{\partial t}+\mathrm{div}\left({\rho }_f\mathbf{Q}\right)=0,0=\mathrm{div}\tau +\mathbf{g}\rho .$$

(1)

Here,

$$\tau =(\lambda \mathrm{div}\mathbf{u}-{\alpha }_{*}p)·\mathrm{I}+2\mu \mathcal{E}\left(u\right),\rho =\varphi {\rho }_f+(1-\varphi ){\rho }_s,$$

where $\varphi$ is the porosity, $\mathbf{Q}$ is the Darcy velocity, ${\rho }_f$ is the fluid density, ${\rho }_s$ is the solid density, $\tau$ is the effective stress tensor, p is the pore pressure, $\mathcal{E}$ is the deformation tensor, $\mathbf{u}$ is the rock displacement vector, ${\alpha }_{*}$ is the Biot number, $\mathbf{g}$ is the gravitational acceleration vector, $\mu$ and $\lambda$ are the elasticity moduli. We use the notations

$${\left(\mathrm{div}\tau \right)}_i=\frac{\partial {\tau }_{ij}}{\partial x_j},\mathrm{div}\mathbf{u}=\frac{\partial u_j}{\partial x_j},{\mathcal{E}}_{ij}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right).$$

An equilibrium state before fracturing is described by the equations

$$0=\mathrm{div}{\tau }_{*}+\mathbf{g}\rho ,{\tau }_{*}=(\lambda \mathrm{div}{\mathbf{u}}_{*}-{\alpha }_{*}{p}_{*})·\mathrm{I}+2\mu \mathcal{E}\left(u_{*}\right).$$

(2)

Here, $\mathrm{I}$ is the identity tensor, ${\tau }_{*}$ is the equilibrium stress tensor in the rock before fracturing, $p_{\infty }={\rho }_{f}gh$ is the equilibrium pore pressure, ${\mathbf{u}}_{*}$ is the equilibrium rock displacement. The equilibrium state is determined by regional stresses as follows. Let us consider a vertical cylinder of the thickness $2h_0$ which is in equilibrium state and which is compressed from above by a poroelastic medium of thickness h, $h_0\ll h$. It is proved in [3] that vertical load is transmitted to horizontal compression by the formula

$$\mathbf{n}·{\tau }_{*}\langle \mathbf{n}\rangle =-{\lambda }_l{\sigma }_h\equiv -{\sigma }_{\infty },$$

where

$${\sigma }_h=gh\rho ,{\lambda }_l=\frac{\nu }{1-\nu }+\frac{(1-2\nu )p_{\infty }{\alpha }_{*}}{{\sigma }_h(1-\nu )},{\left(\tau \langle \mathbf{n}\rangle \right)}_i={\tau }_{ij}{n}_j,$$

$\mathbf{n}$ is the unit external normal vector at the lateral cylinder surface, the point $“·”$ stands for the scalar product, $\nu$ is the Poisson coefficient, ${\lambda }_l$ is the lateral stress coefficient.

Generally, porosity $\varphi$ depends on pore pressure and rock compressibility, i.e., $\varphi =\varphi (p,J)$, $J=\mathrm{tr}\mathcal{E}\left(\mathbf{u}\right)$. By definition of the Biot number ${\alpha }_{*}$, we have the equality $\partial \varphi /\partial J=$ ${\alpha }_{*}$ [12].

Let us introduce the compressibility coefficient $S=\partial \varphi /\partial p$ and the deviation quantities

$${\mathbf{u}}^{\prime }=\mathbf{u}-{\mathbf{u}}_{*},p^{\prime }=p-p_{\infty },{\tau }^{\prime }=\tau -{\tau }_{*}.$$

Then Equation (1) become

$${\alpha }_{*}\frac{\partial }{\partial t}\mathrm{div}{\mathbf{u}}^{\prime }+S{p}_t^{\prime }+\mathrm{div}\left({\rho }_f\mathbf{Q}\right)=0,0=\mathrm{div}{\tau }^{\prime },$$

(3)

where

$${\tau }^{\prime }=(\lambda \mathrm{div}{\mathbf{u}}^{\prime }-{\alpha }_{*}{p}^{\prime })·\mathrm{I}+2\mu \mathcal{E}\left(u^{\prime }\right).$$

The fluid flux $\mathbf{Q}$ obeys the generalized Darcy law which governs electrolyte flows in a porous medium [13,14,15]:

$$\mathbf{Q}=-{\lambda }_{11}\nabla p^{\prime }-{\lambda }_{12}\nabla \psi ,\mathbf{J}=-{\lambda }_{21}\nabla p^{\prime }-{\lambda }_{22}\nabla \psi ,\mathrm{div}\mathbf{J}=0,$$

(4)

where $\mathbf{J}$ is the density of electric current, $\psi$ is the streaming potential, ${\lambda }_{ij}$ are electro-kinetic coefficients. It is the double electric layer (DEL) theory which lays behind the first two equations in (4). Particularly, these equations explain the electro-osmosis effect discovered by F.F. Reuss in 1808, Figure 1. The latter equation in (4) is known as the charge conservation law. By the two-scale homogenization theory, it is proved in [16] that ${\lambda }_{ij}$ are given by the following representation formulas:

$${\lambda }_{11}=\frac{k_r}{{\eta }_r},{\lambda }_{22}={\sigma }_r,{\lambda }_{12}={\lambda }_{21}=F\sqrt{{\lambda }_{11}{\lambda }_{22}},$$

where $k_r$ is the rock permeability, ${\eta }_r$ is the dynamical viscosity of the pore fluid, ${\sigma }_r$ is the effective density of the electric conductivity, F is the dimensionless tortuosity. For sandstones, $F\simeq 0.001$ [8,16].

In [17,18], a mathematical model and a computer code are developed for calculation of the electric conductivity ${\sigma }_r$ of a saturated rock. The model allows one to determine an optimal Archie-like law

$$\frac{{\sigma }_r}{{\sigma }_f}=s_{*}^q{\left(\frac{\varphi -{\varphi }_p}{1-{\varphi }_p}\right)}^m,$$

where ${\sigma }_f$ is the density of the pore fluid electric conductivity, m is the cementation factor, $s_{*}$ water saturation, q mineralization factor, and ${\varphi }_p$ is the percolation limit.

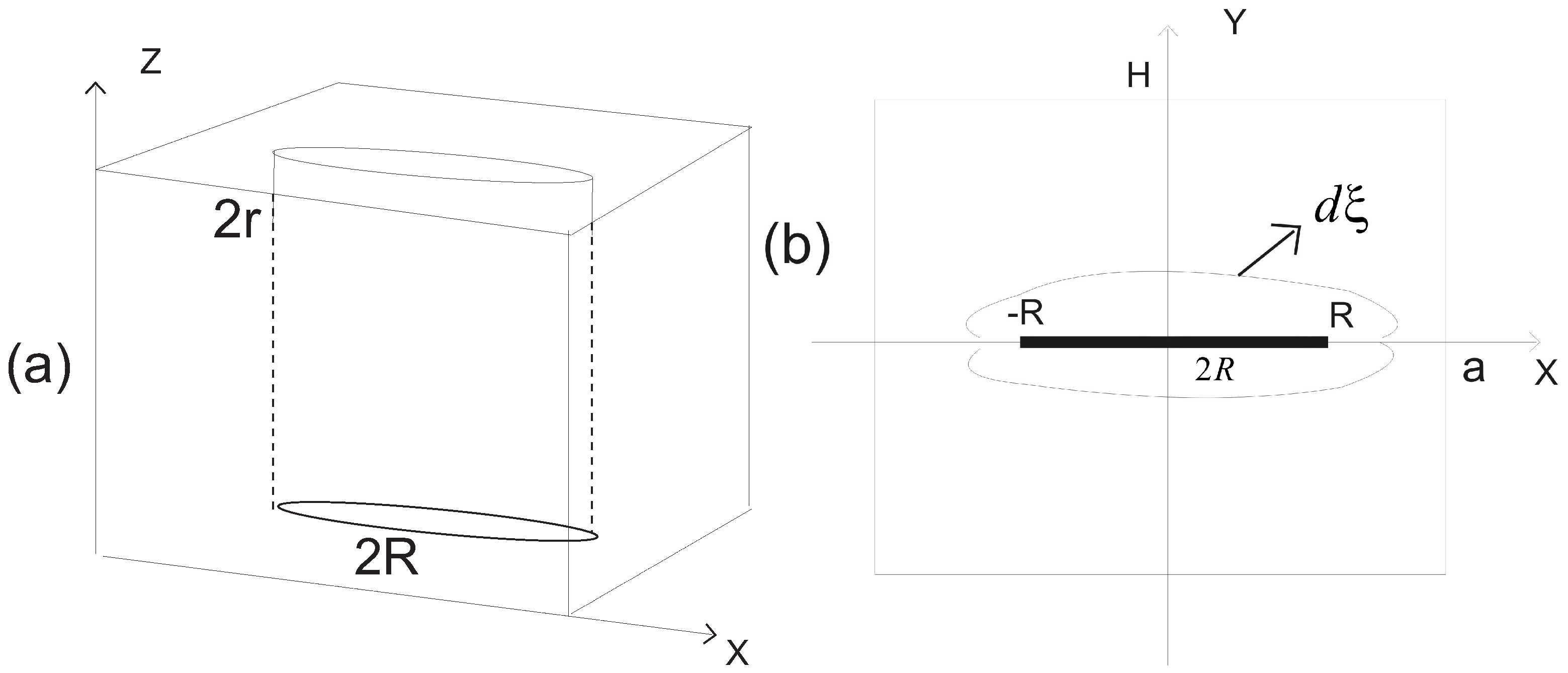
We assume that a vertical fracture of height $2r$ and length $2R$ is extended along the horizontal x-axis and its disclosure along another horizontal y-axis does not depend on the vertical variable z, Figure 2a. We also assume that the fracture is symmetrical with respect to the y-axis, and the rock stress-strain state is symmetrical with respect to the x-axis and y-axis. Thus, in what follows we study a two-dimensional problem with all the vectors lying in the horizontal plane $(x,y)$.

Let us write the mass conservation law for fracture fluid. As in the lubrication theory, we have (Batchelor, 1967)

$$w_t+\frac{\partial }{\partial x}\left(wV\right)=-q.$$

Here, w stands for one-half the fracture aperture. By continuity of displacements,

$$w(x,t)={\mathbf{u}}^{\prime }·{\mathbf{e}}_y{|}_{y=0},$$

(5)

where ${\mathbf{e}}_y$ is the unite vector along the y-axis, q is the fluid leakage, $V(t,x)$ is the fluid velocity along the x-axis. The velocity V enjoys the representation

$$V=-\frac{{\left(2w\right)}^2}{12{\eta }_c}{p}_x^{\prime },$$

(6)

where ${\eta }_c$ is the viscosity of the fracture fluid. It is remarked in [3] that one can use the following alternative formula:

$$V=-\frac{k_c}{{\varphi }_c{\eta }_c}{p}_x^{\prime },$$

(7)

where $k_c$ is the fracture permeability and ${\varphi }_c$ is the fracture porosity.

Leakage from the fracture satisfies the continuity condition

$$q=-({\lambda }_{11}\nabla p-{\lambda }_{12}\nabla \psi )·{\mathbf{e}}_y{|}_{y=0}.$$

(8)

It was proved in [19,20] that the invasion front can be determined by the method of characteristics from the following equation for the position vector $\mathit{\xi }$ $=({\xi }_1,{\xi }_2)$ at the $(x,y)$-plane:

$$\varphi \frac{d}{dt}{\mathit{\xi }=\mathbf{Q}(x,y,t)|}_{x={\xi }_1,y={\xi }_2}.$$

(9)

It means that the infinitesimal displacement $d\mathit{\xi }$ of the front point $({\xi }_1,{\xi }_2)$ is equal to $\mathbf{Q}({\xi }_1,{\xi }_2,t)dt/\varphi$, Figure 2b.

Let us comment on the front since it plays a crucial role in the study. Mathematically, the front can be associated with the interface $F(x,y,t)=0$, with $F(x,y,t)$ being a scalar function. It means that the solution $\mathit{\xi }\left(t\right)$ of (9) satisfies the equation $F\left(\mathit{\xi }\right(t),t)=0$. Propagation of the interface F along the normal vector $\mathbf{n}=$ $\nabla F/|\nabla F|$ can be determined from Equation (9) as follows:

$$\mathbf{n}·\mathbf{Q}+\frac{F_t}{|\nabla F|}=0.$$

Let us denote by ${\left[f\right]}_{\xi }$ the jump of the function $f(x,y)$ across the interface F along the normal vector $\mathbf{n}$ at the point $\mathit{\xi }$:

$${\left[f\right]}_{\xi }=\underset{\delta \to 0}{lim}\left\{f(\mathit{\xi }+\delta \mathbf{n})-f(\mathit{\xi }-\delta \mathbf{n}\right\}.$$

By continuity,

$${\left[p\right]}_{\xi }=0,{\left[\psi \right]}_{\xi }=0,{[\mathbf{J}·\mathbf{n}]}_{\xi }=0,{[\mathbf{Q}·\mathbf{n}]}_{\xi }=0.$$

On the other hand, ${\left[{\lambda }_{ij}\right]}_{\xi }\ne 0$. Hence, ${[\nabla \psi ·\mathbf{n}]}_{\xi }\ne 0$. The latter condition implies that there is a charge concentration at the interface F. In short, our goal is to determine dynamics of the jump ${[\nabla \psi ·\mathbf{n}]}_{\xi }$.

Let us formulate boundary-value conditions for the fracture lying in the rectangular

$${\Omega }_1=\{(x,y):|x|<a,|y|<H\}.$$

Since the fracture aperture is small compared to its length we reduce fracture-rock interactions to its footprint, Figure 1b,

$$F_c=\{(x,y):|x|<R,y=0\}.$$

Because of symmetry we study flows and deformations in the half domain ${\Omega }_1^{+}=$ ${\Omega }_1\cap \{y>0\}$ only.

We assume that the pressure and stress at the external boundary $\partial {\Omega }_1\cap (y>0)$ coincide with the regional values. This is why in terms of deviated quantities we impose the following conditions:

$$\partial {\Omega }_1:\mathbf{n}·{\tau }^{\prime }\langle \mathbf{n}\rangle =0,\mathbf{s}·{\tau }^{\prime }\langle \mathbf{n}\rangle =0,p^{\prime }=0,\psi ={\psi }_{\infty },$$

(10)

where $\mathbf{s}$ is the unite vector tangential to the boundary $\partial {\Omega }_1$, ${\psi }_{\infty }$ is the prescribed streaming potential. Stress continuity at the rock–fracture interface reduces to the footprint $F_c$ as follows

$$y=0,\left|x\right|<L:\mathbf{n}·{\tau }^{\prime }\langle \mathbf{n}\rangle ={\sigma }_{\infty }-p_{\infty }-p^{\prime },\mathbf{s}·{\tau }^{\prime }\langle \mathbf{n}\rangle =0,\psi ={\psi }_c,$$

(11)

where ${\psi }_c$ is the streaming potential inside the fracture. Pressure continuity at the rock–fracture interface implies that the pore pressure and the fracture pressure coincide at $y=0$. Outside the fracture, we impose the following symmetry conditions

$$\frac{\partial }{\partial y}({\mathbf{u}}^{\prime }·{\mathbf{e}}_x)=0,{\mathbf{u}}^{\prime }·{\mathbf{e}}_y=0,\frac{\partial p^{\prime }}{\partial y}=0,\frac{\partial \psi }{\partial y}=0.$$

To complete the picture, one should set initial conditions. We shall do it in what follows.

3. Very Long Fracture

Our goal is determine correlations between streaming potential dynamics and invasion front propagation. To perform asymptotic analysis, we pass to a simplified problem under the following hypotheses. We assume that the fracture aperture is the same along the fracture, with the latter being infinite. In this case $a=L=\infty$ and the solution depends on time and the space variable y only, $0<y<H$.

We denote

$$v(t,y)={\mathbf{u}}^{\prime }·{\mathbf{e}}_y,\xi ={\xi }_2.$$

Omitting the prime in the pressure notation $p^{\prime }$, we arrive at the following equations for the functions $v,p,\psi ,\xi$ in the domain $0<y<H$:

$$0=\frac{\partial }{\partial y}\left[(\lambda +2\mu )v_y-{\alpha }_{*}p\right],$$

(12)

$${\alpha }_{*}{v}_{yt}+S{p}_t=\frac{\partial }{\partial y}\left[{\lambda }_{11}{p}_y+{\lambda }_{12}{\psi }_y\right]$$

(13)

$$0=\frac{\partial }{\partial y}\left[{\lambda }_{21}{p}_y+{\lambda }_{22}{\psi }_y\right]$$

(14)

$$\varphi {\xi }_t=-\left[{\lambda }_{11}{p}_y+{\lambda }_{12}{\psi }_y\right]{|}_{y=\xi }.$$

(15)

Boundary conditions become

$$y=0:v_t={\lambda }_{11}{p}_y+{\lambda }_{12}{\psi }_y,(\lambda +2\mu )v_y+(1-{\alpha }_{*}p)={\sigma }_{\infty }-p_{\infty },\psi ={\psi }_c,$$

(16)

$$y=H:(\lambda +2\mu )v_y-{\alpha }_{*}p=0,p=0,\psi ={\psi }_{\infty }.$$

(17)

It is crucial in the present study that the kinetic coefficients ${\lambda }_{ij}$ undergo jumps at the invasion front:

$${\lambda }_{ij}=\left\{\begin{array}{cc}{\lambda }_{ij}^{-},\hfill & \phantom{,}0<y<\xi \left(t\right),\hfill \\ {\lambda }_{ij}^{+},\hfill & \xi \left(t\right)<y<H,\hfill \end{array}\right.$$

(18)

with ${\lambda }_{ij}^{-}$ and ${\lambda }_{ij}^{+}$ being different constants.

Let us analyse system (12)–(17). Equation (12) implies that the function ${\beta }_1\equiv$ $(\lambda +2\mu )v_y$ $-{\alpha }_{*}p$ does not depend on the variable y. Now, it follows from the boundary condition (17) that ${\beta }_1=0$. Hence, one can exclude the function v by the formula

$$v_y=\frac{{\alpha }_{*}}{\lambda +2\mu }p.$$

One can derive from (17) the following boundary condition for pressure at $y=0$:

$$y=0:p={\sigma }_{\infty }-p_{\infty }$$

(19)

By Equation (14), the function

$$\beta \equiv -{\lambda }_{21}{p}_y-{\lambda }_{22}{\psi }_y$$

(20)

does not depend on y. Clearly,

$${\psi }_y=-\frac{\beta +{\lambda }_{21}{p}_y}{{\lambda }_{22}}.$$

(21)

We conclude from (16) and (21) that the fracture disclosure can be determined from the equation

$$y=0:v_t=\left({\lambda }_{11}-\frac{{\lambda }_{12}{\lambda }_{21}}{{\lambda }_{22}}\right)p_y-\frac{{\lambda }_{12}}{{\lambda }_{22}}\beta .$$

(22)

Let us integrate equality (20) paying attention to jumps of ${\lambda }_{ij}$:

$$\beta \xi =-{\lambda }_{21}^{-}{\left(p\right|}_{\xi }{-p|}_0)-{\lambda }_{22}^{-}{\left(\psi \right|}_{\xi }-\psi {|}_0),$$

$$\beta (H-\xi )=-{\lambda }_{21}^{+}{\left(p\right|}_H{-p|}_{\xi })-{\lambda }_{22}^{+}{\left(\psi \right|}_H-\psi {|}_{\xi }).$$

By excluding ${\psi |}_{\xi }$, we find the following representation for $\beta \left(t\right)$:

$$\beta =\frac{n_1+n_2{p|}_{\xi }}{n_3\xi \left(t\right)+n_4(H-\xi \left(t\right))},p{{|}_{\xi }\equiv p(t,y)|}_{y=\xi \left(t\right)},$$

(23)

where

$$n_1={\psi }_c-{\psi }_{\infty }+\frac{{\lambda }_{21}^{-}}{{\lambda }_{22}^{-}}({\sigma }_{\infty }-p_{\infty }),n_2={\left[\frac{{\lambda }_{21}}{{\lambda }_{22}}\right]}_{\xi },n_3=\frac{1}{{\lambda }_{22}^{-}},n_4=\frac{1}{{\lambda }_{22}^{+}}.$$

Here and in what follows, ${\left[f\right]}_{\xi }$ stands for jump of the function $f\left(y\right)$ at the point $\xi$:

$${\left[f\right]}_{\xi }=f(\xi +)-f(\xi -)\equiv \underset{\delta \to 0}{lim}\left(f(\xi +\delta )-f(\xi -\delta )\right).$$

Thus, by eliminating displacement and potential, we reduce the problem (12)–(17) to the following mathematical model. We look for unknown functions $p(t,y)$, $\xi \left(t\right)$, satisfying the equations:

$$\left(S+\frac{{\alpha }_{*}^2}{\lambda +2\mu }\right)\frac{\partial p}{\partial t}+\frac{\partial Q}{\partial y}=0,Q\equiv -\frac{{\Delta }_{\lambda }}{{\lambda }_{22}}{p}_y+\frac{{\lambda }_{12}}{{\lambda }_{22}}\beta \left(t\right),{\Delta }_{\lambda }\equiv {\lambda }_{11}{\lambda }_{22}-{\lambda }_{12}{\lambda }_{21},$$

(24)

$$\varphi \frac{d\xi }{dt}{=Q(t,y)|}_{y=\xi \left(t\right)-},$$

(25)

$${p|}_{y=0}={\sigma }_{\infty }-p_{\infty }{,p|}_{y=H}=0.$$

(26)

Observe, that solution should obey the no-jump restrictions:

$${\left[p\right]}_{\xi }=0,{\left[Q\right]}_{\xi }=0.$$

Let us pass to dimensionless variables

$$z=\frac{y}{H},\tilde{p}=\frac{p}{p_{*}},\tau =\frac{t}{T},\tilde{\psi }=\frac{\psi }{{\psi }_{*}},\zeta =\frac{\xi }{H}.$$

Now, the functions $\tilde{p}(\tau ,z)$, $\zeta \left(\tau \right)$ satisfy the equations

$$A_1{\tilde{p}}_{\tau }=\frac{\partial }{\partial z}\left(A_2\frac{{\lambda }_{11}}{{\lambda }_{11}^{-}}{\tilde{p}}_z-A_3\tilde{\beta }\left(\tau \right)\frac{{\lambda }_{12}{\lambda }_{22}^{-}}{{\lambda }_{22}{\lambda }_{12}^{-}}\right),\tilde{p}{{|}_{z=0}=\frac{{\sigma }_{\infty }-p_{\infty }}{p_{*}},\tilde{p}|}_{z=1}=0,$$

(27)

$$\varphi {\zeta }_{\tau }=A_6\tilde{\beta }\left(\tau \right)-A_5{\tilde{p}}_z{|}_{z=\zeta -},$$

(28)

on the dimensionless interval $0<z<1$. Here, $A_i$ are dimensionless parameters:

$$A_1=1+\frac{{\alpha }_{*}^2}{S(\lambda +2\mu )},A_2=\frac{T}{H^{2}S}\frac{{\Delta }_{\lambda }^{-}}{{\lambda }_{22}^{-}}=\frac{{\lambda }_{11}^{-}(1-F^2)T}{H^{2}S},A_3=\frac{{\psi }_{*}T{\lambda }_{12}^{-}}{H^{2}S{p}_{*}},$$

$$A_4=\frac{p_{*}{\lambda }_{21}^{-}}{{\psi }_{*}{\lambda }_{22}^{-}},A_5=\frac{p_{*}T}{H^2}\frac{{\Delta }_{\lambda }^{-}}{{\lambda }_{22}^{-}}=\frac{p_{*}T{\lambda }_{11}^{-}(1-F^2)}{H^2},A_6=\frac{{\psi }_{*}T{\lambda }_{12}^{-}}{H^2}.$$

The kinetic coefficients ${\lambda }_{ij}$ are stepwise functions:

$${\lambda }_{ij}=\left\{\begin{array}{cc}{\lambda }_{ij}^{-},\hfill & 0<z<\zeta \left(\tau \right),\hfill \\ {\lambda }_{ij}^{+},\hfill & \zeta \left(\tau \right)<z<1.\hfill \end{array}\right.$$

We denote

$$\Delta \tilde{\psi }=\tilde{\psi }{|}_{z=1}-\tilde{\psi }{|}_{z=0},\Delta \tilde{p}=\tilde{p}{{|}_{z=1}-\tilde{p}|}_{z=0}.$$

The function $\tilde{\beta }\left(\tau \right)$ is given by the formula

$$\tilde{\beta }=\frac{-\Delta \tilde{\psi }-A_4\Delta \tilde{p}+\tilde{p}(\zeta \left(\tau \right),\tau )A_4\left\{{\lambda }_{21}^{+}{\lambda }_{22}^{-}/\left({\lambda }_{21}^{-}{\lambda }_{22}^{+}\right)-1\right\}}{\zeta +(1-\zeta ){\lambda }_{22}^{-}/{\lambda }_{22}^{+}}.$$

By definition, $\tilde{\beta }$ is dimensionless electric current density since $\tilde{\beta }=\frac{\beta H}{{\psi }_{*}{\lambda }_{22}^{-}}$ and $\beta \equiv J$ is dimension electric current density.

We formulate initial conditions as follows:

$$\tilde{p}{{|}_{\tau =0}={\tilde{p}}_0\left(z\right),\zeta |}_{\tau =0}=0.$$

(29)

Choosing $p_{*}={\sigma }_{\infty }-p_{\infty }$, we obtain that $\tilde{p}{|}_{z=0}=1$ and $\Delta \tilde{p}=-1$. Observe that we study electric field induced by the fracture closing. Hence, initial fracture aperture is assumed known and it will appear in what follows.

The solution obeys the following no-jump restrictions:

$${\left[\tilde{p}\right]}_{\zeta }=0,{\left[A_2\frac{{\lambda }_{11}}{{\lambda }_{11}^{-}}{\tilde{p}}_z\right]}_{\zeta }=\tilde{\beta }\left(\tau \right)A_3{\left[\frac{{\lambda }_{12}/{\lambda }_{12}^{-}}{{\lambda }_{22}/{\lambda }_{22}^{-}}\right]}_{\zeta }.$$

(30)

Given the functions $\tilde{p}(z,\tau )$ and $\zeta \left(\tau \right)$, one can determine dimensionless electric field by the formula

$$E^{\prime }=-{\tilde{\psi }}_z=\frac{\tilde{\beta }+({\lambda }_{12}/{\lambda }_{12}^{-})A_4{\tilde{p}}_z}{{\lambda }_{22}/{\lambda }_{22}^{-}}.$$

(31)

4. Asymptotic Analysis

Observe, that (27) is not a differential equation in the common sense since it contains not only partial derivatives of $\tilde{p}(z,\tau )$ at the running point $(z,\tau )$ but at the point $\left(\zeta \right(\tau ),\tau )$ also, with $\zeta \left(\tau \right)$ being unknown function. It is the main mathematical difficulty of the study. Up to now, no tools are developed to solve the problem numerically. This is why we try to solve it analitically applying an asymptotic analysis. There are publications on differential equations which contain partial derivatives at the running point $(z,\tau )$ and a point $(z_0,\tau )$, with $z_0$ being fixed. Such equations are known as loaded differential equations.

We analyse system (27)–(29) under the assumption that jumps of the coefficients ${\lambda }_{ij}$ are small in the sense that there is a small $\epsilon$ such that ${\lambda }_{ij}=k_{ij}\epsilon$ where the step-wise functions $k_{ij}$ do not depend on $\epsilon$. We perform an asymptotic analysis assuming that $\epsilon \to 0$. Clearly, both the functions $\tilde{p}(\tau ,z)$ and $\zeta \left(\tau \right)$ depend on $\epsilon$. But there is a difficulty in addressing the difference ${\tilde{p}}^{{\epsilon }_1}(\tau ,z)-{\tilde{p}}^{{\epsilon }_2}(\tau ,z)$ starting from Equation (27) for ${\tilde{p}}^{\epsilon }(\tau ,z)$. The problem is that the coefficients ${\lambda }_{ij}$ depend on $\epsilon$ also and undergo jumps across the moving unknown line $z={\zeta }^{\epsilon }\left(\tau \right)$. To emphasize that the functions ${\lambda }_{ij}$ depend on $\epsilon$, we write ${\lambda }_{ij}^{\epsilon }(x,\tau )$ instead of ${\lambda }_{ij}(x,\tau )$.

The way to avoid this difficulty is to pass to new variables $(x,\tau )$ such that all the coefficients ${\lambda }_{ij}^{\epsilon }(x,\tau )$ are defined on the same fixed domain. We define the change of variables $(z,\tau )\to (x,\tau )$ as follows:

$$x=\left\{\begin{array}{cc}\frac{z-\zeta \left(\tau \right)}{1-\zeta \left(\tau \right)},\hfill & \zeta \left(\tau \right)<z<1,\hfill \\ \frac{z-\zeta \left(\tau \right)}{\zeta \left(\tau \right)},\hfill & 0<z<\zeta \left(\tau \right).\hfill \end{array}\right.$$

(32)

In new variables, the function ${\tilde{p}}^{\epsilon }(x,\tau )$ is defined on the fixed interval $-1<x<1$ and the functions ${\tilde{p}}^{\epsilon }(x,\tau )$, ${\zeta }^{\epsilon }\left(\tau \right)$ satisfy the equations

$$A_1\left({\tilde{p}}_t^{\epsilon }+x_{\tau }{\tilde{p}}_x^{\epsilon }\right)=x_z\frac{\partial }{\partial x}\left\{A_2{x}_z{a}_1\left(x\right){\tilde{p}}_x^{\epsilon }-A_3\tilde{\beta }\left(\tau \right)a_2\left(x\right)\right\},$$

$${\tilde{p}}^{\epsilon }{{|}_{x=-1}=1,{\tilde{p}}^{\epsilon }|}_{x=1}=0,$$

$$\varphi {\zeta }_{\tau }^{\epsilon }=A_6\tilde{\beta }\left(\tau \right)-\frac{A_5}{{\zeta }^{\epsilon }}{\tilde{p}}_x^{\epsilon }{|}_{x=0-},$$

where

$$\tilde{\beta }=\frac{-\Delta \tilde{\psi }-A_4\Delta {\tilde{p}}^{\epsilon }+{\tilde{p}}^{\epsilon }(0,\tau )A_4{\left[a_2\right]}_0}{{\zeta }^{\epsilon }+(1-\zeta )a_3}.$$

The functions $a_i\left(x\right)$ are defined in Appendix A.

The no-jump conditions at $x=0$ become

$$x=0:{\left[{\tilde{p}}^{\epsilon }\right]}_0=0,{\left[A_2{a}_1\left(x\right)x_z{\tilde{p}}_x^{\epsilon }\right]}_0=\tilde{\beta }\left(\tau \right)A_3{\left[a_2\left(x\right)\right]}_0.$$

We look for ${\tilde{p}}^{\epsilon }(x,\tau )$, ${\zeta }^{\epsilon }\left(\tau \right)$ via the expansion series

$$\tilde{p}(x,\tau )=p^0(x,\tau )+\epsilon p^1(x,\tau )+\cdots ,\zeta \left(\tau \right)={\zeta }^0\left(\tau \right)+\epsilon {\zeta }^1\left(\tau \right)+\cdots .$$

We prove in Appendix A, that the function $p^0(z,\tau )$ in the dimensionless physical variables is given by the formula

$$p^0=1-z-\frac{\gamma }{\pi }{e}^{-A_2{\pi }^2\tau /A_1}sin\pi z.$$

(33)

We derive from (A1) and (A2) that the function ${\zeta }^0\left(\tau \right)$ can be determine by the Cauchy problem

$$\varphi \frac{d{\zeta }^0}{d\tau }=A_6{\beta }^0+A_5\left[1+\gamma e^{-A_2{\pi }^2\tau /A_1}cos\left(\pi {\zeta }^0\right)\right],{\zeta }^0{|}_{\tau =0}=0.$$

Clearly, ${\zeta }^0\left(\tau \right)$ increases in time even if $\Delta \tilde{\psi }=0$.

Let us determine approximate dimensionless electric current ${\beta }_a\left(\tau \right)={\beta }^0+\epsilon {\beta }^1$, making use the formulas

$$\epsilon \frac{k_{ij}}{{\lambda }_{ij}^{-}}=\frac{{\lambda }_{ij}^{+}-{\lambda }_{ij}^{-}}{{\lambda }_{ij}^{-}},\epsilon a_3^1=1-\frac{{\lambda }_{22}^{+}}{{\lambda }_{22}^{-}},$$

$$p^0{{|}_{x=0}=p^0|}_{z={\zeta }^0}=1-{\zeta }^0-\frac{\gamma }{\pi }{e}^{-A_2{\pi }^2\tau /A_1}sin\pi {\zeta }^0.$$

We find that

$${\beta }_a\left(\tau \right)=-\Delta \tilde{\psi }+A_4-A_4(1-{\zeta }^0)\left(1-\frac{{\lambda }_{12}^{+}}{{\lambda }_{12}^{-}}\right)+(1-{\zeta }^0)\left(1-\frac{{\lambda }_{22}^{+}}{{\lambda }_{22}^{-}}\right)\Delta \tilde{\psi }$$

$$-\gamma A_4\left(\frac{{\lambda }_{12}^{+}}{{\lambda }_{12}^{-}}-\frac{{\lambda }_{22}^{+}}{{\lambda }_{22}^{-}}\right)\frac{sin\pi {\zeta }^0}{\pi }{e}^{-A_2{\pi }^2\tau /A_1}.$$

In dimension variables the density of the electric current is given by the formula $J_a={\beta }_a{\psi }_{*}{\lambda }_{22}^{-}/H$ [Vm${}^{-1}$s${}^{-1}$].

Starting from the definition (31), we calculate dimensionless gradient of potential using the formula

$$-{\Psi }_z(z,\tau )=\frac{{\beta }_a\left(\tau \right)+({\lambda }_{12}(z,\tau )/{\lambda }_{12}^{-})A_4{p}_z^0(z,\tau )}{{\lambda }_{22}(z,\tau )/{\lambda }_{22}^{-}}.$$

(34)

Let us introduce the contrast parameters

$$a=\sqrt{\frac{{\lambda }_{11}^{+}}{{\lambda }_{11}^{-}}},b=\sqrt{\frac{{\lambda }_{22}^{+}}{{\lambda }_{22}^{-}}}.$$

When $\Delta \tilde{\psi }=0$, it follows from (34) that

$${\Psi }_z(z,\tau )=-A_4(1-ab)\frac{[1+\mathrm{sign}(z-{\zeta }^0\left(\tau \right))]/2-(1-{\zeta }^0\left(\tau \right))}{1+(b^2-1)[1+\mathrm{sign}(z-{\zeta }^0\left(\tau \right))]/2}+F(z,\tau )e^{-A_2{\pi }^2\tau /A_1},$$

(35)

where

$$F(z,\tau )=\gamma A_4\frac{{\pi }^{-1}(ab+b)sin\left(\pi {\zeta }^0\left(\tau \right)\right)+cos\left(\pi z\right)}{1+(b^2-1)[1+sign(z-{\zeta }^0\left(\tau \right))]/2}.$$

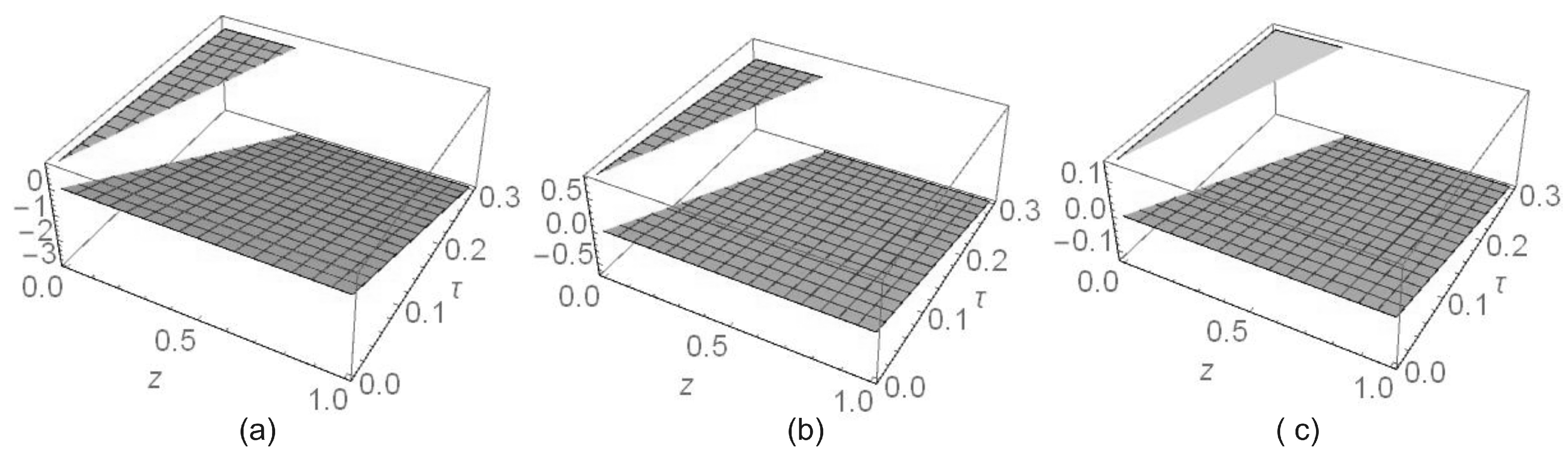
We calculated dynamics of ${\Psi }_z$ neglecting the second term in (35) which decreases exponentially in time. Figure 3 depicts the reduced potential gradient ${\Psi }_Z(z,\tau )\equiv {\Psi }_z/A_4$ across the invasion front $z={\zeta }^0\left(\tau \right)$ for the case $a=0.33$ and different values of b. Potential gradient jump implies charge concentration at the invasion front $z={\zeta }^0\left(\tau \right)$. The charge concentration is build up as b grows. Observe that the signs of ${\Psi }_z$ are different before and after the front.

Let us calculate ${\Psi }_z{|}_{\tau =0}$ within the fracture assuming that $\Delta \tilde{\psi }=0$. We have

$${\Psi }_z{|}_{z=0,\tau =0}=A_4\left(1-\frac{{\lambda }_{12}^{+}}{{\lambda }_{12}^{-}}\right)+\gamma A_4$$

Due to the formula, ${\lambda }_{12}=$ ${\lambda }_{21}=$ $F\sqrt{{\lambda }_{11}{\lambda }_{22}}$, we derive that

$${\Psi }_z{|}_{z=0,\tau =0}=\frac{b}{a}\frac{p_{*}F}{{\psi }_{*}}\sqrt{\frac{{\lambda }_{11}^{+}}{{\lambda }_{22}^{+}}}(1-ab+\gamma )$$

(36)

Let us estimate magnitude of ${\Psi }_z{|}_{z=0,\tau =0}$ for the typical values of data given in Nomenclature setting $\gamma =0$ for simplicity. In this case, $b^2={10}^{-4}/6$. Thus, the dimension initial value of the electric field within the fracture is equal to

$$\frac{{\psi }_{*}}{H}{\Psi }_z{|}_{z=0,\tau =0}=4.53·{10}^{-4}V/m.$$

It follows from (36), that electric field in the fracture can be increased in two ways: when the viscosity of the invasion fluid decreases or when the electric conductivity of the invasion fluid decreases. This conclusion agrees with the recent laboratory experiments [10].

5. Attenuation Time

The induced electric field exists until the fracture aperture disappears. To estimate the closure time, we introduce one more dimensionless parameter $A_7=L/H$, where L is the one-half the initial fracture aperture. Let $\tilde{v}\left(\tau \right)=v/L$ stand for dimensionless fracture aperture at the dimensionless moment $\tau$. Due to (22), $\tilde{v}\left(\tau \right)$ can be determined from the equation

$$x=-1:A_7{\tilde{v}}_{\tau }=A_5{\tilde{p}}_x{x}_z-A_6\tilde{\beta },\tilde{v}{|}_{\tau =0}={\tilde{v}}_0.$$

We remind that $L{\tilde{v}}_0=d_0\left[sm\right]$ is the dimension initial fracture disclosure. A closure time ${\tau }_c$ satisfies the equality

$$-A_7{\tilde{v}}_0=\underset{0}{\overset{{\tau }_c}{\int }}\left(A_5{\tilde{p}}_x{x}_z{|}_{x=-1}-A_6\tilde{\beta }\right)d\tau .$$

Hence, approximately

$$-A_7{\tilde{v}}_0=\underset{0}{\overset{{\tau }_c}{\int }}\left(A_5{p}_x^0{x}_z^0{|}_{x=-1}-A_6{\beta }^0\right)d\tau .$$

With the initial data given by (A2), the above equation is equivalent to

$${\tau }_c\frac{A_5+A_4{A}_6-\Delta \tilde{\psi }{A}_6}{A_7}-{\tilde{v}}_0=-\frac{\gamma A_5}{A_7}·\frac{1-e^{-A_2{\pi }^2{\tau }_c/A_1}}{A_2{\pi }^2/A_1}.$$

Assuming that $\Delta \tilde{\psi }=0$ and using the formula $e^{-x}\simeq 1-x$, we derive that

$${\tau }_c=\frac{A_7{\tilde{v}}_0}{A_5{A}_4+A_6+\gamma A_5}.$$

The dimension closure time is equal to

$$T{\tau }_c=\frac{d_{0}H{\eta }_r^{-}}{p_{*}{k}_r^{-}}·\frac{1}{1+\gamma (1-F^2)}\equiv \frac{d_{0}H{a}^2}{p_{*}{\lambda }_{11}^{+}}·\frac{1}{1+\gamma (1-F^2)},p_{*}={\sigma }_{\infty }-p_{\infty }.$$

Setting $\gamma \simeq 1/2$ and applying the typical conditions given in Nomenclature, we find that the dimension closure time is equal to $T{\tau }_c\simeq 2$ [h], provided $d_0=0.5$ [sm]. One more conclusion is that the closure time decreases as the viscosity of fracture fluid decreases also.

6. Discussions and Conclusions

We formulated a mathematical model to evaluate the streaming potential induced by ionic fracture fluid leak-off after shut-in of a water injection well. Such a potential appears due to electro-kinetic effects relevant to electrolyte flows in a porous medium. The contrast between the virgin fluid and the fluid invading from the fracture is proved to be crucial in a build up of net charge at the invasion front. Calculations reveal that increase of the viscosity and resistivity contrasts results in increase of the streaming potential magnitude. To derive basic equations, we used the scale separation between the fracture disclosure and length. We developed an asymptotic series approach starting from the assumption the contrast parameters is small. The study is motivated by the observation that the vector of electric field correlates with the fracture space orientation since it is directed normally to the fracture surfaces.