Time-Dependent Diffusion Coefficients for Chaotic Advection due to Fluctuations of Convective Rolls

Abstract

The properties of chaotic advection arising from defect turbulence, that is, weak turbulence in the electroconvection of nematic liquid crystals, were experimentally investigated. Defect turbulence is a phenomenon in which fluctuations of convective rolls arise and are globally disturbed while maintaining convective rolls locally. The time-dependent diffusion coefficient, as measured from the motion of a tagged particle driven by the turbulence, was used to clarify the dependence of the type of diffusion on coarse-graining time. The results showed that, as coarse-graining time increases, the type of diffusion changes from superdiffusion → subdiffusion → normal diffusion. The change in diffusive properties over the observed timescale reflects the coexistence of local order and global disorder in the defect turbulence.

1. Introduction

Turbulence occurs by the cascade mechanism (Richardson cascade) because of strong nonlinearities; in ideal cases, the Kolmogorov law (K41) holds [1]. Nevertheless, disorder in fluids arises even in a weakly nonlinear regime through the interaction of a few modes with long timescales based on the slaving principle [2]. For example, in a convective system in which mean flow is hardly relaxed, the convective structure is destabilized or weakly disturbed by the interaction between the convective flow and the mean flow even in the vicinity of the convective threshold [3,4]. A similar phenomenon is observed in an electroconvective system of nematic liquid crystals under an ac electric field [5,6]. For electroconvection in nematics, even in a system in which the mean flow relaxes immediately, the orientation of the rod-shaped molecules of the nematics plays a role corresponding to the mean flow. Because the disturbance in such cases is weak, the convective structure is globally disordered while maintaining local convective rolls. In other words, the correlation length of the disorder is sufficiently longer than the size of the convection roll [7,8]. A disordered state with this property is called weak turbulence (To make a distinction, the K41-type turbulence is called developed turbulence.) Weak turbulence that occurs in a weakly nonlinear regime near a convection threshold has been investigated as one of the experimental subjects of spatiotemporal chaos in spatially extended nonlinear systems [8,9]. However, weak turbulence has seldom been investigated from the viewpoint of turbulent transport. Because order and disorder of different scales coexist, clarifying the differences in properties with coarse-graining scales is required in characterizing it.

Turbulent diffusion that is the transport of mass arising from turbulence is one of the most important phenomena in turbulent transport. Much research on turbulent diffusion caused by developed turbulence have been conducted. Nonetheless, we remark that in time-varying flow, diffusion through mixing occurs even if there is no strong irregularity in the flow. Such phenomenon is called chaotic advection or chaotic mixing. In the context of chaos, it is also called Lagrangian chaos as the chaotic behavior appears within the Lagrangian viewpoint. Chaotic advection arising from weak turbulence is also expected to exhibit properties different from typical turbulent diffusion because of the developed turbulence. Much of the research on weak turbulence as spatiotemporal chaos has been pursued from the Eulerian viewpoint [7,9,10]. In contrast, the chaotic motion of particles driven by weak turbulence is related to the Lagrangian viewpoint and provides other information concerning spatiotemporal chaos.

Electroconvection in nematic liquid crystals under AC electric fields is suitable for investigation of weak turbulence because several advantages exist compared with other systems such as thermal (Rayleigh–Bénard) convection of normal fluids. The timescale of weak turbulence is much shorter than that in Rayleigh-Bénard convection. The refractive index is spatially modulated with the distortion of the nematic director due to convective shear flow. Therefore, the patterns can be optically observed by using the shadowgraph method [11]. An applied voltage used as the control parameter is easily adjustable.

In the electroconvection of nematics, the orientation of the convective roll is determined by the nematic director in the observation plane [12], and the convective flow exerts viscous torque on the director because a nematic substance exhibits viscous anisotropy [13]. These effects act to frustrate the orientation of the convective roll and the nematic director, making the convective roll structure continuously unstable. Thus, weak turbulence occurs. In the electroconvection of nematics, there are two system types of differing symmetry. One is the homeotropic system in which the director can freely rotate as a Nambu-Goldstone mode, and the other is the planar system in which the rotation of the director is limited near the initial orientation of the director. Typical weak turbulence in the homeotropic system is soft-mode turbulence in which the convective roll can also rotate freely [6]. Research aimed at elucidating the transport phenomena arising from soft-mode turbulence has been performed from both the Euler [14] and Lagrange viewpoints. In particular, for the Lagrangian viewpoint, a method called nonthermal Brownian motion has been used that measures the motion of isolated particles and analyses the motion from the analogy with Brownian motion [15,16,17,18,19,20,21]. In the planar system, defect turbulence (see Figure 1) occurs in which defects embedded in the convective stripe pattern nucleate by fluctuations of the convective rolls [22]. Early studies of the defect turbulence focused on the dynamics of defects embedded in the rolls pattern [22]. However, for transport phenomena arising from defect turbulence, fluctuations of the direction of convective rolls (i.e., torsion of the rolls [9]) because of the above-mentioned nonlinear interaction with the director is essential [20,23]. Defect turbulence is similar to the oscillating Rayleigh-Bénard convection by which Lagrangian chaos was studied for the first time [24,25], because it can be regarded as a chaotic oscillation of the convective rolls in a plane normal to the roll axis.

The most important property of weak turbulence is the coexistence of local order and global disorder. Here, this coexistence means there is a hierarchy in the system. This hierarchy was predicted to cause the dependence on observation scale also in the diffusion by chaotic advection. The time-dependent diffusion coefficient is suitable for extracting properties of the diffusion in systems containing such a hierarchy. The time-dependent diffusion coefficient had been already applied to nonthermal Brownian motion in soft-mode turbulence [16,18]. Aside from weak turbulence, biological systems are examples of systems with a hierarchy. The time-dependent diffusion coefficient was also used in extracting properties of biological systems [26,27]. In one study [26], thermal Brownian motion in a system consisting of compartments was simulated to reveal properties of diffusion of a protein molecule in cell membranes. Over very short time scales, a constant time-dependent diffusion coefficient means that the motion within one compartment corresponding to a cell is conventional Brownian motion (normal diffusion). A decreasing time-dependent diffusion coefficient over intermediate time scales means that confinement effect in the compartment by the boundary causes subdiffusion. Over long time scales, the time-dependent diffusion coefficient becomes constant again indicating that hopping diffusion between compartments becomes dominant and consequently normal diffusion occurs. Thus, by increasing the timescale, the type of diffusion in this system changes from normal diffusion → subdiffusion → normal diffusion.

Research on transport phenomena arising from defect turbulence also has been performed from both the Euler [23] and Lagrange [20] viewpoints. The study of chaotic advection in defect turbulence from the Lagrangian viewpoint revealed that hopping is important [20]. That is, a tagged particle is trapped in one convection roll and occasionally hops to an adjacent roll because of fluctuations of the rolls. The activation energy for this hopping was obtained by measuring hopping rates under changes in value of the control parameter. However, detailed analyses using a time-dependent diffusion coefficient have not been conducted. The objective of this paper is to clarify the properties of chaotic advection in the defect turbulence using the time-dependent diffusion coefficients.

2. Results

For applied voltages V beyond a threshold $V_{\mathrm{c}}$, electroconvection occurs and a convective stripe pattern, referred to as normal rolls, appears in the planar nematic system. The wavevector of the stripe pattern is parallel to the x-direction because the initial nematic director is parallel to the x-direction [12]. Hereafter, we use the normalized voltage $\epsilon =(V^2-{V_{\mathrm{c}}}^2)/{V_{\mathrm{c}}}^2$ as the control parameter corresponding to the energy injected into the system. To see the difference resulting from changes in $\epsilon$, measurements were taken for $\epsilon =0.5$ and $1.0$.

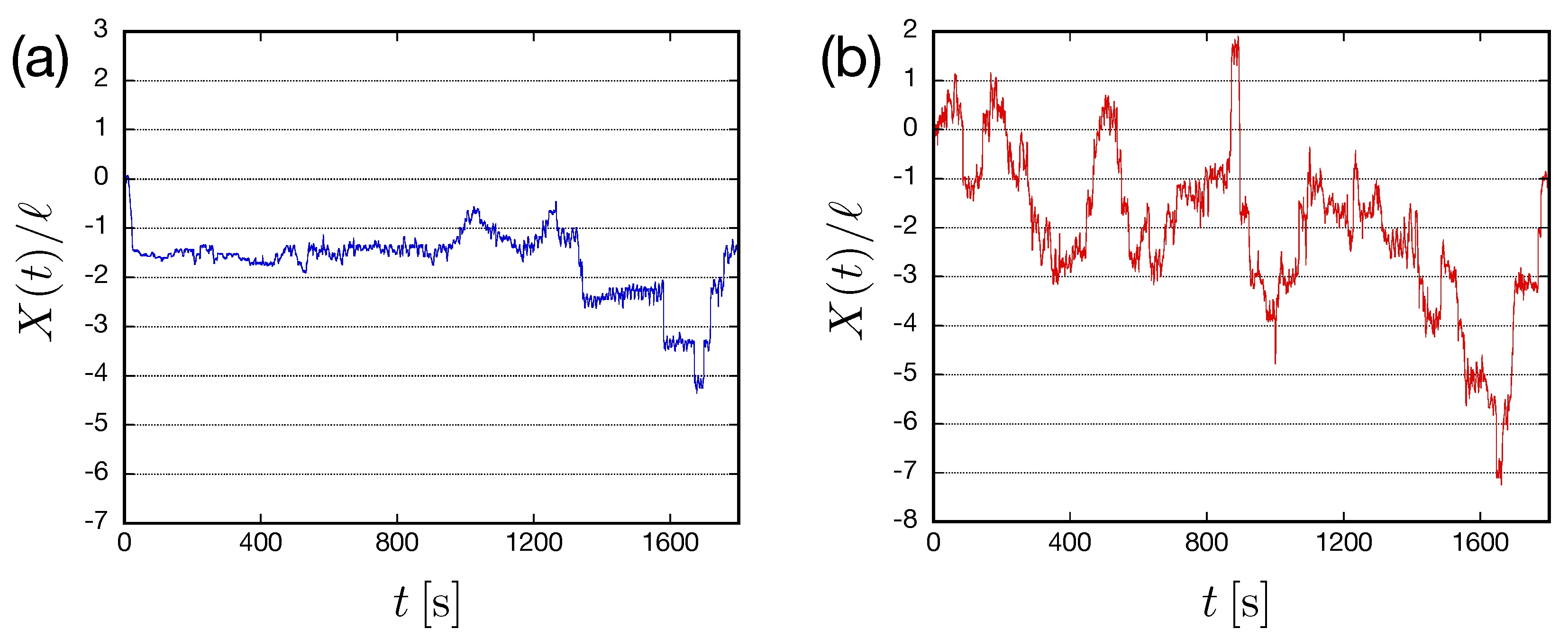
Positions $\mathbf{R}\left(t\right)=\left(X\right(t),Y(t\left)\right)$ of a particle that was driven by defect turbulence were measured. Because the motion in the x-direction characterizes the fluctuations of defect turbulence, only $X\left(t\right)$ was analyzed [20]. Temporal changes in the particle position $X\left(t\right)$ are shown in Figure 2. For $\epsilon =0.5$, the particle was trapped in a convective roll, and sometimes hopped to an adjacent roll. As fluctuations of convective rolls became intense with increases in the energy injected, the range of motion under $\epsilon =1.0$ becomes much larger than that under $\epsilon =0.5$. Furthermore, for $\epsilon =1.0$, the trapping time becomes much shorter, and hopping across several rolls is observed.

To clarify the properties of the random motion of the particle, the type of diffusion should be determined. Therefore, the time-dependent diffusion coefficients, defined by

$$D\left(\tau \right)=\frac{{\langle {|X(t+\tau )-X\left(t\right)|}^2\rangle }_t}{2\tau },$$

(1)

where ${\langle \cdots \rangle }_t$, denoting the average over t, were obtained from the time series of $X\left(t\right)$. The coarse-graining time $\tau$ indicates how much time interval the observation is made. $D\left(\tau \right)$ in short $\tau$ reflects the diffusion in fine structures, and $D\left(\tau \right)$ in long $\tau$ reflects the diffusion in global structures. The types of diffusion are classified by the index $\gamma$ of $D\left(\tau \right)\propto {\tau }^{\gamma }$. In the conventional Brownian motion, also called normal diffusion, $\gamma =0$; that is, $D\left(\tau \right)$ is constant. In contrast, in systems with some complexity, the diffusion behavior becomes anomalous (anomalous diffusion), in which $\gamma \ne 0$. Furthermore, the anomalous diffusion is subclassified as $\gamma >0$ or $\gamma <0$. For $\gamma >0$, $D\left(\tau \right)$ is an increasing function and corresponds to superdiffusion. In this instance, ballistic motion is present [28,29,30]. For $\gamma <0$, $D\left(\tau \right)$ is a decreasing function and corresponds to subdiffusion. In this instance, confinement effects play an important role [31,32,33].

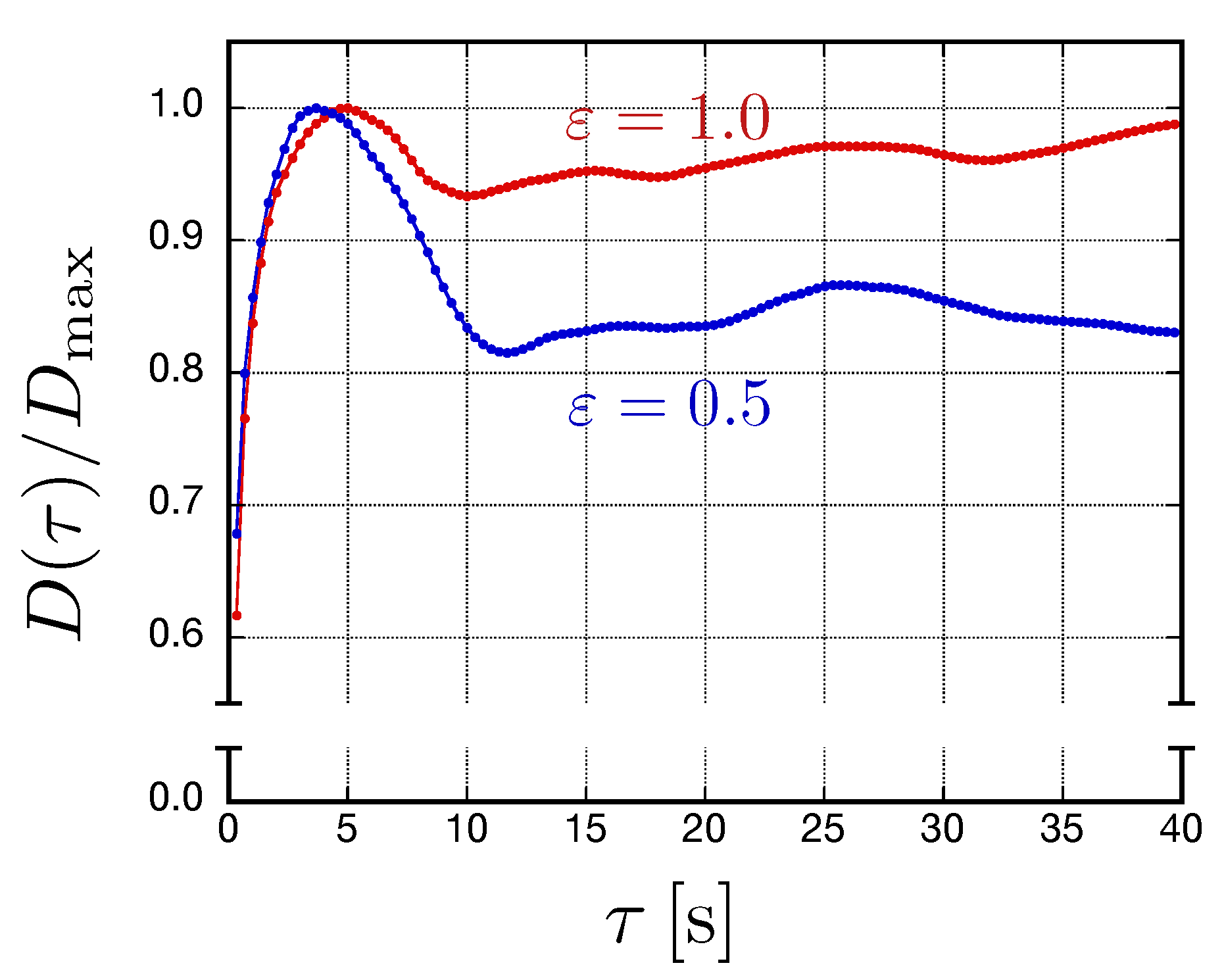
Figure 3 shows the experimental results for $D\left(\tau \right)$. Since order and disorder with different scales coexist in the weak turbulence as mentioned in Introduction, $D\left(\tau \right)$ is not monotonous for $\tau$. The first increase in $D\left(\tau \right)$ means that superdiffusion occurs at short $\tau$ (The conventional (thermal) Brownian motion also exhibits “superdiffusion’’ at timescales shorter than the viscous relaxation time of the fluid system. However, the behaviors over these timescales are unobservable because the viscous relaxation time corresponding to the mean free time is very short. In contrast, the present superdiffusion occurs over an observable timescale.) The following decrease in $D\left(\tau \right)$ means that subdiffusion occurs over intermediate $\tau$. Finally, $D\left(\tau \right)$ becomes almost constant implying that normal diffusion occurs over longer $\tau$. These behaviors are seen in the two instances $\epsilon =0.5$ and $1.0$.

3. Discussion

The result shown in Figure 3 regarding the changes in diffusive properties of the chaotic advection in defect turbulence with the observed timescales may be interpreted as follows. Superdiffusion over short $\tau$ indicates that the particle is moving on the convective flow in a roll (see Figure 4a). Subdiffusion over intermediate $\tau$ is caused by the confinement effect for the particle by being trapped in a convective roll (see Figure 4b) [32]. Normal diffusion over longer $\tau$ arises because the hopping diffusion becomes dominant. Therefore, it is argued that diffusion arising from defect turbulence changes the properties depending on coarse-graining time, reflecting that the local order still exists.

The behavior of $D\left(\tau \right)$ for $\epsilon =1.0$ is qualitatively the same as that for $\epsilon =0.5$. However, the range of subdiffusion for $\epsilon =1.0$ becomes smaller than that for $\epsilon =0.5$. The conjecture is that the confinement effect by the rolls weakens as the hopping rate increases with $\epsilon$ [20]. Furthermore, $D\left(\tau \right)$ for $\epsilon =1.0$ increases slightly in the final range of normal diffusion. This behavior is thought to result from the ballistic motion caused by unidirectional hopping across several convective rolls through intense fluctuations of those rolls with larger amplitudes.

Although this dependence of the diffusive properties on the observation time scale appears also in soft-mode turbulence [16], no subdiffusion was seen. The difference in the homeotropic system in which the soft-mode turbulence appears from the present planar system in which the defect turbulence appears is that the director in the observation plane behaves as a Nambu-Goldstone mode, as mentioned in Introduction [6]. To clarify the reason subdiffusion does not occur in the soft-mode turbulence despite the existence of local convective rolls may lead to elucidating the role of the Nambu-Goldstone mode for chaotic advection.

In conclusion, the properties of chaotic advection arising from defect turbulence were investigated using the time-dependent diffusion coefficients. We found a hierarchy in the diffusive properties that depended on the observation time scale. Specifically, the type of diffusion changes from superdiffusion → subdiffusion → normal diffusion as the coarse-graining time increases. This result reflects the coexistence of the local order and the global disorder in the defect turbulence.

4. Materials and Methods

The sample cell used in the present study was prepared employing the standard method for the planar alignment of the nematic liquid crystal p-methoxybenzylidene-p’-n-butylaniline (MBBA) [20]. The area of the square electrodes was $1.0\times 1.0{\mathrm{cm}}^2$, and polymer films of $50\mathsf{\mu }$m thickness were used to maintain the cell gap. To obtain uniformly planar alignment of the MBBA molecules in the x-y plane parallel to the electrodes, the surfaces of the glass plates with the electrodes were rubbed by a velvet cloth in one direction (defined as the x-direction) after the spin-coating of a surfactant (polyvinyl alcohol). The initial planar director thus obtained was parallel to the x-direction. An ac voltage $V_{\mathrm{ac}}\left(t\right)=\sqrt{2}Vcos\left(2\pi ft\right)$ was applied to the sample in the z-direction. The present study was performed for $f=1000\mathrm{Hz}$ to achieve normal defect turbulence, and specifically to avoid oblique rolls or defect turbulence with abnormal rolls instability [34]. In all measurements, the temperature was kept at $30.00\pm 0.05{}^{\circ }\mathrm{C}$.

To observe the nonthermal Brownian motion in the x-y plane, small particles (Micropearl KBS-5065, Sekisui Chemical, Osaka, Japan) were introduced to the sample cell. The particles had a diameter spread of $6.48\pm 0.17\mathsf{\mu }\mathrm{m}$ and their density of particles was $1.22\times {10}^3\mathrm{kg}/{\mathrm{m}}^3$, which was a little higher than that of the MBBA ($1.02\times {10}^3\mathrm{kg}/{\mathrm{m}}^3$). A CMOS camera (NY-X7i Super System, Canon, Tokyo, Japan) mounted on a stereomicroscope (SMZ1000, Nikon, Tokyo, Japan) was used to capture images including the particles in a period of 1800 s at time intervals of $0.033\mathrm{s}$. The image size was $640\mathrm{pixels}\times 480\mathrm{pixels}$, and the resolution was $2.83\mathsf{\mu }\mathrm{m}/\mathrm{pixel}$. A time series of a particle’s position $\mathbf{R}\left(t\right)=\left(X\right(t),Y(t\left)\right)$ was obtained from the images using motion analysis software (VW-H1MA, Keyence, Osaka, Japan). Since the measuring period (1800 s) was considerably longer than the timescale of the phenomena of interest, the statistical accuracy in the analysis was sufficient. To reduce noise due to thermal Brownian motion and motion blur, coarse-graining by taking averages for every ten intervals of $\mathbf{R}\left(t\right)$ was performed. As a result, the time interval of the time series of $\mathbf{R}\left(t\right)$ is $0.33\mathrm{s}$.