Expanding the Repertoire of Dielectric Fractional Models: A Comprehensive Development and Functional Applications to Predict Metabolic Alterations in Experimentally-Inaccessible Cells or Tissues

Abstract

In this paper, we present the theoretical approach developed by us in the network of dielectric fractional theories. In particular, we mention the general aspects of the non-equilibrium thermodynamics, and after an introduction to the interaction between biological tissues and electrical fields, we highlight the role of phenomenological and state equations; therefore, we recall a general formulation on linear response theory. In Section 6, we introduce the classical fractional model. All of this is essential to show the role and the importance of fractional models in the context of thermodynamic dielectric investigations (of living or inert matter), giving a complete vision of the fractional approach. In Section 7 and Section 8, we introduce our new fractional model derived from non-equilibrium thermodynamic considerations.

1. Introduction

After the inspection of particular phenomena occurring inside living matter (in particular, human blood and its components), we think that they can be best studied in the context of the non-equilibrium Kluitenberg thermodynamic approach with internal variables [1,2,3,4,5,6]. Apart from the non-equilibrium status of biological phenomena, there are suitable reasons that make the theory with internal variables fit to this purpose. The motivation is related to the connection that can be started between internal variables and processes occurring inside biological tissues caused only by internal phenomena, but not by external perturbation. We do not enter into the details of the theory (for which we refer the reader to [7,8,9]), but focus our attention on internal variables. Moreover, no use is made of spring-dashpot models. Generally, the set of variables, polarization, internal energy, specific volume, entropy, and temperature, is, for example, sufficient to characterize the state of a dielectric medium or of a fluid. However, the above-mentioned set of variables is not complete when more complicated phenomena occur, such as chemical reaction, an elastic or plastic strain, and dielectric and magnetic relaxation. For instance, in the Debye theory for dielectric relaxation, it is assumed that the polarization P is additively composed of a part P⁽⁰⁾, which is due to the molecules’ deformation, and a part P⁽¹⁾, which is due to the polar molecules’ orientation in an electric field. Hence, P = P⁽⁰⁾ + P⁽¹⁾. Since P⁽⁰⁾ and P⁽¹⁾ are two different (microscopic) physical phenomena, it is natural to suppose that both P⁽⁰⁾ and P⁽¹⁾ are thermodynamic variables. Hence, the specific entropy assumes the form:

$$s=s(u.\underset{\_}{P},{\underset{\_}{P}}^{(1)})$$

(1)

Here, we have introduced an additional vectorial variable, P⁽¹⁾.

A generalization of this equation can be taken into account by considering a dielectric medium for which the entropy depends on the internal energy of the polarization vector P and some vectorial variables, Ω. We shall assume that Ω is a macroscopic quantity required to give a complete description of the dielectric state of the medium. Without specifying the physical nature of Ω (we shall call it a hidden vectorial variable), we assume that it influences the dielectric properties of the medium. A further generalization of the ideas mentioned above is the assumption that there are several microscopic phenomena that influence the dielectric properties of the medium under consideration; besides, the thermodynamic state of the medium may be described by the internal energy, the polarization vector, and “n” macroscopic internal variables. Therefore, one has:

$$s=s(u.\underset{\_}{P},{\underset{\_}{\Omega }}^{(1)},{\underset{\_}{\Omega }}^{(2)},\dots {\underset{\_}{\Omega }}^{(n)})$$

(2)

Before proceeding with the description of the theory, we want to recall some definitions:

We define thermodynamic variables of the entropy, variables on which the entropy depends, quantities that are obtained by partial differentiation of the entropy (as the temperature), and functions of these quantities (as free energy). Thermodynamic variables—on which the entropy depends and for which the substantial time derivatives occur in the first law of thermodynamics—may be called external thermodynamic variables because the values of these parameters can be prescribed by external influences. Additional variables on which the entropy depends and for which the substantial time derivatives do not occur in the first law may be called internal thermodynamic variables.

The total polarization P can be due to several internal processes that occur simultaneously. Let us suppose that there occur “n” different types of microscopic phenomena giving rise to polarization, and let us further assume that:

$$\underset{\_}{P}={\displaystyle \sum _{h=1}^n{\underset{\_}{P}}^{(h)}}$$

(3)

where P^(h) is the contribution to the polarization of the h-th microscopic phenomenon. It can be shown:

$$s=s(u.\underset{\_}{P},{\underset{\_}{P}}^{(1)},{\underset{\_}{P}}^{(2)},\dots {\underset{\_}{P}}^{(n)})$$

(4)

where we assume that partial polarization vectors ${\underset{\_}{P}}^{(h)}$ (h = 1, 2, …, n) are related to n different microscopic phenomena. From Expression (4), we see that ${\underset{\_}{P}}^{(h)}$ (h = 1, 2, …, n) plays the role of an internal variable. This expression alone allows the possibility to study particular processes that occur in cancer tissues, for example, since we can correlate every partial polarization to particular tumor cell phenomena [10]. The dielectric properties of these tissues are altered, and those electrical changes are revealed as emergent properties at the macroscopic level. This is the case of leukocytosis, which is an abnormal increase in the number of white blood cells; leukemia, which is a neoplastic proliferation of hematopoietic stem cells; and leukopenia, which is an abnormal reduction of circulating white blood cells, especially the granulocytes [11,12,13]. In these cases, the dielectric properties of the blood change, and in particular, the partial polarization vectors associated with each anomalous phenomenon (disease) can change. It may be useful to study the dielectric properties of blood related to neurodegenerative diseases and the protective effects of some natural compounds [14,15,16,17,18]. Obviously, the investigation of these pathologies is very difficult if it is carried out by considering partial polarization directly, since a direct measure of them is very difficult. However, these diseases may be investigated from an electric point of view, as we will show for a particular case in the next sections; there, we will show a “technique” to approach this type of investigation [19,20,21,22]. We will remark that a significant contribution of the developed approach in our previous papers is the knowledge of phenomena associated with each phenomenological and state coefficient and to internal variables [19,20,21,22]. These can highlight the evolution of pathologies that cannot be evidenced in other investigations. In fact, as shown in several previous papers, these coefficients are specific to each system, and this technique can be considered as a new method of characterization [19,20,21,22]. It is like looking at phenomena with a magnifying glass or splitting up a phenomenon into its components. Moreover, this knowledge can be used for the prevention, for example, of tumor pathologies: phenomena that do not appear by using classical techniques of investigation can be pointed out by the aforementioned coefficients, since new processes that can characterize the system are associated with each of them. This result may also be used as a therapeutic interaction with the system [19,20,21,22,23]. However, with respect to the continuity with our thermodynamic point of view and by exploring in depth some peculiarities of several human biological phenomena (in particular human blood and its components), we think that a thermodynamic approach to fractional theory can give more detailed information about biophysical behavior, which cannot be obtained by other ways. In particular, the fractional thermodynamics model proposed by us in the following sections will be useful for conducting an in-depth exploration of the alterations and functionality of red blood cells in the presence of natural and synthetic drugs [24,25,26,27,28,29,30]. The study of these phenomena is very complex, and a direct experimental approach is almost impossible. Thus, we will undertake the non-equilibrium thermodynamics fractional approach—the development of which we hope allows the derivation of new results. In many cases, fractional models are more efficient than non-fractional models, as they better fit experimental data, and this efficiency becomes important when we want to study complex phenomena such as those occurring in the biological field. Our model is based on thermodynamic considerations, and therefore, it is more suited to the investigation of the evolution of the system under study [31,32,33,34,35,36]. We start by introducing a new fractional model in the final sections of this paper. We think the above is enough to justify the need to use non-equilibrium thermodynamics with internal variables in the study of living matter.

1.1. General Considerations

Life has evolved in coexistence with the natural electric and magnetic fields of the Earth. The electromagnetic radiation originating from the Earth is almost static and has low amplitude, so its interaction with biological systems is considered to be almost negligible. However, human evolution and progress, with the expansion of communication networks, have led to a significant increase and expansion of electric fields. Therefore, the daily exposure of humans to these fields is no longer negligible, and it raises the question of their effects on human health. Since the exposure of cells and tissues to electric fields can lead to a variety of physiological changes (most of which are not yet well known), it seems clear that in biological systems, exposure to an electric field can induce a chain of multi-scale responses initiated by the interaction between the incident wave and the atomic structure of biomolecules. For that reason, this interaction can cause changes in the chemical composition and charge distribution of proteins and macromolecules that translates into changes in the biochemical signaling pathways. These conformational changes cause alterations in the cell metabolism, resulting in the switch of biological processes such as proliferation, differentiation, and apoptosis. The accurate estimation of the induced currents by an electric field in the human body has its importance not only in medical research, but also for industrial implications. It should not be forgotten that, a large amount of equipment based on electrical or electronic circuits is used on a daily basis, and therefore, they are potential generators of fields. However, if it is true that electric fields can cause serious damage to health, on the other hand, it must be recognized that the use of these fields could contribute to medical diagnostics and/or to the treatment of specific diseases. In both cases, an in-depth study of the interactions of an electric field with the human body—or, more generally, with biological tissue—would be desirable. In fact, biological material is difficult to study because it is very unusual and varied (from person to person), and the scientific expertise is now very selective, so a physical researcher will be able to assess the physical phenomena resulting from an electric field, but will hardly be able to understand the real implications on the health of the affected cells. In contrast, a biologist or a doctor, in perfect harmony with cellular health, will not be able to understand the physical/mathematical laws that have caused this phenomenon. The goal of this study is to help overcome the current difficulties related to the interpretation of the electrical effects in biological tissues. The intensity of the electric field generally applied to biological tissues depends very much on the dielectric constant of the tissue, since it must be taken into account that an external electric field of intensity ε_r generates an electric field inside the tissues which is reduced by a factor ε_r. So, the intensity of the electric field to apply depends on the tissue being studied (or better, on its dielectric constant). In some cases, we do not go beyond a field of intensity of some kV/m. However, the choice of frequency gives the most important information. In fact, biological tissues are very sensitive in response to the frequency of perturbation, showing different phenomena as the frequency varies. In Figure 1, some of these phenomena are summarily reported.

1.2. Biological Tissues

The human body is very complex; each tissue has specific properties, even if the main constituent is water. In one of the simplest models of approximation, the biological tissue is considered as a set of cells surrounded by a thin semi-permeable membrane, which separates the cytoplasm from the extracellular medium. This membrane not only delimits the cell, but plays an important role in almost all internal metabolic processes [37]. It is a bilayer structure composed of lipid molecules and proteins, where phospholipids are a major component and their hydrophobic ends are sandwiched by their hydrophilic ends. Cell internal structure depends on cell functionality, and may contain various and complex organelles; cell shape and size also depend strongly on the type and function of the cell. For example, nerve cells such as neurons are stellate cells, erythrocytes have biconcave shape, while muscle cells are spindle-shaped. Furthermore, in tissues, cells are connected through junctions that allow exchanges between one cell and the other, favoring local cellular communication. Interstitial and intracellular fluids are mostly aqueous salt solutions, in which the salt content is specified by the presence of inorganic salts and charge ions. The most important ions in solutions are: sodium (Na⁺), potassium (K⁺), chloride (Cl⁻), and calcium (Ca²⁺). From an electrical point of view, these junctions contribute to increasing the sensitivity of the tissue to an externally applied electric field. However, from a medical point of view, these interactions can provide important information on tissue health because some diseases related to cell necrosis and/or degeneration (e.g., cancer) can lead to serious deterioration of these interstitial spaces [38,39].

1.3. Synthetic Description of the Interaction between Electric Field and Biological Tissues

Biological tissues may be considered as an aggregate of ions and molecules interacting with the outer field will give two types of responses: one traced back by electrical conduction phenomena and the other by polarization effects. From a dielectric point of view, biological tissues show dissipative and dispersive effects that may be described with the complex electric conductivity and with a complex dielectric constant, respectively [40,41,42].

Upon perturbing biological tissue by an electric harmonic field, it shows a dielectric relaxation and an Ohmic loss. These responses can be respectively ascribed to the dipole relaxation and migration charge inside the material. There are different modes of polarization: electronic deformation, atomic deformation, dipolar orientation, and interfacial. Each of these depend on the frequency range used, as shown in the following

Table 1. Polarization modes depending on the range of frequencies. Reproduced with permission from [23].

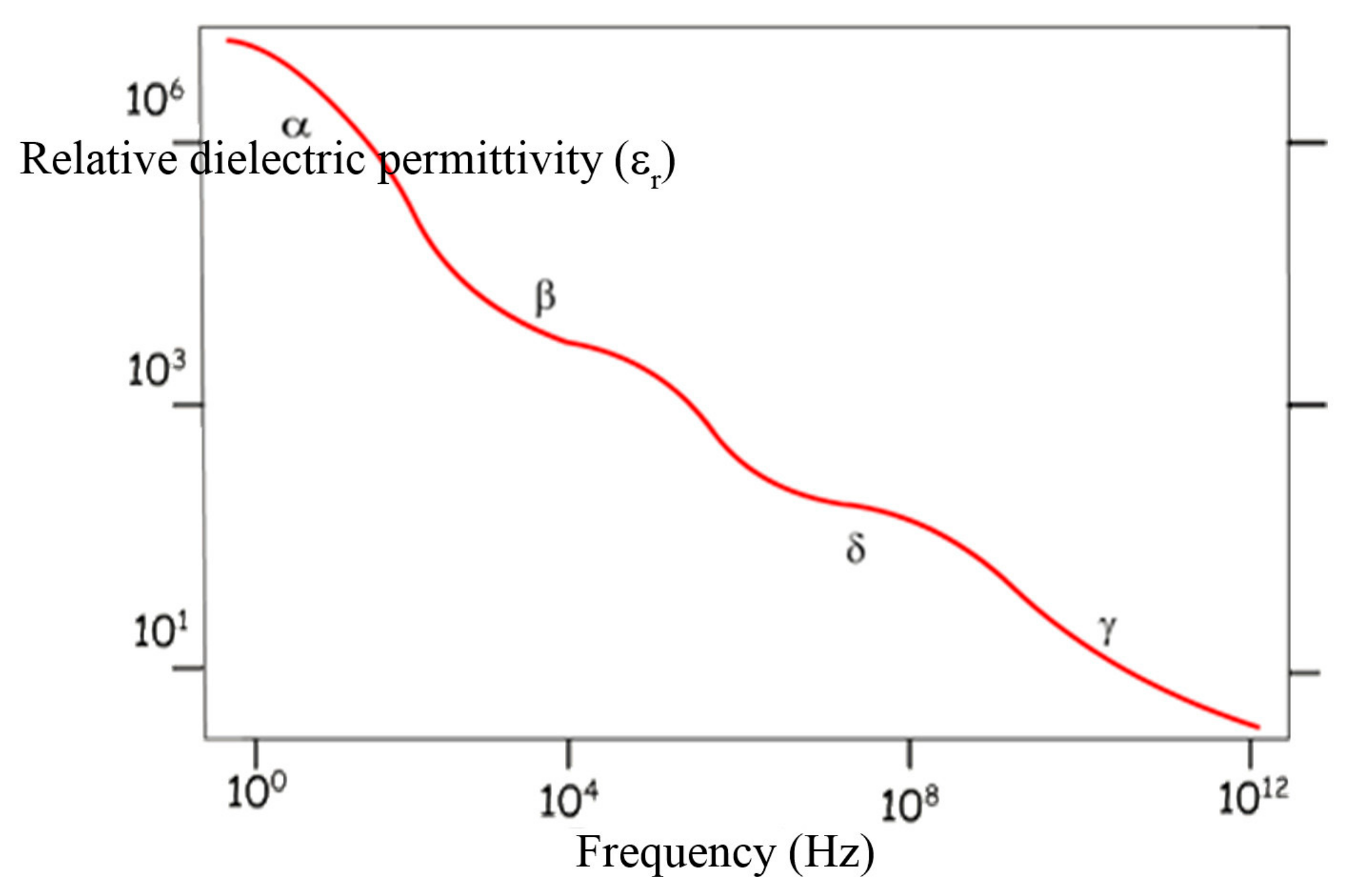
Polarization	Relaxation Time (s)	Frequency (Hz)	Wave
Electronic deformation	10−16	1015	UV
Atomic deformation	10−14–10−13	1013–1012	IR
Dipolar Orientation	10−11–10−3	1010–102	Microwave
Interfacial	10−3–10−1	102–100	Low-frequency

.

Our studies focus on the dipolar orientation, and in particular on the relaxation effects associated with the permanent and induced molecular dipoles that can be observed up to the microwave frequencies (10¹⁰ Hz), as they are characterized by a wide range of time constants on the order of 10⁻¹¹–10⁻³ s. The field changes slowly at low frequencies, allowing the dipole to reach equilibrium before its modification. While at frequencies where the viscosity of the medium prevents the dipole from following the field, the absorption of the energy of the field itself will lead to the dissipation of energy. Furthermore, a changing state of polarization corresponds to charge movements, and is therefore equivalent to a current. This polarization is the displacement current of Maxwell. The effective polarization results from the sum of each contribution to the frequency of the perturbation. The dielectric properties of materials are well described by the complex dielectric constant, but an alternative representation is the complex conductivity associated with a complex dielectric constant from well-known relationships. Even the complex conductivity is a function of the frequency of perturbation. Generally, two types of current can be distinguished in a medium: an Ohmic one associated with a flow charge and the other of displacement associated with the rotation and oscillation of the particles to follow the electric field. The Ohmic current occurs for frequencies lesser than the second. The above-mentioned processes lead to relaxation phenomena indicated as α, β, γ that depend on the range of frequencies considered. Figure 1 shows the dielectric constant values measured in biological tissues at different frequencies.

1.4. Interaction of Electrical Field with Biological Tissue

From the dielectric point of view, the interaction of an electric field with a biological tissue takes place mainly through polarization phenomena. In reality, the electric field is also made up of electric charges (ions), and these are under the effect of the field shift, giving rise to an electric current. In this section, we describe only dielectric relaxation phenomena (omitting the phenomenon of electrical conduction), introducing a new fractional model related to dielectric relaxation phenomena in the context of the thermodynamics of non-equilibrium with internal variables. By placing a biological tissue in a harmonic electric field, the component of the electric moment of each molecule in the direction of the field will be different from zero, and it can be shown that it is proportional to the field. This phenomenon is mainly due to a real deformation which is a deformation polarization and a reorientation which manifests itself on polar molecules (polarization by orientation). Obviously, each molecule follows the course of the field, but if removed from its equilibrium position (deforming and orienting itself), it uses a finite time called relaxation time to reacquire it, thus showing relaxation phenomena due to its inertia or other factors of mechanical nature (e.g., viscosity). We therefore consider a biological tissue as a dielectric medium with dispersion phenomena. The study of such phenomena finds multiple applications in physiology, in diagnostics, and in therapy [20]. One example can be given in cancer diagnostics; in particular, these phenomena allow the comparison of cancer cells to normal cells in order to highlight the evolution of the disease [10,43,44]. This technique can obviously be applied to many other diseases, and it is linked to the knowledge of the complex dielectric function (introduced in paragraph 3). The dielectric function is experimentally measured as a function of the frequency ω of the perturbing electric field. The techniques are summarized in

Table 2. Experimental methods.

Frequency (Hz)	Method
10−4 to 10−1	d.c. Transient measures
10−2 to 102	Ultra-low frequency bridge
10 to 107	Schering bridge
	Transformer bridge
105 to 108	Resonance circuits
108 to 109	Coaxial line
	Re-entrant cavity
109 to 3 × 1010	H01n cavity resonator

, and depend on both the tissue under study and on the frequency ranges investigated. By associating a particular type of polarization to each group, the intervals can in turn be divided into four groups, as shown in Table 2. Obviously, in the table there is no clear distinction between the various types of polarization reported, but the induced relaxation phenomena are indicated with α, β, γ, and δ, and depend on the frequency considered as shown in Figure 1. Observing Figure 1, we note that at low frequencies (relaxations α) there is a very high permittivity (10⁶–10⁷), such as to considerably reduce the field in the tissues. This is a peculiarity of organisms with cell membranes, and the reduction serves to protect the tissues from the fields [45,46]. For higher frequencies, relaxations β, there is a further decrease in the permittivity. These relaxations are influenced by the membranes that act as capacitors between the inside and the outside of the cellular spaces. In particular, at low frequency the electric fields charge these capacitors, but as the frequency increases, the accumulation time of the charges decreases because the field changes before their arrival. This leads to a decrease in the permittivity; this occurs between 10 KHz and 100 MHz (Figure 1). A further increase in frequency triggers the relaxation δ due to the reorientation of the dipolar molecules of water bound to proteins. For frequencies higher than 20 GHz, the rotational and vibrational levels of the polar water macromolecules are affected [23].

2. Importance of Phenomenological and State-Equations

The interaction between electromagnetic field and matter is one of the more important methods to study the electrical properties of inert and biological media. This approach is based on Maxwell’s equations, which is a system of six partial differential equations with 15 unknown functions. For the integration of this system it is necessary to introduce a set of equations in such a way to complete the system. These are the so-called material equations, which are of two types: phenomenological and state equations. They are considered in the network of a thermodynamic approach and specify the material characteristic of the medium. They have a double importance: (i) they are essential for the integration of Maxwell’s differential equations, and (ii) they characterize the medium object of study. Here we are interested only in the characterization of the medium, and we do not consider the integration of the Maxwell equation. Since effects are irreversible phenomena (in particular for biological material), it is worthwhile to study these effects with the help of non-equilibrium thermodynamics (NET) [7,8,9,47]. Here we first synthetically describe the structure of NET and then we introduce the dielectric Kluitenberg’s NET. In this context, our approach is not rigorous, but gives a clear vision of the structure of these theories. We start by observing that the energy is often the cause of the change that occurs in the matter. The phenomena suggest that each form of energy exchanged corresponds to two physical entities, respectively X (extensive variable) and Y (intensive variable), such that the infinitesimal change of this energy dE is:

$$dE=YdX$$

(5)

$$\frac{dE}{dX}=Y$$

(6)

This is a general form of state equation; in the next section we introduce a particular form of this equation. Obviously, if more than one form of energy is exchanged, Equation (5) becomes:

$$dE={\displaystyle \sum _{i=1}^n{Y}_i}d{X}_i$$

where n is the number of exchanged energy. A central role in non-equilibrium thermodynamics is played by the entropy and by its dynamics. By considering the entropy S as function of n extensive variables X_i (i = 1, 2, …, n)

$$S=S(X_1,X_2,\dots ,X_n)$$

(7)

and by introducing generalized forces

$$F_k=\frac{\partial S}{\partial X_k}$$

(8)

called affinities, and related “fluxes”

$$J_k=\frac{d{X}_k}{dt}$$

(9)

the entropy production will be

$$\frac{dS}{dt}={\displaystyle \sum _k{F}_k}{J}_k={\displaystyle \sum _k\frac{\partial S}{\partial X_k}}\frac{d{X}_k}{dt}$$

(10)

However, the entropy balance and the state equation are mathematically insufficient to determine the evolution of the variables describing a system. Thus, it is necessary to introduce the phenomenological equations, which are relations between fluxes and affinities intimately related to the physical phenomena occurring in the medium. The functional dependence between fluxes and affinities can be very complex. However, in a large number of phenomena these relations may be considered linear

$$J_i={\displaystyle \sum _k{M}_{ik}}{F}_k$$

(11)

These are called phenomenological equations and M_ik called phenomenological coefficients satisfying some symmetry relations. In the next sections, following Kluitenberg’s point of view, we introduce particular forms of this relation in the contest of dielectric relaxation phenomena. Here, we introduce the basic axiom on local and instant equilibrium: “For sufficiently small deviations from equilibrium, a system can be divided into tiny (physical) volume elements, each of which can be regarded as a small homogeneous equilibrium system”. Moreover, the length and time scales of these subsystems are infinitesimally small from a macroscopic point of view, but not from a molecular point of view. Molecularly, they are still large, and the subsystem contains enough molecules that the average taken on the number of molecules assumes a deterministic significance. Since our approach is based entirely on linear approximation, in the next section we describe some aspects of the linear response theory.

3. Remarks on Linear Response Theory

As shown in Figure 2, let “S” be a generic system subject to a time-dependent perturbation f(t) (input), and let g(t) be the time-dependent function which represents the response (output) of the system “S” to the perturbation f(t).

For a linear system, it can be shown that the following convolution relation between f(t) and g(t) is valid [48]:

$$g(t)=f(t)\otimes h(t)$$

(12)

where

$$f(t)\otimes h(t)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f(t_1)}h(t-t_1)d{t}_1$$

(13)

From Equation (12) and taking in account convolution theorem, it follows that

$$\stackrel{t}{\mathcal{F}}\left\{g\left(t\right)\right\}=\stackrel{t}{\mathcal{F}}\left\{f\left(t\right)\right\}\stackrel{t}{\mathcal{F}}\left\{h\left(t\right)\right\}$$

(14)

where the symbol $\stackrel{t}{\mathcal{F}}\left\{\dots \right\}$ is the Fourier transform. We have:

$$\stackrel{t}{\mathcal{F}}\left\{g\left(t\right)\right\}=G\left(\omega \right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{e}^{-i\omega t}g\left(t\right)dt}$$

(15)

$$\stackrel{t}{\mathcal{F}}\left\{f\left(t\right)\right\}=F\left(\omega \right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{e}^{-i\omega t}f\left(t\right)dt}$$

(16)

$$\stackrel{t}{\mathcal{F}}\left\{h\left(t\right)\right\}=H\left(\omega \right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{e}^{-i\omega t}h\left(t\right)dt}$$

(17)

where $H(\omega )$ is the transfer function which we propose to determine. From relations (14)–(17), one has

$$H(\omega )=\frac{G(\omega )}{F(\omega )}$$

(18)

and therefore

$$h\left(t\right)=\stackrel{t}{F^{-1}}\left\{H\left(\omega \right)\right\}=\stackrel{t}{F^{-1}}\left\{\frac{G\left(\omega \right)}{F\left(\omega \right)}\right\}$$

(19)

where $\stackrel{t}{F^{-1}}\left\{\dots \right\}$ is the inverse Fourier transform. It is very important for many experiments to utilize a harmonic input as:

$$f(t)=A{e}^{i{\omega }_{0}t}$$

(20)

where A is the amplitude of the oscillation and ω₀ its angular frequency. It can be shown that a very important result for this choice is: “for a L.S.: to a harmonic input corresponds a harmonic output of the same frequency, but with different amplitude and phase, which depend on the angular frequency of input” [29]. Therefore, the output can be expressed as

$$g(t)=B({\omega }_0)e^{i({\omega }_{0}t+\varphi ({\omega }_0))}$$

(21)

where $\varphi ({\omega }_0)$ is a phase lag and the integration is on finite time interval. If we assume an extensive variable f(t) as input (cause) and evaluate the corresponding intensive variable g(t) as output (effect), we are able to determine this transfer function:

$$H(\omega )=\frac{G(\omega )}{F(\omega )}=\frac{B(\omega )}{A}{e}^{i\varphi (\omega )}$$

(22)

and it is introduced the complex quantity

$$\Omega (\omega )={\Omega }_1(\omega )+i{\Omega }_2(\omega )=H(\omega )$$

(23)

with real and imaginary parts given by

$${\Omega }_1=\frac{B(\omega )}{A}\cos \varphi (\omega )$$

(24)

$${\Omega }_2=\frac{B(\omega )}{A}\sin \varphi (\omega )$$

(25)

These functions are very important for the study of the aforementioned relaxation phenomena. In a physical context, these quantities are called storage modulus and loss modulus, respectively, and it is possible to show that they are related to non-dissipative and dissipative phenomena, respectively. Their physical meaning depends on the physical meaning of the amplitude A and B(ω). Moreover, these two quantities are directly experimentally measurable as functions of the angular frequency of input. Now, we will apply this approach to the linear dielectric relaxation.

Dielectric Relaxation Phenomena

Applying a sinusoidal voltage to a dielectric continuum medium placed in a plane capacitor causes a sinusoidal surface charge on its plates, the density of which is characterized by the normal component of induction vector $D=\underset{\_}{D}\times \underset{\_}{n}$ (n is the unit normal to the plates). D is an extensive variable, and is assumed as cause. Inside the capacitor, a sinusoidal electric field characterized by its normal component $E=\underset{\_}{E}\times n$ will be generated. E is an intensive variable, and is assumed as effect. Therefore, if the surface density charge “input” evolves sinusoidally, the input (20) becomes [49]:

$$D^{\ast }=D_0{e}^{i\omega t}$$

(26)

where f = D* and A = D₀. The electric field inside the capacitor is also sinusoidal, and is characterized by the same frequency but by different phase and amplitude; so, the output (21) becomes:

$$E^{\ast }=E_0{e}^{i(\omega t+\varphi (\omega ))}$$

(27)

Taking into account (22)–(25), we have

$$s^{\ast }=\frac{E_0(\omega )}{D_0}{e}^{i\varphi (\omega )}$$

(28)

$$\begin{array}{l}{s}_1(\omega )=\frac{E_0(\omega )}{D_0}\cos \varphi (\omega )\\ \mathrm{or}\\ s_2(\omega )=\frac{E_0(\omega )}{D_0}\sin \varphi (\omega )\end{array}$$

(29)

The quantities s₁ and s₂ are real and imaginary parts of the complex dielectric modulus

$$s^{\ast }=s_1+i{s}_2$$

(30)

Now, we define the complex dielectric function:

$${\epsilon }^{\ast }=\frac{1}{s^{\ast }}={\epsilon }^{\prime }-i{\epsilon }^{″}$$

(31)

with

$${\epsilon }^{\prime }=\frac{s_1}{s_1{}^2+s_2{}^2},{\epsilon }^{″}=\frac{s_2}{s_1{}^2+s_2{}^2}$$

(32)

Relative dielectric functions are defined by

$${\epsilon }_1={\epsilon }^{\prime }/{\epsilon }_0,{\epsilon }_2={\epsilon }^{″}/{\epsilon }_0$$

(33)

where ε₀ is the vacuum dielectric constant. Finally, we provide a detailed report of some experimental methods which are well-known in the literature, and usable for the realization of curves 1 and 2.

4. Remarks on the Dielectric Kluitenberg-Model

Here we refer only to dielectric relaxation phenomena. Kluitenberg’s theory is based on the idea that the usual variables of non-equilibrium thermodynamics are insufficient to describe some phenomena that occur in a medium subjected to perturbation [7,8,9,47]. In particular, they are insufficient to describe relaxation dielectric phenomena in continuous media (we neglect magnetic and mechanical effects). The new Kluitenberg’s idea consists of the assumption that there is a vector field Ω which plays the role of thermodynamical internal degree of freedom and which influences the polarization. So, in the theory it is assumed that the specific entropy (which we still indicate with s) has the following functional dependence:

$$s=s(u,\underset{\_}{p},\underset{\_}{\Omega })$$

(34)

It can be shown that the introduction of vector field Ω allows P to be split in two parts such that

$$\underset{\_}{p}={\underset{\_}{p}}^{(0)}+{\underset{\_}{p}}^{(1)}$$

(35)

and s can be written as

$$s=s(u.\underset{\_}{p},{\underset{\_}{p}}^{(1)})$$

(36)

and one has:

$$\{\begin{array}{l}\frac{1}{T}=\frac{\partial s(u.\underset{\_}{p},{\underset{\_}{p}}^{(1)})}{\partial u}\\ {\underset{\_}{E}}^{(eq)}=-T\frac{\partial s(u.\underset{\_}{p},{\underset{\_}{p}}^{(1)})}{\partial \underset{\_}{p}}\\ {\underset{\_}{E}}^{(1)}=T\frac{\partial s(u.\underset{\_}{p},{\underset{\_}{p}}^{(1)})}{\partial {\underset{\_}{p}}^{(1)}}\end{array}$$

(37)

Moreover, the vector E^(ir) is introduced, defined as:

$${\underset{\_}{E}}^{(ir)}=\underset{\_}{E}-{\underset{\_}{E}}^{(eq)}$$

(38)

where E is the electric field which occurs in Maxwell’s equations. The vector E^(ir) is the irreversible electric field.

4.1. Phenomenological Dielectric Equations

It can be shown that only for dielectric relaxation, the entropy production per unit of volume and time is given by

$${\sigma }^{(s)}=\rho {\underset{\_}{E}}^{(ir)}\frac{d\underset{\_}{p}}{dt}+\rho {\underset{\_}{E}}^{(1)}\frac{d{\underset{\_}{p}}^{(1)}}{dt}$$

(39)

In agreement with Section 1 of this paper and with the method of non-equilibrium thermodynamics developed by De Groot and Mazur [47], linear relations exist for the functions which appear in (39). By assuming that the mass density ρ is constant, the following can be written:

$${\underset{\_}{E}}^{(ir)}=\rho L^{(0,0)}\frac{d\underset{\_}{p}}{dt}+L^{(0,1)}{\underset{\_}{E}}^{(1)}$$

(40)

$$\rho \frac{d{\underset{\_}{p}}^{(1)}}{dt}=\rho L^{(1,0)}\frac{d\underset{\_}{p}}{dt}+L^{(1,1)}{\underset{\_}{E}}^{(1)}$$

(41)

where $L^{(0,0)},L^{(0,1)},L^{(1,0)},L^{(1,1)}$ are phenomenological coefficients and we shall assume that they are constant.

4.2. Linear Approximation State Equations

The free energy f is defined by

$$f=u-Ts$$

(42)

Combining Equation (23) with Equation (32), one has:

$$df=-sdT+{\underset{\_}{E}}^{(eq)}\times d\underset{\_}{p}-{\underset{\_}{E}}^{(1)}\times d{\underset{\_}{p}}^{(1)}$$

(43)

It can be shown that the condition of isotropy and of linearity of the equations of state are fulfilled if it is assumed that f is the sum of two functions f₁ and f₂ [7,8,9]:

$$f=f_1+f_2$$

(44)

where:

$$f_1=f_1(T)$$

(45)

$$f_2=\frac{1}{2}\rho \left[a^{(0,0)}\underset{\_}{p}\cdot (\underset{\_}{p}-2{\underset{\_}{p}}^{(1)})+a^{(1,1)}{\underset{\_}{p}}^{{(1)}^2}\right]$$

(46)

where a^(0,0) and a^(1,1) are state coefficients (assumed constant) which have the dimension of reciprocal dielectric constant. Using (43)–(46) and defining the fields P⁽⁰⁾ and P⁽¹⁾ by

$${\underset{\_}{p}}^{(0)}=\rho {\underset{\_}{p}}^{(0)}$$

$${\underset{\_}{p}}^{(1)}=\rho {\underset{\_}{p}}^{(1)}$$

$$\underset{\_}{p}={\underset{\_}{p}}^{(0)}+{\underset{\_}{p}}^{(1)}$$

We obtain the following state equations:

$${\underset{\_}{E}}^{(eq)}=a^{(0,0)}(\underset{\_}{p}-{\underset{\_}{p}}^{(1)})=a^{(0,0)}{\underset{\_}{p}}^{(0)}$$

(47)

$${\underset{\_}{E}}^{(1)}=a^{(0,0)}\underset{\_}{p}-a^{(1,1)}{\underset{\_}{p}}^{(1)}$$

(48)

In the following, we assume that T is constant. It can be shown that it is possible to eliminate the internal fields and the two fields P⁽⁰⁾ and P⁽¹⁾ from Equations (40), (41), (47), and (48). This leads to the so-called dielectric relaxation equation [7,8,9]:

$${\chi }_{EP}^{(0)}\underset{\_}{E}+\frac{d\underset{\_}{E}}{dt}={\chi }_{PE}^{(0)}\underset{\_}{P}+{\chi }_{PE}^{(1)}\frac{d\underset{\_}{P}}{dt}+{\chi }_{PE}^{(2)}\frac{d^2\underset{\_}{P}}{d{t}^2}$$

(49)

where

$$\begin{array}{l}{\chi }_{EP}^{(0)}=a^{(1,1)}{L}^{(1,1)}\\ {\chi }_{PE}^{(0)}=a^{(0,0)}(a^{(1,1)}-a^{(0,0)})L^{(1,1)}\\ {\chi }_{PE}^{(1)}=a^{(0,0)}(1+L^{(0,1)}-L^{(1,0)})+a^{(1,1)}(L^{(0,0)}{L}^{(1,1)}-L^{(0,1)}{L}^{(1,0)})\\ {\chi }_{PE}^{(2)}=L^{(0,0)}\end{array}$$

(50)

It is important to observe that the constancy of phenomenological and state equations is referred to the time (and space) for each type of perturbation which acts on the medium. However, they vary with the change of the perturbation. For example, if the perturbation is of harmonic type with frequency ω, then the coefficients will depend on ω (we will see this in the next section), which can be considered as a parameter in the functional dependence of the coefficients. In this case, we shall call ${\mathit{a}}^{\left(0,0\right)},{\mathit{a}}^{\left(1,1\right)},{\mathit{L}}^{\left(0,0\right)},{\mathit{L}}^{\left(1,1\right)},{\mathit{L}}^{\left(0,1\right)}$ dynamical coefficients.

5. Classical Fractional Model

As mentioned in previous papers [10,19,20], the study of the dielectric relaxation properties of inert or living materials can be approached in two ways: theoretically and experimentally. We have considered the theoretical approach in previous papers; here we will treat the experimental approach, and in particular the fit of experimental data by taking into account the considerations introduced above on NET. This approach is based on the interaction between the medium under study and the selected external perturbation, and on the reaction of the medium to these perturbations (see Figure 1). This is very important because it gives important information on some characteristics of the medium. However, at the end of an experiment we have a finite set of data to elaborate. These data can be utilized to formulate models for prediction of the behavior of the medium. Frequently, the formulation of such models requires an analytical expression of the experimental data; thus, the process of fitting the data becomes very significant. This has a twofold importance: (i) it leads to the determination of extra data not belonging to the set of experimental data, and therefore it predicts the behavior outside of the experimental limits; (ii) it is essential in the mathematical formulation of the model. The prediction is very important if we consider living matter; for example, the prediction of the evolution of cancer tissues, which can be useful for therapeutic approaches and for diagnostic ones. When the medium is perturbed by a harmonic electric field, the finite set of experimental data obtained to study the dielectric relaxation phenomena is synthesized by the complex dielectric function ε expressed as a function of the frequency of perturbation at constant temperature. The plot of this function can hardly give physical information (although we consider only a linear approximation), because every phenomenon can be the superposition of several ones which—in this case—are hidden variables. Moreover, a spectrum ε = ε(ω) (where ω is the frequency of the perturbation) can be show more than one relaxation time or even a continuum set of relaxation times. In this case, the difficulty in formulating a model which takes into account all the phenomena associated with an increased relaxation time. In this paper, we will consider the collective phenomena showing only one relaxation time, since this is in agreement with the aspects of the biological system which we will study. There are many models for fitting dielectric data, and we mention only those largely used in the case of one relaxation time [31,32,33]:

$$\overline{\epsilon }=\frac{{\epsilon }_R+{\epsilon }_U(i\omega \sigma )}{1+(i\omega \sigma )}\mathrm{DEBYE}$$

(51)

$$\overline{\epsilon }=\frac{{\epsilon }_R+{\epsilon }_U{(i\omega \sigma )}^{\beta }}{1+{(i\omega \sigma )}^{\beta }}\mathrm{COLE}-\mathrm{COLE}$$

(52)

$$\overline{\epsilon }={\epsilon }_U+\frac{{\epsilon }_R+{\epsilon }_U}{{(1-i\omega \sigma )}^{\gamma }}\mathrm{DAVIDSON}-\mathrm{COLE}$$

(53)

$$\overline{\epsilon }={\epsilon }_U+\frac{{\epsilon }_R-{\epsilon }_U}{{(1-{(i\omega \sigma )}^{\alpha })}^{\gamma }}\mathrm{HAVRILIAK}-\mathrm{NEGAMI}$$

(54)

Moreover, we will recall the model proposed by Farsaci [6] for dielectric modulus at low frequencies ($\omega \sigma <<1$):

$$\{\begin{array}{l}{\Gamma }_1(\omega )={\Gamma }_{1R}+{\Gamma }_{2R}\frac{\omega \sigma }{1+{\omega }^2{\sigma }^2}\left(\frac{\omega }{{\omega }_R}-1\right)\\ {\Gamma }_2(\omega )={\Gamma }_{2R}\left(\frac{\omega +{\omega }^2{\sigma }^2{\omega }_R}{(1+{\omega }^2{\sigma }^2){\omega }_R}\right)\end{array}\mathrm{FARSACI}$$

(55)

where

$${\Gamma }^{\ast }={\Gamma }_1+i{\Gamma }_2=\frac{1}{\overline{\epsilon }-1},{\epsilon }^{\prime }=\frac{{\Gamma }_1}{{\Gamma }_1{}^2+{\Gamma }_2{}^2}+1,{\epsilon }^{″}=\frac{{\Gamma }_2}{{\Gamma }_1{}^2+{\Gamma }_2{}^2}$$

(56)

$\sigma$ is the relaxation time, ${\Gamma }_{1R}$, ${\Gamma }_{2R}$, ${\epsilon }_R$, and ${\omega }_R$ are the relaxed and un-relaxed values, respectively, and ω is the angular frequency. It has been shown that Farsaci’s model (which refers to complex dielectric modulus) is in agreement with experimental data for low frequency, since the latter approach to ${\Gamma }_{1R}$ and ${\Gamma }_{2R}$ for $\omega ={\omega }_R$ as occurs in realistic case and not only for ω = 0 as for other models. Here we do not comment on these relations because there is a large body of literature on these questions. However, we will remember that the models (52)–(54) are called fractional models for the presence of the parameters α and β which vary between 0 and 1. Indeed, fractional calculus is a generalization of classical differential and of integral calculus. Sometimes, by increasing the complexity of phenomena occurring in the medium, usual models fail to capture essential details; therefore, in many cases fractional calculus gives better results. Generally, there is no criterion; it is necessary verify the goodness of results to select the model to use. The fractional model which we introduce in the next section is based on NET. Here we do not cover the historic evolution of the fractional calculus, and we do not deepen the development of this calculus because that is not the aim of this work. This paper is devoted to providing a physical-mathematical approach for the study of living matter. So, in order to continue our previous research approach in the network of NET [10,19,20,21,22,23,36] and apply it to biological systems, in the next section we will formulate a dielectric fractional model based on NET.

6. Fractional Model

In this section we introduce our fractional model. The physical formulation of a fractional model is related to the introduction of a fractional differential equation with a certain number of parameters [33,34]. If “n” is this number, the model is named the n-parameter fractional model. Generally, the parameters which appear in the fractional differential equations are not only those of the fractional derivate, but there are other multiplicative constants. Obviously, a model with fewer parameters is better. The model which we are introducing is a two-parameter fractional dielectric model. The coefficients appearing as multiplicative factors in the fractional differential equation are evaluated with a procedure exposed in our previous paper [6]. In agreement with NET (introduced above), we enunciate the following fractional dielectric differential equation for a dielectric medium of order one (approximation with only one relaxation time; this has been shown to be a sufficient approximation for the biological systems which we will study):

$$E+{\left(\frac{1}{k_0}\right)}^{\beta }\frac{d^{\beta }E}{d{t}^{\beta }}=\left(\frac{h_0}{k_0}\right)P+h_1{\left(\frac{1}{k_0}\right)}^{\beta }\frac{d^{\beta }P}{d{t}^{\beta }}+h_2{k}_0{\left(\frac{1}{k_0}\right)}^{\alpha }\frac{d^{\alpha }E}{d{t}^{\beta }}$$

(57)

$$\begin{array}{l}0<\beta \le \alpha \le 1\\ h_i={\chi }_{(PE)}^{(i)}\hspace{1em}(i=0,1,2)k_0={\chi }_{(EP)}^{(0)}=\frac{1}{{\gamma }_0}\end{array}$$

(58)

where P is the polarization and E the electric field. By substituting the well-known relation $P=D-{\epsilon }_{0}E$ into Equation (57), one has:

$$\begin{array}{l}{h}_2\frac{1}{{\gamma }_0}{({\gamma }_0)}^{\alpha }{\epsilon }_0\frac{d^{\alpha }E}{d{t}^{\alpha }}+\left[h_1{\epsilon }_0{({\gamma }_0)}^{\beta }+{({\gamma }_0)}^{\beta }\right]\frac{d^{\beta }E}{d{t}^{\beta }}+(1+h_1{\gamma }_0{\epsilon }_0)E\\ =h_2\frac{1}{{\gamma }_0}{({\gamma }_0)}^{\alpha }\frac{d^{\alpha }D}{d{t}^{\alpha }}+h_1{({\gamma }_0)}^{\beta }\frac{d^{\beta }D}{d{t}^{\beta }}{h}_0{\gamma }_{0}D\end{array}$$

(59)

By considering $D=D_0{e}^{i\omega t}$ as an extensive variable (cause) and $E=E_0{e}^{i(\omega t+\phi )}$ as an intensive one (effect), Equation (59) becomes:

$$\begin{array}{l}{E}_0\left[h_2\frac{1}{{\gamma }_0}{({\gamma }_0)}^{\alpha }{\epsilon }_0{\left(i\omega \right)}^{\alpha }F\left\{e^{i\left(\omega t+\varphi \right)}\right\}+\left(h_1{\epsilon }_0{\left({\gamma }_0\right)}^{\beta }+{\left({\gamma }_0\right)}^{\beta }\right){\left(i\omega \right)}^{\beta }F\left\{e^{i\left(\omega t+\varphi \right)}\right\}+\left(1+h_0{\gamma }_0{\epsilon }_0\right)F\left\{e^{i\left(\omega t+\varphi \right)}\right\}\right]\\ =D_0\left[h_2\frac{1}{{\gamma }_0}{\left({\gamma }_0\right)}^{\alpha }{\left(i\omega \right)}^{\alpha }F\left\{e^{i\omega t}\right\}+h_1{\left({\gamma }_0\right)}^{\beta }{\left(i\omega \right)}^{\beta }F\left\{e^{i\omega t}\right\}+h_0{\gamma }_{0}F\left\{e^{i\omega t}\right\}\right]\end{array}$$

(60)

where the following important relation between Fourier transform $F\left\{\dots \right\}$ and fractional derivative $\frac{d^{\rho }}{d{t}^{\rho }}$ has been used:

$$F\left\{\frac{d^{\rho }f\left(t\right)}{d{t}^{\rho }}\right\}={\left(i\omega \right)}^{\rho }F\left\{f\left(t\right)\right\}$$

The complex dielectric modulus is:

$$s=\frac{F\left\{E_0{e}^{i\left(\omega t+\varphi \right)}\right\}}{F\left\{D_0{e}^{i\omega t}\right\}}=\frac{h_0{\gamma }_0+h_1{\left(i\omega {\gamma }_0\right)}^{\beta }+h_2\frac{1}{{\gamma }_0}{\left(i\omega {\gamma }_0\right)}^{\alpha }}{\left(1+h_0{\gamma }_0{\epsilon }_0\right)+\left(1+h_1{\epsilon }_0\right){\left(i\omega {\gamma }_0\right)}^{\beta }+h_2\frac{1}{{\gamma }_0}{\epsilon }_0{\left(i\omega {\gamma }_0\right)}^{\alpha }}$$

(61)

and finally, from (31):

$$\epsilon =\frac{1}{s}=\frac{(1+h_0{\gamma }_0{\epsilon }_0)+(1+h_1{\epsilon }_0){(i\omega {\gamma }_0)}^{\beta }+\frac{h_2}{{\gamma }_0}{\epsilon }_0{(i\omega {\gamma }_0)}^{\alpha }}{h_0{\gamma }_0+h_1{(i\omega {\gamma }_0)}^{\beta }+\frac{h_2}{{\gamma }_0}{(i\omega {\gamma }_0)}^{\alpha }}$$

(62)

where we remember that the coefficients in (58) are the same as the coefficients of (50). By separating the real and imaginary parts of $\epsilon$ in Equation (62), one obtains:

$${\epsilon }^{\prime }=\frac{AC+BD}{A^2+B^2},{\epsilon }^{″}=\frac{AD-CB}{A^2+B^2}$$

(63)

where:

$$\begin{array}{l}AC+BD=h_0\left(\frac{1}{{\gamma }_0}+h_0{\epsilon }_0\right)+\left[\left(h_0+\frac{1}{{\gamma }_0}{h}_1\right)\frac{1}{{\gamma }_0}+\frac{2h_0{h}_1{\epsilon }_0}{{\gamma }_0}\right]{(\omega {\gamma }_0)}^{\beta })\cos \left(\beta \frac{\pi }{2}\right)+\\ \left(\frac{h_2}{{\gamma }_0{}^3}+\frac{2h_0{h}_2{\epsilon }_0}{{\gamma }_0{}^2}\right){(\omega {\gamma }_0)}^{\alpha }\cos \left(\alpha \frac{\pi }{2}\right)+\frac{h_1}{{\gamma }_0{}^2}(1+h_1{\epsilon }_0){(\omega {\gamma }_0)}^{2\beta }+\frac{h_2{}^2{\epsilon }_0}{{\gamma }_0{}^4}{(\omega {\gamma }_0)}^{2\alpha }+\\ \left(\frac{h_2}{{\gamma }_0{}^3}+\frac{2h_1{h}_2{\epsilon }_0}{{\gamma }_0{}^3}\right){(\omega {\gamma }_0)}^{\alpha +\beta }\cos \left[(\alpha -\beta )\frac{\pi }{2}\right]\end{array}$$

(64)

$$\begin{array}{l}AD-CB=\frac{1}{{\gamma }_0}\left(h_0-h_1\frac{1}{{\gamma }_0}\right){(\omega {\gamma }_0)}^{\beta }\sin \left(\beta \frac{\pi }{2}\right)-\\ \frac{h_2}{{\gamma }_0{}^3}{(\omega {\gamma }_0)}^{\alpha }\sin \left(\alpha \frac{\pi }{2}\right)-\frac{h_2}{{\gamma }_0{}^3}{(\omega {\gamma }_0)}^{\alpha +\beta }\sin \left((\alpha -\beta )\frac{\pi }{2}\right)\end{array}$$

(65)

$$\begin{array}{l}{A}^2+B^2=h_0{}^2+\frac{h_1{}^2}{{\gamma }_0{}^2}{(\omega {\gamma }_0)}^{2\beta }+\frac{h_2{}^2}{{\gamma }_0{}^4}{(\omega {\gamma }_0)}^{2\alpha }+\\ \frac{2h_0{h}_2}{{\gamma }_0}{(\omega {\gamma }_0)}^{\beta }\cos \left(\beta \frac{\pi }{2}\right)+\frac{2h_0{h}_2}{{\gamma }_0{}^2}{(\omega {\gamma }_0)}^{\alpha }\cos \left(\alpha \frac{\pi }{2}\right)+\\ \frac{2h_1{h}_2}{{\gamma }_0{}^3}{(\omega {\gamma }_0)}^{\alpha +\beta }\cos \left((\alpha -\beta )\frac{\pi }{2}\right)\end{array}$$

(66)

This is our two-parameter model, since the values of $h_0,h_1,h_2,{\gamma }_0$ can be evaluated by means of the expressions obtained in our previous paper [6]. In particular:

$$\begin{array}{l}{h}_0=\frac{{\mathsf{\Gamma }}_{1R}}{\tau };h_1=\frac{{\mathsf{\Gamma }}_{2R}+{\mathsf{\Gamma }}_{1R}{\omega }_R\tau }{{\omega }_{R/U}\tau }\\ h_2=\frac{{\mathsf{\Gamma }}_{2R}}{{\omega }_R};{\gamma }_0=\tau \end{array}$$

(67)

where ${\mathsf{\Gamma }}_{1R}$, ${\mathsf{\Gamma }}_{2R}$ are the relaxed values of ${\mathsf{\Gamma }}_1$, ${\mathsf{\Gamma }}_2$ evaluated for $\omega ={\omega }_R$, respectively; $\tau$ is the Debye relaxation time measured for $\omega \tau =1$.

7. Deduction of the Cole–Cole Model

Here we will deduce the Cole–Cole model as a particular case of our model. To this end, we will recall the Cole–Cole differential equation [49]:

$${\tau }_D^{\beta }{\epsilon }_U\frac{d^{\beta }E}{d{t}^{\beta }}+{\epsilon }_{R}E={\tau }_D^{\beta }\frac{d^{\beta }D}{d{t}^{\beta }}+D$$

(68)

By considering $D=D_0{e}^{i\omega t}$ as an extensive variable (cause) and $E=E_0{e}^{i(\omega t+\phi )}$ as an intensive one (effect), Expression (52) is obtained for the dielectric function. If we rewrite Equation (59) with h₂ = 0, we obtain the following expression:

$$\left[\frac{h_1{\epsilon }_0{({\gamma }_0)}^{\beta }+{({\gamma }_0)}^{\beta }}{h_0{\gamma }_0}\right]\frac{d^{\beta }E}{d{t}^{\beta }}+\left(\frac{1+h_1{\gamma }_0{\epsilon }_0}{h_0{\gamma }_0}\right)E=\frac{h_1{({\gamma }_0)}^{\beta }}{h_0{\gamma }_0}\frac{d^{\beta }D}{d{t}^{\beta }}+D$$

(69)

By equating Equations (68) and (69), one obtains the following system:

$$\frac{h_1{\epsilon }_0{({\gamma }_0)}^{\beta }+{({\gamma }_0)}^{\beta }}{h_0{\gamma }_0}={\tau }_D^{\beta }{\epsilon }_U$$

$$\frac{1+h_1{\gamma }_0{\epsilon }_0}{h_0{\gamma }_0}={\epsilon }_R$$

$$\frac{h_1{({\gamma }_0)}^{\beta }}{h_0{\gamma }_0}={\tau }_D^{\beta }$$

The solution of this system is:

$$h_0=\frac{1}{{\tau }_D}\sqrt[\beta ]{\frac{{\epsilon }_R-{\epsilon }_0}{{\epsilon }_U-{\epsilon }_0}}\frac{1}{{\epsilon }_R-{\epsilon }_0};\hspace{1em}{h}_1=\frac{1}{{\epsilon }_U-{\epsilon }_0};\hspace{1em}{k}_0=\frac{1}{{\gamma }_0}=\frac{1}{{\tau }_D}\sqrt[\beta ]{\frac{{\epsilon }_R-{\epsilon }_0}{{\epsilon }_U-{\epsilon }_0}}$$

(70)

Thus, if we choose these values for $h_0,h_1,k_0$ from Equation (69) we obtain Equation (68).

8. Conclusions

In the network of dielectric relaxation phenomena, there exist numerous fractional models for fitting experimental data. Depending on the material object of study, one can select the model to use. Some of these models are based on an “empirical” mathematical approach and are not deduced by physical considerations. Our results are derived from a thermodynamic theory by introducing a thermodynamic fractional dielectric differential equation. This allows us to determine an expression for a complex dielectric function that we think would be more coherent from a thermodynamics point of view. Moreover, it is an important development for all of the studies that require an analytical expression of a dielectric function for the formulation of biophysical models. The new approach may be used for other development even in media with more than one relaxation time. Finally, we will remark that our model is a two-parameter model α and β from which—in this particular case—can be obtained from the Cole–Cole model. These parameters are related to each material, and are calculated for each one after a fitting process. In our case, the knowledge of an analytical form of complex dielectric function contributes in a consistent way to the theoretical study of phenomena which cannot be approached experimentally. Moreover, the model can predict processes which are experimentally inaccessible and—as mentioned above from a thermodynamic point of view—the model allows the investigation of phenomena not appearing in classical models. These peculiarities make the model useful for prevention and therapeutic techniques.