Entropy Generation and Exergy Destruction in Flow of Multiphase Dispersions of Droplets and Particles in a Polymeric Liquid
Abstract
:1. Introduction
2. Theoretical Background
2.1. Entropy Balance in Fluid Flow
2.2. Momentum and Energy Balance Equations for Fluid Flow
2.3. Application of the Gibbs Equation to Fluid Flow
2.4. Exergy Destruction in Fluid Flow
3. Experimental Work
3.1. Experimental Set Up
3.2. Preparation of Multiphase Dispersions
4. Results and Discussion
4.1. Two-Phase Dispersions
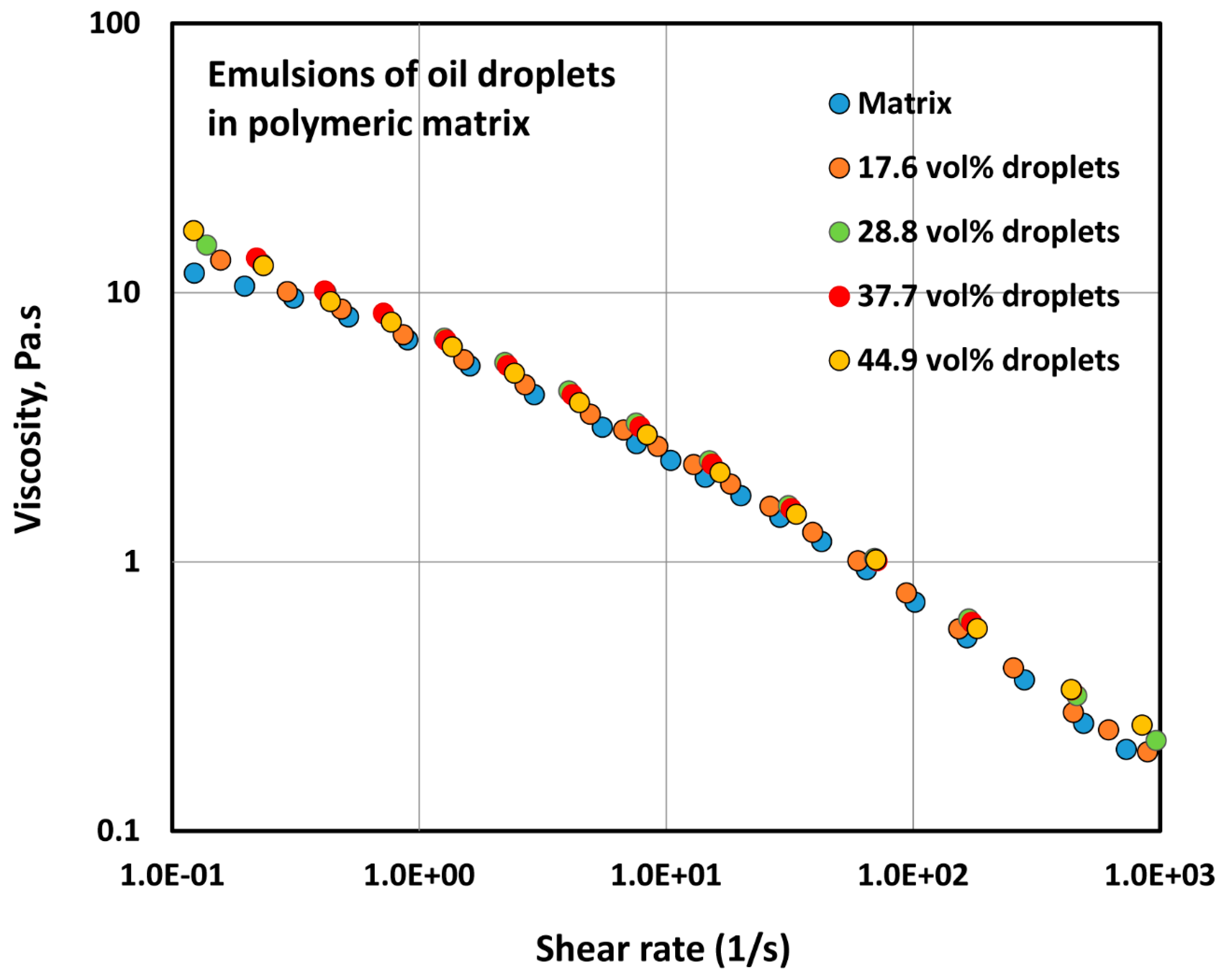
4.1.1. Rheology of Two-Phase Dispersions
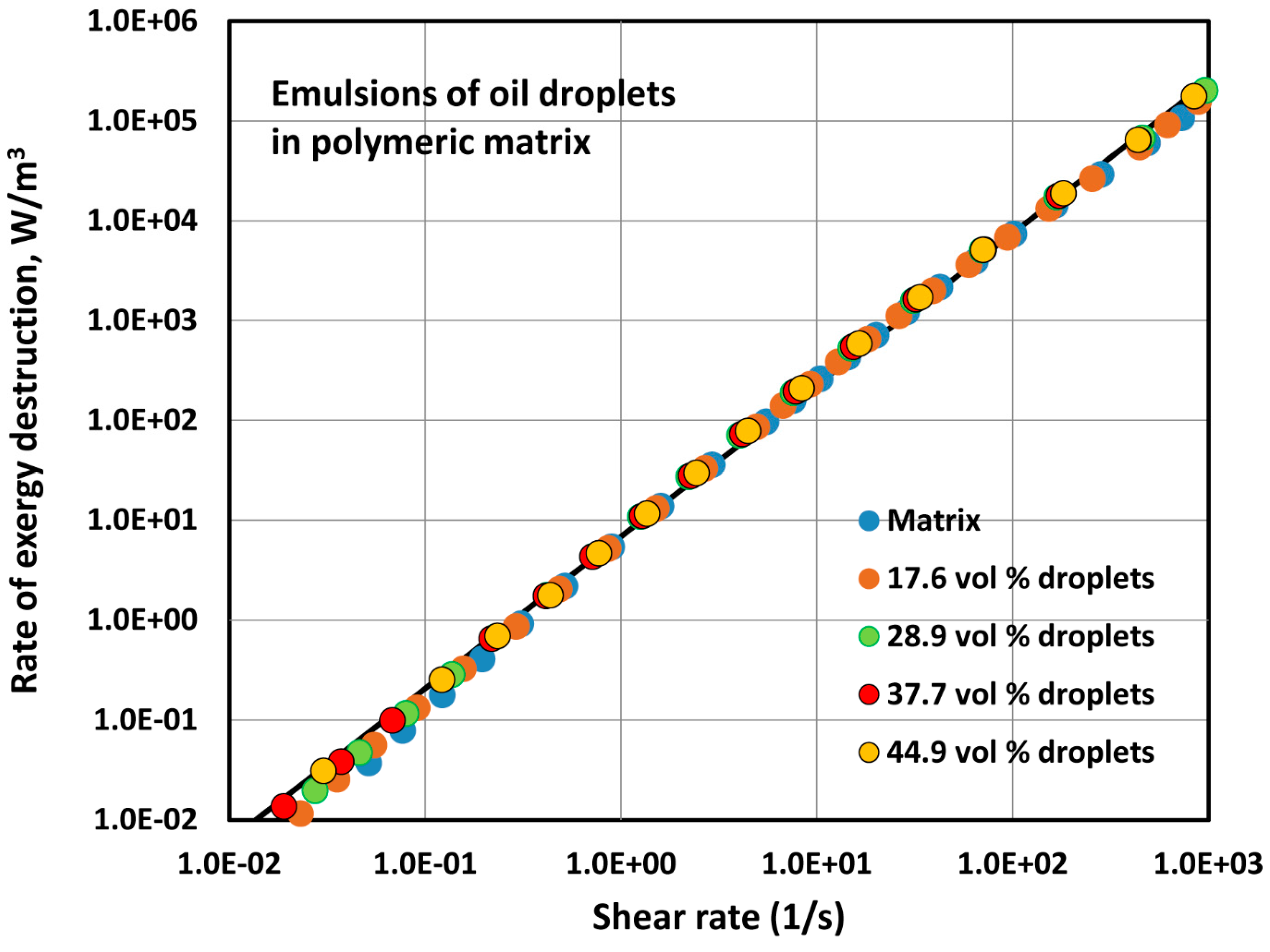
4.1.2. Exergy Destruction in Flow of Two-Phase Dispersions
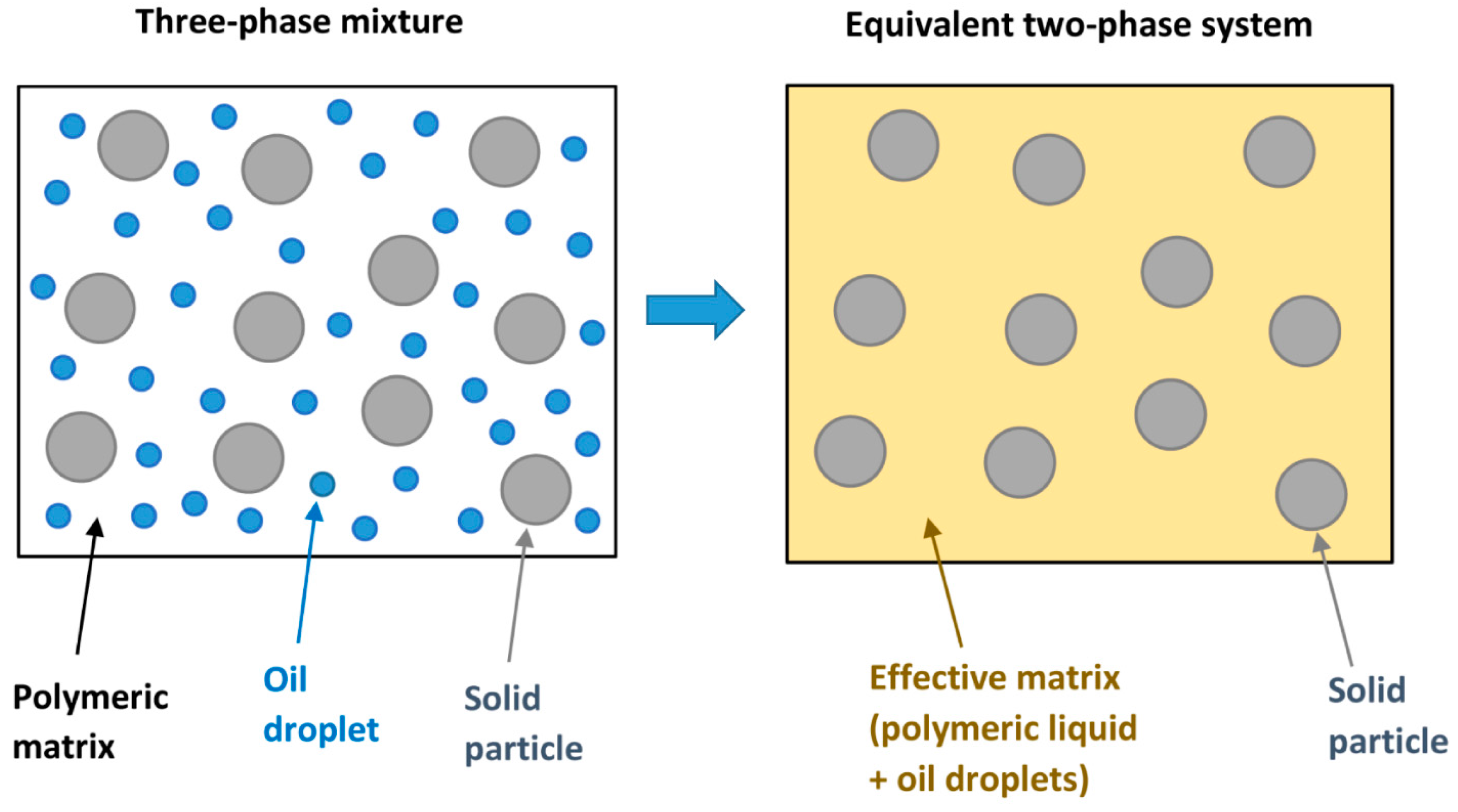
4.2. Multi-Phase Dispersions of Oil and Water in a Polymeric Matrix
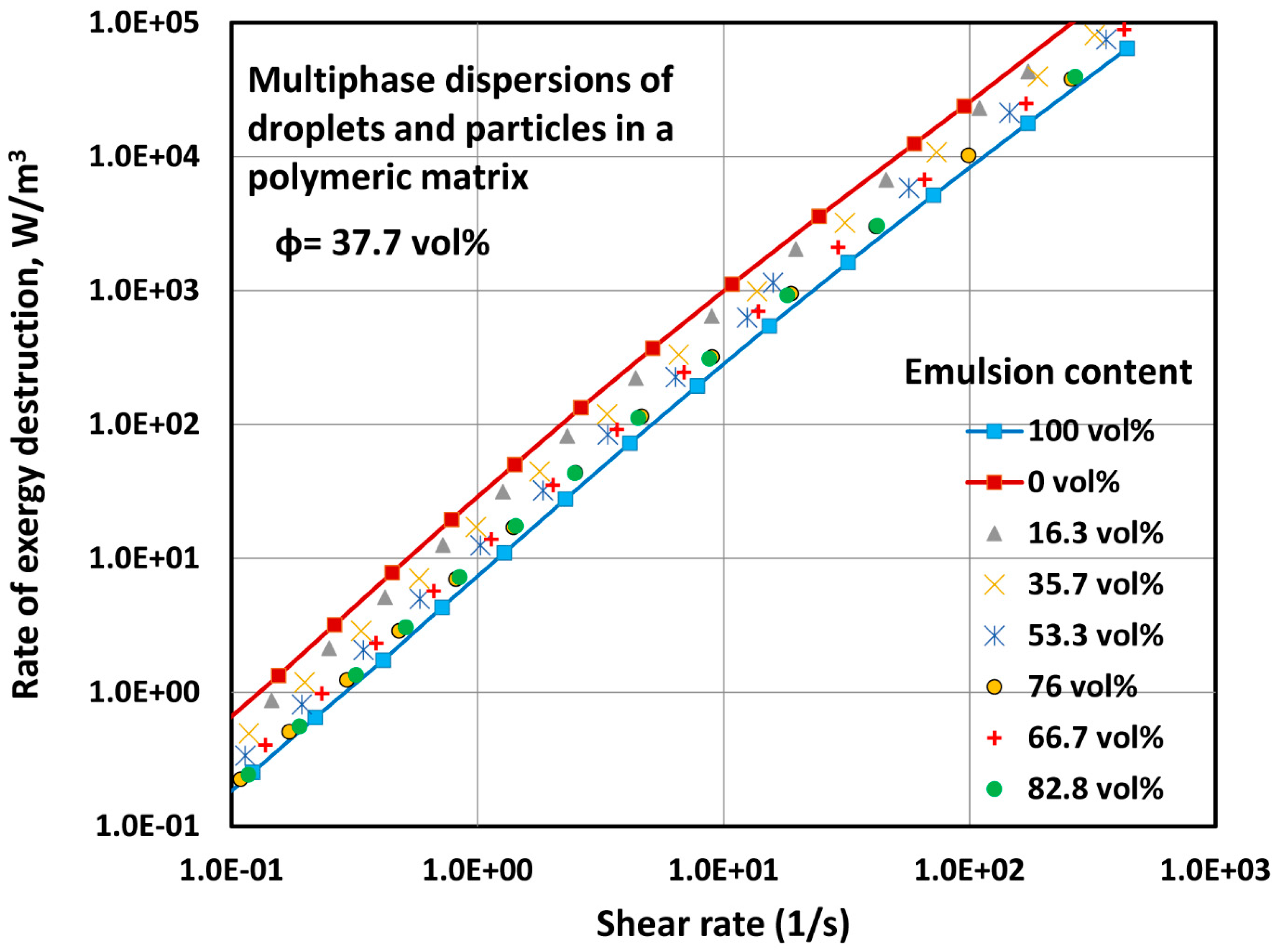
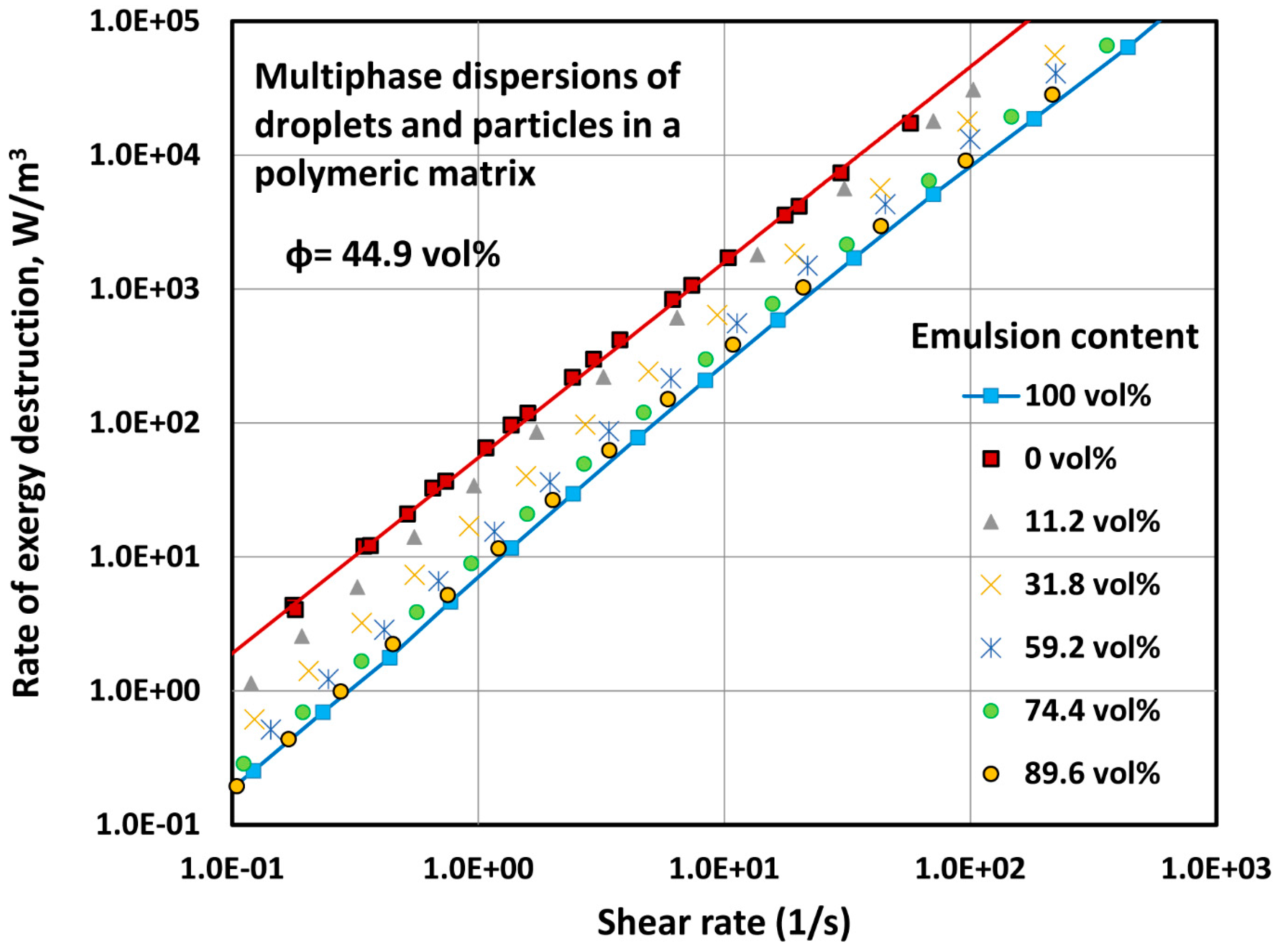
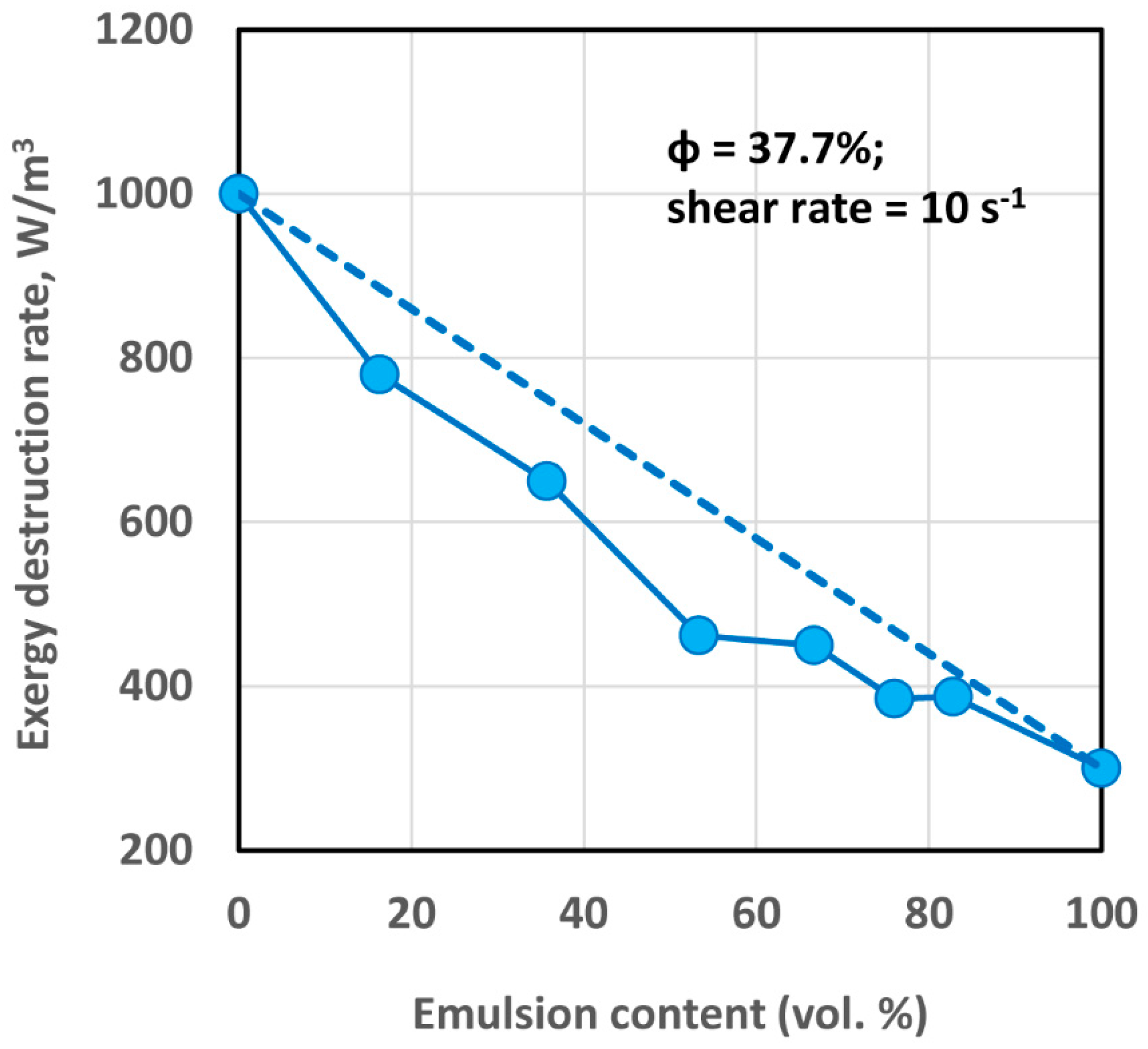
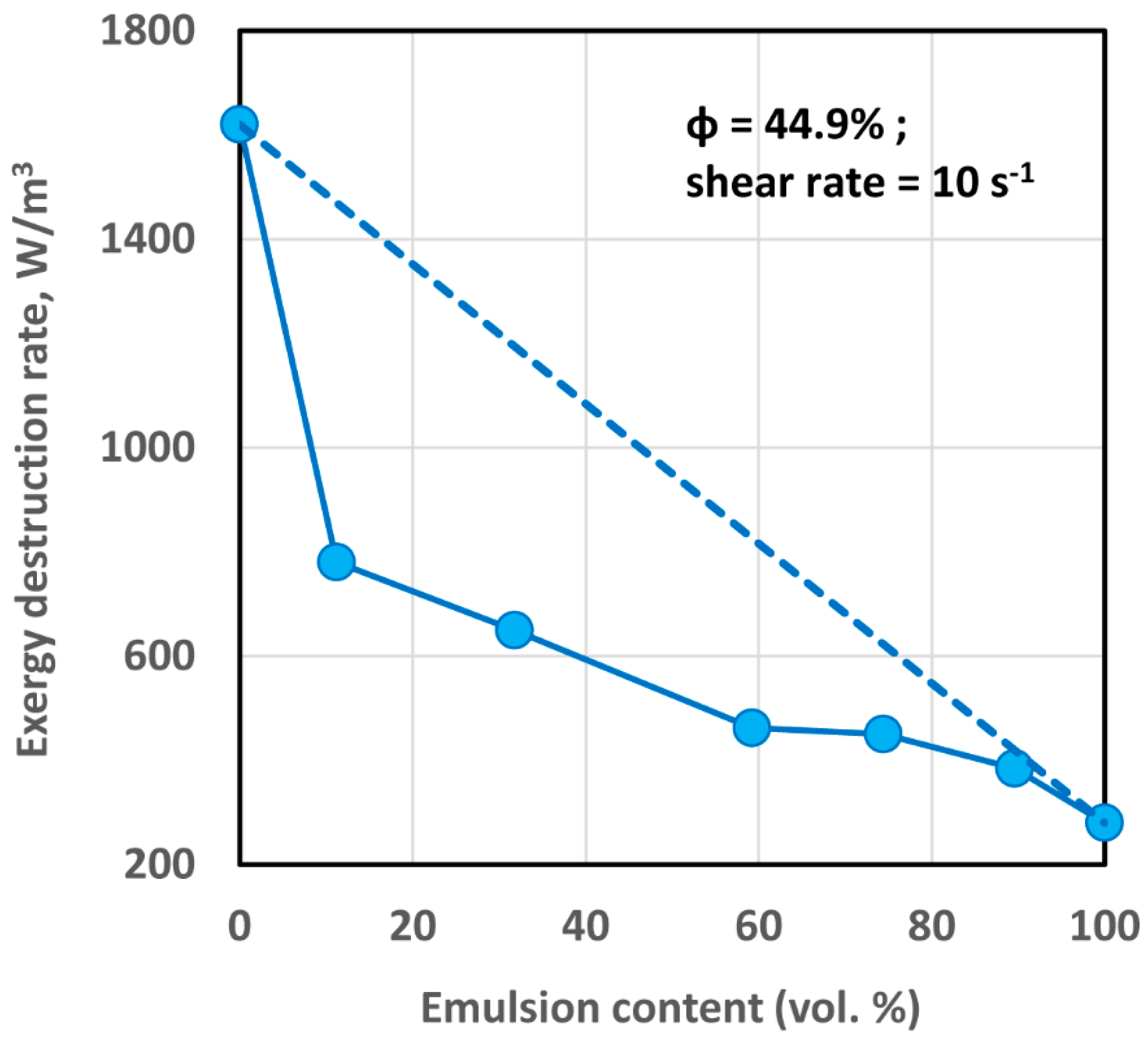
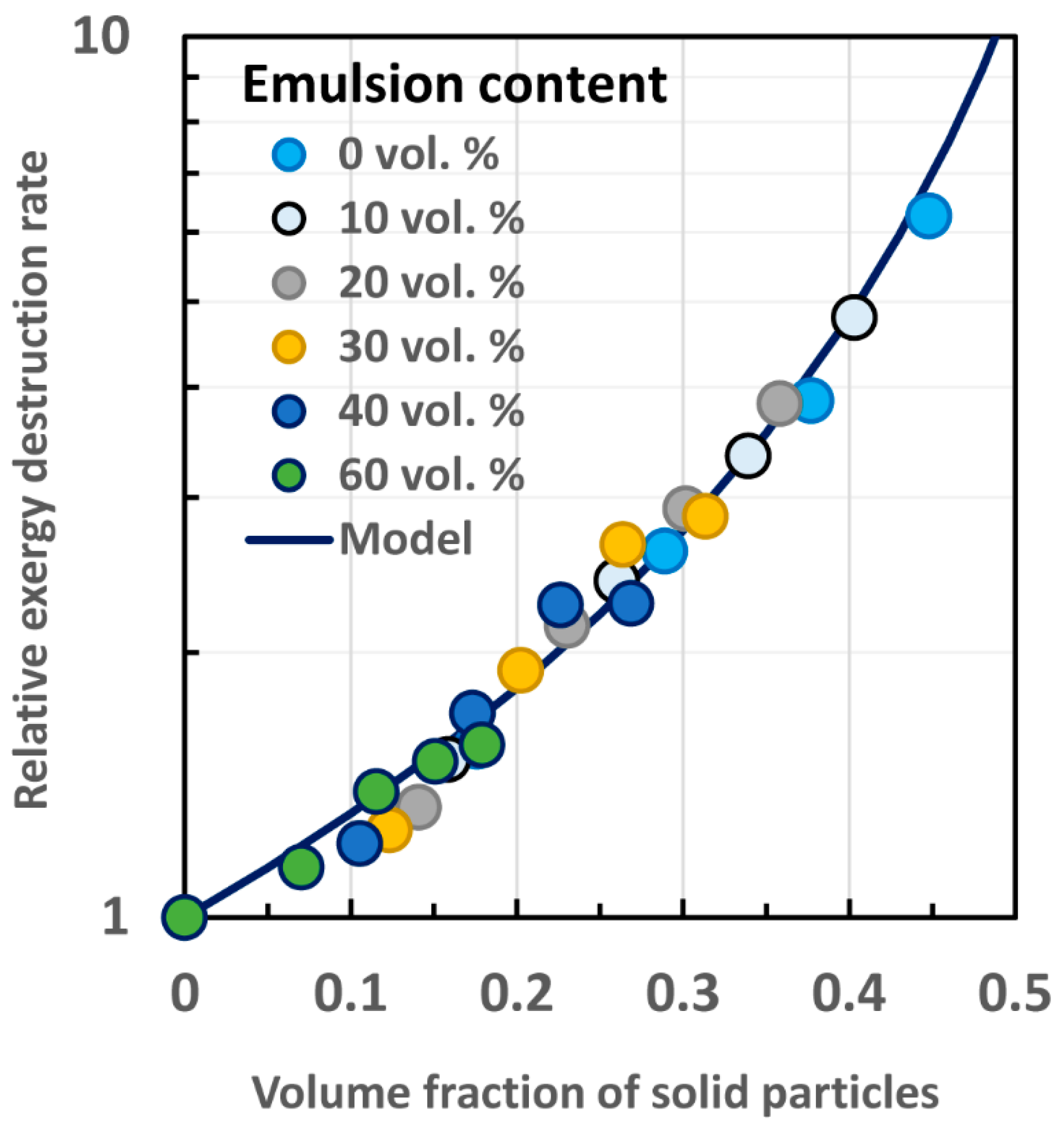
4.2.1. Exergy Destruction in Multi-Phase Dispersions
4.2.2. Model for Calculation of Exergy Destruction in Multi-Phase Dispersions
5. Practical Implications of This Work
6. Conclusions
- (a)
- The addition of oil droplets to a polymeric matrix does not alter the consistency index and flow behavior index of the system to any appreciable extent.
- (b)
- The addition of solid particles to a polymeric matrix does not alter the flow behavior index significantly, but the consistency index increases sharply with the increase in the particle concentration.
- (c)
- The exergy destruction rate in flow of emulsions of oil droplets and polymeric matrix does not change to any appreciable extent with the increase in the concentration of oil droplets.
- (d)
- The exergy destruction rate in flow of suspensions of solid particles and polymeric matrix increases with the increase in particle concentration.
- (e)
- Three-phase blends of oil droplets, solid particles, and polymeric matrix, can be modelled as two-phase blends of solid particles dispersed in an effective matrix composed of oil droplets and polymeric matrix.
- (f)
- A model is proposed to estimate the exergy destruction rates in flow of three-phase dispersions of oil droplets, solid particles, and polymeric matrix.
Conflicts of Interest
References
- Conley, R.F. Practical Dispersion; VCH: New York, NY, USA, 1996. [Google Scholar]
- Tadros, T.F. Solid/Liquid Dispersions; Academic Press: London, UK, 1987. [Google Scholar]
- Bennett, H.; Bishop, J.L.; Wulfinghoff, M.F. Practical Emulsions-Applications; Chemical Publishing: New York, NY, USA, 1968. [Google Scholar]
- Lissant, K.J. Emulsions and Emulsion Technology; Dekker: New York, NY, USA, 1974. [Google Scholar]
- Torrey, S. Emulsions and Emulsifier Applications-Recent Developments; Noyes Data Corporation: Park Ridge, NJ, USA, 1984. [Google Scholar]
- Friberg, S. Food Emulsions; Dekker: Rumson, NJ, USA, 1976. [Google Scholar]
- Becher, P. Encyclopedia of Emulsion Technology; Dekker: New York, NY, USA, 1985; Volume 2. [Google Scholar]
- Han, C.D. Multiphase Flow in Polymer Processing; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Kissa, E. Dispersions: Characterization, Testing, and Measurement; Dekker: New York, NY, USA, 1999. [Google Scholar]
- Pal, R. Rheology of emulsions containing polymeric liquids. In Encyclopedia of Emulsion Technology; Becher, P., Ed.; Dekker: New York, NY, USA, 1996; Volume 4, pp. 93–263. [Google Scholar]
- Pal, R. Quantification of irreversibilities in practical cyclic processes using exergy analysis and Gouy-Stodola theorem. Int. J. Mech. Eng. Educ. 2017. [Google Scholar] [CrossRef]
- Pal, R. Influence of droplet size on exergy destruction in flow of concentrated non-Newtonian emulsions. Energies 2016, 9, 293. [Google Scholar] [CrossRef]
- Pal, R. Entropy production in pipeline flow of dispersions of water in oil. Entropy 2014, 16, 4648–4661. [Google Scholar] [CrossRef]
- Pal, R. Exergy destruction in pipeline flow of surfactant-stabilized oil-in-water emulsions. Energies 2014, 7, 7602–7619. [Google Scholar] [CrossRef]
- Pal, R. Entropy generation in flow of highly concentrated non-Newtonian emulsions in smooth tubes. Entropy 2014, 16, 5178–5197. [Google Scholar] [CrossRef]
- Pal, R. Second law analysis of adiabatic and non-adiabatic pipeline flows of unstable and surfactant-stabilized emulsions. Entropy 2016, 18, 113. [Google Scholar] [CrossRef]
- Lebon, G.; Jou, D.; Casas-Vazquez, J. Understanding Non-Equilibrium Thermodynamics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Pal, R. Rheology of Particulate Dispersions and Composites; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids—Fluid Mechanics; Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
- Pal, R. Anomalous wall effects in parallel plate torsional flow of highly concentrated emulsions. ASME FED 1999, 249, 137–150. [Google Scholar]
- Pal, R. Modeling the viscosity of concentrated nanoemulsions and nanosuspensions. Fluids 2016, 1, 11. [Google Scholar] [CrossRef]
- Stickel, J.J.; Powell, R.L. Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 2005, 37, 129–149. [Google Scholar] [CrossRef]
- Van der Werf, J.C.; De Kruif, C.G. Hard-sphere colloidal dispersions: The scaling of rheological properties with particle size, volume fraction, and shear rate. J. Rheol. 1989, 33, 421–454. [Google Scholar] [CrossRef]
- Shikata, T.; Pearson, D.S. Viscoelastic behavior of concentrated spherical suspensions. J. Rheol. 1994, 38, 601. [Google Scholar] [CrossRef]
- Cheng, Z.D.; Zhu, J.X.; Chaikin, P.M.; Phan, S.E.; Russel, W.B. Nature of the divergence in low shear viscosity of colloidal hard-sphere dispersions. Phys. Rev. E 2002, 65, 041405. [Google Scholar] [CrossRef] [PubMed]
- Mewis, J.; Wagner, N.J. Colloidal Suspension Rheology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]


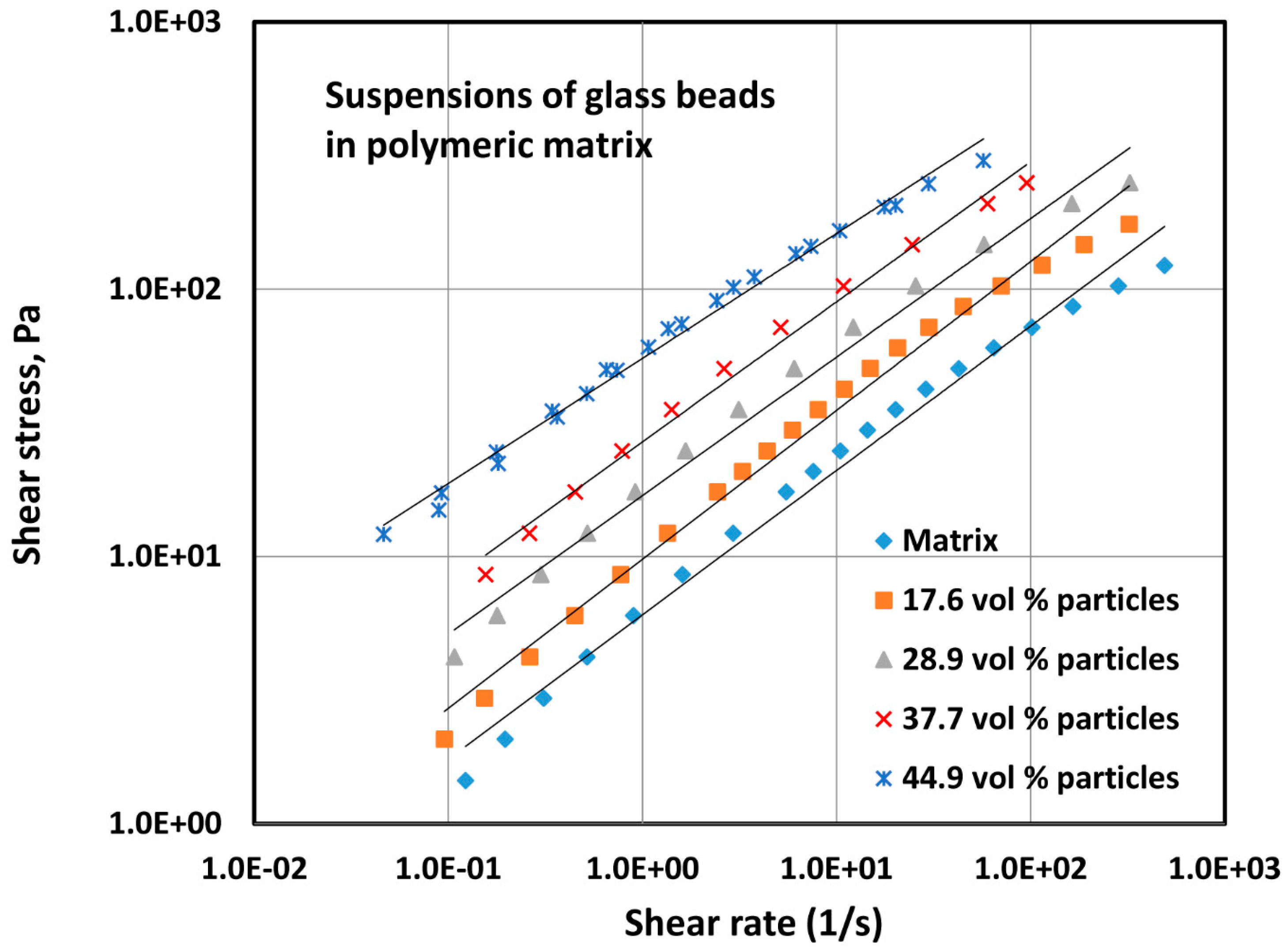
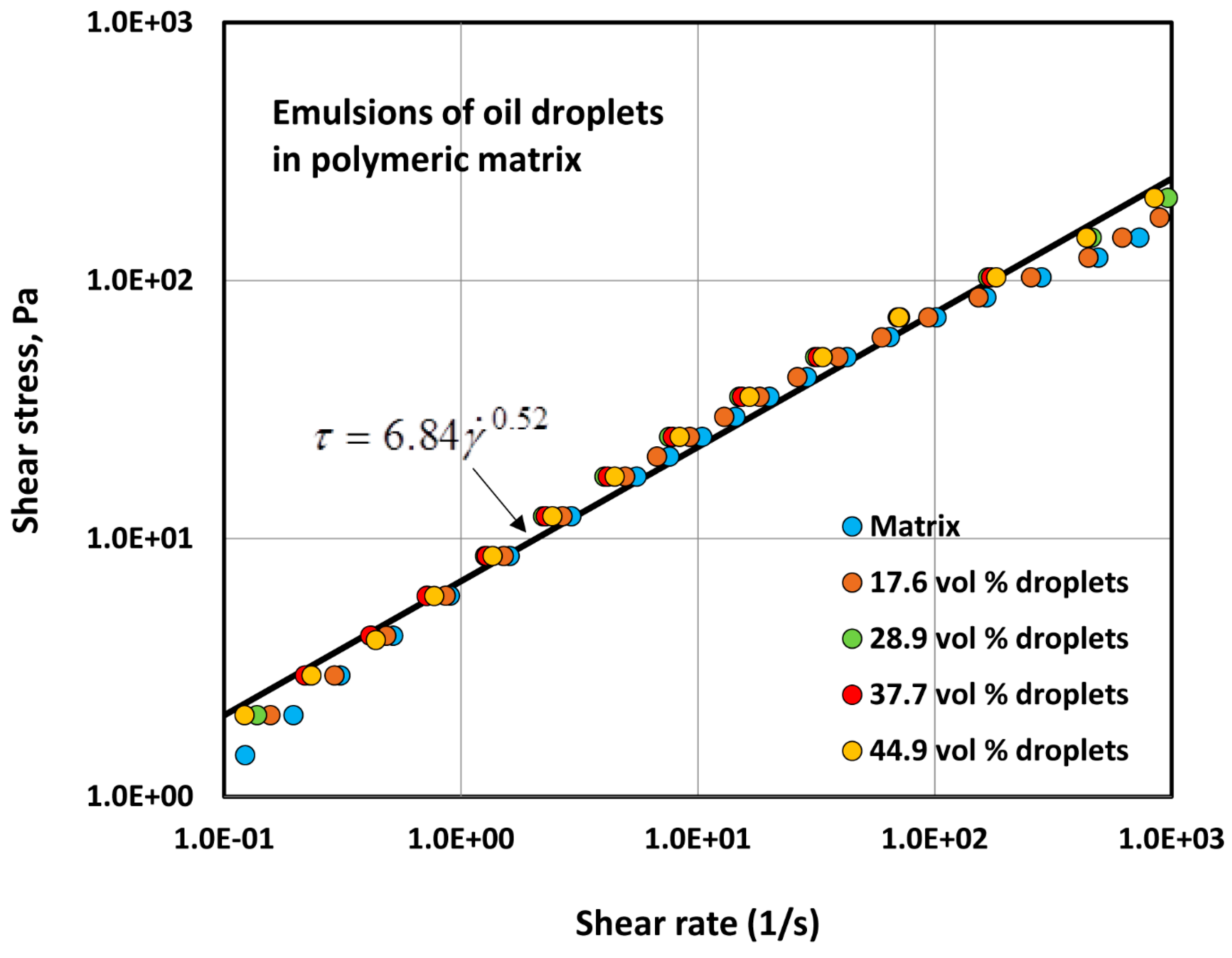



| Volume Percent of Glass Particles | Regression Correlation Coefficient, R2 | Flow Behavior Index, n | Consistency Index, K (Units of Pa.sn) | 95% Confidence Interval of n | 95% Confidence Interval of K |
|---|---|---|---|---|---|
| 0 | 0.9863 | 0.540 | 6.05 | [0.507, 0.573] | [5.45, 6.73] |
| 17.6 | 0.9884 | 0.557 | 9.76 | [0.527, 0.587] | [8.94, 10.58] |
| 28.9 | 0.9866 | 0.518 | 16.91 | [0.479, 0.558] | [15.10, 18.94] |
| 37.7 | 0.9908 | 0.524 | 26.85 | [0.488, 0.560] | [24.61, 29.26] |
| 44.9 | 0.9913 | 0.468 | 55.09 | [0.452, 0.484] | [53.36, 56.88] |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pal, R. Entropy Generation and Exergy Destruction in Flow of Multiphase Dispersions of Droplets and Particles in a Polymeric Liquid. Fluids 2018, 3, 19. https://doi.org/10.3390/fluids3010019
Pal R. Entropy Generation and Exergy Destruction in Flow of Multiphase Dispersions of Droplets and Particles in a Polymeric Liquid. Fluids. 2018; 3(1):19. https://doi.org/10.3390/fluids3010019
Chicago/Turabian StylePal, Rajinder. 2018. "Entropy Generation and Exergy Destruction in Flow of Multiphase Dispersions of Droplets and Particles in a Polymeric Liquid" Fluids 3, no. 1: 19. https://doi.org/10.3390/fluids3010019
APA StylePal, R. (2018). Entropy Generation and Exergy Destruction in Flow of Multiphase Dispersions of Droplets and Particles in a Polymeric Liquid. Fluids, 3(1), 19. https://doi.org/10.3390/fluids3010019




