Rapid Assessment of Relative Hemolysis Amidst Input Uncertainties in Laminar Flow
Abstract
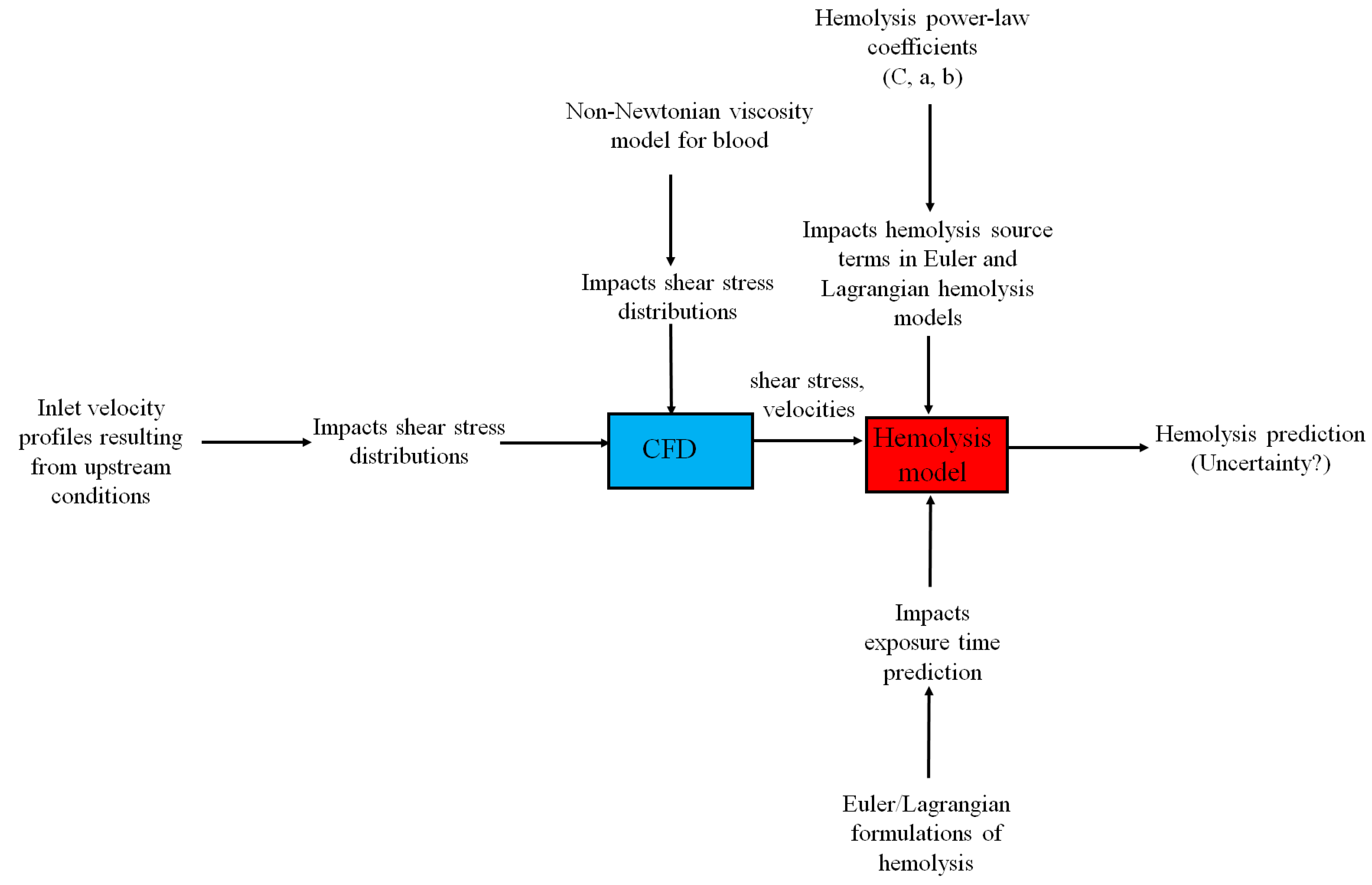
1. Introduction
1.1. Assessing Prediction Sensitivity to Inflow Velocity Profiles
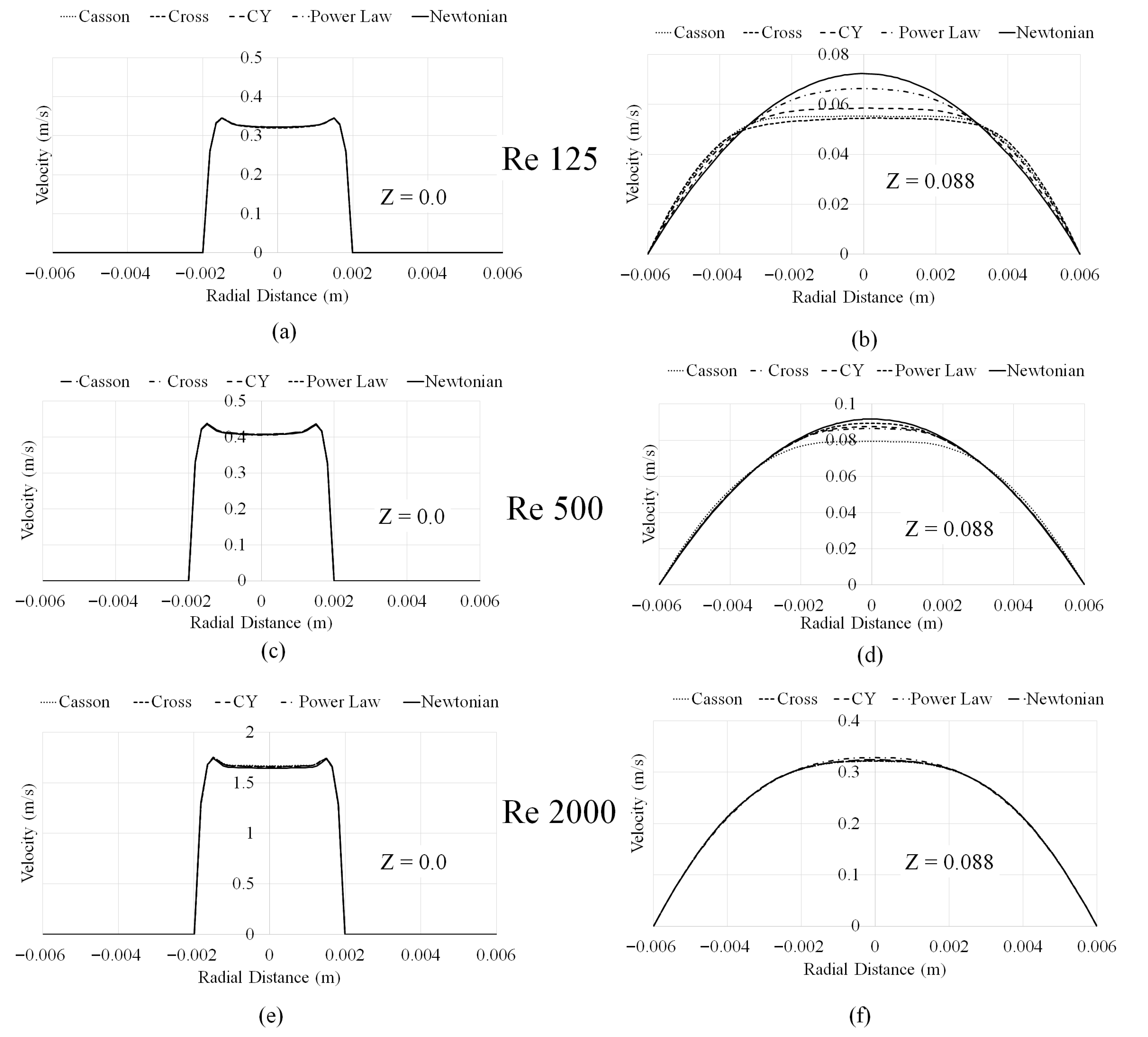
1.2. Prediction Sensitivity to Blood Viscosity Models
1.3. Prediction Sensitivity to Hemolysis Power Law Constants
1.4. Prediction Sensitivity to Eulerian and Lagrangian Formulations of the Hemolysis Power Law
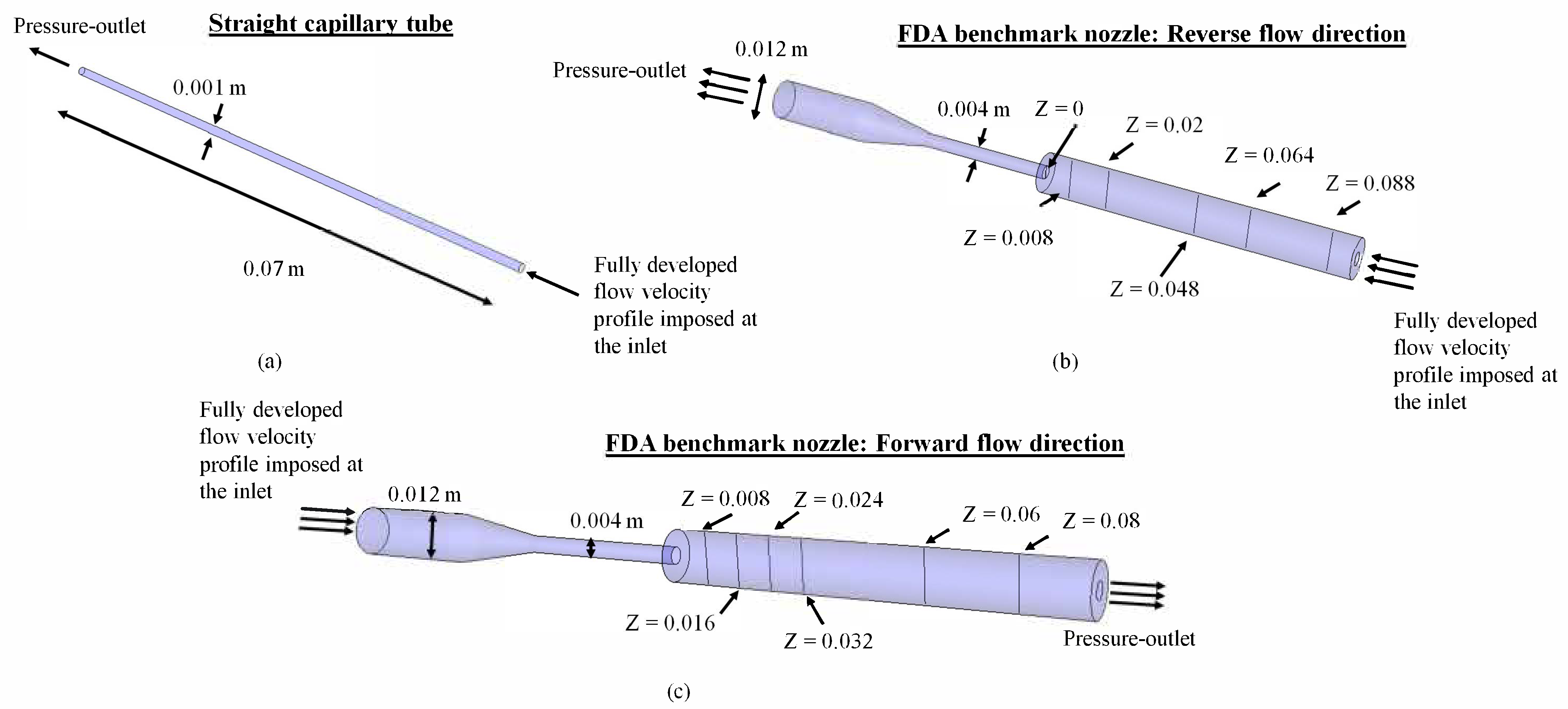
2. Methods
3. Results and Discussion
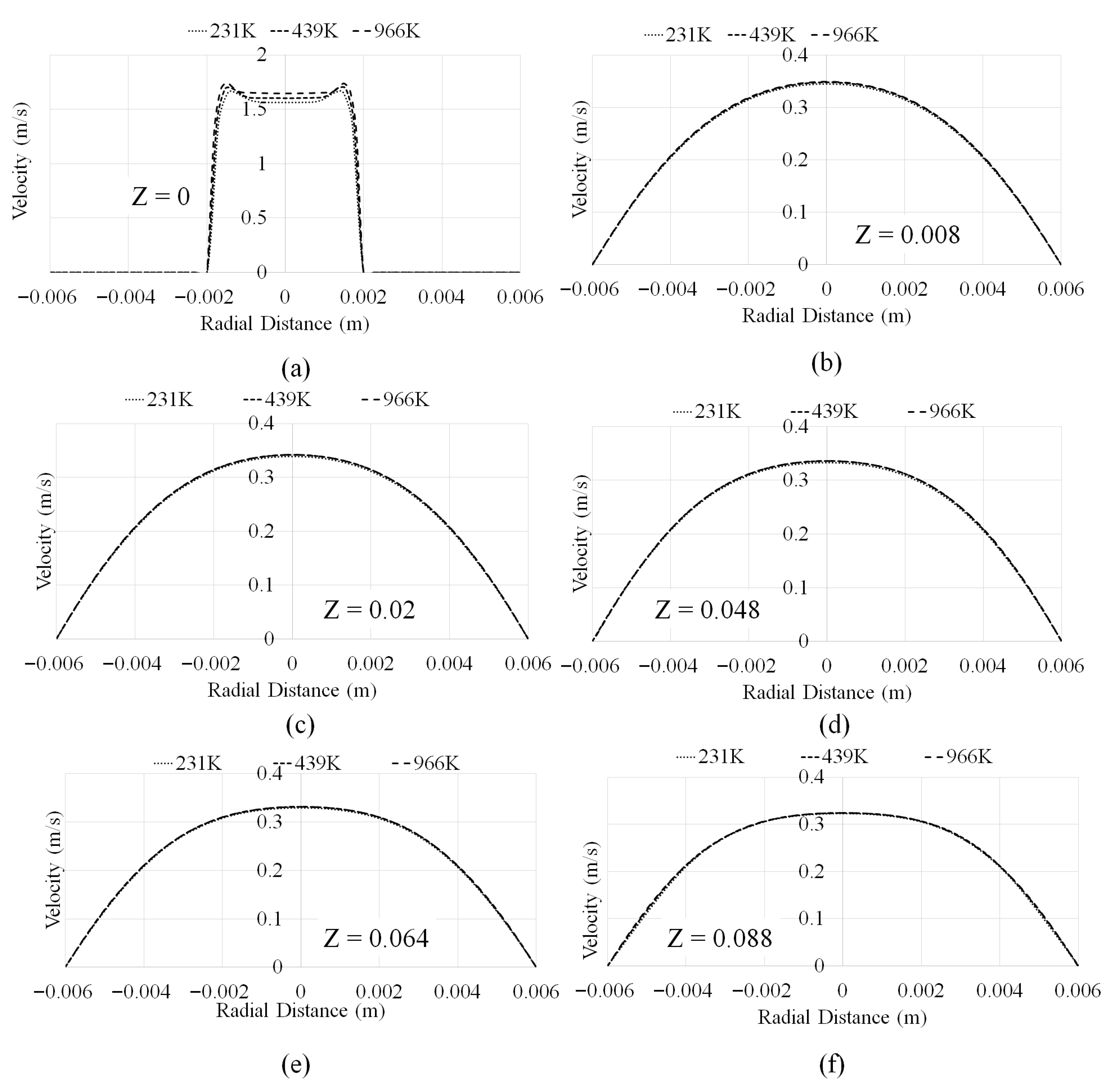
3.1. Mesh Convergence and Velocity Profiles
3.2. Hemolysis Assessments
4. Conclusions
- 1.
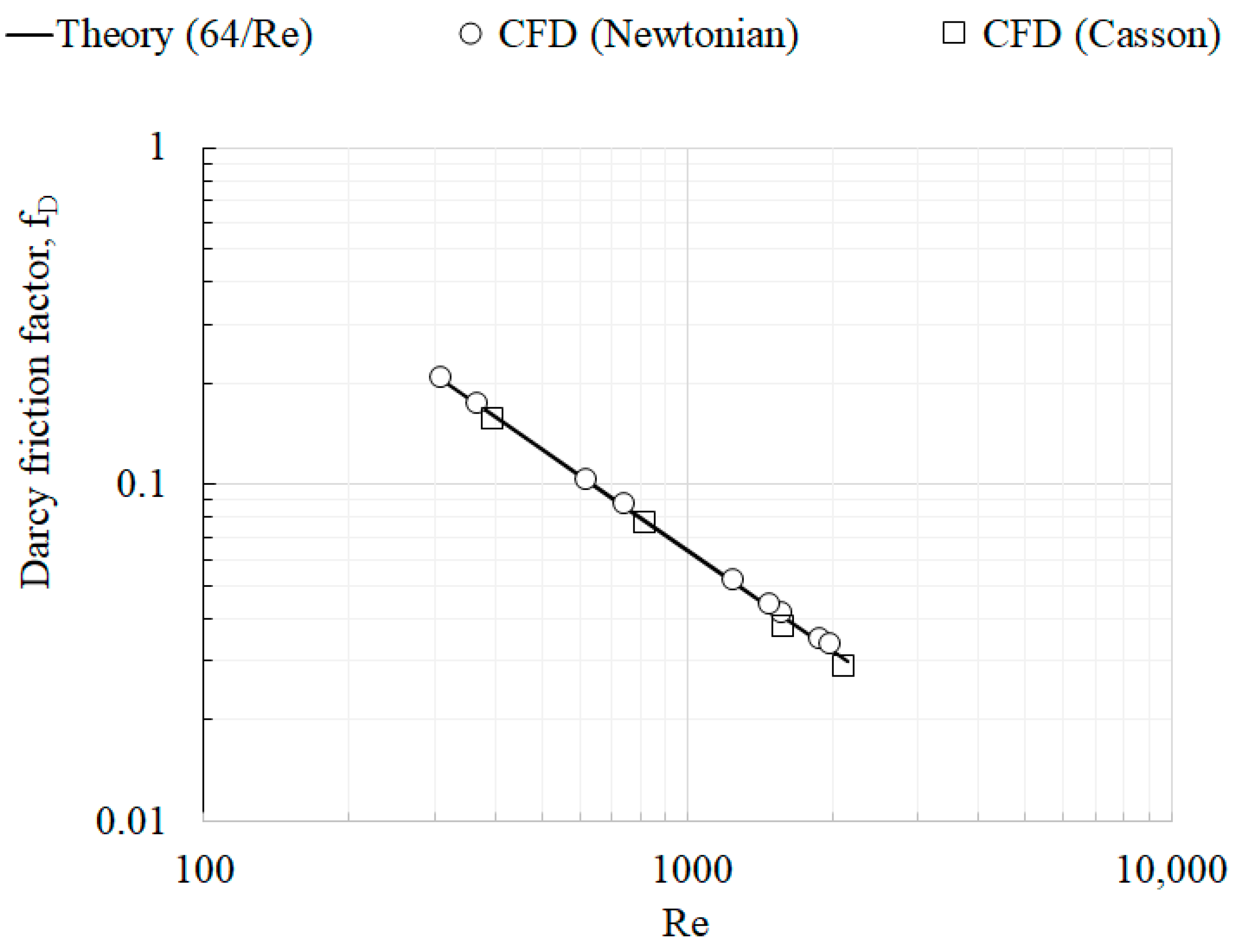
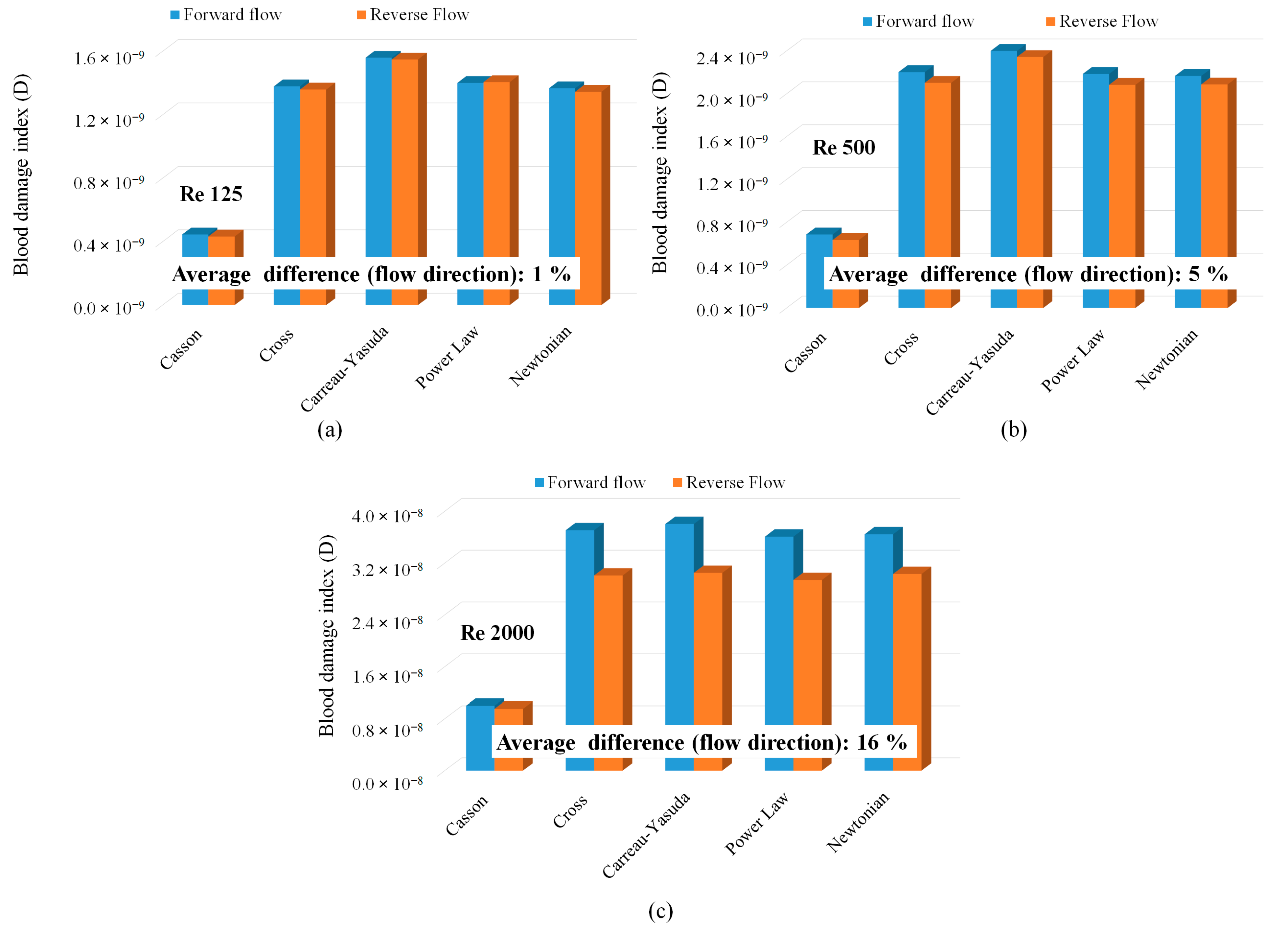
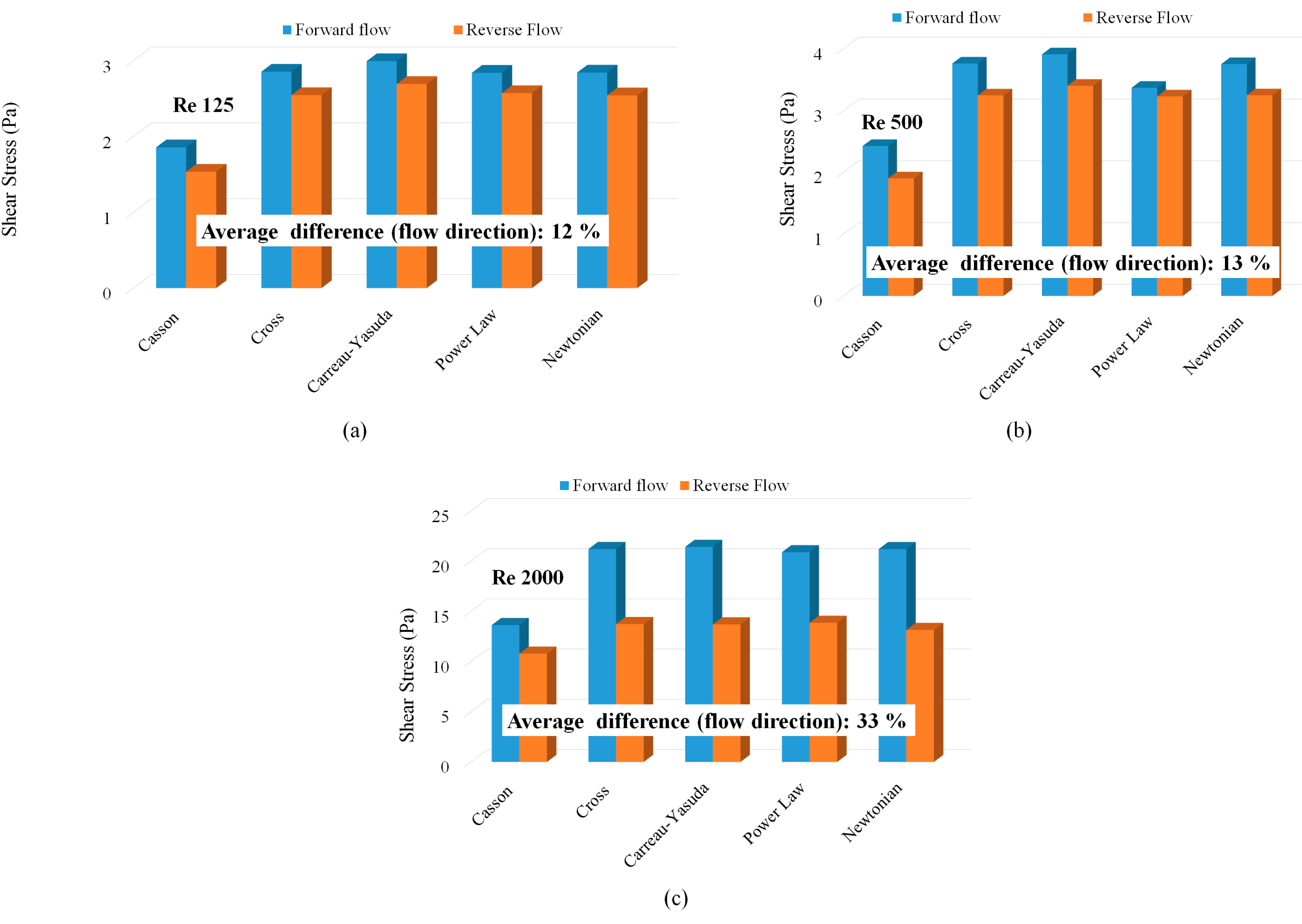
- At laminar, fully developed flow conditions, both Newtonian and Non-Newtonian models showed identical shear stress variations with Reynolds number.
- 2.
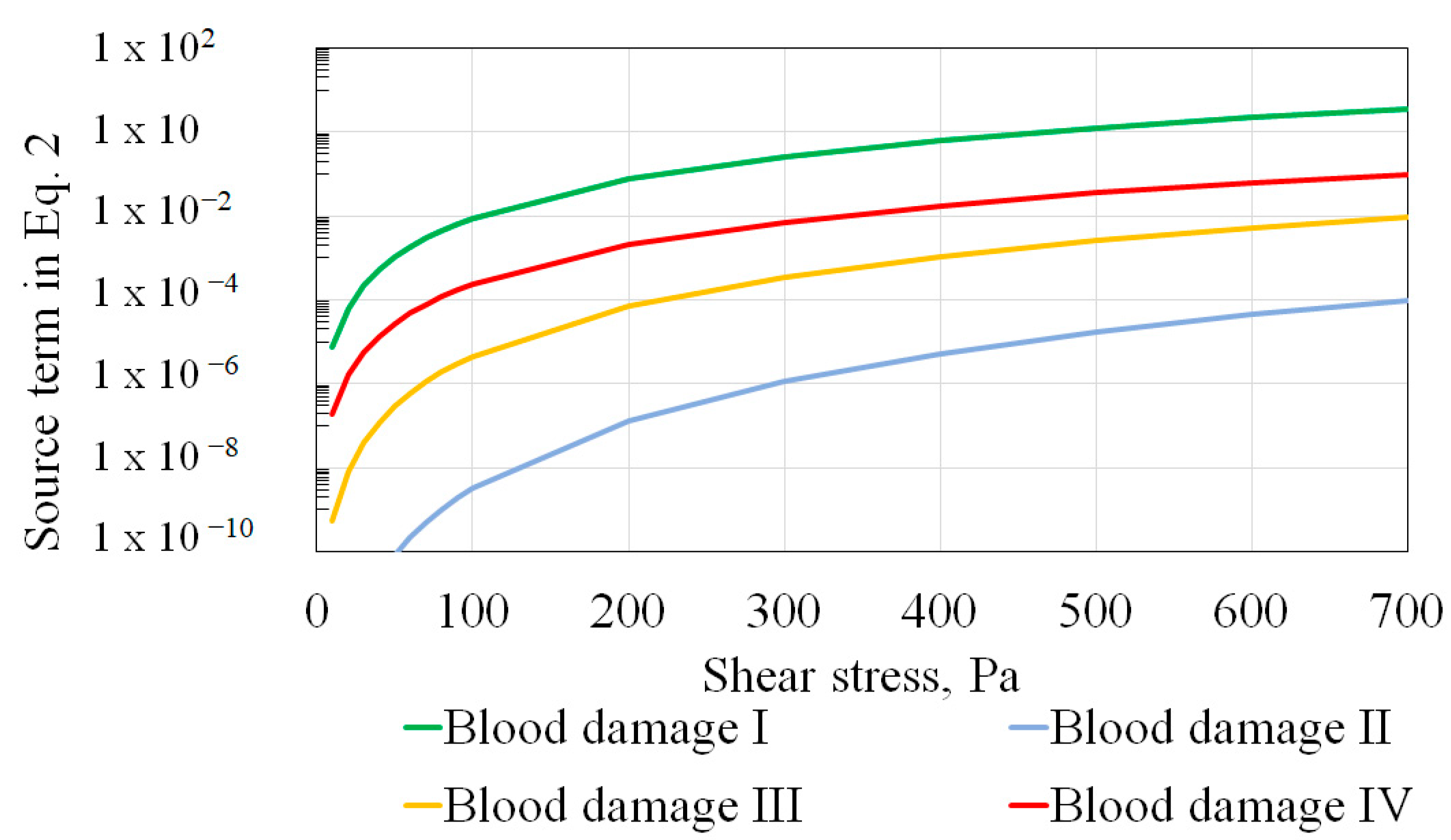
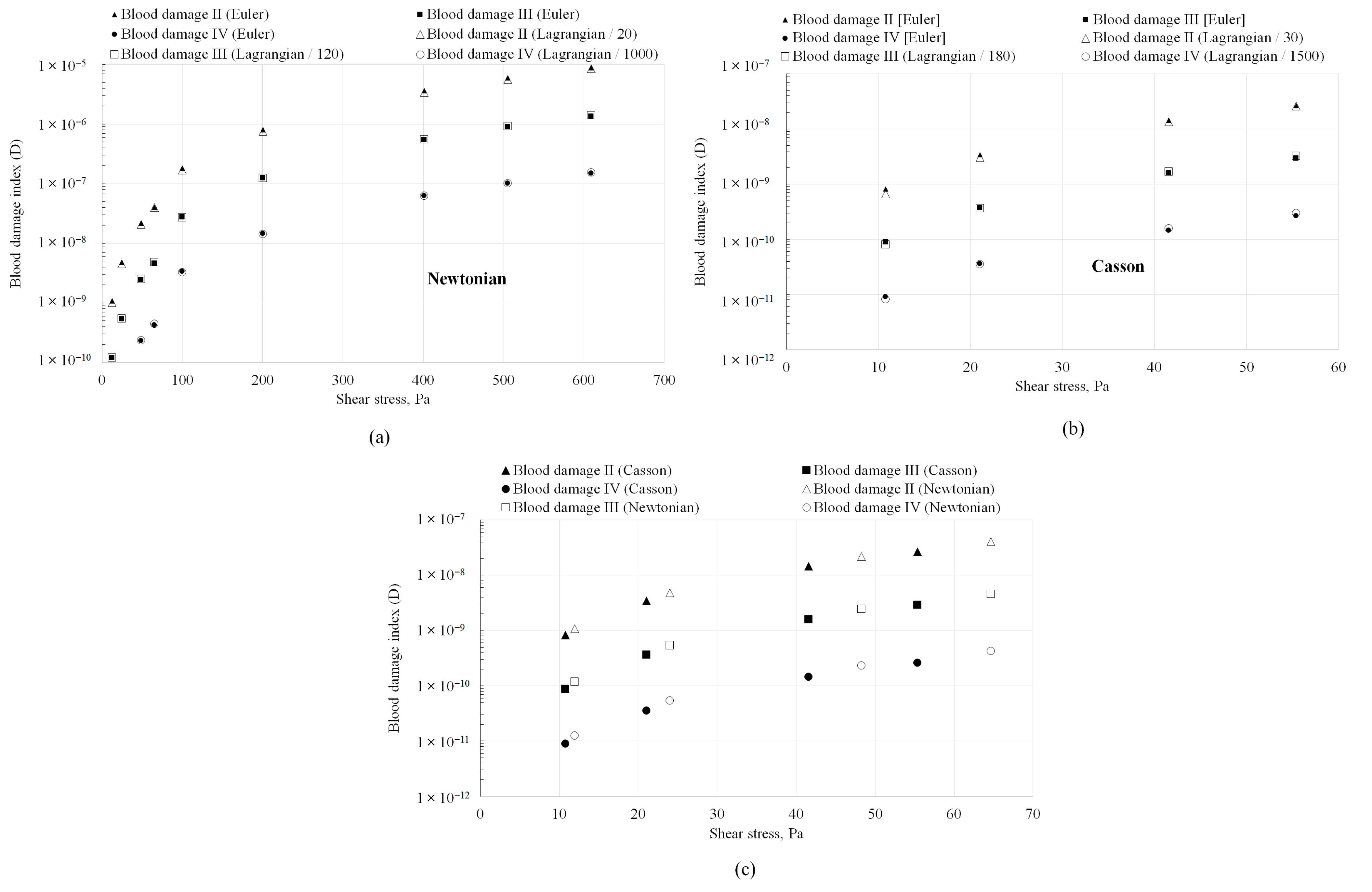
- When fully developed flow conditions persist throughout the geometry, absolute hemolysis predictions (in both Eulerian and Lagrangian formulations) were proportional to each other and independent of the blood viscosity model or the hemolysis power law coefficients. However, the value of the proportionality constant was specific to the power law coefficients employed in the analysis. The value of the proportionality constant was also different for the Casson non-viscosity model.
- 3.
- While recent studies [7] have suggested that the erroneous treatment of residence time in the Eulerian formulation (resulting from flow acceleration) may necessitate the formulation/deduction of separate sets of coefficients for each (Eulerian/Lagrangian) formulation, the results from this study suggest that this requirement may be alleviated for relative hemolysis assessments when the conditions of fully developed flow are present, since Eulerian and Lagrangian absolute hemolysis predictions are simply proportional to each other.
- 4.
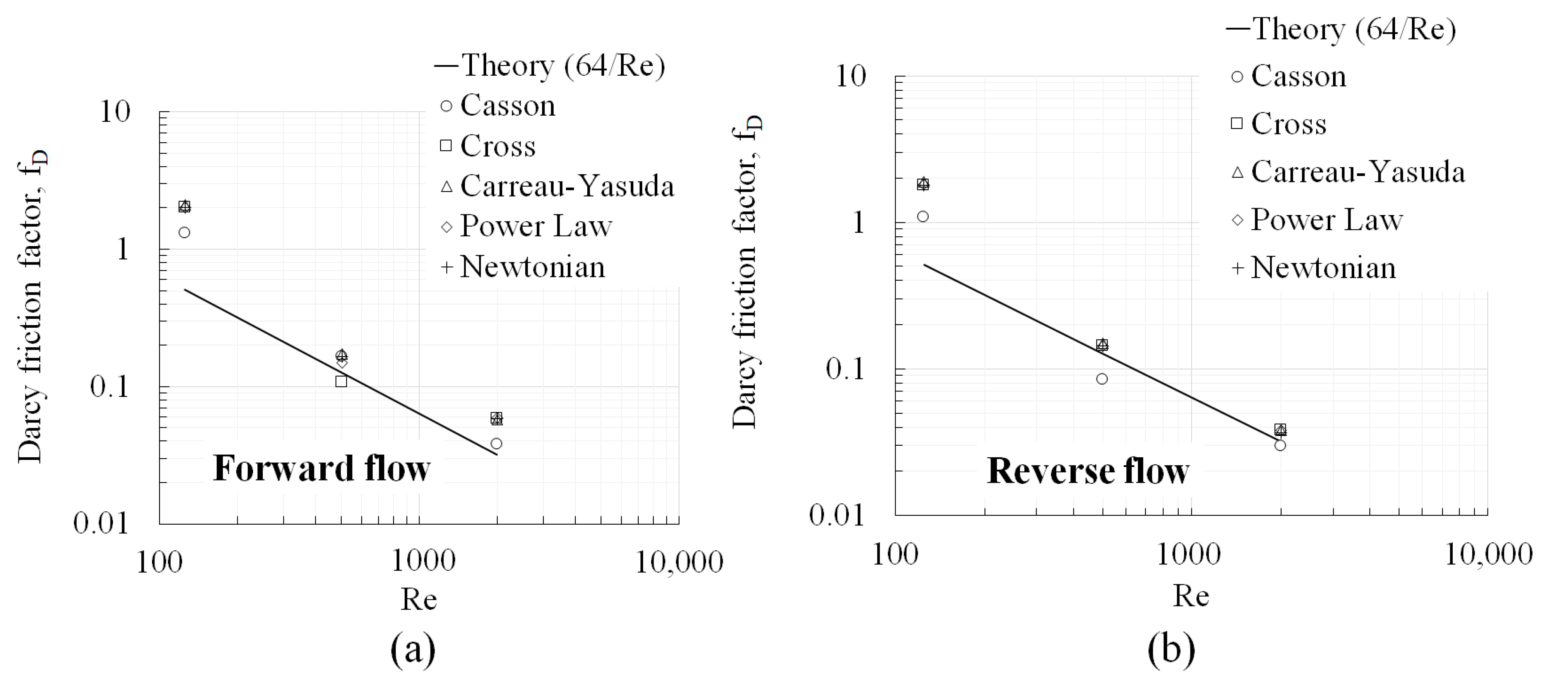
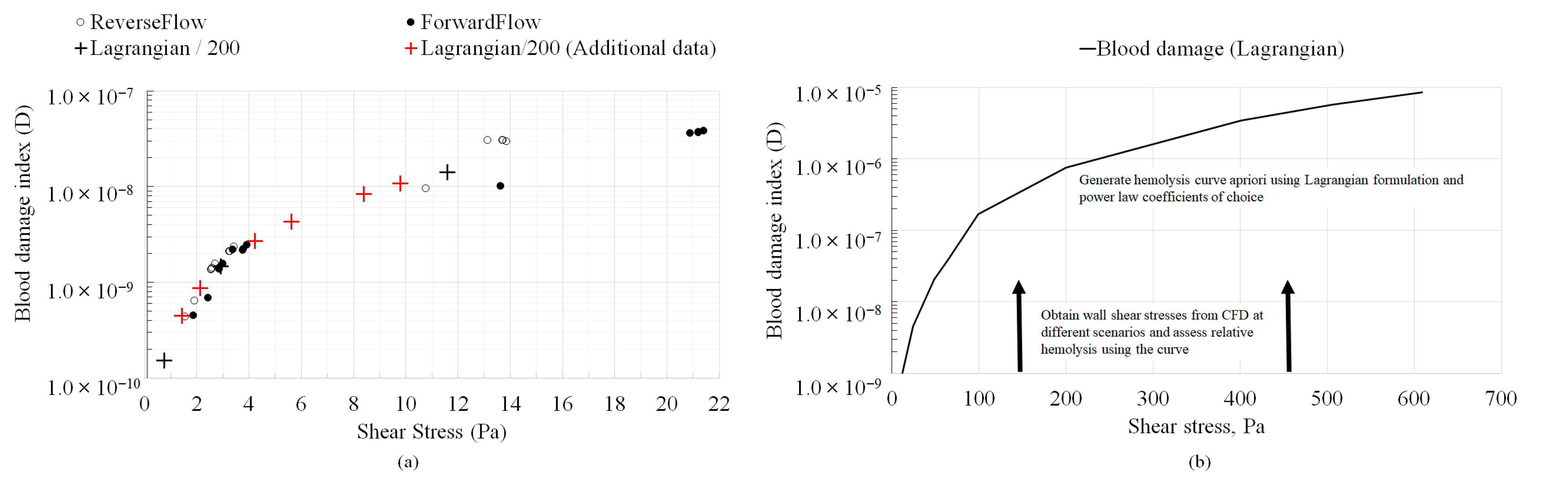
- Even when developing flow conditions persist throughout the geometry, identical variations in absolute hemolysis as a function of wall shear stresses were observed between the Eulerian and Lagrangian frameworks that were generally independent of the viscosity model. Therefore, in simple geometries similar to the ones investigated in this study (capillary tubes, FDA benchmark nozzle), where hemolysis is dominated by wall shear and hemolysis in recirculation regions is absent, the simplified Lagrangian hemolysis modeling methodology formulated based on fully developed Newtonian fluid flow could be employed as a surrogate for quick relative hemolysis assessments. This could be done by generating an absolute hemolysis versus shear stress curve a priori using any set of power law coefficients of choice. Next, wall shear stress values could be obtained from CFD simulations for different design prototypes or flow situations and relative hemolysis assessments made based on the curve.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kameneva, M.V.; Burgreen, G.W.; Kono, K.; Repko, B.; Antaki, J.F.; Umezu, M. Effects of turbulent stresses upon mechanical hemolysis: Experimental and computational analysis. ASAIO J. 2004, 50, 418–423. [Google Scholar] [CrossRef]
- Hariharan, P.; Giarra, M.; Reddy, V.; Day, S.; Manning, K.B.; Deutsch, S.; Stewart, S.F.C.; Myers, M.R.; Berman, M.R.; Burgreen, G.W.; et al. Experimental particle image velocimetry protocol and results database for validating computational fluid dynamic simulations of the FDA benchmark nozzle model. J. Biomech. Eng. 2011, 133, 041002. [Google Scholar] [CrossRef]
- Stewart, S.F.C.; Hariharan, P.; Paterson, E.G.; Burgreen, G.W.; Reddy, V.; Day, S.W.; Giarra, M.; Manning, K.B.; Deutsch, S.; Berman, M.R.; et al. Results of FDA’s First Interlaboratory Computational Study of a Nozzle with a Sudden Contraction and Conical Diffuser. Cardiovasc. Eng. Technol. 2013, 4, 374–391. [Google Scholar] [CrossRef]
- Stewart, S.F.C.; Paterson, E.G.; Burgreen, G.W.; Hariharan, P.; Giarra, M.; Reddy, V.; Day, S.W.; Manning, K.B.; Deutsch, S.; Berman, M.R.; et al. Assessment of CFD performance in simulations of an idealized medical device: Results of FDA’s first computational Interlaboratory study. Cardiovasc. Eng. Technol. 2012, 3, 139–160. [Google Scholar] [CrossRef]
- Herbertson, L.H.; Olia, S.E.; Daly, A.; Noatch, C.P.; Smith, W.A.; Kameneva, M.V.; Malinauskas, R.A. Multilaboratory study of flow-induced Hemolysis using the FDA benchmark nozzle model. Artif. Organs 2014, 39, 237–248. [Google Scholar] [CrossRef]
- Mantegazza, A.; Tobin, N.; Manning, K.B.; Craven, B.A. Examining the universality of the hemolysis power law model from simulations of the FDA nozzle using calibrated model coefficients. Biomech. Model. Mechanobiol. 2023, 22, 433–451. [Google Scholar] [CrossRef]
- Faghih, M.M.; Craven, B.A.; Sharp, M.K. Practical implications of the erroneous treatment of exposure time in the Eulerian hemolysis power law model. Artif. Organs 2023, 47, 1531–1538. [Google Scholar] [CrossRef]
- Menon, K.; Hu, Z.; Marsden, A.L. Cardiovascular fluid dynamics: A journey through our circulation. Flow 2024, 4, E7. [Google Scholar] [CrossRef]
- Kopernik, M. Modelling of blood thrombosis at microscopic and mesoscopic scales. Comput. Assist. Methods Eng. Sci. 2019, 25, 21–45. [Google Scholar]
- Giersiepen, M.; Wurzinger, L.J.; Opitz, R.; Reul, H. Estimation of shear stress-related blood damage in heart valve prostheses-in vitro comparison of 25 aortic valves. Int. J. Artif. Organs 1990, 13, 300–306. [Google Scholar] [CrossRef]
- Craven, B.A.; Aycock, K.I.; Herbertson, L.H.; Malinauskas, R.A. A CFD-based Kriging surrogate modeling approach for predicting device-specific hemolysis power law coefficients in blood-contacting medical devices. Biomech. Model. Mechanobiol. 2019, 18, 1005–1030. [Google Scholar] [CrossRef] [PubMed]
- Stiehm, M.; Wüstenhagen, C.; Siewert, S.; Grabow, N.; Schmitz, K.P. Numerical simulation of pulsatile flow through a coronary nozzle model based on FDA’s benchmark geometry. Curr. Dir. Biomed. Eng. 2017, 3, 775–778. [Google Scholar] [CrossRef]
- Good Bryan, C. The Effects of non-Newtonian Blood Modeling and Pulsatility on Hemodynamics in the Food and Drug Administration’s Benchmark Nozzle Model. Biorheology 2023, 59, 1–18. [Google Scholar] [CrossRef]
- Trias, M.; Arbona, A.; Massó, J.; Miñano, B.; Bona, C. FDA’s nozzle numerical simulation challenge: Non-Newtonian fluid effects and blood damage. PLoS ONE 2014, 9, e92638. [Google Scholar] [CrossRef]
- Hussein, B.K.; Al-Azawy, M.G.; Al-Waaly, A.A.; Hamza, Z.A. Evaluation of Turbulence and Non-Newtonian Blood Rheology Models Through FDA Nozzle. In Proceedings of the 2021 International Conference on Advance of Sustainable Engineering and its Application (ICASEA), Wasit, Iraq, 27–28 October 2021; IEEE: New York, NY, USA, 2021; pp. 1–5. [Google Scholar]
- Zakaria, M.S.; Zainudin, S.H.; Abdullah, H.; Yuan, C.S.; Abd Latif, M.J.; Osman, K. CFD Simulation of Non-Newtonian Effect on Hemodynamics Characteristics of Blood Flow through Benchmark Nozzle. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 64, 117–125. [Google Scholar]
- Krishnamoorthy, G.; Gholizadeh, N. Blood Damage Analysis within the FDA Benchmark Nozzle Geometry at Laminar Conditions: Prediction Sensitivities to Software and Non-Newtonian Viscosity Models. Symmetry 2024, 16, 1165. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent. Version 2023 R2. 2023. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 1 January 2024).
- McCabe, W.L.; Smith, J.C.; Harriott, P. Unit Operations of Chemical Engineering; McGraw-Hill: New York, NY, USA, 1967; Volume 5. [Google Scholar]
- Metzner, A.B.; Reed, J.C. Flow of non-newtonian fluids—Correlation of the laminar, transition, and turbulent-flow regions. Aiche J. 1955, 1, 434–440. [Google Scholar] [CrossRef]
- Hong, J.K.; Gao, L.; Singh, J.; Goh, T.; Ruhoff, A.M.; Neto, C.; Waterhouse, A. Evaluating medical device and material thrombosis under flow: Current and emerging technologies. Biomater. Sci. 2020, 8, 5824–5845. [Google Scholar] [CrossRef]
- Taskin, M.E.; Fraser, K.H.; Zhang, T.; Wu, C.; Griffith, B.P.; Wu, Z.J. Evaluation of Eulerian and Lagrangian models for hemolysis estimation. ASAIO J. 2012, 58, 363–372. [Google Scholar] [CrossRef]
- Wu, P.; Gao, Q.; Hsu, P.L. On the representation of effective stress for computing hemolysis. Biomech. Model. Mechanobiol. 2019, 18, 665–679. [Google Scholar] [CrossRef]
- Fogelson, A.L.; Neeves, K.B. Fluid mechanics of blood clot formation. Annu. Rev. Fluid Mech. 2015, 47, 377–403. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Diacovo, T.G.; Chen, J.; Freund, J.B.; King, M.R. Simulation of platelet, thrombus and erythrocyte hydrodynamic interactions in a 3D arteriole with in vivo comparison. PLoS ONE 2013, 8, e76949. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Hosseinzadegan, H.; Tafti, D.K. Modeling thrombus formation and growth. Biotechnol. Bioeng. 2017, 114, 2154–2172. [Google Scholar] [CrossRef] [PubMed]
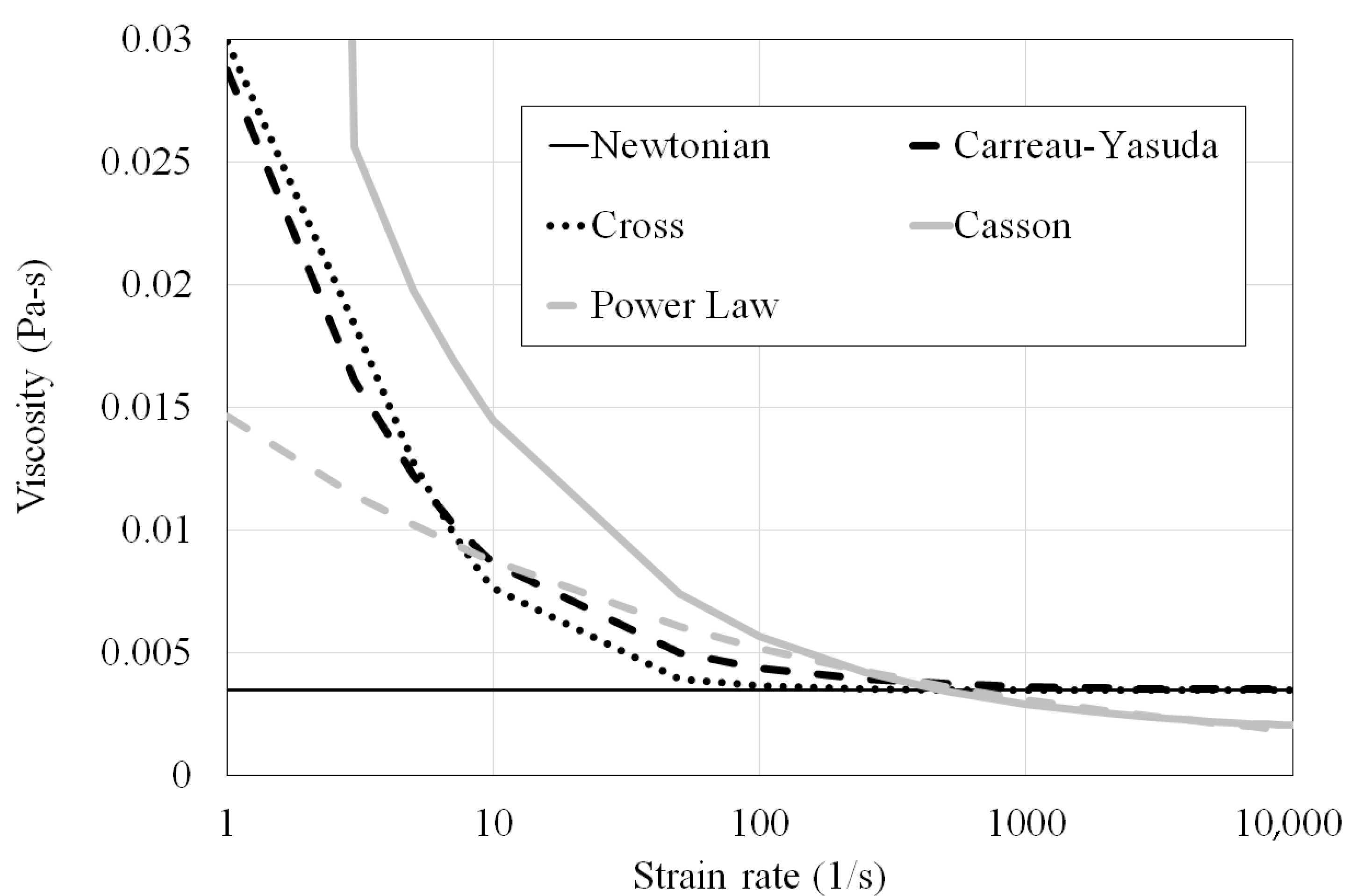
| Type | Viscosity Model | Constants |
|---|---|---|
| Carreau–Yasuda (CY) | ||
| Casson | ||
| Cross | ||
| Power Law | n = 0.7755 λ = 0.01467 |
| Model Name | Constants Source | a | b | C |
|---|---|---|---|---|
| Blood damage I | Giersiepen et al. [10] | 0.785 | 2.416 | 3.620 × 10−7 |
| Blood damage II * | Craven et al. [11] (ξ = 0.5) | 0.5 | 2.65 | 2.88 × 10−10 |
| Blood damage III * | Craven et al. [11] (ξ = 0.75) | 0.7375 | 2.9 | 1.81 × 10−10 |
| Blood damage IV * | Craven et al. [11] (ξ = 1.0) | 1.0 | 3.1 | 1.5 × 10−10 |
| Geometry | Viscosity Model | Power Law Constants (Table 2) | Shear Stress Ranges (Pa) | Average Exposure Time (s) Ranges * |
|---|---|---|---|---|
| Straight capillary tube (hemolysis from inlet to outlet) | Newtonian (0.002 Pa-s, 0.0063 Pa-s), Casson | Blood damage II, III, IV | 10–600 | 5.8 × 10−3–93 × 10−3 |
| FDA nozzle forward flow (hemolysis from inlet to outlet across the throat only) | Newtonian (0.0035 Pa-s), 5 Non-Newtonian (Table 1, Figure 3) | Blood damage I | 1–20 | 24 × 10−3–386 × 10−3 |
| FDA nozzle reverse flow (hemolysis from inlet to outlet across the throat only) | Newtonian (0.0035 Pa-s), 5 Non-Newtonian (Table 1, Figure 3) | Blood damage I | 1–20 | 24 × 10−3–386 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gholizadeh, N.; Wang, R.; Gautham, G.; Krishnamoorthy, G. Rapid Assessment of Relative Hemolysis Amidst Input Uncertainties in Laminar Flow. Fluids 2025, 10, 228. https://doi.org/10.3390/fluids10090228
Gholizadeh N, Wang R, Gautham G, Krishnamoorthy G. Rapid Assessment of Relative Hemolysis Amidst Input Uncertainties in Laminar Flow. Fluids. 2025; 10(9):228. https://doi.org/10.3390/fluids10090228
Chicago/Turabian StyleGholizadeh, Nasim, Ryan Wang, Gayatri Gautham, and Gautham Krishnamoorthy. 2025. "Rapid Assessment of Relative Hemolysis Amidst Input Uncertainties in Laminar Flow" Fluids 10, no. 9: 228. https://doi.org/10.3390/fluids10090228
APA StyleGholizadeh, N., Wang, R., Gautham, G., & Krishnamoorthy, G. (2025). Rapid Assessment of Relative Hemolysis Amidst Input Uncertainties in Laminar Flow. Fluids, 10(9), 228. https://doi.org/10.3390/fluids10090228







