Effects of Airfoil Parameters on the Cavitation Performance of Water Jet Propulsion Pumps
Abstract
1. Introduction
2. Numerical Calculation Method
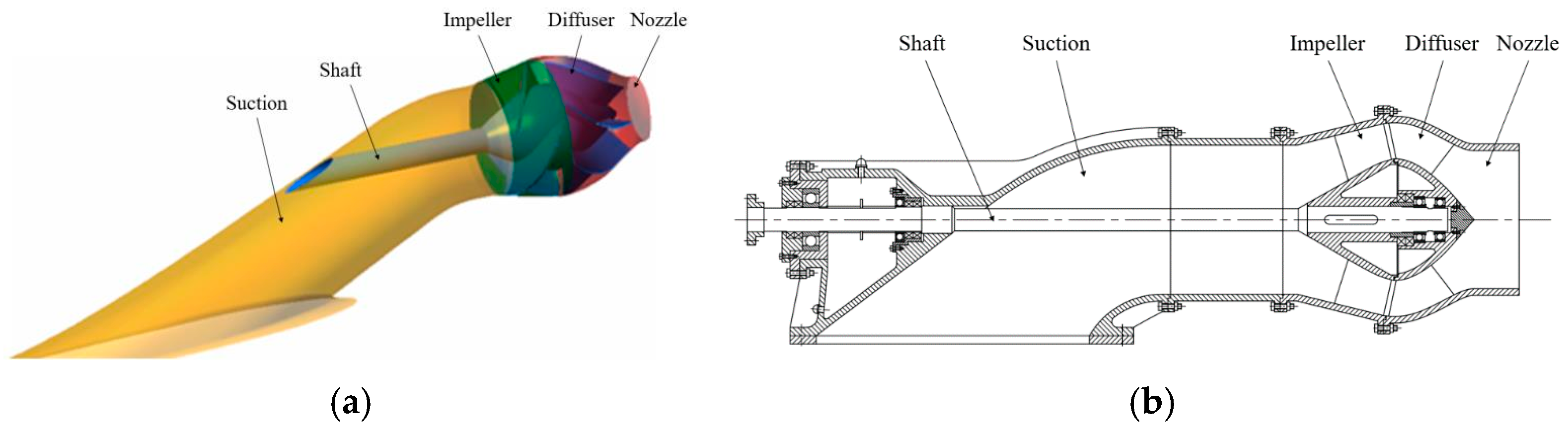
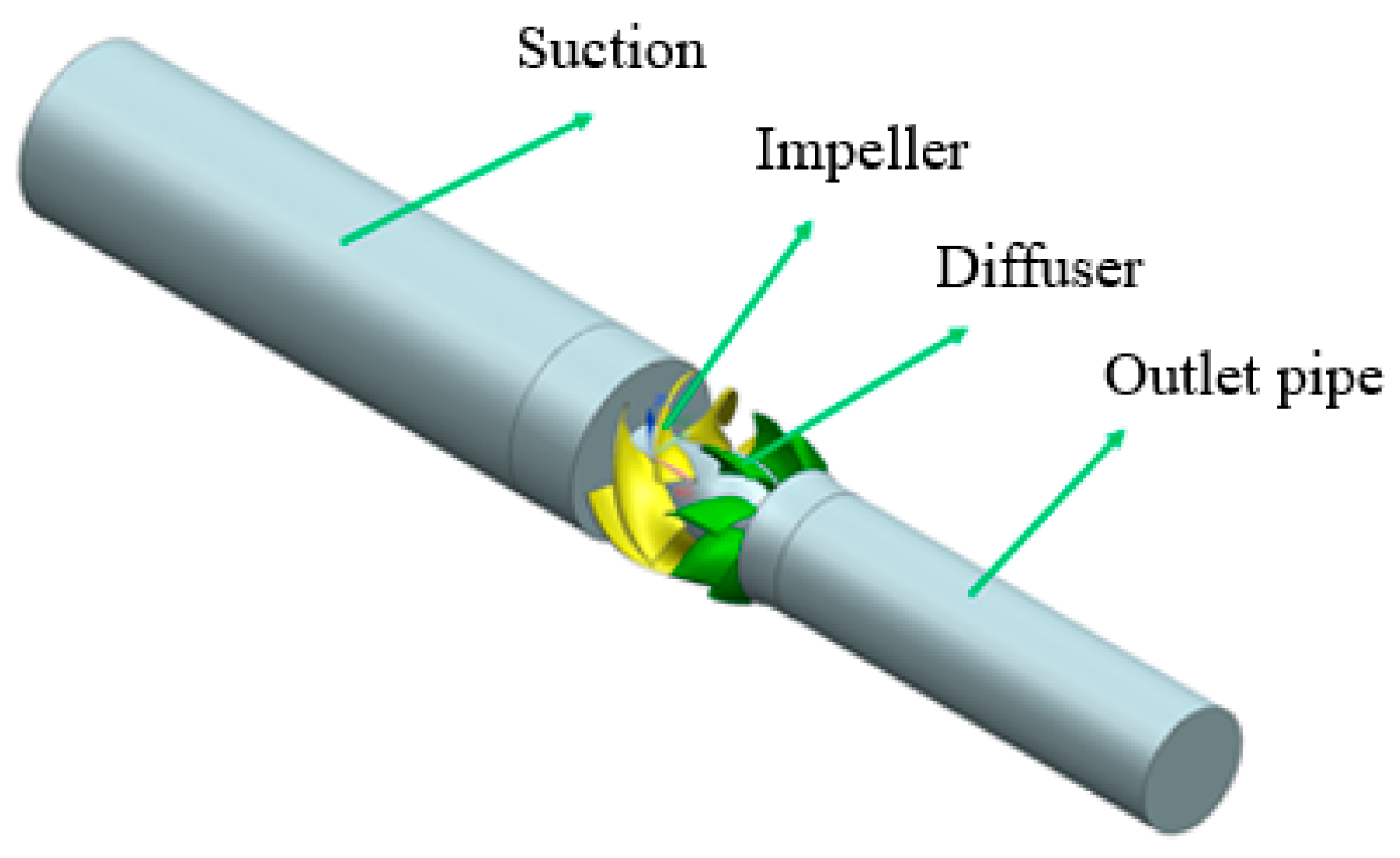
2.1. Numerical Calculation Model
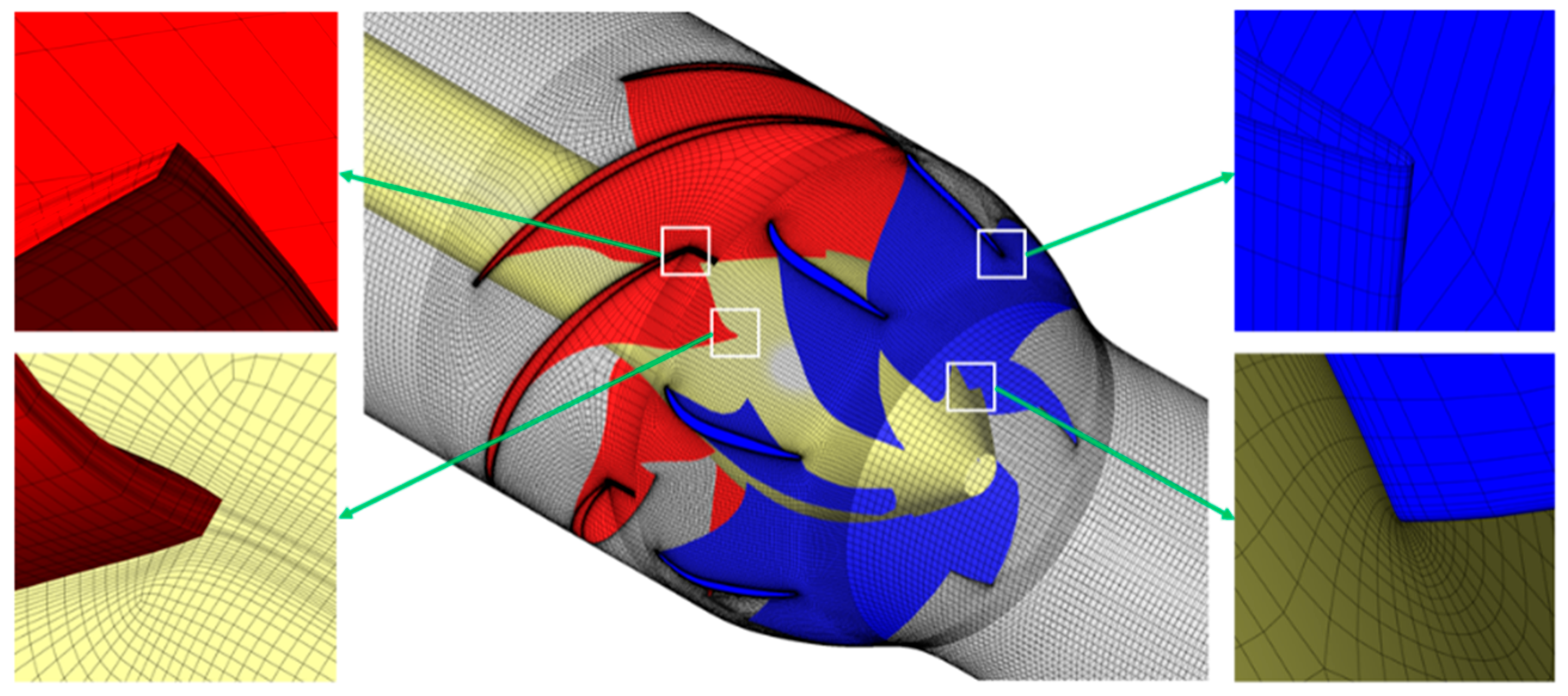
2.2. Mesh Generation
2.3. Turbulence Model
2.4. Cavitation Model
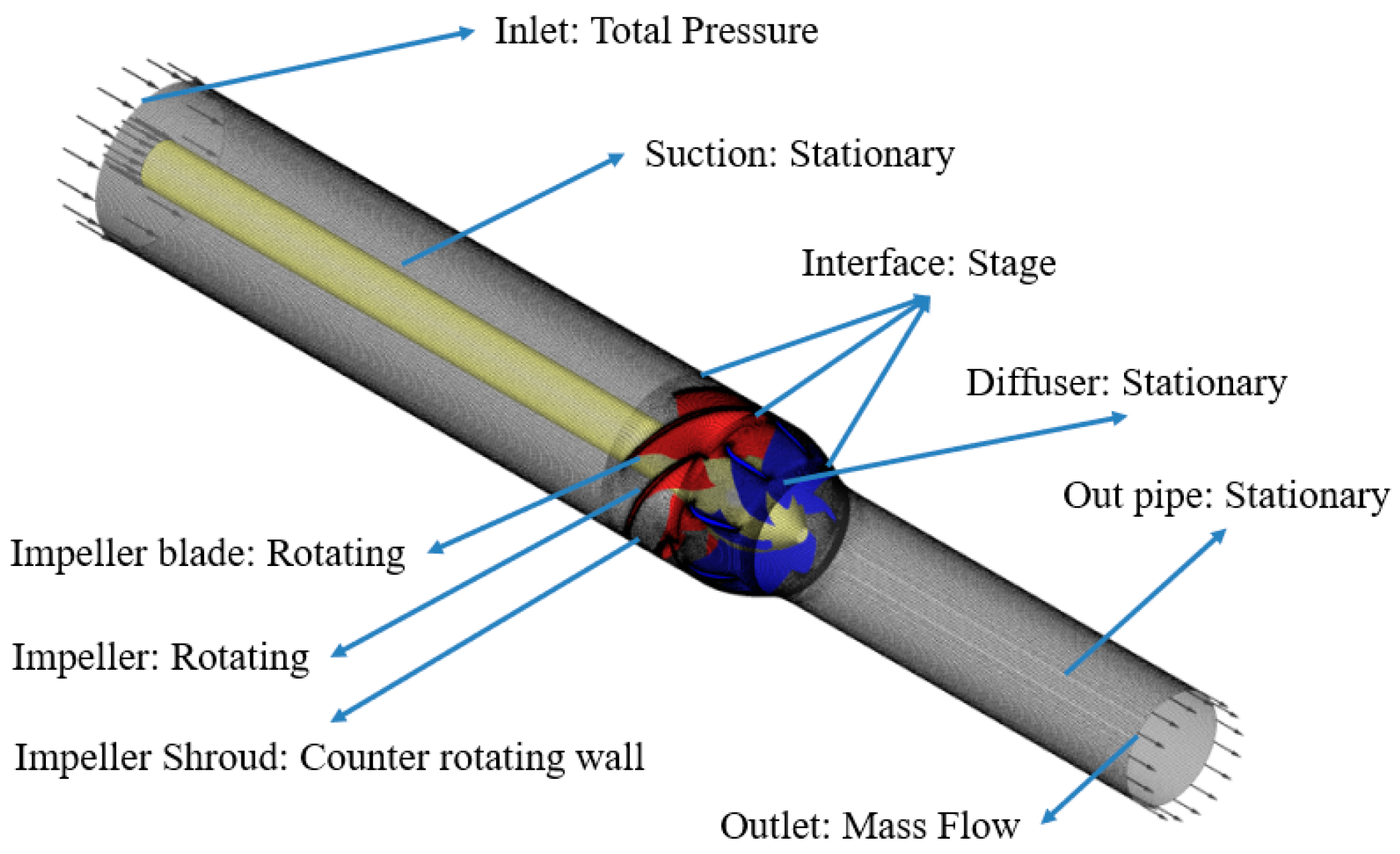
2.5. Boundary Condition
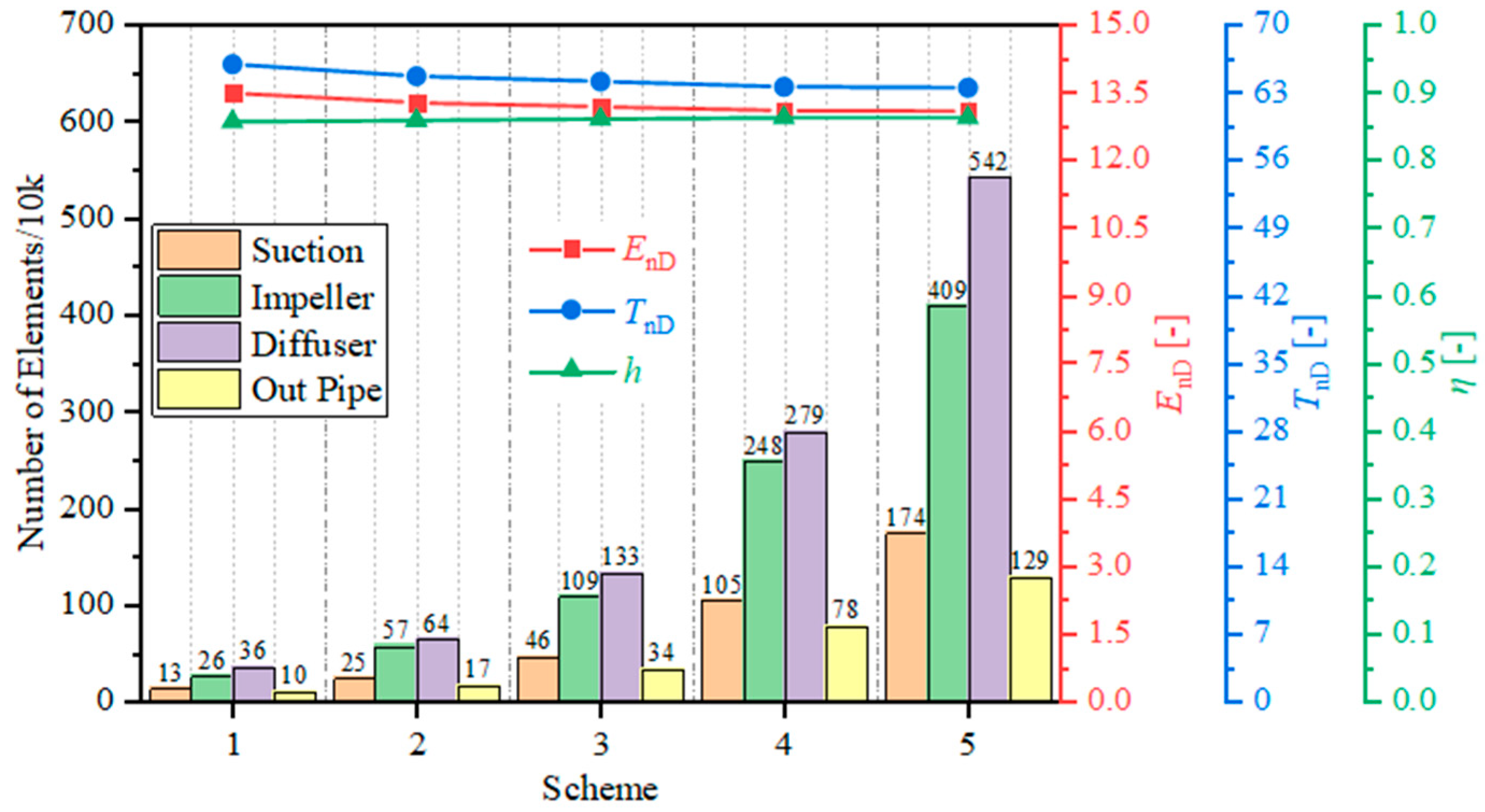
2.6. Mesh Independence Verification
3. Cavitation Experiment
Experimental Bench
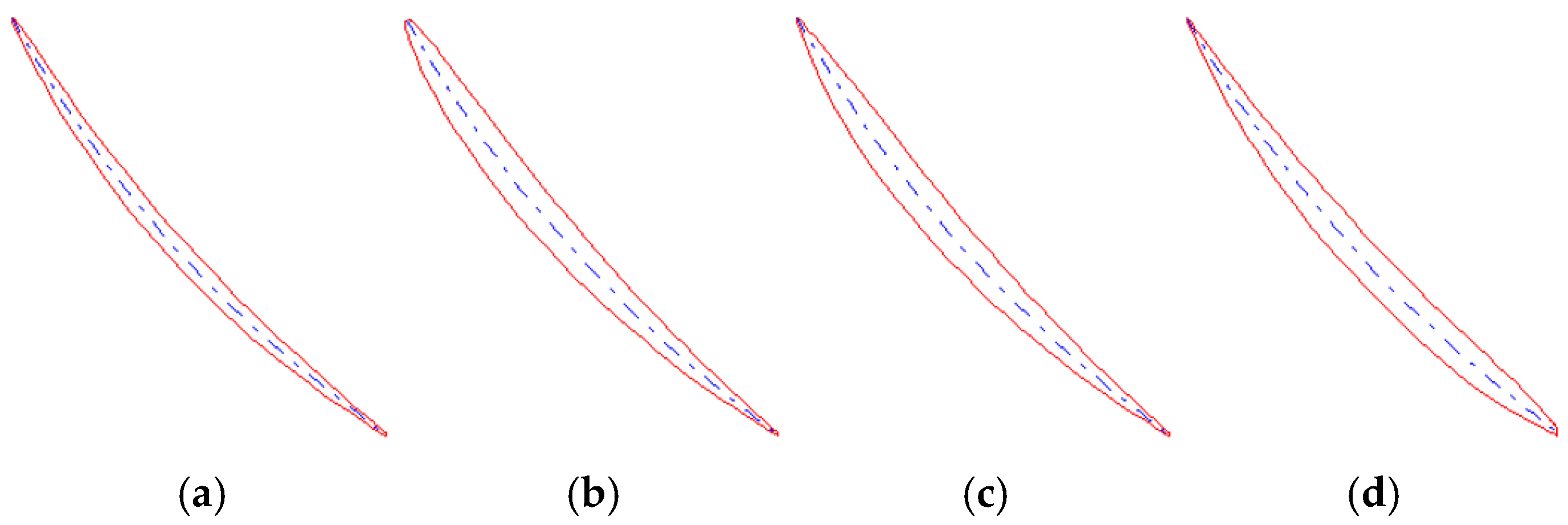
4. Different Airfoil Schemes
5. Result Analysis
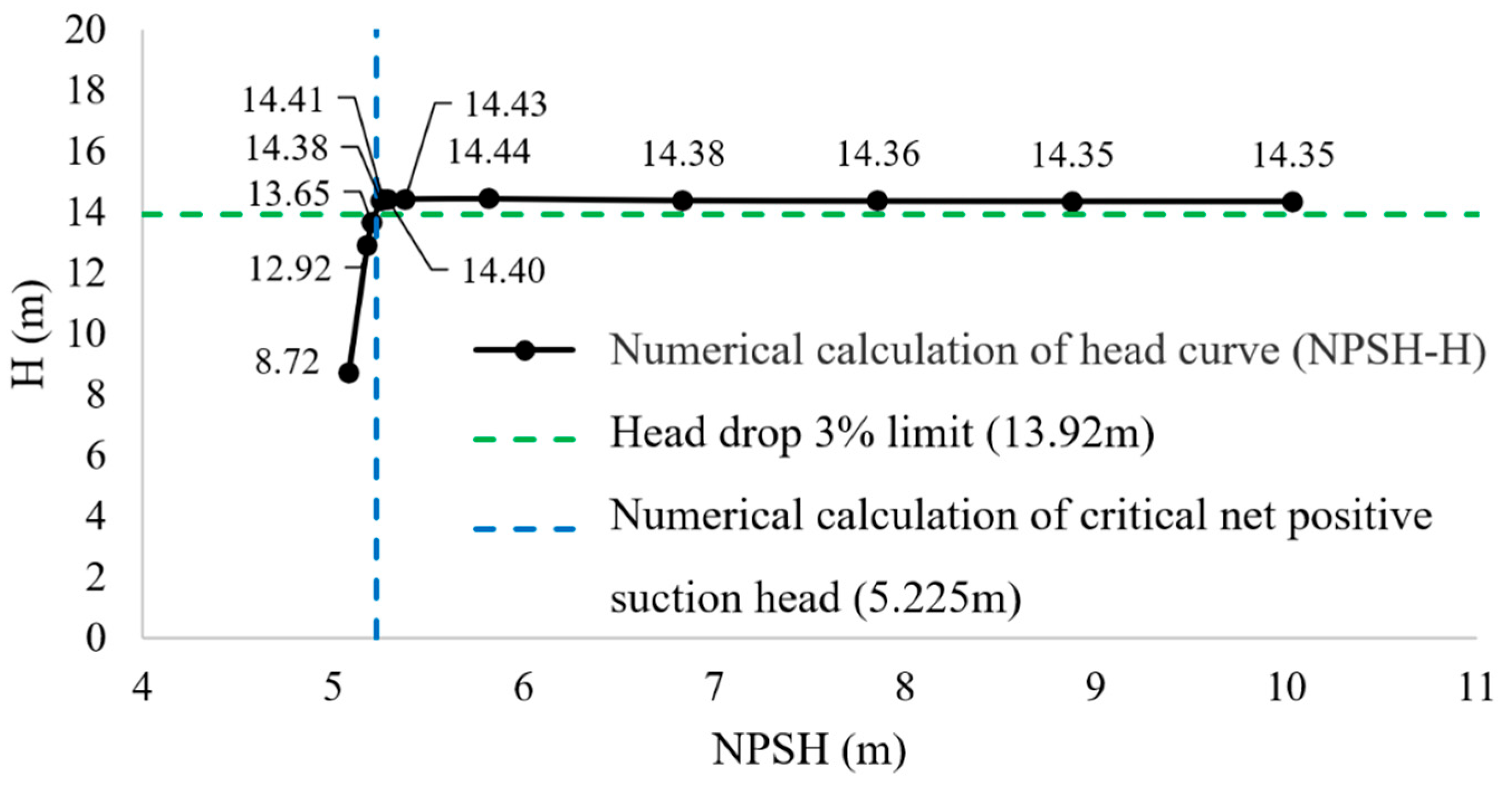
5.1. Cavitation Performance Test
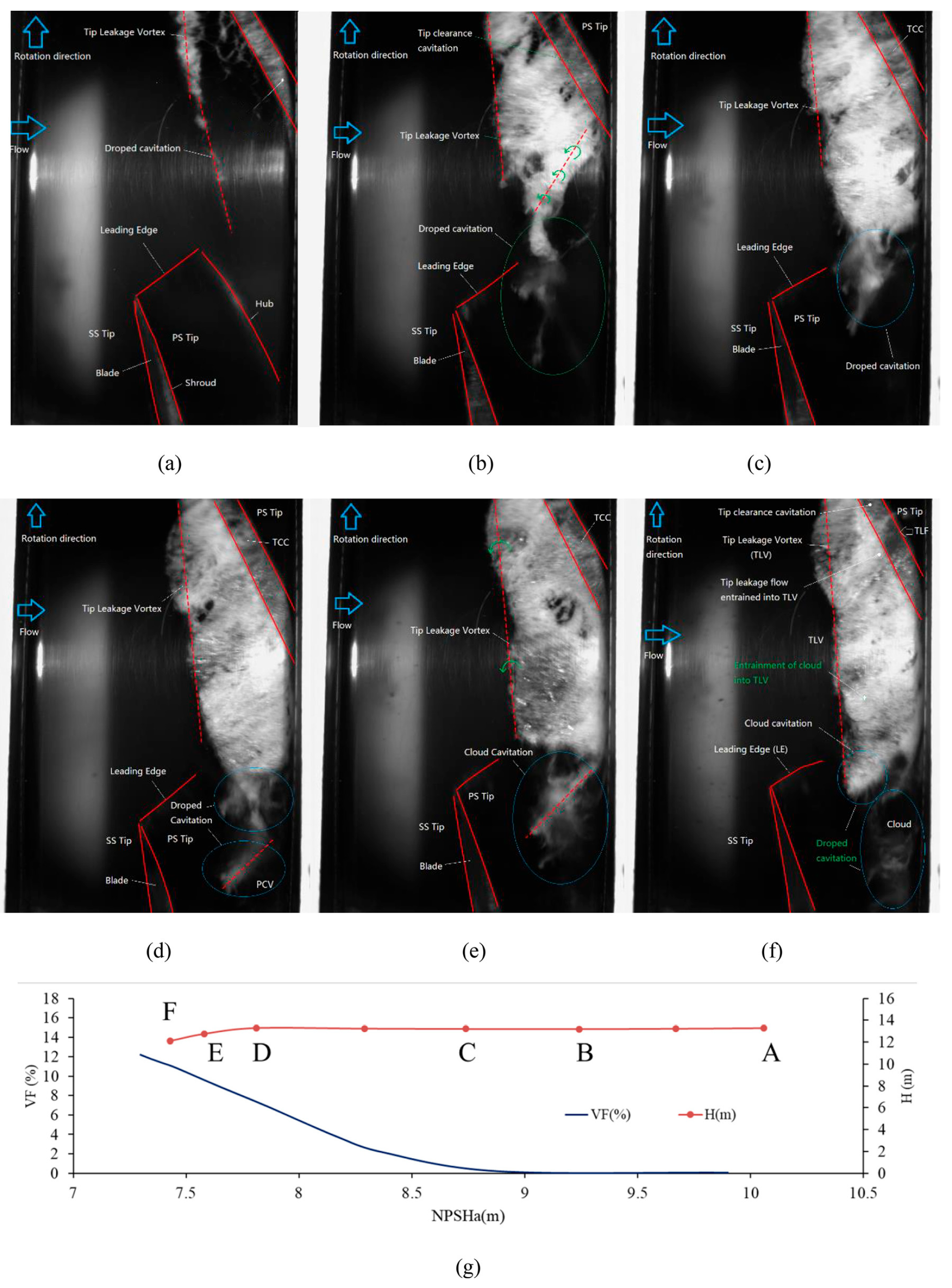
5.2. Cavitation Flow Analysis
5.3. Influence of Airfoil on Cavitation Performance
5.3.1. Original Model
5.3.2. NACA0009_0004 Airfoil
5.3.3. NACA0009-13_0004-13 Airfoil
5.3.4. NACA0009-16_0004-16 Airfoil
5.3.5. Summary of Cavitation Performance Curves Under Different Airfoil Schemes
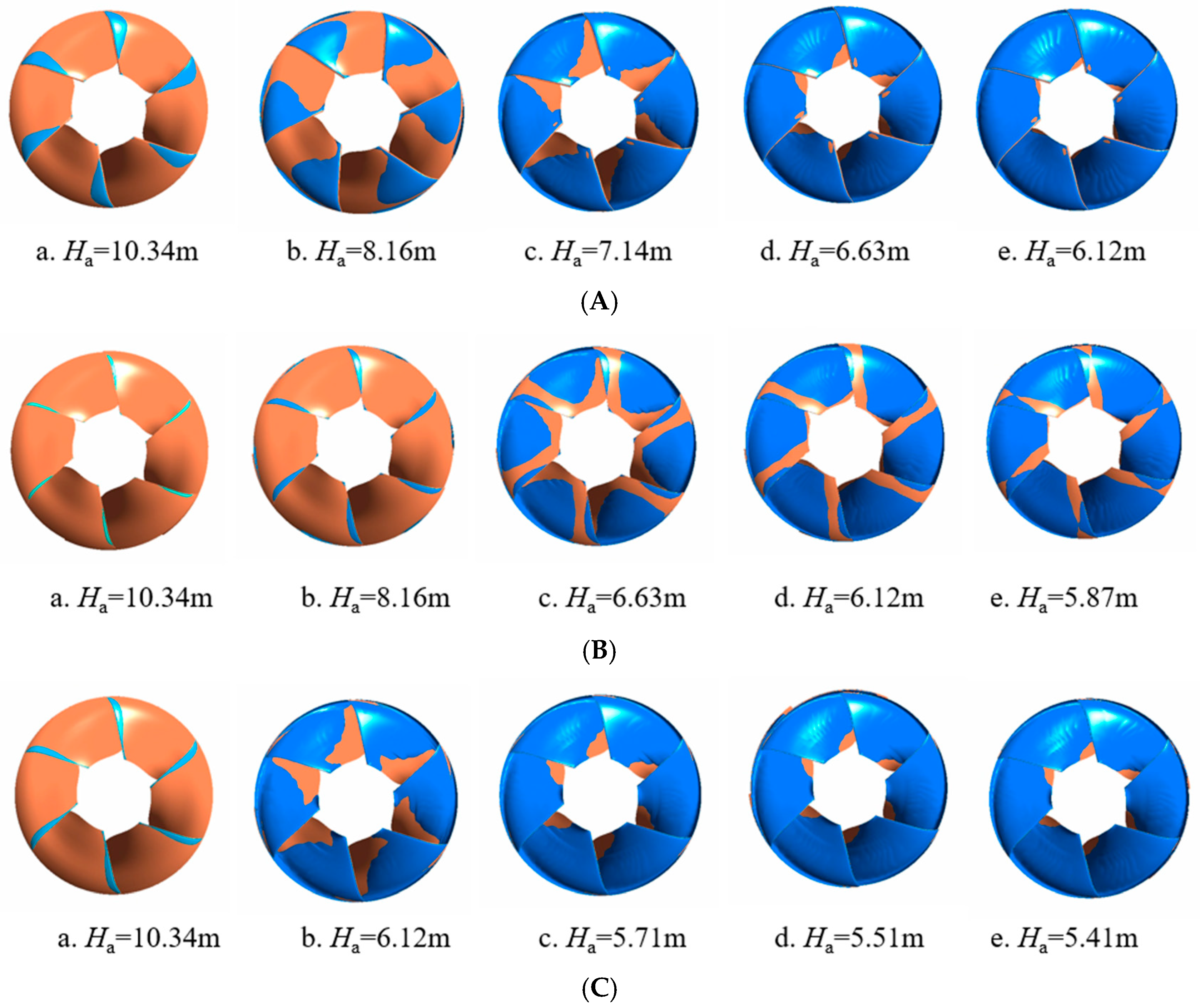
5.4. Evolution of Cavitation Flow Structure in Pumps
5.5. Flow Analysis of Airfoils Cavitation
5.6. Numerical Simulation Results and Experimental Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiao, W.; Wang, Y.; Cheng, L.; Zhao, H. Experimental study on thrust pulsation characteristics of water jet propulsion pump units. Ocean Eng. 2023, 284, 115079. [Google Scholar] [CrossRef]
- Long, Y. Study on the Hydraulic Optimization Design Method and Cavitation of Waterjet Pump. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2018. (In Chinese). [Google Scholar]
- Long, Y.; Zhong, J.; Chen, Y.; Zhang, Y.; Wan, C.; Zhu, R. Numerical simulation of internal flow of built-up rudder of the waterjet assembly under different navigate states. Ship Sci. Technol. 2023, 45, 111–117. (In Chinese) [Google Scholar]
- Luo, X.; Li, Q.; Zhang, Z.; Zhang, J. Research on the underwater noise radiation of high pressure water jet propulsion. Ocean Eng. 2021, 219, 108438. [Google Scholar] [CrossRef]
- Jiao, W.; Chen, H.; Cheng, L.; Zhang, B.; Yang, Y.; Luo, C. Experimental study on flow evolution and pressure fluctuation characteristics of the underwater suction vortex of water jet propulsion pump unit in shallow water. Ocean Eng. 2022, 266, 112569. [Google Scholar] [CrossRef]
- Park, W.G.; Jang, J.H.; Chun, H.H.; Kim, M.C. Numerical flow and performance analysis of waterjet propulsion system. Ocean Eng. 2005, 32, 1740–1761. [Google Scholar] [CrossRef]
- Luo, X.; Ye, W.; Huang, R.; Wang, Y.; Du, T.; Huang, C. Numerical investigations of the energy performance and pressure fluctuations for a waterjet pump in a non-uniform inflow. Renew. Energy 2020, 153, 1042–1052. [Google Scholar] [CrossRef]
- Cao, P.; Wang, Y.; Kang, C.; Li, G.; Zhang, X. Investigation of the role of non-uniform suction flow in the performance of water-jet pump. Ocean Eng. 2017, 140, 258–269. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, X.; Liu, H.; Zhou, F.; Tang, T.; Lai, X. Analysis of the impeller’s tip clearance size on the operating characteristics of the underwater vehicle with a new high-speed water jet propulsion pump. Ocean Eng. 2021, 236, 109524. [Google Scholar] [CrossRef]
- Ji, L.; Li, W.; Shi, W.; Tian, F.; Agarwal, R. Diagnosis of internal energy characteristics of mixed-flow pump within stall region based on entropy production analysis model. Int. Commun. Heat Mass Transf. 2020, 117, 104784. [Google Scholar] [CrossRef]
- Sun, Y.; Peng, H.; Liu, W.; Guo, J.; Guo, Y. Comparison of the hydrodynamic performance of front and rear-stator pump-jet propulsors in an oblique wake under the cavitation condition. Phys. Fluids 2022, 34, 1–17. [Google Scholar] [CrossRef]
- Huang, R.; Dai, Y.; Luo, X.; Wang, Y.; Huang, C. Multi-objective optimization of the flush-type intake duct for a waterjet propulsion system. Ocean Eng. 2019, 187, 106172. [Google Scholar] [CrossRef]
- Huang, R.F.; Zhai, Z.H.; Zhou, J.J.; Luo, X.W. Cavitating flow analysis and design optimization for a waterjet mixed flow pump. IOP Conf. Ser. Earth Environ. Sci. 2018, 163, 012073. [Google Scholar] [CrossRef]
- Tian, D.; Lu, R.; Zhu, H.; Liu, J.; Zhang, Y.; Wei, G.; Li, G.; Si, Q. Cavitation performance analysis and optimal design of the portable electric-driven axial flow pump. J. Phys. Conf. Ser. 2024, 2707, 012055. [Google Scholar] [CrossRef]
- Kunz, R.F.; Boger, D.A.; Stinebring, D.R.; Chyczewski, T.S.; Lindau, J.W.; Gibeling, H.J.; Venkateswaran, S.; Govindan, T.R. A preconditioned navier–stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Merkle, C.; Feng, J.; Buelow, P. Computational Modeling of the Dynamics of Sheet Cavitation. In Proceedings of the 3rd International Symposium on Cavitation, Grenoble, France, 7–10 April 1998. [Google Scholar]
- Saito, Y. Numerical analysis of unsteady vaporous cavitating flow around a hydrofoil. J. Kyushu Univ. Health Welf. 2003, 12, 171–176. [Google Scholar]
- Singhal, A.K.; Athavale, M.M.; Li, H.; Jiang, Y. Mathematical basis and validation of the full cavitation model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Gunter, H.; Sauer, J. Physical and numerical modeling of unsteady cavitation dynamics. In Proceedings of the Icmf-2001, International Conference on Multiphase Flow, New Orleans, LO, USA, 27 May–1 June 2001. [Google Scholar]
- Yuan, W.; Sauer, J.; Schnerr, G. Modeling and computation of unsteady cavitation flows in injection nozzles. Mécanique Ind. 2001, 2, 383–394. [Google Scholar] [CrossRef]
- Katz, J. Cavitation phenomena within regions of flow separation. J. Fluid Mech. 1984, 140, 397–436. [Google Scholar] [CrossRef]
- Laberteaux, K.R.; Ceccio, S.L.; Mastrocola, V.J.; Lowrance, J.L. High speed digital imaging of cavitating vortices. Exp. Fluids 1998, 24, 489–498. [Google Scholar] [CrossRef][Green Version]
- Gehrer, A.; Benigni, H.; Jaberg, H.; Penninger, G. Dimensioning and simulation of process pumps. In Proceedings of the 2004 Pump Users International Forum, Karlsruhe, Germany, 29–30 September 2004; pp. 29–30. [Google Scholar]
- Xu, S.; Long, X.P.; Ji, B.; Li, G.B.; Song, T. Vortex dynamic characteristics of unsteady tip clearance cavitation in a waterjet pump determined with different vortex identification methods. J. Mech. Sci. Technol. 2019, 33, 5901–5912. [Google Scholar] [CrossRef]
- Han, C.Z.; Xu, S.; Cheng, H.Y.; Ji, B.; Zhang, Z.Y. LES method of the tip clearance vortex cavitation in a propelling pump with special emphasis on the cavitation-vortex interaction. J. Hydrodyn. 2020, 32, 1212–1216. [Google Scholar] [CrossRef]
- Tan, D.; Li, Y.; Wilkes, I.; Miorini, R.L.; Katz, J. Visualization and time-resolved particle image velocimetry measurements of the flow in the tip region of a subsonic compressor rotor. J. Turbomach. 2015, 137, 041007. [Google Scholar] [CrossRef]
- Long, Y.; An, C.; Zhu, R.; Chen, J. Research on hydrodynamics of high velocity regions in a water-jet pump based on experimental and numerical calculations at different cavitation conditions. Phys. Fluids 2021, 33, 045124. [Google Scholar] [CrossRef]
- Long, Y.; Feng, C.; Wang, L.; Wang, D.; Cai, Y.; Zhu, R. Experiment on cavitation flow in critical cavitation condition of water-jet propulsion pump. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 1512–1518. (In Chinese) [Google Scholar]
- Long, Y.; Zhu, R.; Wang, D. A cavitation performance prediction method for pumps PART1-Proposal and feasibility. Nucl. Eng. Technol. 2020, 52, 2471–2478. [Google Scholar] [CrossRef]
- Long, Y.; Zhang, Y.; Chen, J. A cavitation performance prediction method for pumps: Part2-sensitivity and accuracy. Nucl. Eng. Technol. 2021, 53, 3612–3624. [Google Scholar] [CrossRef]
- Long, Y.; Zhang, M.; Zhou, Z.; Zhong, J.; An, C.; Chen, Y.; Wan, C.; Zhu, R. Research on cavitation wake vortex structures near the impeller tip of a water-jet pump. Energies 2023, 16, 1576. [Google Scholar] [CrossRef]
- Xu, S.; Xiong, Y.; Tang, F.; Li, G.; Long, X.; Ji, B.; Huang, R. The investigation on the flow characteristics during the continuous development of the tip leakage vortex cavitation in an axial pump-jet propulsion. Phys. Fluids 2024, 36, 055152. [Google Scholar] [CrossRef]
- Qiu, J.T.; Liu, T.Y.; Liu, X.Y.; Dai, Y.X.; Wang, Z.L.; Cai, Y.L. Experimental and numerical study on cavitation pulsating pressure of water-jet propulsion axial-flow pump. PLoS ONE 2024, 19, e0310167. [Google Scholar] [CrossRef] [PubMed]
- Xia, C.Z.; Cheng, L.; Shang, Y.N.; Zhou, J.R.; Yang, F.; Jin, Y. Numerical simulation on the cavitation of waterjet propulsion pump. IOP Conf. Ser. Mater. Sci. Eng. 2016, 129, 012011. [Google Scholar] [CrossRef]
- Gong, B.; Zhang, Z.; Feng, C.; Yin, J.; Li, N.; Wang, D. Experimental investigation of characteristics of tip leakage vortex cavitation-induced vibration of a pump. Ann. Nucl. Energy 2023, 192, 109935. [Google Scholar] [CrossRef]
- Xu, Z.; Lai, H. Comparison of Cavitation in Two Axial-Flow Water Jet Propulsion Pumps. Processes 2023, 11, 2137. [Google Scholar] [CrossRef]
- Huang, R.; Qiu, R.; Wang, Y.; Luo, X.; Zhang, W. Space-time frequency spectra analyses of the unsteady cavitating vortical flows inside a mixed-flow pump. Ocean Eng. 2021, 238, 109758. [Google Scholar] [CrossRef]
- Zheng, K.; Long, Y.; Xiang, Q.; Xu, C.; Chen, J.; Wang, D. Study on the experiment and numerical simulation of cavitation flow mechanisms at different flow rates in water-jet propulsion pumps. J. Phys. Conf. Ser. 2024, 2707, 012050. [Google Scholar]
- Husband, B.; Bu, M.; Evans, A.G.; Melvin, T. Investigation for the operation of an integrated peristaltic micropump. J. Micmmech. Mieroeng. 2004, 14, 64–69. [Google Scholar] [CrossRef]
- Tsunenofi, O.; Yoshiro, I. Comparison of surface damage caused by sliding wear and cavitation erosion on mechanical face seals. Trans. ASME 1987, 107, 200–205. [Google Scholar]
- Mishra, C. Investigation of Hydrodynamic Cavitation in Microfluidic System Micro Orifices and Microventuris; Rensselaer Polytechnic Institute: Troy, NY, USA, 2005. [Google Scholar]
- Zwaan, E.; Le Gac, S.; Tsuji, K.; Ohl, C.D. Controlled cavitation in microfluidic systems. Virtual J. Nanoscale Sci. Technol. 2007, 16, 2545011–2545014. [Google Scholar] [CrossRef] [PubMed]
- Shao, H. Investigation on Cavitation Inside Micro Channel; Zhejiang University: Hangzhou, China, 2012. [Google Scholar]
- Su, X.; Song, F.; Xie, W.; Chang, H.; Wang, L. Study on characteristics of internal flow field of water-jet pumps based on bionic airfoil. J. Harbin Univ. Commer. (Nat. Sci. Ed.) 2021, 37, 739–744. (In Chinese) [Google Scholar]
- Su, X.Z.; Li, W.J.; Xie, W.C.; Song, F.; Chang, H.Y. Cavitation characteristics of impeller of water jet propulsion pumps based on bionic airfoil. J. Qingdao Agric. Univ. (Ziran Kexueban) 2022, 39, 147–152. (In Chinese) [Google Scholar]
- Lu, J.; Zhou, D.; Wang, X.; Su, X.; Zhang, S. Biomimetic airfoil design and flow characteristics based on sturgeon. J. Harbin Univ. Commer. (Nat. Sci. Ed.) 2024, 40, 688–697. (In Chinese) [Google Scholar]
- Li, Q.; Xia, S. The impact of airfoil blade tip on the internal flow of small water-jet pumps. China Rural Water Hydropower 2018, 131–135, 139. (In Chinese) [Google Scholar]
- Hao, Z.R.; Li, C.; Ren, W.L.; Wang, Y.; Hua, Z.L.; Liu, G. Optimization design of water jet propulsion pump blade based on improved PSO algorithm. J. Drain. Irrig. Mach. Eng. (JDIME) 2020, 38, 566–570. (In Chinese) [Google Scholar]
- Menter, F.R. Improved two-equation k-omega turbulence models for aerodynamic flows. NASA Tech. Memo. 1992, 93, 103975. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the 5th International Conference on Multiphase Flow, ICMF’04, Yokohama, Japan, 30 May–4 June 2004. [Google Scholar]




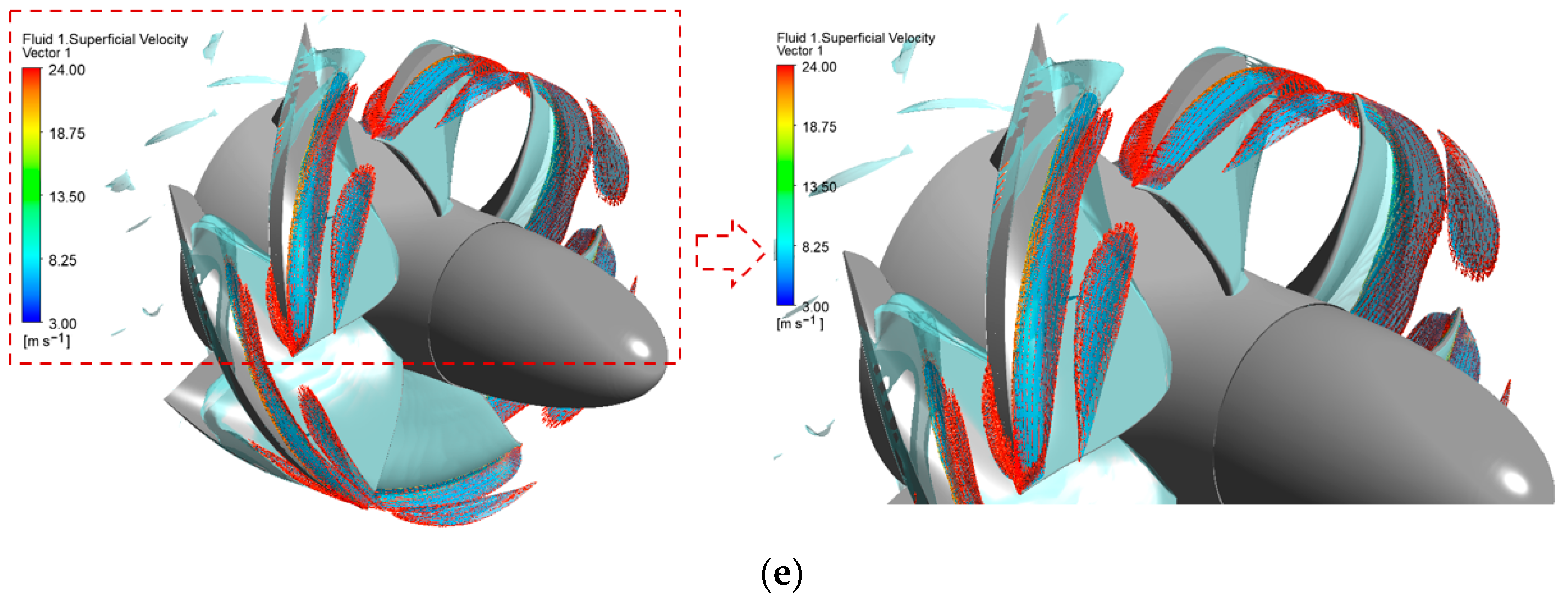

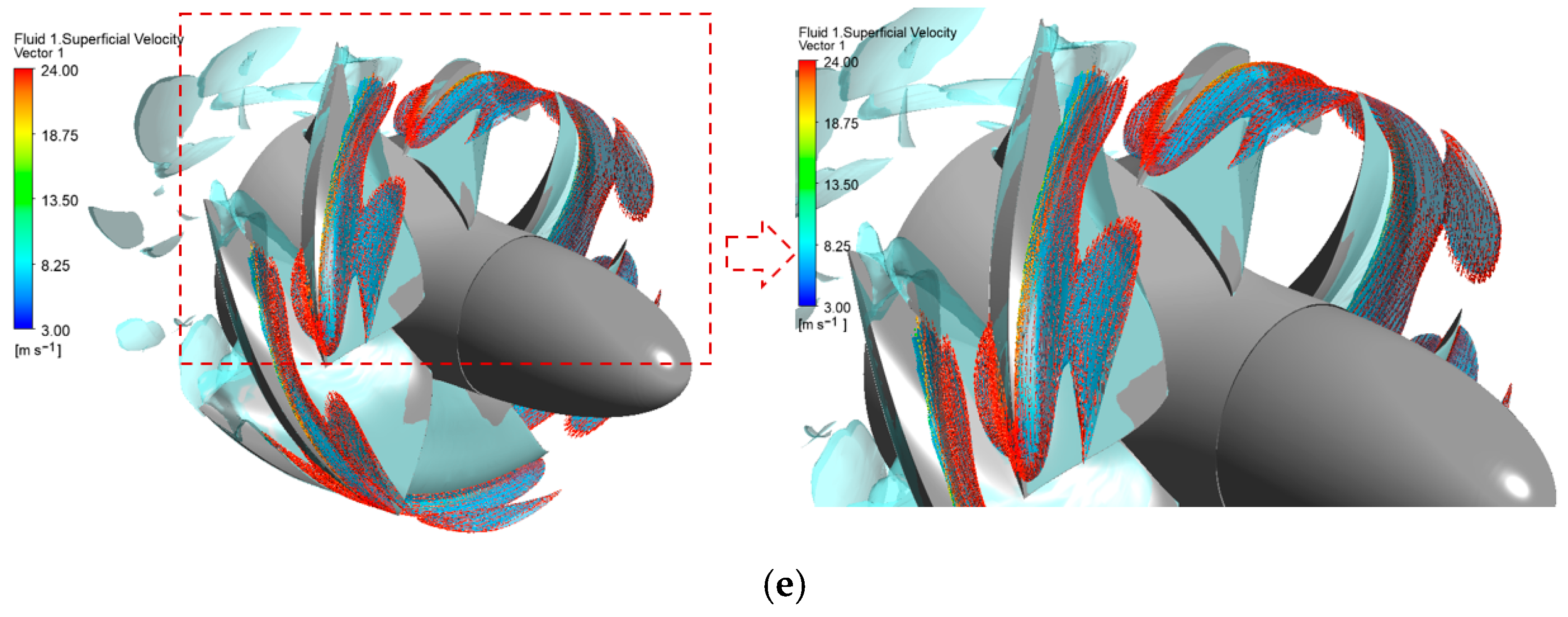
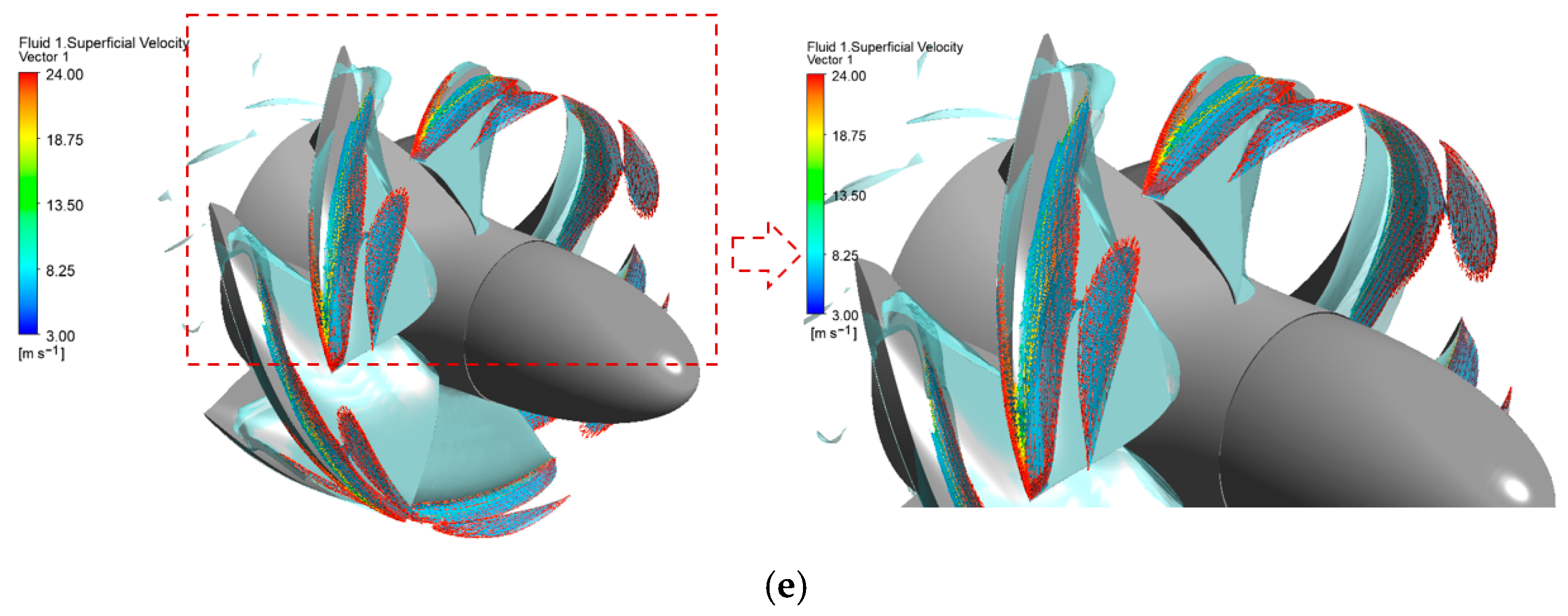
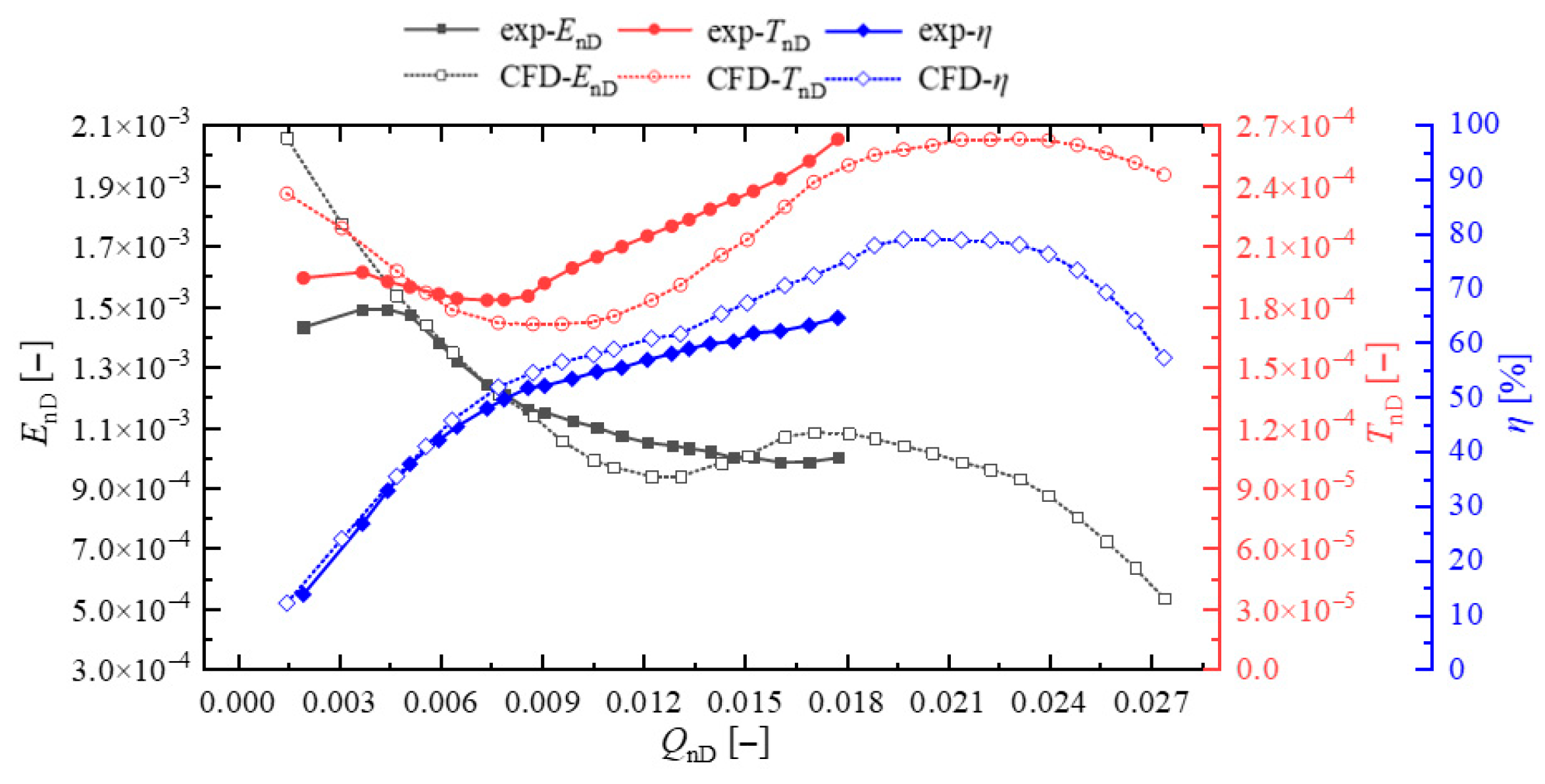
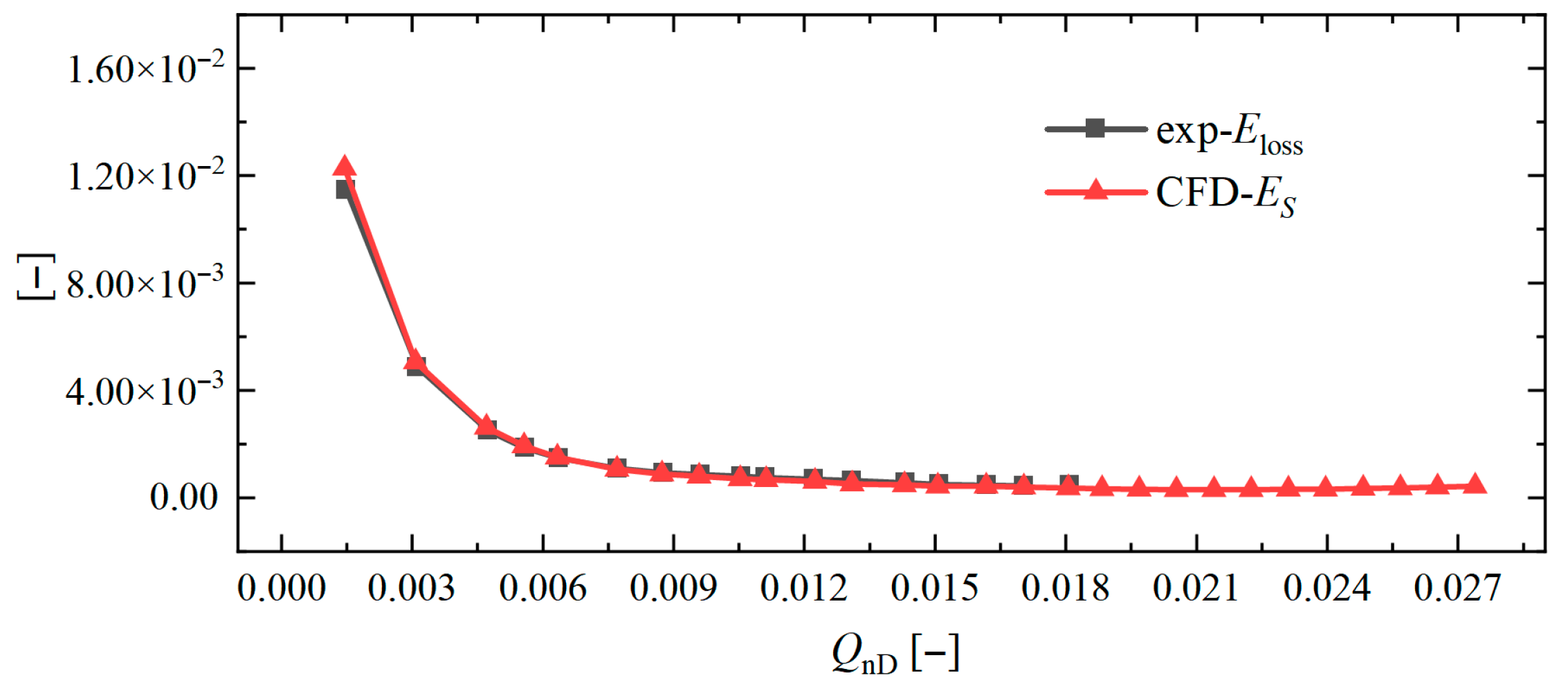
| Component | Wall | Minimum Wall Value | Maximum Wall Value | Average Wall Value | Average Component Value |
|---|---|---|---|---|---|
| Inlet pipe | Pipe wall | 1.083 | 15.882 | 4.110 | 4.151 |
| Deflector | 1.168 | 17.727 | 6.549 | ||
| Impeller | Hub | 0.038 | 4.739 | 2.004 | 3.504 |
| Blade | 0.051 | 15.673 | 4.212 | ||
| Edge | 0.131 | 10.202 | 3.198 | ||
| Diffuser | Hub | 0.049 | 7.150 | 2.075 | 3.714 |
| Blade | 0.041 | 10.330 | 4.035 | ||
| Edge | 0.131 | 10.202 | 3.937 | ||
| Outlet pipe | Shaft | 5.495 | 12.737 | 8.000 | 7.518 |
| Pipe wall | 5.323 | 9.857 | 7.368 |
| Categories | EFF | H (m) | HDP (%) | NPSH (m) |
|---|---|---|---|---|
| 101,325 | 0.8906 | 14.35 | 0.00 | 10.04 |
| 90,000 | 0.8910 | 14.35 | 0.03 | 8.88 |
| 80,000 | 0.8916 | 14.36 | 0.08 | 7.86 |
| 70,000 | 0.8910 | 14.38 | 0.20 | 6.84 |
| 60,000 | 0.8814 | 14.44 | 0.63 | 5.82 |
| 55,000 | 0.8393 | 14.43 | 0.55 | 5.38 |
| 54,750 | 0.8351 | 14.40 | 0.36 | 5.29 |
| 54,500 | 0.8356 | 14.41 | 0.47 | 5.26 |
| 54,000 | 0.8101 | 13.65 | −4.87 | 5.20 |
| 53,750 | 0.7954 | 12.92 | −9.93 | 5.18 |
| 52,500 | 0.6797 | 8.72 | −39.25 | 5.08 |
| Categories | EFF | H (m) | HDP (%) | NPSH (m) |
|---|---|---|---|---|
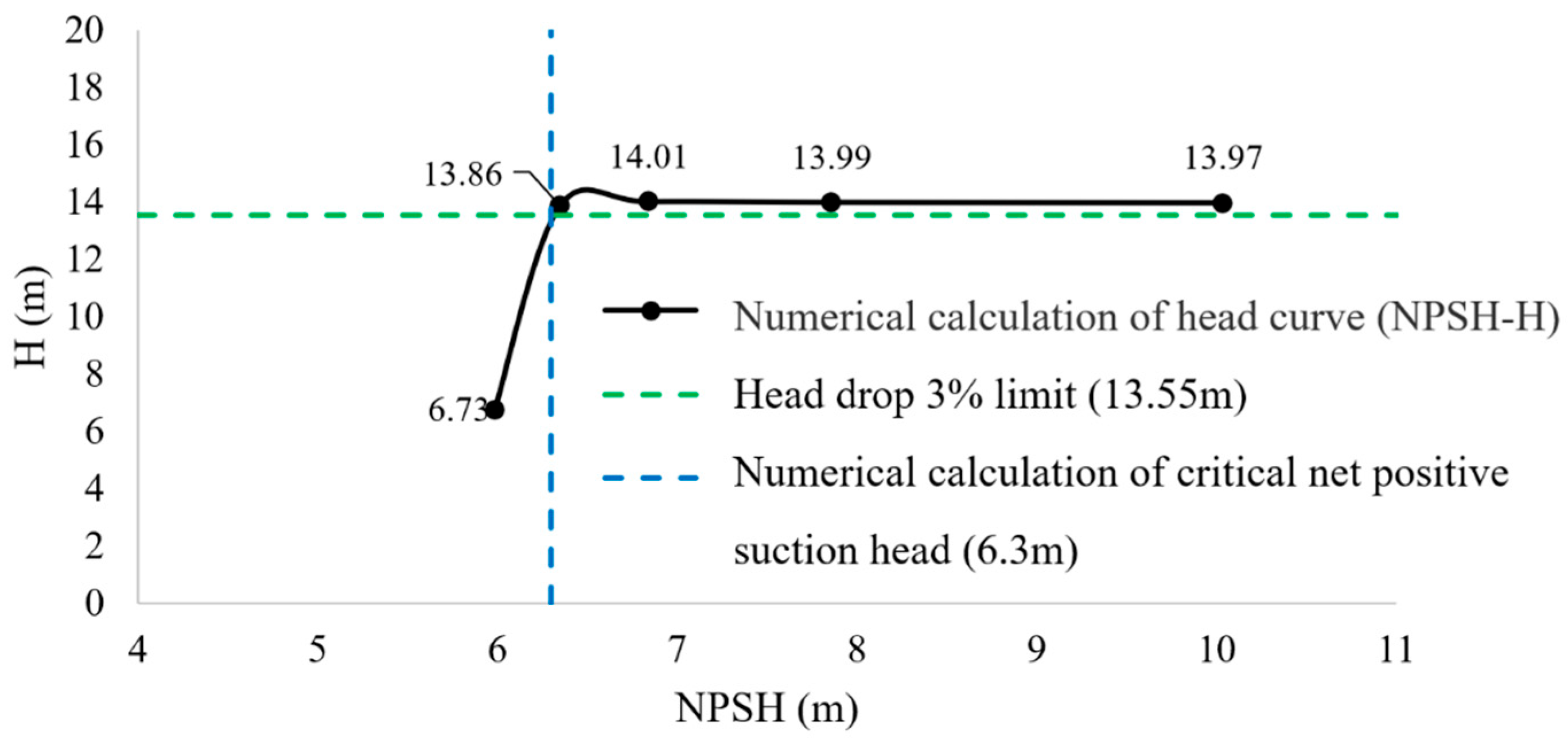
| 101,325 | 0.8850 | 13.97 | 0.00 | 10.04 |
| 80,000 | 0.8862 | 13.99 | 0.12 | 7.86 |
| 70,000 | 0.8810 | 14.01 | 0.29 | 6.84 |
| 65,000 | 0.8371 | 13.86 | −0.80 | 6.34 |
| 60,000 | 0.5826 | 6.73 | −51.84 | 5.98 |
| Categories | EFF | H (m) | HDP (%) | NPSH (m) |
|---|---|---|---|---|
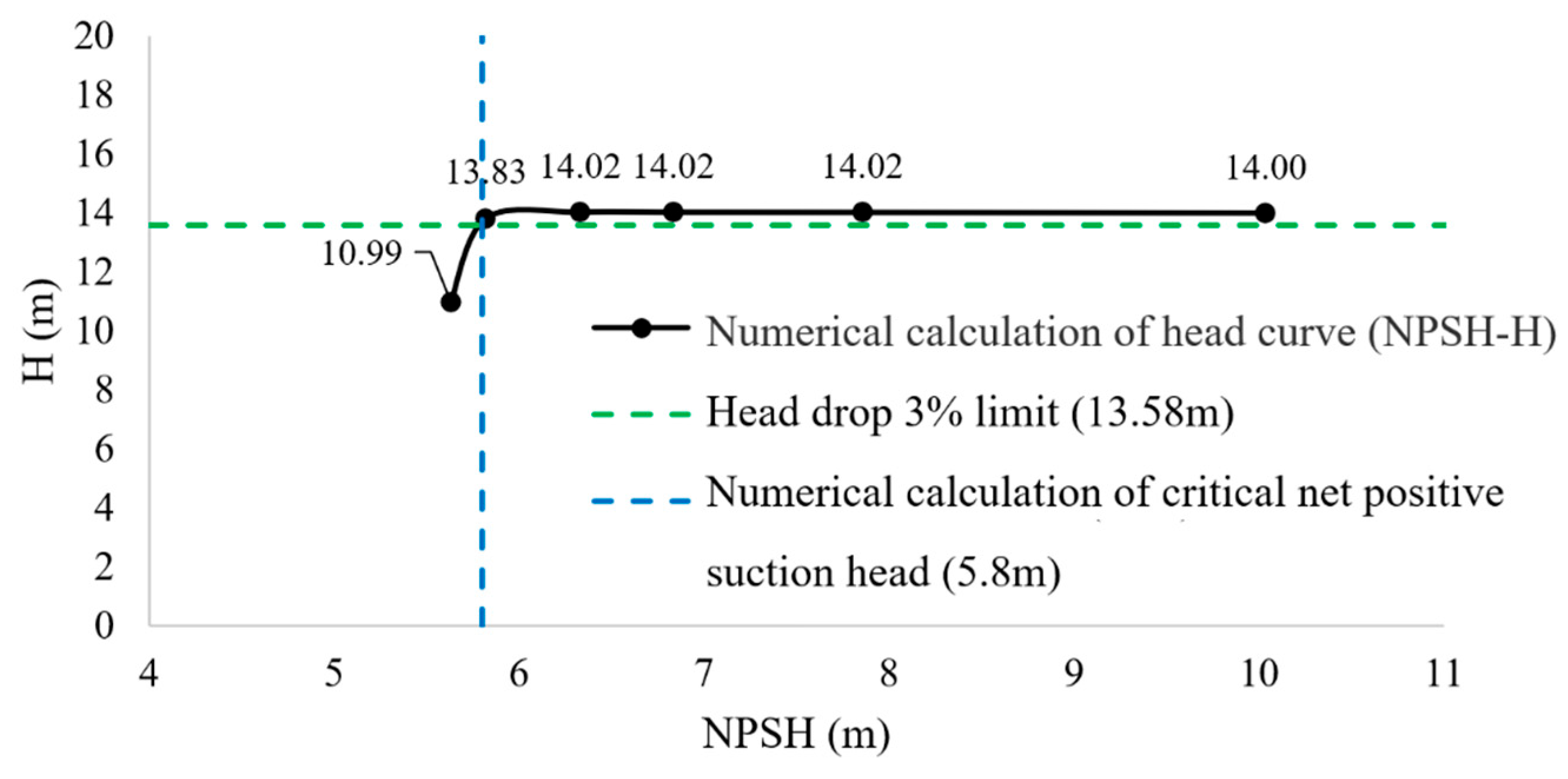
| 101,325 | 0.8877 | 14.00 | 0.00 | 10.04 |
| 80,000 | 0.8887 | 14.02 | 0.13 | 7.86 |
| 70,000 | 0.8886 | 14.02 | 0.17 | 6.83 |
| 65,000 | 0.8817 | 14.02 | 0.18 | 6.33 |
| 60,000 | 0.8202 | 13.83 | −1.22 | 5.82 |
| 57,500 | 0.7561 | 10.99 | −21.47 | 5.63 |
| Categories | EFF | H (m) | HDP (%) | NPSH (m) |
|---|---|---|---|---|
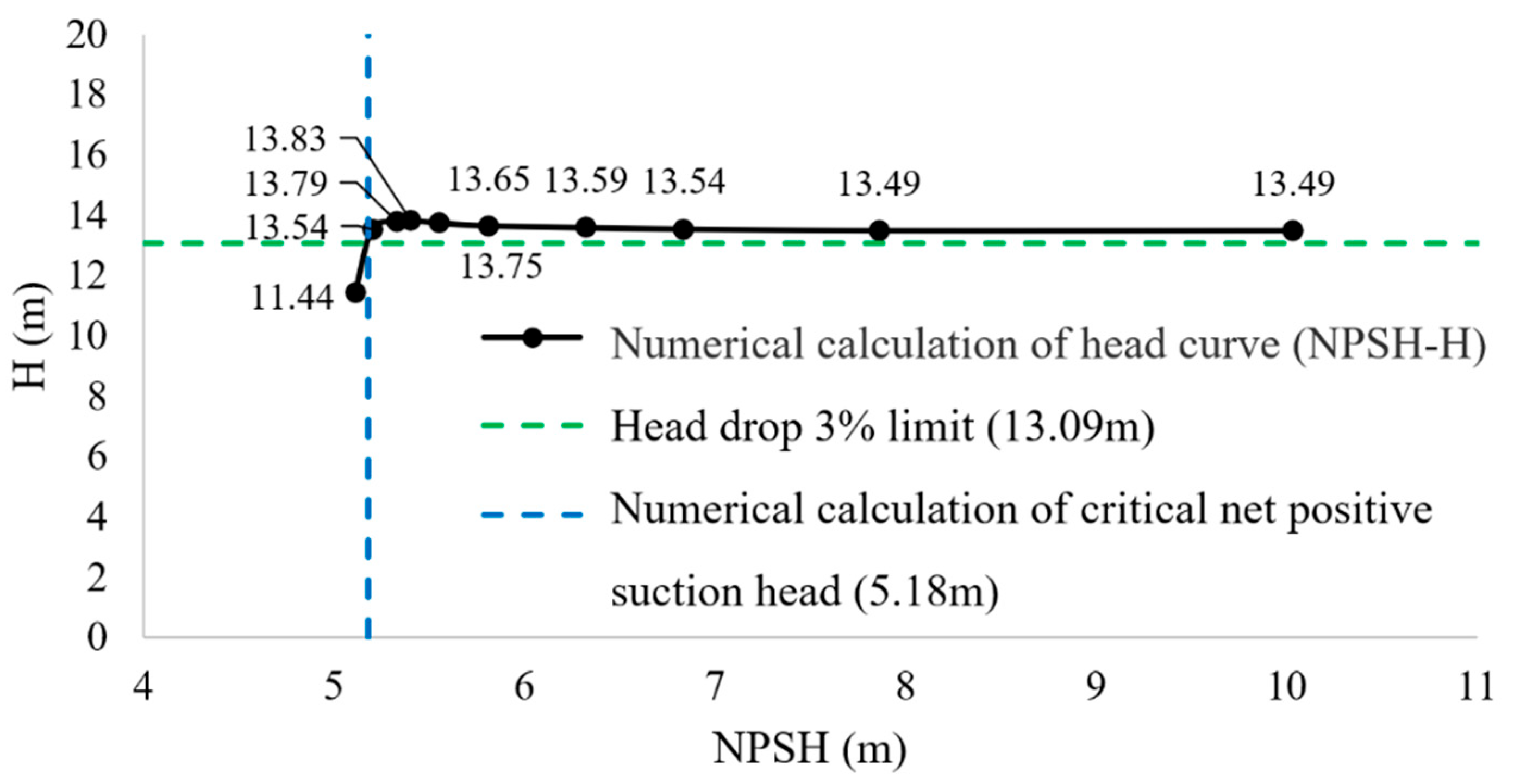
| 101,325 | 0.8836 | 13.49 | 0.00 | 10.04 |
| 80,000 | 0.8828 | 13.49 | −0.01 | 7.86 |
| 70,000 | 0.8870 | 13.54 | 0.38 | 6.84 |
| 65,000 | 0.8894 | 13.59 | 0.71 | 6.32 |
| 60,000 | 0.8847 | 13.65 | 1.18 | 5.81 |
| 57,500 | 0.8870 | 13.75 | 1.89 | 5.55 |
| 56,000 | 0.8785 | 13.83 | 2.51 | 5.40 |
| 55,000 | 0.8709 | 13.79 | 2.21 | 5.33 |
| 54,000 | 0.8423 | 13.54 | 0.39 | 5.20 |
| 53,000 | 0.7833 | 11.44 | −15.19 | 5.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Long, Y.; Wan, C.; Chen, J.; Cai, Y.; Zhong, J. Effects of Airfoil Parameters on the Cavitation Performance of Water Jet Propulsion Pumps. Fluids 2025, 10, 227. https://doi.org/10.3390/fluids10090227
Zheng Y, Long Y, Wan C, Chen J, Cai Y, Zhong J. Effects of Airfoil Parameters on the Cavitation Performance of Water Jet Propulsion Pumps. Fluids. 2025; 10(9):227. https://doi.org/10.3390/fluids10090227
Chicago/Turabian StyleZheng, Yingying, Yun Long, Churui Wan, Jianping Chen, Youlin Cai, and Jinqing Zhong. 2025. "Effects of Airfoil Parameters on the Cavitation Performance of Water Jet Propulsion Pumps" Fluids 10, no. 9: 227. https://doi.org/10.3390/fluids10090227
APA StyleZheng, Y., Long, Y., Wan, C., Chen, J., Cai, Y., & Zhong, J. (2025). Effects of Airfoil Parameters on the Cavitation Performance of Water Jet Propulsion Pumps. Fluids, 10(9), 227. https://doi.org/10.3390/fluids10090227







