Investigation of Heart Valve Dynamics: A Fluid-Structure Interaction Approach

Abstract

This study presents a numerical investigation into the heart valve through a fluid–structure interaction (FSI) framework using a two-dimensional, steady-state, Newtonian flow assumption. While simplified, this approach captures core biomechanical effects and provides a baseline for future extension toward non-Newtonian, pulsatile, and three-dimensional models. The analysis focuses on the influence of magnetic field intensity characterized by the Hartmann number (Ha) and flow regime defined by the Reynolds number (Re) on critical hemodynamic parameters, including wall shear stress (WSS), velocity profiles, and pressure gradients in the valve region. The results demonstrate that stronger magnetic fields significantly stabilize intravalvular flow by suppressing recirculation zones and reducing flow separation distal to valve constrictions, offering protective hemodynamic benefits and serving as a non-invasive method to modulate vascular behavior and reduce the risk of cardiovascular pathologies such as atherosclerosis and hypertension.

1. Introduction

Cardiovascular diseases remain one of the leading causes of mortality worldwide, often linked to complex hemodynamic behaviors within arterial systems—particularly in regions of stenosis, bifurcation, or valve dysfunction [1,2,3]. Flow disturbances such as recirculation zones and oscillatory wall shear stress (WSS) have been implicated in endothelial dysfunction and atherogenesis [4,5]. A key contributor to these phenomena is the interaction between blood flow and the deformable arterial wall, formally treated as a fluid–structure interaction (FSI) problem [6,7,8,9].

Advances in computational biomechanics have enabled the use of fully coupled FSI models to simulate heart valve dynamics with greater accuracy. Borowski et al. [10] demonstrated that Arbitrary Lagrangian–Eulerian (ALE) methods improve the fidelity of valve deformation prediction in transcatheter aortic valve simulations. Kaiser et al. [11] employed an immersed boundary approach validated against 4D flow MRI, capturing realistic flow dynamics around pulmonary valves. Mao et al. [12] combined smoothed particle hydrodynamics with nonlinear finite elements to simulate coupled ventricular and valvular motion. These frameworks account for intricate interactions between pressure gradients, tissue motion, and geometric nonlinearity.

Recent developments in immersed methods such as the immersed finite element method (IFEM) [13,14] and immersogeometric analysis [15] have further expanded the capability of FSI modeling to handle anatomically complex valve geometries. These methods offer robust strategies for simulating the detailed interplay between fluid and structure, particularly when sharp interfaces or complex material interfaces are present.

Beyond traditional hemodynamic considerations, there is growing clinical interest in the use of magnetic fields to modulate blood flow in cardiovascular applications. Given the weakly conducting nature of blood, external magnetic fields generate Lorentz forces that can dampen velocity fluctuations, suppress vortex formation, and enhance flow coherence. This is particularly relevant in heart valve regions, where shear-induced platelet activation, stagnation zones, and turbulent jets are common. These pathological flow features contribute to adverse outcomes such as thrombus formation, embolic risk, and accelerated bioprosthetic degeneration. By improving WSS uniformity and reducing peak stresses on the valve leaflets, magnetic modulation may offer a non-invasive therapeutic pathway to mitigate these risks and improve the functional longevity of both native and prosthetic valves [16,17].

Despite these promising insights, prior magnetohydrodynamics (MHD) studies have largely focused on rigid-walled arterial segments, simplified axisymmetric geometries, or steady-state flow assumptions. Very few incorporate realistic valve-adjacent conditions, let alone the dynamic FSI effects present in living tissues. The combined influence of magnetic field intensity (Hartmann number) and biomechanical compliance on flow-induced stress patterns remains underexplored. Furthermore, little is known about how magnetic fields might interact with leaflet motion or influence fatigue cycles in flexible valve supports. This study addresses these gaps by simulating magnetically influenced blood flow through a bifurcated, stenosed artery with elastic walls using a fully coupled ALE-based FSI framework. Our goal is to quantify how varying magnetic field strengths modulate flow separation, WSS, and wall displacement, thereby offering new computational insights into the design of magnetically augmented cardiovascular therapies [18,19,20].

This work contributes a novel perspective to the intersection of magnetohydrodynamics and cardiovascular biomechanics by providing the first fully coupled numerical simulation of biomagnetic blood flow through a bifurcated, stenosed geometry with compliant arterial walls. Unlike earlier studies that treat fluid and structure separately or assume simplified vessel mechanics, our model captures the nonlinear interplay between magnetic field intensity, flow separation, and elastic wall deformation using an Arbitrary Lagrangian–Eulerian (ALE) framework. The ability to systematically vary Hartmann and Reynolds numbers within this setting allows for controlled investigation of magnetic field effects on clinically relevant metrics such as wall shear stress (WSS), pressure gradients, and mechanical fatigue indicators. This work lays the groundwork for magnetically assisted flow modulation strategies in valve-adjacent regions and presents a computational platform that can be extended toward prosthetic valve optimization and thrombosis risk assessment.

While the model adopts a two-dimensional, steady-state formulation with Newtonian blood properties, these assumptions were chosen to reduce computational cost and focus on fundamental magnetic–hemodynamic interactions. Nevertheless, it is acknowledged that real heart valve dynamics involve pulsatile, non-Newtonian, and three-dimensional effects. As such, the current results offer qualitative insights rather than direct patient-specific predictions. Future studies will aim to incorporate pulsatile flow and complex geometries to improve physiological realism.

The remainder of this paper is structured as follows: Section 2 develops the governing equations, outlining the ALE formulation for fluid–structure interaction under magnetic influence, along with constitutive models for both blood flow and arterial elasticity, and details the computational methodology, including domain geometry, boundary conditions, and spatial discretization using the $P_2/P_1$ finite element pair. Section 3 presents a comprehensive analysis of the simulation results, examining the impact of varying Hartmann and Reynolds numbers on flow behavior, wall displacement, and WSS distribution. Finally, Section 4 summarizes the key findings, discusses implications for magnetically guided cardiovascular therapies, and outlines future directions for clinical translation and model refinement.

2. Mathematical Formulation

In this study, a two-dimensional, viscous, steady-state, incompressible laminar flow of a biomagnetic fluid is analyzed as it passes through a simplified representation of a heart valve. The computational domain reflects asymmetric valve geometry with a central constriction, mimicking the narrowing between deformable valve leaflets. It is assumed that the increase in effective viscosity due to the magnetic field is negligible and that the walls of the domain are electrically non-conductive, with no significant electric field effects present. The outer boundaries representing the vessel walls are modeled as linearly elastic, while the valve leaflets are treated as hyperelastic structures.

The blood, modeled as a Newtonian fluid, is assumed to be electrically conducting and is subjected to a transverse uniform magnetic field. A fully developed parabolic velocity profile is imposed at the inlet, whereas the outlet boundary is maintained at a fixed reference pressure, commonly set to zero. This setup provides a physiologically relevant approximation of flow conditions in the vicinity of the heart valve.

To effectively capture the coupled fluid–structure interactions inherent in such systems, the Arbitrary Lagrangian–Eulerian (ALE) framework is employed. This approach enables simultaneous treatment of fluid and solid domains by allowing mesh motion to be defined independently from both the material (Lagrangian) and spatial (Eulerian) frames. As such, ALE is particularly well suited for simulating heart valve dynamics, where fluid motion interacts strongly with the deformable leaflet structures without prescribing a fixed mesh movement.

The dimensional variables used in the governing equations are defined as follows (SI units are used unless stated otherwise):

• $u^{*},v^{*}$ [m/s]: Velocity components in the x- and y-directions.
• $w^{*}$ [m/s]: Mesh velocity in the ALE formulation.
• $p^{*}$ [Pa = N/m²]: Fluid pressure.
• ${\rho }_f$ [kg/m³]: Fluid density.
• ${\mu }^{*}$ [Pa·s]: Dynamic viscosity of the fluid.
• ${\sigma }^{*}$ [S/m]: Electrical conductivity of the fluid.
• $B^{*}$ [T]: Magnitude of the externally applied magnetic field (Tesla).
• ${\sigma }^{*}{u}^{*}{\left(B^{*}\right)}^2$ [N/m³]: Lorentz force term per unit volume.
• $F_v^{*}$ [N/m³]: External body force acting on the solid (neglected in this study).
• ${\sigma }_s^{*}$ [Pa]: Cauchy stress tensor in the solid domain.
• $E^{*}$ [Pa]: Young’s modulus of the solid wall.
• h [m]: Characteristic length scale, taken as the arterial diameter.

These dimensional variables are then used to construct the dimensionless variables and governing equations described below, following standard non-dimensionalization procedures. The resulting dimensionless system retains generality and reduces computational complexity while preserving the essential physics of the problem.

Considering the above assumption and methodology, the governing equations in the Arbitrary Lagrangian-Eulerian (ALE) formulation for the fluid flow are given below (for more detail, see Donea et al. [21]) and the monolithic ALE formulation of the fluid–structure interaction is given in Razzaq et al. [22].

Conservation of mass

$${\displaystyle \frac{\partial u^{*}}{\partial x^{*}}}+{\displaystyle \frac{\partial v^{*}}{\partial y^{*}}}=0,$$

(1)

and conservation of momentum

$${\rho }_f[(u^{*}-w^{*}){\displaystyle \frac{\partial u^{*}}{\partial x^{*}}}+(v^{*}-w^{*}){\displaystyle \frac{\partial u^{*}}{\partial y^{*}}}]=-{\displaystyle \frac{\partial p^{*}}{\partial x^{*}}}-{\sigma }^{*}{u}^{*}{\left(B^{*}\right)}^2+{\mu }^{*}\left({\displaystyle \frac{{\partial }^2{u}^{*}}{\partial {\left(x^{*}\right)}^2}}+{\displaystyle \frac{{\partial }^2{u}^{*}}{\partial {\left(y^{*}\right)}^2}}\right),$$

(2)

$${\rho }_f[(u^{*}-w^{*}){\displaystyle \frac{\partial v^{*}}{\partial x^{*}}}+(v^{*}-w^{*}){\displaystyle \frac{\partial v^{*}}{\partial y^{*}}}]=-{\displaystyle \frac{\partial p^{*}}{\partial y^{*}}}+{\mu }^{*}\left({\displaystyle \frac{{\partial }^2{v}^{*}}{\partial {\left(x^{*}\right)}^2}}+{\displaystyle \frac{{\partial }^2{v}^{*}}{\partial {\left(y^{*}\right)}^2}}\right),$$

(3)

where $u^{*}$ and $v^{*}$ are the dimensional velocity components, and $w^{*}$ is the dimensional mesh coordinate velocity. ${\sigma }^{*}$ is the electrical conductivity of the biomagnetic fluid. The fluid electric conductivity generates a term, ${\sigma }^{*}{u}^{*}{\left(B^{*}\right)}^2$, in Equation (2), representing the Lorentz force per unit volume.

The governing equations for the solid displacement in dimensional form is given by

Conservation of momentum:

$$\nabla {\sigma }_s^{*}+F_v^{*}=0,$$

(4)

now, assuming that there is no external force acting on the solid body, i.e., $F_v^{*}=0$.

$$\begin{array}{cc}\hfill \sigma & ={\displaystyle \frac{{\sigma }_s^{*}}{E^{*}}},E={\displaystyle \frac{E^{*}h}{{\rho }_f{v}_0^2}},(x,y)=({\displaystyle \frac{x^{*}}{h}},{\displaystyle \frac{y^{*}}{h}}),(u,v,w)=({\displaystyle \frac{u^{*}}{v_0}},{\displaystyle \frac{v^{*}}{v_0}},{\displaystyle \frac{w^{*}}{v_0}}),\hfill \\ \hfill u_s& ={\displaystyle \frac{u_s^{*}}{h}},p={\displaystyle \frac{p^{*}}{{\rho }_f{v}_0^2}},Re={\displaystyle \frac{{\rho }_{f}h{v}_0}{\mu }},Ha={\displaystyle \frac{{\sigma }^{*}{B}^{*2}{h}^2}{\mu }},\hfill \end{array}$$

(5)

where h is the diameter of the artery, and $v_0$ is the maximum velocity of the blood at the inlet. The dimensionless parameters $Re$ and $Ha$ denote the Reynolds number and Hartmann number, respectively.

Equation (4) with the help of the dimensionless parameters given in Equation (5) can be written as

$$\nabla \sigma =0,$$

(6)

where $\sigma$ is the strain tensor, and, in the case of linearly elastic walls, the strain tensor can be written as

$$\sigma =J^{-1}FS{F}^T,$$

(7)

where J is the determinant value of F, and F is defined as $F=1+\nabla u_s$. Also, the relation for the second Piola–Kirchhoff stress tensor S with strain $ϵ$ is, $S=C:ϵ$ and $C=C(E,\nu )$, where E is Young’s modulus, $\nu$ is the Poisson ratio of the solid wall, and the strain tensor is defined as

$$ϵ={\displaystyle \frac{1}{2}}\left({(\nabla u_s)}^T+\nabla u_s+{(\nabla u_s)}^T·\nabla u_s\right).$$

(8)

By considering the dimensionless parameter, we can write Equations (1)–(3) as

$${\displaystyle \frac{\partial u}{\partial x}}+{\displaystyle \frac{\partial v}{\partial y}}=0,$$

(9)

$$(u-w){\displaystyle \frac{\partial u}{\partial x}}+(v-w){\displaystyle \frac{\partial u}{\partial y}}=-{\displaystyle \frac{\partial p}{\partial x}}-{\displaystyle \frac{H{a}^2}{Re}}u+{\displaystyle \frac{1}{Re}}\left({\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}\right),$$

(10)

$$(u-w){\displaystyle \frac{\partial v}{\partial x}}+(v-w){\displaystyle \frac{\partial v}{\partial y}}=-{\displaystyle \frac{\partial p}{\partial y}}+{\displaystyle \frac{1}{Re}}\left({\displaystyle \frac{{\partial }^{2}v}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}v}{\partial y^2}}\right),$$

(11)

$$\nabla \sigma =0.$$

(12)

The parabolic velocity profile is assumed at the inlet.

$$u(x,y)=y{u}_0(1-y).$$

(13)

where $u_0=0.01$, and the outlet boundary conditions are prescribed on pressure. The pressure sets equal to zero at the outlet. On the interface of the fluid and solid, regular no-slip boundary conditions are employed. The maximum velocity $u_0=0.01$ was selected in a dimensionless context to reduce the computational cost while capturing key flow characteristics. This value does not represent peak systolic flow but rather corresponds to a simplified approximation of early systolic conditions. As such, the results aim to demonstrate qualitative trends in magnetic damping rather than reproduce exact clinical hemodynamics. Future studies will incorporate pulsatile inflow conditions with higher peak velocities to better simulate mid-to-late systolic behavior, where flow separation is most prevalent.

2.1. Geometrical Configuration

To provide anatomical context for the numerical investigation, Figure 1 presents a schematic of the human circulatory system, highlighting the pathways of deoxygenated and oxygenated blood through the heart chambers and major vessels. Of particular interest is the pulmonary valve and its adjacent vasculature, which play a central role in regulating blood flow from the right ventricle to the pulmonary artery. Although the true anatomy is three-dimensional and highly complex, this illustration helps orient the reader to the general flow direction and key anatomical landmarks relevant to the modeled domain.

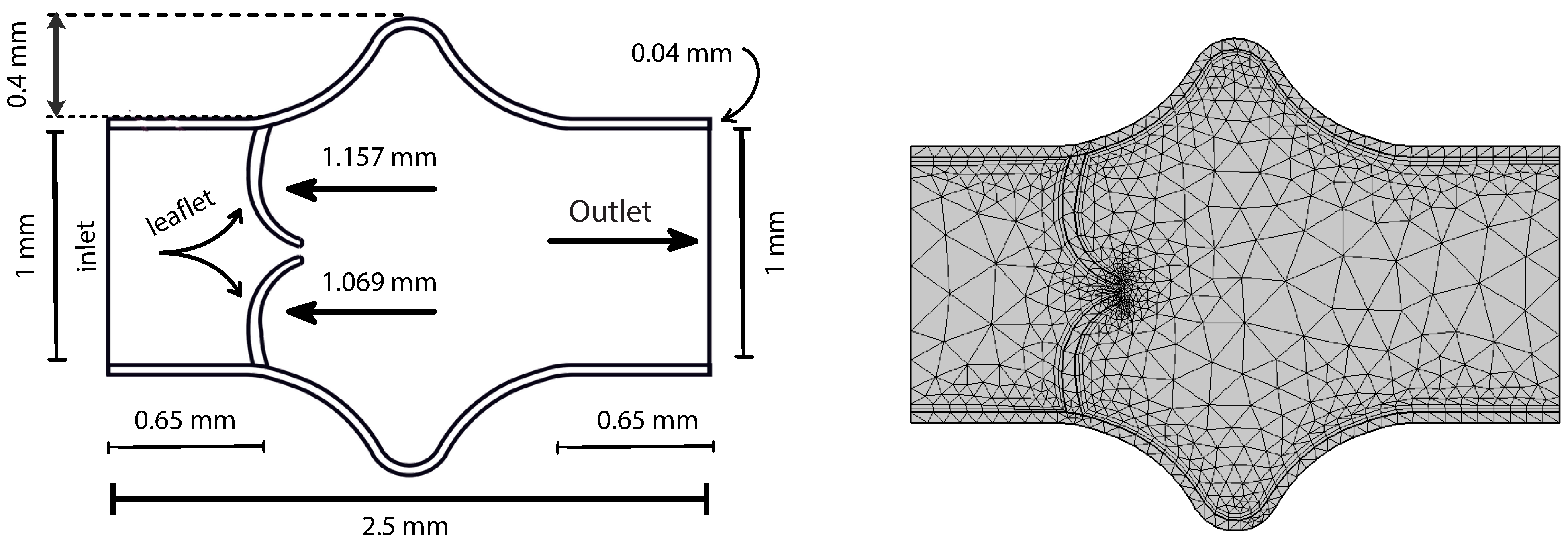
A simplified two-dimensional representation of the valve region is employed in this study, as shown in Figure 2. This abstraction facilitates computational efficiency while capturing the essential structural and flow characteristics near the valve. The geometry consists of a constricted channel mimicking the narrowed orifice created by opposing valve leaflets, forming a stenosis-like throat region. The domain features asymmetric, smoothly curved upper and lower boundaries that idealize the shape of valve leaflets in a planar section. The left side of the domain defines the inlet, where a fully developed parabolic velocity profile is prescribed, while the right side acts as the outlet. This configuration represents a cross-section of a valve chamber and includes gradual expansions upstream and downstream to model flow entrance and exit effects.

In this model, the vessel walls are treated as linearly elastic and isotropic, described using Young’s modulus E and Poisson’s ratio $\nu$, capturing their relatively stiff mechanical response under flow-induced pressure loads. The material parameters used for the walls are

$$E=5\times {10}^5,\nu =0.49.$$

In contrast, the leaflets are modeled using a Saint Venant–Kirchhoff (SVK) hyperelastic material model. While SVK is a relatively simple hyperelastic formulation—best suited for small to moderate deformations—it provides a nonlinear constitutive response needed for modeling valve leaflet flexibility under pulsatile flow. The material behavior is expressed in terms of the Lamé parameters $\lambda$ and $\mu$, which relate to E and $\nu$ through

$$\begin{array}{cc}\hfill \nu & ={\displaystyle \frac{\lambda }{2(\lambda +\mu )}},E={\displaystyle \frac{\mu (3\lambda +2\mu )}{\lambda +\mu }},\hfill \\ \hfill \mu & ={\displaystyle \frac{E}{2(1+\nu )}},\lambda ={\displaystyle \frac{\nu E}{(1+\nu )(1-2\nu )}}.\hfill \end{array}$$

It is important to note that while the SVK model allows for some degree of nonlinear elastic response, it is most accurate under moderate strain levels. For small-deformation static studies such as this, it offers a reasonable compromise between simplicity and capturing the essential mechanical effects of leaflet flexibility.

Nonetheless, native heart valve tissue is known to exhibit anisotropic, fiber-reinforced properties due to its collagenous microstructure, which contributes to a highly nonlinear, direction dependent mechanical response. To more accurately represent the physiological behavior of the valve leaflets, future studies could incorporate more advanced constitutive models, such as the Holzapfel–Gasser–Ogden formulation (see [23] or other anisotropic hyperelastic laws), which can account for the fiber architecture and large deformation effects typical of real valve tissue.

The initial coarse mesh configuration is illustrated in Figure 2. A triangular discretization strategy is employed to partition the computational domain, resulting in a structured mesh of 1303 elements. The geometry includes the lower elastic wall, along which wall shear stress (WSS) is evaluated. The mesh ensures adequate resolution of the flow and structural interfaces while maintaining computational efficiency at the coarsest level.

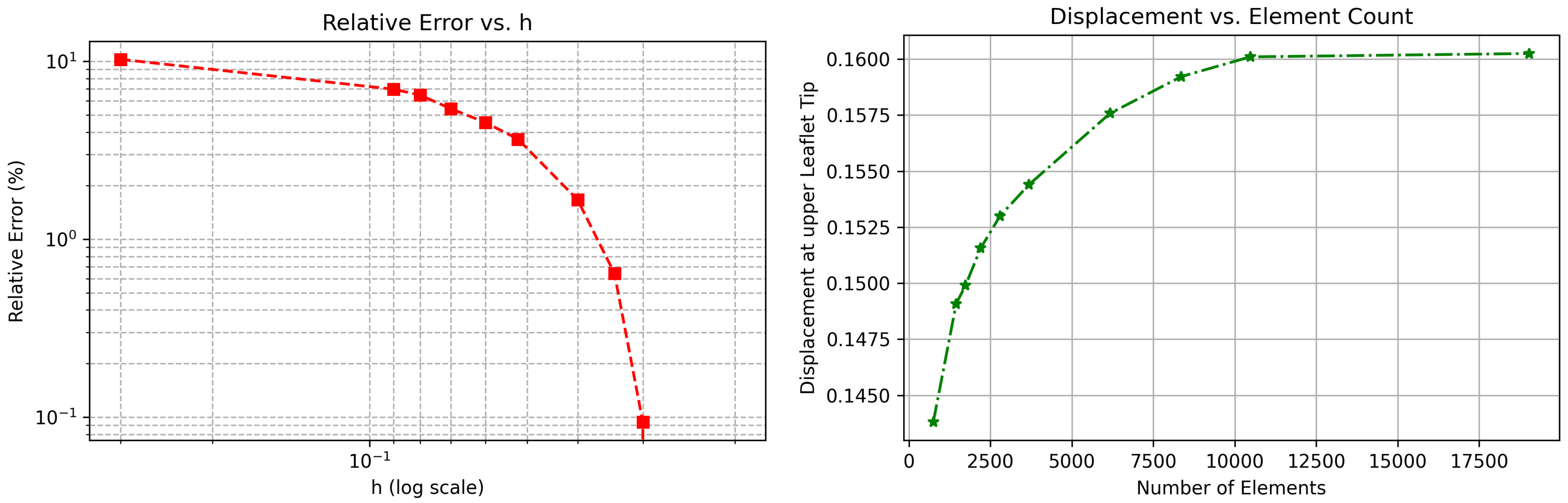
A summary of the mesh refinement study is provided in

Table 1. Mesh refinement levels with corresponding element counts, total wall shear stress (WSS) on the lower boundary, and relative errors computed with respect to Level 4.

Level	No. of Elements	Total WSS on Lower Wall ($\times {10}^{-4}$)	Relative Error (%)
0	1998	1.6210	6.59
1	3672	1.7063	1.67
2	5715	1.7102	1.45
3	10,432	1.7230	0.71
4	25,123	1.7353	0.00

, where each refinement level is characterized by the total number of elements, the computed WSS on the lower elastic boundary, and the corresponding relative error with respect to the finest mesh solution. All simulations reported in this study are based on the mesh at Level 4, which comprises 25,123.

2.2. Mesh Convergence Verification

To ensure the numerical accuracy and mesh independence of the FSI model, a detailed mesh convergence study was performed. Specifically, the total displacement at the tip of one of the valve leaflets was evaluated across a series of uniformly refined meshes. A probe was positioned at the leaflet tip, and displacement values were recorded for each refinement level. The relative error $\epsilon \left(h\right)$ was computed as

$$\epsilon \left(h\right)={\displaystyle \frac{\left|u\left(h\right)-u_{\mathrm{ref}}\right|}{\left|u_{\mathrm{ref}}\right|}}\times 100\%,$$

(14)

where $u\left(h\right)$ denotes the computed displacement at a given mesh size h, and $u_{\mathrm{ref}}$ represents the reference displacement obtained from the finest mesh.

As shown in Figure 3, both plots indicate consistent and monotonic convergence. The relative error in displacement decreases steadily as the mesh is refined, and the displacement values plateau beyond approximately 10,000 elements. These results confirm the robustness and numerical reliability of the proposed FSI framework under mesh refinement.

3. Results and Discussion

In this section, we present and analyze the numerical results obtained from the fluid–structure interaction simulations of blood flow under the influence of an external magnetic field. The effects of varying Hartmann numbers $(Ha=0,4,8,12)$ are examined for different Reynolds numbers $(Re=400,800,1200)$. The magnetic field strengths corresponding to the Hartmann numbers used (Ha = 0–12) were estimated to be in the range of 0.0–0.85 Tesla. These values are within the limits of modern clinical MRI systems. However, this study is not designed to propose direct clinical application but to assess the fundamental biomechanical effects of Lorentz forces in cardiovascular flows. Future studies may explore the feasibility of using dynamic magnetic modulation in controlled settings or evaluate safety thresholds based on tissue interaction studies. The results focus on flow velocity, wall displacement, wall shear stress (WSS), and the general hemodynamic response under magnetic field influence.

3.1. Velocity Field Analysis

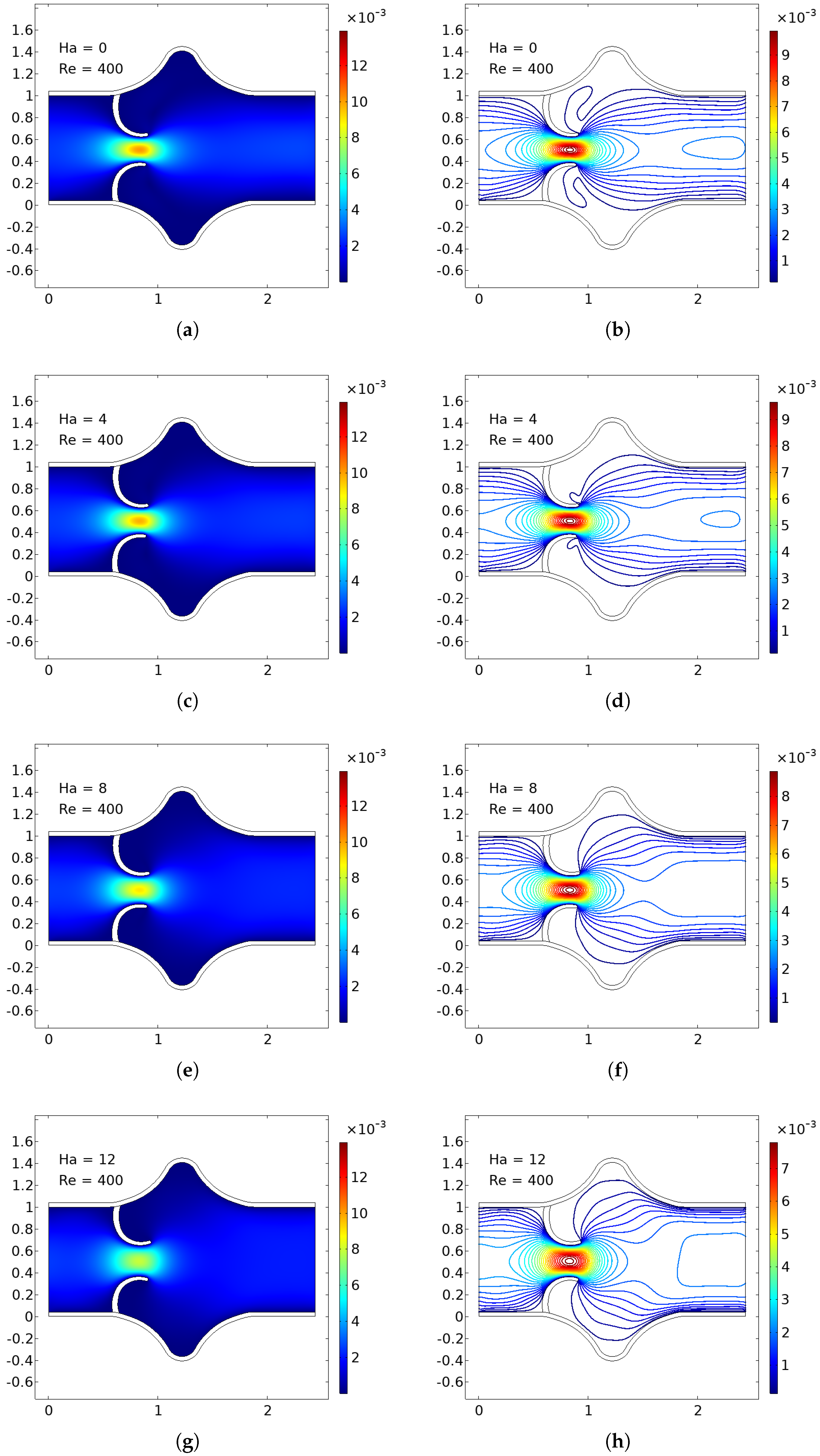
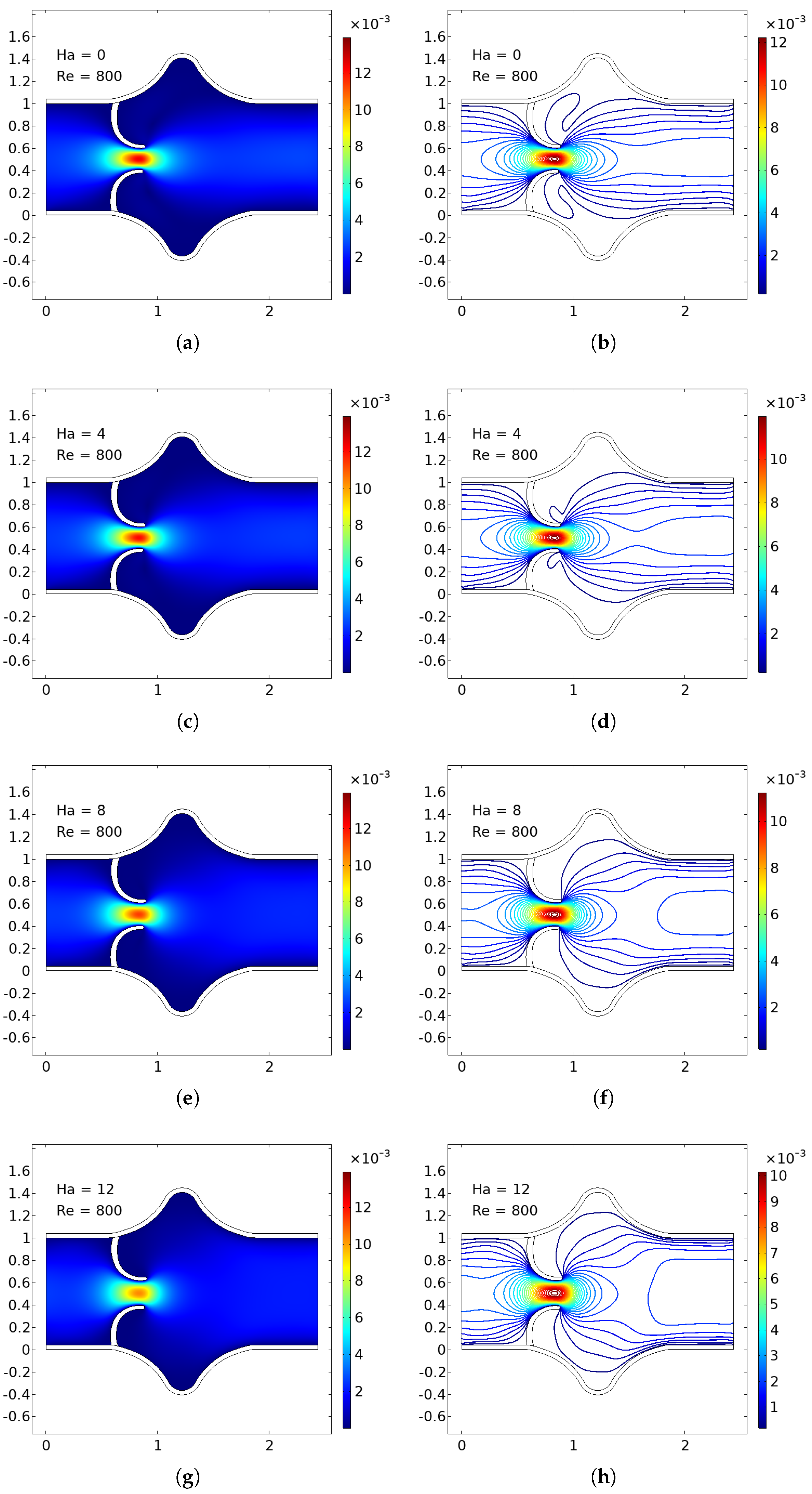
The numerical simulations present a comprehensive picture of intravalvular blood flow through a stenosed valve model subjected to various Hartmann numbers (Ha) and Reynolds numbers (Re), as shown in Figure 4, Figure 5 and Figure 6. The velocity fields were obtained from stationary fluid–structure interaction (FSI) computations on a two-dimensional domain resembling a simplified heart valve geometry with flexible leaflets and elastic walls. A parabolic inlet flow was prescribed, mimicking physiologically relevant conditions in the absence of pulsatility.

In the baseline case (Ha = 0), the velocity distribution demonstrates strong flow acceleration through the throat region due to geometric narrowing. Downstream of the stenosis, a pair of well-defined vortices emerge asymmetrically near the leaflet tips, accompanied by a noticeable drop in core velocity and a widening of low-velocity recirculation zones. These patterns are more pronounced at higher Reynolds numbers, where inertial effects dominate over viscous dissipation, leading to intensified flow separation and longer wake regions. The presence of these vortices is indicative of adverse pressure gradients and shear layer instability typically observed in pathological or prosthetic valvular configurations.

As the magnetic field intensity increases (Ha = 8, 10, 12), the velocity field exhibits a progressive suppression of flow separation and damping of recirculation zones. This is attributed to the Lorentz force generated by the imposed magnetic field, which acts as a momentum sink, introducing an effective damping mechanism. The Lorentz force resists lateral deviations of flow, promoting alignment along the axial direction and mitigating rotational structures. At lower Re (e.g., Re = 400), the magnetic field is highly effective in stabilizing the flow, nearly eliminating recirculation zones at moderate Ha values. At higher Re (e.g., Re = 1200), the inertia of the fluid is stronger, requiring correspondingly higher Ha values to achieve the same degree of stabilization, but the trend remains consistent.

Additionally, the velocity magnitude profiles near the leaflet tips show an observable reduction in peak jet velocity with increasing Ha. This attenuation is associated with an increased effective viscosity due to magnetic damping, leading to broader and more uniform velocity contours across the channel. The core jet narrows less dramatically, and velocity gradients near the wall and leaflet surfaces become smoother. This has significant biomechanical implications, especially regarding shear stress and its influence on endothelial integrity, blood element activation, and mechanical loading on the leaflet surfaces.

The observed velocity patterns highlight the interplay between inertial, viscous, and magnetic forces in shaping the hemodynamics of valvular flow. In the absence of magnetic influence, the velocity field reflects classic features of post-stenotic flow: jet acceleration through the throat, followed by separation, recirculation, and vortex shedding. These are pathological hallmarks in diseased valves and are often associated with hemolysis, platelet activation, and tissue degeneration due to elevated shear stresses and oscillatory flows.

The introduction of magnetic fields alters this behavior substantially. The suppression of vortices and stabilization of the flow field are particularly beneficial in mitigating shear-related damage and promoting hemodynamic efficiency. In essence, the magnetic field behaves as an active flow control mechanism, analogous to mechanical or geometric flow stabilizers but with the advantage of being externally tunable and non-invasive.

These findings align well with established principles of magnetohydrodynamics in biological flows and extend prior studies by demonstrating the effect within a coupled FSI framework. Importantly, the model incorporates deformable leaflet and wall boundaries, thereby capturing secondary interactions between fluid motion and structural deformation. Although a stationary formulation was adopted, the trends are expected to persist under transient flow regimes.

From a clinical or device-design perspective, the results suggest that magnetic field application could be employed as a passive stabilization strategy in valve prostheses or bio-hybrid systems, potentially prolonging device lifespan and reducing adverse flow-induced phenomena. Future work should consider full transient simulations and pulsatile inflow conditions to extend the current conclusions, and experimental validation would be essential to quantify the practical thresholds of magnetic field strengths in physiological settings.

3.2. Arterial Wall Displacement

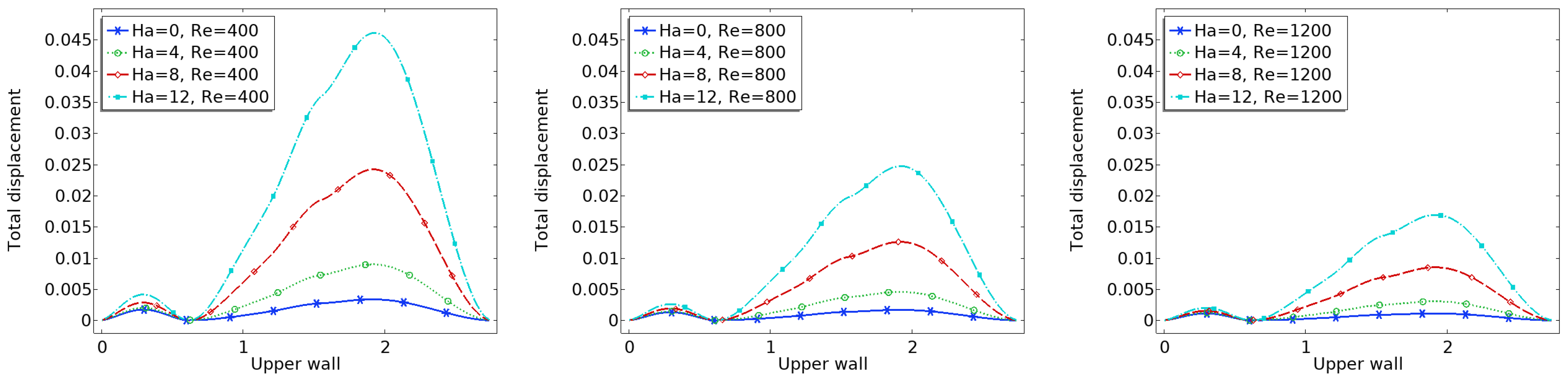
The interaction between fluid flow and the elastic vessel wall is further assessed through the displacement of the upper wall, as shown in Figure 7. In the case of the zero magnetic field, the deformation is significantly higher, particularly at the post-stenotic region, where high-velocity jets impinge on the wall.

When the magnetic field is applied, the Lorentz force reduces the flow momentum, thereby decreasing the fluid pressure on the wall. Consequently, the displacement magnitude is reduced across the entire upper wall. This effect is more significant near the bifurcation and downstream of the stenosis, where flow-induced forces are usually high.

Reduced displacement implies less wall fatigue and a lower risk of damage due to excessive mechanical stress. It also suggests that magnetic regulation could offer protective biomechanical benefits in arteries with compromised elasticity.

3.3. Pressure

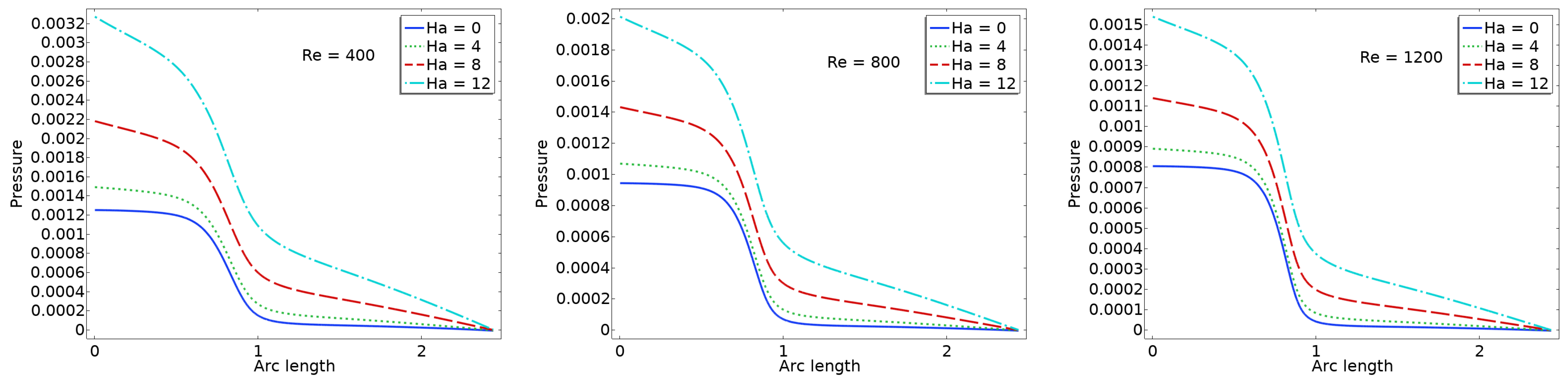
The pressure plots shown in Figure 8 illustrate the centerline pressure distribution obtained under varying Ha and Re numbers. These simulations are conducted within a stationary framework to capture the pressure field resulting from the interaction between blood flow and valve leaflet deformation. Each subplot corresponds to a specific Reynolds number (Re = 400, 800, 1200), while curves within each plot represent different Hartmann numbers (Ha = 0, 4, 8, 12). As the Reynolds number increases, the inertial forces in the flow become more dominant, leading to sharper pressure gradients, particularly downstream of the valve region. The pressure consistently decreases along the flow direction, indicative of forward flow through a constricted passage such as a heart valve.

The effect of the magnetic field, represented by the Hartmann number, is clearly evident in the flattening of the pressure profiles as Ha increases. At higher Hartmann numbers, the pressure drop becomes more gradual due to the magnetic damping effects, which suppress flow instabilities and reduce velocity gradients. This behavior suggests a stabilizing influence of the magnetic field on the flow, resulting in a more uniform pressure distribution. In the context of cardiovascular applications, such as artificial or bio-prosthetic heart valves, this reduction in pressure fluctuation may translate into lower mechanical stresses on the valve leaflets. Consequently, incorporating magnetohydrodynamic effects in the design or operation of heart valve systems could potentially enhance their durability and functional performance.

3.4. Wall Shear Stress (WSS) Distribution

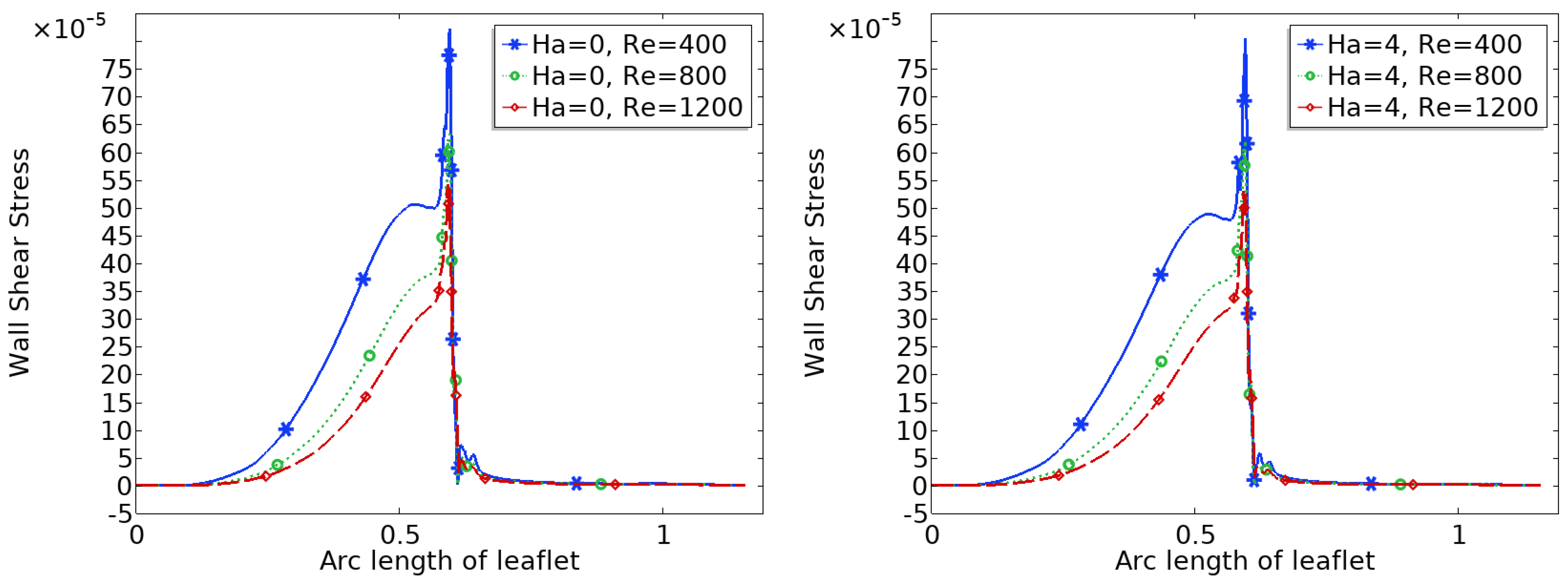
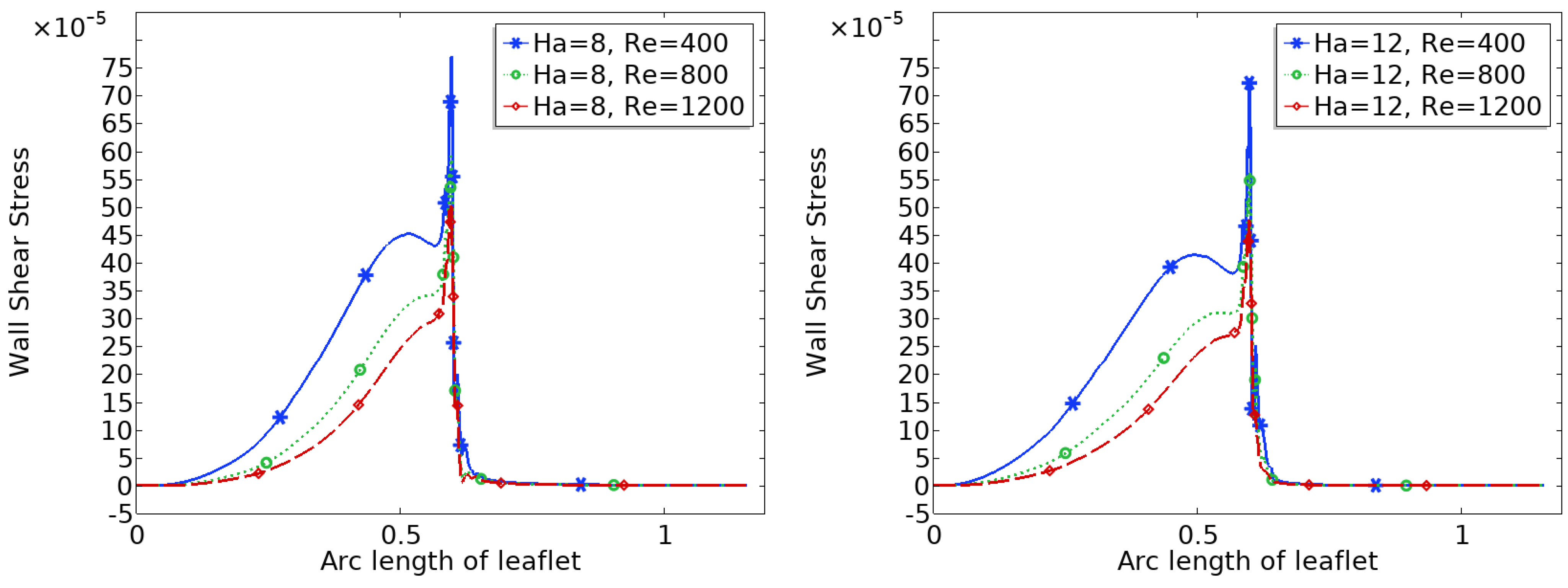
Figure 9 and Figure 10 show the distribution of wall shear stress (WSS) over the surface of the upper heart valve leaflet under varying magnetic field strengths. WSS is a critical biomechanical stimulus influencing endothelial function and the progression of valve related pathologies. The magnitude and spatial variation of WSS are key indicators of the mechanical environment experienced by the valve tissue.

In the baseline configuration without magnetic influence (Ha = 0), WSS exhibits significant spatial variation across the leaflet surface. The face of the leaflet directly exposed to the bloodstream experiences relatively high shear stress due to stronger flow interaction, while the back face, shielded from direct flow, is subjected to much lower WSS. Notably, a sharp peak in WSS is observed at the leaflet tip, where the geometry induces strong flow acceleration and shear concentration.

With increasing magnetic field strength, the WSS distribution becomes more uniform, and the magnitude increases especially in regions that initially experienced low shear, such as the back face of the leaflet. The peak at the leaflet tip becomes broader but less sharp, indicating a stabilizing effect on the shear field. These trends suggest that magnetic modulation not only smoothens the flow but also redistributes mechanical loading more evenly across the leaflet, potentially mitigating localized stress concentrations and reducing the risk of mechanical fatigue or endothelial damage.

Figure 11 illustrates the effect of magnetic field strength (Ha) on the total WSS over the upper leaflet across a range of Reynolds numbers. At each fixed Re, increasing Ha leads to a clear increase in WSS magnitude, indicating that the applied magnetic field enhances shear stresses on the leaflet surface. While WSS generally decreases with increasing Re, the trend of increasing WSS with Ha remains consistent across all Re values.

Table 2. Quantitative values of normalized displacement, pressure, wall shear stress (WSS), and velocity magnitude on upper leaflet for various Hartmann (Ha) and Reynolds (Re) numbers.

Ha	Re	Displacement	Pressure	WSS	Velocity
0.0000	400.00	0.16788	−3.48 × ${10}^{-4}$	4.09 × ${10}^{-6}$	2.38 × ${10}^{-7}$
0.0000	800.00	0.13168	−2.65 × ${10}^{-4}$	4.78 × ${10}^{-6}$	3.14 × ${10}^{-7}$
0.0000	1200.0	0.11339	−2.23 × ${10}^{-4}$	4.22 × ${10}^{-6}$	3.01 × ${10}^{-7}$
4.0000	400.00	0.17336	−2.19 × ${10}^{-4}$	3.85 × ${10}^{-5}$	3.22 × ${10}^{-7}$
4.0000	800.00	0.13501	−1.94 × ${10}^{-4}$	2.76 × ${10}^{-5}$	3.87 × ${10}^{-7}$
4.0000	1200.0	0.11585	−1.73 × ${10}^{-4}$	1.69 × ${10}^{-5}$	3.52 × ${10}^{-7}$
8.0000	400.00	0.18889	1.21 × ${10}^{-4}$	1.20 × ${10}^{-4}$	5.38 × ${10}^{-7}$
8.0000	800.00	0.14453	−4.00 × ${10}^{-6}$	7.71 × ${10}^{-5}$	5.76 × ${10}^{-7}$
8.0000	1200.0	0.12294	−4.06 × ${10}^{-5}$	5.28 × ${10}^{-5}$	5.43 × ${10}^{-7}$
12.000	400.00	0.21297	6.03 × ${10}^{-4}$	1.93 × ${10}^{-4}$	8.10 × ${10}^{-7}$
12.000	800.00	0.15961	2.73 × ${10}^{-4}$	1.28 × ${10}^{-4}$	8.32 × ${10}^{-7}$
12.000	1200.0	0.13427	1.58 × ${10}^{-4}$	9.31 × ${10}^{-5}$	7.14 × ${10}^{-7}$

presents the quantitative variations in normalized displacement, pressure, WSS, and velocity magnitude measured on the upper leaflet across a range of Ha and Re numbers. As the magnetic field strength increases (i.e., higher Ha), there is a noticeable increase in leaflet displacement and WSS, particularly at lower Re. The velocity magnitude on the leaflet surface also increases with Ha, indicating enhanced structural motion under the influence of the magnetic field. Additionally, the pressure values transition from negative to positive with increasing Ha, suggesting altered loading conditions on the leaflet surface due to magnetically influenced flow behavior.

4. Conclusions

This study presents a detailed numerical analysis of heart valve behavior under stationary conditions using a fluid–structure interaction (FSI) framework that incorporates biomagnetic effects. By employing an Arbitrary Lagrangian–Eulerian (ALE) formulation, the model captures the coupled behavior of blood flow and deformable valve-like elastic walls under various magnetic field strengths, represented by the Hartmann number (Ha).

The results demonstrate that increasing the magnetic field intensity has a significant stabilizing influence on intravalvular flow. Specifically, higher Hartmann numbers suppress recirculation zones and flow separation downstream of the constriction, promoting smoother, more aligned velocity fields. This effect is particularly relevant in valve regions, where disturbed flow patterns contribute to shear-induced damage, thrombogenic risks, or calcific degeneration.

In addition, the simulations reveal that magnetic fields attenuate wall displacement and dampen fluid-induced oscillations of the valve structure. This suggests potential benefits in terms of reducing mechanical fatigue and prolonging the functional lifespan of biological or prosthetic valve tissues.

Furthermore, the pressure distribution along the centerline shows a consistent decrease in pressure downstream, with the magnitude of pressure drop moderated by increasing Hartmann numbers. At higher magnetic intensities, the damping effect leads to smoother pressure gradients, reducing localized pressure spikes that could otherwise contribute to mechanical stress and fatigue in valve structures. These findings support the hypothesis that magnetic modulation not only stabilizes flow velocity but also results in a more favorable pressure profile within the valve domain.

Critically, the wall shear stress (WSS) distribution increases in magnitude with stronger magnetic fields. Since abnormal WSS has been linked to valvular endothelial dysfunction and disease progression, the findings imply that controlled magnetic exposure could have protective hemodynamic effects in heart valve environments.

While idealized geometries were used to approximate heart valve behavior, and the flow was assumed to be two-dimensional, steady, and laminar, these simplifications inherently limit the full physiological representation of cardiac hemodynamics. In practice, blood flow through valves is three-dimensional and pulsatile, characterized by transient vortices, secondary flow structures, and time-varying wall shear stresses. Additionally, complex leaflet mechanics may be better captured through advanced anisotropic material models. Future studies should, therefore, aim to integrate patient-specific valve geometries, fully pulsatile inlet conditions, and three-dimensional flow modeling to capture transitional or turbulent behavior and provide a more realistic prediction of in vivo cardiovascular performance.

Overall, this work highlights the potential role of magnetic field manipulation in modulating heart valve hemodynamics, reducing pathological flow features, and improving long-term biomechanical outcomes in valvular heart disease.