Heat Transfer and Pressure Drop in Fully Developed Turbulent Flows of Graphene Nanoplatelets–Silver/Water Nanofluids
Abstract
:1. Introduction
2. Nanofluid Properties
3. Physical Model
4. Empirical Expressions
5. Governing Equations for CFD Simulation
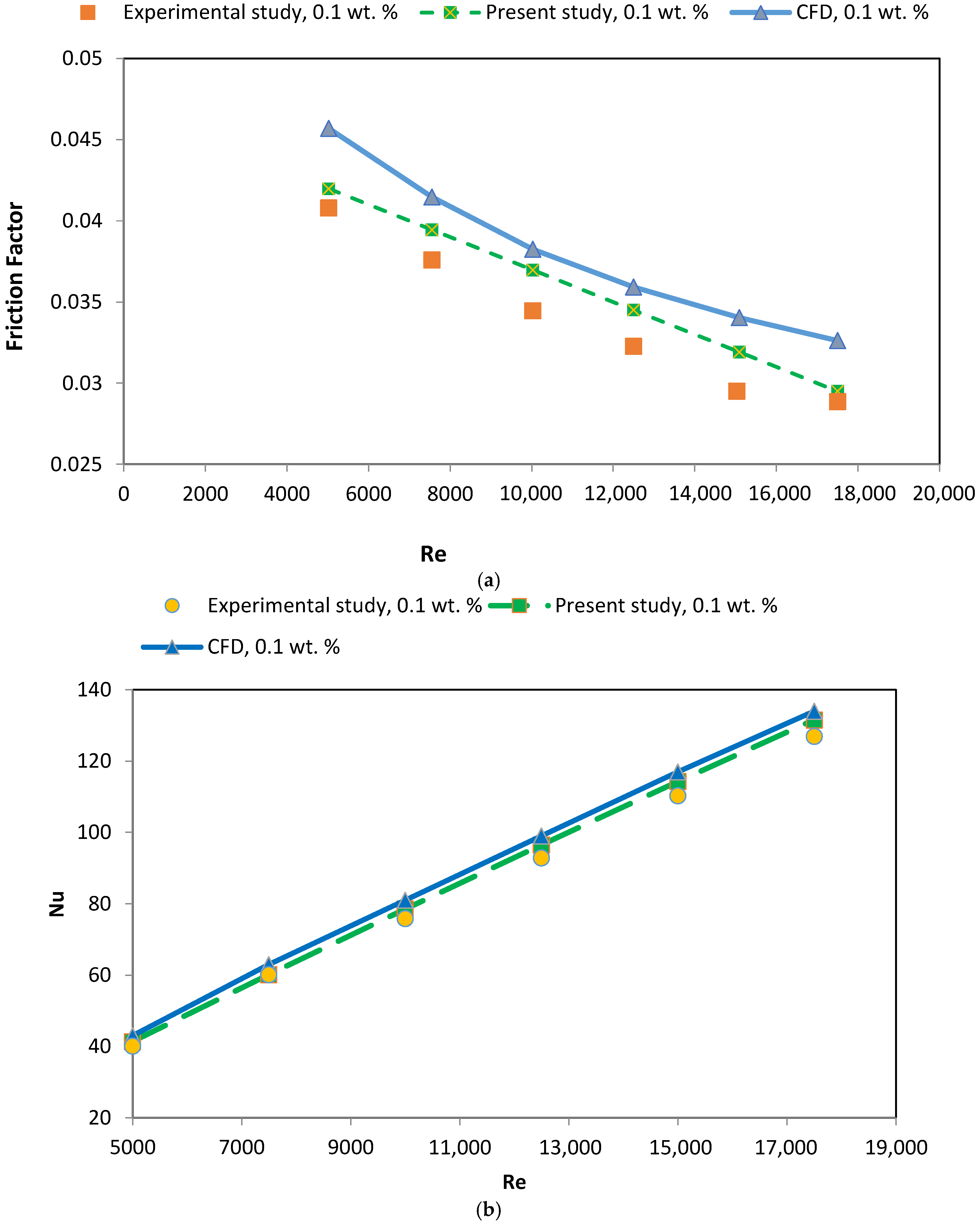
6. Validation
Validation of Heat Transfer for Graphene Nanoplatelets–Silver/Wate Nanofluids
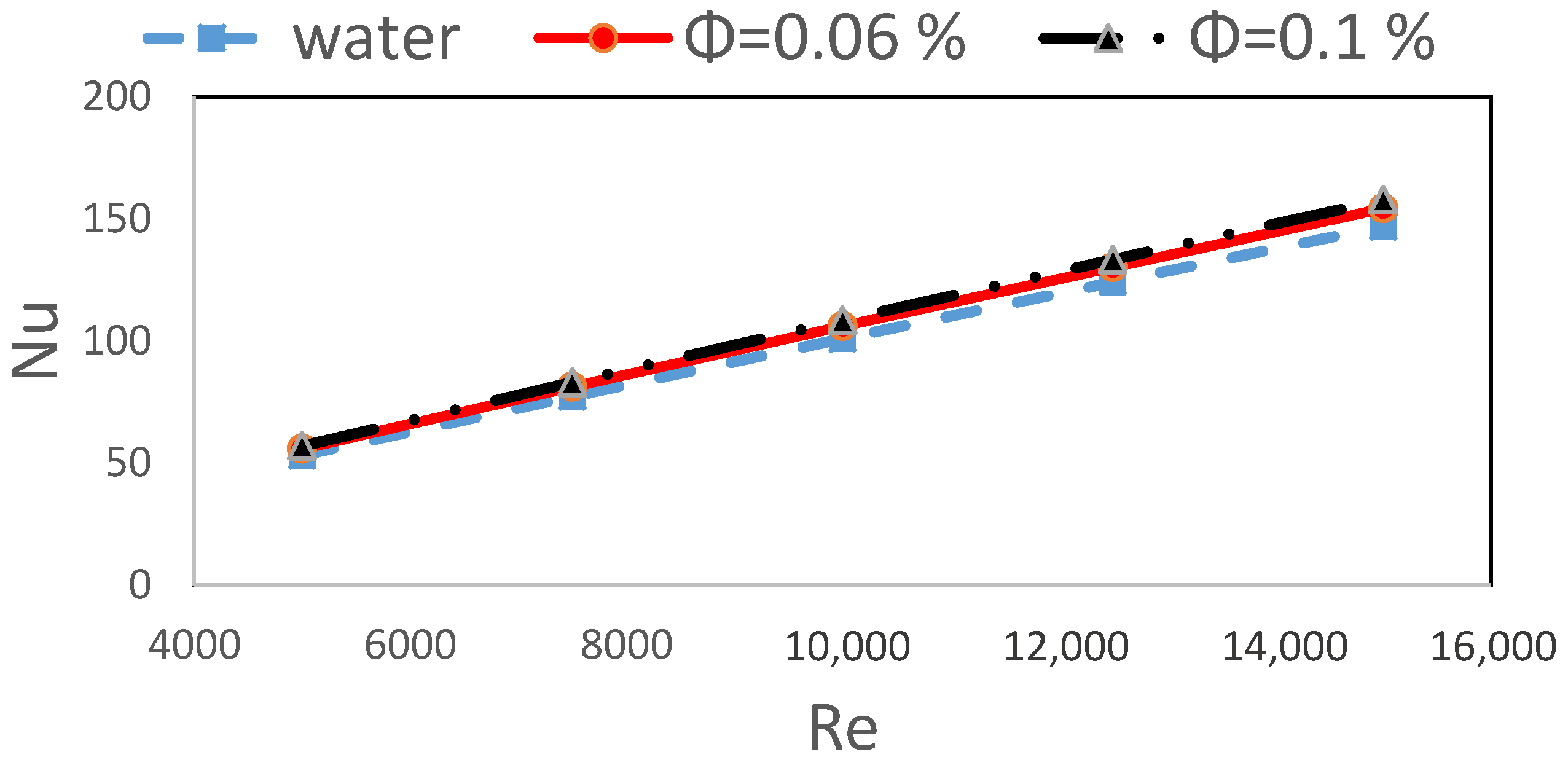
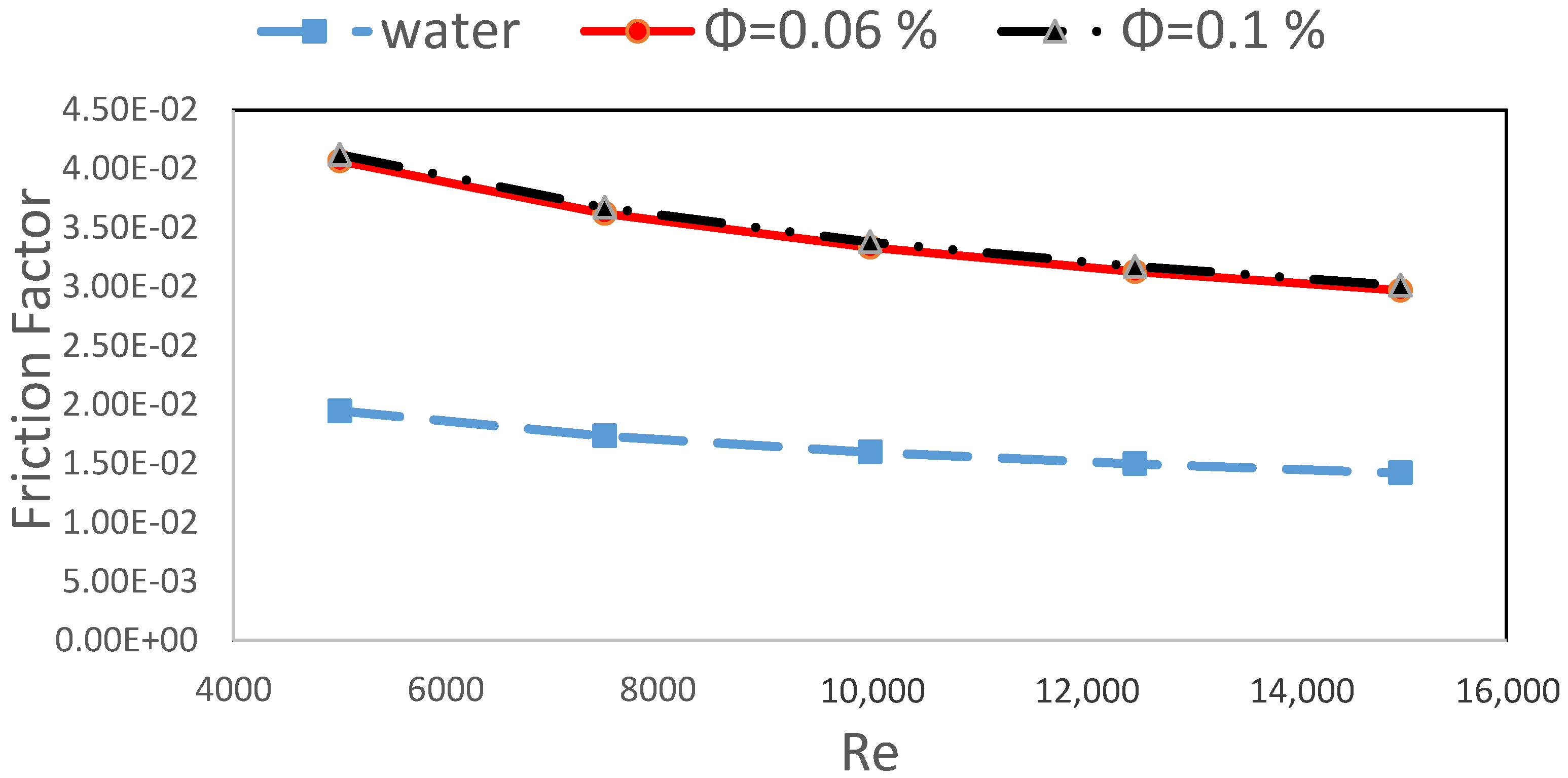
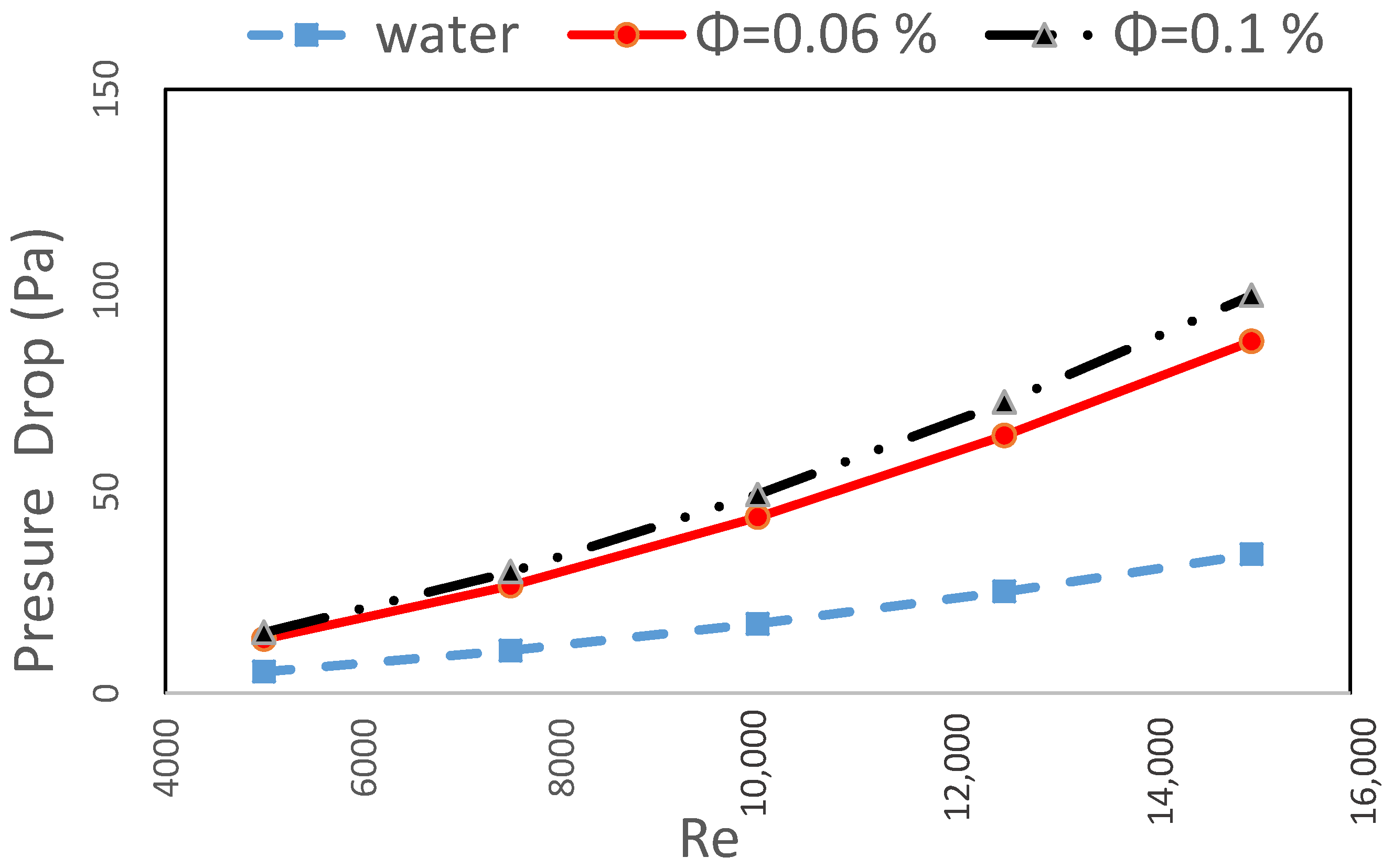
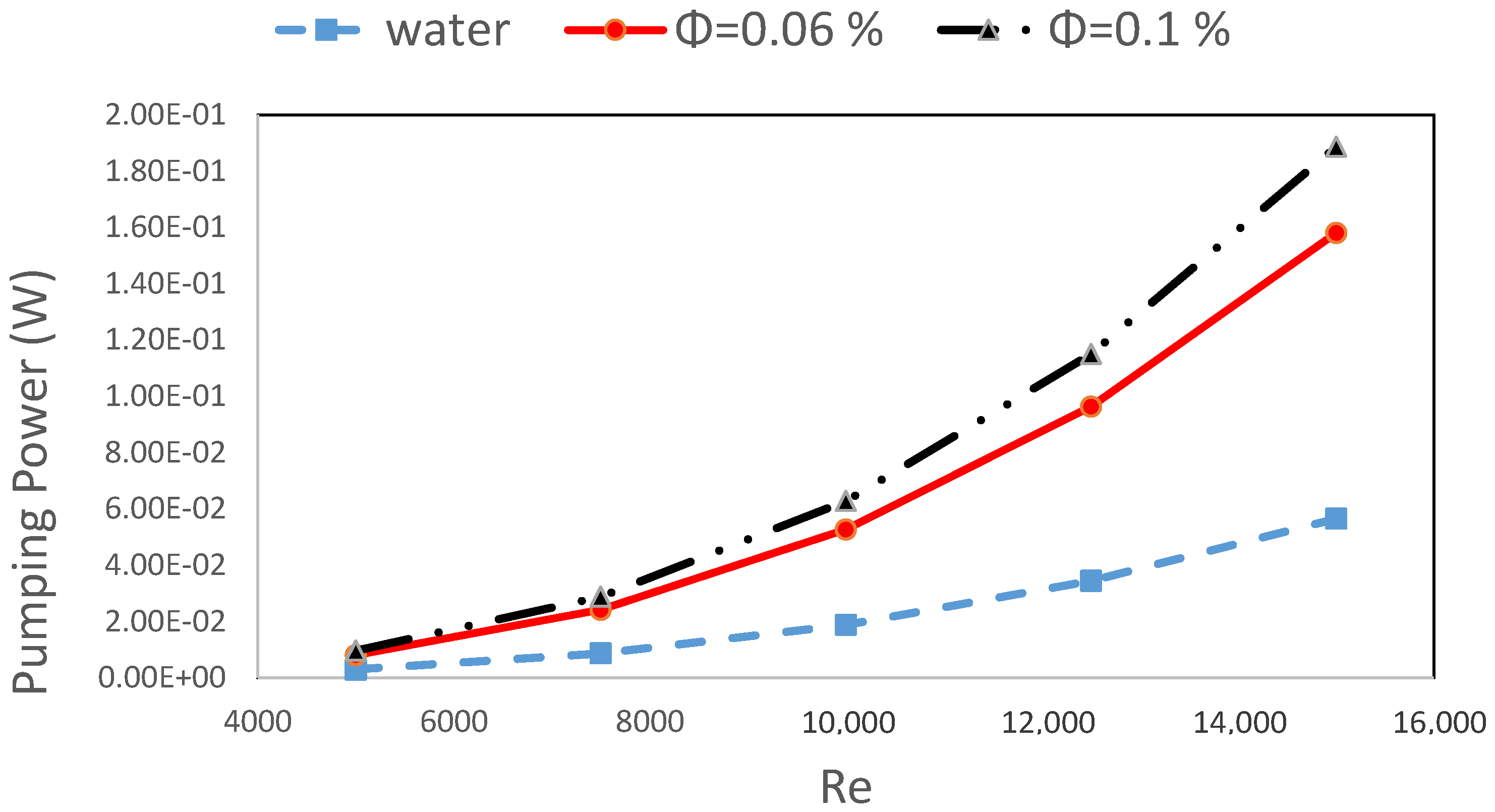
7. Results and Discussion
- (1)
- The Brownian motion of nanosheets and the associated micro-scale fluid motion.
- (2)
- An increase in the overall thermal conductivity of the suspension as a result of the high thermal conductivity of nanosheets suspended in the carrying fluid.
- (3)
- A rise in the effective heat transfer surface area among the dispersed nanosheets and the base fluid [16].
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| A | Area (m) |
| H | Depth of the channel (m) |
| f | Friction factor |
| h | Heat transfer coefficient (W·m−2·K−1) |
| Dh | Hydraulic diameter (m) |
| l | Length of each surface in contact with the aqueous body (m) |
| L | Length of the channel (m) |
| Nu | Nusselt number |
| Pr | Prandtl number |
| Pe | Peclet number |
| p | Pressure (Pa) |
| Pp | Pumping power (W) |
| Re | Reynolds number |
| Cp | Specific heat capacity (J·kg−1·K−1) |
| T | Temperature (K) |
| κ | Thermal conductivity (W·m−1·K−1) turbulence |
| V | Velocity (m·s−1) |
| u | Velocity, x-component (m·s−1) |
| v | Velocity, y-component (m·s−1) |
| P | Wetted perimeter (m) |
| W | Width of the channel (m) |
Greek Symbols
Density (kg·m−3) | |
| μ | Dynamic viscosity (Pa·s) |
| υ | Kinematics viscosity (m²·s−1) |
| α | Thermal diffusivity (m²·s−1) |
| κ | Thermal conductivity (m²·s−2) |
| ε | Turbulence dissipation (m²·s−3) |
| η | Thermal performance factor |
Weight percentage of nanosheets |
Subscripts
| bf | Base fluid |
| m | Mixture |
| i | Indices |
| t | Turbulence |
References
- Huminic, G.; Huminic, A. Application of nanofluids in heat exchangers: a review. Renew. Sustain. Energy Rev. 16, 5625–5638. [CrossRef]
- Mehrizi, A.A.; Farhadi, M.; Sedighi, K.; Delavar, M.A. Effect of fin position and porosity on heat transfer improvement in a plate porous media heat exchanger. J. Taiwan Inst. Chem. Eng. 2013, 44, 420–431. [Google Scholar] [CrossRef]
- Gut, J.A.W.; Fernandes, R.; Pinto, J.M.; Tadini, C.C. Thermal model validation of plate heat exchangers with generalized configurations. Chem. Eng. Sci. 2004, 59, 4591–4600. [Google Scholar] [CrossRef]
- Dwivedi, A.K.; Das, S.K. Dynamics of plate heat exchangers subject to flow variations. Int. Heat Mass Transf. 2007, 50, 2733–2743. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab.: Lemont, IL, USA, 1995.
- Safaei, M.; Mahian, O.; Garoosi, F.; Hooman, K.; Karimipour, A.; Kazi, S.; Gharehkhani, S. Investigation of micro-and nanosized particle erosion in a 90° pipe bend using a two-phase discrete phase model. Sci. World J. 2014, 2014, 740578. [Google Scholar] [CrossRef] [PubMed]
- Safaei, M.R.; Togun, H.; Vafai, K.; Kazi, S.N.; Badarudin, A. Investigation of Heat Transfer Enhancement in a Forward-Facing contracting Channel using FMWCNT Nanofluids. Numer. Heat Transf. 2014, 66, 1321–1340. [Google Scholar] [CrossRef]
- Goodarzi, M.; Safaei, M.R.; Vafai, K.; Ahmadi, G.; Dahari, M.; Kazi, S.N.; Jomhari, N. Investigation of nanofluid mixed convection in a shallow cavity using a two-phase mixture model. Int. J. Therm. Sci. 2014, 75, 204–220. [Google Scholar] [CrossRef]
- Wu, J.M.; Zhao, J. A review of nanofluid heat transfer and critical heat flux enhancement—Research gap to engineering application. Prog. Nucl. Energy 2013, 66, 13–24. [Google Scholar] [CrossRef]
- Sonawane, S.S.; Khedkar, R.S.; Wasewar, K.L. Study on concentric tube heat exchanger heat transfer performance using Al2O3-water based nanofluids. Int. Commun. Heat Mass Transf. 2013, 49, 60–68. [Google Scholar] [CrossRef]
- Pandey, S.D.; Nema, V.K. Experimental analysis of heat transfer and friction factor of nanofluid as a coolant in a corrugated plate heat exchanger. Exp. Therm. Fluid Sci. 2012, 38, 248–256. [Google Scholar] [CrossRef]
- Taws, M.; Nguyen, C.T.; Galanis, N.; Gherasim, I. Experimental Investigation of Nanofluid Heat Transfer in a Plate Heat Exchanger, Proceedings of the ASME 2012 Heat Transfer Summer Conference Collocated with the ASME 2012 Fluids Engineering Division Summer Meeting and the ASME 2012 10th International Conference on Nanochannels, Microchannels, and Minichannels, Rio Grande, Puerto Rico, 8–12 July 2012; American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 1–8.
- Elias, M.M.; Saidur, R.; Rahim, N.A.; Sohel, M.R.; Mahbubul, I.M. Performance Investigation of a Plate Heat Exchanger Using Nanofluid with Different Chevron Angle. Adv. Mater. Res. 2014, 832, 254–259. [Google Scholar] [CrossRef]
- Sarafraz, M.M.; Hormozi, F. Heat transfer, pressure drop and fouling studies of multi-walled carbon nanotube nano-fluids inside a plate heat exchanger. Exp. Therm. Fluid Sci. 2016, 72, 1–11. [Google Scholar] [CrossRef]
- Goodarzi, M.; Kherbeet, A.S.; Afrand, M.; Sadeghinezhad, E.; Mehrali, M.; Zahedi, P.; Wongwises, S.; Dahari, M. Investigation of heat transfer performance and friction factor of a counter-flow double-pipe heat exchanger using nitrogen-doped, graphene-based nanofluids. Int. Commun. Heat Mass Transf. 2016, 76, 16–23. [Google Scholar] [CrossRef]
- Goodarzi, M.; Amiri, A.; Goodarzi, M.S.; Safaei, M.R.; Karimipour, A.; Languri, E.M.; Dahari, M. Investigation of heat transfer and pressure drop of a counter flow corrugated plate heat exchanger using MWCNT based nanofluids. Int. Commun. Heat Mass Transf. 2015, 66, 172–179. [Google Scholar] [CrossRef]
- Hassan, M.; Sadri, R.; Ahmadi, G.; Dahari, M.B.; Kazi, S.N.; Safaei, M.R.; Sadeghinezhad, E. Numerical study of entropy generation in a flowing nanofluid used in micro-and minichannels. Entropy 2013, 15, 144–155. [Google Scholar] [CrossRef]
- Yarmand, H.; Gharehkhani, S.; Ahmadi, G.; Shirazi, S.F.S.; Baradaran, S.; Montazer, E.; Zubir, M.N.M.; Alehashem, M.S.; Kazi, S.N.; Dahari, M. Graphene nanoplatelets-silver hybrid nanofluids for enhanced heat transfer. Energy Convers. Manag. 2015, 100, 419–428. [Google Scholar] [CrossRef]
- Togun, H.; Ahmadi, G.; Abdulrazzaq, T.; Shkarah, A.J.; Kazi, S.; Badarudin, A.; Safaei, M.R. Thermal performance of nanofluid in ducts with double forward-facing steps. J. Taiwan Inst. Chem. Eng. 2015, 47, 28–42. [Google Scholar] [CrossRef]
- Sadeghinezhad, E.; Mehrali, M.; Tahan Latibari, S.; Mehrali, M.; Kazi, S.N.; Oon, C.S.; Metselaar, H.S.C. Experimental investigation of convective heat transfer using graphene nanoplatelet based nanofluids under turbulent flow conditions. Ind. Eng. Chem. Res. 2014, 53, 12455–12465. [Google Scholar] [CrossRef]
- Yarmand, H.; Ahmadi, G.; Gharehkhani, S.; Kazi, S.N.; Safaei, M.R.; Sadat Alehashem, M.; Mahat, A.B. Entropy generation during turbulent flow of zirconia-water and other nanofluids in a square cross section tube with a constant heat flux. Entropy 2014, 16, 6116–6132. [Google Scholar] [CrossRef]
- Yarmand, H.; Gharehkhani, S.; Kazi, S.N.; Sadeghinezhad, E.; Safaei, M.R. Numerical investigation of heat transfer enhancement in a rectangular heated pipe for turbulent nanofluid. Sci. World J. 2014, 2014, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Safaei, M.R.; Goshayshi, H.R.; Saeedi Razavi, B.; Goodarzi, M. Numerical investigation of laminar and turbulent mixed convection in a shallow water-filled enclosure by various turbulence methods. Sci. Res. Essays 2011, 6, 4826–4838. [Google Scholar]
- Safaei, M.R.; Goodarzi, M.; Mohammadi, M. Numerical modeling of turbulence mixed convection heat transfer in air filled enclosures by finite volume method. Int. J. Multiphys. 2011, 5, 307–324. [Google Scholar] [CrossRef]
- Ray, D.R.; Das, D.K.; Vajjha, R.S. Experimental and numerical investigations of nanofluids performance in a compact minichannel plate heat exchanger. Int. J. Hea Mass Transf. 2014, 71, 732–746. [Google Scholar] [CrossRef]
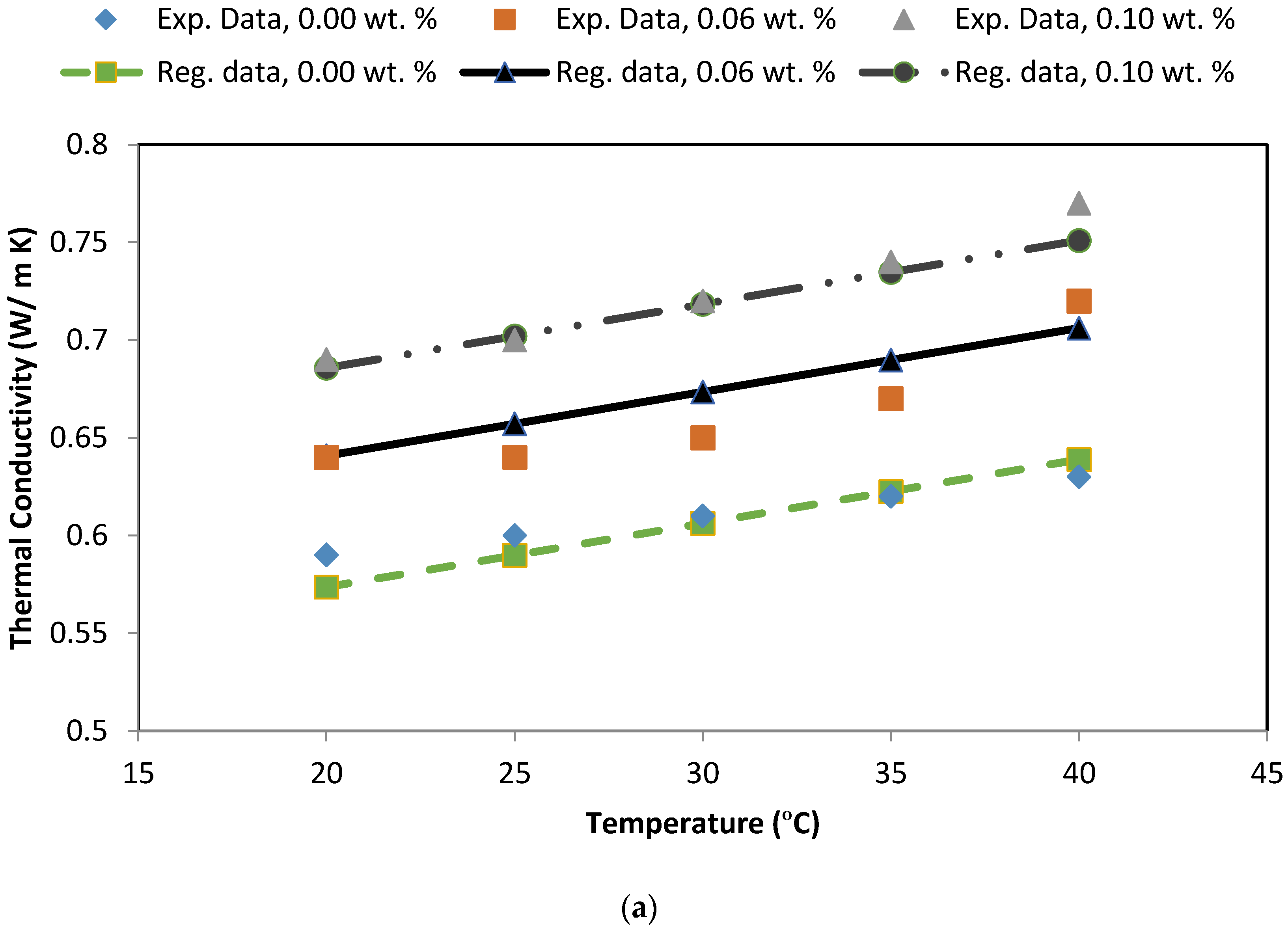
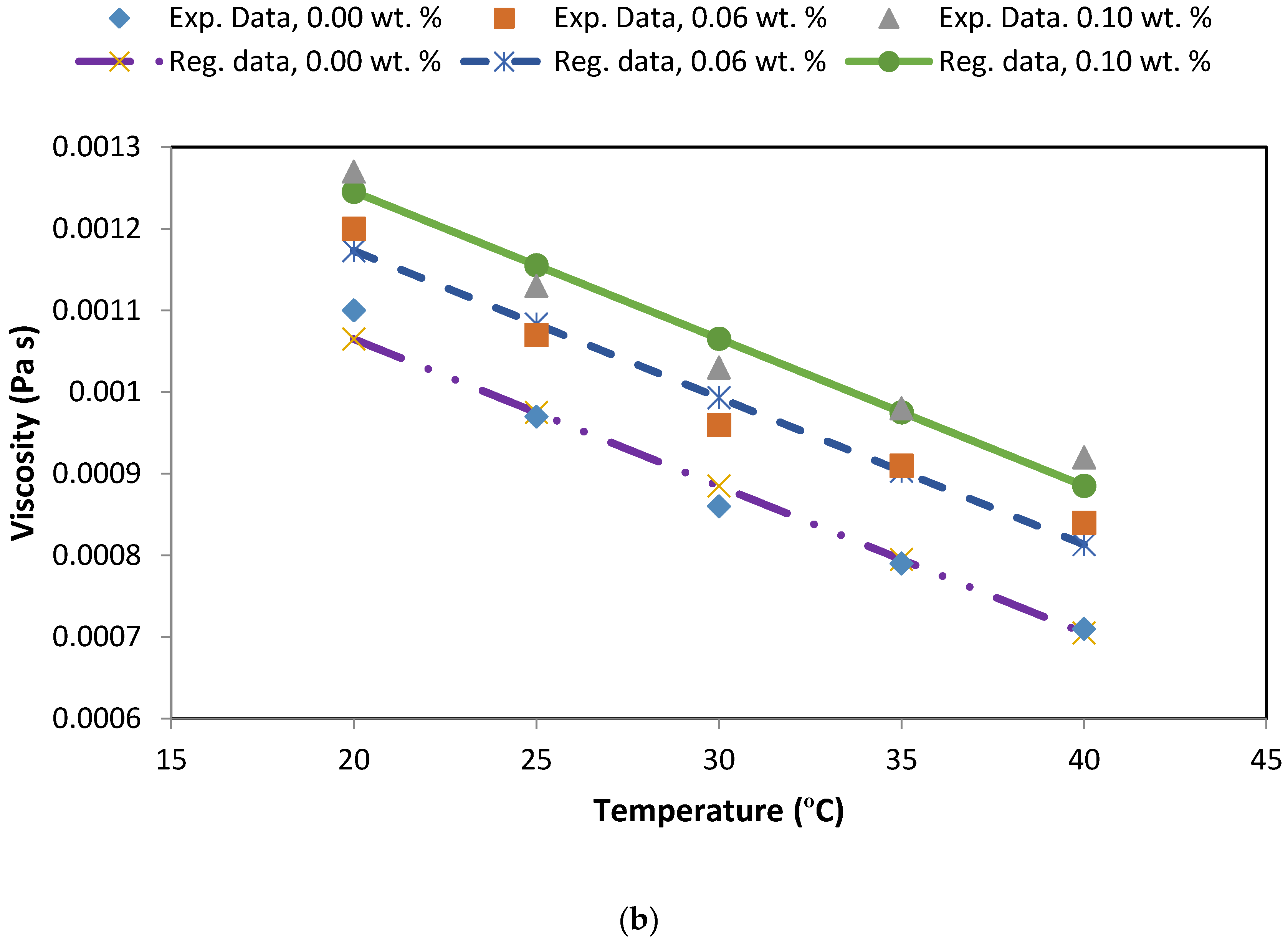
| Thermophysical Properties | Weight Percentage | 20 °C | 25 °C | 30 °C | 35 °C | 40 °C |
|---|---|---|---|---|---|---|
| Density (Kg/m3) | φ = 0.00% | 997.91 | 996.68 | 995.29 | 993.68 | 991.99 |
| φ = 0.06% | 998.5 | 997.40 | 996.01 | 994.45 | 992.53 | |
| φ = 0.10% | 998.90 | 997.80 | 996.30 | 994.67 | 992.93 | |
| Thermal Conductivity (W/m·K) | φ = 0.00% | 0.59 | 0.60 | 0.61 | 0.62 | 0.63 |
| φ = 0.06% | 0.64 | 0.64 | 0.65 | 0.67 | 0.72 | |
| φ = 0.10% | 0.69 | 0.70 | 0.72 | 0.74 | 0.77 | |
| Viscosity (Pa·s) | φ = 0.00% | 1.1 × 10−3 | 9.7 × 10−4 | 8.6 × 10−4 | 7.9 × 10−4 | 7.1 × 10−4 |
| φ = 0.06% | 1.20 × 10−3 | 1.07 × 10−3 | 9.6 × 10−4 | 9.1 × 10−4 | 8.4 × 10−4 | |
| φ = 0.10% | 1.27 × 10−3 | 1.13 × 10−3 | 1.03 × 10−3 | 9.8 × 10−4 | 9.2 × 10−4 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safaei, M.R.; Ahmadi, G.; Goodarzi, M.S.; Safdari Shadloo, M.; Goshayeshi, H.R.; Dahari, M. Heat Transfer and Pressure Drop in Fully Developed Turbulent Flows of Graphene Nanoplatelets–Silver/Water Nanofluids. Fluids 2016, 1, 20. https://doi.org/10.3390/fluids1030020
Safaei MR, Ahmadi G, Goodarzi MS, Safdari Shadloo M, Goshayeshi HR, Dahari M. Heat Transfer and Pressure Drop in Fully Developed Turbulent Flows of Graphene Nanoplatelets–Silver/Water Nanofluids. Fluids. 2016; 1(3):20. https://doi.org/10.3390/fluids1030020
Chicago/Turabian StyleSafaei, Mohammad Reza, Goodarz Ahmadi, Mohammad Shahab Goodarzi, Mostafa Safdari Shadloo, Hamid Reza Goshayeshi, and Mahidzal Dahari. 2016. "Heat Transfer and Pressure Drop in Fully Developed Turbulent Flows of Graphene Nanoplatelets–Silver/Water Nanofluids" Fluids 1, no. 3: 20. https://doi.org/10.3390/fluids1030020






