Boundary Layer Flow and Heat Transfer of FMWCNT/Water Nanofluids over a Flat Plate
Abstract
:1. Introduction
2. Governing Equations for Nanofluids Heat Transfer
3. Nanofluid Properties
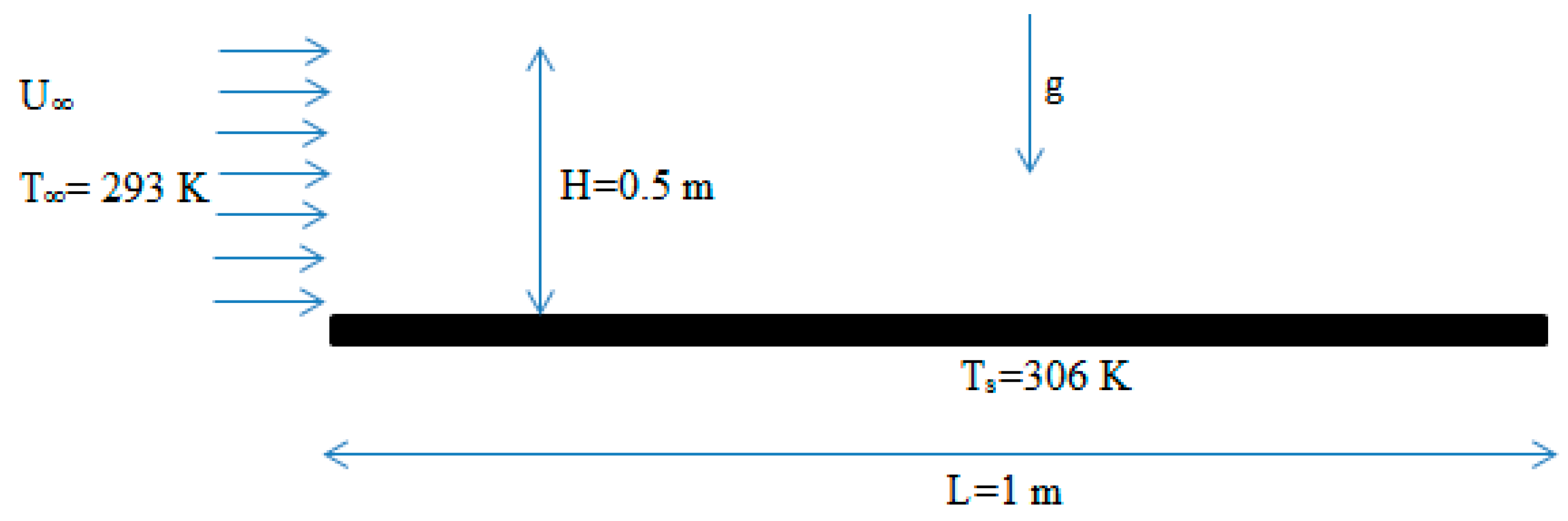
4. Boundary Conditions
5. Numerical Procedure
6. Validation
7. Grid Independence
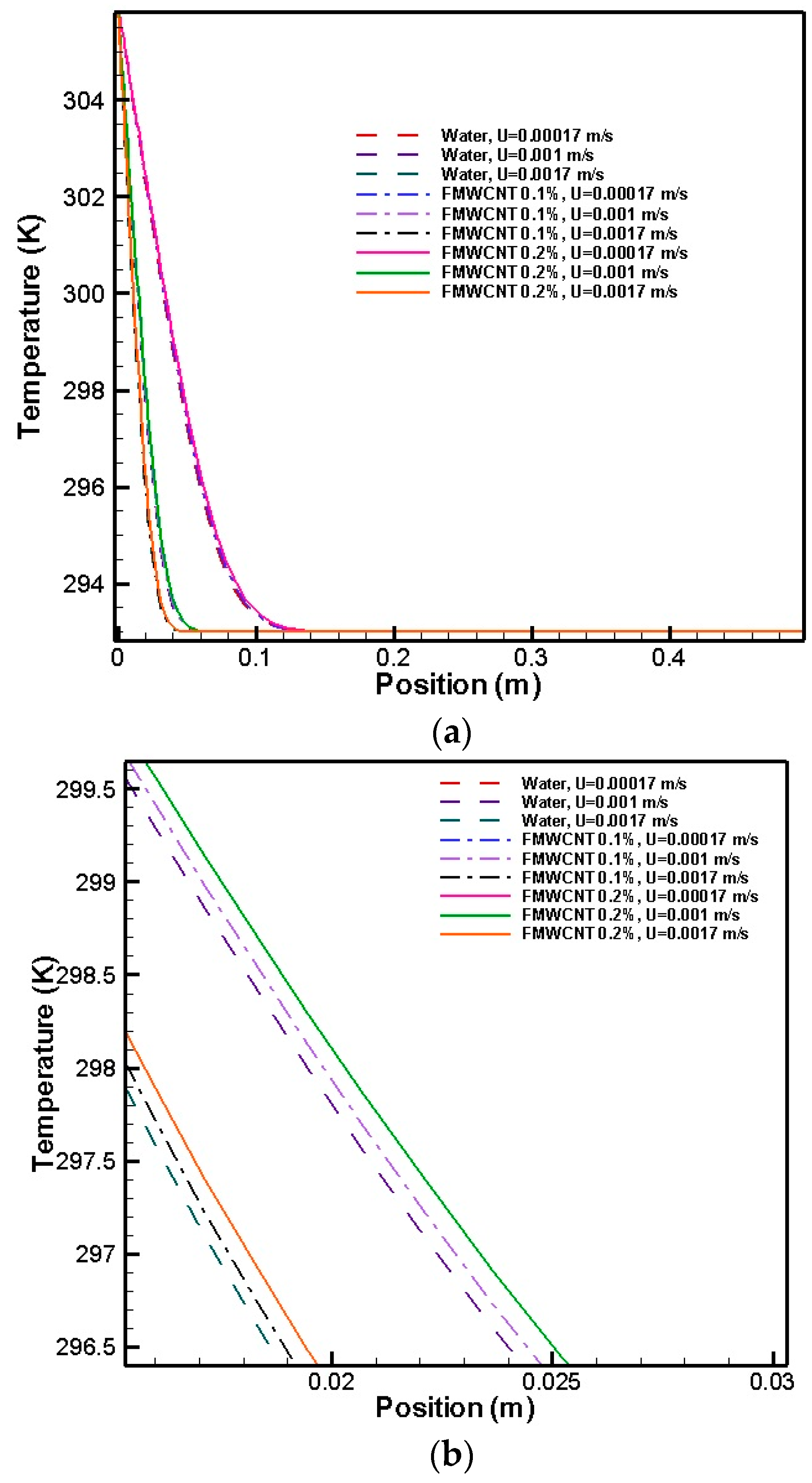
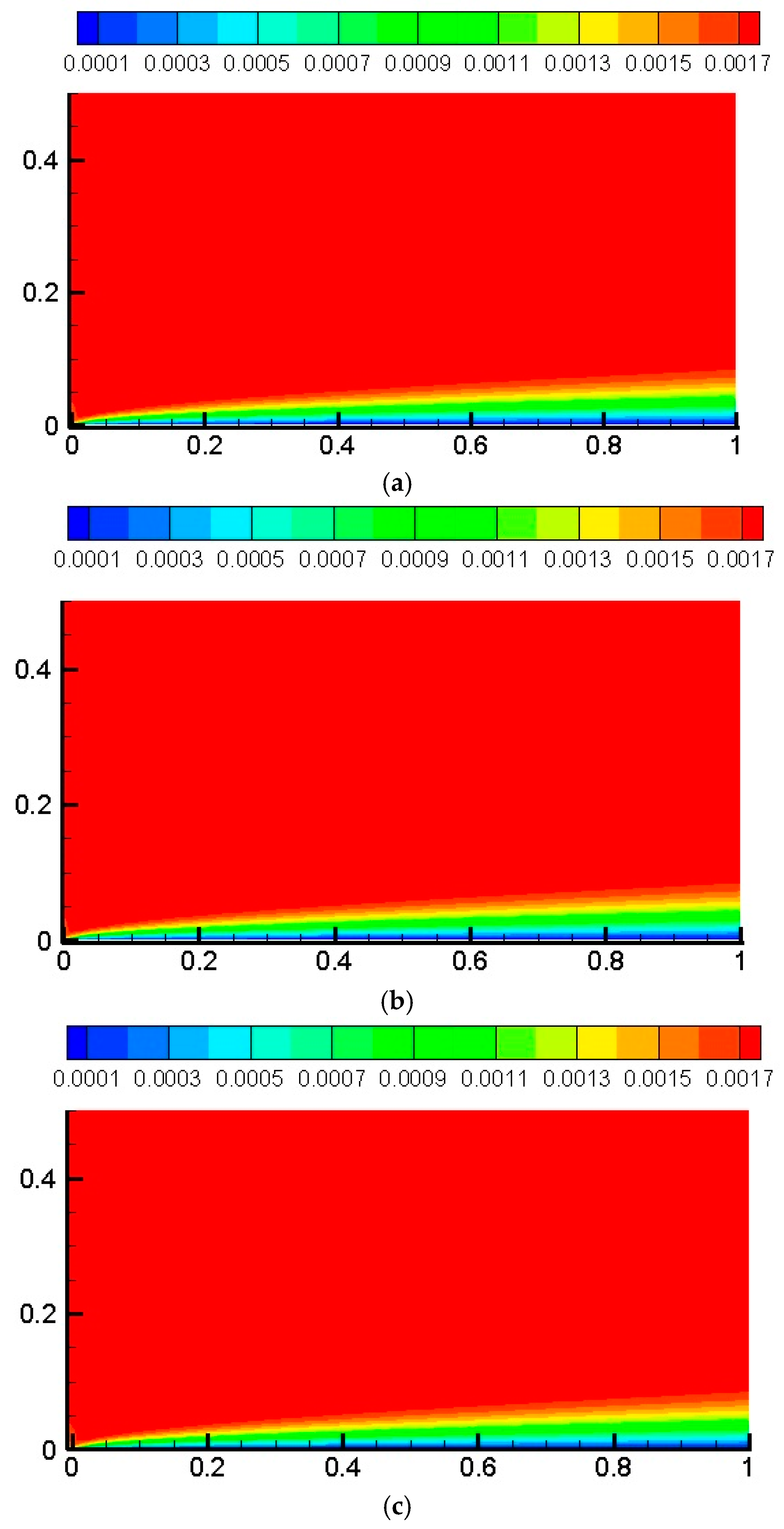
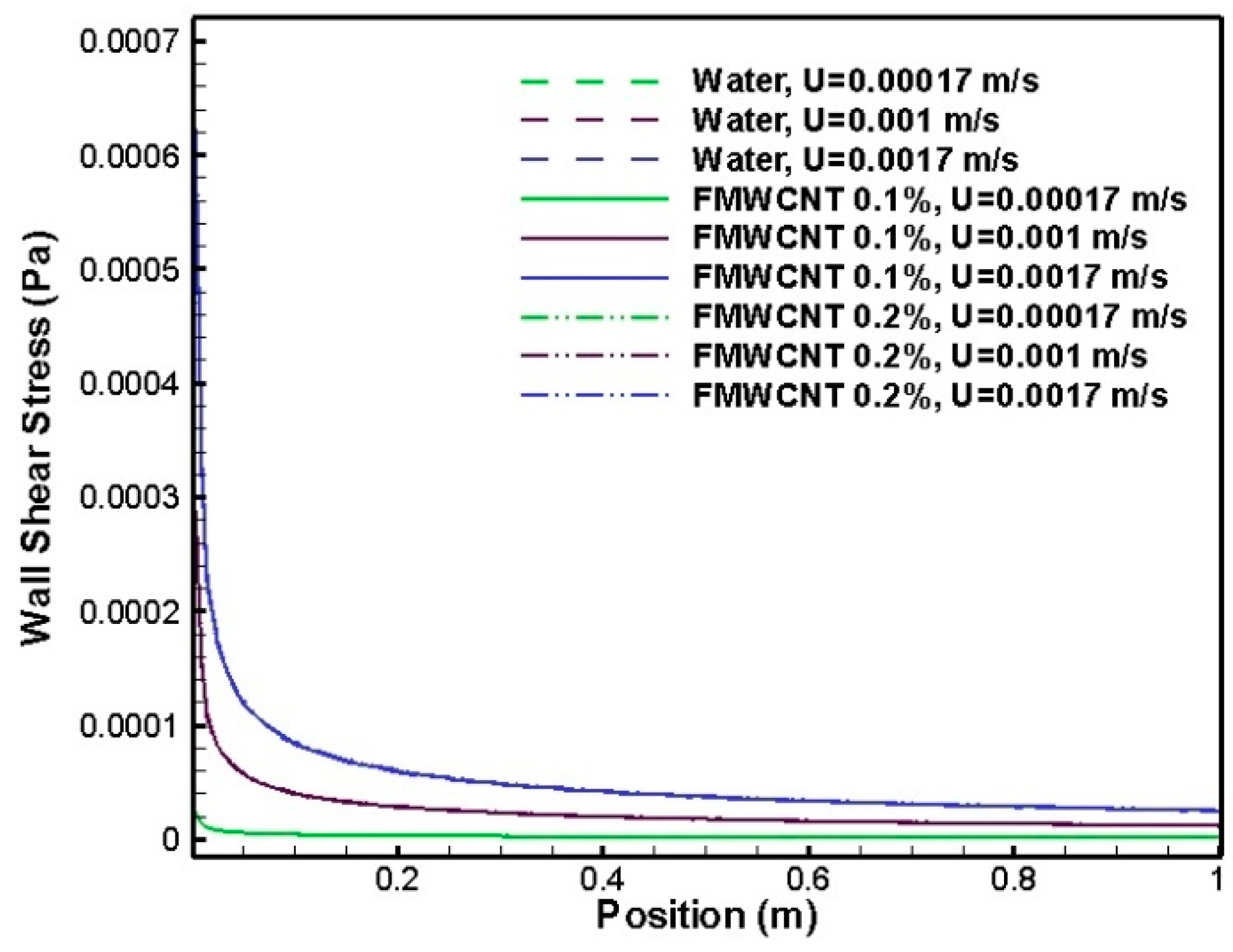
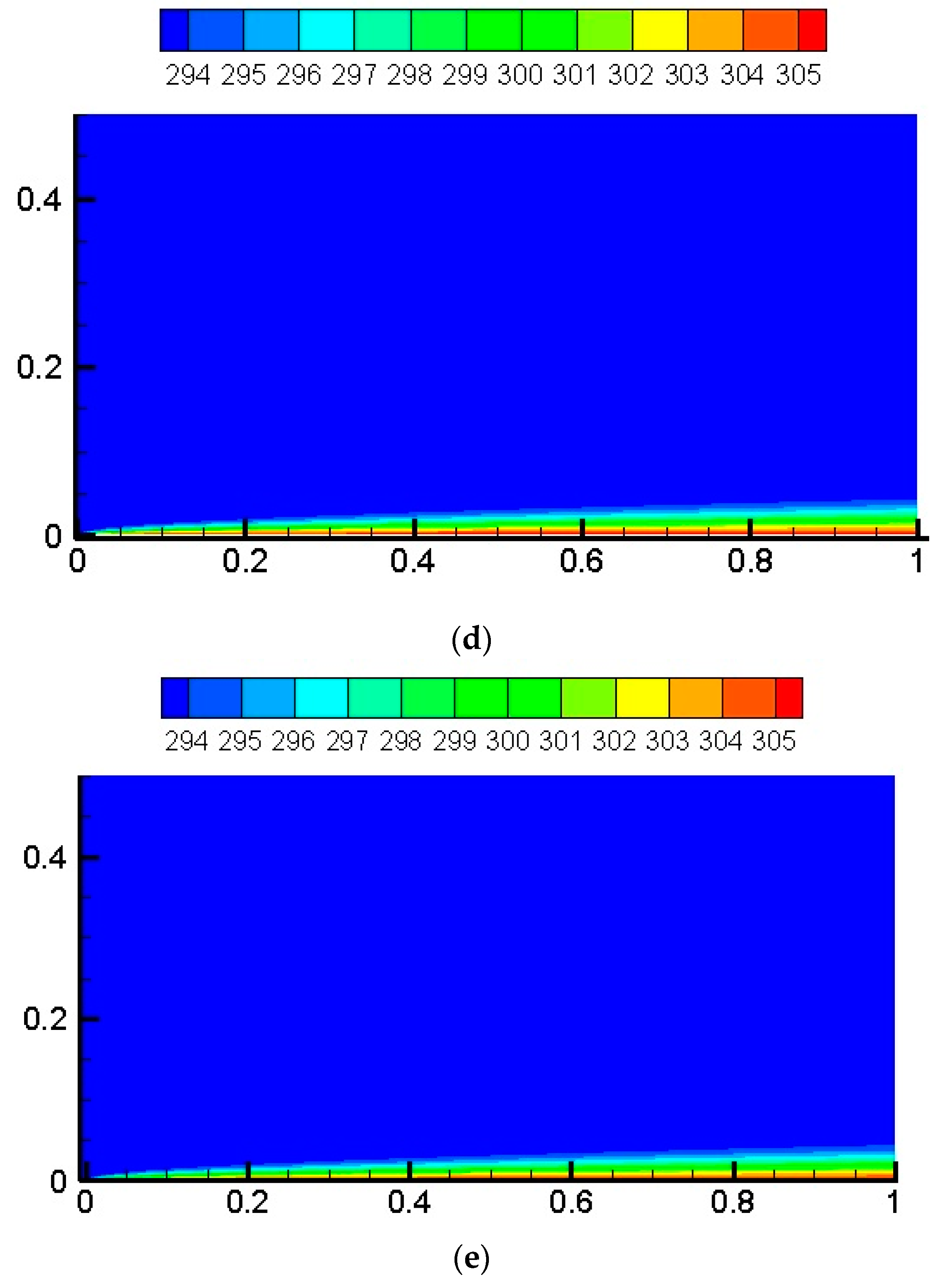
8. Results and Discussion
9. Conclusions
- (1)
- The Nusselt number of a nanofluid is augmented by increasing the weight percentage of nanotubes and the free stream velocity.
- (2)
- For the range of concentration less than 0.2% FMWCNT, the effect of the nanotube weight percentage on wall shear stress is insignificant.
- (3)
- Under similar conditions, the boundary layer thickness increases as free stream velocity decreases or particle volume fraction increases.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| T | temperature (K) |
| k | thermal conductivity (W·m−2·K−1) |
| t | time (s) |
| P | pressure (Pa) |
| Cp | specific heat capacity (J·kg−1·K−1) |
| u, v | Velocity components (m·s−1) |
| Greek Symbols | |
| δ | Boundary layer thickness (m) |
| ρ | Density (kg·m−3) |
| μ | Dynamic viscosity (Pa·s) |
| υ | Kinematic viscosity (m2·s−1) |
| ϕ | Weight percentage of nanotubes |
| Subscripts | |
| Bf | Base fluid |
| nf | Nanofluid |
| ∞ | Infinity |
References
- Hassan, M.; Sadri, R.; Ahmadi, G.; Dahari, M.B.; Kazi, S.N.; Safaei, M.R.; Sadeghinezhad, E. Numerical Study of Entropy Generation in a Flowing Nanofluid Used in Micro-and Minichannels. Entropy 2013, 15, 144–155. [Google Scholar] [CrossRef]
- Asadian, A.M.; Abouali, O.; Yaghoubi, M.; Ahmadi, G. The Effect of Temperature Dependent Electrical Conductivity on the MHD Natural Convection of Al2O3–Water Nanofluid in a Rectangular Enclosure. In Proceedings of the ASME 2014 12th International Conference on Nanochannels, Microchannels and Minichannels, Chicago, IL, USA, 3–7 August 2014.
- Herwig, H.; Hausner, O. Critical view on “new results in micro-fluid mechanics”: An example. Int. J. Heat Mass Transf. 2003, 46, 935–937. [Google Scholar] [CrossRef]
- Goodarzi, M.; Safaei, M.R.; Vafai, K.; Ahmadi, G.; Dahari, M.; Kazi, S.N.; Jomhari, N. Investigation of nanofluid mixed convection in a shallow cavity using a two-phase mixture model. Int. J. Therm. Sci. 2014, 75, 204–220. [Google Scholar] [CrossRef]
- Yarmand, H.; Ahmadi, G.; Gharehkhani, S.; Kazi, S.N.; Safaei, M.R.; Alehashem, M.S.; Mahat, A.B. Entropy generation during turbulent flow of zirconia-water and other nanofluids in a square cross section tube with a constant heat flux. Entropy 2014, 16, 6116–6132. [Google Scholar] [CrossRef]
- Goshayeshi, H.R.; Goodarzi, M.; Safaei, M.R.; Dahari, M. Experimental study on the effect of inclination angle on heat transfer enhancement of a ferrofluid in a closed loop oscillating heat pipe under magnetic field. Exp. Therm. Fluid Sci. 2016, 74, 265–270. [Google Scholar] [CrossRef]
- Safaei, M.R.; Ahmadi, G.; Goodarzi, M.S.; Safdari Shadloo, M.; Goshayeshi, H.R.; Dahari, M. Heat Transfer and Pressure Drop in Fully Developed Turbulent Flows of Graphene Nanoplatelets–Silver/Water Nanofluids. Fluids 2016, 1, 20. [Google Scholar] [CrossRef]
- Malvandi, A.; Ganji, D.D.; Hedayati, F.; Yousefi Rad, E. An analytical study on entropy generation of nanofluids over a flat plate. Alex. Eng. J. 2013, 52, 595–604. [Google Scholar] [CrossRef]
- Ahmad, S.; Pop, I. Mixed convection boundary layer flow from a vertical flat plate embedded in a porous medium filled with nanofluids. Int. Commun. Heat Mass Transf. 2010, 37, 987–991. [Google Scholar] [CrossRef]
- Hamad, M.A.A.; Pop, I.; Md Ismail, A.I. Magnetic field effects on free convection flow of a nanofluid past a vertical semi-infinite flat plate. Nonlinear Anal. Real World Appl. 2011, 12, 1338–1346. [Google Scholar] [CrossRef]
- Malvandi, A.; Hedayati, F.; Ganji, D.D. Slip effects on unsteady stagnation point flow of a nanofluid over a stretching sheet. Powder Technol. 2014, 253, 377–384. [Google Scholar] [CrossRef]
- Safaei, M.R.; Gooarzi, M.; Akbari, O.A.; Shadloo, M.S.; Dahari, M. Performance Evaluation of Nanofluids in an Inclined Ribbed Microchannel for Electronic Cooling Applications. Available online: http://www.intechopen.com/books/electronics-cooling/performance-evaluation-of-nanofluids-in-an-inclined-ribbed-microchannel-for-electronic-cooling-appli (accessed on 20 September 2016).
- Bejan, A. Convection Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 4. [Google Scholar]
- Aboulhasan Alavi, S.M.; Safaei, M.R.; Mahian, O.; Goodarzi, M.; Yarmand, H.; Dahari, M.; Wongwises, S. A Hybrid Finite-Element/Finite-Difference Scheme for Solving the 3-D Energy Equation in Transient Nonisothermal Fluid Flow over a Staggered Tube Bank. Numer. Heat Transf. Part B Fundam. 2015, 68, 169–183. [Google Scholar] [CrossRef]
- Goodarzi, M.; Safaei, M.R.; Karimipour, A.; Hooman, K.; Dahari, M.; Kazi, S.N.; Sadeghinezhad, E. Comparison of the finite volume and lattice boltzmann methods for solving natural convection heat transfer problems inside cavities and enclosures. Abstr. Appl. Anal. 2014, 2014, 762184. [Google Scholar] [CrossRef]
- Nikkhah, Z.; Karimipour, A.; Safaei, M.R.; Forghani-Tehrani, P.; Goodarzi, M.; Dahari, M.; Wongwises, S. Forced convective heat transfer of water/functionalized multi-walled carbon nanotube nanofluids in a microchannel with oscillating heat flux and slip boundary condition. Int. Commun. Heat Mass Transf. 2015, 68, 69–77. [Google Scholar] [CrossRef]
- Amrollahi, A.; Rashidi, A.M.; Lotfi, R.; Emami Meibodi, M.; Kashefi, K. Convection heat transfer of functionalized MWNT in aqueous fluids in laminar and turbulent flow at the entrance region. Int. Commun. Heat Mass Transf. 2010, 37, 717–723. [Google Scholar] [CrossRef]
- Safaei, M.R.; Togun, H.; Vafai, K.; Kazi, S.; Badarudin, A. Investigation of heat transfer enhancement in a forward-facing contracting channel using FMWCNT nanofluids. Numer. Heat Transf. Part A 2014, 66, 1321–1340. [Google Scholar] [CrossRef]
- Wasistho, B.; Geurts, B.; Kuerten, J. Simulation techniques for spatially evolving instabilities in compressible flow over a flat plate. Comput. Fluids 1997, 26, 713–739. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical heat transfer and fluid flow, Series in Computational Methods in Mechanics and Thermal Sciences; Hemisphere Publishing Corporation: Washington, DC, USA, 1980. [Google Scholar]
- Safaei, M.R.; Goodarzi, M.; Mohammadi, M. Numerical modeling of turbulence mixed convection heat transfer in air filled enclosures by finite volume method. Int. J. Multiphys. 2011, 5, 307–324. [Google Scholar] [CrossRef]
- Rahmanian, B.; Safaei, M.R.; Kazi, S.N.; Ahmadi, G.; Oztop, H.F.; Vafai, K. Investigation of pollutant reduction by simulation of turbulent non-premixed pulverized coal combustion. Appl. Therm. Eng. 2014, 73, 1222–1235. [Google Scholar] [CrossRef]
- Togun, H.; Ahmadi, G.; Abdulrazzaq, T.; Shkarah, A.J.; Kazi, S.; Badarudin, A.; Safaei, M. Thermal performance of nanofluid in ducts with double forward-facing steps. J. Taiwan Inst. Chem. Eng. 2015, 47, 28–42. [Google Scholar] [CrossRef]
- Karimipour, A.; Afrand, M.; Akbari, M.; Safaei, M.R. Simulation of Fluid Flow and Heat Transfer in the Inclined Enclosure. Int. J. Mech. Aerosp. Eng. 2012, 6, 86–91. [Google Scholar]
- Schlichting, H. Boundary-Layer Theory; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- White, F.M.; Corfield, I. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 2006; Volume 3. [Google Scholar]
- Ahmadi, G. On mechanics of saturated granular materials. Int. J. Non-Linear Mech. 1980, 15, 251–262. [Google Scholar] [CrossRef]
- Ahmadi, G. On the mechanics of incompressible multiphase suspensions. Adv. Water Resour. 1987, 10, 32–43. [Google Scholar] [CrossRef]
- Safaei, M.R.; Mahian, O.; Garoosi, F.; Hooman, K.; Karimipour, A.; Kazi, S.N.; Gharehkhani, S. Investigation of Micro- and Nanosized Particle Erosion in a 90° Pipe Bend Using a Two-Phase Discrete Phase Model. Sci. World J. 2014, 2014, 740578. [Google Scholar] [CrossRef] [PubMed]



| Wt. % FMWCNT/Water | Density (kg·m−3) | Viscosity (kg·m−1·s−1) | Thermal Conductivity (W·m−1·K−1) | ||||
|---|---|---|---|---|---|---|---|
| 20 °C | 27 °C | 33 °C | 20 °C | 27 °C | 33 °C | ||
| 0 | 995.8 (26.6 °C) | 0.000980 | 0.000860 | 0.000765 | 0.59 | 0.61 | 0.62 |
| 0.1 | 1003 (23.4 °C) | 0.000998 | 0.000881 | 0.000781 | 0.62 | 0.64 | 0.66 |
| 0.2 | 1006 (23.1 °C) | 0.00103 | 0.000901 | 0.000790 | 0.67 | 0.69 | 0.71 |
| U (m/s) | Exact Solution | Present Study | |||
|---|---|---|---|---|---|
| Cf | τ (Pa) | Nu | τ (Pa) | Nu | |
| 0.00017 | 0.051 | 7.37 × 10−7 | 8.326 | 7.79 × 10−7 | 8.798 |
| 0.001 | 0.021 | 1.05 × 10−5 | 20.193 | 1.12 × 10−5 | 21.538 |
| 0.0017 | 0.016 | 2.30 × 10−5 | 26.328 | 2.45 × 10−5 | 27.998 |
| Local Coefficient of Friction | Number of Grids |
|---|---|
| 0.02342 | 50 × 25 |
| 0.02286 | 75 × 40 |
| 0.02252 | 100 × 50 |
| 0.02249 | 110 × 55 |
| 0.02247 | 125 × 65 |
| 0.02245 | 150 × 75 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safaei, M.R.; Ahmadi, G.; Goodarzi, M.S.; Kamyar, A.; Kazi, S.N. Boundary Layer Flow and Heat Transfer of FMWCNT/Water Nanofluids over a Flat Plate. Fluids 2016, 1, 31. https://doi.org/10.3390/fluids1040031
Safaei MR, Ahmadi G, Goodarzi MS, Kamyar A, Kazi SN. Boundary Layer Flow and Heat Transfer of FMWCNT/Water Nanofluids over a Flat Plate. Fluids. 2016; 1(4):31. https://doi.org/10.3390/fluids1040031
Chicago/Turabian StyleSafaei, Mohammad Reza, Goodarz Ahmadi, Mohammad Shahab Goodarzi, Amin Kamyar, and S. N. Kazi. 2016. "Boundary Layer Flow and Heat Transfer of FMWCNT/Water Nanofluids over a Flat Plate" Fluids 1, no. 4: 31. https://doi.org/10.3390/fluids1040031
APA StyleSafaei, M. R., Ahmadi, G., Goodarzi, M. S., Kamyar, A., & Kazi, S. N. (2016). Boundary Layer Flow and Heat Transfer of FMWCNT/Water Nanofluids over a Flat Plate. Fluids, 1(4), 31. https://doi.org/10.3390/fluids1040031







