Heat Transfer and Dissipation Effects in the Flow of a Drilling Fluid
Abstract
:1. Introduction
2. Governing Equations
- Conservation of masswhere ρ is the density of the fluid, is the partial derivative with respect to time, and is the velocity vector. For an isochoric motion we have .
- Conservation of linear momentumwhere b is the body force vector, T is the Cauchy stress tensor, and is the total time derivative, given by . The conservation of angular momentum indicates that in the absence of couple stresses the stress tensor is symmetric, that is, .
- Conservation of concentration
- Conservation of Energy:where is the specific internal energy, L is the gradient of velocity, q is the heat flux vector, is the specific radiant energy, and “ designates the scalar product of two tensors. Thermodynamical considerations require the application of the second law of thermodynamics or the entropy inequality. The local form of the entropy inequality is given by (see [18], p. 130):where is the specific entropy density, the dot implies the material time derivative, is the entropy flux, and s is the entropy supply density. If it is assumed that , and , where θ is the absolute temperature, then Equation (5) reduces to the Clausius-Duhem inequality:
3. Constitutive Equations
3.1. Stress Tensor
3.2. Heat Flux Vector
3.3. Particle Flux
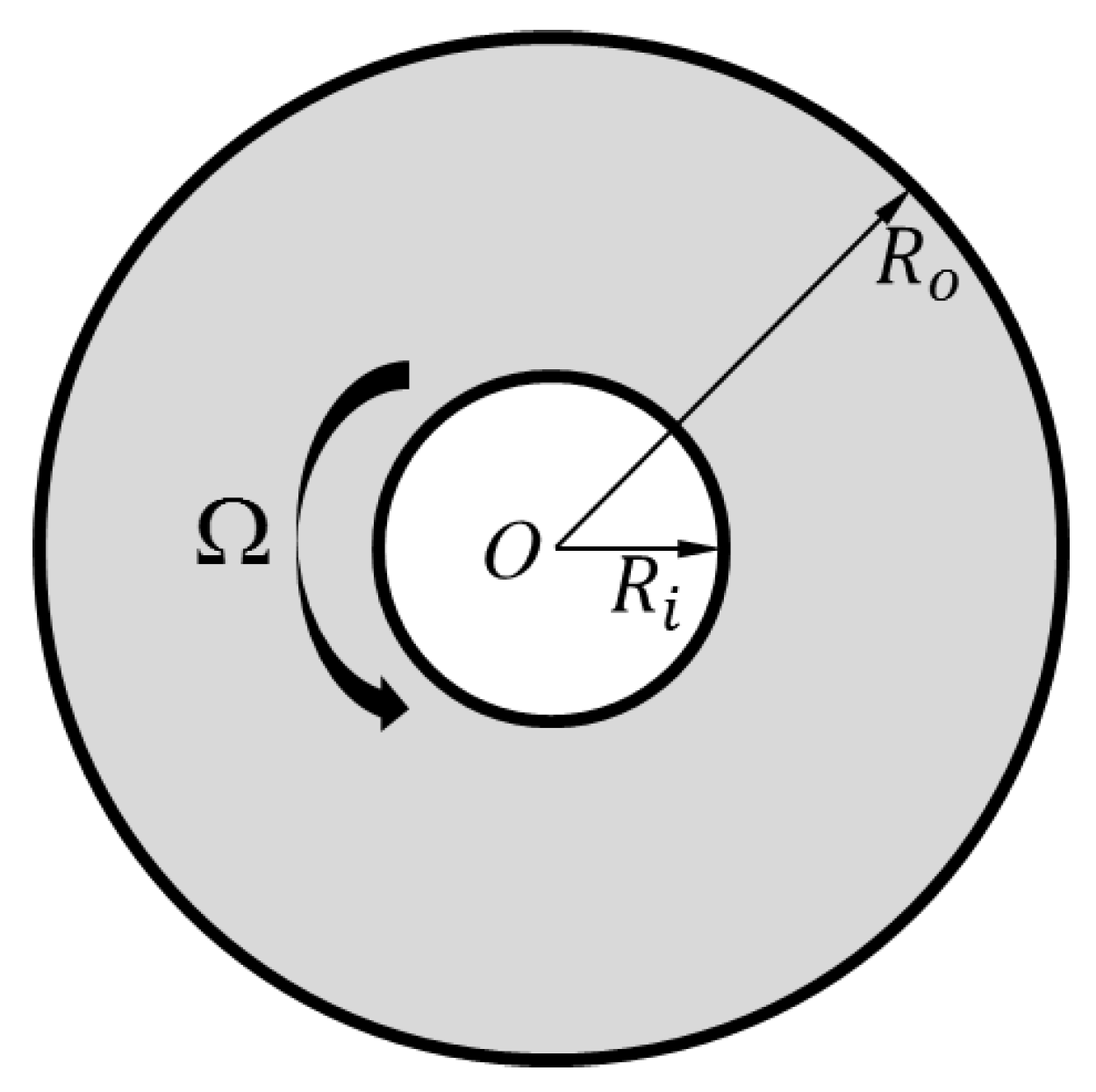
4. Couette Flow
- (i)
- the motion is steady;
- (ii)
- the particle flux due to the Brownian diffusion is neglected;
- (iii)
- the constitutive equation for the stress tensor is given by Equation (8), the constitutive relation for the particle flux is given by Equations (18)–(20), the constitutive relation for the heat flux is given by Equations (13)–(16).
- (iv)
- the velocity, the volume fraction, and the temperature profiles are of the form:
5. Numerical Results
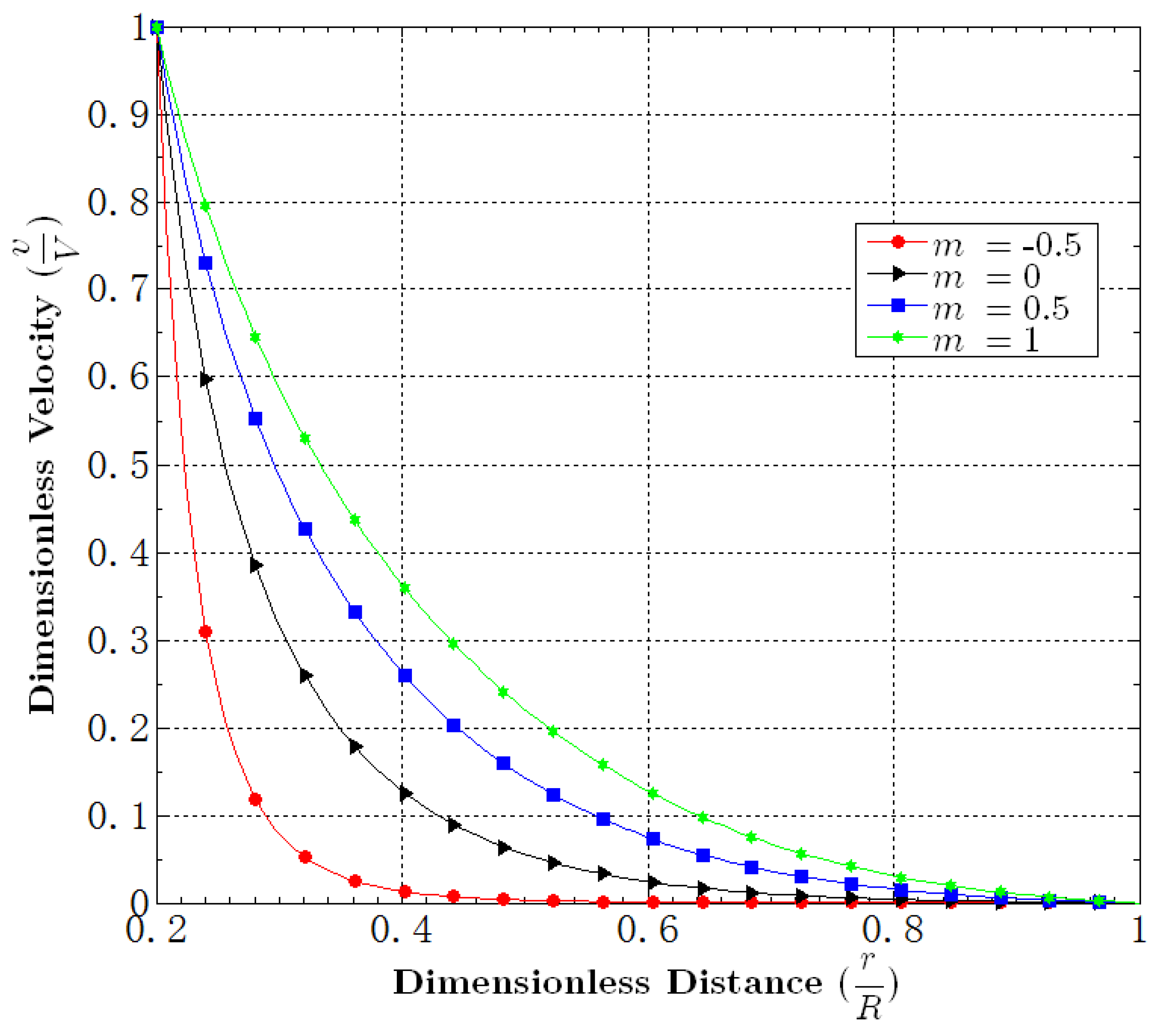
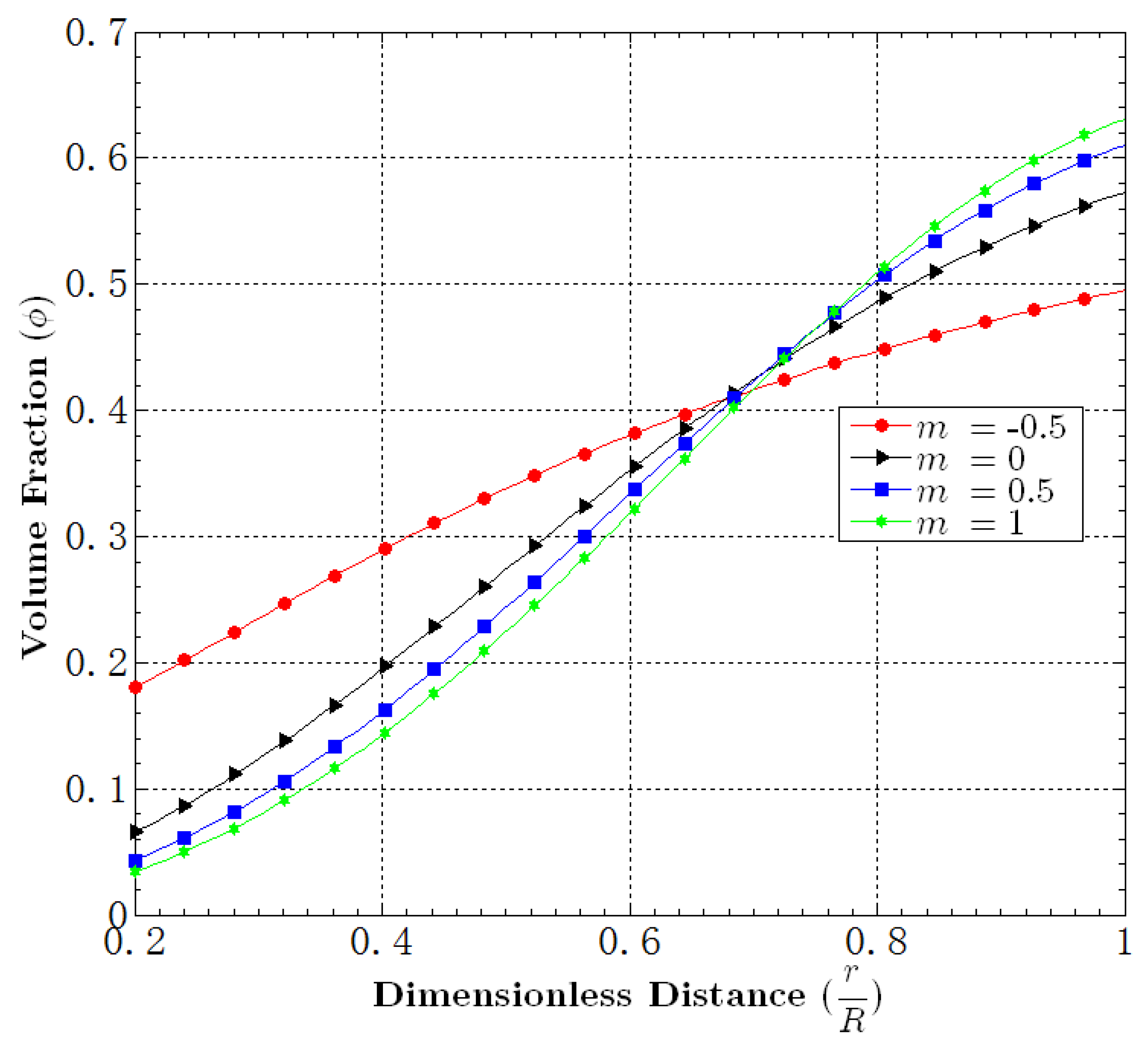
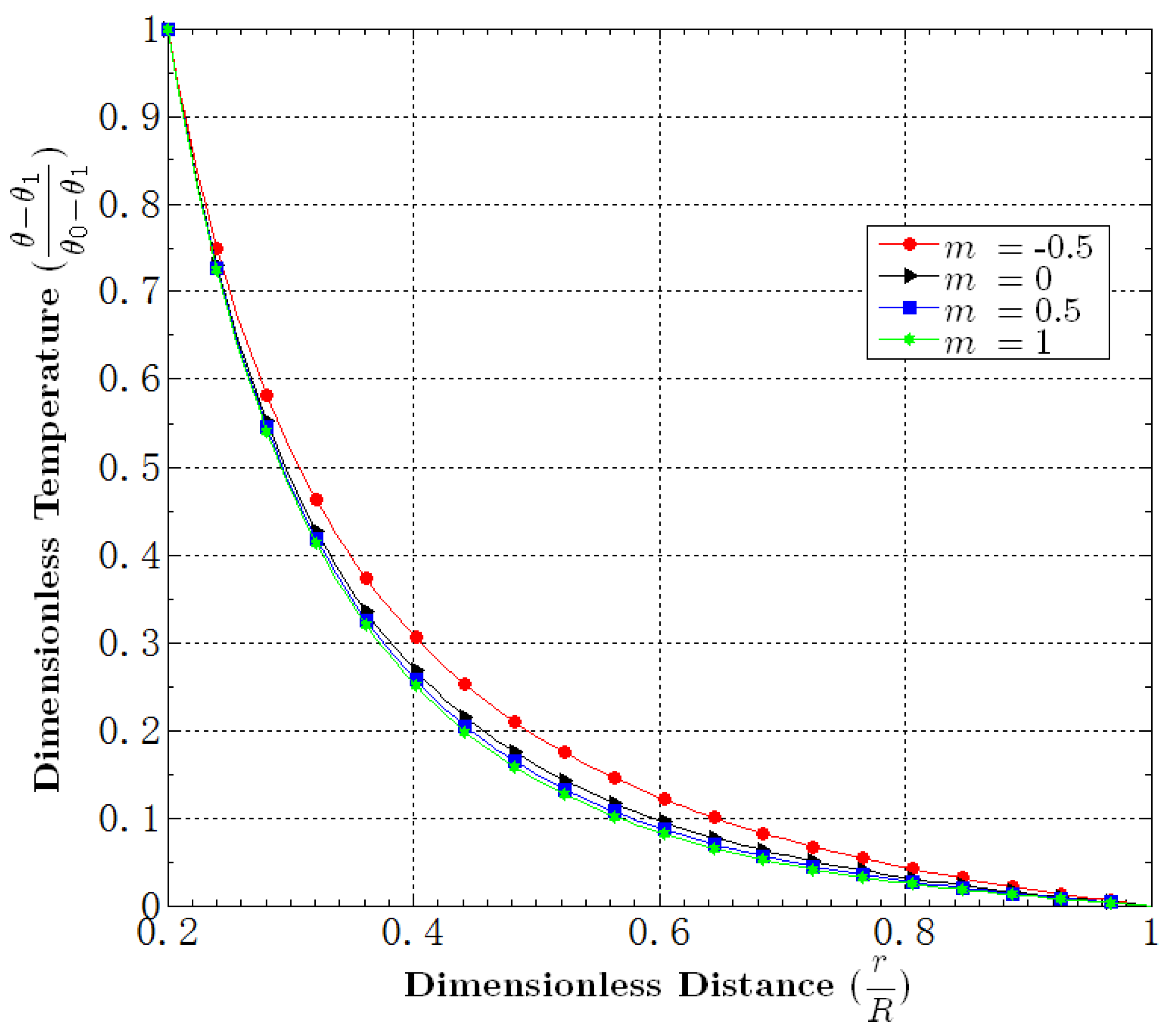
5.1. Effect of m
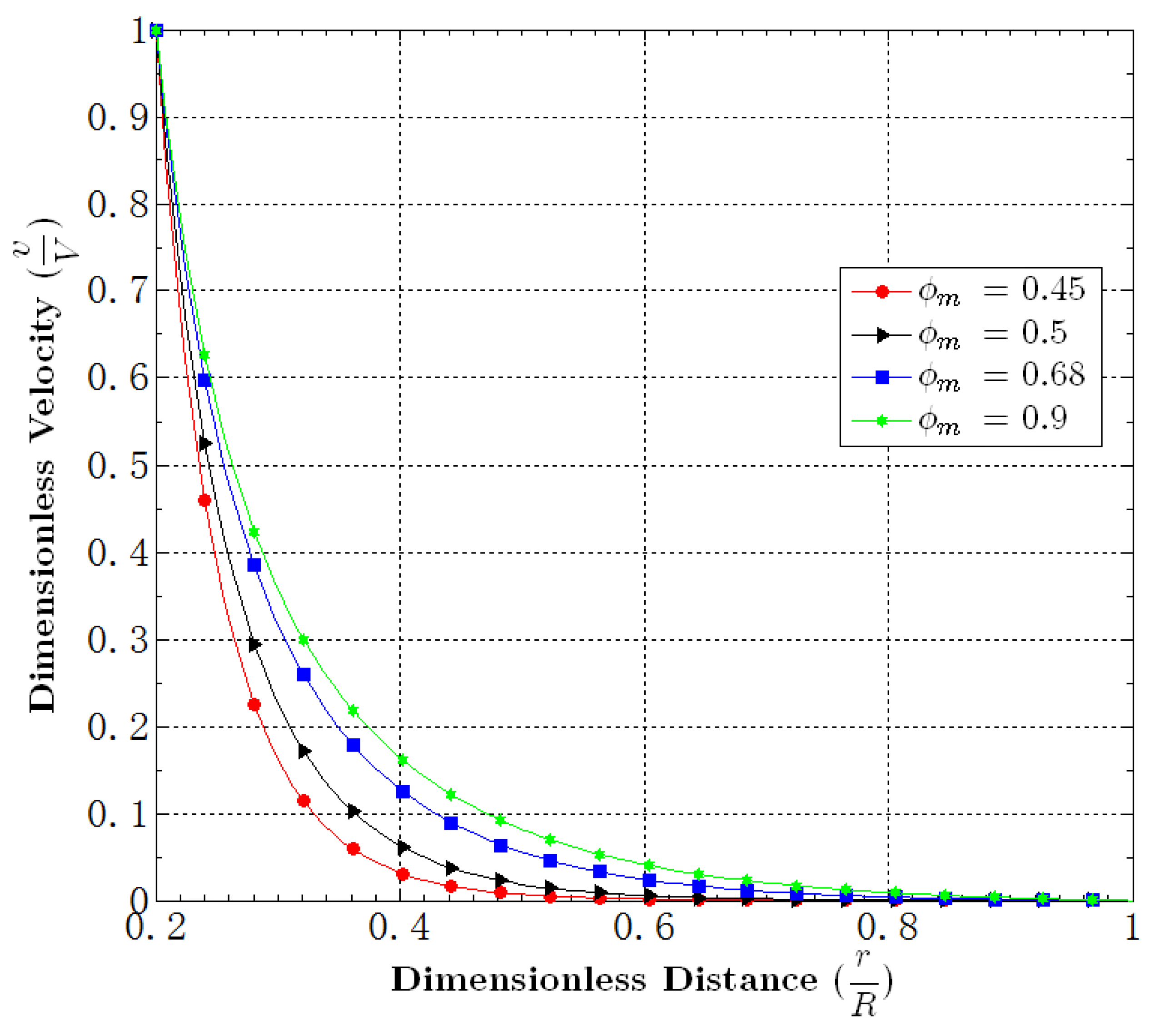
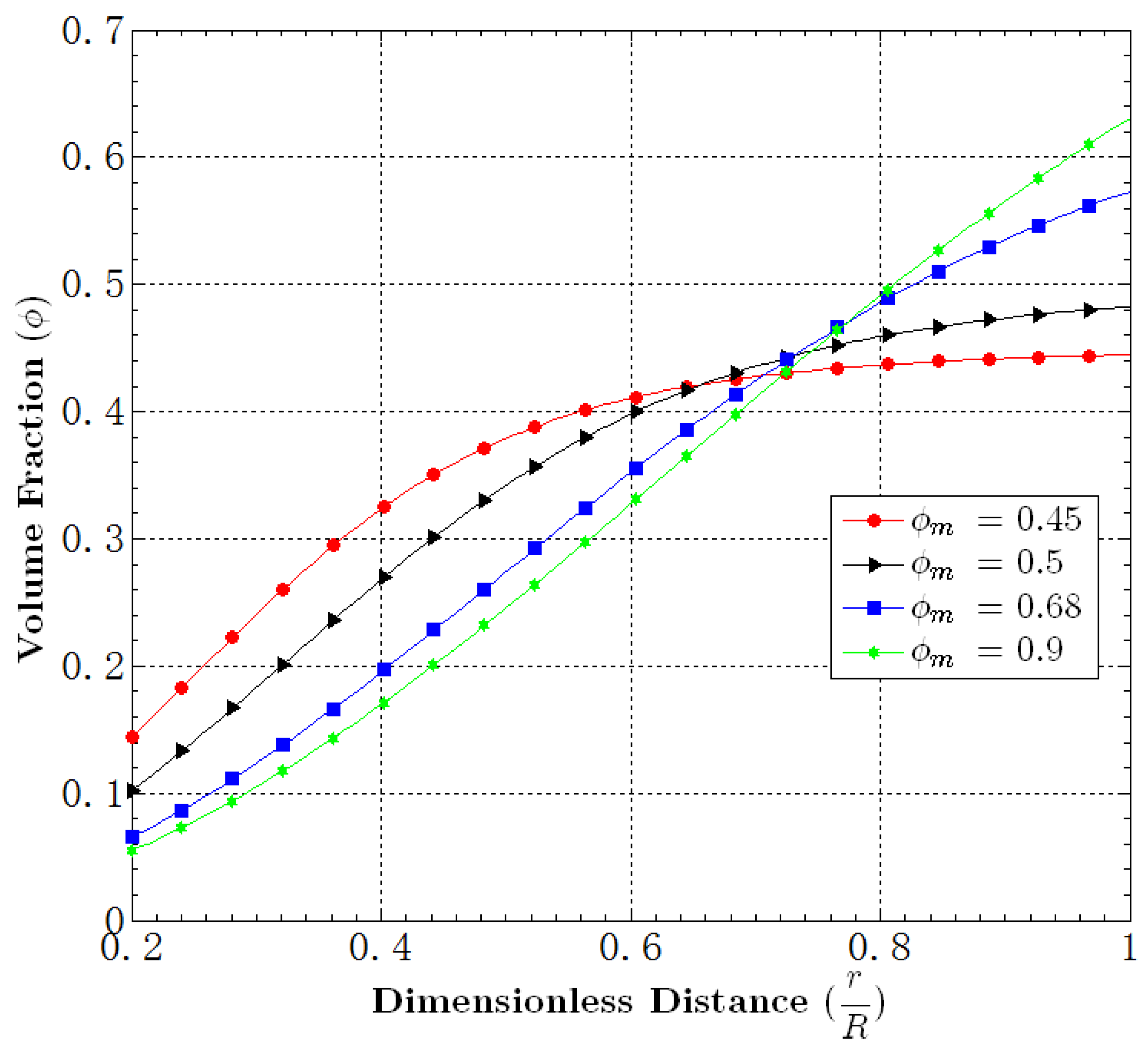
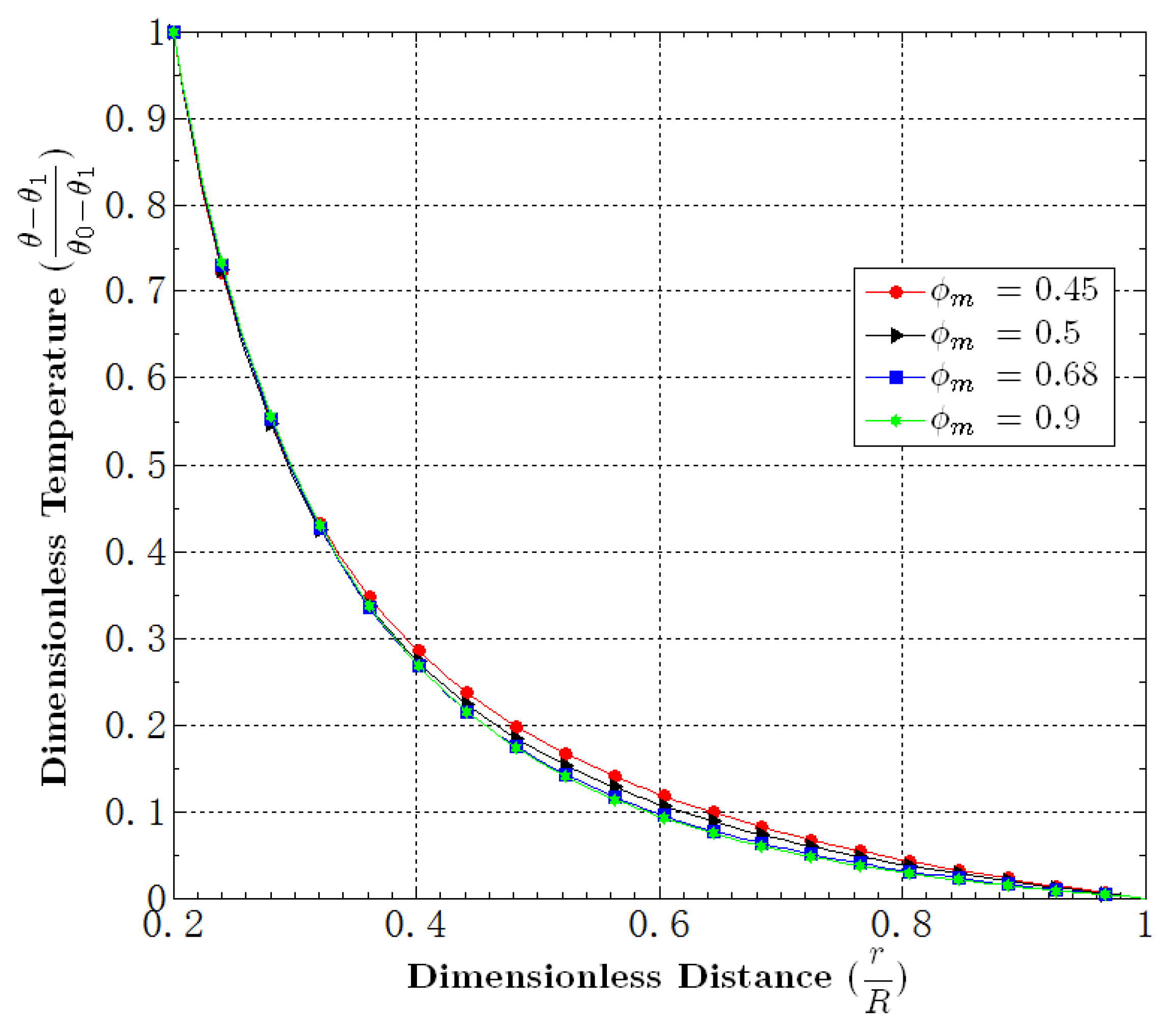
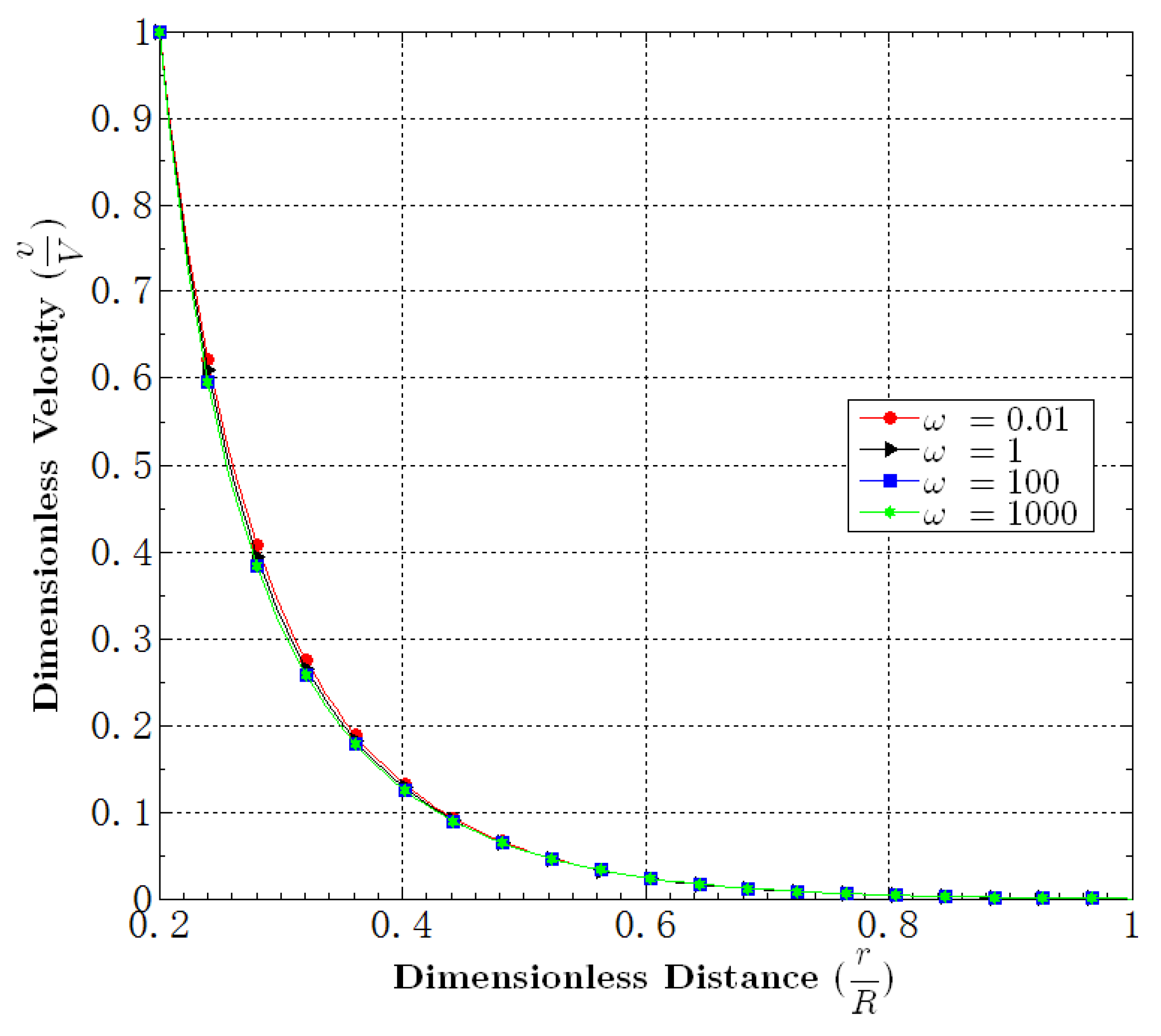
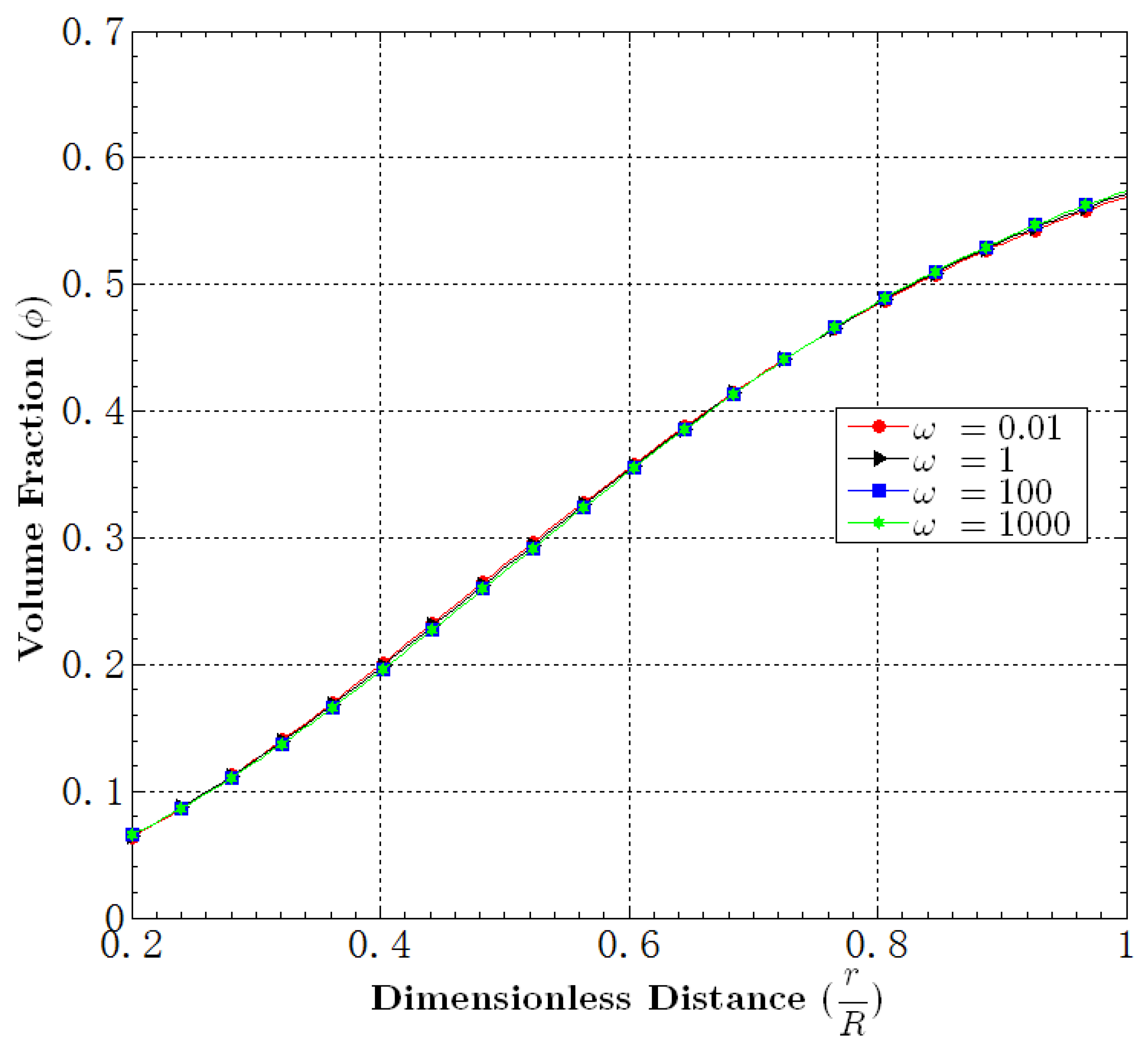
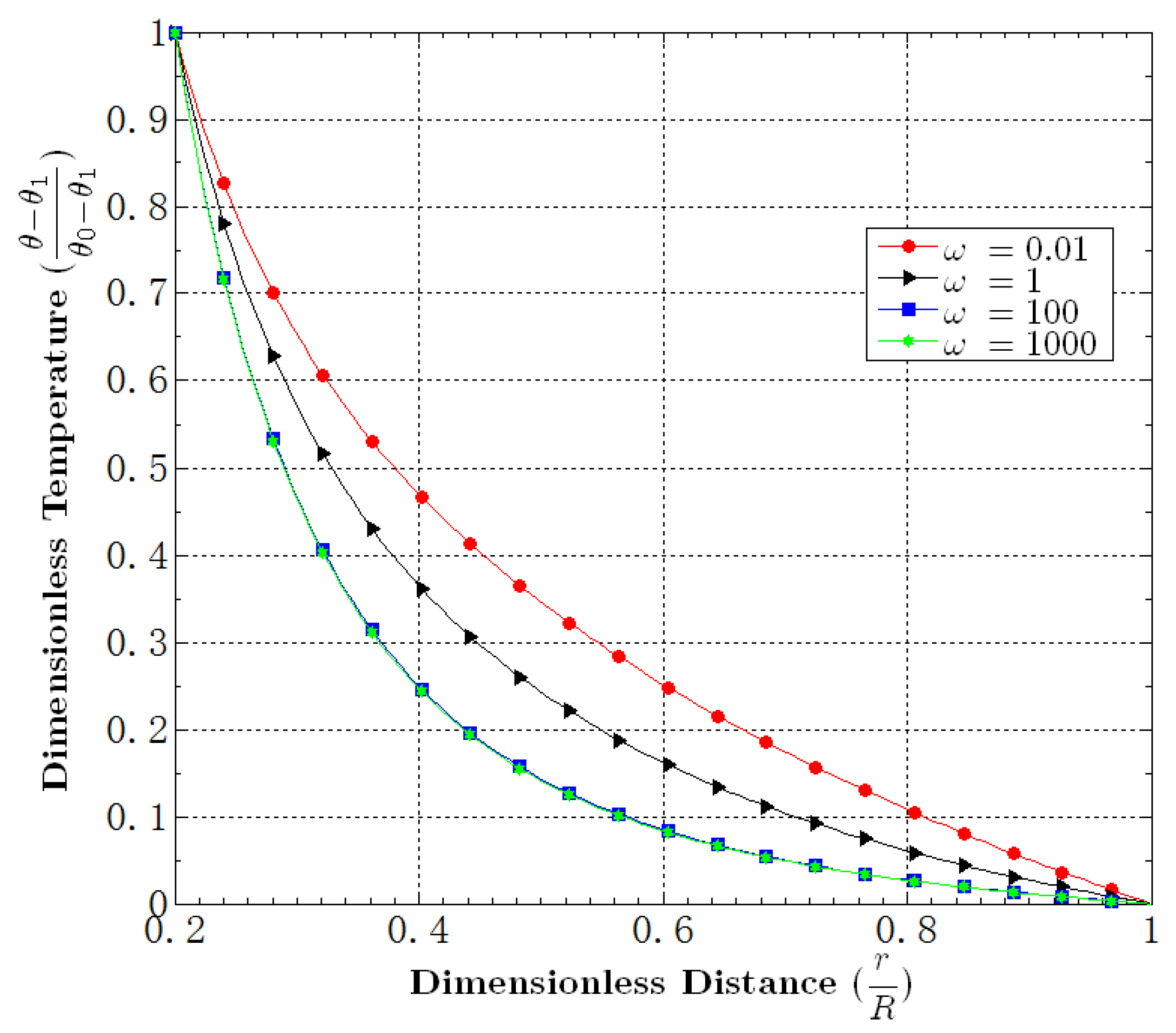
5.2. Effect of
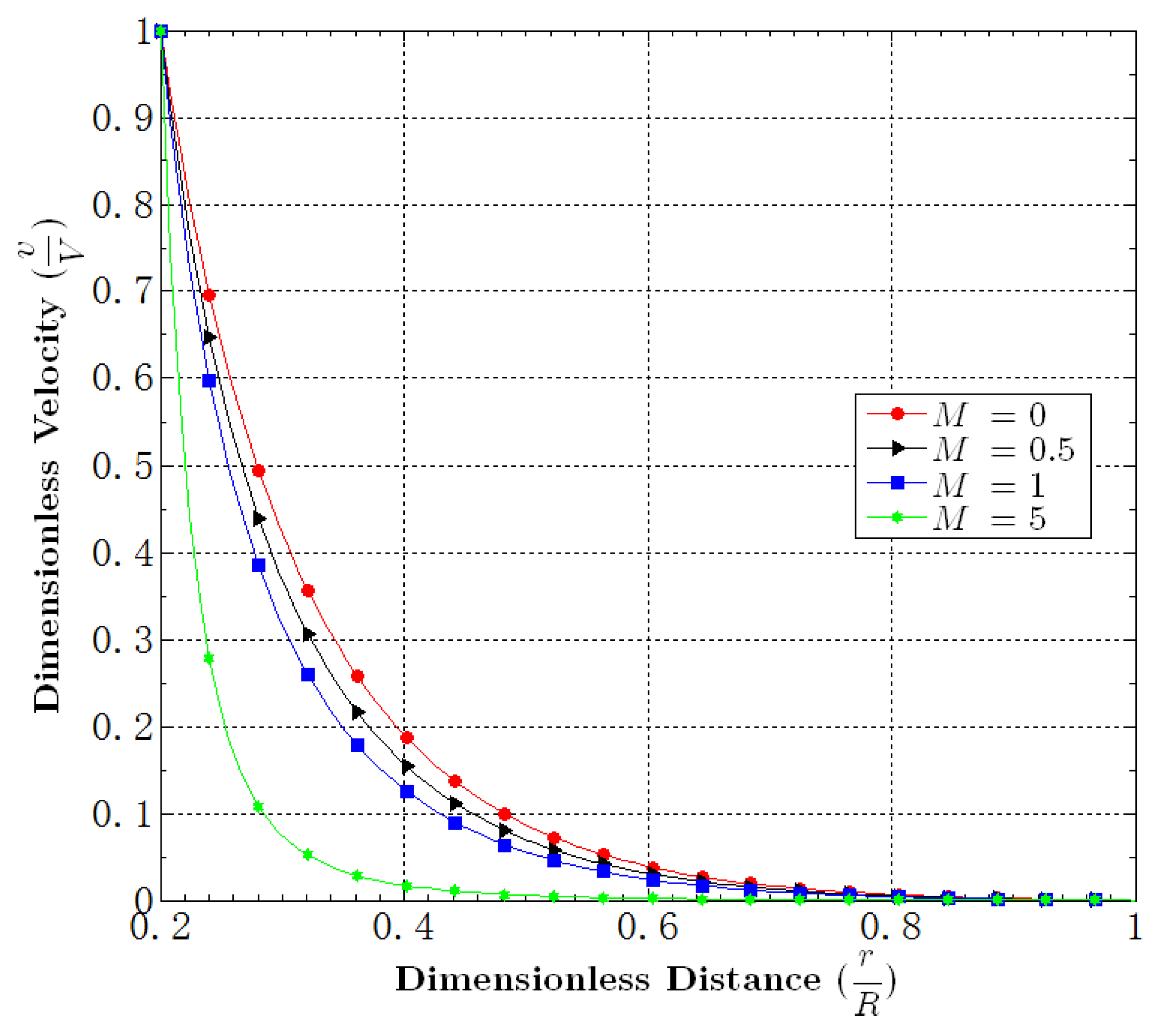
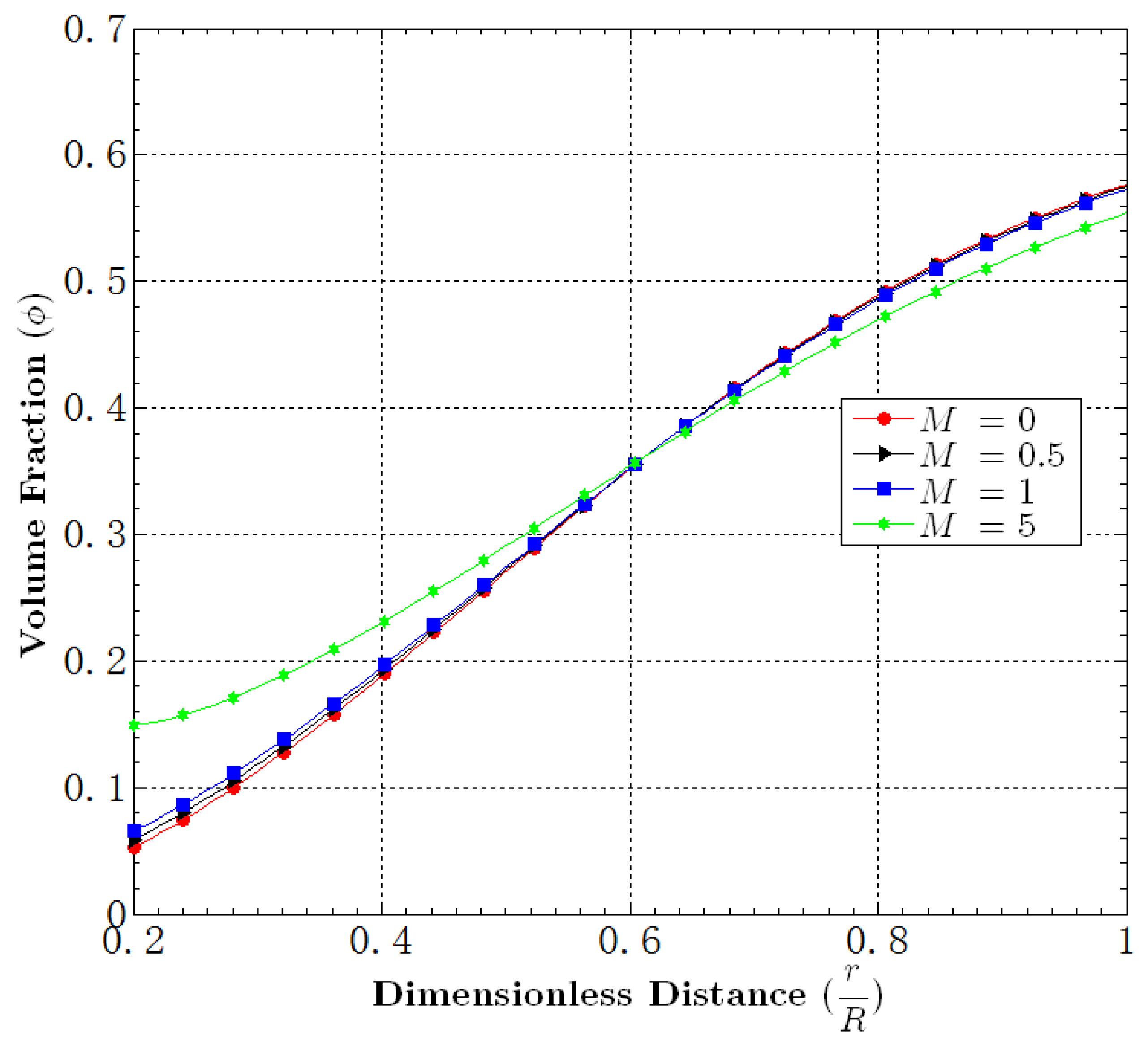
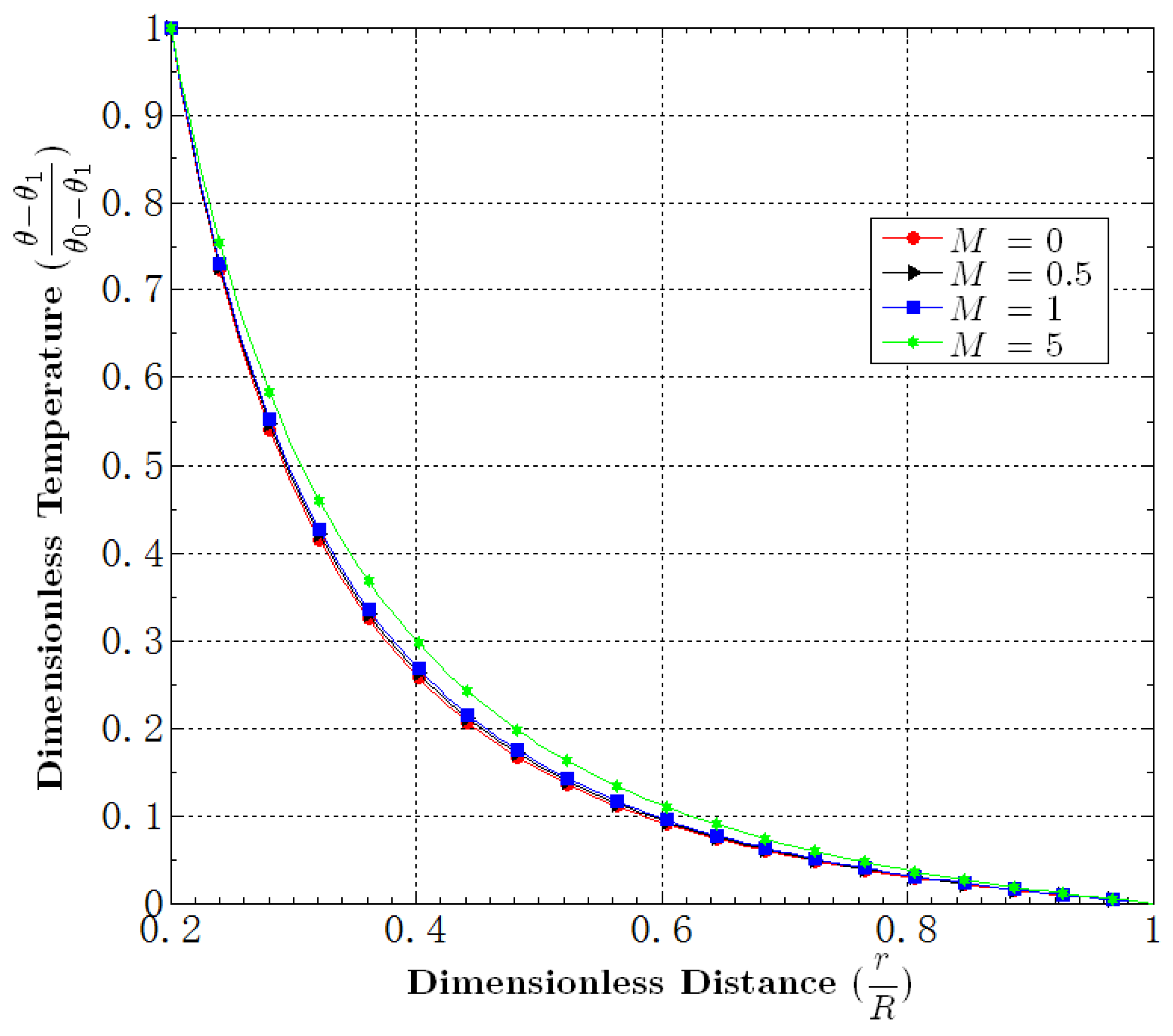
5.3. Effect of M
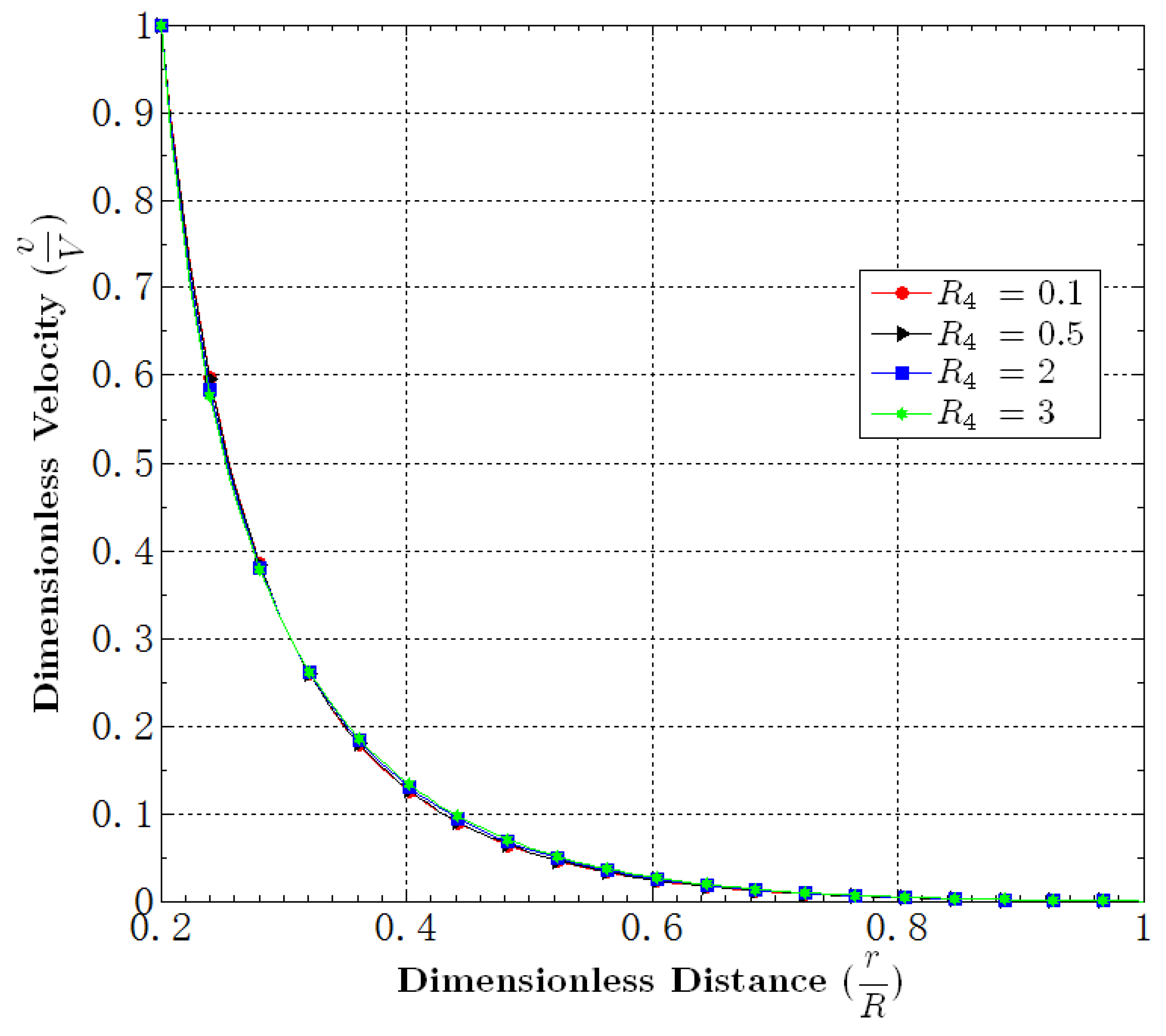
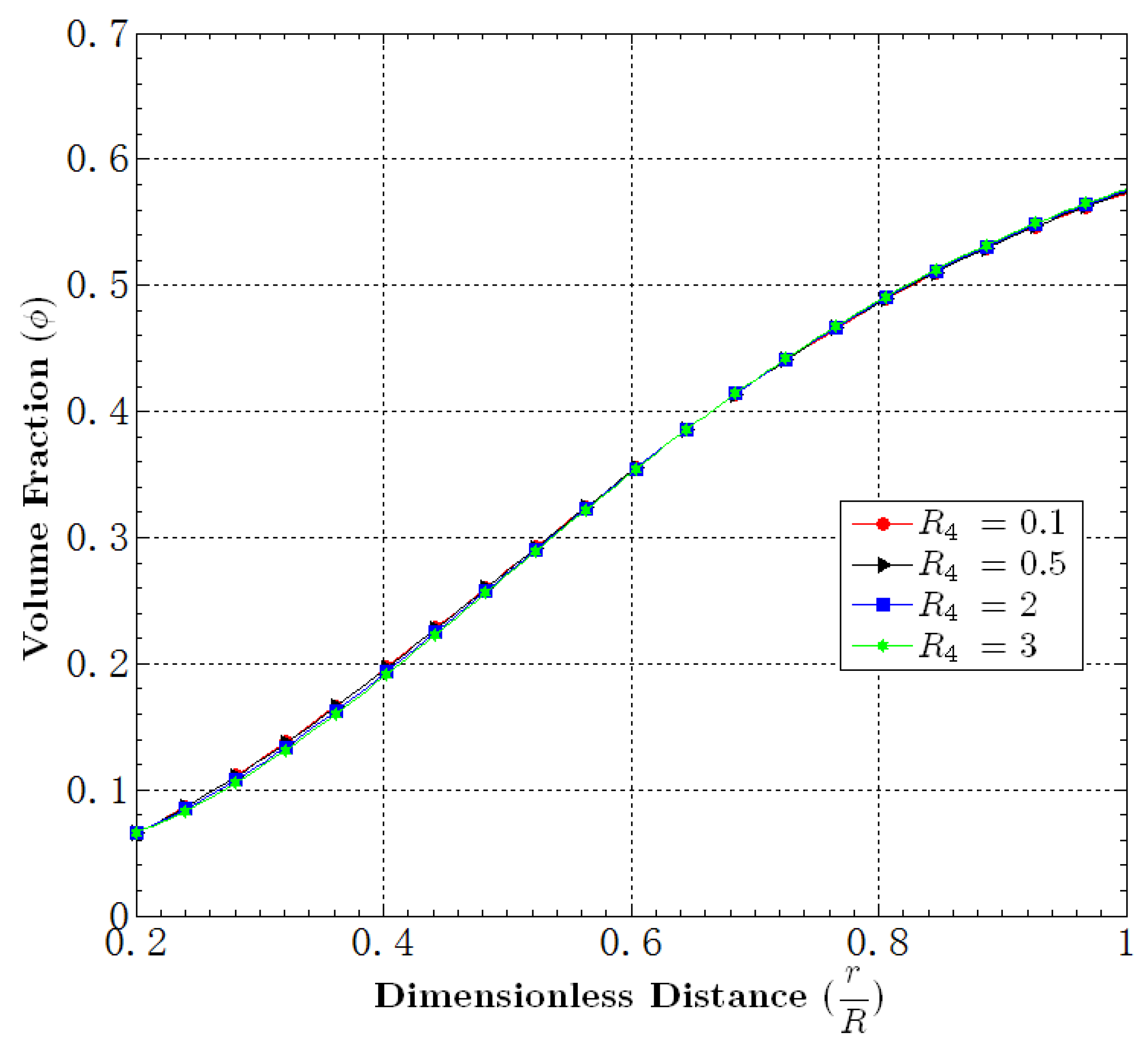
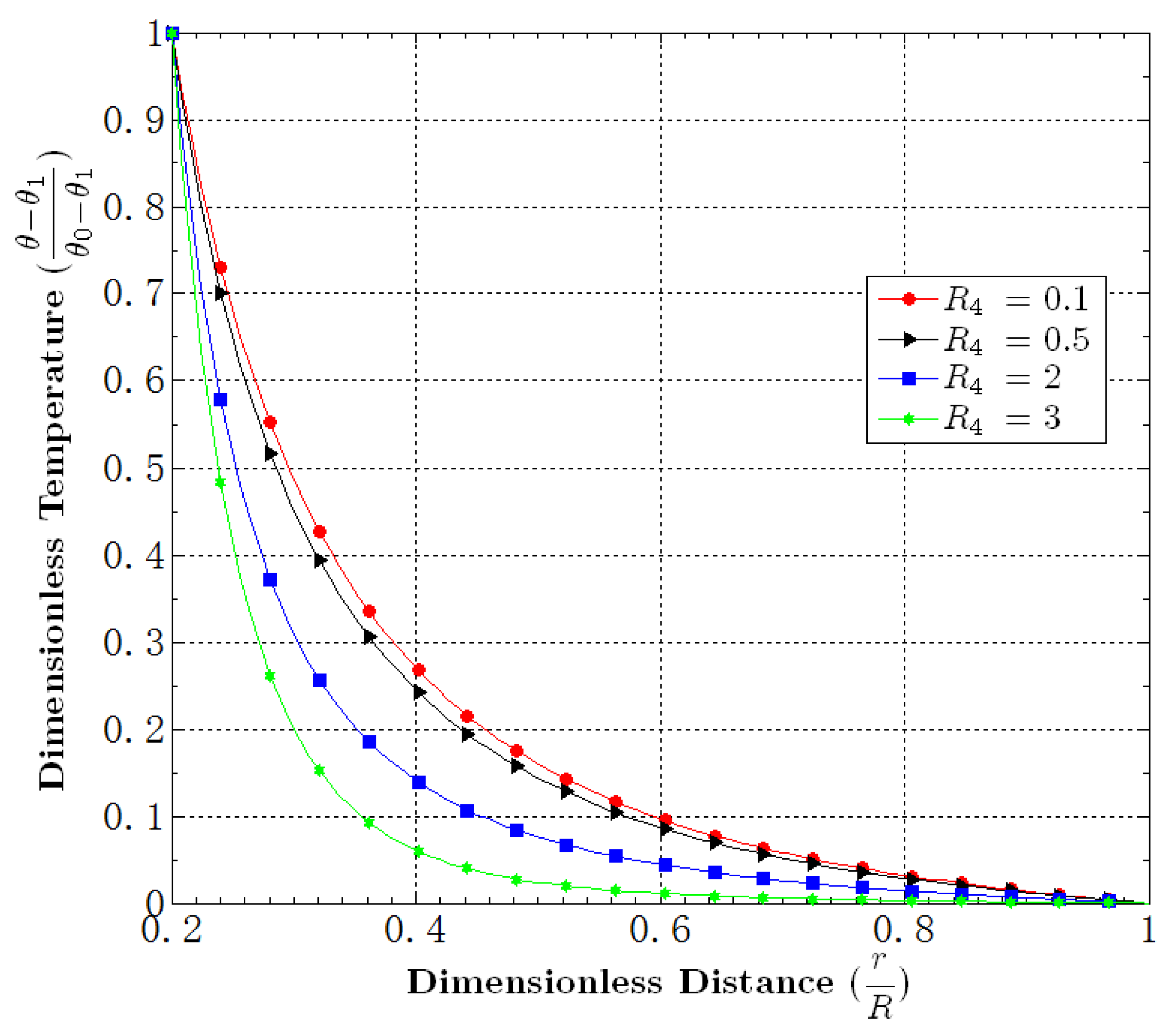
5.4. Effect of
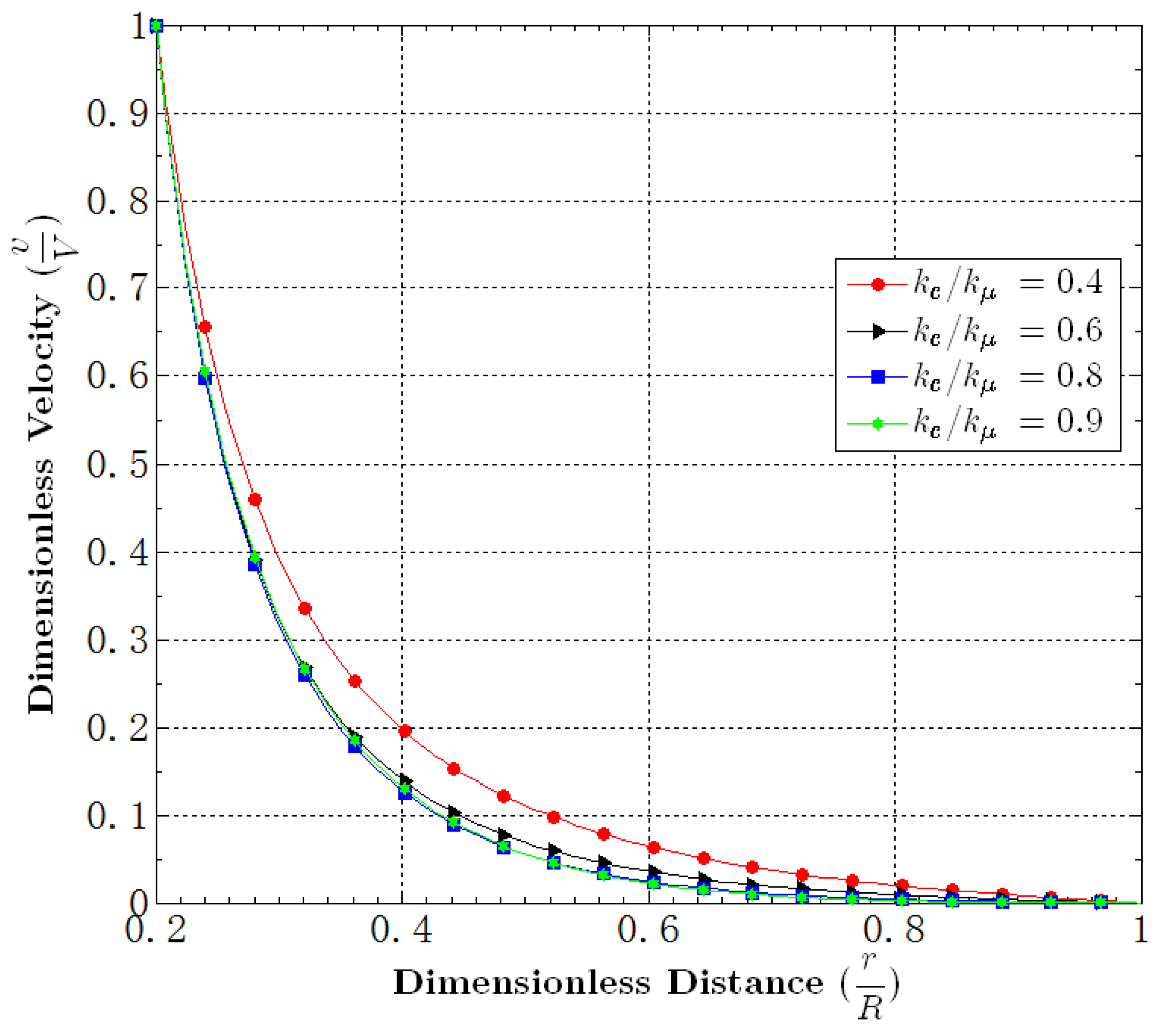
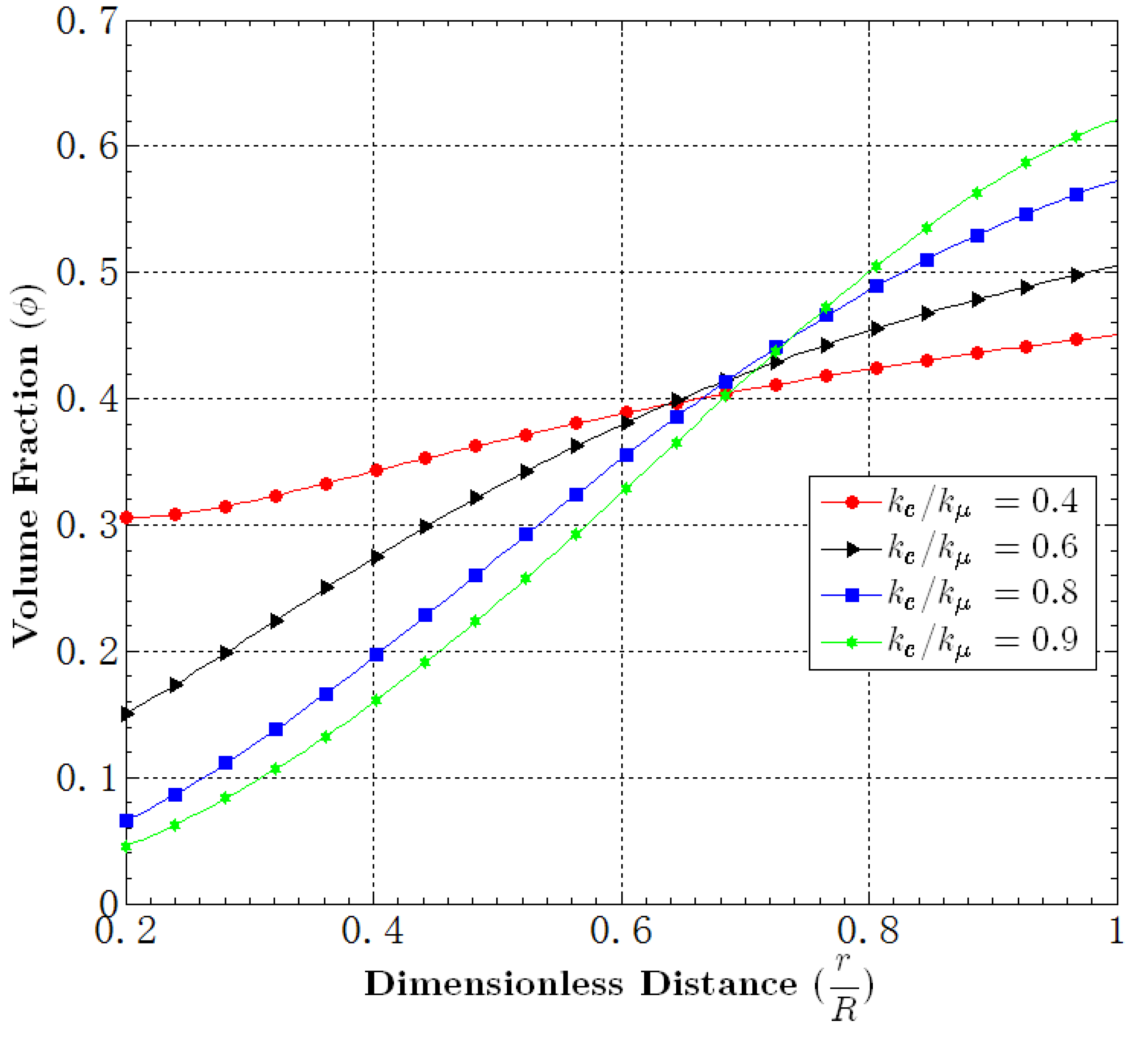
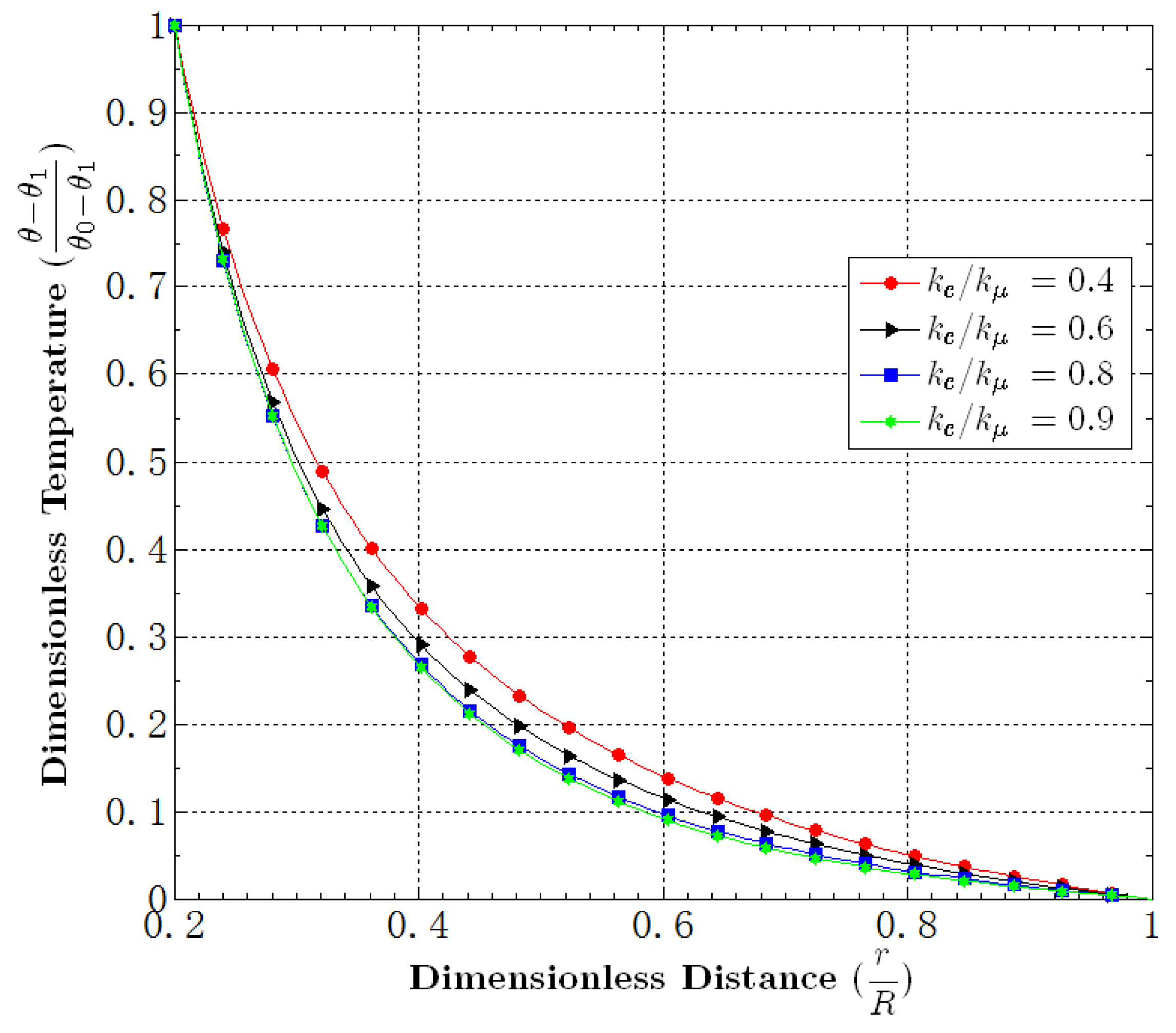
5.5. Effect of
5.6. Effect of
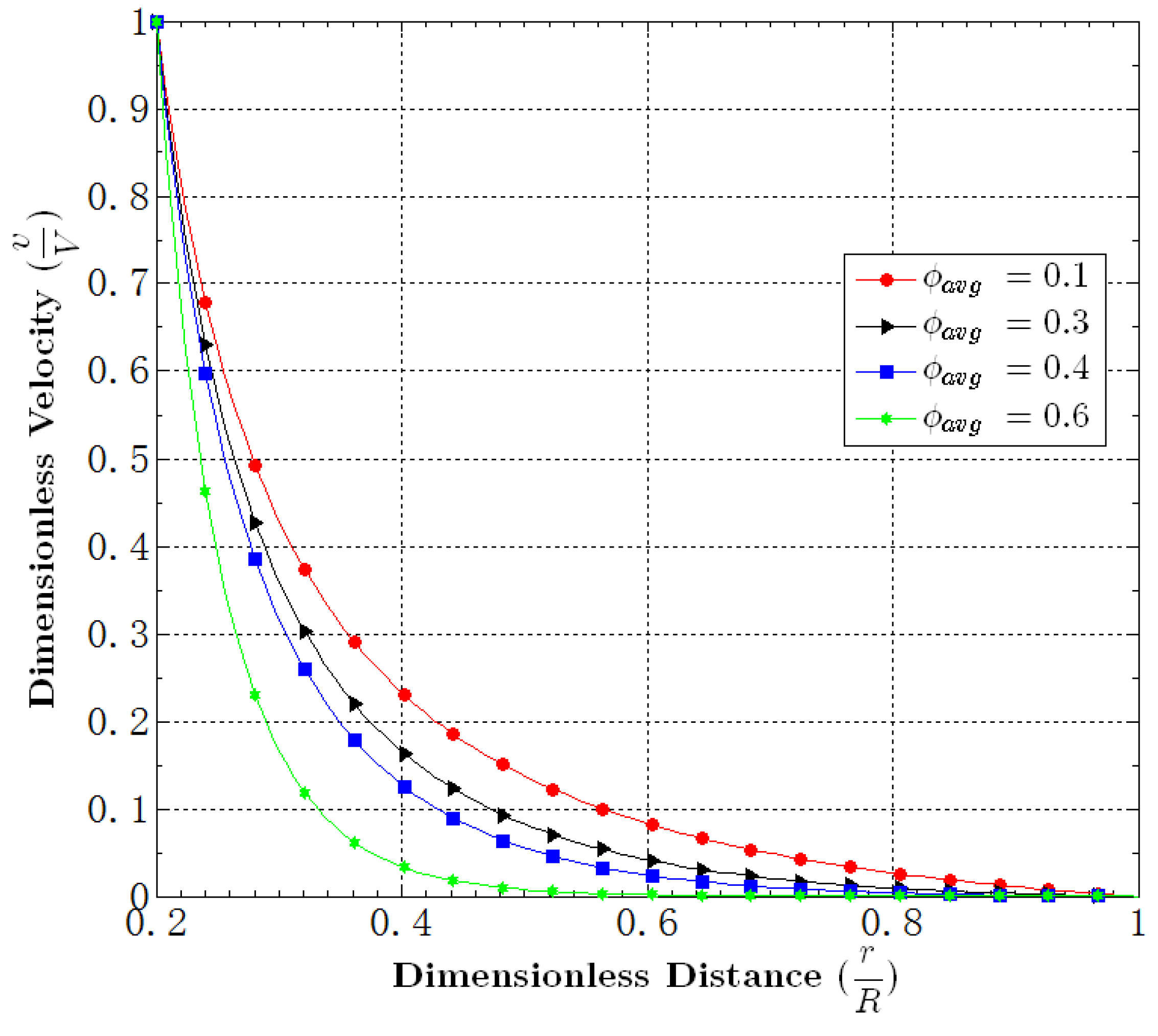
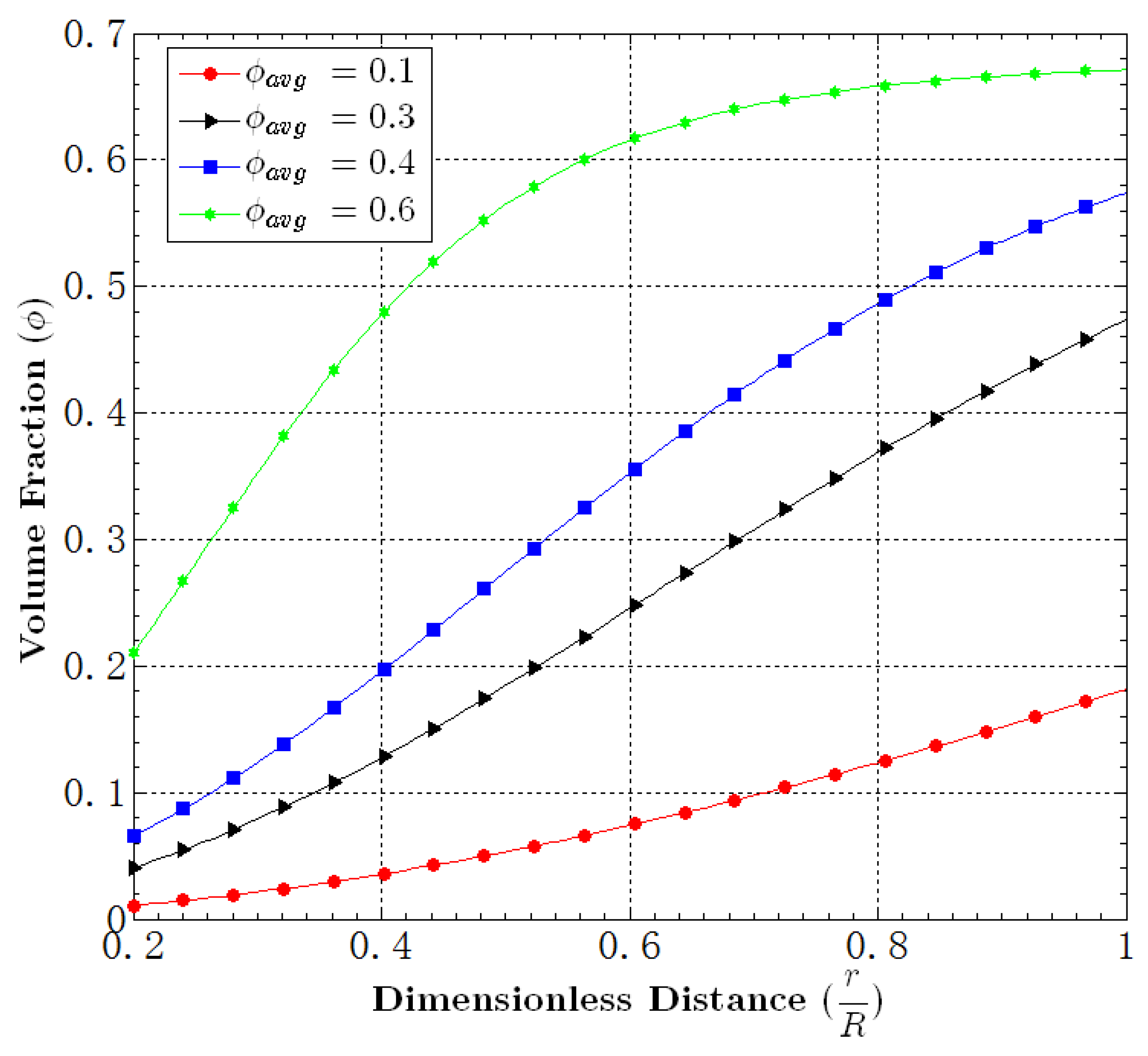
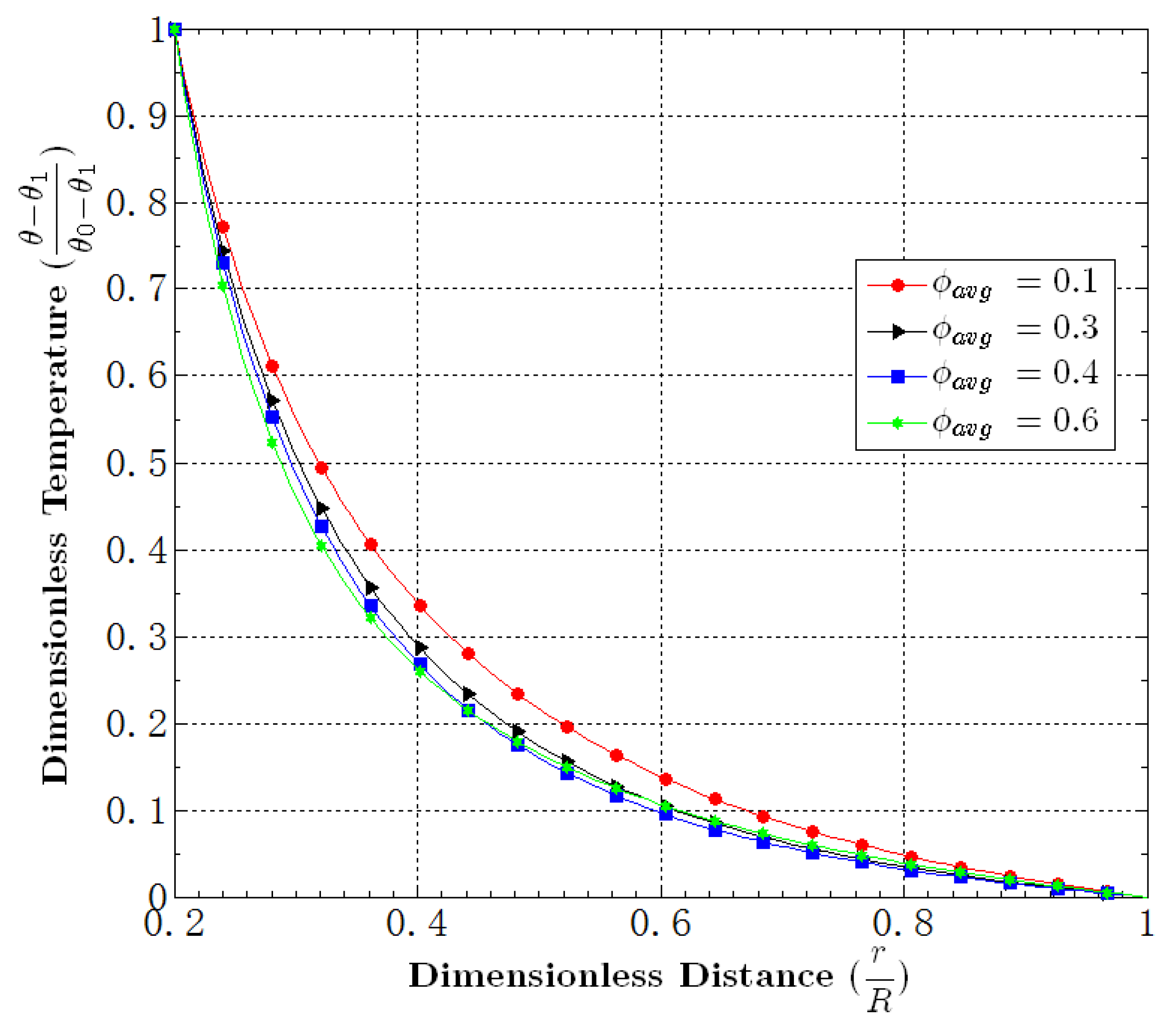
5.7. Effect of the Average Volume Fraction
6. Concluding Remarks
Author Contributions
Conflicts of Interest
Nomenclature
| Symbol | Explanation |
| b | body force vector |
| concentration | |
| D | symmetric part of the velocity gradient |
| g | acceleration due to gravity |
| l | identity tensor |
| L | gradient of the velocity vector |
| m | Power-law index |
| t | time |
| T | Cauchy stress tensor |
| bulk density | |
| reference viscosity | |
| effective viscosity | |
| θ | temperature |
| div | divergence operator |
| ∇ (or grad) | gradient operator |
References
- Joseph, D.; Renardy, Y. Fundamentals of two-fluid dynamics. J. Fluid Mech. 1995, 282, 405–406. [Google Scholar]
- Rajagopal, K.; Tao, L. Mechanics of Mixtures; Series on Advances in Mathematics for Applied Sciences; World Scientific: Singapore, 1995; Volume 35. [Google Scholar]
- Zhou, Z.; Wu, W.-T.; Massoudi, M. Fully developed flow of a drilling fluid between two rotating cylinders. Appl. Math. Comput. 2016, 281, 266–277. [Google Scholar] [CrossRef]
- Gray, G.R.; Darley, H. Composition and Properties of Oilwell Drilling Fluids; Gulf Publishing Company: London, UK, 1981. [Google Scholar]
- Rabia, H. Oilwell Drilling Engineering: Principles and Practice; Graham and Trotman Ltd: London, UK, 1985. [Google Scholar]
- Caenn, R.; Chillingar, G.V. Drilling fluids: State of the art. J. Pet. Sci. Eng. 1996, 14, 221–230. [Google Scholar] [CrossRef]
- Siginer, D.A.; Bakhtiyarov, S.I. Flow of drilling fluids in eccentric annuli. J. Non-Newton. Fluid Mech. 1998, 78, 119–132. [Google Scholar] [CrossRef]
- Fam, M.A.; Dusseault, M.B.; Fooks, J.C. Drilling in mudrocks: Rock behavior issues. J. Pet. Sci. Eng. 2003, 38, 155–166. [Google Scholar] [CrossRef]
- Valluri, S.G.; Miska, S.Z.; Yu, M.; Ahmed, R.M.; Takach, N. Experimental study of effective hole cleaning using “sweeps” in horizontal wellbores. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006.
- Coussot, P. Mudflow Rheology and Dynamics; Balkema: Amsterdam, The Netherlands, 1997. [Google Scholar]
- Yield-power Law Model More Accurately Predicts Mud Rheology. Available online: http://www.ogj.com/articles/print/volume-91/issue-34/in-this-issue/drilling/yield-power-law-model-more-accurately-predicts-mud-rheology.html (accessed on 17 March 2016).
- Sławomirski, M.R. Rheological behavior of oil well drilling fluids. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1975, 12, 115–123. [Google Scholar] [CrossRef]
- Briscoe, B.; Luckham, P.; Ren, S. The properties of drilling muds at high pressures and high temperatures. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 1994, 348, 179–207. [Google Scholar] [CrossRef]
- Massoudi, M. A mixture theory formulation for hydraulic or pneumatic transport of solid particles. Int. J. Eng. Sci. 2010, 48, 1440–1461. [Google Scholar] [CrossRef]
- Massoudi, M. A note on the meaning of mixture viscosity using the classical continuum theories of mixtures. Int. J. Eng. Sci. 2008, 46, 677–689. [Google Scholar] [CrossRef]
- Subia, S.R.; Ingber, M.S.; Mondy, L.A.; Altobelli, S.A.; Graham, A.L. Modelling of concentrated suspensions using a continuum constitutive equation. J. Fluid Mech. 1998, 373, 193–219. [Google Scholar] [CrossRef]
- Phillips, R.J.; Armstrong, R.C.; Brown, R.A.; Graham, A.L.; Abbott, J.R. A constitutive equation for concentrated suspensions that accounts for shear-induced particle migration. Phys. Fluids A Fluid Dyn. (1989–1993) 1992, 4, 30–40. [Google Scholar] [CrossRef]
- Liu, I.-S. Continuum Mechanics; Springer: Berlin, Germany, 2002. [Google Scholar]
- Müller, I. On the entropy inequality. Arch. Ration. Mech. Anal. 1967, 26, 118–141. [Google Scholar] [CrossRef]
- Ziegler, H. An Introduction to Thermomechanics; North-Holland Publishing Company: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Truesdell, C.; Noll, W. The Nonlinear Field Theories of Mechanics; Springer-Verlag: Berlin, Geramny, 1992. [Google Scholar]
- Massoudi, M.; Wang, P. Slag behavior in gasifiers. Part II: Constitutive modeling of slag. Energies 2013, 6, 807–838. [Google Scholar] [CrossRef]
- Gupta, G.; Massoudi, M. Flow of a generalized second grade fluid between heated plates. Acta Mech. 1993, 99, 21–33. [Google Scholar] [CrossRef]
- Miao, L.; Wu, W.-T.; Aubry, N.; Massoudi, M. Heat transfer and flow of a slag-type non-linear fluid: Effects of variable thermal conductivity. Appl. Math. Comput. 2014, 227, 77–91. [Google Scholar] [CrossRef]
- Miao, L.; Massoudi, M. Heat transfer analysis and flow of a slag-type fluid: Effects of variable thermal conductivity and viscosity. Int. J. Non-Linear Mech. 2015, 76, 8–19. [Google Scholar] [CrossRef]
- Krieger, I.M. Rheology of monodisperse latices. Adv. Colloid Interface Sci. 1972, 3, 111–136. [Google Scholar] [CrossRef]
- Roscoe, R. The viscosity of suspensions of rigid spheres. Br. J. Appl. Phys. 1952, 3, 267–269. [Google Scholar] [CrossRef]
- Roscoe, R. Flow Properties of Disperse Systems; Hermans, J., Ed.; Interscience Publishers: New York, NY, USA, 1953; pp. 1–38. [Google Scholar]
- Massoudi, M.; Vaidya, A. Unsteady flows of inhomogeneous incompressible fluids. Int. J. Non-Linear Mech. 2011, 46, 738–741. [Google Scholar] [CrossRef]
- Massoudi, M.; Vaidya, A. Analytical solutions to stokes-type flows of inhomogeneous fluids. Appl. Math. Comput. 2012, 218, 6314–6329. [Google Scholar] [CrossRef]
- Fourier, J. The Analytical Theory of Heat; Dover Publications: New York, NY, USA, 1955. [Google Scholar]
- Winterton, R.H. Early study of heat transfer: Newton and fourier. Heat Transf. Eng. 2001, 22, 3–11. [Google Scholar] [CrossRef]
- Kaviany, M. Principles of Heat Transfer in Porous Media; Springer: Berlin, Germany, 1995. [Google Scholar]
- Bashir, Y.; Goddard, J. Experiments on the conductivity of suspensions of ionically-conductive spheres. AIChE J. 1990, 36, 387–396. [Google Scholar] [CrossRef]
- Prasher, R.S.; Koning, P.; Shipley, J.; Devpura, A. Dependence of thermal conductivity and mechanical rigidity of particle-laden polymeric thermal interface material on particle volume fraction. J. Electron. Packag. 2003, 125, 386–391. [Google Scholar] [CrossRef]
- Lee, D.-L.; Irvine, T.F., Jr. Shear rate dependent thermal conductivity measurements of non-newtonian fluids. Exp. Therm. Fluid Sci. 1997, 15, 16–24. [Google Scholar] [CrossRef]
- Jeffrey, D.J. Conduction through a random suspension of spheres. Proc. R. Soc. Lond. A Math. Phys. Sci. 1973, 335, 355–367. [Google Scholar] [CrossRef]
- Batchelor, G.; O’Brien, R. Thermal or electrical conduction through a granular material. Proc. R. Soc. Lond. A Math. Phys. Sci. 1977, 355, 313–333. [Google Scholar] [CrossRef]
- Pabst, W. Simple second-order expression: For the porosity dependence of thermal conductivity. J. Mater. Sci. 2005, 40, 2667–2669. [Google Scholar] [CrossRef]
- Miao, L.; Wu, W.T.; Aubry, N.; Massoudi, M. Falling film flow of a viscoelastic fluid along a wall. Math. Methods Appl. Sci. 2014, 37, 2840–2853. [Google Scholar] [CrossRef]
- Massoudi, M.; Christie, I. Effects of variable viscosity and viscous dissipation on the flow of a third grade fluid in a pipe. Int. J. Non-Linear Mech. 1995, 30, 687–699. [Google Scholar] [CrossRef]
| m | M | ||
|---|---|---|---|
| −0.5, 0.0, 0.5, 1.0 | 0.45, 0.5, 0.68, 0.9 | 0.0, 0.5, 1.0, 5.0 | 0.1, 0.5, 2.0, 3.0 |
| -- | |||
| 0.01, 1.0, 100.0, 1000.0 | 0.4, 0.6, 0.8, 0.9 | 0.1, 0.3, 0.4, 0.6 | -- |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.-T.; Massoudi, M. Heat Transfer and Dissipation Effects in the Flow of a Drilling Fluid. Fluids 2016, 1, 4. https://doi.org/10.3390/fluids1010004
Wu W-T, Massoudi M. Heat Transfer and Dissipation Effects in the Flow of a Drilling Fluid. Fluids. 2016; 1(1):4. https://doi.org/10.3390/fluids1010004
Chicago/Turabian StyleWu, Wei-Tao, and Mehrdad Massoudi. 2016. "Heat Transfer and Dissipation Effects in the Flow of a Drilling Fluid" Fluids 1, no. 1: 4. https://doi.org/10.3390/fluids1010004
APA StyleWu, W.-T., & Massoudi, M. (2016). Heat Transfer and Dissipation Effects in the Flow of a Drilling Fluid. Fluids, 1(1), 4. https://doi.org/10.3390/fluids1010004






