On the Flows of Fluids Defined through Implicit Constitutive Relations between the Stress and the Symmetric Part of the Velocity Gradient

Abstract

Though implicit constitutive relations have been in place for a long time, wherein the stress, the strain (or the symmetric part of the velocity gradient), and their time derivatives have been used to describe the response of viscoelastic and inelastic bodies, it is only recently purely algebraic relationships between the stress and the displacement gradient (or the velocity gradient) have been introduced to describe the response of non-linear fluids and solids. Such models can describe phenomena that the classical theory, wherein the stress is expressed explicitly in terms of kinematical variables, is incapable of describing, and they also present a sensible way to approach important practical problems, such as the flows of colloids and suspensions and the turbulent flows of fluids, and that of the fracture of solids. In this paper we review this new class of algebraic implicit constitutive relations that can be used to describe the response of fluids.

1. Introduction

Most commonly used fluid models such as the Euler fluid model, the Navier-Stokes fluid model, and the power-law fluid model, as well as models of the differential and integral type assume explicit expressions for the Cauchy stress in terms of the density and appropriate kinematical variables. Rate type fluids on the other hand are usually implicit relationships between the stress, its several objective time derivatives, and the symmetric part of the velocity gradient and its various time derivatives (Implicit constitutive relations have been used to describe non-Newtonian fluids, as well as the inelastic response of solids (see Burgers [1], Oldroyd [2], Prandtl [3], Reuss [4]).The Maxwell fluid model which is a rate type fluid model is an exception in that an explicit expression can be provided for the velocity gradient in terms of the stress and an objective time derivative of the stress, that is it is not a truly implicit fluid model. Also, some rate type constitutive relations can be integrated and expressed in the integral form.). These rate type models, which are implicit, were introduced to capture the stress relaxation exhibited by viscoelastic fluids and always involve objective time derivatives of the stress tensor. It is however possible that one could have an implicit relationship between the stress, density and the symmetric part of the velocity gradient that can describe several non-Newtonian response characteristics that cannot be adequately described by the Navier-Stokes fluid model (The Navier-Stokes fluid is often referred to as a Newtonian fluid and hence a non-Newtonian fluid is one that is not describable by the Navier-Stokes fluid model. As discussed by Dugas [5] and Truesdell [6], the terminology “Newtonian fluid” is not warranted to describe the classical linearly viscous Navier-Stokes fluid. Navier [7,8,9] developed a model on a molecular basis that had only one of the two viscosities associated with what is currently referred to as the Navier-Stokes fluid. Poisson [10] was the first, on a molecular basis, to obtain the model that is referred to as the Navier-Stokes fluid. Stokes [11] obtained exactly the same model as that obtained by Poisson, from a phenomenological point of view. Stokes [12] is very clear in his writing that he has merely obtained the same model as that developed by Poisson, but from a totally different perspective.). This paper is concerned with a review of results of the flows of fluids, which are defined through a relation between the stress and the symmetric part of the velocity gradient, no time derivatives of the stress or the symmetric part of the velocity gradient are involved. However, as we shall see, this class of models can be used to characterize a very rich class of material response such as shear thinning/shear thickening, nonlinear creep, pressure dependence of viscosity, “yield”, non-monotonicity of relationship between stress and shear rate, thixotropy, etc. However, such algebraic models cannot describe normal stress differences in simple shear flows (hence cannot describe the effects such as “die-swell” and “rod climbing”), stress relaxation, etc.

A special sub-class of models wherein one has a relation between the stress and the symmetric part of the velocity gradient leads to a generalization of the generalized Stokesian fluid model that allows the material moduli to depend on the invariants of both the stress, the symmetric part of the velocity gradients and their mixed invariants and allows one to model very interesting phenomena that cannot be described by the general Stokesian fluid model. (We are using the term “relation” in the mathematical sense, that is, it might not be possible to express either the stress explicitly in terms of the symmetric part of the velocity gradient or vice-versa. Of course, a function is a very special relation.Also, a fluid whose stress is a function of the density and the symmetric part of the velocity gradient is referred to as a Stokesian fluid. The Navier-Stokes fluid and the power-law fluids are a very special sub-class of Stokesian fluids.)

As mentioned above, until recently the implicit models used to describe fluid behavior invariably involved time derivatives of the stresses and the symmetric part of the velocity gradient as in rate type models used to describe non-Newtonian fluids. Rajagopal in a series of papers developed implicit models to describe both fluids and solids where an implicit relationship is assumed between the stress and appropriate kinematical variables [13,14,15]. The algebraic class of implicit models being considered includes models that can explain phenomena that cannot be described by the classical linearly viscous or power-law models. It also includes as a special sub-class fluids whose material moduli depend on the mean value of the stress, a situation that has been amply demonstrated to be the case in numerous experiments (experimental literature prior to 1930 that discuss the dependence of the material properties on the mean value of the stress can be found in Bridgman [16] and a documentation of more recent experimental literature can be found in Bulicek et al. [17]).

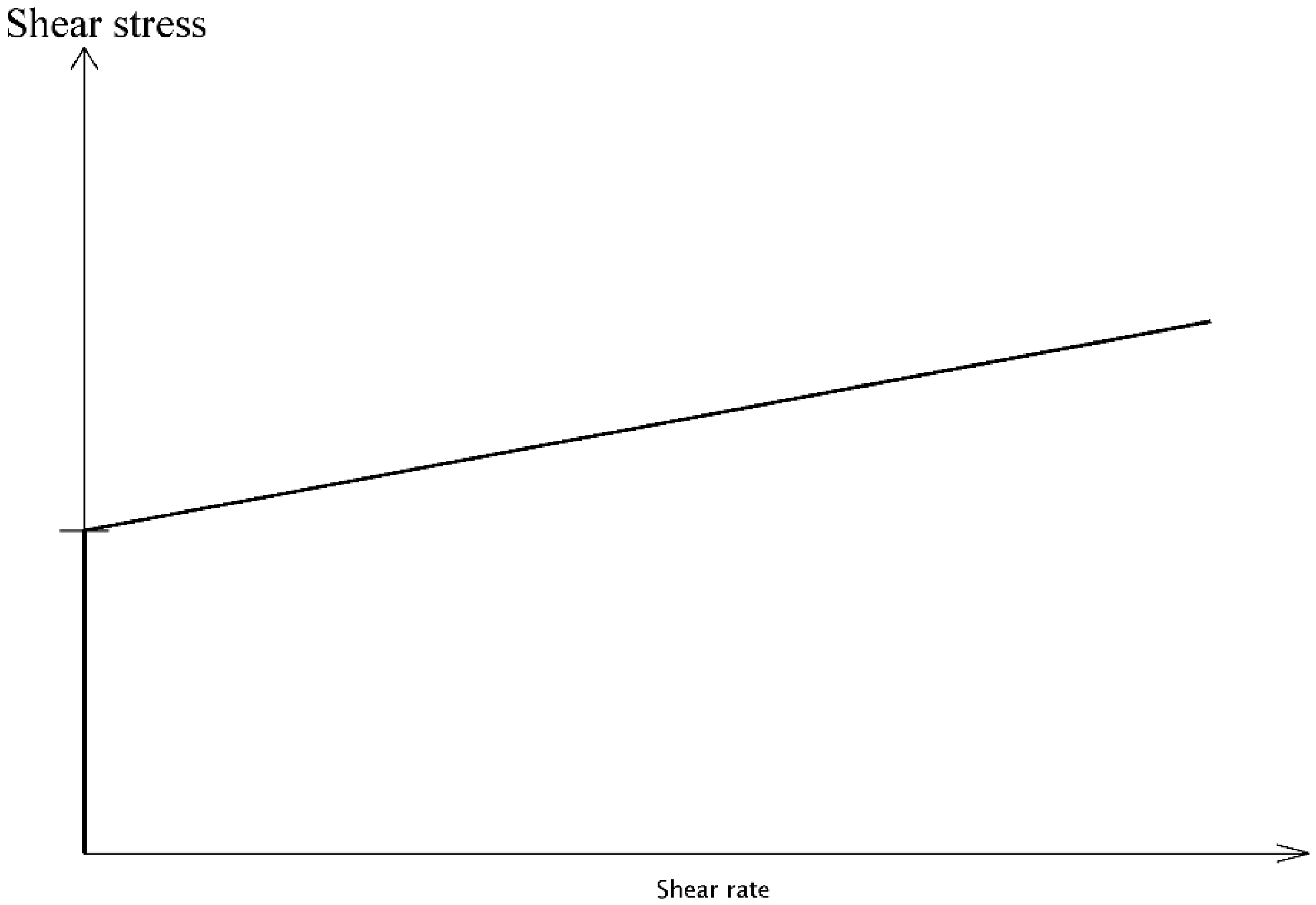
We conclude the introduction with a brief discussion of several observed phenomena, which necessarily need one to use implicit constitutive relations, or the specification of appropriate kinematical quantities in terms of the stress rather than the standard procedure of prescribing the stress as a function of the kinematical quantities to describe the behavior of bodies. The simplest example is the idealization that goes by the name “Bingham fluid” which describes fluids that seem to have a threshold for the stress (see Figure 1) before they start flowing (Of course, if one were to define a fluid as a body that cannot resist shear, then by definition one cannot have a fluid that exhibits a threshold for the shear stress. However, the definition that a body cannot resist shear is meaningless unless one specifies a time scale, force scale and length scale for the observation being made. A body that seems to not flow when observed for even a day, could flow if one waited long enough and if enough stress were applied (the experiment on asphalt that is being carried out since 1930 (see Edgeworth et al. [18] bears testimony to this fact). We shall not get into a discussion of these issues here, suffice it is to say there is no adequate definition as to what is meant by a fluid or for that matter a solid.). Such fluids cannot be described by constitutive expressions for the stress in terms of the shear rate, they however can be described by a constitutive expression for the shear rate in terms of the stress. Of course, such a constitutive relation is not an implicit relation, however, if in such a fluid the viscosity were to depend on the shear rate as well as the mean value of the stress, we would have a fluid which would need an implicit constitutive relation to describe its response characteristics. Since there are several real fluids whose material properties depend on both the mean value of the stress and the shear rate, such implicit constitutive relations are definitely necessary to describe the behavior of real fluids.

When one considers the homogenized modeling of colloids and suspensions as a single continuum one finds the behavior to warrant the need for implicit constitutive relations. The experiments of Boltenhagen et al. [19] on Tris (2-hydroxyethyl) tallowalkyl ammonium acetate (TTAA) surfactant dissolved in water containing sodium salicylate (NaSal) clearly shows the need for implicit constitutive relations (see the figure in the paper by Boltenhagen et al. [19])). The experiments of Boltenhagen have been corroborated using an implicit model by Perlocova and Prusa (see the figure in Perlocova and Prusa [20]). There are numerous such examples and the reader can find references to some of them in the paper by Perlocova and Prusa [20].

2. Preliminaries

I shall provide a very brief review of the kinematical terms and other concepts that we need to make this paper self-contained (a more detailed discussion of the kinematics can be found in Truesdell [21]). Let $x$ denote the current position of a particle in the body, which is at $X$ in a stress-free reference configuration. Let

$$x=\mathsf{\chi }\left(X,t\right)$$

(1)

denote the motion of the particle $X$ at time t. We shall assume that the motion is one to one and hence invertible.

Let $F$ denote the deformation gradient defined through:

$$F=\frac{\partial \mathsf{\chi }}{\partial X}$$

(2)

The velocity is defined through:

$$v=\frac{\partial \mathsf{\chi }}{\partial t},$$

(3)

the velocity gradient $L$, and its symmetric part $D$ and its skew part $W$ are defined through:

$$L=\frac{\partial v}{\partial x},D=\frac{1}{2}[L+{(L)}^T],W=\frac{1}{2}[L-{(L)}^T].$$

(4)

The Cauchy-Green tensors $B$ and $C$ are defined through:

$$B:=F{F}^T,C:=F^{T}F.$$

(5)

Let $\mathsf{\xi }$ be the position occupied by the point $X$ at time $\tau ;$ that is:

$$\mathsf{\xi }=\mathsf{\chi }(X,\tau )=\mathsf{\chi }({\mathsf{\chi }}^{-1}(x,t),\tau ):={\mathsf{\chi }}_t(x,\tau ).$$

(6)

The above allows one to use the configuration at time t as a reference configuration and the mapping ${\mathsf{\chi }}_t$ is referred to as the relative deformation gradient (Since all measurements are made with regard to some reference, and is hence relative to that, to give this mapping the nomenclature relative motion is not very meaningful. This motion ought to be called precisely what it is, namely motion relative to the configuration at time t being the reference. Since such a statement is cumbersome, we shall continue with the customary nomenclature, namely relative motion.). The relative deformation gradient $F_t(x,\tau )$ is defined through:

$$F_t(x,\tau )=\frac{\partial {\mathsf{\chi }}_t}{\partial x}.$$

(7)

One can define the relative stretches, relative rotations, the relative Cauchy-Green tensors and the relative strains in a standard manner. We shall not do so here (see Truesdell [21] for a detailed discussion of the relevant issues).

Before introducing the algebraic implicit constitutive relations, we shall very briefly discuss implicit models wherein the histories of the stress, density and appropriate kinematical quantities are related. A sub-class of such implicit constitutive relations are those wherein the stress at a point in the material depends on the history of how the body has been deformed. In order to define such constitutive relations we need to define the history of a function $f^t$ of $f$ through:

$$f^t(s)=f(t-s),$$

(8)

where $f$ can stand for a scalar, vector or second order tensor.

Let $\rho$ and $T$ denote the density and Cauchy stress, respectively. A Simple Fluid (see Noll [22]) is defined as one wherein the Cauchy stress is related to the history of the density and the deformation gradient in the following manner:

$$\begin{gathered} T= \underset{s=o}{\overset{\infty }{\Im }}\left[{\rho }^t\left(x,s\right),F_t{}^t\left(x,s\right)\right], \\ =\underset{s=o}{\overset{\infty }{\Im }}\left[\rho \left(x,t-s\right),F_t\left(x,t-s\right)\right] \end{gathered}$$

(9)

where $\underset{s=o}{\overset{\infty }{\Im }}$ denotes an operator which assigns to histories, tensors (Coleman and Noll [23] call the operator a “functional”, a term that is used in the mathematical literature to denote the special class of operators that map vectors belonging to vector spaces into the Reals. Also, in this paper, in all the equations in which the symbol $\underset{s=o}{\overset{\infty }{\Im }}$ appears, it does not mean the exact same operator but stands for a general operator.).

3. The Implicit Model Defined through $f(\rho ,T,D)=0$

Before discussing the class of algebraic implicit models of the form $f(\rho ,T,D)=0,$ we briefly introduce general implicit models for fluids of the form:

$$\underset{s=o}{\overset{\infty }{\Im }}\left[\rho \left(x,t-s\right),F_t\left(x,t-s\right),T\left(x,t-s\right)\right]=0$$

(10)

Such models are however too general to be of any use with regard to practical problems. A sub-class of the above general class are rate type implicit models that take the form:

$$f\left(\rho ,F,\dot{F},\mathrm{...}\stackrel{\left(n\right)}{F},T,\dot{T},\mathrm{...}\stackrel{\left(m\right)}{T}\right)=0,$$

(11)

where the superscripts denote derivative with respect to time. The classical models due to Maxwell [24], Burgers [1], Oldroyd [2] and others fall into the above class. Fluids of the differential type given by the constitutive expression

$$T=f(\rho ,A_1,--—,A_n),$$

(12)

where:

$$A_1=2D,$$

(13)

and:

$$A_n=\frac{d{A}_{n-1}}{dt}+A_1(\frac{\partial v}{\partial x})+{(\frac{\partial v}{\partial x})}^T{A}_1,$$

(14)

$A_n$, $n=1,2,--$, being the Rivlin-Ericksen tensors (see Rivlin-Ericksen [25] also are a special sub-class of the implicit constitutive Relation (11).We shall not consider such general rate type or differential type models in this article but we shall consider a far simpler class of models which we shall introduce next.

While implicit constitutive models that are used to describe non-Newtonian fluids such as the models due to Maxwell [24], Burgers [1] and Oldroyd [2] involve time derivatives of the stress and/or the time derivatives of the symmetric part of the velocity gradient, implicit models of the form $f(\rho ,T,D)=0,$ do not involve such time derivatives and hence we shall refer to them as implicit algebraic constitutive relations. Interestingly, such constitutive relations, while they are incapable of describing stress relaxation, seem to be capable of explaining the response that is exhibited by several colloidal solutions (see Perlocava and Prusa [20]). They also describe fluids those whose material properties can depend on the mean value of the stress, and as most fluids do exhibit dependence of material properties such as the viscosity on the mean value of the stress (see Andrade [26], Bridgman [16]) such models are very useful and deserve much more attention than they have been given thus far.

Before we investigate the implications of a model given by the constitutive relation $f(\rho ,T,D)=0,$ let us consider the physical motivation for the existence of such models. The fact that the viscosity of fluids can depend on the mean value of the stress goes back to the beginnings of fluid dynamics (a detailed history of the same can be found in book by Bridgman [16] who however is not careful in differentiating the distinctionbetween the thermodynamic pressure and the mean value of the stress, the mechanical pressure (The terminology “pressure” is unfortunately used in a variety of senses and the exact sense in which it is used is invariably left unsaid. It is used to describe the thermodynamic pressure in compressible fluids, it is used as a surrogate for the mean value of the stress, referred to as the mechanical pressure in incompressible fluids, it is used to refer to the Lagrange multiplier that enforces the constraint of incompressibility in incompressible fluids, etc. None of these terminologies refer to the same quantity in general (see Rajagopal [27]. In fact, Andrade, Bridgman and others play fast and loose with the terminology.). In Bridgman’s book he provides the following dependence of the viscosity on the density, pressure and temperature:

$$\mu (\rho ,p,\theta )=A{(\rho )}^{\frac{1}{2}}(\exp [p+\rho r^2]\frac{s}{\theta }),$$

(15)

where $A,s$ are constants, and $\theta$ is the absolute temperature. The problem with the above expression for the viscosity is that the meaning of the pressure “$p$” is not just left ambiguous, unacceptable liberties are taken with regard to the usage of the terminology. In the above equation, “p”cannot stand for the thermodynamic pressure for in this case it could be expressed in terms of the density and temperature and can be eliminated from the above expression. Thus “p”has to stand for the mean value of the stress, but there is no notion of a tensorial stress introduced in the text (see Rajagopal [27]) for a detailed discussion of the relevant issues). In nonlinear fluids, the viscosity, which is a material property can depend on the invariants of the stress and the invariants of appropriate kinematic quantities and it makes sense to assume that it depends on the mean value of the stress.

The sloppiness of Bridgman [16] in not delineating whether in the formula for the viscosity that he gives “p” stands for the thermodynamic pressure or the mean value of the stress becomes irrelevant in the case of an incompressible fluid for which we can unambiguously interpret the “pressure” as the mean value of the stress, and the constitutive relation for the fluid takes the form (Fluids whose viscosity is a function of the stress are also referred to as Piezo-viscous fluids.)

$$T=-pI+2\mu (\mathrm{p})D,$$

(16)

and since the fluid is incompressible and can undergo only isochoric motions that implies that:

$$trD=0,$$

(17)

and hence:

$$p=-\frac{1}{3}(trT),$$

(18)

which implies that the Equation (16) takes the form:

$$T=\frac{1}{3}(trT)I+2\mu (\frac{1}{3}trT)D.$$

(19)

While such an equation allows one to express $D$ as a function of $T$ we see that $T$ is not necessarily expressible explicitly as a function of $D$. (It makes eminent sense in the case of the Navier-Stokes theory to express the symmetric part of the velocity gradient in terms of the density and the stress rather than what is done customarily. In fact, were one to adopt such an approach one would not give any credence to the Stokes relation that is invoked in the classical Navier-Stokes theory as it would be evident that such an assumption is fatally flawed. It is unfortunate that Stokes [11] suggested such an assumption (which he later doubted seriously (Stokes [12]) and Maxwell [24] compounded the folly by claiming that he could derive it from the kinetic theory of gases (see Rajagopal [28] for a detailed discussion of the relevant issues). Despite a plethora of experimental evidence to the contrary, the assumption is yet being used bearing witness to the power of authority.).

One can ask whether it is reasonable to assume that the variation in pressure is sufficiently high that it changes the viscosity significantly while the changes to the density are yet sufficiently small that the fluid can be considered to be incompressible. In the case of many organic liquids, while material properties like viscosity can change by as much as a factor of ${10}^8$, the density changes by just a few percent (see Rajagopal [14]) when the mean value of the stress is varied over a large range, and thus such fluids can be modeled as incompressible fluids whose material properties depend on the mean value of the stress. Such as assumption is at the heart of the field of elastohydrodynamics (see Szeri [29]).

Stokes (Stokes [11] remarks “‘If we suppose μ to be independent of the pressure also, and substitute . . . ’ and he also comments soon afterward that ‘Let us now consider in what cases it is allowable to suppose μ to be independent of the pressure. It has been concluded by Du Buat from his experiments on the motion of water in pipes and canals, that the total retardation of the velocity due to friction is not increased by increasing the pressure . . . I shall therefore suppose that for water, and by analogy for other incompressible fluids, μ is independent of the pressure’”.) recognized that the viscosity of fluids could in general depend upon the pressure (the mean value of the stress) but in certain special flows this dependence on the pressure could be ignored. It is also well established that in many fluids the viscosity depends on the shear rate. Suppose we have a generalization of the classical compressible Navier-Stokes fluid wherein we only consider the shear viscosity to depend on the mean value of the stress and shear rate so that it takes the form:

$$T=-p(\rho )I+\lambda (\rho )(trD)I+2\mu (\rho ,trT,tr{D}^2)D,$$

(20)

or the generalization of the classical incompressible Navier-Stokes fluid that takes the form:

$$T=-pI+2\mu (\rho ,trT,tr{D}^2)D.$$

(21)

In both these cases, we cannot express either the stress explicitly as a function of the symmetric part of the velocity gradient or the symmetric part of the velocity gradient explicitly as a function of the stress. Both these constitutive relations are of the form:

$$f(\rho ,T,D)=0.$$

(22)

Let us now suppose that $f$ that appears in the Relation (22) is an isotropic function of the tensors $T$ and $D$. Then $f$ has to satisfy

$$Qf\left(\rho ,T,D\right)Q^T=f\left(\rho ,QT{Q}^T,QD{Q}^T\right)\forall Q\in {\rm O},$$

(23)

where ${\rm O}$ denotes the set of all orthogonal transformations. It then follows that:

$${\alpha }_{0}1+{\alpha }_{1}T+{\alpha }_{2}D+{\alpha }_3{T}^2+{\alpha }_4{D}^2+{\alpha }_5\left(DT+TD\right)+{\alpha }_6\left(T^{2}D+D^{2}T\right)+{\alpha }_7\left(T{D}^2+D^{2}T\right)+{\alpha }_8\left(T^2{D}^2+D^2{T}^2\right)=0$$

(24)

where the material functions ${\alpha }_i,i=0,\mathrm{...},8,$ depend on the density $\rho$ and the invariants

$$trT,trD,tr{T}^2,tr{D}^2,tr{T}^3,tr{D}^3,tr\left(TD\right),tr\left(T^{2}D\right),tr\left(D^{2}T\right),tr\left(D^2{T}^2\right).$$

(25)

Perlocova and Prusa [20] consider a special case of the above model to describe the experiments on colloidal systems by Boltenhagen et al. [19] that cannot be described by the fluid models wherein the stress is expressed as an explicit function of the velocity gradient.

The class of models defined by Equations (24) and (25) includes as sub-classes fluids defined through:

$$T={\lambda }_{0}I+{\lambda }_{1}D+\alpha {\lambda }_2{D}^2,$$

(26)

where the material moduli ${\lambda }_i,i=1,2,3$ are functions of density $\rho$ and the invariants $trT$, $tr{T}^2$ and $tr{T}^3$, that is the general Stokesian fluid model (see Stokes [11]), and also:

$$D={\beta }_{0}1+{\beta }_{1}T+{\beta }_2{T}^2,$$

(27)

where the material moduli ${\beta }_i,i=1,2,3$ depend on the density $\rho$ and the invariants $trD,$ $tr{D}^2$ and $tr{D}^3$.

The classical Navier-Stokes fluid model (Navier [7], Stokes [11]) can be expressed either as:

$$T=-p(\rho )I+\lambda (\rho )(trD)I+2\mu (\rho )D,$$

(28)

where $p(\rho )$ is identified as the thermodynamic pressure and $\lambda (\rho )$ and $\mu (\rho )$ refer to the bulk-viscosity (The bulk viscosity $\lambda$ cannot be determined directly from any experiment. Once can measure the shear viscosity $\mu$ and the bulk modulus $(3\lambda +2\mu )$ and hence infer $\lambda$.) and the shear viscosity. The classical Navier-Stokes fluid can also be expressed as (see Rajagopal [29])

$$D={\gamma }_0(\rho )I+{\gamma }_1(\rho )(\mathrm{tr}T)I+{\gamma }_2(\rho )T.$$

(29)

In fact, as explained in detail by Rajagopal [28], the above representation for the model is preferable, both from the perspective of the philosophy behind the development of models and also as it shows an assumption that has been given far more importance than it should have been, is in fact incorrect, namely the Stokes’ assumption. Stokes makes the assumption for some special flows wherein he feels that the assumptions might be applicable (Stokes [11] remarks “Of course we may at once put k=0 if we assume that in the case of a uniform motion of dilatation the pressure at any instant depends only on the actual density and temperature at that instant and not the rate at which the former changes with time. In most cases in which it would be interesting to apply the theory of the friction of fluids the density is either constant or may without sensible error be regarded as constant, or else changes slowly with time. In the first two cases the result would be the same and in the third nearly the same whether k were equal to zero or not. Consequently, if theory and experiment should in such cases agree, the experiments must not be regarded as confirming that the part of the theory which relates to supposing k to be equal to zero.” Stokes however had serious doubts about his assumption for a few years later (Stokes [12]) he remarks “Although I have shown (Vol. I., p. 119) that on the admission of a supposition which Poisson would probably have allowed the two constants in his equations of motion are reduced to one, and the equations take the form (1t), and although Maxwell obtained the same equations from his kinetic theory of gases (Philosophical Transactions for 1867, p. 81) I have always felt that the correctness of the value $\frac{\mu }{3}$ for the coefficient of the last term in (1) does not rest on as firm a basis as the correctness of the equations of motion of an incompressible fluid, for which the last term does not come in at all. If the supposition made above be not admitted, we must replace the coefficient $\frac{\mu }{3}$ by a different coefficient, which may be written $\frac{\mu }{3}+\varpi$ and $\varpi$ must be positive, as otherwise the mere alternate expansion and contraction, alike in all directions, of a fluid, instead of demanding the exertion of work upon it, would cause it to give out work. But if the positive constant exists, the coefficient of the squared velocity of dilatation in the transformed expression for DV in p. 43, instead of being $\frac{2\mu }{3}$, will be $-\frac{2\mu }{3}+\varpi$ and in order that the quantity under the sign of triple integration may vanish, we must have in addition to the Equations (137) on p. 44 the further equation $\delta =0$, and the conclusion is the same as in the case of an incompressible fluid.”). However, not one experiment bears witness to the Stokes assumption. In fact, as Rajagopal [28] has shown, starting from the representation Equation (29), that such an assumption is untenable.

It has been established beyond any dispute that properties of materials, mechanical properties such as viscosity and shear modulus, and thermal, electrical, optical, magnetic and other properties depend on the mean value of the stress. With regard to the viscosity of fluids, as early as 1893 based on experiments Barus [30] concluded that it varies exponentially with pressure. The recent experiments of Bair and Koptke [31] show an increase of a factor of over ${10}^8$ over the range of pressures that they considered. Clearly, one cannot ignore such a strong variation of the viscosity with pressure and as most fluids also shear thin or shear thicken at the very least we need to use algebraic implicit constitutive relations to describe the response of many fluids over a reasonable range of pressure and shear rates.

Henceforth, we will confine our attention to incompressible homogeneous fluids and hence the density $\rho$ will be considered a constant.

4. A Sub-Class of Fluids in whichViscosity Depends only on Pressure

We shall briefly discuss flows of fluids that are described by a special sub-class of constitutive relations (24) and (25). In particular we shall discuss incompressible fluids defined by the constitutive relation

$$T+pI-2\mu (\mathrm{p},\mathrm{tr}{D}^2)D=0.$$

(30)

Since the fluid is incompressible, it can undergo only isochoric motions and hence one has to meet the constraint Equation (13), that is $trD=0.$ Thus Equation (30) is an implicit equation and in general neither the stress nor the symmetric part of the velocity gradient can be explicitly defined in terms of the other.

A special sub-class of the class defined by Equation (30) is incompressible fluids wherein the stress is given by the relation:

$$T+pI-2\mu (\mathrm{p})D=0.$$

(31)

Since $p$ is the negative of the mean value of the stress, we note that in the case of the above model $D$ can be expressed explicitly as a function of the stress $T,$ and thus the constitutive relation is not an implicit relation. Local existence and uniqueness results for the equations governing the flow of a fluid defined by Equation (31) have been established by Renardy [32] under assumptions for the viscosity that clearly violates experimental observations (While the viscosity grows exponentially with pressure, Renardy [32] needs the ratio of the viscosity to the pressure to tend to zero as the pressure tends to infinity.). Gazzola [33] and Gazzola and Sechi [34] have established short time existence of a smooth solution for small data.

The first rigorous existence results for the equations governing the motion of fluids described by Equation (30) for large data were established by Malek, et al. [35,36], Hron et al. [37] and Franta et al. [38]. Interestingly, it is essential for the existence results that the viscosity depends on the shear rate, that is they are unable to prove existence results for the case of the viscosity depending only on the pressure. Malek et al. [35] were able to establish the existence of weak solutions for spatially periodic three-dimensional flows that are global in time, for a large class of viscosity-pressure relationships. However, it is essential that the viscosity depend on the shear rate in a certain manner for all these results to hold; none of the above results apply to the special sub-class of models described by Equation (30). This is an interesting open problem that deserves attention. Hron et al. [39] considered the flows of fluids modeled by Equation (30) wherein the viscosity depends only on the pressure. Even simple unidirectional flows of such fluids exhibit solutions that are markedly different from the flow of the incompressible Navier-Stokes model. (Suslov and Tran [40] examined the several solutions obtained by Hron et al. [39] and claimed that one of them for the flow between two parallel plates that showed an inflection point could not be correct. Suslov and Tran [40] are indeed correct if one were to restrict oneself to determining classical solutions to the problem wherein the pressure field is assumed to be continuous. However, as pointed out later by Hron et al. [39], if one allows for discontinuities in the pressure field, then the a solution such as that obtained by Hron et al. [39] is admissible (see Hron et al. [41] for a detailed discussion of the nature of various solutions to the problem). However, Suslov and Tran [40] are totally justified in their claim as Hron et al. [39] did not have any discussion whatsoever about the class of solutions that were being sought for the problem, classical solution, weak solution, etc. In fact, Hron et al. [39] were not aware of the discontinuity in the pressure field corresponding to their solution and only realized it in the light of the paper by Suslov and Tran [40]. In fact, it is wholly possible that the solutions with inflection points might not be stable to even infinitesimal disturbances, and thus a study of the stability of the solutions established by Hron et al. [39] is warranted.) (see Figure 2) After showing that unidirectional flows are only possible for special dependence of the viscosity on pressure, for viscosities wherein such unidirectional flows are possible, Hron et al. [37] show that non-unique solutions are possible unlike the situation in the case of the classical Navier-Stokes model.

Rajagopal et al. [42] have studied the flows of fluids with pressure dependent viscosity wherein the effects of gravity could be important. They are able to establish uniqueness of flows to the governing equation and also carry out a qualitative analysis concerning the nature of the solution to the governing equations. In the case of two special boundary value problems, which are modifications of Stokes’ first and second problem wherein the effect of gravity is incorporated, they are able to obtain exact solutions.

There is a considerable amount of work on fluids with pressure dependent viscosity within the context of lubrication theory as the flows of such fluids have relevance to problems in elastohydrodynamics. An approximation introduced by Reynolds [43] that is applicable to flows of the classical Navier-Stokes fluid that are relevant to problems concerning lubrication problems, has been extended to the case of fluids with pressure dependent viscosity in an ad hoc manner and studied by several authors. These derivations however are incorrect as observed by Schaffer et al. [44] and Greenwood [45], and Rajagopal and Szeri [4] have given a detailed and general discussion of the errors that were made in the modification of the Reynolds equation for fluids with pressure dependent viscosities. Using the modified equations developed by Rajagopal and Szeri [46], Saccomandi and Vergori [47] studied the flow of a fluid with pressure dependent viscosity down an inclined plane. They studied time dependent problems wherein one also has a free surface and incorporating the effects of surface tension and gravity they find several families of traveling wave solutions to the problems. Recently, a rigorous derivation of the modified Reynolds equation for fluids with pressure dependent viscosity has been put into place by Gustafsson et al. [48] who show that the modified equation implies that the pressure and viscosity are higher than that determined by the erroneous equation in certain specific boundary value problems that they considered.

In the case of a fluid whose viscosity depends both on the pressure and the shear rate, Rajagopal et al. [49] study the flows of such a fluid down an inclined plane and considered two distinct regimes, one in which the viscous and gravitational effects are of the same order and another wherein the effects of the pressure gradient is balanced by the viscous stresses in the bulk. In the first regime wherein the effects of gravity are of the same order as the viscous effects they find the possibility of breaking waves wherein the pressure dependence delays the breaking time, the effect being more pronounced in shear thinning fluids than shear thickening fluids. In the second regime where the effects of the pressure gradient are balanced by the viscous stresses, they are able to find traveling waves (see Rajagopal et al. [49] for a detailed discussion of the relevant issues).

5. Stress Power-Law Fluids

A sub-class of fluid models that has been studied in some detail recently that belongs to the class defined by Equation (27) is the class of incompressible stress power-law fluids whose constitutive relation takes the form (One could study compressible stress-power law fluids wherein the symmetric part of the velocity gradient is expressed as $D=\varphi (\rho )I+\alpha {[1+\beta \mathrm{tr}{T}^2]}^{n}T.$ In the case of such a constitutive relation $trD$ is not necessarily zero.):

$$D=\alpha [1+\beta {(tr{(T_d)}^2]}^n{T}_d,$$

(32)

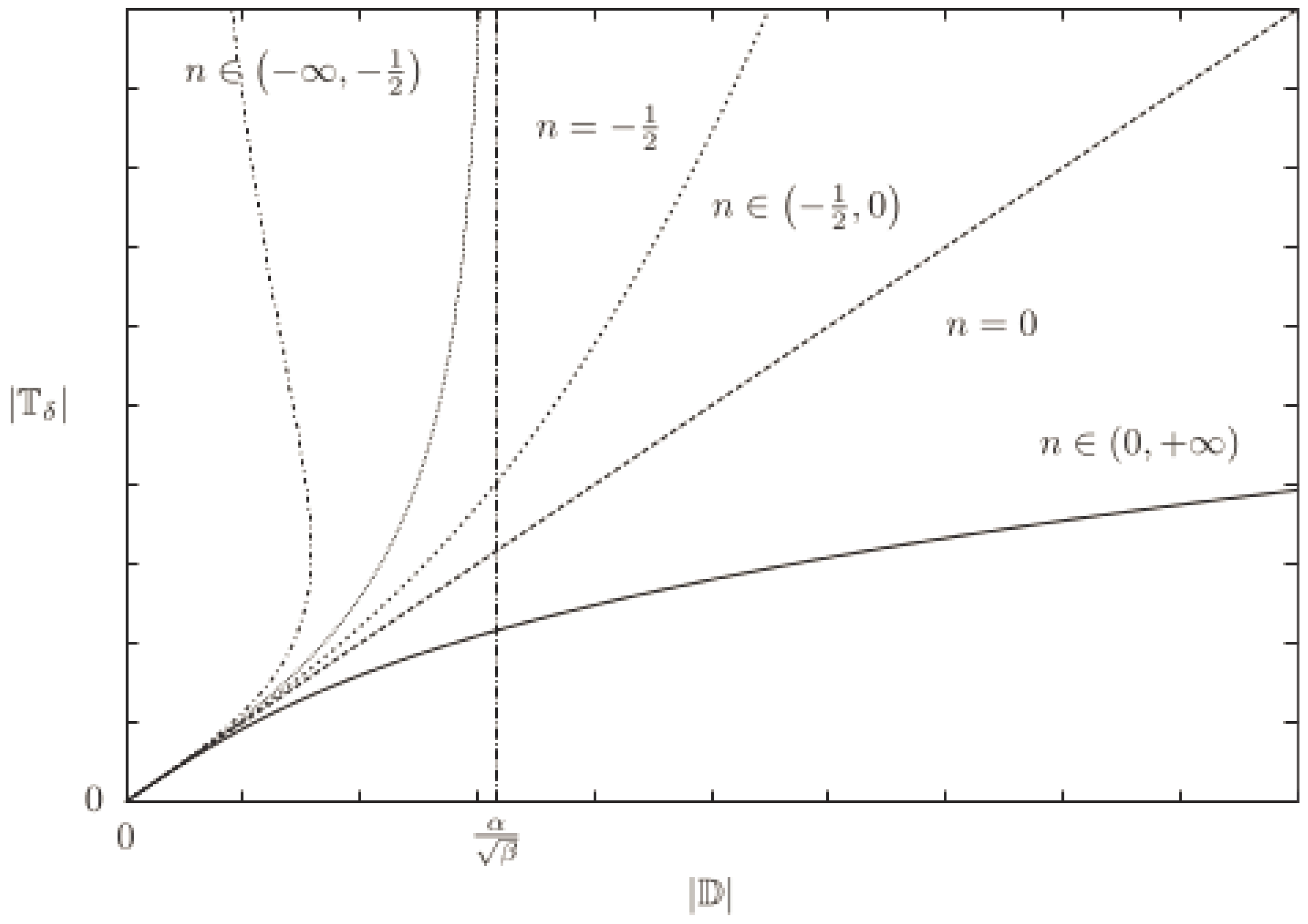
where $T_d$ denotes the deviatoric part of the stress. Such fluids can exhibit behavior that is not possible within the context of the classical power-law fluid model. Figure 3 shows the relationship between the shear stress and the shear rate for various values of n. The response exhibited for $n\in (-\infty ,-\frac{1}{2})$ cannot be described by the classical power-law fluid model.

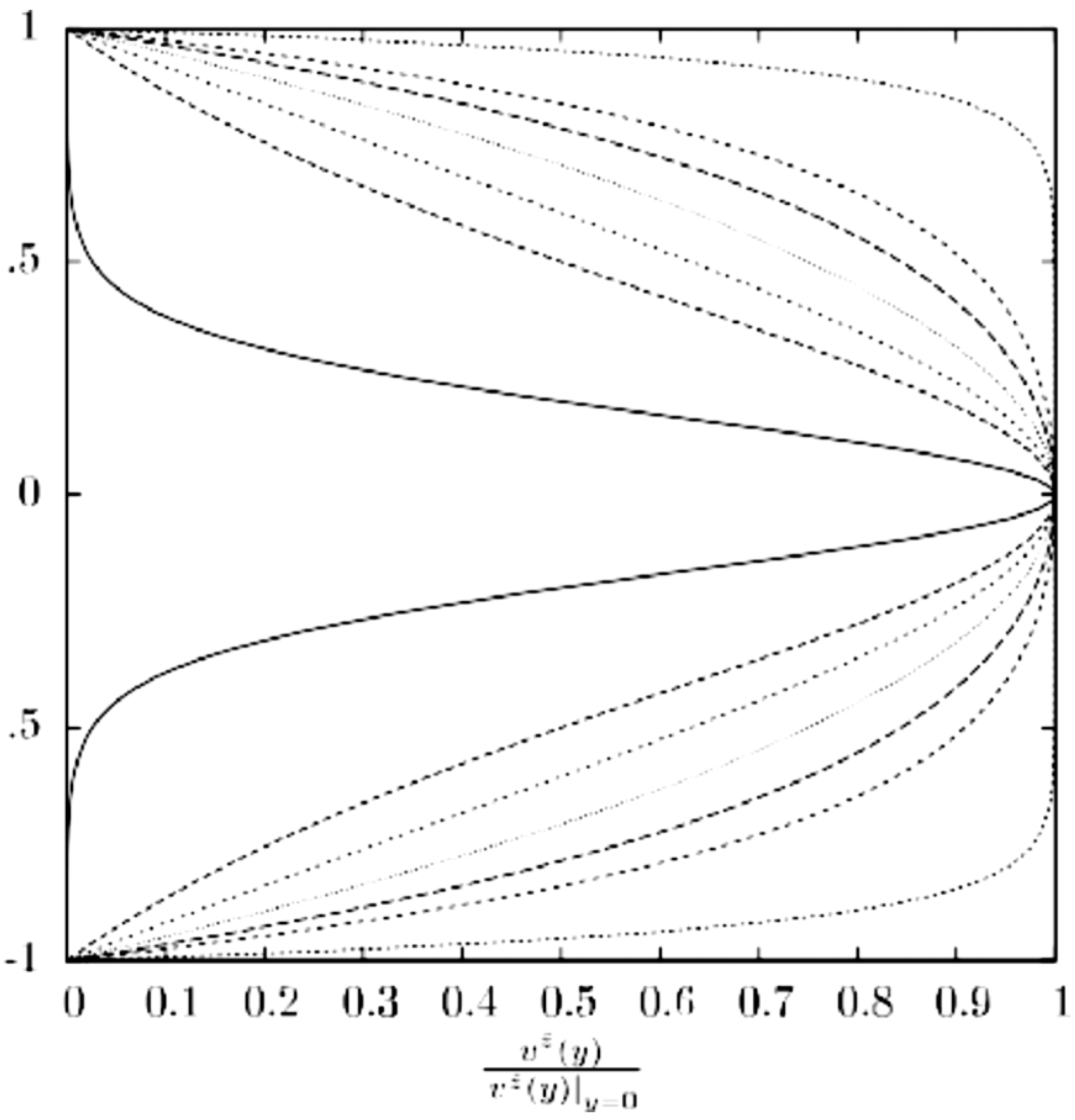
Malek, Prusa and Rajagopal [50] considered several simple flows of the stress power-law fluid given through the above constitutive relation: Plane Couette and Poiseuille flows, Hagen-Poiseuille flow, Cylindrical Couette flow, etc. In the case of Plane Poiseuille flow, the solutions for the stress power-law fluid can be very different from that for the classical power-law fluid (see the various velocity profiles in Malek, Prusa and Rajagopal [50]). Interestingly in the case of cylindrical Couette flow, they find that non-unique solutions are possible (see the discussion in Malek, Prusa and Rajagopal [50]. They also find that the boundary condition that is imposed can have a profound effect on the solvability of the governing equations.

Narayanan and Rajagopal [51] studied the counterparts to exact solutions to problems referred to as the Stokes’ first problem and Stokes’ second problem (see Stokes [12], Rayleigh [52]) in the case of the Navier-Stokes fluid. In the case of stress-power law fluids that can stress thin or stress thicken, they find the development of stress boundary layers. Recently, Mohankumar et al. [53] studied a variant of Stokes’ first problem within the context of stress power-law fluids. When the power-law index n = 0, they find a new exact solution wherein the stress is given in terms of a convolution integral. They also solve the governing equations numerically when the power law index is not zero.

A generalization of the power-law fluid that seems to be capable of describing the response of colloids takes the form (see Le Roux and Rajagopal [54], Perlacova and Prusa [20]):

$$D=\alpha ([1+\beta {(tr{(T_d)}^2]}^n+\lambda )T_d.$$

(33)

Such a constitutive relation allows one to describe non-monotone relationship between the shear stress and the shear rate, a situation that cannot be described by the classical fluid models.

Le Roux and Rajagopal [54] considered Plane Poiseuille flow of a fluid described by the constitutive Model (33). Even in the case of simple flows such as the counterparts to plane Couette and Poiseuille flows, one finds solutions with interesting new characteristics. In the case of the flow corresponding to plane Couette flow, different stress fields in the flow domain can have an identical velocity field and also satisfy the no slip boundary condition. When the fluid is slipping freely at one of the parallel plates while it meets either the no-slip or Navier-slip condition at the other plate, the boundary value problem has a unique solution. However, if the flowing fluid satisfies the Navier slip condition at both plates then the solution is quite uncharacteristic. The problem can have one, two or three solutions (velocity fields), depending on the values of the parameters that describe the model, the velocities of the plates and the shear forces applied to the fluid at the plates. One finds similar characteristics with regard to the solution to the counterpart to the classical Poiseuille flow problems.

6. Relevance of Implicit Models to Turbulence

The most important open problem in fluid mechanics and possibly physics is that of turbulence. Though intense research has been going on in the field for several decades there is no satisfactory model that can describe even a few of the numerous turbulent flows that abound. The two most prominent stumbling blocks that impede the progress in turbulence modeling are the propensity to think of the model as some minor departure from the classical Navier-Stokes fluid model and the susceptibility to treat the velocity and pressure as the sum of a basic part and a fluctuating part. Such an assumption goes against the dictates of causality, which would require one to think of the forces as the cause and kinematics as the effect. If fluctuations are to be taken into account, then one ought to take into account the fluctuations in the stresses and also the velocities. Fluctuations in the “pressure”, if by that one means the “mechanical pressure”akes into account only the mean value of the stress in the case of an incompressible fluid, and does not even take the mean valu of the stress into account in the case of a compressible fluid; and hence only partial fluctuations in the stress are taken into account. Implicit constitutive relations do away with both these stumbling blocks as implicit models need not be minor departures from the classical Navier-Stokes fluid model and more importantly one can incorporate fluctuations in both the velocity, as well as all the components of the stress in developing the turbulence model. It would be a very worthwhile effort to pursue the development of models for turbulence within the framework of implicit constitutive theories.

7. Concluding Remarks

After introducing general implicit constitutive relations, we have primarily discussed algebraic stress power-law model. Rate type-implicit models like the Oldroyd-B model, Burgers model, etc. have been studied in great detail by several authors and hence are not discussed here. However, in these studies the material parameters that characterize these models are either assumed to be constant or are only assumed to depend on the invariants of the symmetric part of the velocity gradient and not on the invariants of the stress. It seems reasonable that the material moduli of such fluids would also depend on the mean value of the stress and possibly the second and third invariants of the stress, as well as mixed invariants of the stress and the symmetric part of the velocity gradient. Such models have not been studied and deserve to be studied as there are several applications where such a dependence needs to be taken into consideration.