Partial Desalination of Saline Groundwater, including Flowback Water, to Produce Irrigation Water
Abstract
1. Introduction
1.1. Saline Groundwater Sources
1.2. Desalination Solutions
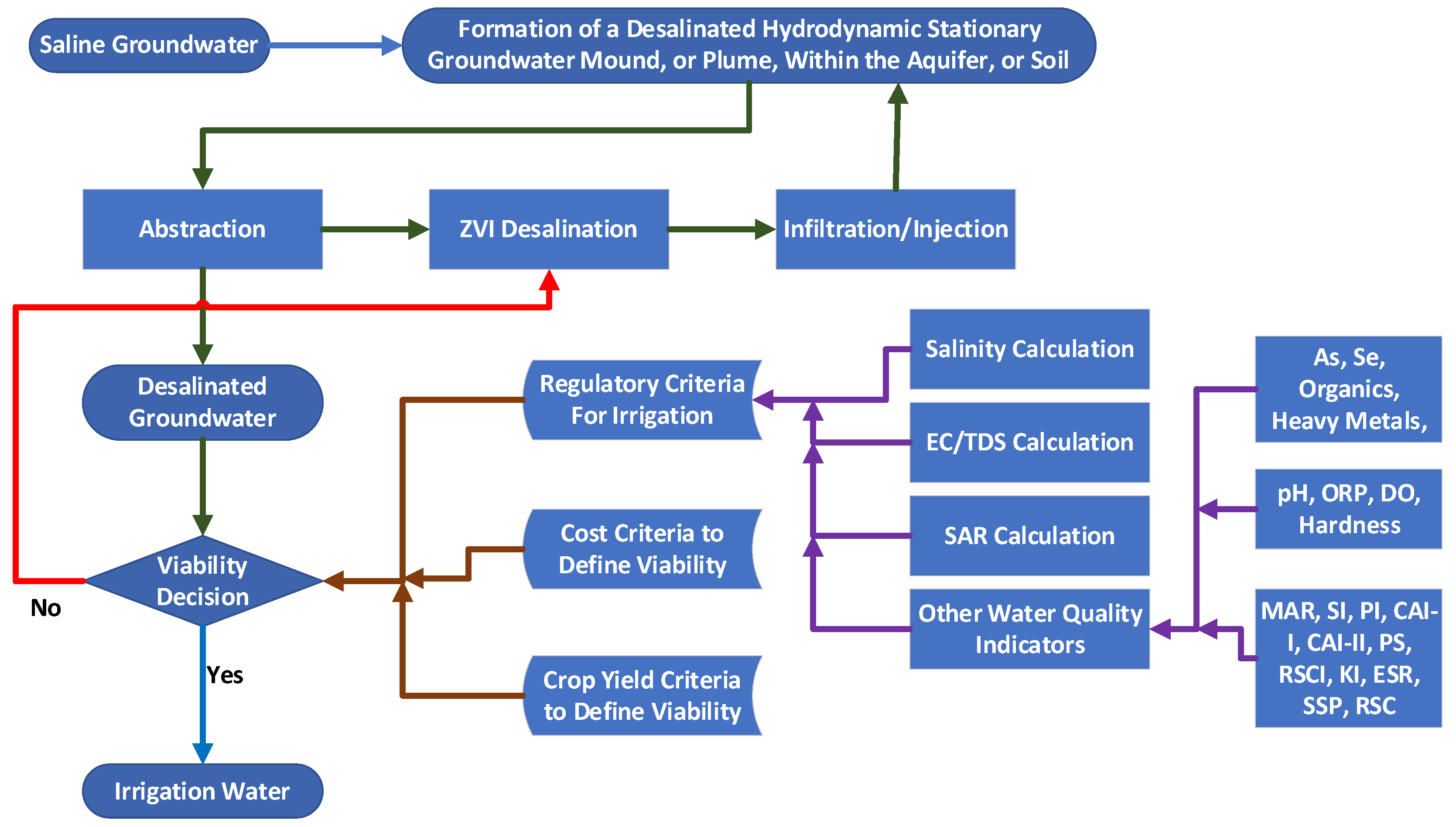
1.3. ZVI Desalination Considerations
1.4. Production of Irrigation Quality Water
1.5. Desalination Decision
- The expected crop yield and value following the use of the water;
- The expected costs associated with using the water,
- Whether the water complies with local regulations in terms of its chemistry and water quality indicators. Most global regulators have standards that have to be complied with.
2. Terminology, Materials and Methods
2.1. ZVI Terminology, Groundwater Salinity Indices and Patent Terminology
2.1.1. ZVI Definition
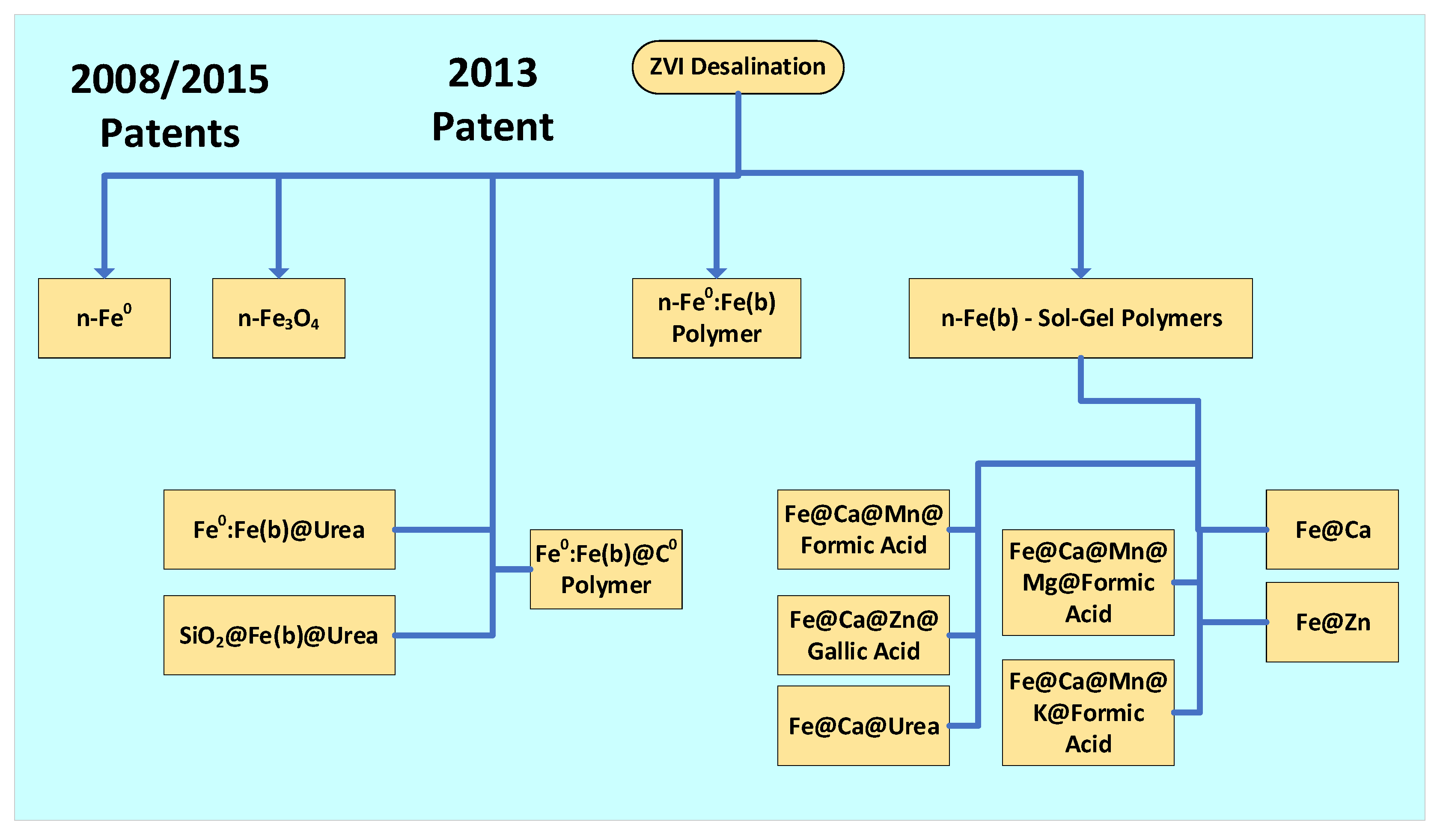
2.1.2. Patent Terminology
2.1.3. Desalination Pattern Classification
2.1.4. Salinity Indices
2.2. Assessment of Crop Yield Resulting from the Use of Partially Desalinated Irrigation Water
Yield Increase Assessment Methodology
- Increased crop yield and increased gross revenue;
- Increased choice of crops which can be grown on a holding; and
- Increased agricultural land value.
2.3. Polymer Terminology
2.3.1. Initial Polymer Product
2.3.2. Polymer Characterization
2.3.3. Polymer Terminology
2.4. ZVI Desalination Measurement
- Electrical conductivity (EC, mScm−1, dSm−1);
- Ion Selective Electrodes (ISE) for Na+ ions and Cl- ions;
- Evaporation of product and feed waters to produce a residual measurable product;
- Ion chromatography and spectroscopy to identify Na+ and Cl- ions;
- Flame emission photometry to identify Na+ ions
- Chemical titration to identify Cl- ions;
2.4.1. Desalination Assessment
2.4.2. Relationship between EC and Salinity
2.4.3. Significance of Fe0 Dissolution to Fen+ ions
2.4.4. Uncoated Fe0
2.4.5. Coated Fe0
2.5. Desalination Mechanism
- Fe0 surfaces corrode to form FexOyHz species and release Fen+ ions [56];
2.6. Desalination Pattern
- A plot of ion concentration at time t = n (Ct = n) versus reaction time, tr, or a plot of Ln(Ct = n) versus tr, will equate to a straight line for each time segment, where Ct = n either declines with time, or increases with time, indicating that the reaction is zero-order, or pseudo-zero order, or first-order, or pseudo-first order [6,7,59,60].
2.7. Statistical Methodology Used
- PCC = 0.9 to 1.0 (R2 = 0.81 to 1.00): Interpretation = very strong correlation
- PCC = 0.7 to 0.89 (R2 = 0.49 to 0.79): Interpretation = strong correlation
- PCC = 0.4 to 0.69 (R2 = 0.16 to 0.47): Interpretation = moderate correlation
- PCC = 0.1 to 0.39 (R2 = 0.01 to 0.15): Interpretation = weak correlation
- PCC = 0.0 to 0.10 (R2 = 0.00 to 0.01): Interpretation = negligible correlation
2.8. Data
2.9. Measurement Equipment
- ORP (oxidation reduction potential) meter (HM Digital) calibrated at ORP = 200 mV; Measured ORP (oxidation reduction potential) values are converted to Eh, mV as: Eh, mV = −65.667pH + 744.67 + ORP (mV), using a quinhydrone calibration at pH = 4 and pH = 7.
- pH meter (HM Digital) calibrated at pH = 4.01; 7.0; 10.0.
- EC (electrical conductivity) meter (HM Digital meter calibrated at EC = 1.431 mScm−1).
- Cl- ISE (Ion Selective Electrode); Bante Cl- ISE, EDT Flow Plus Combination Cl- ISE; Cole Parmer Cl- ISE attached to a Bante 931 Ion meter. Calibration was undertaken using 0.001, 0.01, 0.1, and 1.0 M NaCl calibration solutions.
- Na+ ISE (Ion Selective Electrode); Bante Na ISE, Sciquip Na ISE, Cole Parmer Na ISE attached to a Bante 931 Ion Meter. Calibration was undertaken using 0.001, 0.01, 0.1, and 1.0 M NaCl calibration solutions.
- Temperature measurements, were made using a temperature probe, attached to a Bante 931 Ion Meter.
2.10. Reactor Size Used
2.11. Materials Used
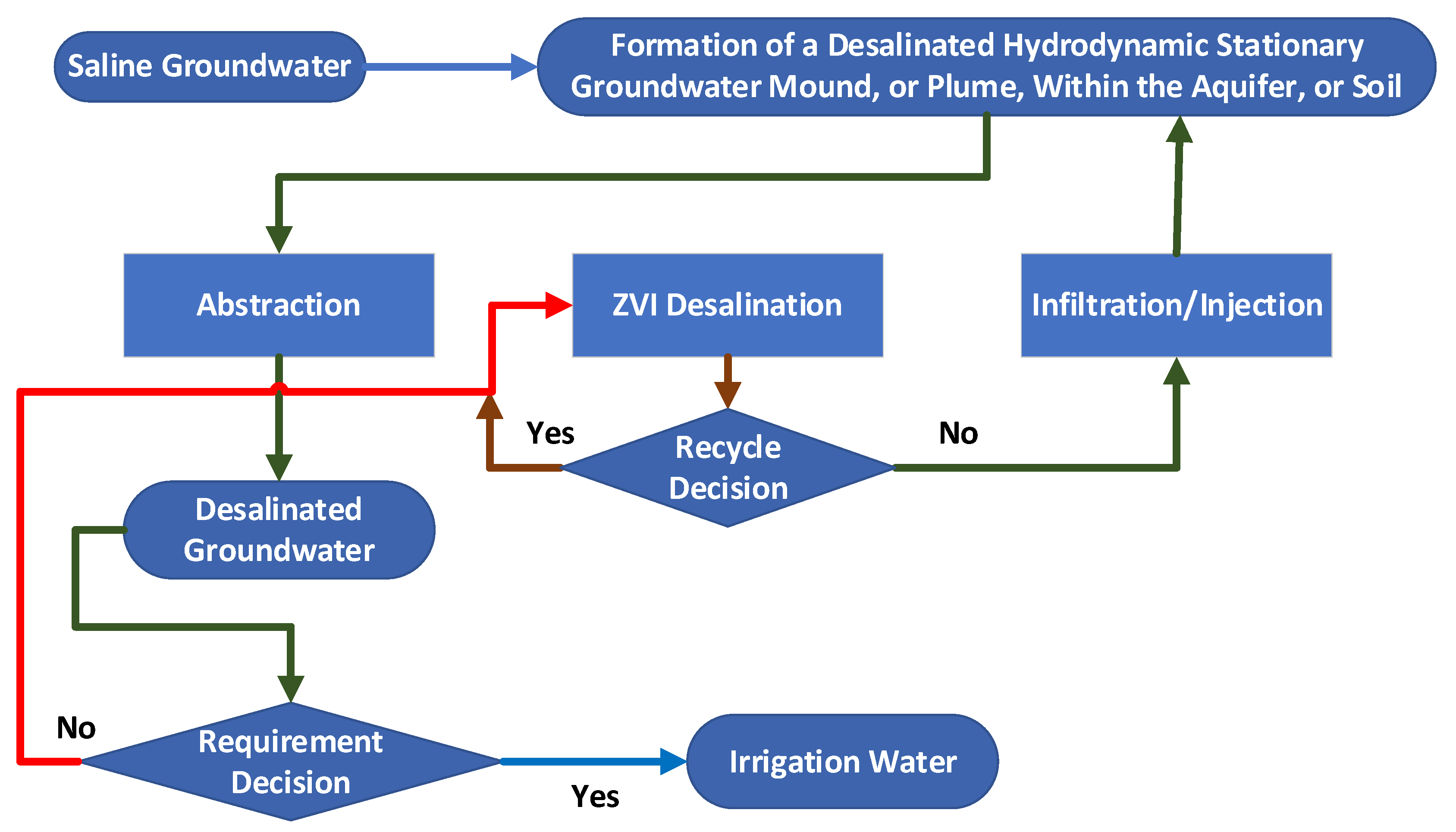
2.12. Hydrology of a Stationary Plume
2.13. Past ZVI Desalination Processes
3. n-Fe0:Fe(a,b,c) Polymers
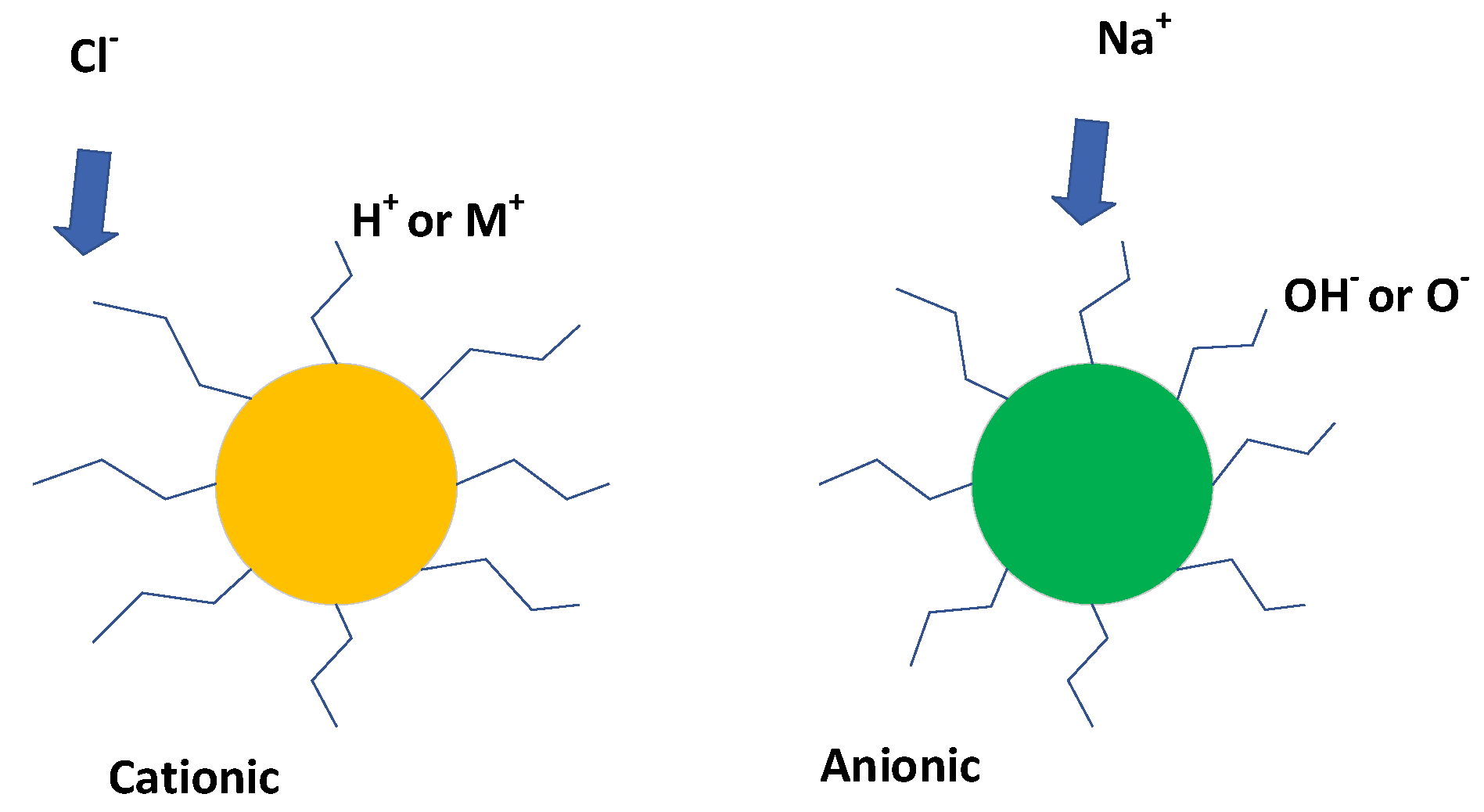
3.1. Functionalized Fe-Polymer Colloids
3.2. Possible Ion Transport Model
3.3. Fe:Fe(a,b,c) Polymer Spheres
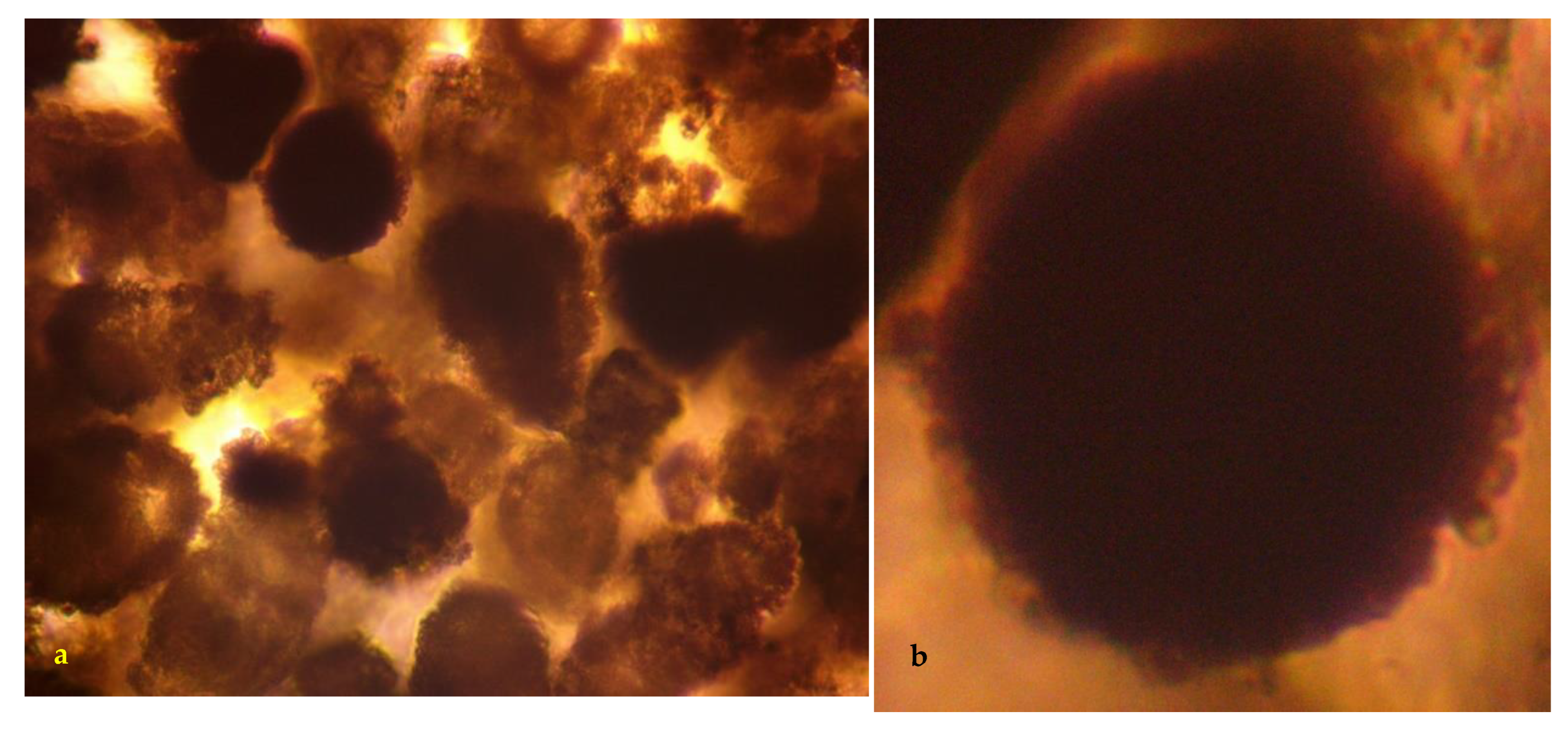
3.4. Colloidal Spheres
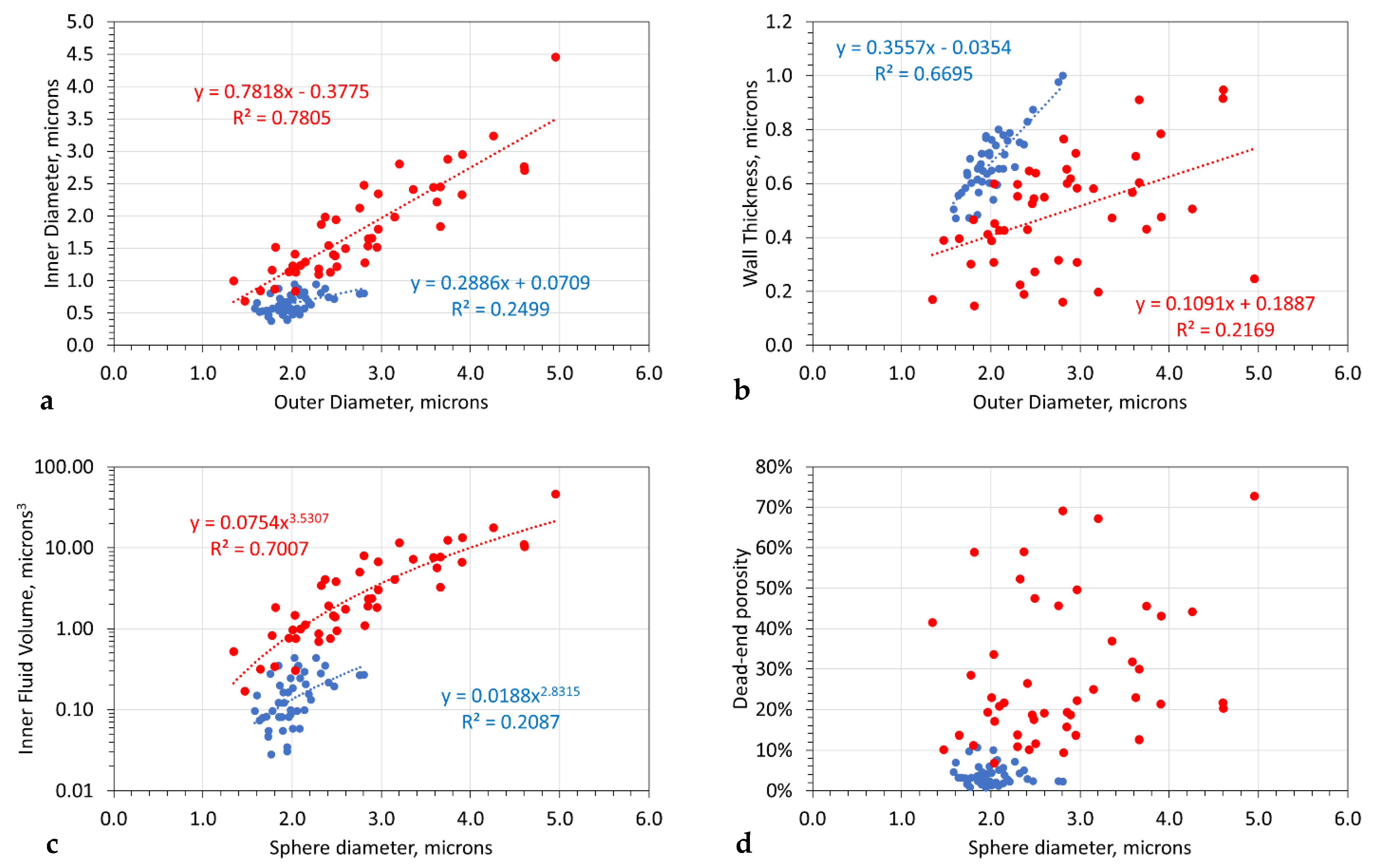
3.5. Colloidal Sphere Diameter
3.6. Fluid Core Volume of the Spheres
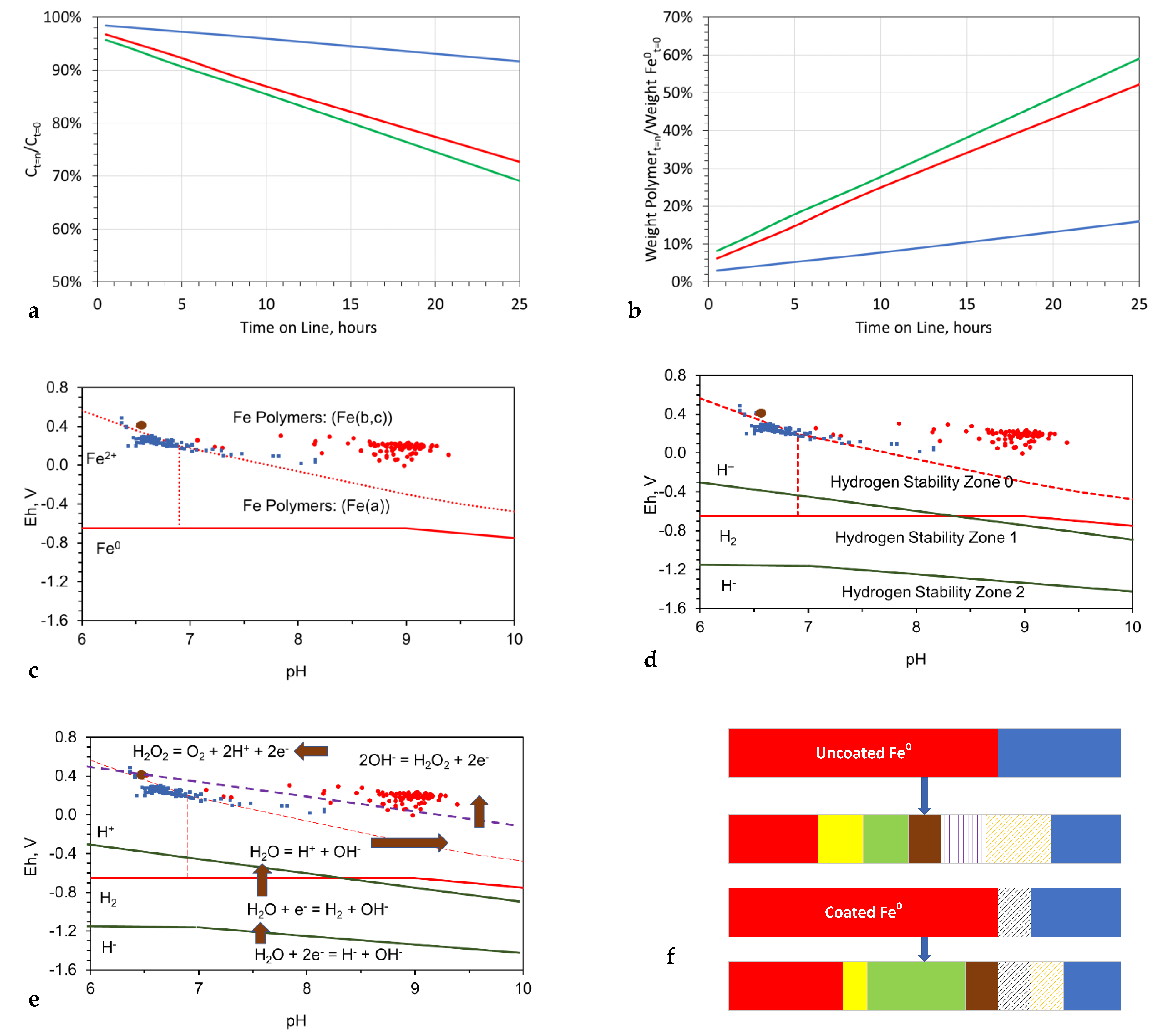
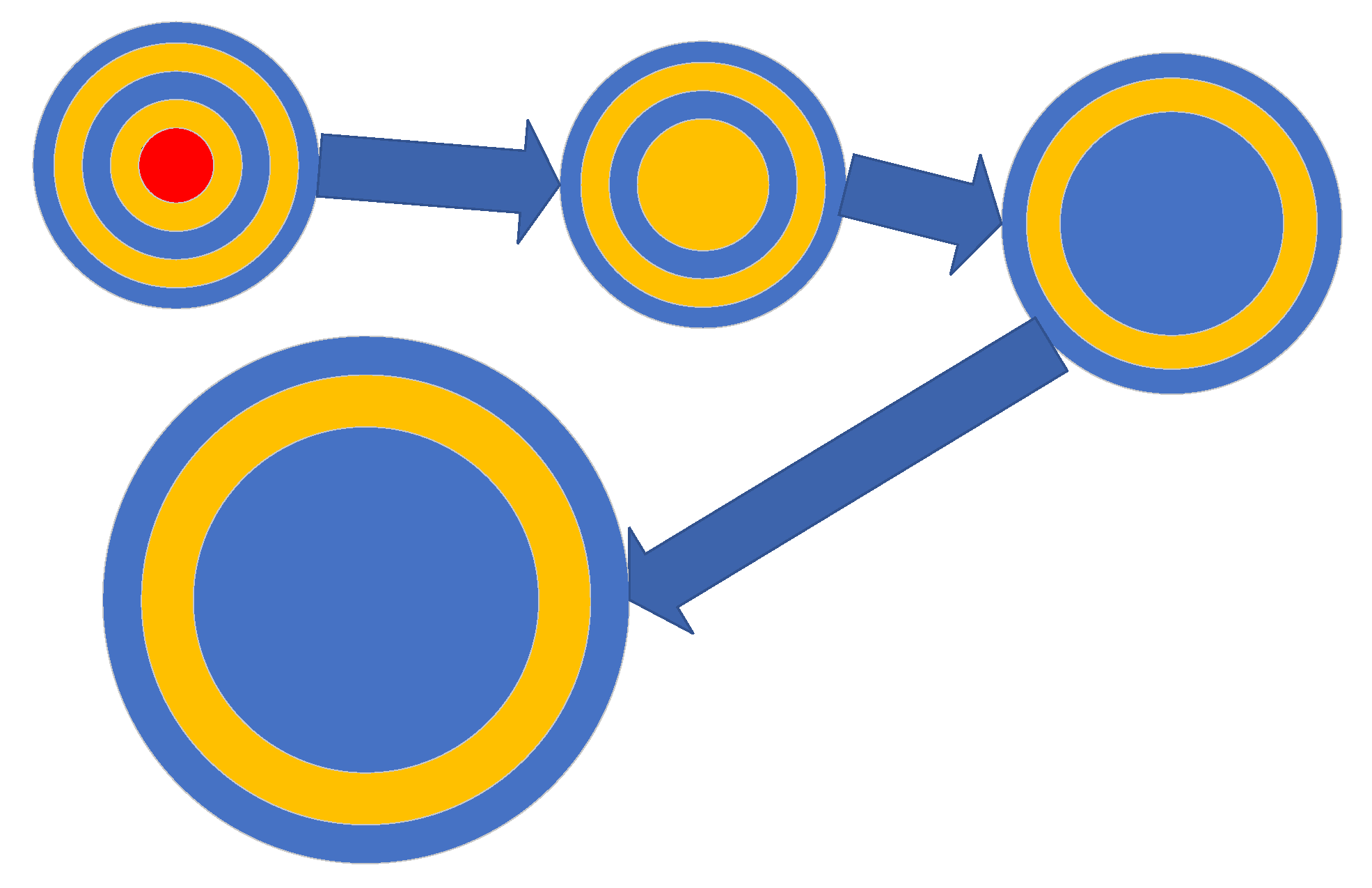
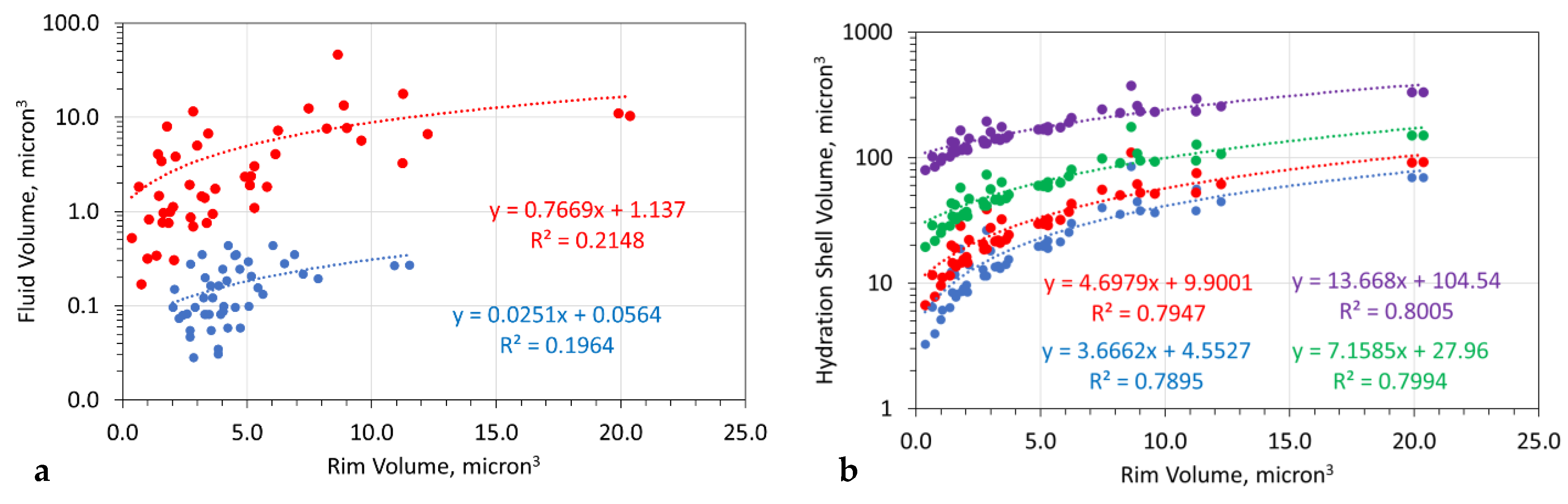
3.7. Change in Sphere Rim Thickness with Time
- For a sphere with a specific outer diameter, the inner diameter of the fluid sphere increases with time (Figure 7a);
- The average sphere outer diameter and the sphere size range increase with time (Figure 7a);
- Increasing reaction time results in an increase in the internal fluid volume of the spheres and a positive correlation developing between internal fluid volume and sphere size (Figure 7c);
- After 4000 h, the spheres appear to be completely mineralized (Figure 6c).
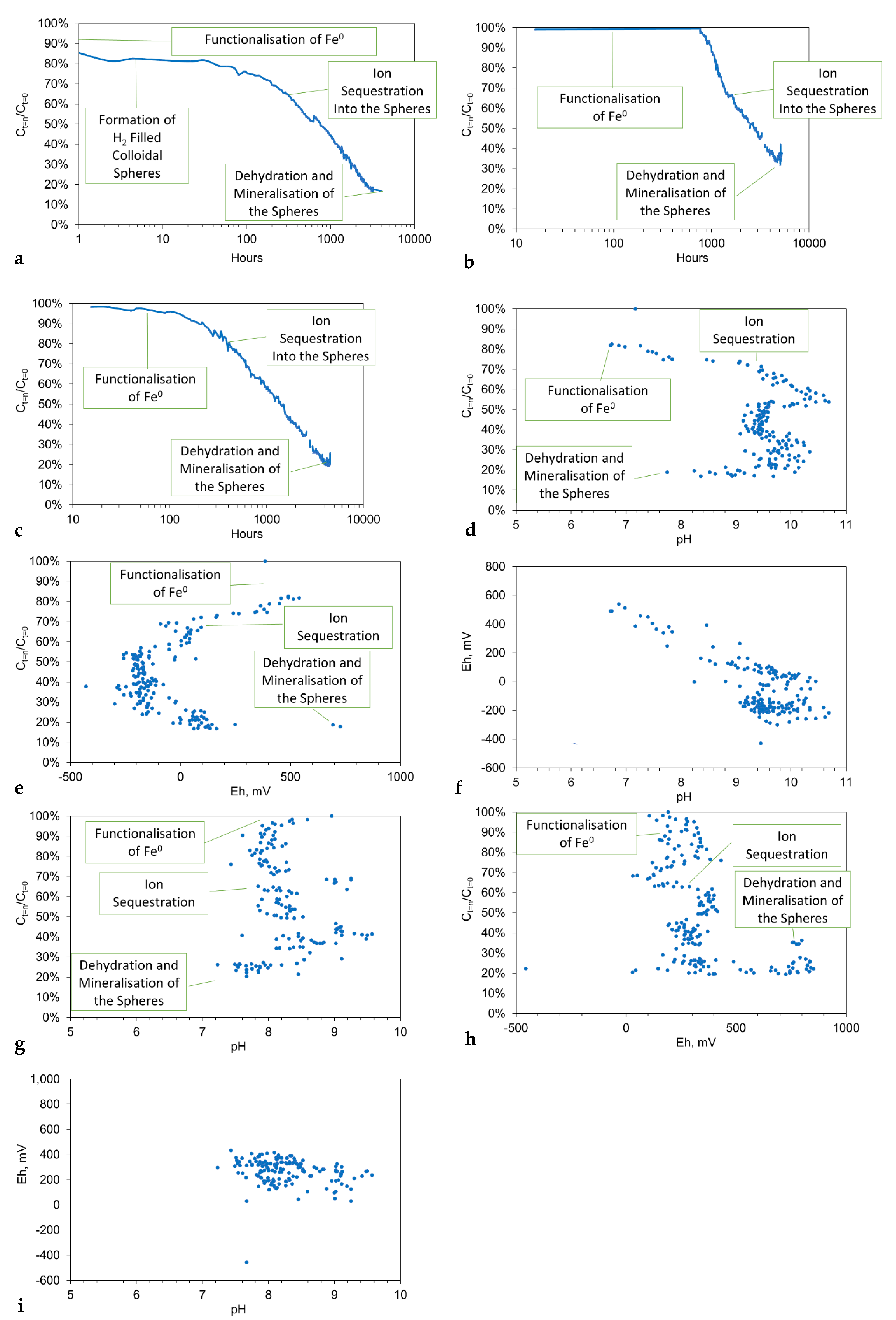
3.8. Model for Desalination by the Polymer Spheres
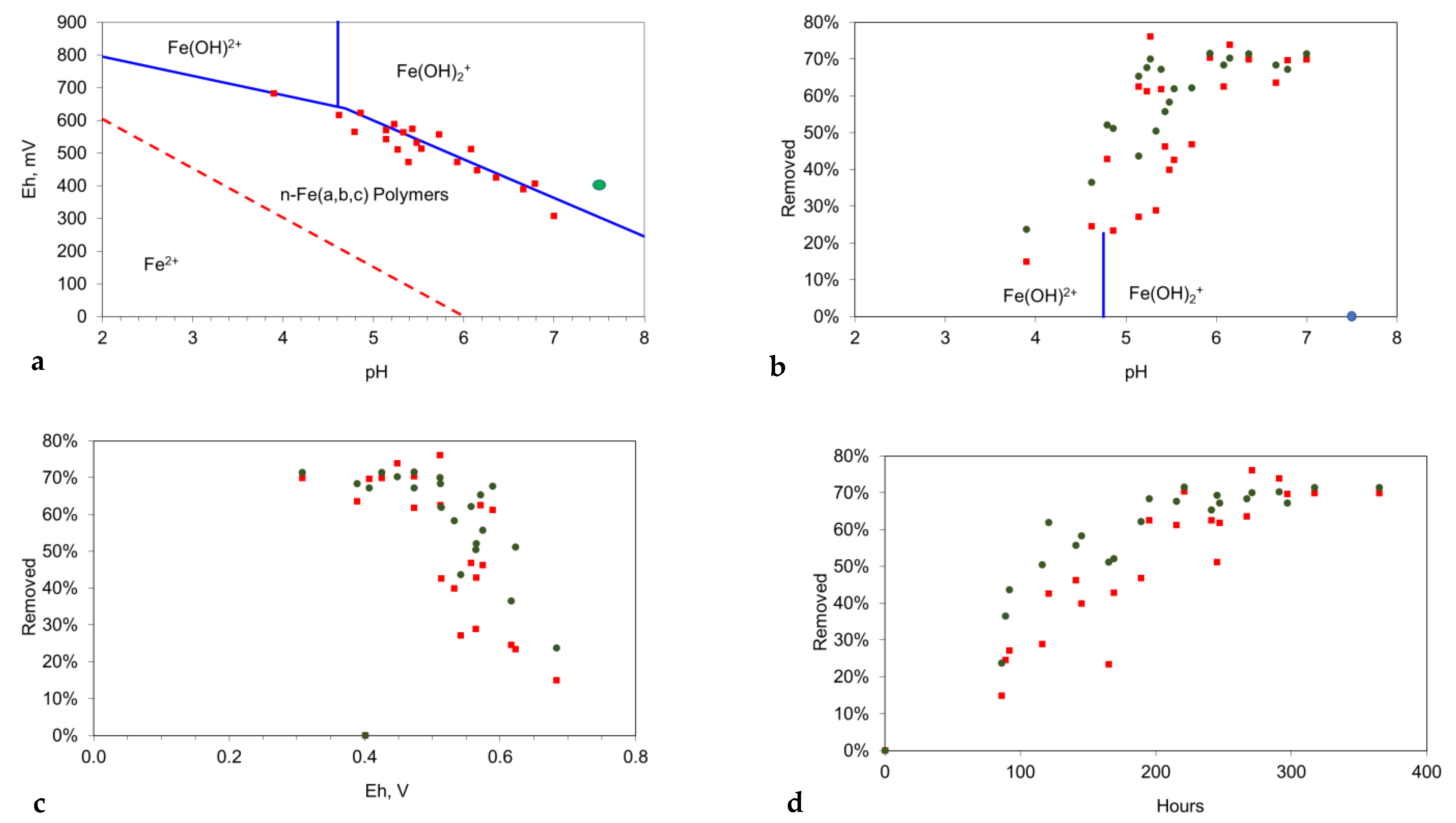
- The initial functionalization of the n-Fe0 is associated with a pH shift into the range 8.5 to 11, and a decrease in Eh (Figure 8d–f);
- The trend of decreasing salinity continues while the pH remains in the range of 9 to 11, and the Eh is below 0 mV (Figure 8d–f);
- The cessation of salinity removal is associated with a decrease in pH into the range of 7 to 9, combined with an increase in Eh (Figure 8d–f).
- The removal of NaCl occurs in the redox (Eh:pH) regime, where the dominant Fe oxidation number is 3 (Figure 8d–f). This redox regime is consistent with desalination being associated with nFe0:n-Fe(a,b,c) polymers.
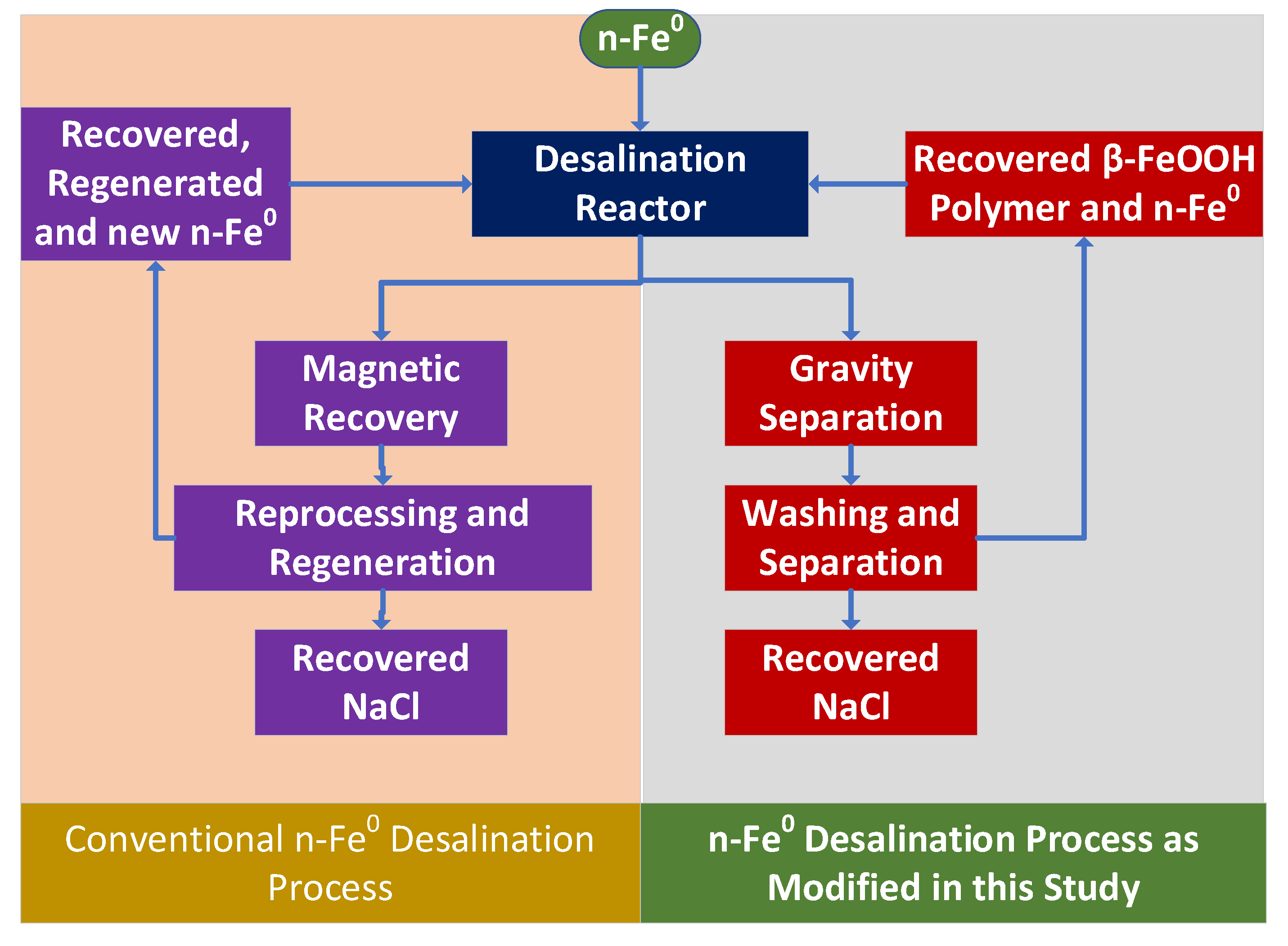
3.9. Reuse of n-Fe0
- Desalination is associated with a pH within the range of 8 to 11;
- Desalination is associated with an Eh of <500 mV.
- All n-Fe0, m-Fe0 particles and Fe-polymers change the Eh and pH of water flowing through them. The degree of change decreases with increasing throughput and increasing space velocity (SV), where:
3.10. Creating a Viable Desalination Process from the Experimental Results
3.10.1. Uncoated n-Fe0
3.10.2. Coated n-Fe0
- it acts as a protection of the particle from corrosion;
- it allows the removed Na+ ions and Cl- ions to be recovered;
- it allows the nanoparticles to be reused;
- it can allow the nanoparticles to be stable in air, thereby improving safe handling; and
- it can prevent the annealing and cementation of the particles.
3.10.3. Formation of β-FeOOH and Green Rust Chloride Polymer Spheres
3.10.4. Sphere Growth
3.10.5. Relationship between Sphere Rim Volume, Fluid Volume and Hydration Shell
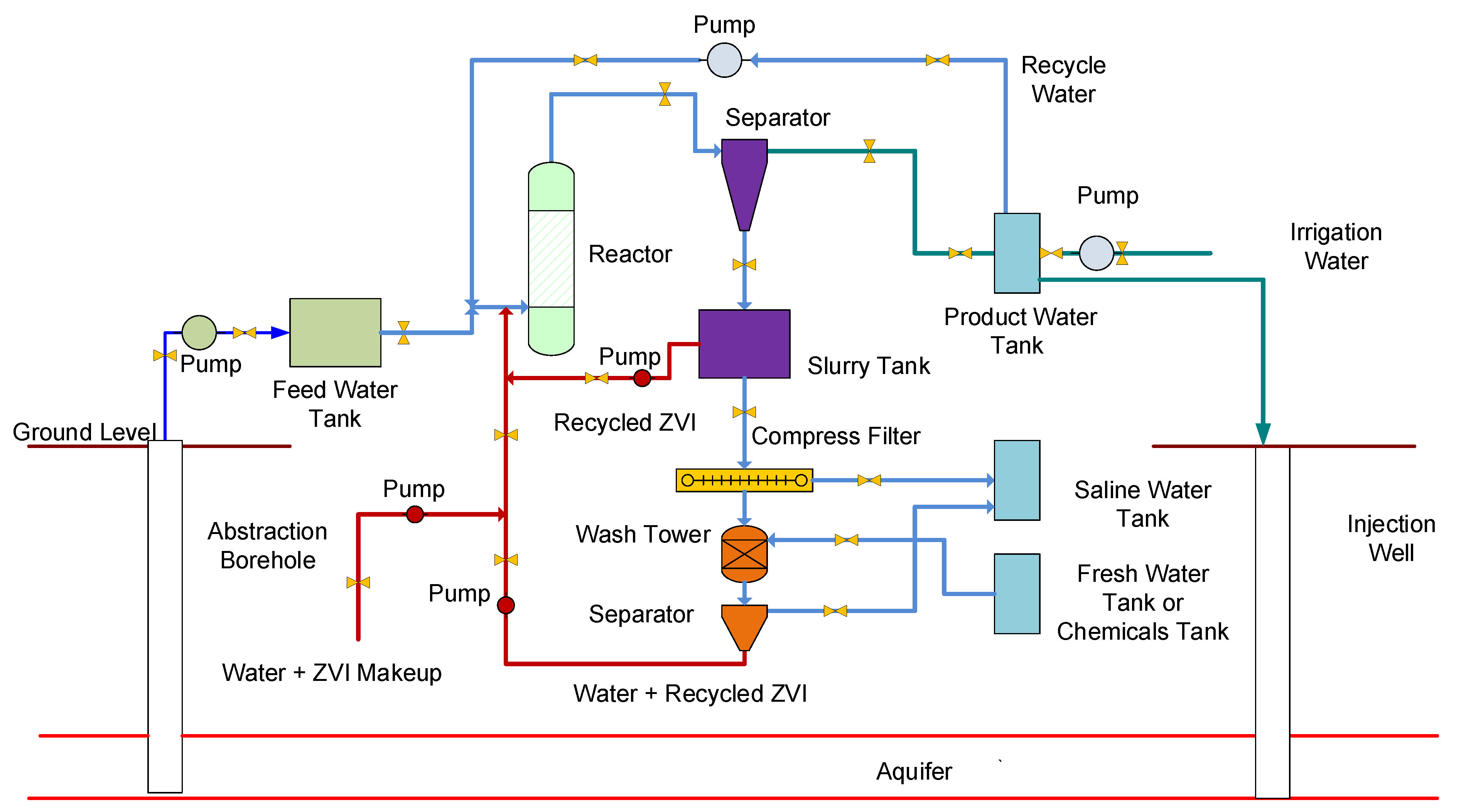
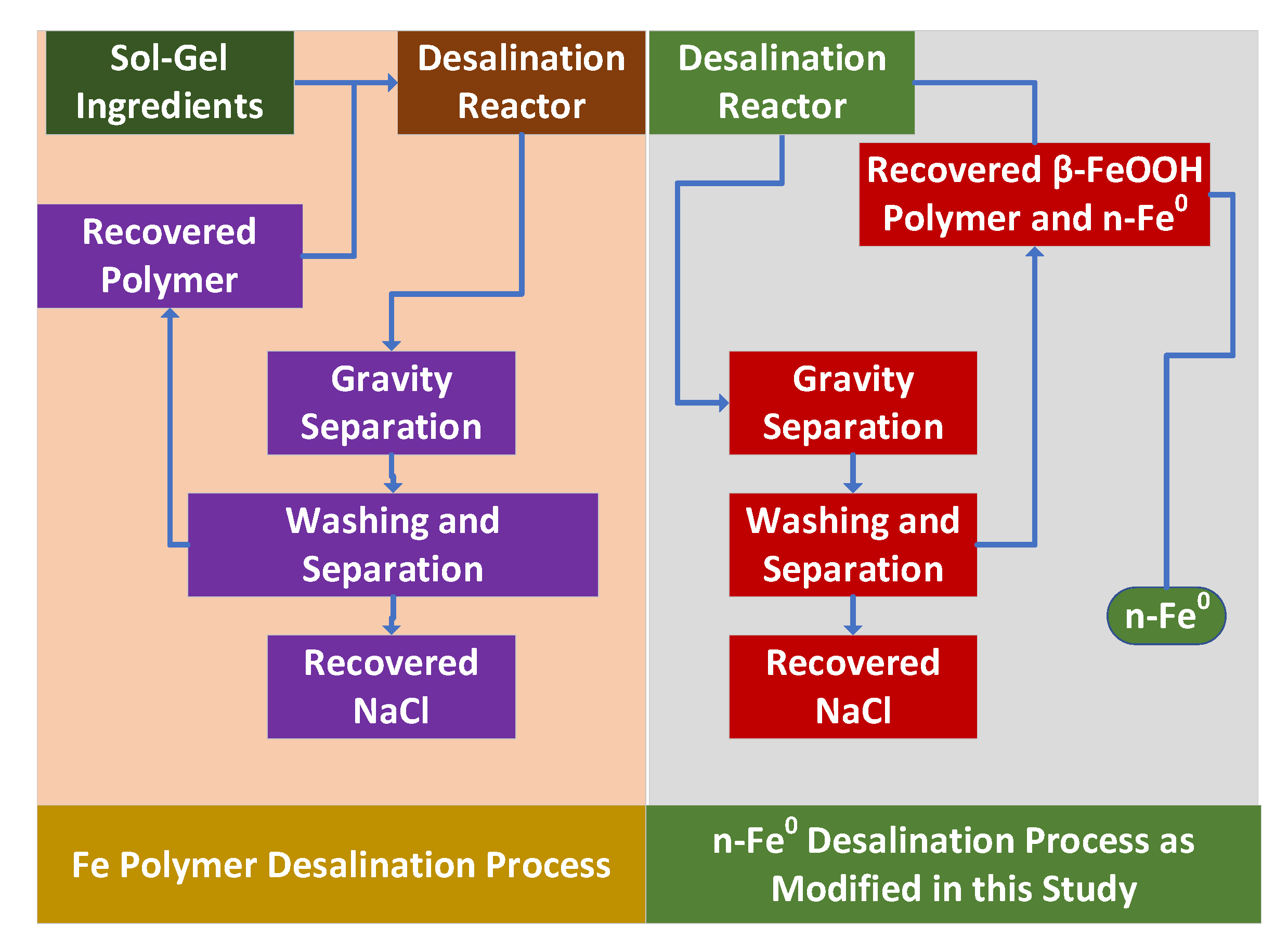
- a tank, reservoir, or impoundment to hold the saline groundwater or saline flowback water;
- A reactor that receives water from the tank or impoundment plus a charge of [n-Fe0 + n-Fe0:Fe polymer + n-Fe polymer];
- A gravity separation unit that recovers the [n-Fe0 + n-Fe0:Fe polymer + n-Fe polymer] and then discharges a product water (partially desalinated irrigation water). Optionally, part of the product water may be recycled;
- The recovered [n-Fe0 + n-Fe0:Fe polymer + n-Fe polymer] is recycled, with or without additional processing to remove the adsorbed Na+ and Cl- ions.
3.11. Desalination Modeling Associated with n-Fe0 or a β-FeOOH Polymer or a Fe(b) Polymer
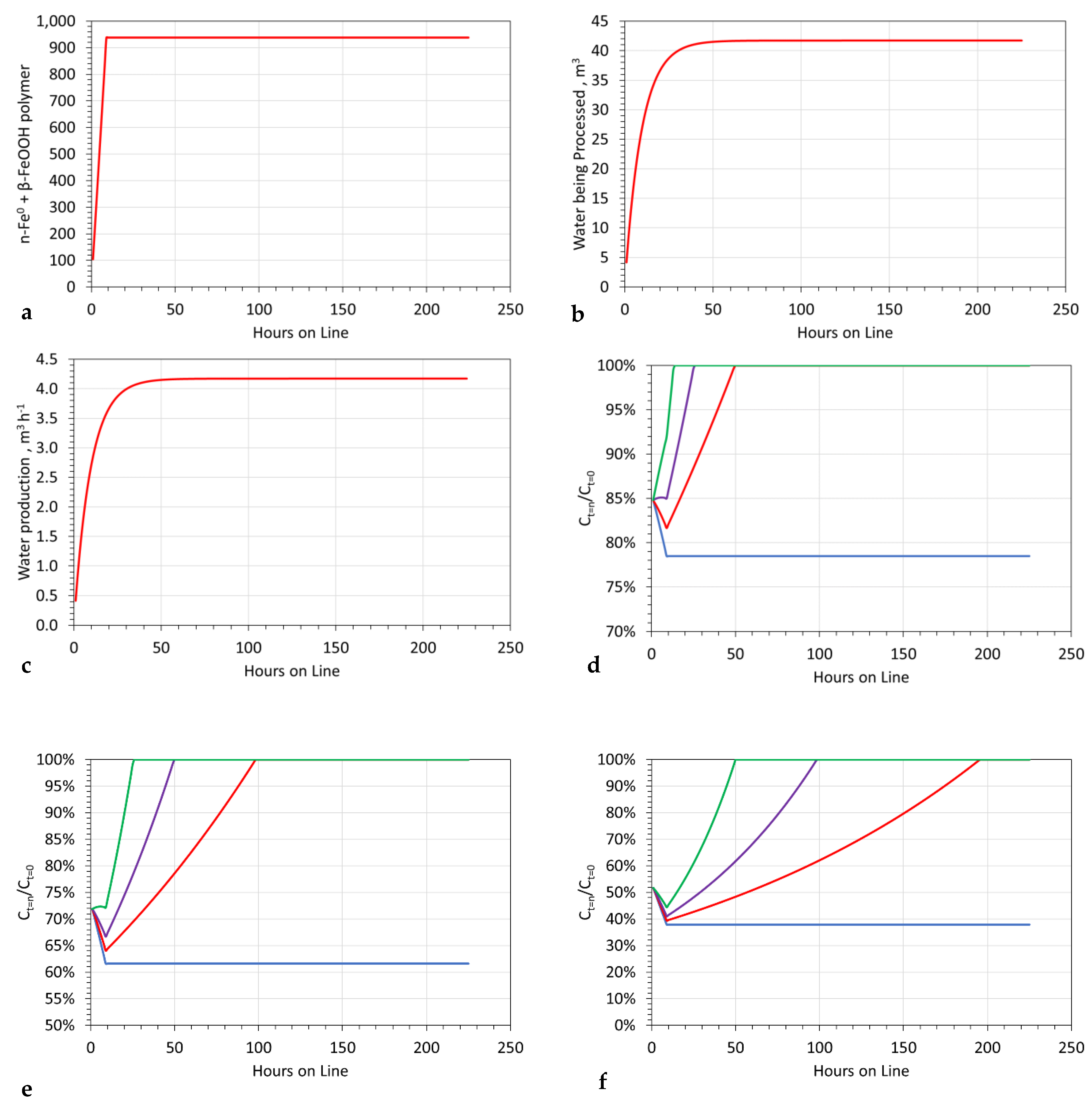
3.11.1. Example Viability Assessment of the n-Fe0:Fe(b) Polymer
Example Reactor Size Assessment
- The feed water equates to 4.17 m3 h−1;
- The n-Fe0 feed equates to 104.25 kg h−1 (25 g L−1);
- The required desalination in the initial hour is 15% (Ct = 1h/Ct = 0 = 0.85);
- The required reactor volume is 4.17 m3.
- 1.
- Example Reactor Specification
- 2.
- Example Reactor Operation: Without Recycle
- 3.
- Example Reactor Operation: With Recycle
- 4.
- Example Reactor Operation: With Recycle—Economies of Scale
Assessing Expected Yield
Impact of Adsorption/Reaction Site Blocking on the Particles
- Example Reaction Time and Reactor Size
- Example Product Water Salinity
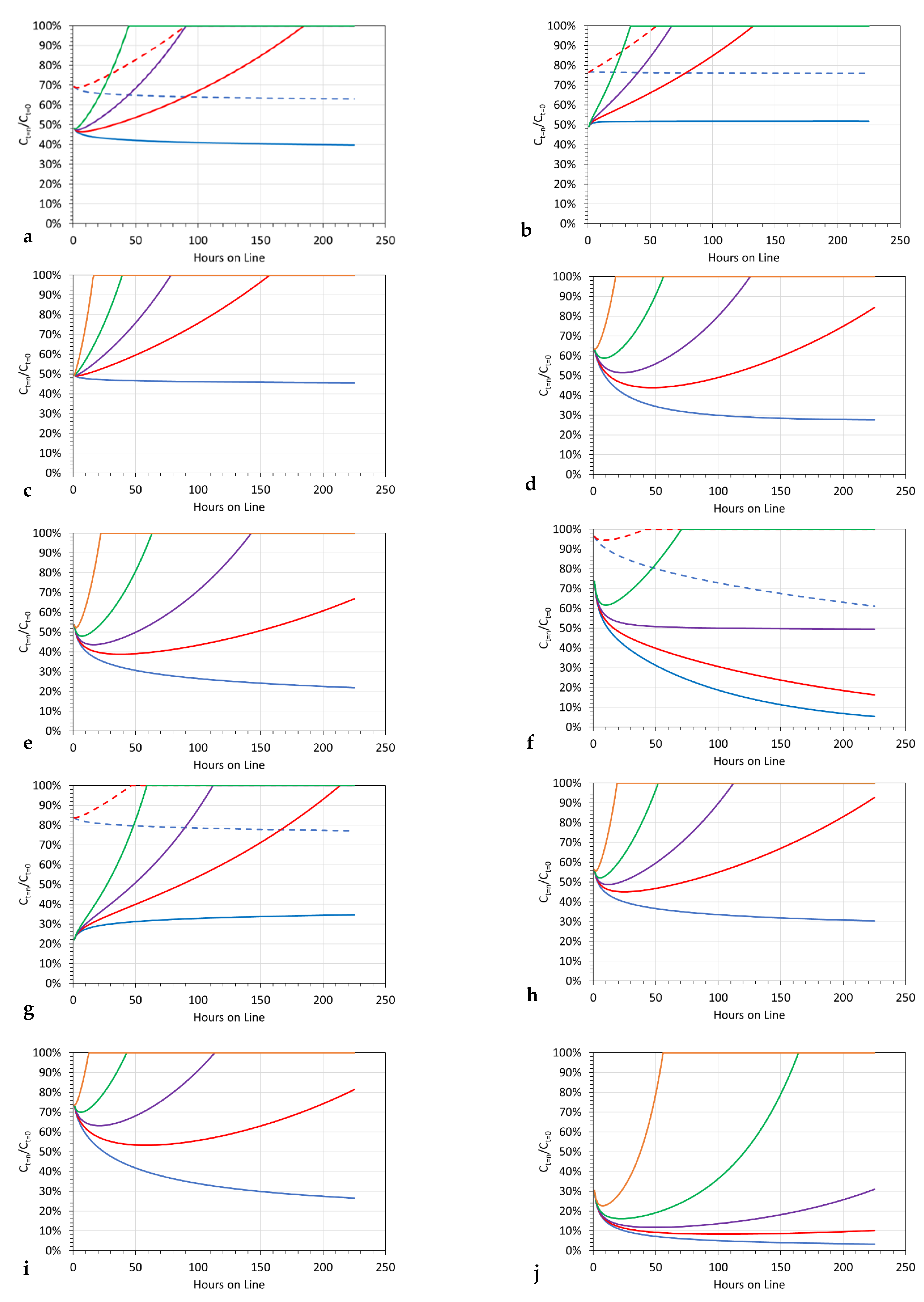
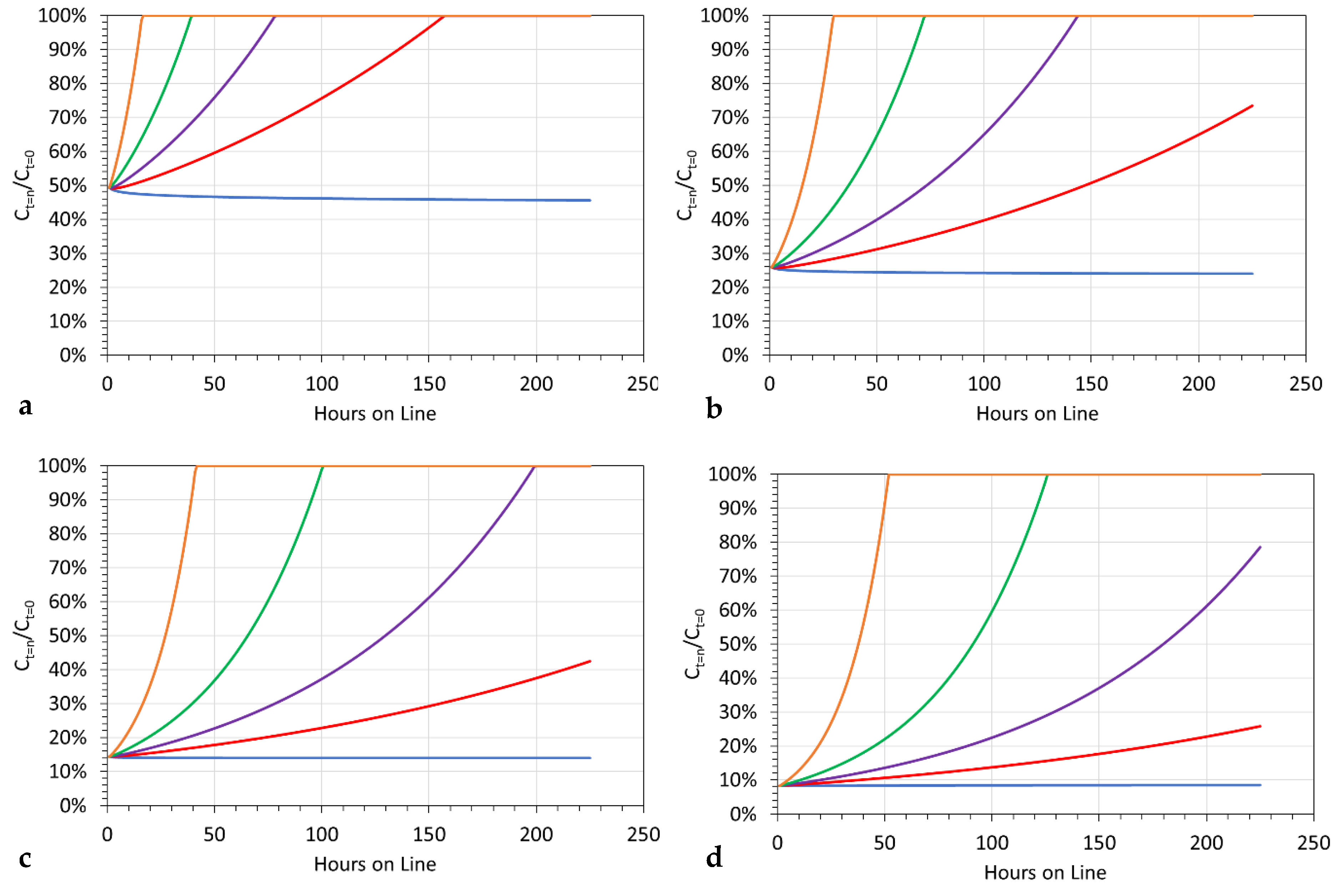
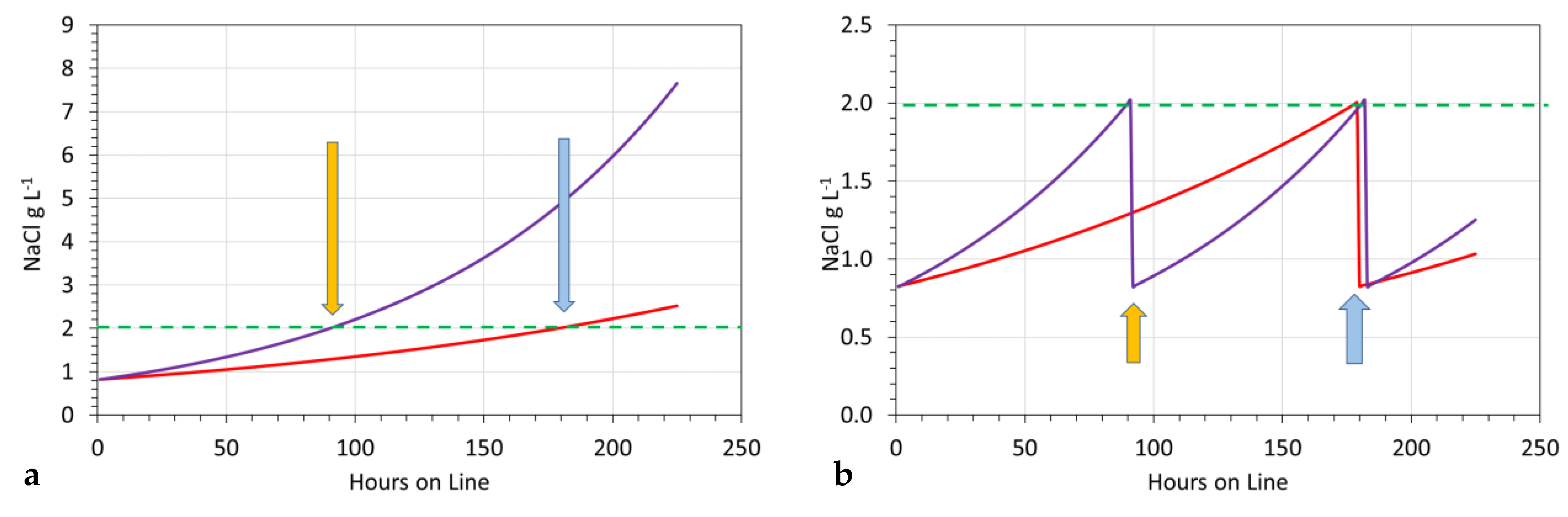
3.11.2. Significance of Increasing Pw
- [d] = 1.02, replacement is at 15-h intervals (processing 62 m3);
- [d] = 1.01, replacement is at 29-h intervals (processing 120 m3);
- [d] = 1.005, replacement is at 56-h intervals (processing 233 m3).
4. Boosting Desalination Using Sol-Gel Polymers
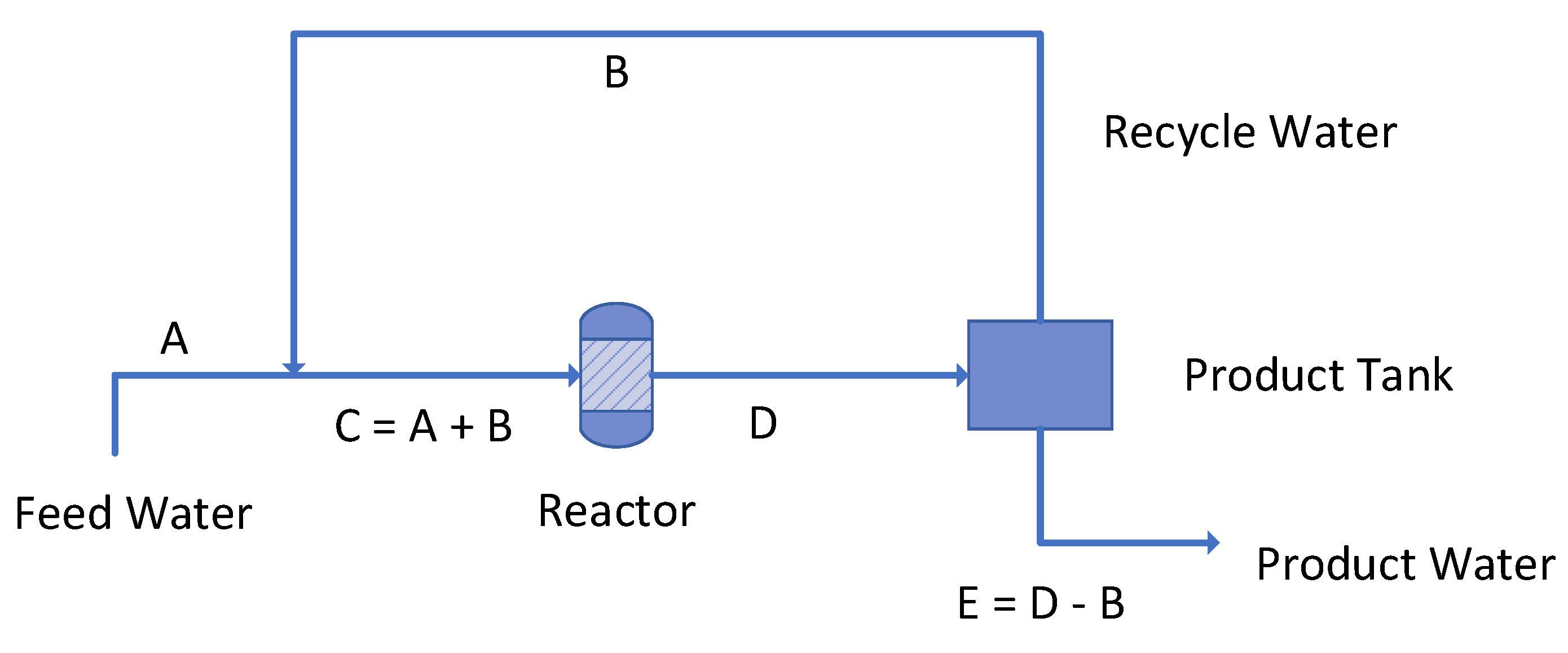
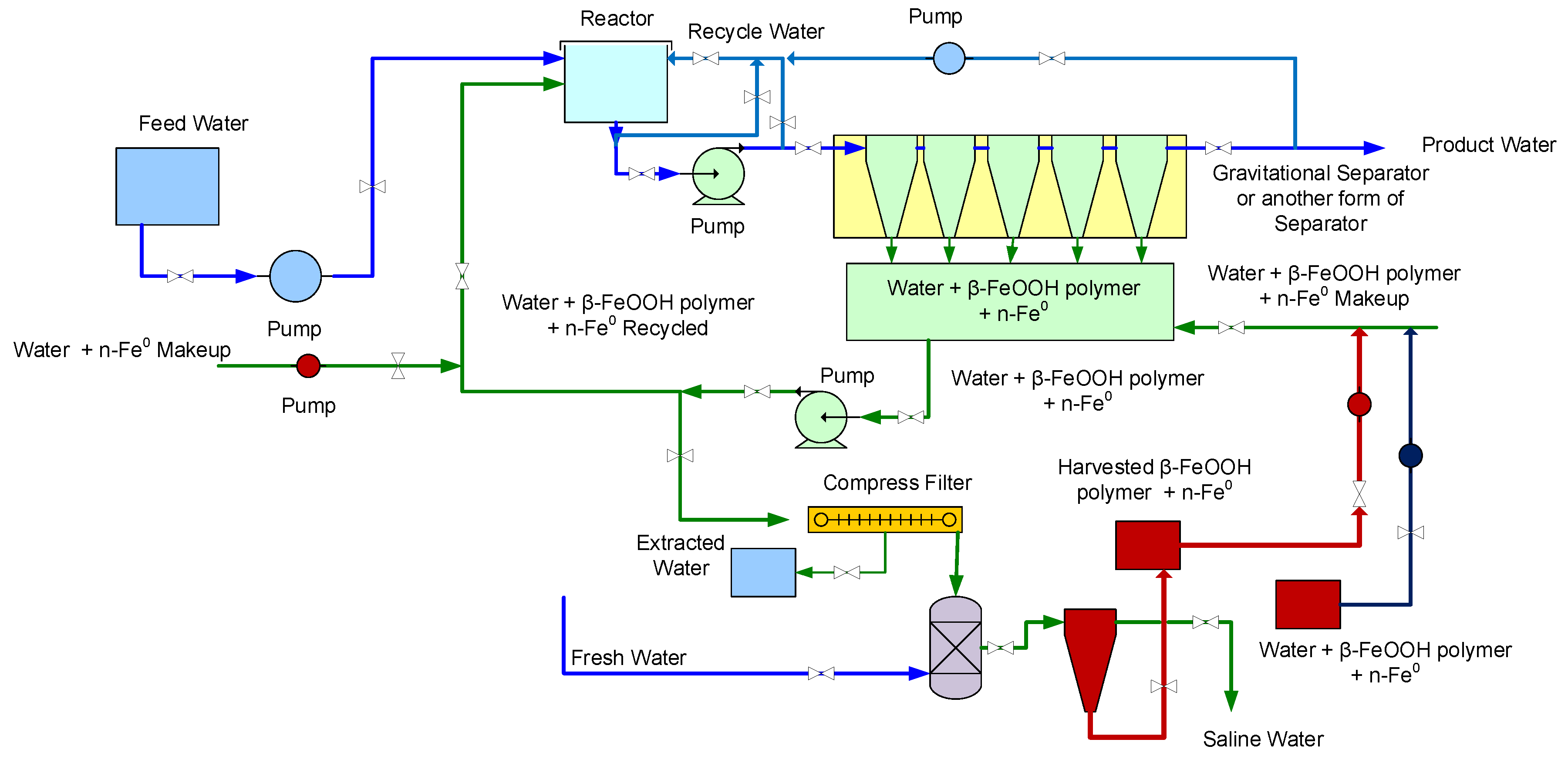
4.1. Reactor Process Flow
4.2. Increasing pH to Facilitate Sol-Gel Formation
4.3. Fe-Ca Polymer
4.4. Fe-Ca-Urea Polymer
4.5. Fe-Ca-Mn-Formic Acid Polymer
4.6. Fe-Ca-Zn-Galic Acid Polymer
4.7. Fe-Zn Polymer
4.8. Fe-Ca-Mn-Mg-Formic Acid Polymer
4.9. Fe-Ca-Mn-K-Formic Acid Polymer
4.10. Fe-Ca-Zn-Tartaric Acid Polymer
5. Expected Desalination
- The technology should be able to partially desalinate the irrigation water;
- The pH of the irrigation water and composition of the residual polymers and ions in the water should not adversely affect either the plant (crop) growth or the soil structure;
- The technology should improve the standard measures used by the regulatory agricultural authorities to assess the suitability of water for irrigation;
- The amount of desalination achieved should be sufficient to induce an increase in crop yield (t ha−1), without inducing a decrease in crop value (USD t−1);
- Application of the partially desalinated irrigation water should decrease soil salinization and should not contribute to soil salinization. Increasing soil salinization is associated with decreasing agricultural land values (USD ha−1);
- The cost of providing the partially desalinated irrigation water should be less than the increased net revenue resulting from increased crop yields associated with using the water;
- The regulatory authorities provide approval for the use of the appropriate desalination polymer, provide approval for irrigation overland flow to enter the local riparian environment, and provide approval for the resultant soil throughflow to enter both the shallow groundwater environment and the local riparian environment, through field drainage to ditches and streams, etc.
5.1. Environmental Impact
5.2. Indicative Costs
5.3. Regulatory Indices
5.4. Example Fe-Ca-Urea Polymer Analysis
Example Impact of Polymer Recycle on Product Water Composition
- Feed water flow rate = 4.17 m3 h−1;
- Product water flow rate = 4.17 m3 h−1;
- Rr = 0% for product water; Rr = 100% for polymer recovered from the separator;
- Reactor volume = 4.17 m3, including flowlines to the separator (Figure 17).
- tr = 1 h;
- [d] is between 1.005 and 1.01.
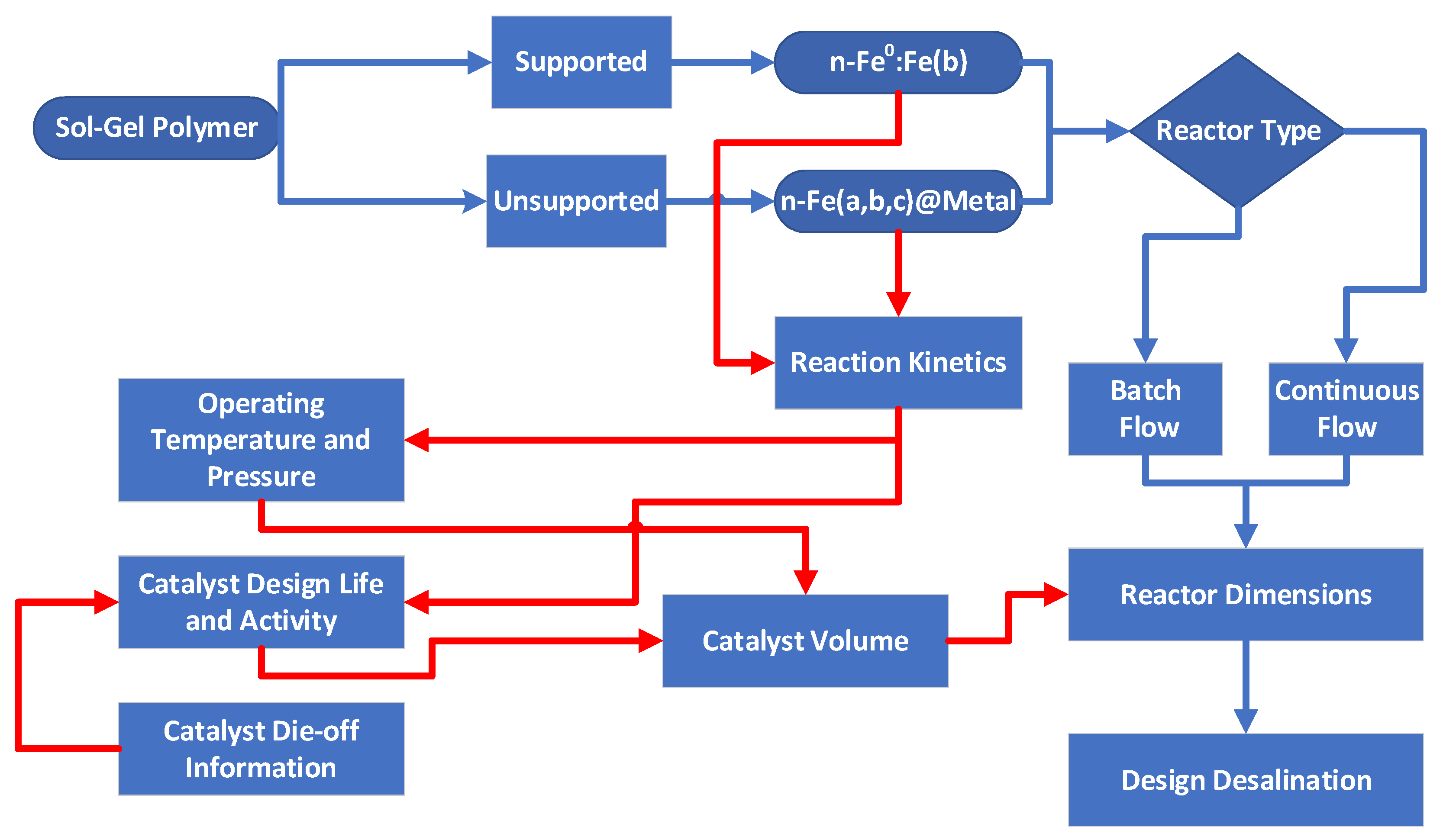
6. Application to Groundwater Management
- Reaction kinetics (Figure 14) considering:
- ∘
- Polymer Type
- ■
- Supported: n-Fe0:Fe(b);
- ■
- Unsupported: n-Fe(b);
- ∘
- Static diffusion operating conditions;
- ∘
- Pressure of 0.1 MPa and temperature of 273–298 K;
- ∘
- Different Pw;
- ∘
- Different activity dieback relationships;
- Reactor Operation (Figure 13) considering:
- ∘
- desalination with no product water recycled to the reactor;
- ∘
- desalination with product water recycled to the reactor;
- ∘
- desalination with polymer recycled to the reactor.
- Above ground in tanks or impoundments. This is the conventional approach. The typical irrigation requirement is 1000–10,000 m3 ha−1 a−1. An agricultural holding of 100 ha, would require surface-based storage (e.g., 3 m deep) covering 33,000–330,000 m2 (3.3 to 33 ha). This large land take for desalinated water storage may be both physically and economically impractical.
7. Commerciality
- The turbulence within the reaction environment increases; and
- The pH in the turbulent environment increased.
8. Conclusions
- Magnetic separation route (n-Fe0; n-Fe3O4);
- Gravitational separation route (Fe0:Fe(b)@C0; n-Fe:Fe(b), n-Fe(b)).
- The kinetic desalination results from a 2.3 L reactor operation are effectively replicated in a 240 L reactor, indicating that it may be reasonable to expect that the desalination results from a 240 L reactor will be replicated in a 24 m3 reactor;
- The site blocking constant [d] was increased to between 1.01 and 1.015, relative to the 2.3 L reactor;
- Desalination increases as pH increases and Eh decreases.
- It is technically feasible to use existing saline aquifers to store desalinated water in hydrodynamic stationary plumes, and it will be possible to abstract this water for irrigation use when required.
- This concept could be used to reverse or contain seawater incursion into an aquifer.
- It will be possible to create perched hydrodynamic stationary mounds in some soils, which could be used to desalinate the soil and/or store desalinated water within the mounds for future use as irrigation water.
- This study has highlighted five areas for future investigation:
- The formation of colloids and micron-sized hollow polymer agglomerates and their role in desalination;
- The ability of n-polymers to catalytically remove Na+ and Cl- ions, their selectivity, and associated kinetic controls;
- Scalability and statistical repeatability analysis of desalination observations;
- Influence of reactor type and reactor operating conditions on the desalination outcome;
- Field demonstration of the creation and stability of desalinated hydrodynamic stationary plumes in saline aquifers and desalinated perched hydrodynamic groundwater mounds in saline soil as potential reservoirs and sources of desalinated water.
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Magnetic Zero Valent Iron Desalination and Fe0:Fe(b)@C0 Polymers
Appendix A.1. Magnetic n-Fe0 Desalination: Spanish Patent ES2598032
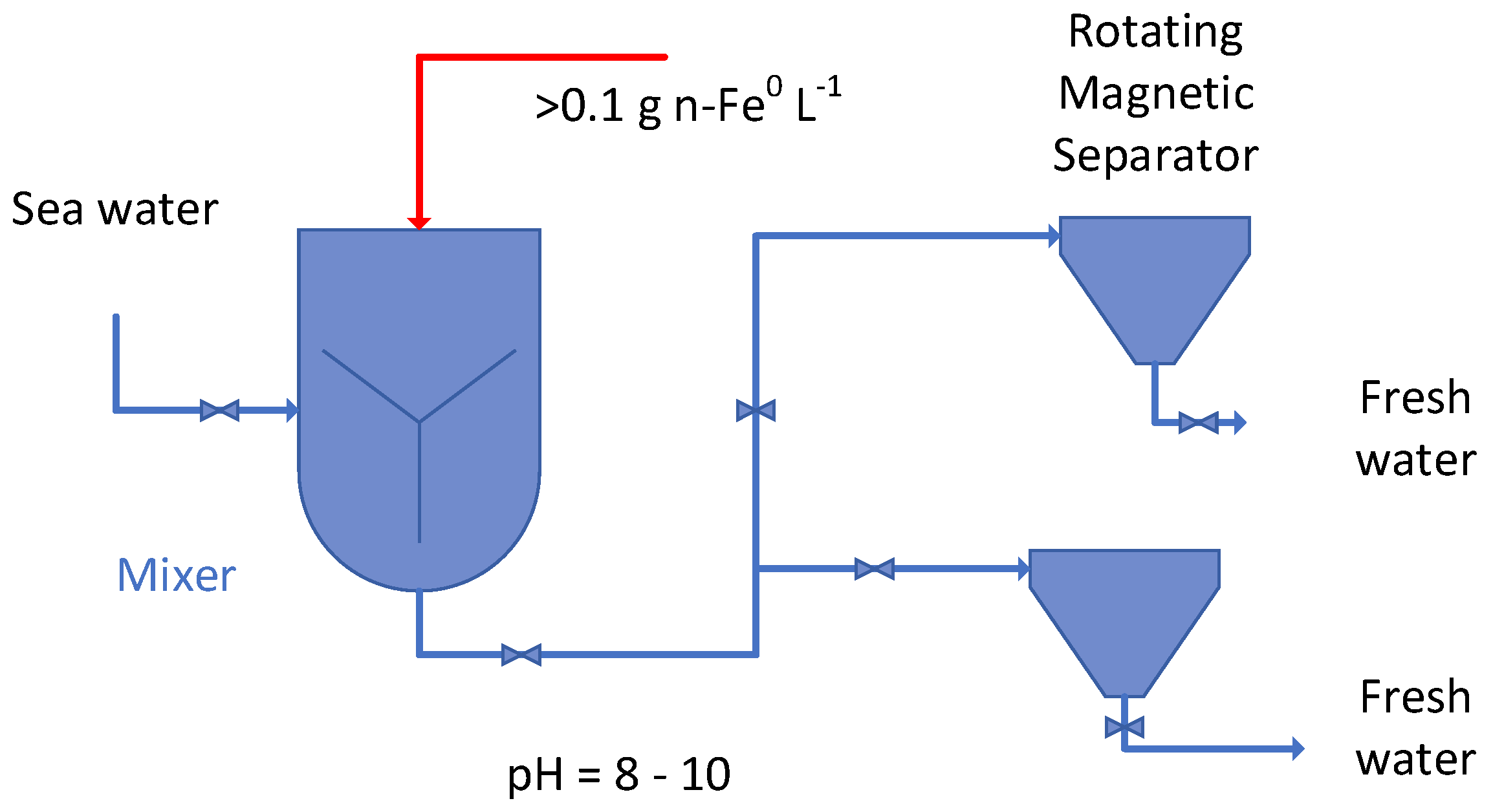
Appendix A.1.1. Removal Potential of a Functionalized n-Fe0 Particle
- Approach 1: Saturation of the water in a bubble column reactor with a reducing gas [6] selected from H2, CO, CH4, and NH3. This approach is not practical in most agricultural environments.
- Approach 2: Saturation of the water with hydrogen in a diffusion reactor containing one or more of Fe0 + Al0 + Cu0 [56];
- Approach 3: Saturation of water in a bubble column reactor using hydrogen generated from the reaction of ferrosilicon, or silicon, with NaOH [e.g., GB147519A; GB191111640A; GB191109623A]
- Approach 4: Saturation of water in a bubble column reactor using hydrogen generated from the reaction of native iron, a perchlorate, and slaked (hydrated) lime, e.g., [GB191109623A]
Appendix A.1.2. Economic Viability
- 25 g n-Fe0 L−1 = USD 250 m−3
- 2.5 g n-Fe0 L−1 = USD 25 m−3
- 0.25 g n-Fe0 L−1 = USD 2.5 m−3
- 0.025 b n-Fe0 L−1 = USD 0.25 m−3.
Appendix A.1.3. Corrosion Analysis
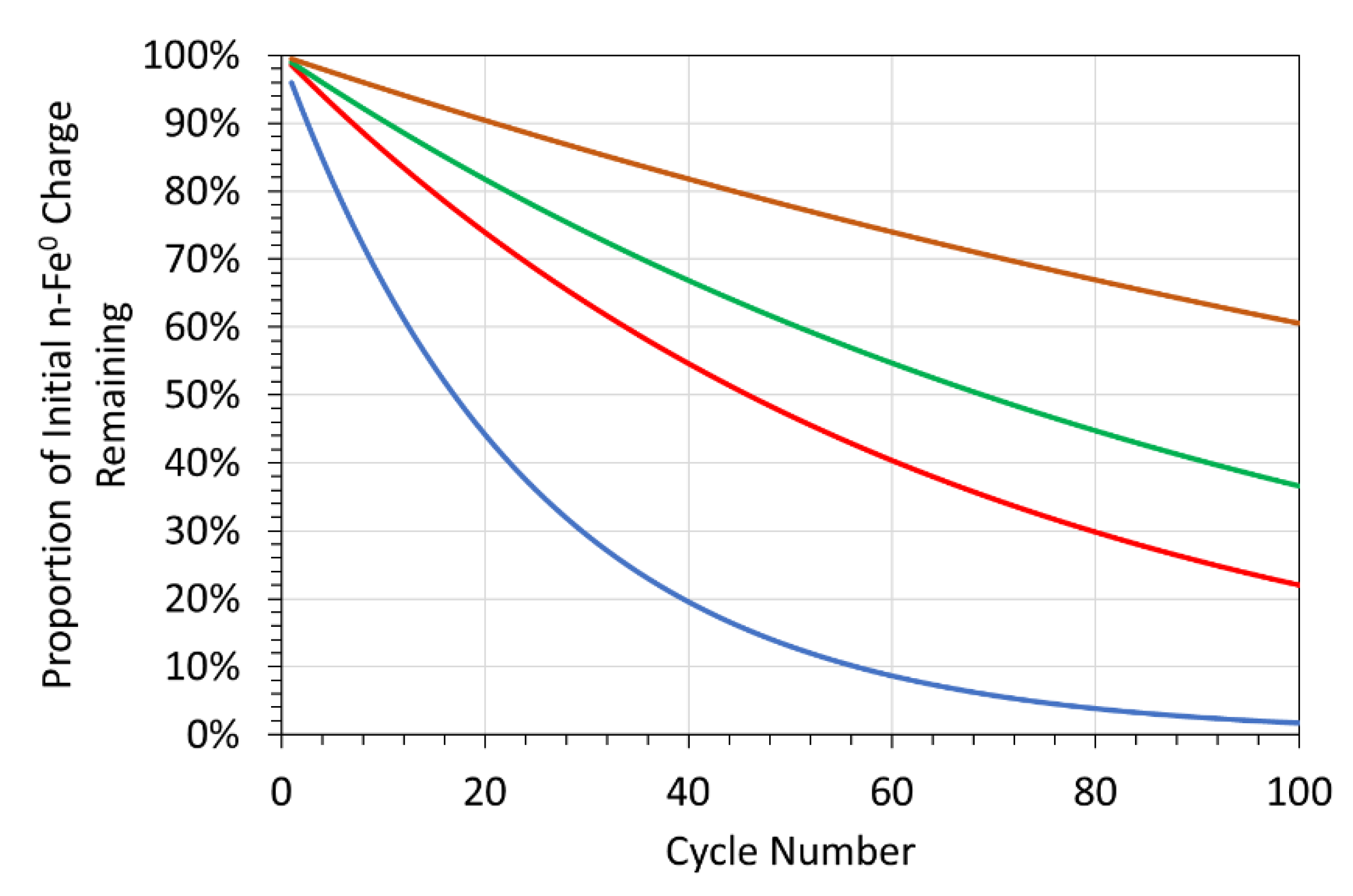
Appendix A.2. Magnetic n-Fe3O4 Desalination: US Patent US8636906B2
Appendix A.2.1. Example Magnetic Nanoparticle Formation
Appendix A.2.2. Binding Capacity of a Nanoparticle
Appendix A.2.3. Regeneration and Reuse of a Nanoparticle
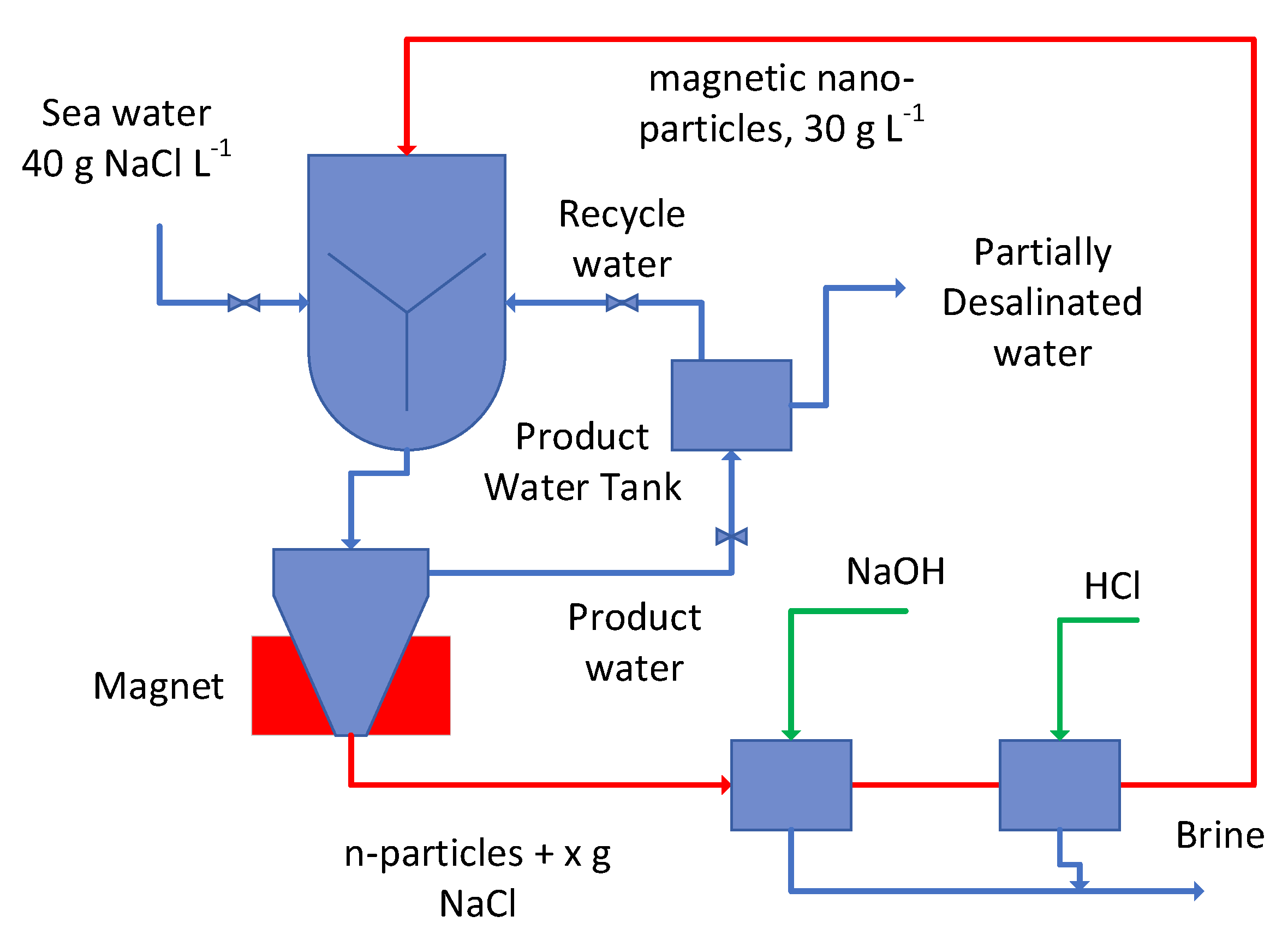
Appendix A.2.4. Desalination Operation
Appendix A.2.5. Economic Viability
Appendix A.3. UK Patent GB2520775A
Fe0:Fe(b)@C0 Polymers
[m-Fe0:Fe(a,b,c)@C0@H+]@Cl-,

Appendix B. Classification of Common Desalination Patterns Associated with ZVI Desalination
- Pattern 1: Near-instantaneous ion decline followed by:
- ∘
- Pattern 1a: a stable ion concentration followed by:
- ▪
- Pattern 1aa: a rising ion concentration;
- ▪
- Pattern 1ab: an ion concentration decline followed by:
- Pattern 1aba: a stable ion concentration;
- Pattern 1abb: a rising ion concentration;
- Pattern 1abc: a continued ion concentration decline, at a slower rate:
- ∘
- Pattern 1b: a rising ion concentration followed by:
- ▪
- Pattern 1ba: a stable ion concentration;
- ▪
- Pattern 1bb: an ion concentration decline followed by:
- Pattern 1bba: a stable ion concentration;
- Pattern 1bbb: a rising ion concentration;
- Pattern 1bbc: a continued ion concentration decline, at a slower rate:
- ∘
- Pattern 1c: a declining ion concentration followed by:
- ▪
- Pattern 1ca: a stable ion concentration;
- ▪
- Pattern 1cb: a rising ion concentration;
- ▪
- Pattern 1cc: a continued ion concentration decline, at a slower rate:
- Pattern 2: No initial ion decline followed by:
- ∘
- Pattern 2a: a declining ion concentration followed by:
- ▪
- Pattern 2aa: a stable ion concentration;
- ▪
- Pattern 2ab: a rising ion concentration;
- ▪
- Pattern 2ac: a continued ion concentration decline, at a slower rate:
- ∘
- Pattern 2b: an instantaneous decline followed by:
- ▪
- Pattern 2ba: a stable ion concentration;
- ▪
- Pattern 2bb: a rising ion concentration;
- ▪
- Pattern 2bc: a continued ion concentration decline
- Pattern 3: A slow initial ion decline followed by:
- ∘
- Pattern 3a: a stable ion concentration;
- ∘
- Pattern 3b: a rising ion concentration;
- ∘
- Pattern 3c: a continued ion concentration decline, at a slower rate:
- ∘
- Pattern 3d: a continued ion concentration decline, at a faster rate followed by:
- ▪
- Pattern 3da: a stable ion concentration;
- ▪
- Pattern 3db: a rising ion concentration;
Appendix C. Groundwater Chemical Indices
Appendix D. Creating a Hydrodynamic Stationary Groundwater Plume or Mound
Appendix D.1. Creating a Stationary Desalinated Plume
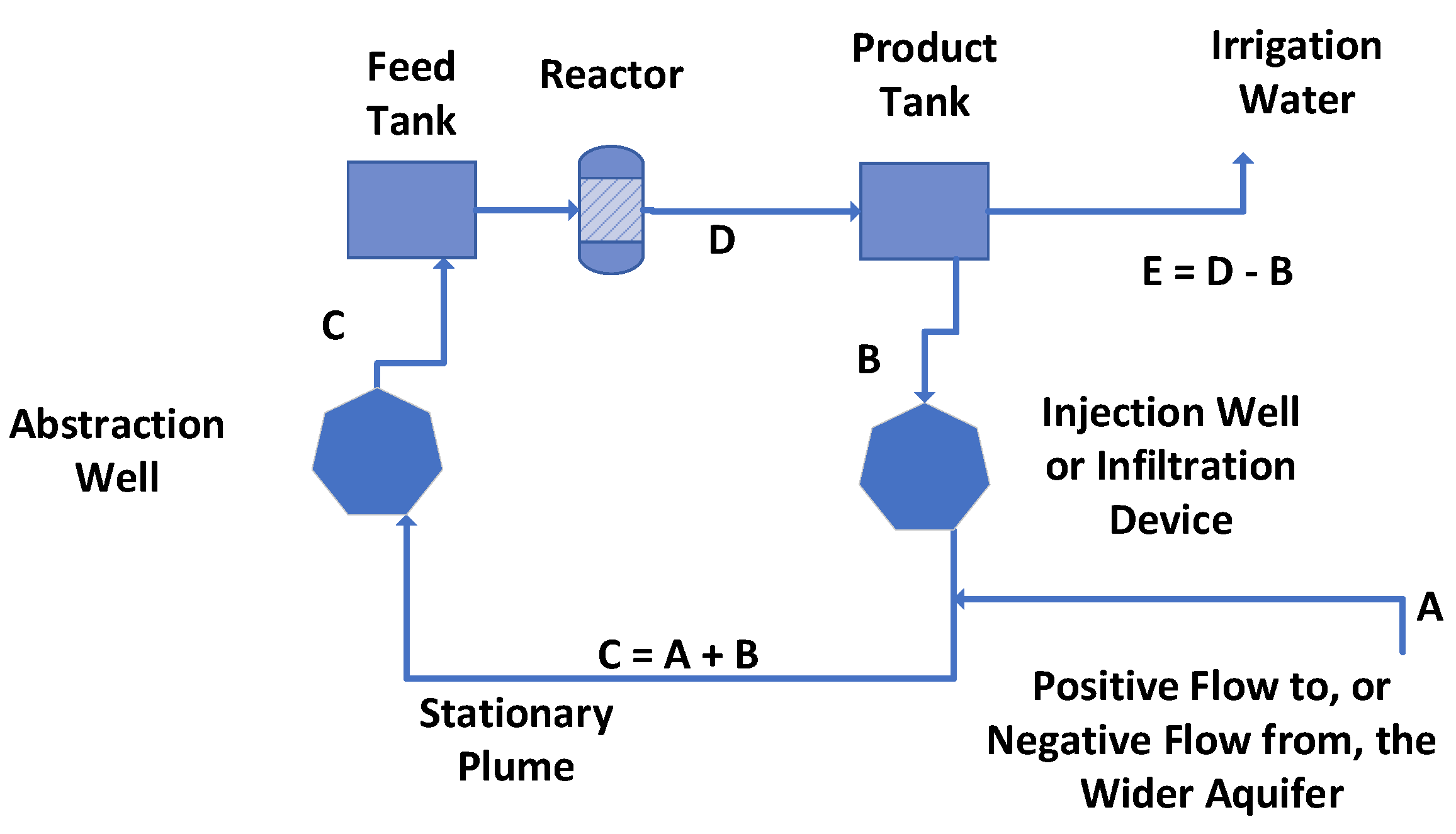
Appendix D.1.1. Normalized Reactor Conditions
- (i)
- (ii)
- The aquifer water (A) (Figure A6) is assumed to have the following composition Ca2+ = 0.2669 g L−1; K+ = 0.0302 g L−1; Mg2+ = 0.0381 g L−1; Na+ = 6.9340 g L−1; Cl- = 11.6500 g L−1; HCO3- = 0.5793 g L−1; SO42- = 0.087 g L−1; total salinity = 18.58 g L−1; total dissolved solids (TDS) = 19.58 g L−1; SAR = 148.35;
- (iii)
- The associated reaction temperature is 0 to 25 °C;
- (iv)
- The required product water (D) salinity is <2.5 g L−1.
Appendix D.1.2. Modeling the Stationary Plume
- (i)
- Water abstraction is through a 150-mm-diameter well located in the center of the stationary plume;
- (ii)
- The regional potentiometric slope, within the aquifer, has a gradient across the plume area of <1 m per 1000 lateral meters;
- (iii)
- The surface ground area over the stationary plume is level;
- (iv)
- The top of the saline aquifer is located at 150 m depth;
- (v)
- The sandstone aquifer has a thickness of 5 m;
- (vi)
- The constructed stationary plume has a radius of 100 m and covers 31,415 m2 (3.1 ha);
- (vii)
- The porosity of the aquifer is 30%. The effective storage volume of the stationary plume is 47,123 m3. As a simplification, for modeling purposes, it is assumed that [A] (Figure A6) = [E], and it is assumed that [A] is either positive or zero. Setting [A] as a negative value would result in the size of the stationary plume volume declining with time.
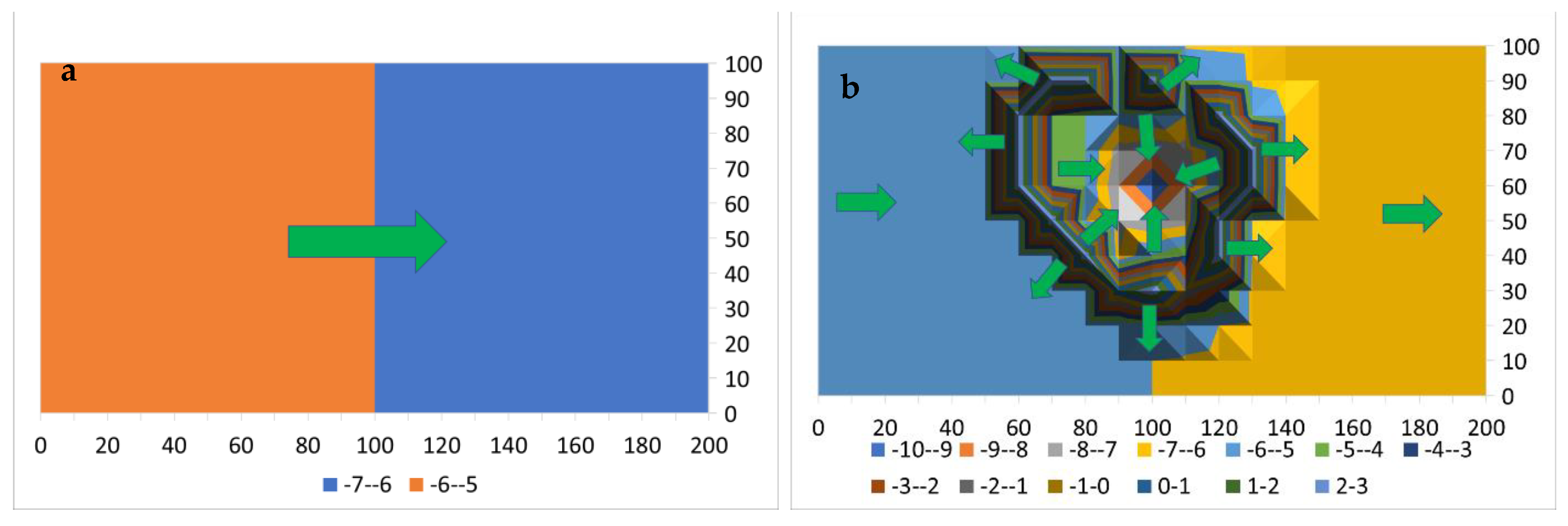
Appendix D.1.3. Adsorption and Catalytic Reaction Modeling
- (i)
- Reactor with no recycle and a maximum residence time of the water in the reactor of 1 h;
- (ii)
- Reactor with recycle of all or part of the product water.
Adsorption Modeling: Constructing the Stationary Plume
Adsorption Modeling: Operating the Stationary Plume
- Stationary plume creation
- ∘
- Assumptions
- ▪
- Vd = 47123.89 m3,
- ▪
- As = 18.58 g L−1,
- ▪
- Target As = 1.0 g L−1,
- ∘
- Modeled plume salinity vs. time
- ▪
- Processing rate: 40 m3 h−1,
- ▪
- Product salinity leaving the reactor: <2.5 g L−1,
- ▪
- n-Fe3O4 adsorbent used = 12.846 t.
- ▪
- Adsorption rate:
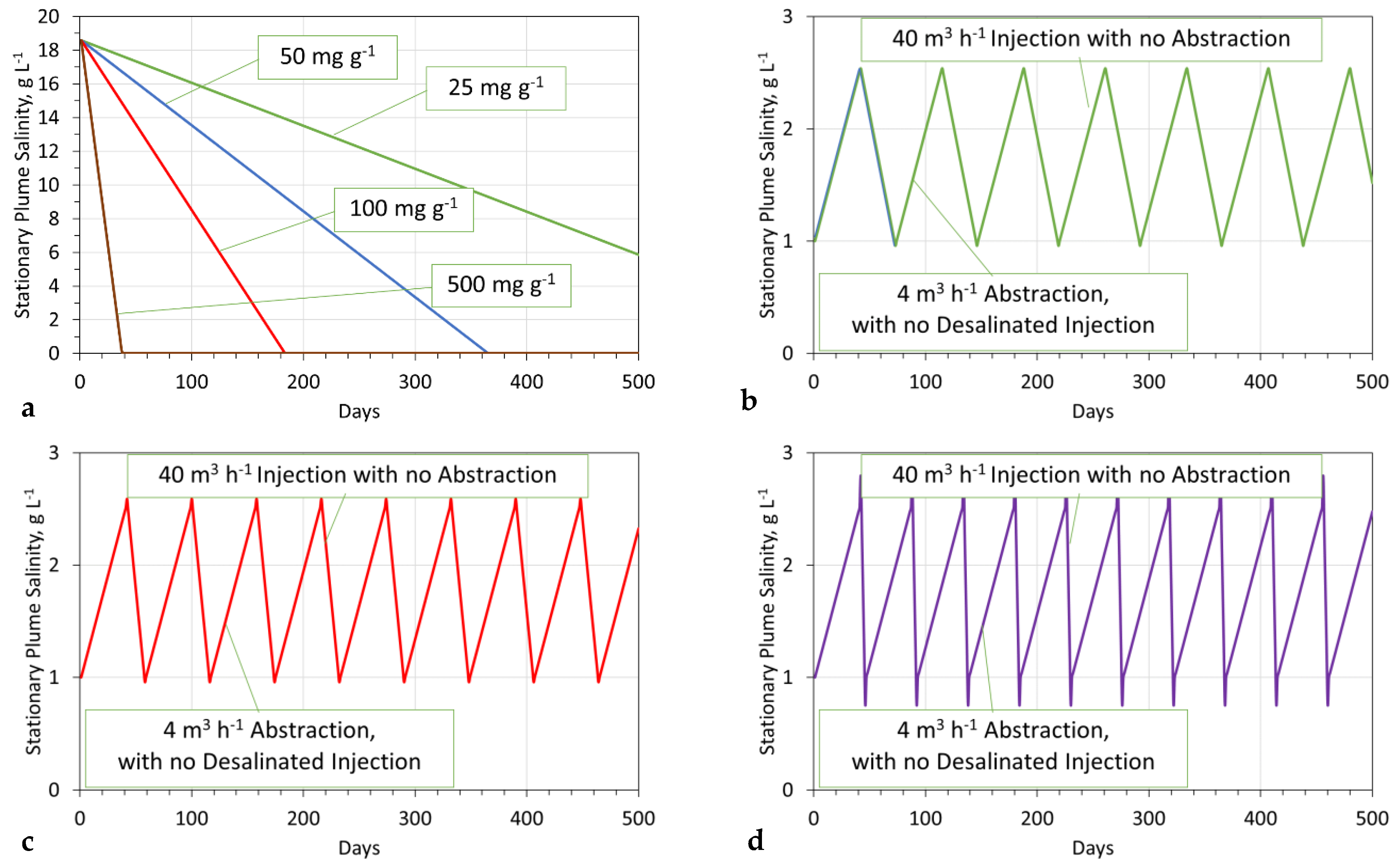
- 25 mg g−1 Fe3O4; Stabilization time = >500 days;
- 50 mg g−1 Fe3O4; Stabilization time = 346 days;
- 100 mg g−1 Fe3O4; Stabilization time = 173 days;
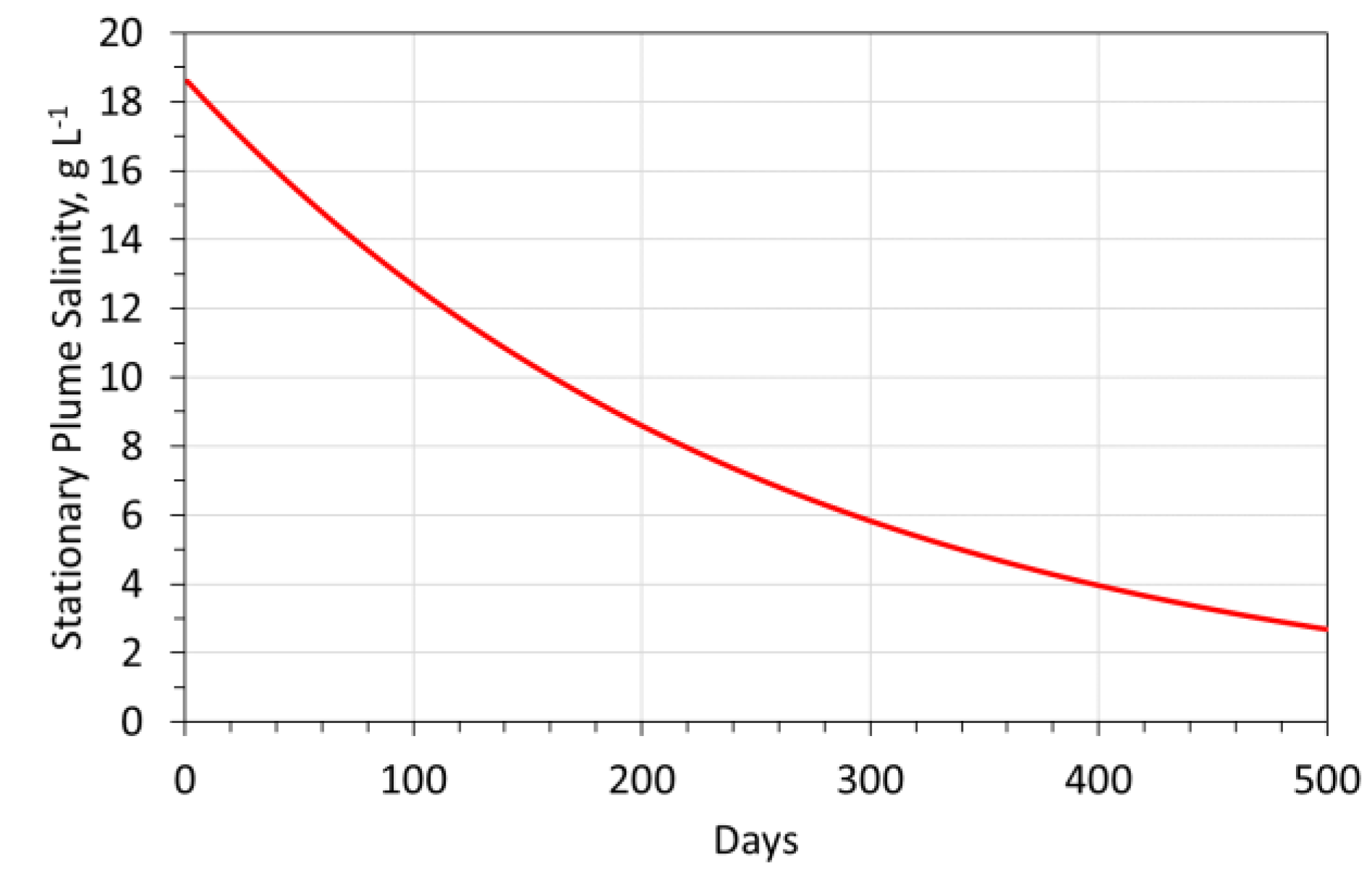
- 500 mg g−1 Fe3O4; Stabilization time = 36 days;The stabilization time required to achieve As = 1 g L−1, decreases as the adsorbent quality increases (Figure A9a).
- ∘
- Modeled plume salinity vs. time during operation
- ▪
- Extracted Irrigation water [E]: 4 m3 h−1,
- ▪
- Makeup water from aquifer [A]: 4 m3 h−1,
- ▪
- Period of extraction of 96 m3 d−1 = 42 days (4032 m3). Minimum salinity = 1 g L−1; maximum salinity = 2.5 g L−1,
- ▪
- Aquifer reconstruction period, to reduce salinity from 2.5 g L−1 to 1.0 g L−1 (Figure A9b–d)
- 50 mg g−1 Fe3O4; Stabilization time = 30 days;
- 100 mg g−1 Fe3O4; Stabilization time = 16 days;
- 500 mg g−1 Fe3O4; Stabilization time = 5 days.
Catalytic Modeling
- Fe0:Fe(b)@Urea polymer: Further details in Reference [4];
- ∘
- Stationary plume creation
- ▪
- Assumptions
- Vd = 47123.89 m3;
- As = 18.58 g L−1;
- Target As = 1.0 g L−1.
- ∘
- Modeled plume salinity vs. time
- ▪
- Processing rate: 40 m3 h−1,
- ▪
- Processing time: 3 h;
- ▪
- Product desalination leaving the reactor = 19%,
- ▪
- Fe0:Fe(b)@Urea catalyst used = 8.33 kg;
- ▪
- Stabilization time = >500 days (Figure A10).
- SiO2@Fe(b)@Urea polymer: Further details in Reference [7];
- ∘
- Stationary plume creation
- ▪
- Assumptions
- Vd = 47123.89 m3,
- As = 18.58 g L−1,
- Target As = 1.0 g L−1,
- ∘
- Modeled plume salinity vs. time
- ▪
- Processing rate: 40 m3 h−1,
- ▪
- Processing time: 24 h;
- ▪
- Product desalination leaving the reactor = 40%,
- ▪
- Fe0:Fe(b)@Urea catalyst used = 1.11 kg Fe (78 L catalyst);
- ▪
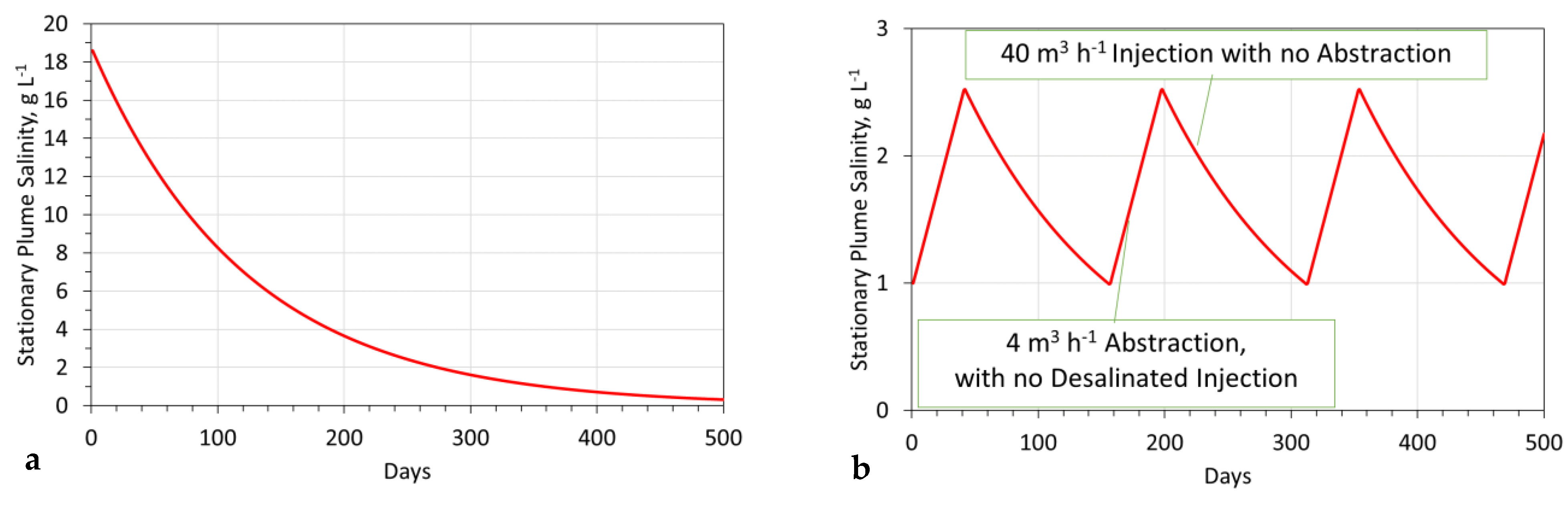
- Stabilization time = 365 days (Figure A11a);The stabilization time = time required to achieve As = 1 g L−1.
- ∘
- Modeled plume salinity vs. time during operation
- ▪
- Extracted Irrigation water [E]: 4 m3 h−1,
- ▪
- Makeup water from aquifer [A]: 4 m3 h−1,
- ▪
- Period of extraction of 96 m3 d−1 = 42 days (4032 m3). Minimum salinity = 1 g L−1; maximum salinity = 2.5 g L−1,
- ▪
- Aquifer reconstruction period to reduce salinity from 2.5 g L−1 to 1.0 g L−1 is 113 days (Figure A11b)
- ∘
- Stationary plume creation
- ▪
- Assumptions
- Vd = 47123.89 m3,
- As = 18.58 g L−1,
- Target As = 1.0 g L−1,
- ∘
- Modeled plume salinity vs. time
- ▪
- Processing rate: 40 m3 h−1,
- ▪
- Processing time: 24 h;
- ▪
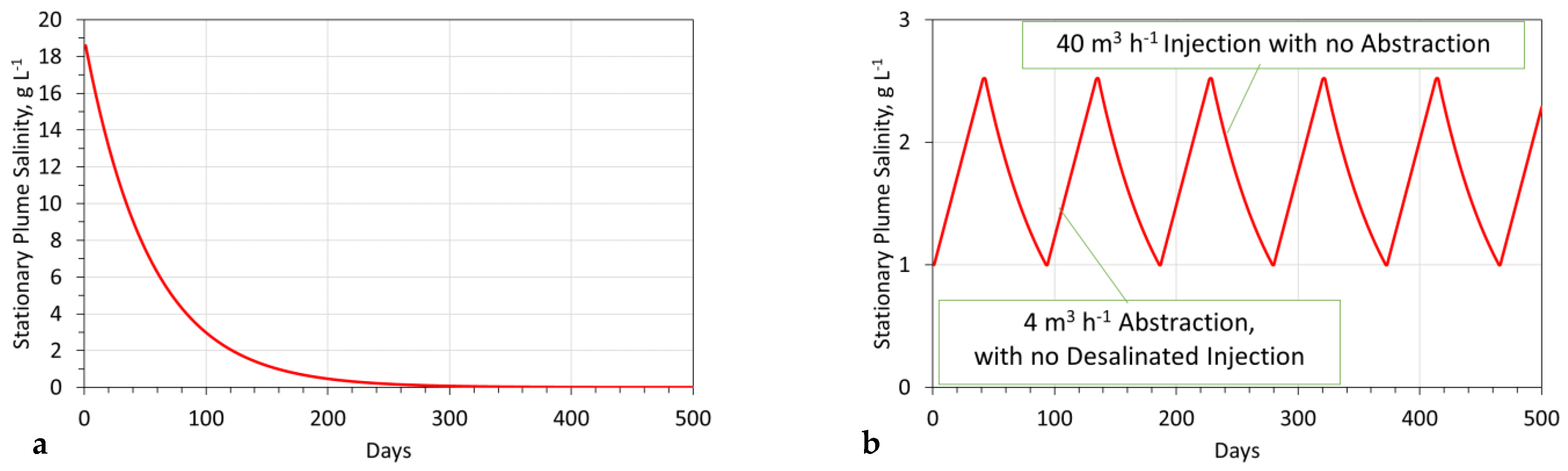
- Product desalination leaving the reactor = 90%;
- ▪
- Fe0:Fe(b)@Urea catalyst used = 229.6 kg FeSO4 + 547.8 kg CaO + 216.5 kg Urea;
- ▪
- Stabilization time = 160 days (Figure A12a);The stabilization time = time required to achieve As = 1 g L−1.
- ∘
- Modeled plume salinity vs. time during operation
- ▪
- Extracted Irrigation water [E]: 4 m3 h−1;
- ▪
- Makeup water from aquifer [A]: 4 m3 h−1;
- ▪
- Period of extraction of 96 m3 d−1 = 42 days (4032 m3). Minimum salinity = 1 g L−1; maximum salinity = 2.5 g L−1;
- ▪
- Aquifer reconstruction period to reduce salinity from 2.5 g L−1 to 1.0 g L−1 is 50 days (Figure A12b).
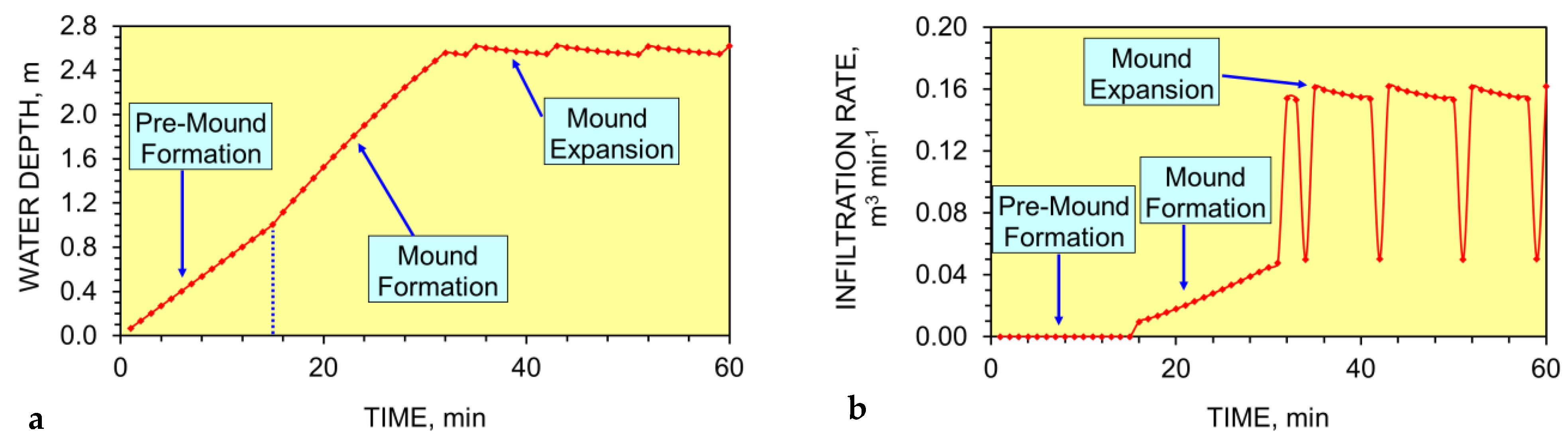
Appendix D.2. Modeling a Perched Pressure Mound
- The soil body is located above a regional or perched water table;
- The soil porosity contains an irreducible water saturation, an irreducible air saturation, a mobile air saturation, and when saturated contains a mobile water saturation. Additionally, salinized soil may contain dissolvable, crystallized ions and salts within their porosity.
- The soil contains a very low permeability, e.g., <10−14 m3 m−2 s−1 Pa−1.
- The soil contains a network of sealed nano-, micro-, and macro-fractures.
- Increasing the hydraulic pressure, P, applied will progressively and abruptly unseal the sealed nano-, micro-, and macro-fractures, and result in water flow into and water storage within the fractures. Reducing the hydraulic pressure applied will result in the progressive and abrupt resealing of the nano-, micro-, and macro-fractures.
- The fractures create an anisotropic permeability distribution where kx >> kz and ky >> kz. The dominant fracture propagation direction is in the x and y directions.
- A 2 m × 2 m × 4 m pit is dug in the clay;
- A 1 m-deep, 1.2 m-wide perforated preformed concrete ring segment is placed in the pit. It is overlain by three 1 m-deep, 1.2 m-wide non-perforated pre-formed concrete segments;
- The perforated zone is surrounded by coarse gravel (5–15 cm particle size), estimated porosity = 30%. Estimated storage volume, net of the storage chamber = 0.86 m3. The surrounding clay permeability is anisotropic, with a ratio of horizontal permeability to vertical permeability of 30. The remaining 3 m of the pit are infilled with clay.
References
- Wu, B.; Tian, F.; Zhang, M.; Piao, S.; Zeng, H.; Zhu, W.; Liu, J.; Elnashar, A.; Lu, Y. Quantifying global agricultural water appropriation with data derived from earth observations. J. Clean. Prod. 2022, 358, 131891. [Google Scholar] [CrossRef]
- Negacz, K.; Malek, Ž.; de Vos, A.; Vellinga, P. Saline soils worldwide: Identifying the most promising areas for saline agriculture. J. Arid. Environ. 2022, 203, 104775. [Google Scholar] [CrossRef]
- Fischer, C.; Aubron, C.; Trouvé, A.; Sekhar, M.; Ruiz, L. Groundwater irrigation reduces overall poverty but increases socioeconomic vulnerability in a semiarid region of southern India. Sci. Rep. 2022, 12, 8850. [Google Scholar] [CrossRef] [PubMed]
- Antia, D.D.J. Provision of Desalinated Irrigation Water by the Desalination of Groundwater Abstracted from a Saline Aquifer. Hydrology 2022, 9, 128. [Google Scholar] [CrossRef]
- Cheng, M.; Wang, H.; Fan, J.; Wang, X.; Sun, X.; Yang, L.; Zhang, S.; Xiang, Y.; Zhang, F. Crop yield and water productivity under salty water irrigation: A global meta-analysis. Agric. Water Manag. 2021, 256, 107105. [Google Scholar] [CrossRef]
- Antia, D.D.J. Purification of Saline Water Using Desalination Pellets. Water 2022, 14, 2639. [Google Scholar] [CrossRef]
- Antia, D.D.J. Catalytic Partial Desalination of Saline Water. Water 2022, 14, 2893. [Google Scholar] [CrossRef]
- Sefelnasr, A.; Ebraheem, A.A.; Faiz, M.A.; Shi, X.; Alghafli, K.; Baig, F.; Al-Rashed, M.; Alshamsi, D.; Ahamed, M.B.; Sherif, M. Enhancement of Groundwater Recharge from Wadi Al Bih Dam, UAE. Water 2022, 14, 3448. [Google Scholar] [CrossRef]
- Chenoweth, J.; Al-Masri, R.A. Cumulative effects of large-scale desalination on the salinity of semi-enclosed seas. Desalination 2022, 526, 115522. [Google Scholar] [CrossRef]
- GebreEgziabher, M.; Jasechko, S.; Perrone, D. Widespread and increased drilling of wells into fossil aquifers in the USA. Nat. Commun. 2022, 13, 2129. [Google Scholar] [CrossRef]
- Mir, R.; Azizyan, G.; Massah, A.; Gohari, A. Fossil water: Last resort to resolve long-standing water scarcity? Agric. Water Manag. 2022, 261, 107358. [Google Scholar] [CrossRef]
- Singh, A. Long-term (44 Years) regional groundwater recharge estimation for agricultural sustainability. Nat. Resour. Res. 2022, 31, 301–314. [Google Scholar] [CrossRef]
- Singh, A. Groundwater recharge assessment and long-term simulation for managing the threat of salinization of irrigated lands. J. Hydrol. 2022, 609, 127775. [Google Scholar] [CrossRef]
- Zhao, M.; Meng, X.; Wang, B.; Zhang, D.; Zhao, Y.; Li, R. Groundwater Recharge Modeling under Water Diversion Engineering: A Case Study in Beijing. Water 2022, 14, 985. [Google Scholar] [CrossRef]
- Dubois, E.; Larocque, M.; Gagné, S.; Braun, M. Climate Change Impacts on Groundwater Recharge in Cold and Humid Climates: Controlling Processes and Thresholds. Climate 2022, 10, 6. [Google Scholar] [CrossRef]
- Vendrell-Puigmitja, L.; Proia, L.; Espinosa, C.; Barral-Fraga, L.; Cañedo-Argüelles, M.; Osorio, V.; Casas, C.; Llenas, L.; Abril, M. Hypersaline mining effluents affect the structure and function of stream biofilm. Sci. Total Environ. 2022, 843, 156966. [Google Scholar] [CrossRef]
- Maritz, L.; Pillay, D.; Branch, G.M. The ecology of coastal wetland ponds created by diamond mining in southern Namibia. 1. Physical conditions. Afr. J. Mar. Sci. 2022, 44, 49–60. [Google Scholar] [CrossRef]
- Pumjan, S.; Long, T.T.; Loc, H.H.; Park, E. Deep well injection for the waste brine disposal solution of potash mining in Northeastern Thailand. J. Environ. Manag. 2022, 311, 114821. [Google Scholar] [CrossRef]
- Chen, X.; Sheng, Y.; Wang, G.; Guo, L.; Zhang, H.; Zhang, F.; Yang, T.; Huang, D.; Han, X.; Zhou, L. Microbial compositional and functional traits of BTEX and salinity co-contaminated shallow groundwater by produced water. Water Res. 2022, 215, 118277. [Google Scholar] [CrossRef]
- Samuel, O.; Othman, M.H.D.; Kamaludin, R.; Sinsamphanh, O.; Abdullah, H.; Puteh, M.H.; Kurniawan, T.A.; Li, T.; Ismail, A.F.; Rahman, M.A.; et al. Oilfield-produced water treatment using conventional and membrane-based technologies for beneficial reuse: A critical review. J. Environ. Manag. 2022, 308, 114556. [Google Scholar] [CrossRef]
- Emmons, R.V.; Shyam Sunder, G.S.; Liden, T.; Schug, K.A.; Asfaha, T.Y.; Lawrence, J.G.; Kirchhoff, J.R.; Gionfriddo, E. Unraveling the Complex Composition of Produced Water by Specialized Extraction Methodologies. Environ. Sci. Technol. 2022, 56, 2334–2344. [Google Scholar] [CrossRef] [PubMed]
- Jarma, Y.A.; Karaoğlu, A.; Tekin, Ö.; Senan, I.R.A.; Baba, A.; Kabay, N. Integrated pressure-driven membrane separation processes for the production of agricultural irrigation water from spent geothermal water. Desalination 2022, 523, 115428. [Google Scholar] [CrossRef]
- Kaczmarczyk, M.; Tomaszewska, B.; Bujakowski, W. Innovative desalination of geothermal wastewater supported by electricity generated from low-enthalpy geothermal resources. Desalination 2022, 524, 115450. [Google Scholar] [CrossRef]
- Prajapati, M.; Shah, M.; Soni, B. A comprehensive review of the geothermal integrated multi-effect distillation (MED) desalination and its advancements. Groundw. Sustain. Dev. 2022, 19, 100808. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, J.Y. Analysis of Compositions of Flowback Water from Marcellus Shale Wells by Utilizing Data Mining Techniques. J. Energy Resour. Technol. 2022, 144, 013004. [Google Scholar]
- Fajfer, J.; Lipińska, O.; Konieczyńska, M. Hydraulic fracturing flowback chemical composition diversity as a factor determining possibilities of its management. Environ. Sci. Pollut. Res. 2022, 29, 16152–16175. [Google Scholar] [CrossRef]
- Yang, Y.; Tian, L.; Borch, T.; Tariq, H.; Li, T.; Bai, Y.; Su, Y.; Tiraferri, A.; Crittenden, J.C.; Liu, B. Safety and Technical Feasibility of Sustainable Reuse of Shale Gas Flowback and Produced Water after Advanced Treatment Aimed at Wheat Irrigation. ACS Sustain. Chem. Eng. 2022, 10, 12540–12551. [Google Scholar] [CrossRef]
- Manivannan, V.; Manoj, S.; RamyaPriya, R.; Elango, L. Delineation and quantification of groundwater resources affected by seawater intrusion along the east coast of India. Environ. Earth Sci. 2022, 81, 300. [Google Scholar] [CrossRef]
- Benaafi, M.; Tawabini, B.; Abba, S.I.; Humphrey, J.D.; AL-Areeq, A.M.; Alhulaibi, S.A.; Usman, A.G.; Aljundi, I.H. Integrated Hydrogeological, Hydrochemical, and Isotopic Assessment of Seawater Intrusion into Coastal Aquifers in Al-Qatif Area, Eastern Saudi Arabia. Molecules 2022, 27, 6841. [Google Scholar] [CrossRef]
- Selvakumar, S.; Chandrasekar, N.; Srinivas, Y.; Selvam, S.; Kaliraj, S.; Magesh, N.S.; Venkatramanan, S. Hydrogeochemical processes controlling the groundwater salinity in the coastal aquifers of Southern Tamil Nadu, India. Mar. Pollut. Bull. 2022, 174, 113264. [Google Scholar] [CrossRef]
- Al-Asadi, S.A.; Alhello, A.A.; Ghalib, H.B.; Muttashar, W.R.; Al-Eydawi, H.T. Seawater intrusion into Shatt Al-Arab River, Northwest Arabian/Persian Gulf. J. Appl. Water Eng. Res. 2022, 1–14. [Google Scholar] [CrossRef]
- Liu, Z.; Hou, P.; Zha, Y.; Muhammad, T.; Li, Y. Salinity threshold of desalinated saline water used for drip irrigating: The perspective of emitter clogging. J. Clean. Prod. 2022, 361, 132143. [Google Scholar] [CrossRef]
- Said, I.; Salman, S.A.; Elnazer, A.A. Salinization of groundwater during 20 years of agricultural irrigation, Luxor, Egypt. Environ. Geochem. Health 2022, 44, 3821–3835. [Google Scholar] [CrossRef] [PubMed]
- Pouladi, P.; Nazemi, A.R.; Pouladi, M.; Nikraftar, Z.; Mohammadi, M.; Yousefi, P.; David, J.Y.; Afshar, A.; Aubeneau, A.; Sivapalan, M. Desiccation of a saline lake as a lock-in phenomenon: A socio-hydrological perspective. Sci. Total Environ. 2022, 811, 152347. [Google Scholar] [CrossRef] [PubMed]
- Varghese, P.; Varma, A. Catalytic reactions in transport-line reactors. Chem. Eng. Sci. 1979, 34, 337–343. [Google Scholar] [CrossRef]
- Carberry, J.J. Chemical and Catalytic Reaction Engineering; Dover Publications, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Bottero, J.Y.; Manceau, A.; Villieras, F.; Tchoubar, D. Structure and mechanisms of formation of iron oxide hydroxide (chloride) polymers. Langmuir 1994, 10, 316–319. [Google Scholar] [CrossRef]
- Spiro, T.G.; Allerton, S.E.; Renner, J.; Terzis, A.; Bils, R.; Saltman, P. The Hydrolytic Polymerization of Iron (III). J. Am. Chem. Soc. 1966, 88, 2721–2726. [Google Scholar] [CrossRef]
- Dong, H.; Gao, B.; Yue, Q.; Sun, S.; Wang, Y.; Li, Q. Floc properties and membrane fouling of different monomer and polymer Fe coagulants in coagulation–ultrafiltration process: The role of Fe (III) species. Chem. Eng. J. 2014, 258, 442–449. [Google Scholar] [CrossRef]
- Chen, D.-W.; Liu, C.; Lu, J.; Mehmood, T.; Ren, Y.-Y. Enhanced phycocyanin and DON removal by the synergism of H2O2 and micro-sized ZVI: Optimization, performance, and mechanisms. Sci. Total Environ. 2020, 738, 140134. [Google Scholar] [CrossRef]
- Misstear, B.; Banks, D.; Clark, L. Water Wells and Boreholes; John Wiley and Sons: Hoboken, NJ, USA, 2007; 498p. [Google Scholar]
- Lide, D. CRC Handbook of Chemistry and Physics, 2008–2009, 89th ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Konadu-Amoah, B.; Hu, R.; Ndé-Tchoupé, A.I.; Gwenzi, W.; Noubactep, C. Metallic iron (Fe0)-based materials for aqueous phosphate removal: A critical review. J. Environ. Manag. 2022, 315, 115157. [Google Scholar] [CrossRef]
- Fronczyk, J.; Pawluk, K.; Michniak, M. Application of permeable reactive barriers near roads for chloride ions removal. Ann. Wars. Univ. Life Sci. SGGW Land Reclam. 2010, 42, 249–259. [Google Scholar] [CrossRef]
- Rebello, L.R.B.; Siepman, T.; Drexler, S. Correlations between TDS and electrical conductivity for high-salinity formation brines characteristic of South Atlantic pre-salt basins. Water SA 2020, 46, 602–609. [Google Scholar]
- Hildebrant, B.; Ndé-Tchoupé, A.I.; Lufingo, M.; Licha, T.; Noubactep, C. Steel Wool for Water Treatment: Intrinsic Reactivity and Defluoridation Efficiency. Processes 2020, 8, 265. [Google Scholar] [CrossRef]
- Fu, J.; Jiang, X.; Han, W.; Cao, Z. Enhancing the Cycling Stability of Transition-Metal-Oxide-Based Electrochemical Electrode via Pourbaix Diagram Engineering. Energy Storage Mater. 2021, 42, 252–258. [Google Scholar] [CrossRef]
- Li, X.; Sheng, A.; Ding, Y.; Liu, J. A model towards understanding stabilities and crystallization pathways of iron (oxyhydr) oxides in redox-dynamic environments. Geochim. Cosmochim. Acta 2022, 336, 92–103. [Google Scholar] [CrossRef]
- Perry, S.C.; Gateman, S.M.; Stephens, L.I.; Lacasse, R.; Schulz, R.; Mauzeroll, J. Pourbaix diagrams as a simple route to first principles corrosion simulation. J. Electrochem. Soc. 2019, 166, C3186–C3192. [Google Scholar] [CrossRef]
- Génin, J.M.R.; Ruby, C.; Géhin, A.; Refait, P. Synthesis of green rusts by oxidation of Fe (OH) 2, their products of oxidation and reduction of ferric oxyhydroxides; Eh–pH Pourbaix diagrams. Comptes Rendus Geosci. 2006, 338, 433–446. [Google Scholar] [CrossRef]
- Beverskog, B.; Puigdomenech, I. Revised pourbaix diagrams for iron at 25–300 °C. Corros. Sci. 1996, 38, 2121–2135. [Google Scholar] [CrossRef]
- Pourbaix, M. Atlas of Electrochemical Equilibria in Aqueous Solutions, 2nd ed.; Library of Congress Catalog Card No 65-11670; Franklin, J.A., Translator; NACE International: Houston, TX, USA, 1974; p. 644. [Google Scholar]
- Antia, D.D.J. Remediation of Saline Wastewater Producing a Fuel Gas Containing Alkanes and Hydrogen Using Zero Valent Iron (Fe0). Water 2022, 14, 1926. [Google Scholar] [CrossRef]
- Sato, M. Persistency-field Eh-pH diagrams for sulfides and their application to supergene oxidation and enrichment of sulfide ore bodies. Geochim. Cosmochim. Acta 1992, 56, 3133–3156. [Google Scholar] [CrossRef]
- Rezaei, F.; Vione, D. Effect of pH on Zero Valent Iron Performance in Heterogeneous Fenton and Fenton-Like Processes: A Review. Molecules 2018, 23, 3127. [Google Scholar] [CrossRef] [PubMed]
- Antia, D.D.J. Water Treatment and Desalination Using the Eco-materials n-Fe0 (ZVI), n-Fe3O4, n-FexOyHz[mH2O], and n-Fex[Cation]nOyHz[Anion]m [rH2O]. In Handbook of Nanomaterials and Nanocomposites for Energy and Environmental Applications, 1st ed.; Kharissova, O.V., Torres-Martínez, L.M., Kharisov, B.I., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 3159–3242. [Google Scholar] [CrossRef]
- Ebbing, D.D.; Gammon, S.D. General Chemistry, 8th ed.; Houghton Mifflin Company: New York, NY, USA, 2005; ISBN 0618399429. [Google Scholar]
- Pilling, M.J.; Seakins, P.W. Reaction Kinetics; Oxford Science Publications, Oxford University Press: New York, NY, USA, 1996; 305p. [Google Scholar]
- Antia, D.D.J. Desalination of irrigation water using metal polymers. Water 2022, 14, 3224. [Google Scholar] [CrossRef]
- Antia, D.D.J. Desalination of groundwater and impoundments using Nano-Zero Valent Iron, n-Fe0. Meteorol. Hydrol. Water Manag. Res. Oper. Appl. 2015, 3, 21–38. [Google Scholar] [CrossRef]
- BSI British Standards Institute. Quality Management Systems. In Statistical Interpretation of Data; BSI Handbook; British Standards Institute: London, UK, 1985; p. 318. ISBN 0580150712. [Google Scholar]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef]
- Taylor, R. Interpretation of the Correlation Coefficient: A Basic Review. J. Diagn. Med. Sonogr. 1990, 6, 35–39. [Google Scholar] [CrossRef]
- Cao, V.; Bakari, O.; Kenmogne-Tchidjo, J.F.; Gatcha-Bandjun, N.; Ndé-Tchoupé, A.I.; Gwenzi, W.; Njau, K.N.; Noubactep, C. Conceptualizing the Fe0/H2O System: A Call for Collaboration to Mark the 30th Anniversary of the Fe0-Based Permeable Reactive Barrier Technology. Water 2022, 14, 3120. [Google Scholar] [CrossRef]
- Shende, R.; Vats, A.; Doorenbos, Z.; Kapoor, D.; Puszynski, J. Formation of pyrophoric alpha-Fe nanoparticles from Fe (II)-oxalate. NSTI-Nanotech 2008, 1, 692–695. [Google Scholar]
- Shende, R.V.; Vats, A.; Doorenbos, Z.D.; Kapoor, D.; Martin, D.; Puszynski, J. Formation of pyrophoric iron particles by H2 reduction of oxalate and oxides. Int. J. Energ. Mater. Chem. Propuls. 2008, 7, 87–97. [Google Scholar] [CrossRef]
- Refait, P.; Benali, O.; Abdelmoula, M.; Génin, J.M. Formation of ‘ferric green rust’ and/or ferrihydrite by fast oxidation of iron (II–III) hydroxychloride green rust. Corros. Sci. 2003, 45, 2435–2449. [Google Scholar] [CrossRef]
- Génin, J.M.; Olowe, A.A.; Refait, P.; Simon, L. On the stoichiometry and Pourbaix diagram of Fe (II)-Fe (III) hydroxy-sulphate or sulphate-containing green rust 2: An electrochemical and Mössbauer spectroscopy study. Corros. Sci. 1996, 38, 1751–1762. [Google Scholar] [CrossRef]
- Rémazeilles, C.; Refait, P. On the formation of β-FeOOH (akaganéite) in chloride-containing environments. Corros. Sci. 2007, 49, 844–857. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, T.; Xiao, X.; Fang, X.; Liu, X.; Dong, Y.; Li, Y.; Li, J. Nature-inspired phytic acid-based hybrid complexes for fabricating green and transparent superhydrophobic and anti-mildew coating on bamboo surface. Colloids Surf. A Physicochem. Eng. Asp. 2022, 651, 129769. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, J.; Xie, M.; Xu, J.; Li, Y.; Shen, H.; Hao, J. Synthesis of polyethyleneimine-modified magnetic iron oxide nanoparticles without adding base and other additives. Mater. Lett. 2017, 193, 122–125. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L.; Song, X.; Gu, X.; Sun, H.; Fu, C.; Meng, F. Synthesis of superparamagnetic iron oxide nanoparticles modified with MPEG-PEI via photochemistry as new MRI contrast agent. J. Nanomater. 2015, 16, 31. [Google Scholar] [CrossRef]
- Cai, J.; Liu, J.; Gao, Z.; Navrotsky, A.; Suib, S.L. Synthesis and anion exchange of tunnel structure akaganeite. Chem. Mater. 2001, 13, 4595–4602. [Google Scholar] [CrossRef]
- Scheck, J.; Lemke, T.; Gebauer, D. The Role of Chloride Ions during the Formation of Akaganéite Revisited. Minerals 2015, 5, 778–787. [Google Scholar] [CrossRef]
- Post, J.E.; Buchwald, V.F. Crystal structure refinement of akaganeite. Am. Miner. 1991, 76, 272–277. [Google Scholar]
- Reguer, S.; Mirambet, F.; Dooryhee, E.; Hodeau, J.-L.; Dillmann, P.; Lagarde, P. Structural evidence for the desalination of akaganeite in the preservation of iron archaeological objects, using synchrotron X-ray powder diffraction and absorption spectroscopy. Corros. Sci. 2009, 51, 2795–2802. [Google Scholar] [CrossRef]
- Wang, J.; Shui, L.; Segerink, L.I.; Eijkel, J.C.T. Microfluidic Construction of Hierarchically Composite Superballs for Sensing Applications. Proceedings 2018, 2, 750. [Google Scholar] [CrossRef]
- Cao, S.W.; Zhu, Y.J. Iron oxide hollow spheres: Microwave–hydrothermal ionic liquid preparation, formation mechanism, crystal phase and morphology control and properties. Acta Mater. 2009, 57, 2154–2165. [Google Scholar] [CrossRef]
- Sabir, S.; Arshad, M.; Chaudhari, S.K. Zinc oxide nanoparticles for revolutionizing agriculture: Synthesis and applications. Sci. World J. 2014, 2014, 925494. [Google Scholar] [CrossRef] [PubMed]
- Chambers, O.; Sešek, A.; Tasič, J.F.; Trontelj, J. Fertiliser characterisation using optical and electrical impedance methods. Comput. Electron. Agric. 2018, 155, 69–75. [Google Scholar] [CrossRef]
- Lanauskas, J.; Kvikliene, N. Effect of calcium foliar application on some fruit quality characteristics of ‘Sinap Orlovskij’ apple. Agron. Res. 2006, 4, 31–36. [Google Scholar]
- Salama, D.M.; Abd El-Aziz, M.E.; Osman, S.A.; Abd Elwahed, M.S.; Shaaban, E.A. Foliar spraying of MnO2-NPs and its effect on vegetative growth, production, genomic stability, and chemical quality of the common dry bean. Arab. J. Basic Appl. Sci. 2022, 29, 26–39. [Google Scholar] [CrossRef]
- Sadana, U.S.; Manchanda, J.S.; Khurana, M.P.S.; Dhaliwal, S.S.; Singh, H. The current scenario and efficient management of zinc, iron, and manganese deficiencies. Better Crops–South Asia 2010, 4, 24–26. [Google Scholar]
- Rasht, I. Effect of application of iron fertilizers in two methods’ foliar and soil application on growth characteristics of Spathyphyllum illusion. Eur. J. Exp. Biol. 2013, 3, 232–240. [Google Scholar]
- Torabian, S.; Zahedi, M.; Khoshgoftar, A.H. Effects of foliar spray of nano-particles of FeSO4 on the growth and ion content of sunflower under saline condition. J. Plant Nutr. 2017, 40, 615–623. [Google Scholar] [CrossRef]
- Fazekas, C.; Péntek, A.; Vojnich, V.J. effect of foliar fertilizers applications on the nectar production of sunflower (Heliathus annuus L.) and on the foraging behaviour of honeybees (Apis mellifera L.). Ann. Fac. Eng. Hunedoara 2019, 17, 153–160. [Google Scholar]
- Härdter, R.; Rex, M.; Orlovius, K. Effects of different Mg fertilizer sources on the magnesium availability in soils. Nutr. Cycl. Agroecosystems 2005, 70, 249–259. [Google Scholar] [CrossRef]
- Song, C.; Liu, C.; Han, G.; Liu, C. Impact of different fertilizers on carbonate weathering in a typical karst area, Southwest China: A field column experiment. Earth Surf. Dyn. 2017, 5, 605–616. [Google Scholar] [CrossRef]
- Castle, M.E.; Watson, J.N. Silage and milk production, a comparison between grass silages made with and without formic acid. Grass Forage Sci. 1970, 25, 65–71. [Google Scholar] [CrossRef]
- Ha, C.N.T.; Ngoc, N.D.; Ngoc, C.P.; Trung, D.D.; Quang, B.N. Synthesis and application of rare earth organic fertilizers on cucumbers. Vietnam. J. Catal. Adsorpt. 2021, 10, 17–22. [Google Scholar] [CrossRef]
- Xiaoyu, N.; Yuejin, W.; Zhengyan, W.; Lin, W.; Guannan, Q.; Lixiang, Y. A novel slow-release urea fertiliser: Physical and chemical analysis of its structure and study of its release mechanism. Biosyst. Eng. 2013, 115, 274–282. [Google Scholar] [CrossRef]
- Liu, W.; Price, S.; Bennett, G.; Maxwell, T.M.; Zhao, C.; Walker, G.; Bunt, C. A landscape review of controlled release urea products: Patent objective, formulation and technology. J. Control. Release 2022, 348, 612–630. [Google Scholar] [CrossRef]
- Sugimoto, T.; Kobayashi, M.; Adachi, Y. The effect of double layer repulsion on the rate of turbulent and Brownian aggregation: Experimental consideration. Colloids Surf. A Physicochem. Eng. Asp. 2014, 443, 418–424. [Google Scholar] [CrossRef]
- Antia, D.D.J. Desalination of Water Using ZVI (Fe0). Water 2015, 7, 3671–3831. [Google Scholar] [CrossRef]
- Piper, A.M. A graphic procedure in the geochemical interpretation of water-analyses. Eos Trans. Am. Geophys. Union 1944, 25, 914–928. [Google Scholar] [CrossRef]
- Yidana, S.M. Groundwater classification using multivariate statistical methods: Southern Ghana. J. Afr. Earth Sci. 2010, 57, 455–469. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, J.; Wang, S.; Zou, J.; Zhen, P. Multivariate statistical analysis of chemical and stable isotopic data as indicative of groundwater evolution with reduced exploitation. Geosci. Front. 2023, 14, 101476. [Google Scholar] [CrossRef]
- El Osta, M.; Masoud, M.; Alqarawy, A.; Elsayed, S.; Gad, M. Groundwater Suitability for Drinking and Irrigation Using Water Quality Indices and Multivariate Modeling in Makkah Al-Mukarramah Province, Saudi Arabia. Water 2022, 14, 483. [Google Scholar] [CrossRef]
- Anoop, S.; Sayana, C.; Pillai, R.S. Groundwater quality and chemical characteristics of Bekal watershed, Kasaragod district, Kerala, India. Sustain. Water Resour. Manag. 2022, 8, 42. [Google Scholar] [CrossRef]
- Agoubi, B.; Kharroubi, A.; Abida, H. Hydrochemistry of groundwater and its assessment for irrigation purpose in coastal Jeffara Aquifer, southeastern Tunisia. Arab. J. Geosci. 2013, 6, 1163–1172. [Google Scholar] [CrossRef]
- Arulbalaji, P.; Gurugnanam, B. Groundwater quality assessment using geospatial and statistical tools in Salem District, Tamil Nadu, India. Appl. Water Sci. 2017, 7, 2737–2751. [Google Scholar] [CrossRef]
- Sisodiya, S.; Mehar, R.K.; Mathur, A.K. Datasets for Assessment of Water Quality Indices for Irrigation and Drinking for Hadoti Lakes, Rajasthan. Int. J. Lakes Rivers 2020, 13, 121–130. [Google Scholar]
- Brutsaert, W. Hydrology an Introduction; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Gao, Y.; Du, E.; Yi, S.; Han, Y.; Zheng, C. An improved numerical model for groundwater flow simulation with MPFA method on arbitrary polygon grids. J. Hydrol. 2022, 606, 127399. [Google Scholar] [CrossRef]
- Atangana, A. (Ed.) Mathematical Analysis of Groundwater Flow Models; CRC Press: Boca Raton, USA, 2022; 634p. [Google Scholar]
- Dahlberg, E.C. Applied Hydrodynamics in Petroleum Exploration; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Hubbert, M.K. Entrapment of petroleum under hydrodynamic conditions. AAPG Bull. 1953, 37, 1954–2026. [Google Scholar]
- Stewart, S.A.; Albertz, M. Hydrostatic pore water pressure revisited. Basin Res. 2022. [Google Scholar] [CrossRef]
- Wendebourg, J.; Biteau, J.J.; Grosjean, Y. Hydrodynamics and hydrocarbon trapping: Concepts, pitfalls and insights from case studies. Mar. Pet. Geol. 2018, 96, 190–201. [Google Scholar] [CrossRef]
- Stewart, S.A.; Riddell, L.A. Hydrodynamic invalidation of synformal traps for dissolved CO2. Geology 2022, 50, 1121–1124. [Google Scholar] [CrossRef]
- Alhama, I.; García-Ros, G.; Icardi, M. Non-Stationary Contaminant Plumes in the Advective-Diffusive Regime. Mathematics 2021, 9, 725. [Google Scholar] [CrossRef]
- da Silva, D.V.; Oleinik, P.H.; Costi, J.; de Paula Kirinus, E.; Marques, W.C.; Moller, O.O. Variability of the Spreading of the Patos Lagoon Plume Using Numerical Drifters. Coasts 2022, 2, 51–69. [Google Scholar] [CrossRef]
- Antia, D.D.J. Provision of Desalinated Irrigation Water by the Desalination of Groundwater within a Saline Aquifer. Hydrology 2017, 4, 1. [Google Scholar] [CrossRef]
- Antia, D.D.J. ZVI (Fe0) desalination: Catalytic partial desalination of saline aquifers. Appl. Water Sci. 2018, 8, 71. [Google Scholar] [CrossRef]
- Singh, A. Soil salinization management for sustainable development: A review. J. Environ. Manag. 2021, 277, 111383. [Google Scholar] [CrossRef] [PubMed]
- Singh, A. Soil salinization and waterlogging: A threat to environment and agricultural sustainability. Ecol. Indic. 2015, 57, 128–130. [Google Scholar] [CrossRef]
- Machado, R.M.A.; Serralheiro, R.P. Soil Salinity: Effect on Vegetable Crop Growth. Management Practices to Prevent and Mitigate Soil Salinization. Horticulturae 2017, 3, 30. [Google Scholar] [CrossRef]
- Antia, D.D.J. Formation and Control of Self-Sealing High Permeability Groundwater Mounds in Impermeable Sediment: Implications for SUDS and Sustainable Pressure Mound Management. Sustainability 2009, 1, 855–923. [Google Scholar] [CrossRef]
- Antia, D.D.J. Interpretation of Overland Flow Associated with Infiltration Devices Placed in Boulder Clay and Construction Fill. In Overland Flow and Surface Runoff; Wong, T.S.W., Ed.; Nova Science Publishers Inc.: New York, NY, USA, 2012; Chapter 9; pp. 211–286. ISBN 978-1-61122-868-7. [Google Scholar]
- Khan, M.Y.; Kirkham, D.; Handy, R.L. Shapes of steady state perched groundwater mounds. Water Resour. Res. 1976, 12, 429–436. [Google Scholar] [CrossRef]
- Schneider, A.D.; Luthin, J.N. Simulation of groundwater mound perching in layered media. Trans. ASAE 1978, 21, 920–0923. [Google Scholar] [CrossRef]
- Lu, P.; Sheng, Z.; Zhang, Z.; Miller, G.; Reinert, S.; Huang, M. Effect of multilayered groundwater mounds on water dynamics beneath a recharge basin: Numerical simulation and assessment of surface injection. Hydrol. Process. 2021, 35, e14193. [Google Scholar] [CrossRef]
- Yihdego, Y. Simulation of Groundwater Mounding Due to Irrigation Practice: Case of Wastewater Reuse Engineering Design. Hydrology 2017, 4, 19. [Google Scholar] [CrossRef]
- Currie, D.; Laattoe, T.; Walker, G.; Woods, J.; Smith, T.; Bushaway, K. Modelling Groundwater Returns to Streams from Irrigation Areas with Perched Water Tables. Water 2020, 12, 956. [Google Scholar] [CrossRef]


| Cl- | Na+ | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Polymer | Trial | [a] | [b] | R2 | PCC | [a] | [b] | R2 | PCC |
| Fe-Ca | 1 | 0.000120540 | −0.9842 | 0.999 | 1.000 | 0.0000851 | −0.92801 | 0.997 | 0.998 |
| 2 | 0.000168210 | −0.9867 | 0.999 | 0.999 | 0.0000039 | −1.61133 | 1.000 | 1.000 | |
| Fe-Ca-Urea | 3 | 0.000278500 | −0.9542 | 0.954 | 0.977 | 0.0001331 | −1.01025 | 1.000 | 1.000 |
| Fe-Ca-Mn-Formic Acid | 4 | 0.000049800 | −0.4236 | 0.918 | 0.958 | 0.0002348 | −1.05551 | 0.842 | 0.918 |
| 5 | 0.000135500 | −0.7804 | 0.975 | 0.987 | 0.0002164 | −0.88604 | 0.955 | 0.977 | |
| Fe-Ca-Zn-Gallic Acid | 6 | 0.000020820 | −0.5451 | 1.000 | 1.000 | 14.4647000 | −0.00100 | 1.000 | 1.000 |
| Fe-Zn | 7 | 0.000027580 | −1.1817 | 1.000 | 1.000 | 0.0000730 | −0.86425 | 0.999 | 0.999 |
| Fe-Ca-Mn-Mg-Formic Acid | 8 | 0.000179580 | −0.7637 | 0.990 | 0.995 | 0.0001411 | −0.94756 | 0.996 | 0.998 |
| Fe-Ca-Mn-Formic Acid | 9 | 0.000031490 | −0.4312 | 0.732 | 0.856 | 0.0001519 | −0.92883 | 0.906 | 0.952 |
| Fe-Ca-Zn- Tartaric Acid | 10 | 0.000289940 | −0.7276 | 0.963 | 0.981 | 0.0003781 | −0.86185 | 0.988 | 0.994 |
| FeSO4 | CaO | ZnO | Tartaric Acid | Urea | Polymer A | Polymer B | |
|---|---|---|---|---|---|---|---|
| Low | 80 | 60 | 2900 | 1500 | 15 | 34.25 | 0.33 |
| High | 150 | 120 | 3200 | 30,000 | 150 | 63.60 | 0.81 |
| Ca | K | Mg | Na | Cl | HCO3 | SO4 | NaCl | SAR | EC1 | EC2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Example Well | 0.1633 | 0.0327 | 0.0262 | 4.659 | 7.64 | 1.036 | 0.0656 | 12.3 | 125.94 | 24.77 | 19.46 |
| 0% Desalination | 2.5490 | 0.0327 | 0.0262 | 4.659 | 7.64 | 1.036 | 0.0656 | 12.3 | 35.58 | 29.11 | 22.87 |
| 20% Desalination | 2.5490 | 0.0327 | 0.0262 | 3.727 | 6.11 | 1.036 | 0.0656 | 9.8 | 28.47 | 24.63 | 19.36 |
| 50% Desalination | 2.5490 | 0.0327 | 0.0262 | 2.330 | 3.82 | 1.036 | 0.0656 | 6.1 | 17.79 | 17.93 | 14.08 |
| 80% Desalination | 2.5490 | 0.0327 | 0.0262 | 0.932 | 1.53 | 1.036 | 0.0656 | 2.5 | 7.12 | 11.22 | 8.81 |
| 100% Desalination | 2.5490 | 0.0327 | 0.0262 | 0.000 | 0.00 | 1.036 | 0.0656 | 0.0 | 0.00 | 6.74 | 5.30 |
| Ca | K | Mg | Na | Cl | HCO3 | SO4 | NaCl | SAR | EC1 | EC2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Example Well | 0.1633 | 0.0327 | 0.0262 | 4.659 | 7.64 | 1.036 | 0.0656 | 12.3 | 125.94 | 24.77 | 19.46 |
| 0% Desalination | 9.7062 | 0.0327 | 0.0262 | 4.659 | 7.64 | 1.036 | 0.0656 | 12.3 | 18.35 | 42.12 | 33.09 |
| 20% Desalination | 9.7062 | 0.0327 | 0.0262 | 3.727 | 6.11 | 1.036 | 0.0656 | 9.8 | 14.68 | 37.65 | 29.58 |
| 50% Desalination | 9.7062 | 0.0327 | 0.0262 | 2.330 | 3.82 | 1.036 | 0.0656 | 6.1 | 9.17 | 30.94 | 24.31 |
| 80% Desalination | 9.7062 | 0.0327 | 0.0262 | 0.932 | 1.53 | 1.036 | 0.0656 | 2.5 | 3.67 | 24.23 | 19.04 |
| 90% Desalination | 9.7062 | 0.0327 | 0.0262 | 0.466 | 0.76 | 1.036 | 0.0656 | 1.2 | 1.83 | 21.99 | 17.28 |
| 100% Desalination | 9.7062 | 0.0327 | 0.0262 | 0.000 | 0.00 | 1.036 | 0.0656 | 0.0 | 0.00 | 19.76 | 15.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antia, D.D.J. Partial Desalination of Saline Groundwater, including Flowback Water, to Produce Irrigation Water. Hydrology 2022, 9, 219. https://doi.org/10.3390/hydrology9120219
Antia DDJ. Partial Desalination of Saline Groundwater, including Flowback Water, to Produce Irrigation Water. Hydrology. 2022; 9(12):219. https://doi.org/10.3390/hydrology9120219
Chicago/Turabian StyleAntia, David D. J. 2022. "Partial Desalination of Saline Groundwater, including Flowback Water, to Produce Irrigation Water" Hydrology 9, no. 12: 219. https://doi.org/10.3390/hydrology9120219
APA StyleAntia, D. D. J. (2022). Partial Desalination of Saline Groundwater, including Flowback Water, to Produce Irrigation Water. Hydrology, 9(12), 219. https://doi.org/10.3390/hydrology9120219






