Groundwater Temperature Modelling at the Water Table with a Simple Heat Conduction Model
Abstract
1. Introduction
- To analyze the long-term trends of air temperature and temperature below the surface at depths of up to 10 m based on the observed average monthly temperature series from the stations of the SHMI;
- The second part of the study aimed at the modelling of the groundwater temperature at the water table (depth of 0.6–15 m). The Fourier model of heat propagation in soil was used to model the groundwater temperature. The given model can be used to simulate groundwater temperature as a function of air temperature, groundwater table depth, and soil type.
2. Materials and Methods
2.1. Data Used
- Soil moisture (%) and soil temperature (°C) (at eight horizons: 0.10, 0.20, 0.40, 0.60, 0.80, 1.00, 1.20, and 1.60 m below the soil surface);
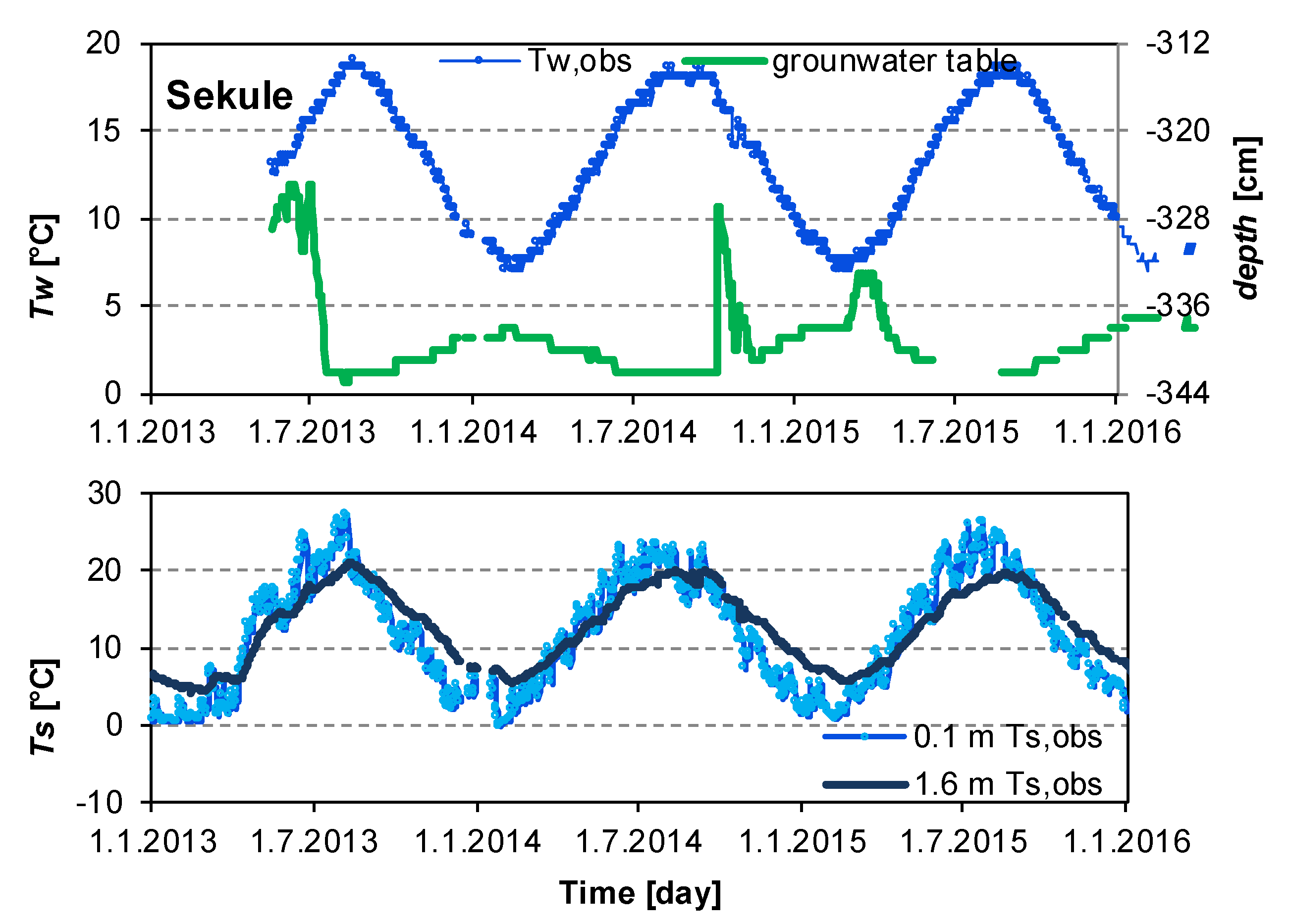
- The depth of the groundwater table (m below the ground surface);
- Groundwater temperature (°C);
- Air temperature (°C) and Rainfall depth (mm).
2.2. Groundwater Temperature Modelling with Time and Depth
- A cosinusoidal temperature variation at the soil surface z = 0.
- At an infinite depth, the soil temperature was assumed to be constant and equal to the average soil temperature.
- The thermal diffusivity was assumed to be constant throughout the soil profile and throughout the year.
3. Results
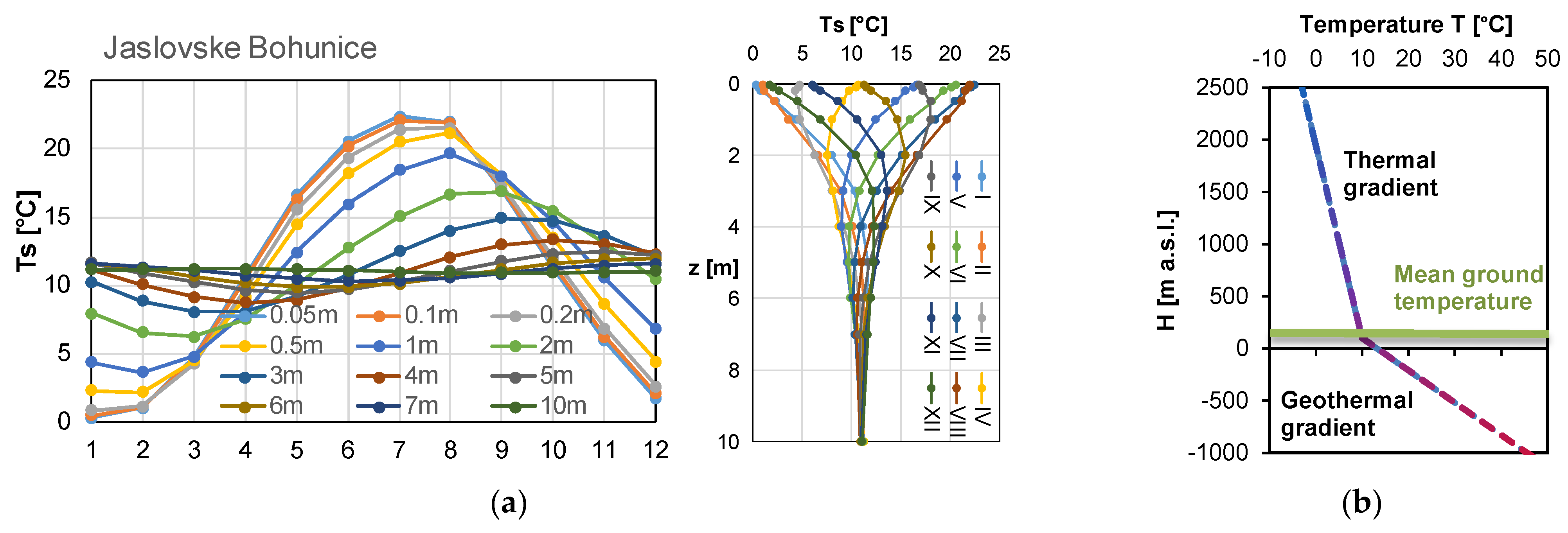
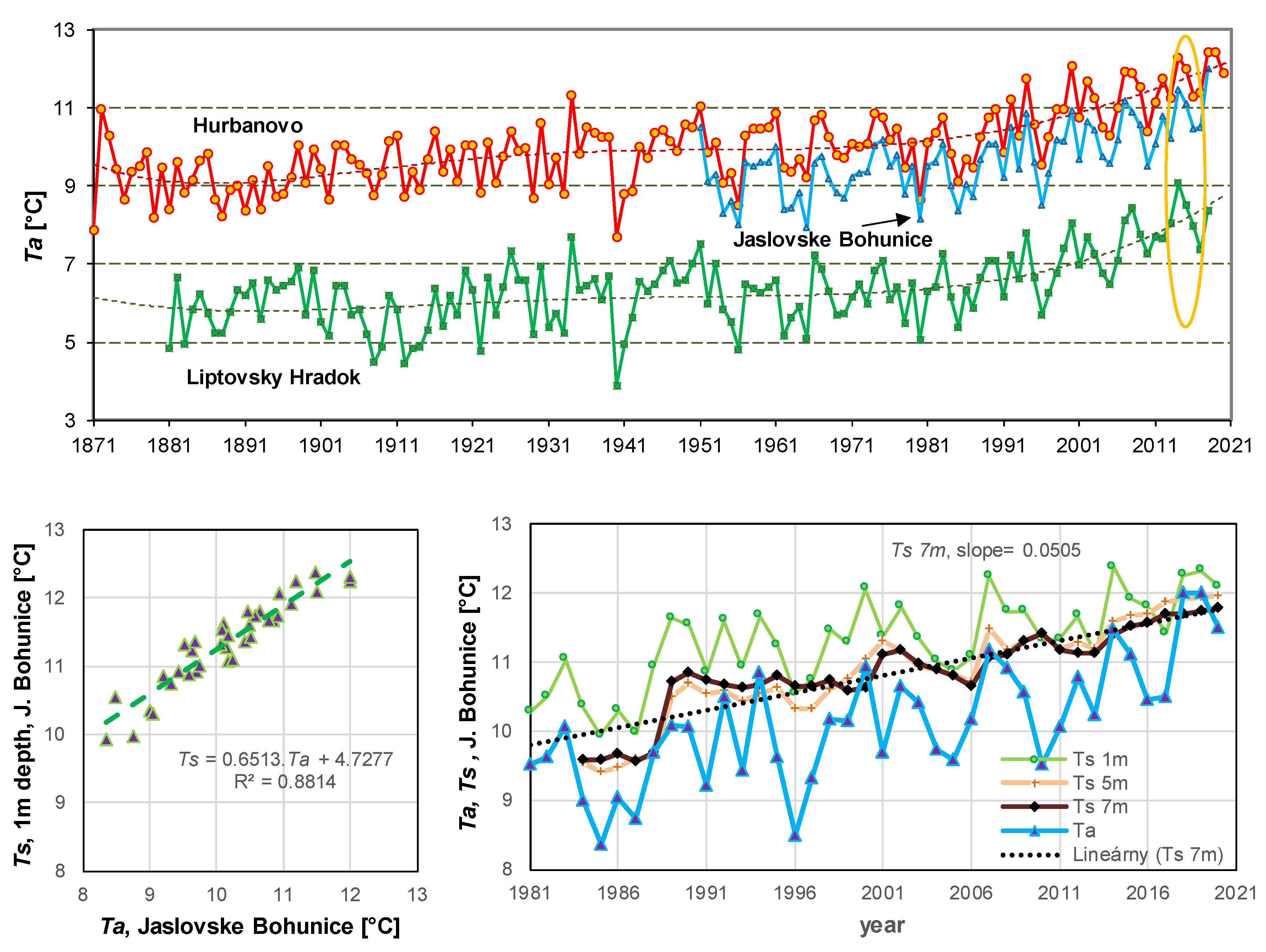
3.1. Long-Term Trends of Air and Soil Temperature Series
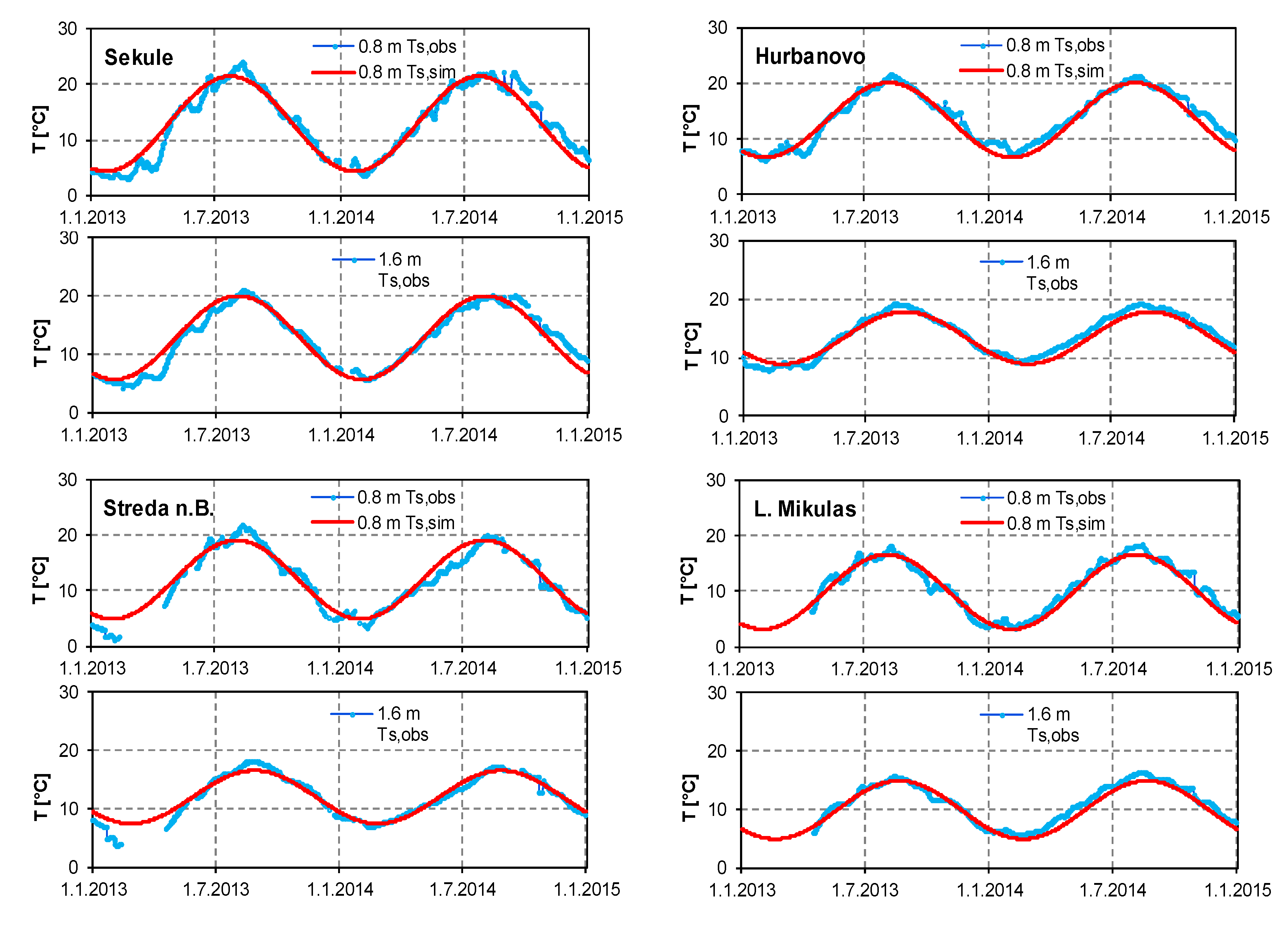
Characteristics of the Soil and Groundwater Temperature Series at Different Stations
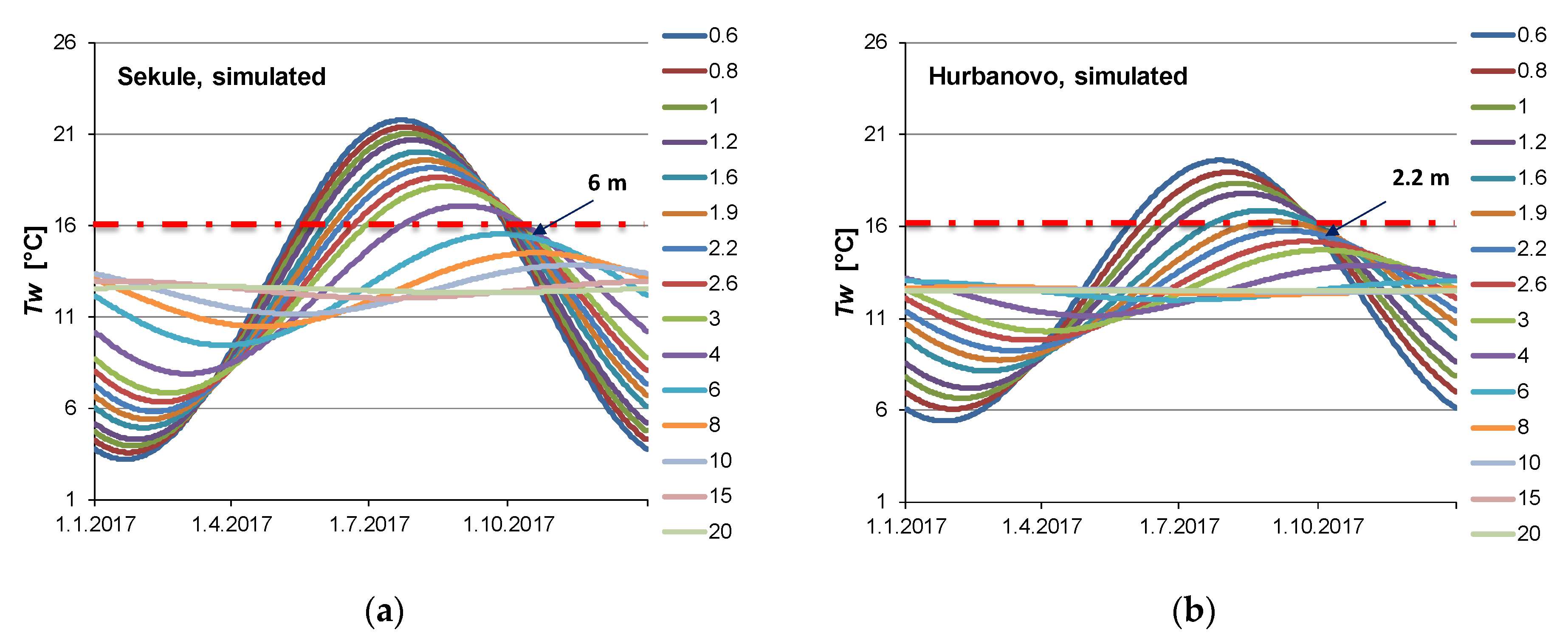
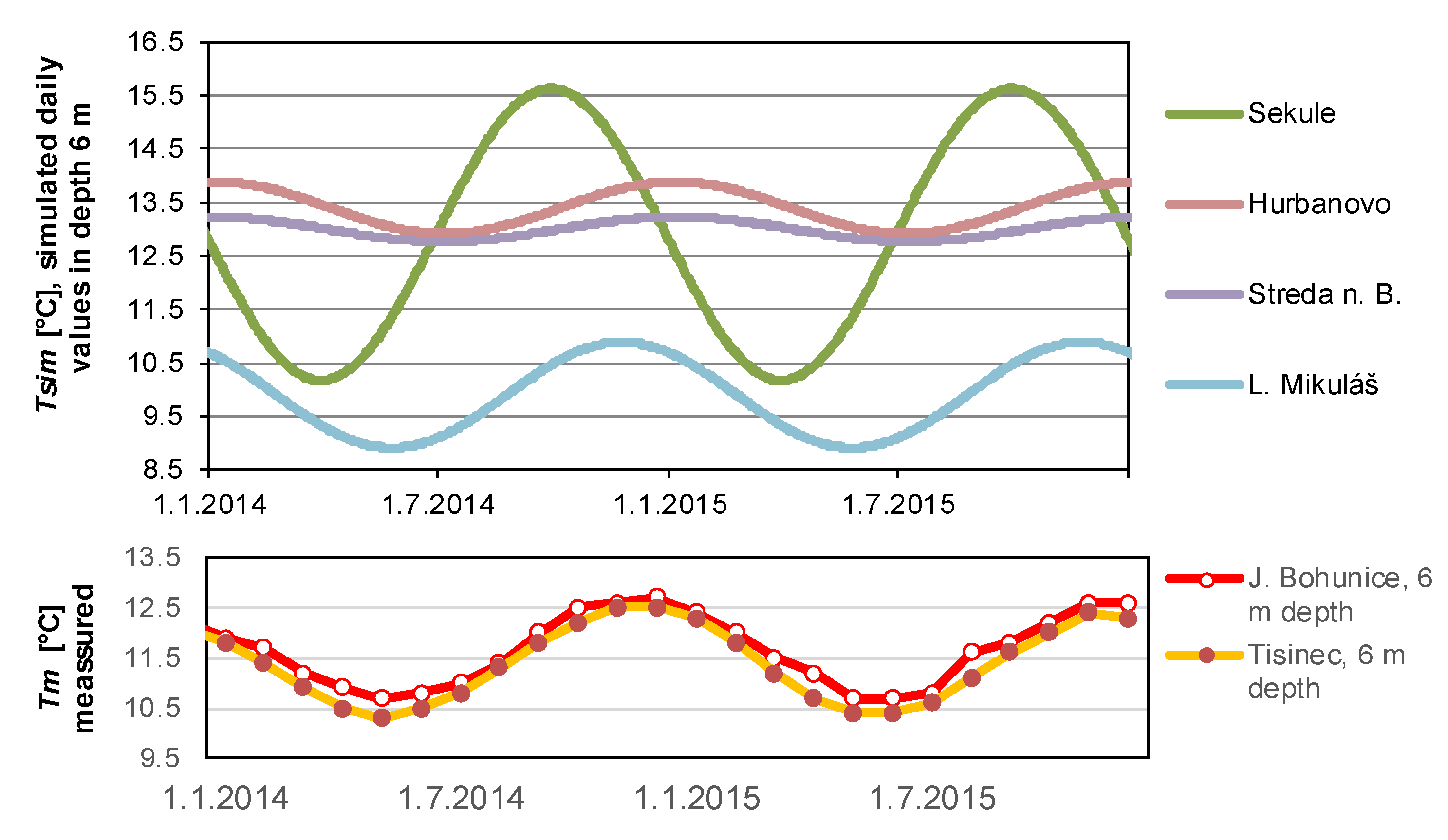
3.2. Results of the Groundwater Temperature Simulation
4. Discussion and Conclusions
- From the long-term trend analysis of air temperature and temperatures at depths of up to 10 m, we can see that in Slovakia the air temperature increased by 0.6 and the soil temperature increased by 0.5 °C per 10 years over the past 30 years.
- The long-term average temperatures at depths up to 10 m were higher compared to the air temperature by around 0.8–0.9 °C at all the used stations during the period 2013–2016.
- The groundwater temperature at a depth of approximately 6 m in Hurbanovo was highest in the coldest winter months of January–February. This finding should be taken into account when using heat pumps in the construction industry [38] for cooling and heating buildings.
- Long-term temperature measurements at a depth of approximately 10 m would be useful to verify the atmospheric temperature rise, as this temperature, unlike air temperature measurements, is minimally affected by daily and seasonal variations, by changes in vegetation on the surface, and by the fact that the mass heat capacity of ice is half that of water and a quarter that of air [39].
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davidson, E.A.; Janssens, I.A. Temperature sensitivity of soil carbon decomposition and feedbacks to climate change. Nature 2006, 440, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Riedel, T. Temperature-associated changes in groundwater quality. J. Hydrol. 2019, 572, 206–212. [Google Scholar] [CrossRef]
- Miklánek, P.; Martincová, M.; Pekárová, P.; Mészároš, I. Seasonal changes of the soil temperature in different depths. In Proceedings of the 13th International Multidisciplinary Scientific GeoConference SGEM 2013: Hydrology and Water Resources, Soil, Forest Ecosystems, Marine and Ocean Ecosystems, Sofia, Bulgaria, 16–22 June 2013; pp. 285–292, ISSN 1314-2704. [Google Scholar]
- Dunajsky, E. Soil Temperature in Greater Depths, Slovakia. Available online: http://www.shmu.sk/File/sms/dunajsky_teplota.pdf (accessed on 1 September 2022). (In Slovak).
- Limberg, A.; Henning, A. Auswertung von Temperaturmessungen des Berliner Untergrundes über einen Zeitraum von 150 Jahren. Brandenbg. Geowiss. Beitr. 2019, 26, 15–31. [Google Scholar]
- Marcin, D.; Benková, K.; Fričovský, B.; Bodiš, D.; Bottlik, F.; Kordík, J.; Stríček, I. Assessment of the State of Geothermal Bodies of Ground Water in the Territory of the Slovak Republic; Geological study; State Geological Institute of Dionýz Štúr: Bratislava, Slovak, 2020; p. 295, 22 appendixes. [Google Scholar]
- Martincová, M.; Pekárová, P.; Škoda, P.; Pekár, J. Long-term trends in water temperature in the Slovak rivers and the impact of climatic and orographic factors. Acta Hydrol. Slovaca. 2011, 12, 276–285. [Google Scholar]
- Bedrna, Z.; Gašparovič, J. Types of temperature regime of the soils in the Czechoslovak socialist republic. Geogr. Časopis. 1986, 38, 60–77. (In Slovak) [Google Scholar]
- Song, Y.T.; Zhou, D.W.; Zhang, H.X.; Li, G.D.; Jin, Y.H.; Li, Q. Effects of vegetation height and density on soil temperature variations. Chin. Sci. Bull. 2013, 58, 907–912. [Google Scholar] [CrossRef]
- Nikiforova, T.; Savytskyi, M.; Limam, K.; Bosschaerts, W.; Belarbi, R. Methods and results of experimental researches of thermal conductivity of soils. Energy Procedia. 2013, 42, 775–783. [Google Scholar] [CrossRef]
- Kodešová, R.; Vlasáková, M.; Fér, M.; Teplá, D.; Jakšík, O.; Neuberger, P.; Adamovský, R. Thermal properties of representative soils of the Czech Republic. Soil Water Res. 2013, 8, 141–150. [Google Scholar] [CrossRef]
- Özkan, U.; Gökbulak, F. Effect of vegetation change from forest to herbaceous vegetation cover on soil moisture and temperature regimes and soil water chemistry. Catena 2017, 149, 158–166. [Google Scholar] [CrossRef]
- Šimůnek, J.; Šejna, M.; Saito, H.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media; Department of Environmental Science, University of California Riverside: Riverside, CA, USA, 2013. [Google Scholar]
- Valuš, G. Soil temperatures. In Climatic and Phenological Conditions of the East Slovak Region, 1st ed.; HMI: Prague, Czech Republic, 1966; pp. 118–123. [Google Scholar]
- Coufal, V.; Kott, I.; Moãný, M. Soil temperature in the cold part of the year in the period 1961–1991 in the Czech Republic. In National Climate Program of the Czech Republic; Czech Hydrometeorological Institute: Prague, Czech Republic, 1993; p. 37. (In Czech) [Google Scholar]
- Hora, P. Relationship between soil temperature and different soil types. In Mikroklima a Mezoklima Krajinných Struktur a Antropogenních Prostředí; Středová, H., Rožnovský, J., Litschmann, T., Eds.; CHMI: Praha, Czech Republic, 2011. [Google Scholar]
- Kutílek, M. Hypothermic soil regimes. In Pedologie a Paleo-Pedologie; Němeček, J., Smolíková, L., Kutílek, M., Eds.; Academia: Praha, Czech Republic, 1990; pp. 86–99. (In Czech) [Google Scholar]
- Kočárek, M.; Kodešová, R. Influence of temperature on soil water content measured by ECH2O-TE sensors. Int. Agrophys. 2012, 26, 259–269. [Google Scholar] [CrossRef]
- Lehnert, M. The soil temperature regime in the urban and suburban landscapes of Olomouc, Czech Republic. Morav. Geogr. Rep. 2013, 21, 3, 27–36. [Google Scholar] [CrossRef]
- Zheng, D.; Hunt, E.R., Jr.; Running, S.W. A daily soil temperature model based on air temperature and precipitation for continental applications. Clim. Res. 1993, 2, 183–191. [Google Scholar] [CrossRef]
- Taylor, C.A.; Stefan, H.G. Shallow groundwater temperature response to climate change and urbanization. J. Hydrol. 2009, 375, 601–612. [Google Scholar] [CrossRef]
- Riedel, J.W.; Peterson, E.W.; Dogwiler, T.J.; Seyoum, W.M. Investigating thermal controls on the hyporheic flux as evaluated using numerical modeling of flume-derived data. Hydrology 2022, 9, 156. [Google Scholar] [CrossRef]
- Kassaye, K.T.; Boulange, J.; Tu, L.; Saito, H.; Watanabe, H. Soil water content and soil temperature modeling in a vadose zone of Andosol under temperate monsoon climate. Geoderma 2021, 384, 114797. [Google Scholar] [CrossRef]
- Singh, R.K.; Sharma, R.V. Numerical analysis for ground temperature variation. Geotherm Energy 2017, 5, 22. [Google Scholar] [CrossRef]
- Wang, J.; Lee, W.F.; Ling, P.P. Estimation of Thermal Diffusivity for Greenhouse Soil Temperature Simulation. Appl. Sci. 2020, 10, 653. [Google Scholar] [CrossRef]
- Park, K.; Kim, Y.; Lee, K.; Kim, D. Development of a Shallow-Depth Soil Temperature Estimation Model Based on Air Temperatures and Soil Water Contents in a Permafrost Area. Appl. Sci. 2020, 10, 1058. [Google Scholar] [CrossRef]
- Sándor, R.; Fodor, N. Simulation of soil temperature dynamics with models using different concepts. Sci. World J. 2012, 8, 590287. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Gao, Z.; Horton, R.; Lenschow, D.H.; Meng, K.; Jaynes, D.B. An analytical solution to the one-dimensional heat conduction–convection equation in soil. Soil Sci. Soc. Am. J. 2012, 76, 1978–1986. [Google Scholar] [CrossRef]
- Islam, M.A.; Lubbad, R.; Amiri, S.A.G.; Isaev, V.; Shevchuk, Y.; Uvarova, A.V.; Afzal, M.S.; Kumar, A. Modelling the seasonal variations of soil temperatures in the Arctic coasts. Polar Sci. 2021, 30, 100732. [Google Scholar] [CrossRef]
- Andújar Márquez, J.M.; Martínez Bohórquez, M.Á.; Gómez Melgar, S. Ground thermal diffusivity calculation by direct soil temperature measurement. Application to very low enthalpy geothermal energy systems. Sensors 2016, 16, 306. [Google Scholar] [CrossRef] [PubMed]
- Farouki, O.T. Thermal Properties of Soils. Ser. Rock Soil Mech. 1986, 11, 136. [Google Scholar]
- Peters-Lidard, C.D.; Blackburn, E.; Liang, X.; Wood, E.F. The Effect of Soil Thermal Conductivity Parameterization on Surface Energy Fluxes and Temperatures. J. Atmos. Sci. 1998, 55, 1209–1223. [Google Scholar] [CrossRef]
- Kodešová, R.; Fér, M.; Klement, A.; Nikodem, A.; Teplá, D.; Neuberger, P.; Bureš, P. Impact of various surface covers on water and thermal regime of Technosol. J. Hydrol. 2014, 519, 2272–2288. [Google Scholar] [CrossRef]
- Figura, S.; Livingstone, D.M.; Kipfer, R. Forecasting groundwater temperature with linear regression models using historical data. Groundwater 2015, 53, 943–954. [Google Scholar] [CrossRef]
- Riedel, T.; Weber, T.K.D. Review: The influence of global change on Europe’s water cycle and groundwater recharge. Hydrogeol J. 2020, 28, 1939–1959. [Google Scholar] [CrossRef]
- Michel, A.; Schaefli, B.; Wever, N.; Zekollari, H.; Lehning, M.; and Huwald, H. Future water temperature of rivers in Switzerland under climate change investigated with physics-based models. Hydrol. Earth Syst. Sci. 2022, 26, 1063–1087. [Google Scholar] [CrossRef]
- Lei, N.; Han, J. Effect of precipitation on respiration of different reconstructed soils. Sci. Rep. 2020, 10, 7328. [Google Scholar] [CrossRef]
- Leski, K.; Luty, P.; Gwadera, M.; Larwa, B. Numerical Analysis of Minimum Ground Temperature for Heat Extraction in Horizontal Ground Heat Exchangers. Energies 2021, 14, 5487. [Google Scholar] [CrossRef]
- Pekárová, P.; Pekár, J.; Miklánek, P. Why do some places show a bimodal distribution of daily air temperature? In Water Regime of Natural Areas: Book of Peer-Reviewed Papers; IH SAS: Bratislava, Slovakia, 2022; pp. 20–29. ISBN 978-80-89139-52-1. (In Slovak) [Google Scholar]
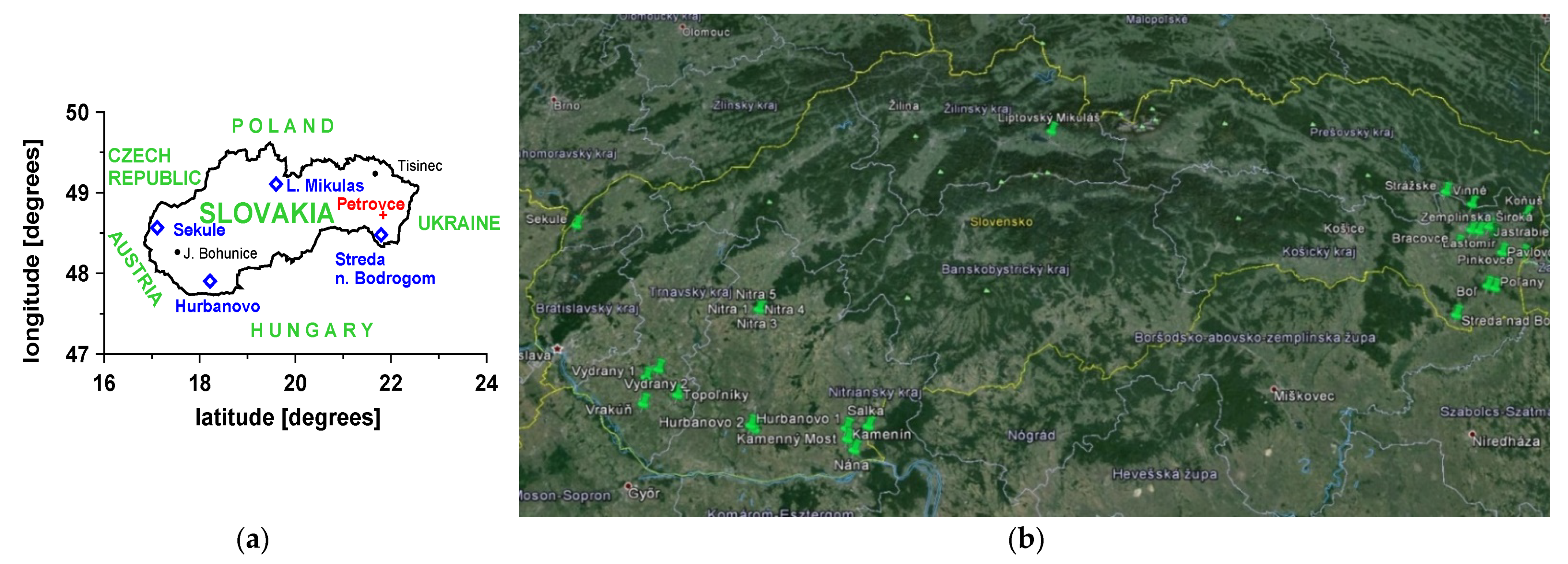


| No. | Locality | Land Use | Type of Soil | GPS | |
|---|---|---|---|---|---|
| N | E | ||||
| 01 | Vinné | Vineyard, grass | Clay loam | 48°48.842′ | 21°57.812′ |
| 02 | Bracovce | Orchard, grass | Clay loam | 48°38.584′ | 21°50.094′ |
| 03 | Pavlovce | Orchard, grass | Clay loam | 48°36.702′ | 22°04.170′ |
| 04 | Lastomír | Orchard, grass | Sandy loam | 48°42.230′ | 21°55.631′ |
| 05 | Strážske | Orchard, grass | Clay loam | 48°52.069′ | 21°49.836′ |
| 06 | Sekule | Orchard, grass | Loamy sand | 48°36.383′ | 16°59.675′ |
| 07 | Hurbanovo 1 | Orchard, grass | Loamy sand | 47°53.055′ | 18°10.298′ |
| 08 | Nitra 1 | Lawn | Clay loam | 48°18.150′ | 18°05.980′ |
| 09 | Iňačovce | Pastureland, grass | Silty-clay loam | 48°41.304′ | 22°03.198′ |
| 10 | Streda n. Bodrogom | Agricultural crops | Clay loam | 48°21.526′ | 21°44.659′ |
| 11 | Poľany | Pastureland, grass | Sandy loam | 48°27.997′ | 21°59.044′ |
| 12 | Boľ | Pastureland, grass | Clay loam | 48°28.495′ | 21°56.774′ |
| 13 | Liptovský Mikuláš | Lawn | Loam | 49°05.838′ | 19°35.392′ |
| 14 | Jastrabie | Agricultural crops | Clay loam | 48°43.199′ | 22°01.727′ |
| 15 | Koňuš | Vineyard, grass | Clay loam | 48°46.383′ | 22°15.639′ |
| 16 | Pinkovce | Orchard, grass | Clay loam | 48°36.325′ | 22°11.056′ |
| 17 | Zemplínska Široká | Orchard, grass | lay loam | 48°42.007′ | 21°58.192′ |
| 18 | Nitra 3 | Orchard, grass | Clay loam | 48°18.082′ | 18°06.117′ |
| 19 | Nitra 2 | Orchard, grass | Clay loam | 48°18.121′ | 18°06.054′ |
| 20 | Hurbanovo 2 | Lawn | Loam | 47°52.345′ | 18°11.573′ |
| 21 | Nitra 4 | Orchard, grass | Clay loam | 48°18.010′ | 18°05.971′ |
| 22 | Nitra 5 | Orchard, grass | Clay loam | 48° 18.208′ | 18° 05.791′ |
| 23 | Vrakúň | Agricultural crops | Loamy sand | 47°56.428′ | 17°37.025′ |
| 24 | Topoľníky | Orchard, grass | Loam | 47° 58.593′ | 17° 46.623′ |
| 25 | Kamenín | Vineyard, grass | Loam | 47°53.315′ | 18°38.463′ |
| 26 | Vydrany 1 | Agricultural crops | Loam | 48°01.988′ | 17°35.907′ |
| 27 | Vydrany 2 | Agricultural crops | Loam | 48°03.884′ | 17°39.005′ |
| 28 | Salka | Agricultural crops | Loamy sand | 47°53.918′ | 18°44.795′ |
| 29 | Nána | Agricultural crops | Loam | 47°49.010′ | 18°41.593′ |
| 30 | Kamenný Most | Orchard, grass | Sandy loam | 47°51.130′ | 18°39.218′ |
| Depth | Mean Particle Density | Bulk Density | Soil Texture | |||
|---|---|---|---|---|---|---|
| ρs | ρb | Clay | Silt | Sand | Textural Class | |
| <0.002 mm | 0.002–0.05 mm | 0.05–2.00 mm | ||||
| [cm] | [g·cm−3] | [g·cm−3] | [%] | [%] | [%] | |
| Sekule (48°36.383′ N, 16°59.675′ E) | ||||||
| 10 | 2.58 | 1.46 | 10.81 | 5.09 | 84.10 | Loamy sand |
| 20 | 2.63 | 1.53 | 7.89 | 10.31 | 81.80 | Loamy sand |
| 40 | 2.60 | 1.71 | 10.52 | 6.08 | 83.40 | Loamy sand |
| 60 | 2.58 | 1.78 | 10.61 | 0.99 | 88.40 | Loamy sand |
| 80 | 2.61 | 1.77 | 10.62 | 0.48 | 88.90 | Loamy sand |
| 100 | 2.73 | 1.70 | 10.42 | 0.08 | 89.50 | Loamy sand |
| 120 | 2.63 | 1.84 | 10.52 | 0.18 | 89.30 | Loamy sand |
| 160 | 2.66 | 1.70 | 10.62 | 0.08 | 89.30 | Loamy sand |
| Hurbanovo (47°52.345′ N, 18°11.573′ E) | ||||||
| 10 | 2.59 | 1.10 | 13.54 | 33.76 | 52.70 | Sandy loam |
| 20 | 2.65 | 1.21 | 14.91 | 30.09 | 55.00 | Sandy loam |
| 40 | 2.69 | 1.72 | 7.62 | 27.08 | 65.30 | Sandy loam |
| 60 | 2.66 | 1.23 | 15.77 | 28.23 | 56.00 | Sandy loam |
| 80 | 2.69 | 1.39 | 16.93 | 25.87 | 57.20 | Sandy loam |
| 100 | 2.69 | 1.48 | 15.52 | 28.08 | 56.40 | Sandy loam |
| 120 | 2.69 | 1.53 | 12.86 | 19.34 | 67.80 | Sandy loam |
| 160 | 2.70 | 1.46 | 19.57 | 24.73 | 55.70 | Sandy loam |
| Streda nad Bodrogom (48°21.526′ N, 21°44.659′ E) | ||||||
| 10 | 2.66 | 1.41 | 23.01 | 57.69 | 19.30 | Silt loam |
| 20 | 2.65 | 1.49 | 24.69 | 56.91 | 18.40 | Silt loam |
| 40 | 2.64 | 1.38 | 22.93 | 51.47 | 25.60 | Silt loam |
| 60 | 2.68 | 1.35 | 23.16 | 54.14 | 22.70 | Silt loam |
| 80 | 2.75 | 1.31 | 20.12 | 55.28 | 24.60 | Silt loam |
| 100 | 2.77 | 1.31 | 20.70 | 60.80 | 18.50 | Silt loam |
| 120 | 2.67 | 1.21 | 15.18 | 43.52 | 41.30 | Loam |
| 160 | 2.69 | 1.43 | 35.16 | 55.64 | 9.20 | Silty clay loam |
| Sekule | Hurbanovo | Streda n. Bodrogom | L. Mikuláš | |
|---|---|---|---|---|
| Groundwater level [m] | 3 | 1.9 | 2.4 | 3 |
| Tw mean [°C] | 12.80 | 12.85 | 11.80 | 9.65 |
| Tw min [°C] | 7.63 | 9.56 | 9.08 | 6.92 |
| Tw max [°C] | 18.17 | 17.24 | 14.92 | 12.88 |
| Tw stdev [°C] | 3.73 | 2.71 | 2.07 | 2.11 |
| Ta mean [°C] | 11.99 | 11.71 | 11.00 | 8.27 |
| Sekule | Hurbanovo | Streda n Bodrogom | L. Mikuláš | |
|---|---|---|---|---|
| Soil textural class | loamy sand | sandy loam | silt loam | loam |
| [m2.day−1] | 0.1652 | 0.0364 | 0.0318 | 0.0533 |
| [rad] | 0.25 | 0.18 | 0.20 | 0.24 |
| Groundwater level [m] | 3.4 | 1.74 | 2.43 | 3 |
| Tw average [°C] | 12.90 | 12.85 | 11.80 | 9.65 |
| Ta average [°C] | 11.99 | 11.71 | 11.00 | 8.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pekárová, P.; Tall, A.; Pekár, J.; Vitková, J.; Miklánek, P. Groundwater Temperature Modelling at the Water Table with a Simple Heat Conduction Model. Hydrology 2022, 9, 185. https://doi.org/10.3390/hydrology9100185
Pekárová P, Tall A, Pekár J, Vitková J, Miklánek P. Groundwater Temperature Modelling at the Water Table with a Simple Heat Conduction Model. Hydrology. 2022; 9(10):185. https://doi.org/10.3390/hydrology9100185
Chicago/Turabian StylePekárová, Pavla, Andrej Tall, Ján Pekár, Justína Vitková, and Pavol Miklánek. 2022. "Groundwater Temperature Modelling at the Water Table with a Simple Heat Conduction Model" Hydrology 9, no. 10: 185. https://doi.org/10.3390/hydrology9100185
APA StylePekárová, P., Tall, A., Pekár, J., Vitková, J., & Miklánek, P. (2022). Groundwater Temperature Modelling at the Water Table with a Simple Heat Conduction Model. Hydrology, 9(10), 185. https://doi.org/10.3390/hydrology9100185








