Development of a Machine Learning Framework to Aid Climate Model Assessment and Improvement: Case Study of Surface Soil Moisture
Abstract
1. Introduction
2. Methodology
2.1. Machine Learning Framework
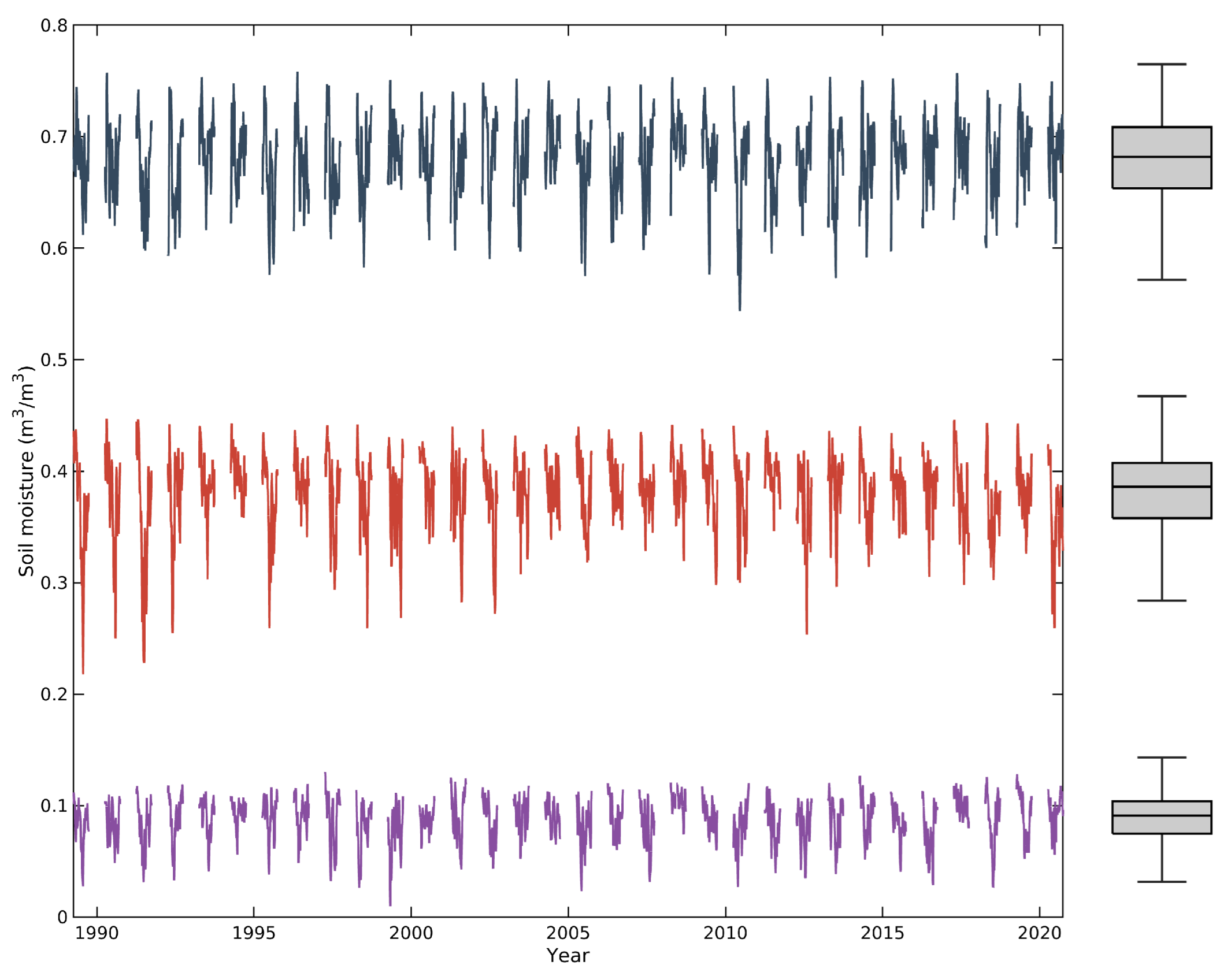
2.2. Case Study
3. Results
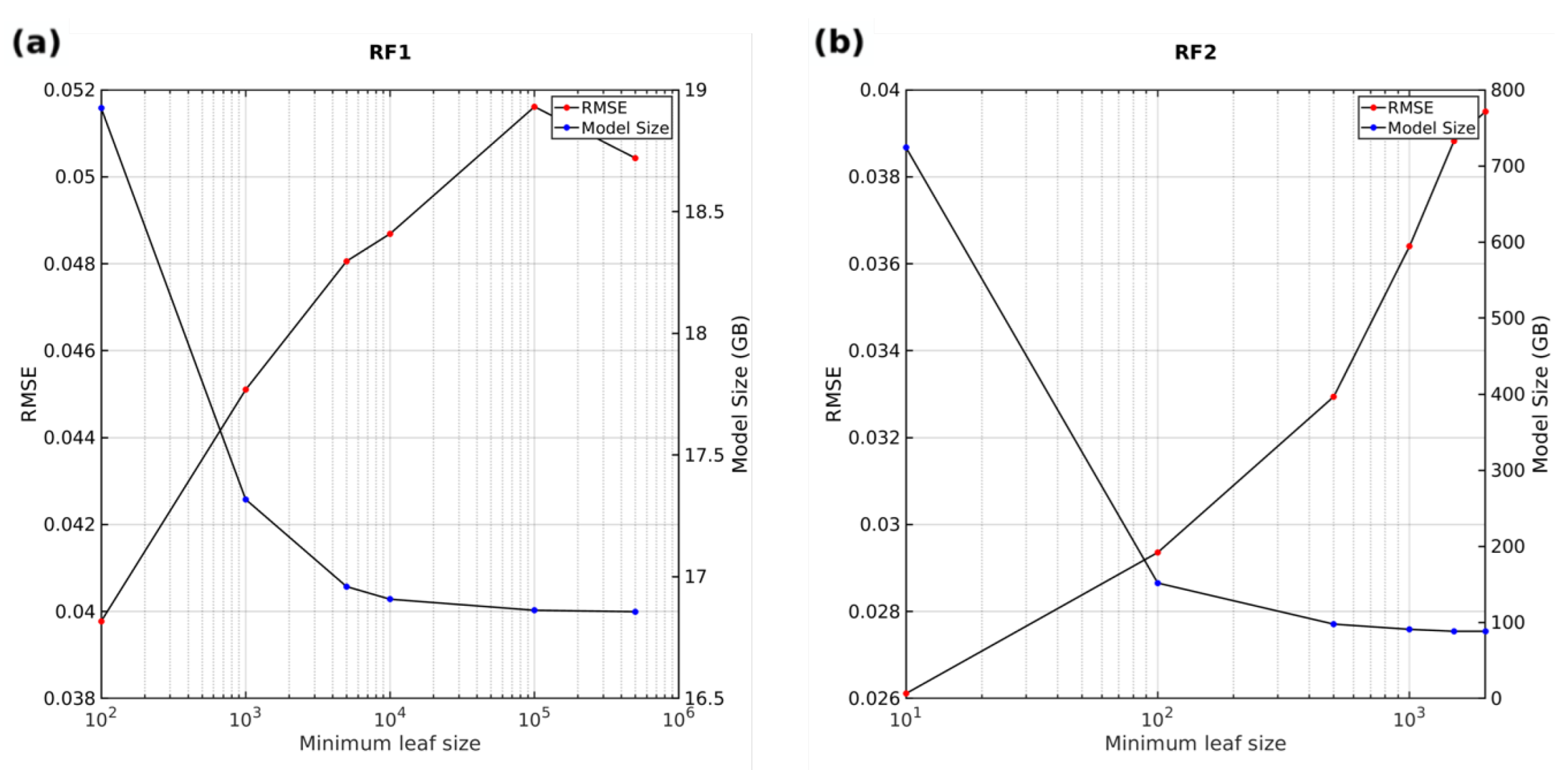
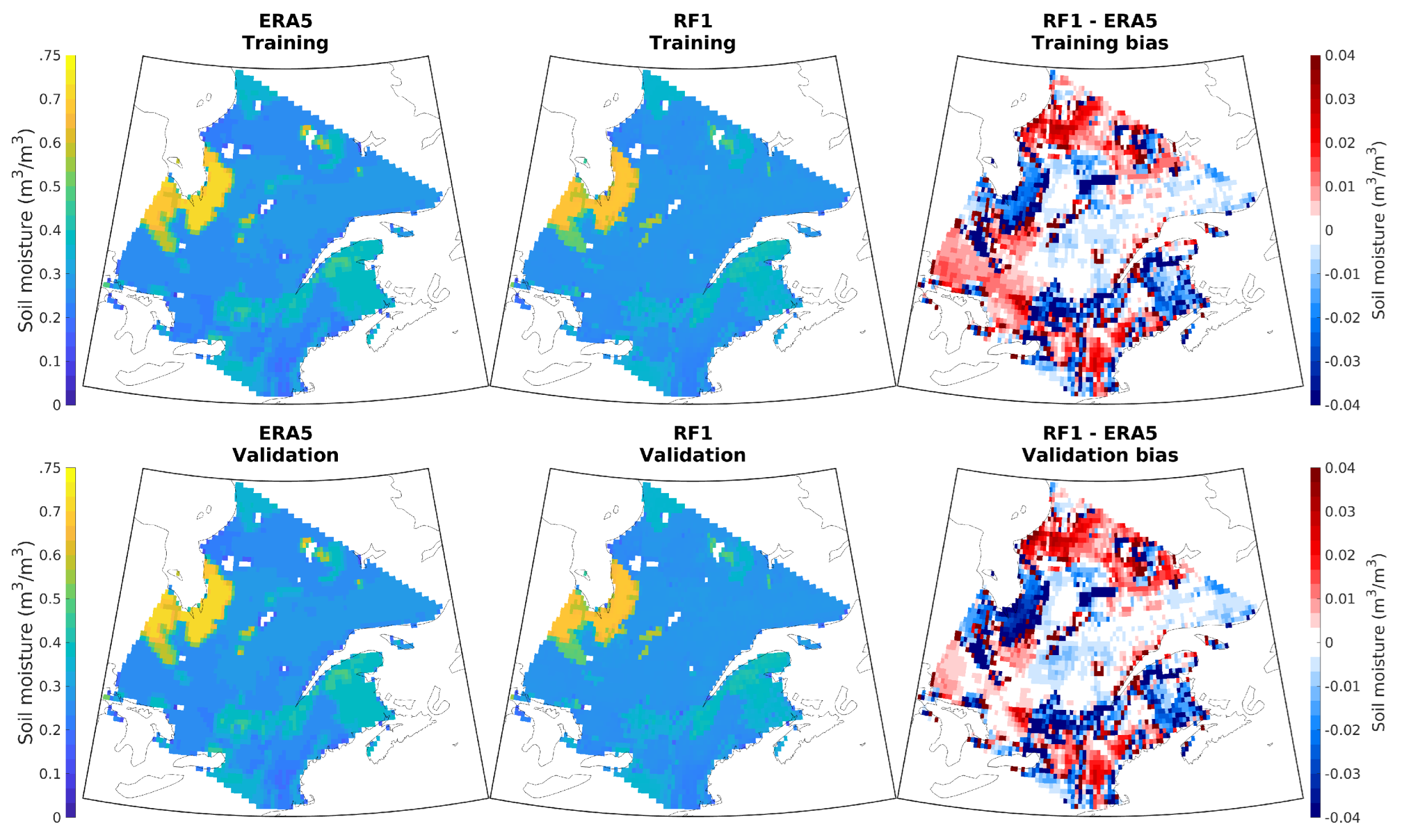
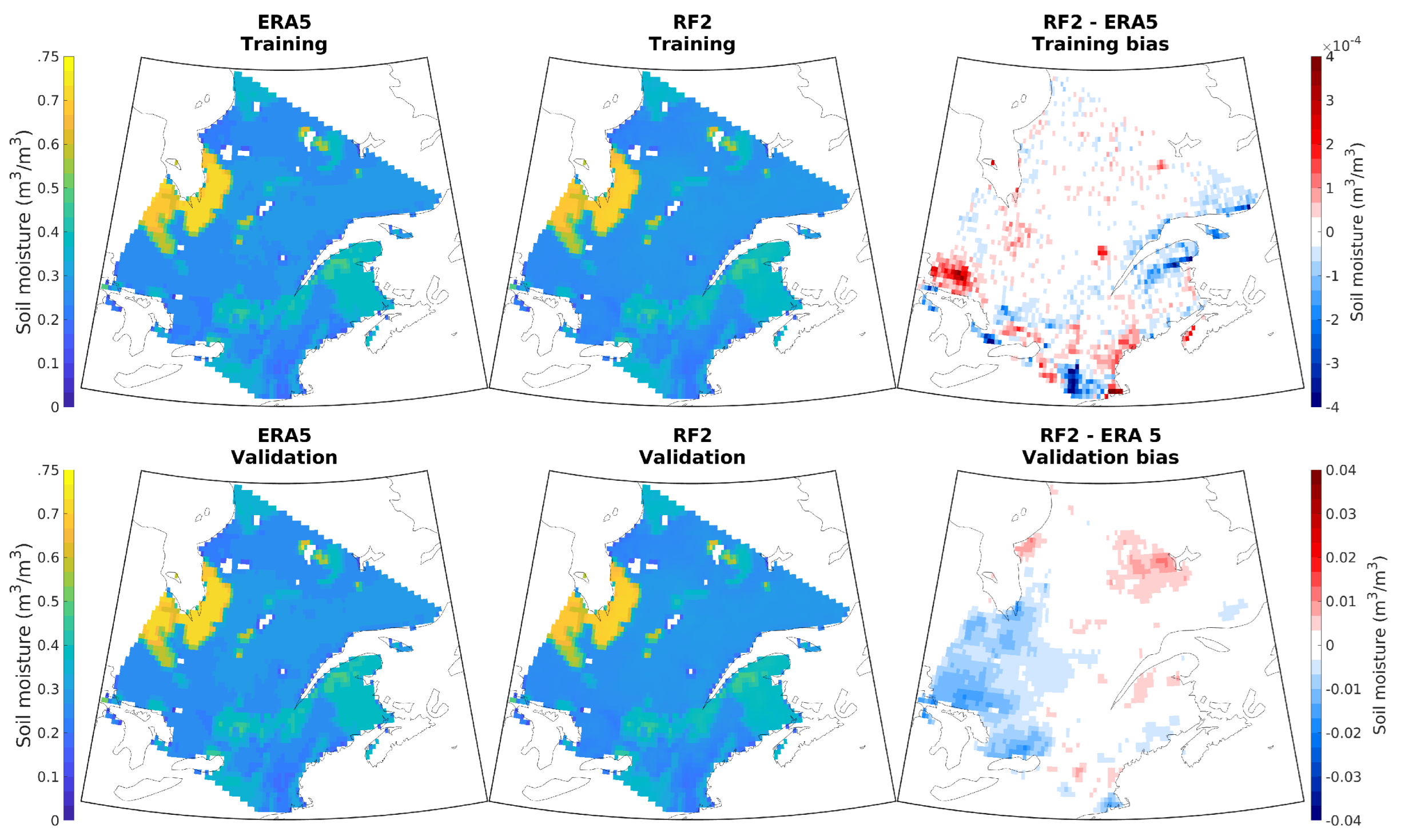
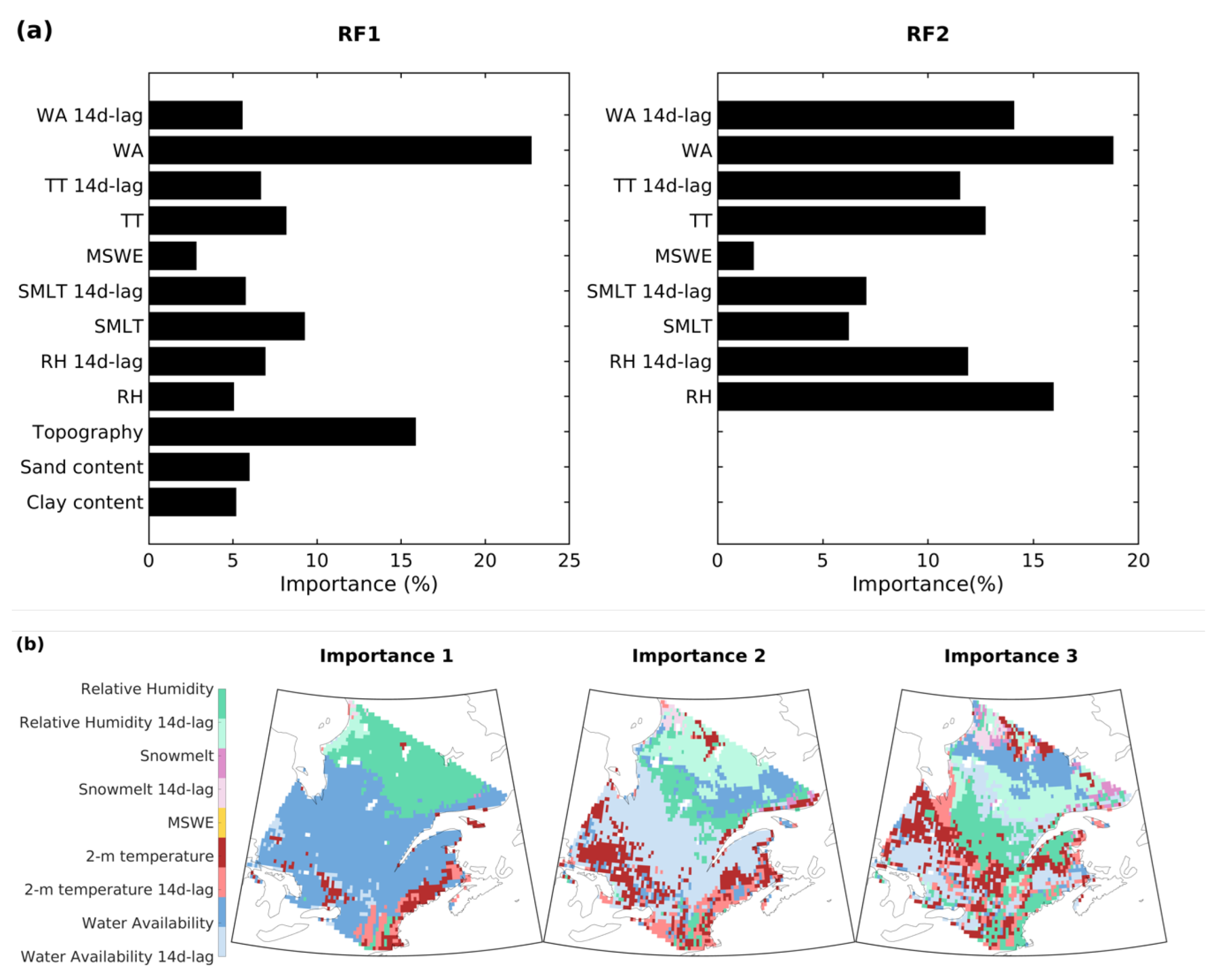
3.1. Development of Random Forest Models
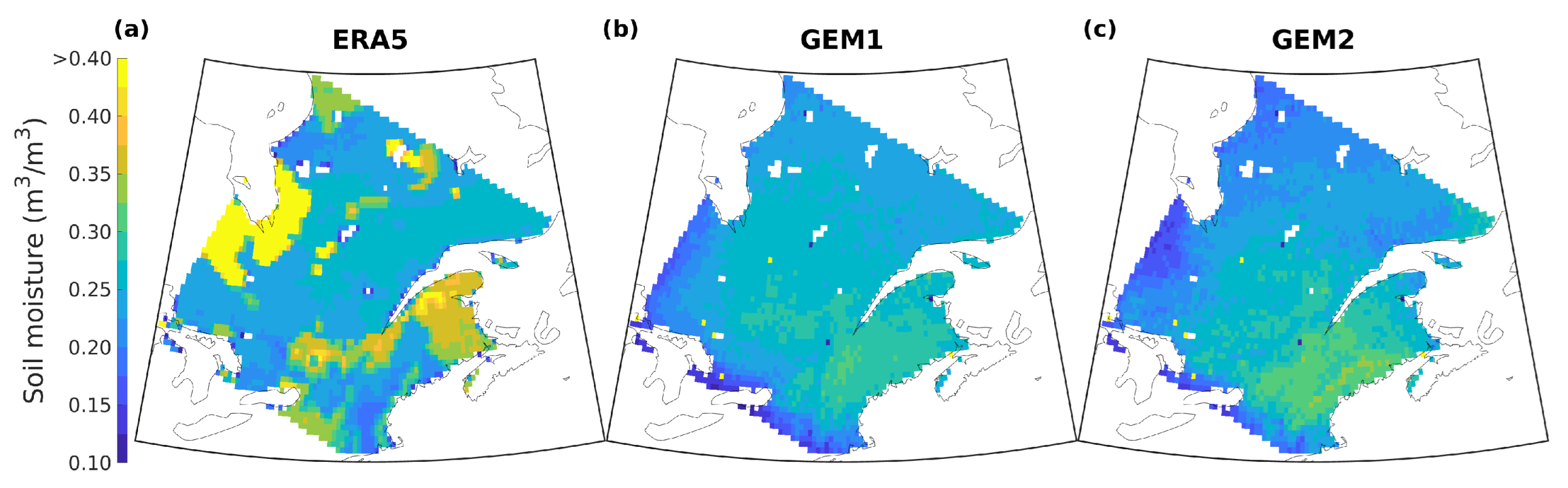
3.2. GEM Simulations
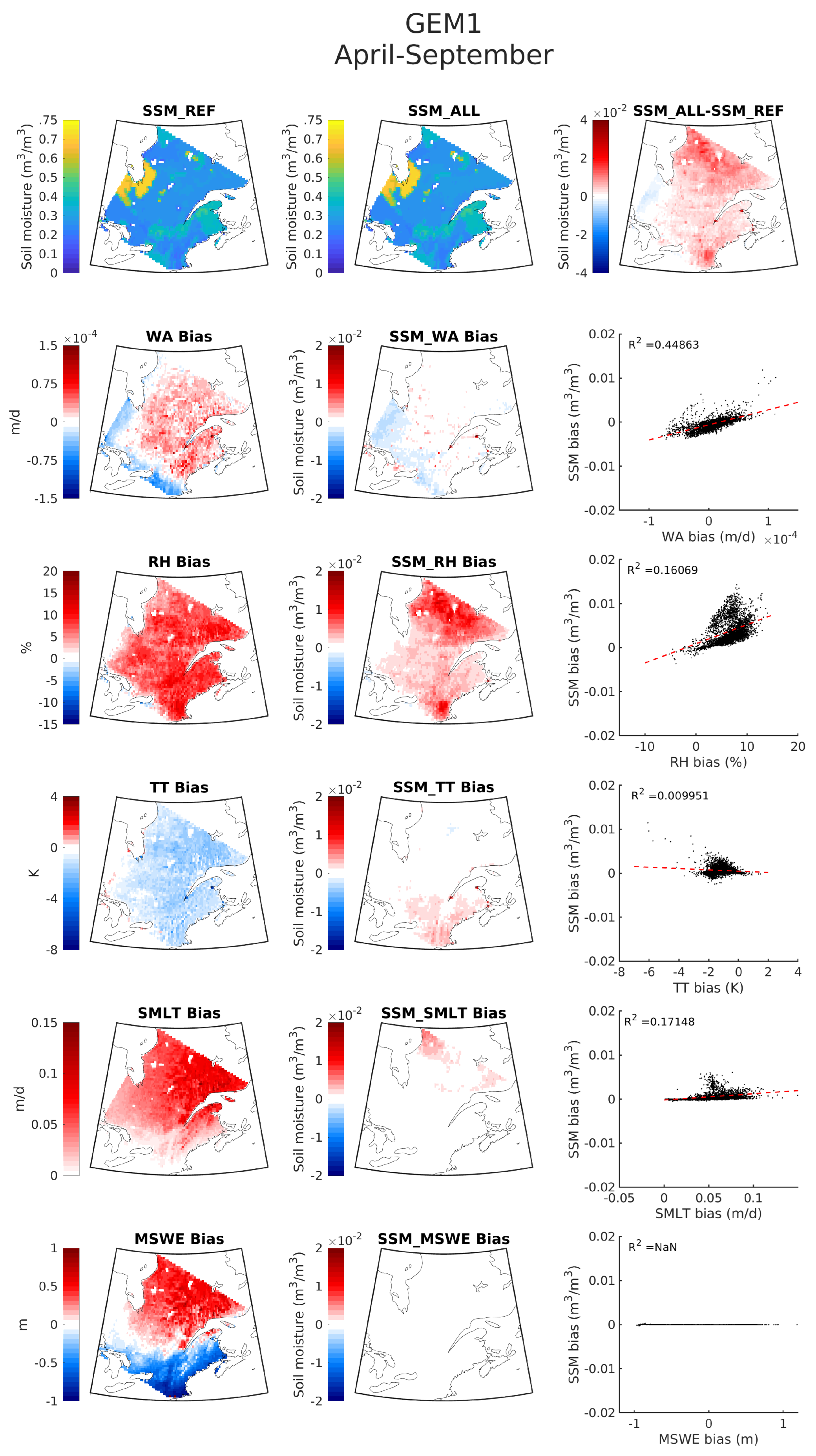
3.2.1. Case 1: ’Normal’ GEM Simulation
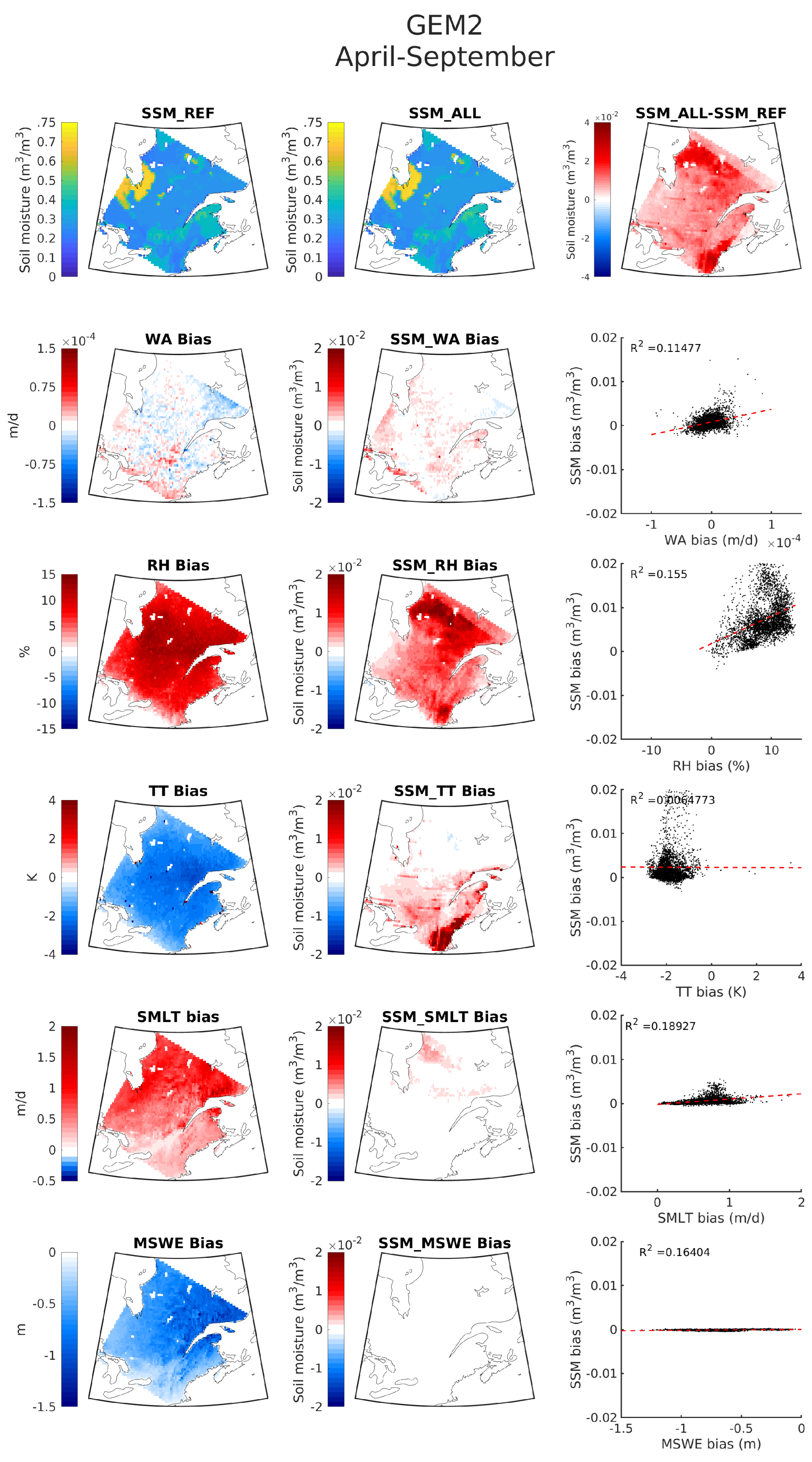
3.2.2. Case 2: ‘Perturbed’ GEM Simulation
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CLASS | Canadian Land Surface Scheme |
| COSMO-CLM | Cosmo-Climate Lokalmodell(German regional climate model) |
| CMIIP5 | Coupled Model Intercomparison Project Phase 5 |
| CO2 | Carbon dioxide |
| DT | Decision Tree |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| ERA5 | ECMWF Re-Analysis |
| GCM | Global Climate Model |
| GEM | Global Environmental Multiscale |
| ML | Machine Learning |
| MLS | Minimum Leaf Size |
| MSWE | Maximum Snow Water Equivalent |
| RCA4 | Rosby Centre Regional Atmospheric Model Version 4 |
| RCM | Regional Climate Model |
| RF | Random Forest |
| RH | Relative Humidity |
| RMSE | Root Mean Square Error |
| RTM | Radiative Transfer Model |
| SM | Soil Moisture |
| SMLT | Snowmelt |
| SSM | Surface Soil Moisture |
| TT | 2 m Temperature |
| WA | Water Availability |
References
- Watson-Parris, D. Machine learning for weather and climate are worlds apart. Philos. Trans. R. Soc. 2021, 379, 20200098. [Google Scholar] [CrossRef] [PubMed]
- Schneider, T.; Lan, S.; Stuart, A.; Texeira, J. Earth System Modeling 2.0: A Blueprint for ModelsThat Learn from Observations and Targeted High-Resolution Simulations. Geophys. Res. Lett. 2017, 44, 12396–12417. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature. 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- O’Hagan, A. Probabilistic uncertainty specification: Overview, elaboration techniques and their application to a mechanistic model of carbon flux. Environ. Model. Softw. 2012, 36, 35–48. [Google Scholar] [CrossRef]
- Bellprat, O.; Kotlarski, S.; Lüthi, D.; Schär, C. Objective calibration of regional climate models. J. Geophys. Res. 2012, 117, D23115. [Google Scholar] [CrossRef]
- Castruccio, S.; McInerney, D.J.; Stein, M.L.; Crouch, F.L.; Jacob, R.L.; Moyer, E.J. Statistical Emulation of Climate Model Projections Based on Precomputed GCM Runs. J. Clim. 2014, 27, 1829–1844. [Google Scholar] [CrossRef]
- Verrelst, J.; Sabater, N.; Rivera, J.P.; Muñoz-Marí, J.; Vicent, J.; Camps-Valls, G.; Moreno, J. Emulation of Leaf, Canopy and Atmosphere Radiative Transfer Models for Fast Global Sensitivity Analysis. Remote Sens. 2016, 8, 673. [Google Scholar] [CrossRef]
- Babaousmail, H.; Hou, R.; Gnitou, G.T.; Ayugi, B. Novel statistical downscaling emulator for precipitation projections using deep Convolutional Autoencoder over Northern Africa. J. Atmos. Sol.-Terr. Phys. 2021, 218, 105614. [Google Scholar] [CrossRef]
- Wu, Y.; Teufel, B.; Sushama, L.; Belair, S.; Sun, L. Deep learning-based super-resolution climate simulator-emulator framework for urban heat studies. Geophys. Res. Lett. 2021, 48, e2021GL094737. [Google Scholar] [CrossRef]
- Teufel, B.; Carmo, F.; Sushama, L.; Sun, L.; Khaliq, M.N.; Belair, S.; Shamseldin, A.Y.; Kumar, D.N.; Vaze, J. Physically Based Deep Learning Framework to Model Intense Precipitation Events at Engineering Scales. Geophys. Res. Lett. 2022; Submitted. [Google Scholar]
- Breiman, L. Randon Forests. Mach. Lear. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Verseghy, D.L. Class-the Canadian Land Surface Scheme Version 3.5 Technical Documentation (Version 1). Environment Canada 2011. Available online: https://wiki.usask.ca/download/attachments/223019286/CLASS%20v3.5%20Documentation.pdf?version=1&modificationDate=1314718459000&api=v2 (accessed on 5 July 2022).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Mishra, A.K. Multi-layer high-resolution soil moisture estimation using machine learning over the United States. Remote Sens. Environ. 2021, 266, 112706. [Google Scholar] [CrossRef]
- Carranza, C.; Nolet, C.; Pezij, M.; van der Ploeg, M. Root zone soil moisture estimation with Random Forest. J. Hydrol. 2021, 593, 125840. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez Casas, F.A.; Sushama, L.; Teufel, B. Development of a Machine Learning Framework to Aid Climate Model Assessment and Improvement: Case Study of Surface Soil Moisture. Hydrology 2022, 9, 186. https://doi.org/10.3390/hydrology9100186
Ramírez Casas FA, Sushama L, Teufel B. Development of a Machine Learning Framework to Aid Climate Model Assessment and Improvement: Case Study of Surface Soil Moisture. Hydrology. 2022; 9(10):186. https://doi.org/10.3390/hydrology9100186
Chicago/Turabian StyleRamírez Casas, Francisco Andree, Laxmi Sushama, and Bernardo Teufel. 2022. "Development of a Machine Learning Framework to Aid Climate Model Assessment and Improvement: Case Study of Surface Soil Moisture" Hydrology 9, no. 10: 186. https://doi.org/10.3390/hydrology9100186
APA StyleRamírez Casas, F. A., Sushama, L., & Teufel, B. (2022). Development of a Machine Learning Framework to Aid Climate Model Assessment and Improvement: Case Study of Surface Soil Moisture. Hydrology, 9(10), 186. https://doi.org/10.3390/hydrology9100186




