Improving Urban Runoff in Multi-Basin Hydrological Simulation by the HYPE Model Using EEA Urban Atlas: A Case Study in the Sege River Basin, Sweden
Abstract
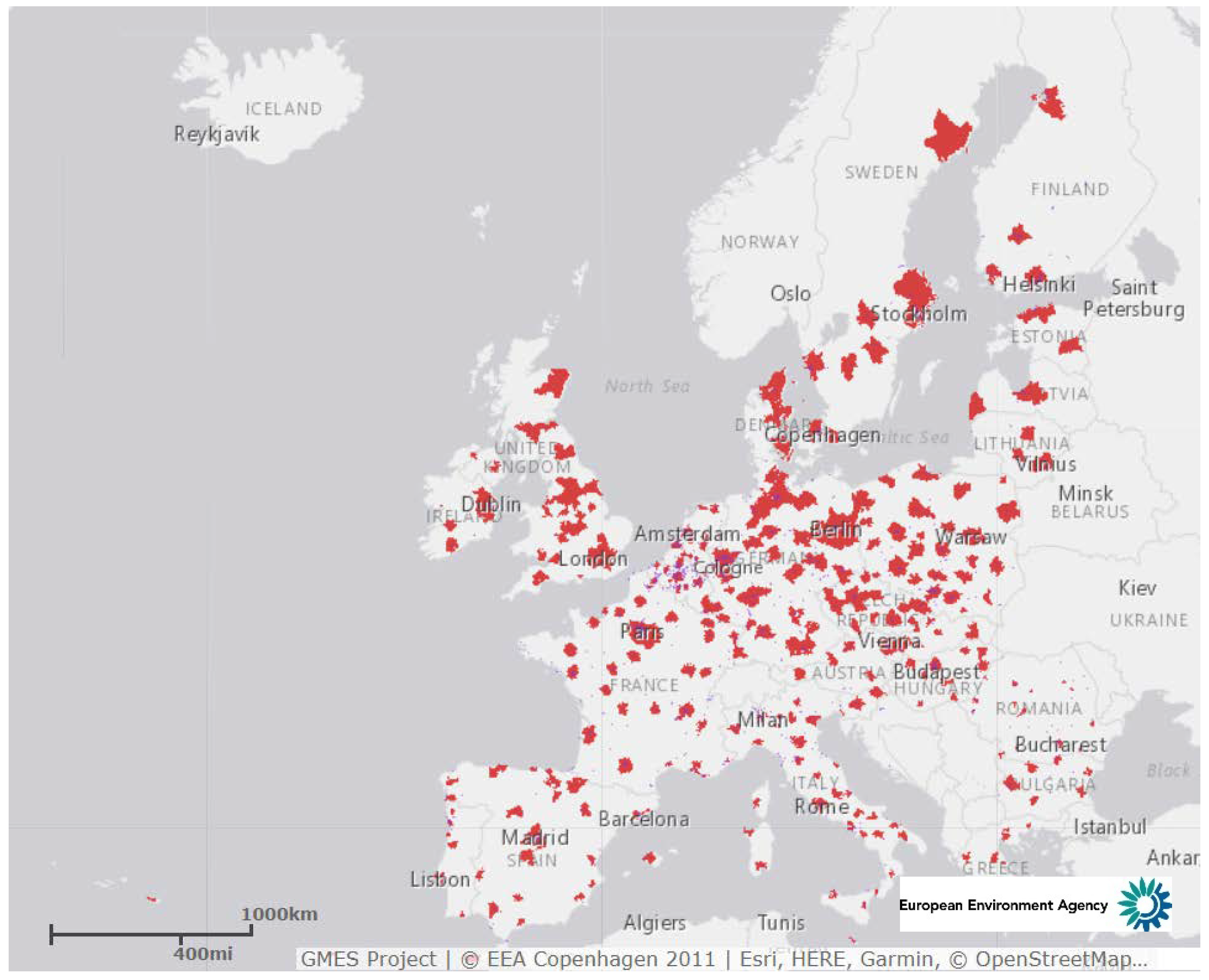
1. Introduction
2. Materials and Methods
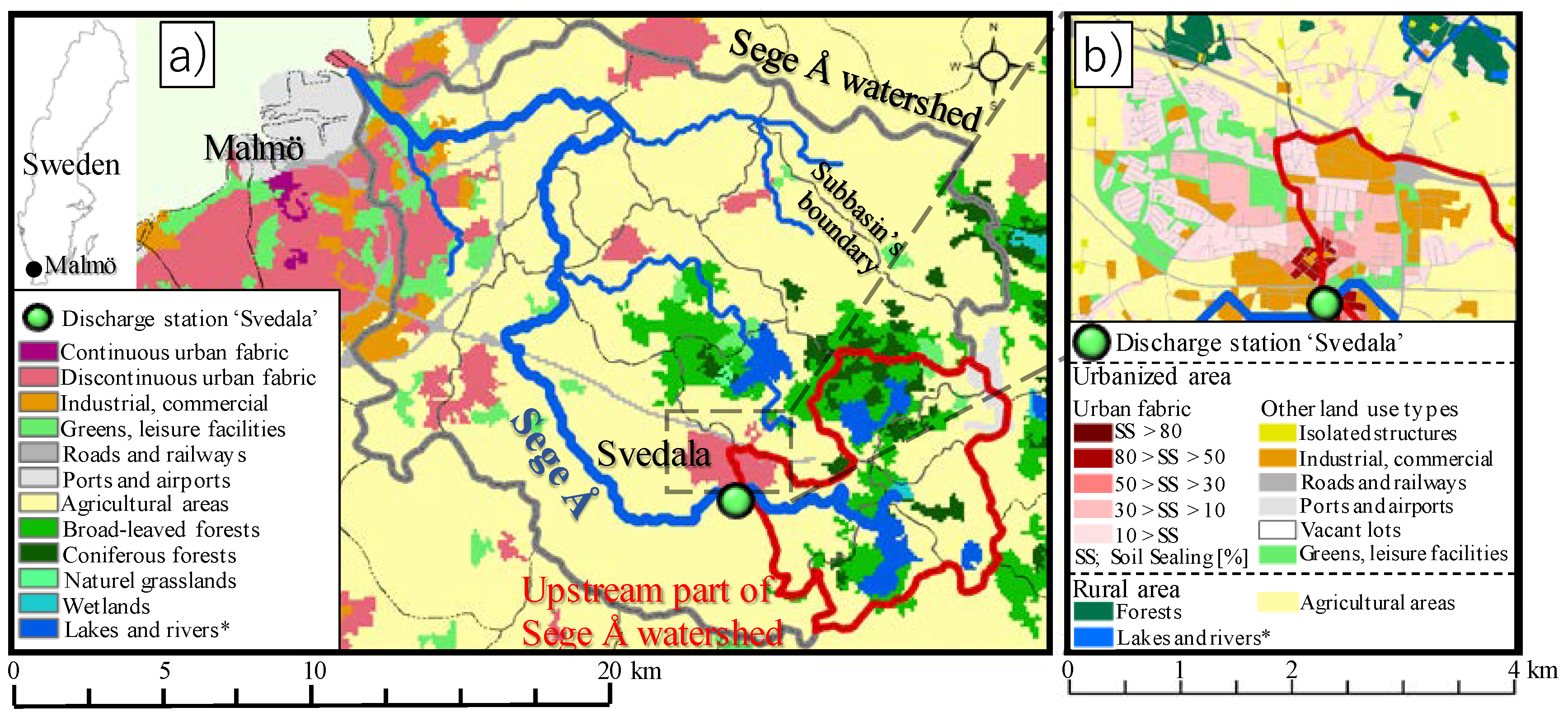
2.1. Study Basin and Hydrological Model
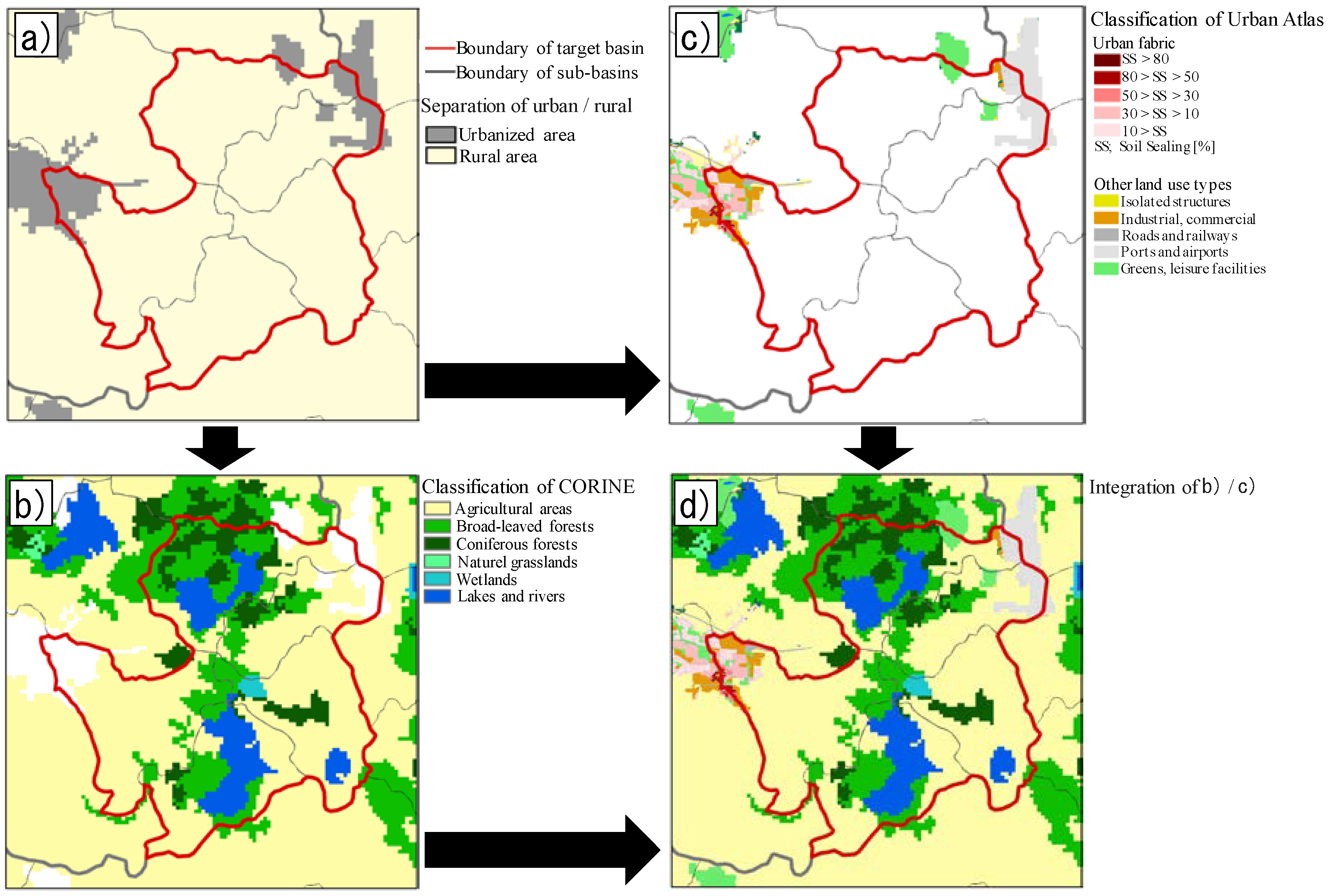
2.2. GIS Process and SLC Set-Up
2.3. Experimental Set-Up and Evaluation
3. Results
3.1. The Impervious SLC
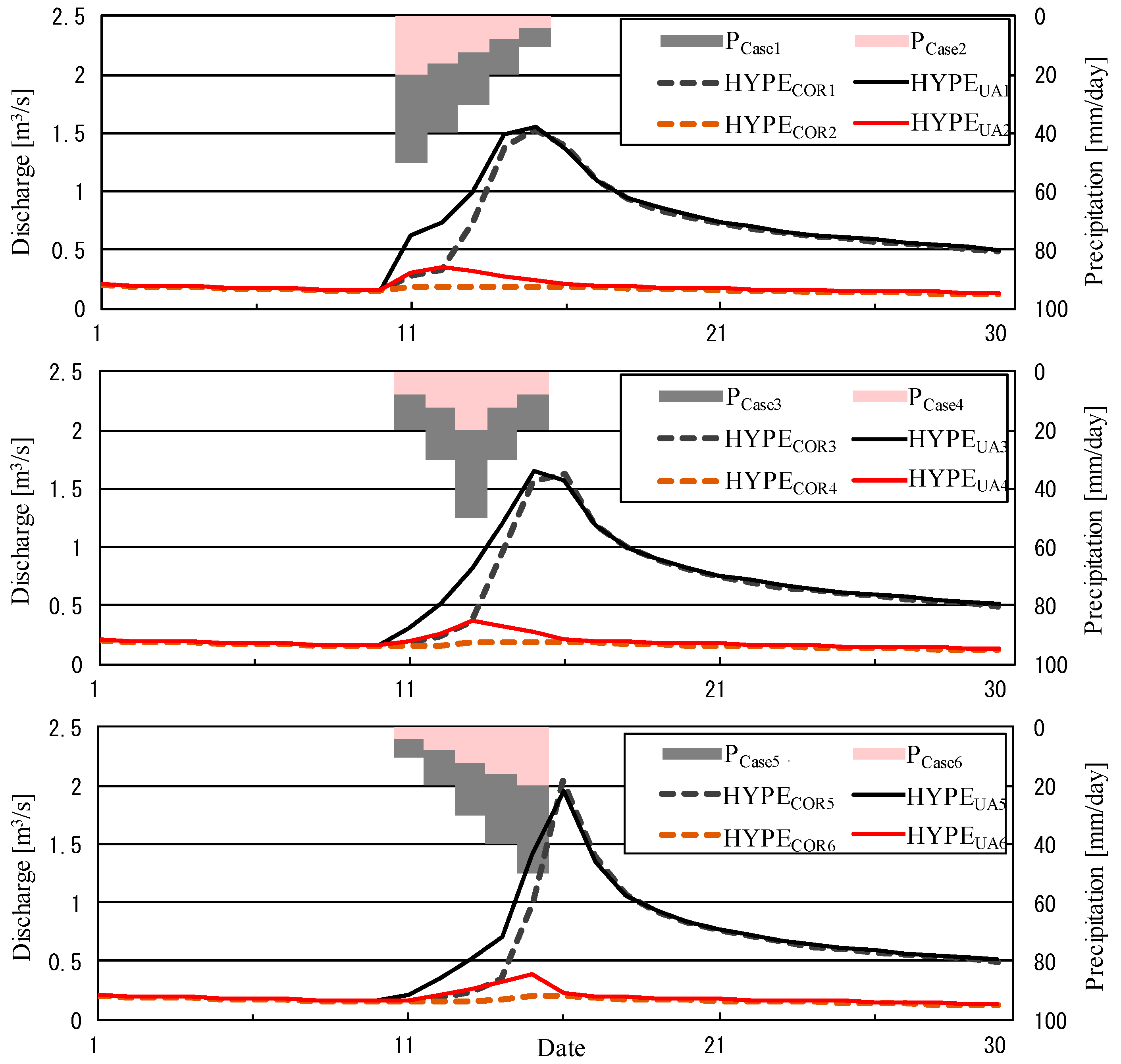
3.2. Synthetic Experiments
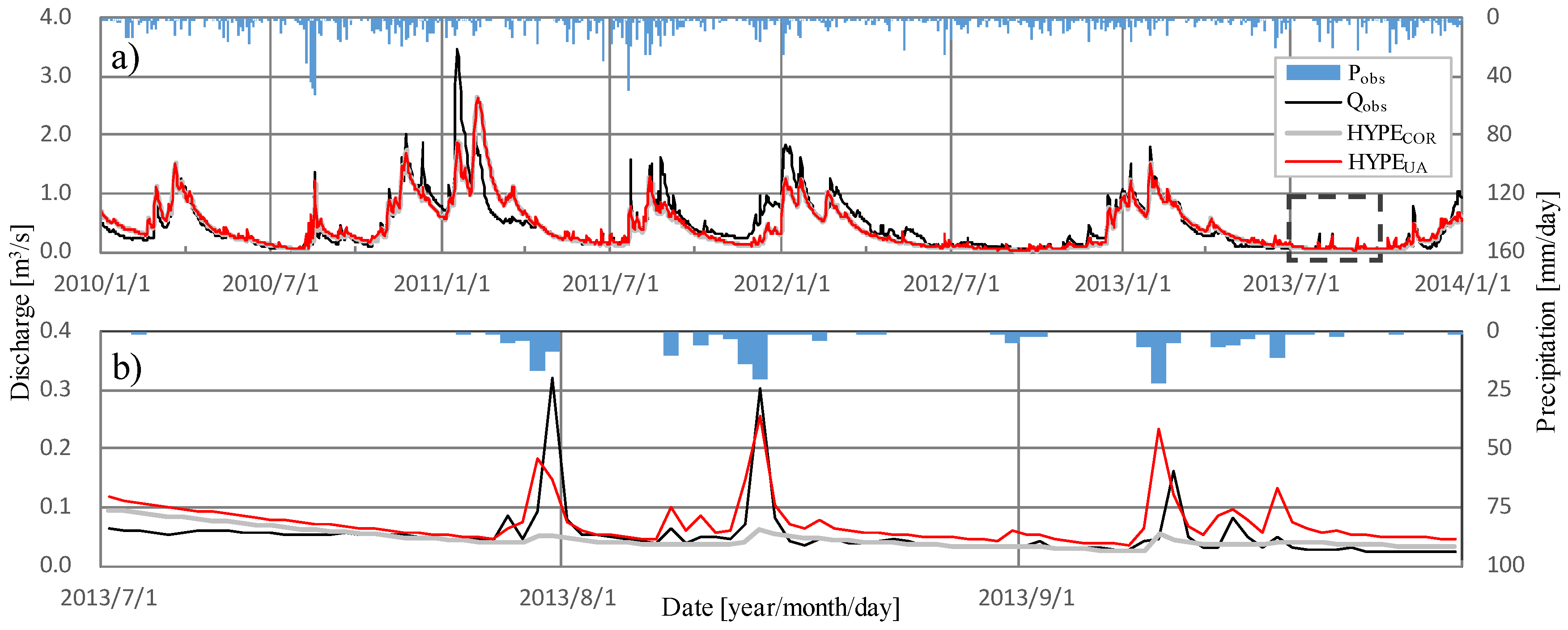
3.3. Real-World Simulations
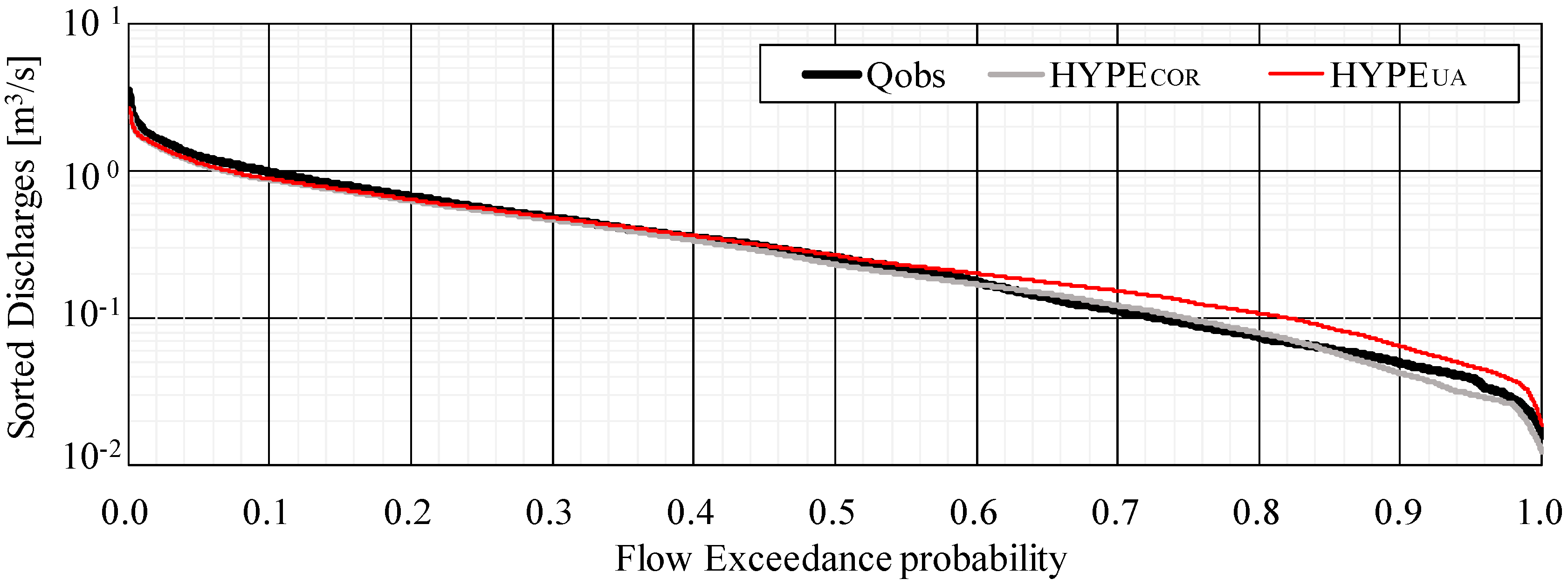
3.4. Model Verification using Flow Duration Curves
4. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arnold, J.G.; Srinivasin, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment: Part I. Model development. JAWRA 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Whitehead, P.G.; Wilson, E.J.; Butterfield, D. A semi-distributed integrated nitrogen model for multiple source assessment in catchments (INCA): Part I - Model structure and process equations. Sci. Total Environ. 1998, 210, 547–558. [Google Scholar] [CrossRef]
- Wade, A.J.; Durand, P.; Beaujouan, V.; Wessel, W.W.; Raat, K.J.; Whitehead, P.G.; Butterfield, D.; Rankinen, K.; Lepistö, A. A nitrogen model for European catchments: INCA, new model structure and equations. Hydrol. Earth Syst. Sci. 2002, 6, 559–582. [Google Scholar] [CrossRef]
- Futter, N.M.; Erlandsson, M.A.; Butterfield, D.; Whitehead, P.G.; Oni, S.K.; Wade, A.J. PERSiST: A flexible rainfall-runoff modelling toolkit for use with the INCA family of models. Hydrol. Earth Syst. Sci. 2014, 18, 855–873. [Google Scholar] [CrossRef]
- Bergström, S. The HBV model. In Computer Models of Watershed Hydrology; Singh, V., Ed.; Water Resources Publications: Highlands Ranch, CO, USA, 1995; pp. 443–476. [Google Scholar]
- Andersson, L.; Rosberg, J.; Pers, C.B.; Olsson, J.; Arheimer, B. Estimating catchment nutrient flow with the HBV-NP Model: Sensitivity to input data, AMBIO. J. Hum. Environ. 2005, 34, 521–532. [Google Scholar] [CrossRef]
- Lindström, G.; Pers, C.; Rosberg, J.; Strömqvist, J.; Arheimer, B. Development and test of the HYPE (Hydrological Predictions for the Environment) model—A water quality model for different spatial scales. Hydrol. Res. 2010, 41, 295–319. [Google Scholar] [CrossRef]
- Strömqvist, J.; Arheimer, B.; Dahné, J.; Donnelly, C.; Lindström, G. Water and nutrient predictions in ungauged basins: Set-up and evaluation of a model at the national scale. Hydrol. Sci. J. 2012, 57, 229–247. [Google Scholar] [CrossRef]
- Leopold, L.B. Hydrology for Urban Land Planning—A Guidebook on the Hydrologic Effects of Urban Land Use. Geol. Surv. Circular 1968, 554, 1–18. [Google Scholar]
- Zelenáková, M.; Diaconub, D.C.; Haarstadc, K. Urban water retention measures, structural and physical aspects of construction engineering. Procedia Eng. 2017, 190, 419–426. [Google Scholar] [CrossRef]
- Jartun, M.; Ottesen, R.T.; Steinnes, E.; Volden, T. Runoff of particle bound pollutants from urban impervious surfaces studied by analysis of sediments from stormwater traps. Sci. Total Environ. 2008, 396, 147–163. [Google Scholar] [CrossRef]
- Van der Knijff, J.M.; Younis, J.; De Roo, A.P.J. LISFLOOD: A GIS-based distributed model for river basin scale water balance and flood simulation. Int. J. Geogr. Inf. Sci. 2008, 24, 1–24. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Tuttle, B.T.; Sutton, P.C.; Baugh, K.E.; Howard, A.T.; Milesi, C.; Bhaduri, B.L.; Nemani, R. Global distribution and density of constructed impervious surfaces. Sensors 2007, 7, 1962–1979. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.; Liao, A.; Cao, X.; Chen, L.; Chen, X.; He, C.; Han, G.; Peng, S.; Lu, M.; et al. Global land cover mapping at 30 m resolution: A POK-based operational approach. ISPRS J. Photogramm. Remote Sens. 2017, 103, 7–27. [Google Scholar] [CrossRef]
- European Environment Agency (EEA). CORINE Land Cover. 2014. Available online: http://www.eea.europa.eu/publications/COR0-landcover/ (accessed on 11 July 2016).
- Grillakis, M.G.; Tsanis, I.K.; Koutroulis, A.G. Application of the HBV hydrological model in a flash flood case in Slovenia. Nat. Hazards Earth Syst. Sci. 2010, 10, 2713–2725. [Google Scholar] [CrossRef]
- Panagopoulosa, Y.; Makropoulosa, C.; Baltasb, E.; Mimikoua, M. SWAT parameterization for the identification of critical diffuse pollution source areas under data limitations. Ecol. Model. 2011, 222, 3500–3512. [Google Scholar] [CrossRef]
- European Environment Agency (EEA). Urban Atlas. 2010. Available online: http://www.eea.europa.eu/data-and-maps/data/urban-atlas/ (accessed on 11 July 2016).
- Tanouchi, H.; Kawamura, A.; Amaguchi, H.; Olsson, J. Study on a precision improvement of runoff prediction by hype model using polygonal impervious area ratio data in an urbanized area. Ann. J. Hydraul. Eng. JSCE 2016, 72, I_427–I_432. (In Japanese) [Google Scholar]
- Tanouchi, H.; Kawamura, A.; Amaguchi, H.; Olsson, J. A study on hype model application considering impervious surface in urbanized watershed. J. Jpn. Soc. Civil Eng. Ser. G (Environ. Res.) 2016, 72, I_21–I_26. (In Japanese) [Google Scholar]
- Pechlivanidis, I.G.; Arheimer, B. Large-scale hydrological modelling by using modified PUB recommendations: the India-HYPE case. Hydrol. Earth Syst. Sci. 2015, 19, 4559–4579. [Google Scholar] [CrossRef]
- Hundecha, Y.; Arheimer, B.; Donnelly, C.; Pechlivanidis, I. A regional parameter estimation scheme for a pan-European multi-basin model. J. Hydrol. Reg. Stud. 2016, 6, 90–111. [Google Scholar] [CrossRef]
- Swedish Meteorological and Hydrological Institute (SMHI). HYPE Wiki. 2016. Available online: http://www.smhi.net/hype/wiki/doku.php (accessed on 11 July 2016).
- Johansson, B. Estimation of Areal Precipitation for Hydrological Modeling in Sweden. Ph.D. Thesis, Earth Science Center, Department of Physical Geography, Göteborg University, Göteborg, Sweden, 2002. [Google Scholar]
- European Environment Agency (EEA). EEA Fast Track Service Precursor on Land Monitoring—Degree of soil sealing. 2019. Available online: https://www.eea.europa.eu/data-and-maps/data/eea-fast-track-service-precursor-on-land-monitoring-degree-of-soil-sealing-100m (accessed on 19 March 2019).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models Part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Gupta, H.V.; Wagener, T. A process-based diagnostic approach to model evaluation: Application to the NWS distributed hydrologic model. Water Resour. Res. 2008, 44, W09417. [Google Scholar] [CrossRef]
- Shafii, M.; Tolson, B.A. Optimizing hydrological consistency by incorporating hydrological signatures into model calibration objectives. Water Resour. Res. 2015, 5, 3796–3814. [Google Scholar] [CrossRef]
- Shuster, D.W.; Bonta, J.; Thurston, H.; Warnemuende, E.; Smith, R.D. Impacts of impervious surface on watershed hydrology: A review. Urban Water J. 2005, 2, 263–275. [Google Scholar] [CrossRef]
- Cuo, L.; Lettenmaier, D.P.; Mattheussen, B.V.; Storck, P.; Wiley, M. Hydrologic prediction for urban watersheds with the Distributed Hydrology-Soil-Vegetation Model. Hydrol. Process. 2008, 22, 4205–4213. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, Y.; Chen, Y.L.; Xu, C.Y.; Gao, Y.; Du, J. Hydrological response to urbanization at different spatio-temporal scales simulated by coupling of CLUE-S and the SWAT model in the Yangtze River Delta region. J. Hydrol. 2013, 485, 113–125. [Google Scholar] [CrossRef]
- Brandes, D.; Cavallo, G.J.; Nilson, M.L. Base flow trends in urbanizing watersheds of the delaware river basin. JAWRA 2007, 44, 1377–1391. [Google Scholar] [CrossRef]

| Soil types | Total | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Clay | Sandy | Coarse | Peat | Moraine | Impervious | Water | |||||
| Land use types | Rural Area | Lake | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 11.0 | 11.0 | 94.3 |
| Marsh | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.6 | 0.6 | |||
| Wetland | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |||
| Broadleaf forest | 2.8 | 0.0 | 0.4 | 3.9 | 9.8 | 0.0 | 0.0 | 17.5 | |||
| Conifer forest | 0.4 | 0.0 | 0.0 | 3.2 | 5.1 | 0.0 | 0.0 | 9.0 | |||
| Farmland | 15.1 | 0.7 | 3.9 | 6.1 | 29.6 | 0.0 | 0.0 | 56.2 | |||
| Urbanized area | Impervious area | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 2.6 | 0.0 | 2.6 | 5.7 | |
| Pervious area | 0.3 | 0.0 | 0.0 | 0.1 | 2.5 | 0.0 | 0.0 | 2.9 | |||
| Green land | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 | 0.0 | 0.1 | |||
| Grass/parks | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | |||
| Total | 19.4 | 0.7 | 4.8 | 14.4 | 49.7 | 2.6 | 10.9 | 100.0 | |||
| Parameter | Dependence | Unit | Impervious SLC in HYPEUA | Urbanized SLC in HYPECOR | Description |
|---|---|---|---|---|---|
| cevp | land use | mm/degree/h | 0.00208 | 0.00728 | Evapotranspiration parameter |
| rrcs1 | soil | /h | 0.000417 | 0.025 | Recession coefficient * |
| srrate | soil | - | 0.9 | 0.01 | Fraction surface runoff of rainfall above infiltration threshold |
| macrate | soil | - | 0 | 0.3 | Fraction macro-pore flow of rainfall above infiltration threshold |
| mactrinf | soil | mm/h | 0.25 | 0.83 | Infiltration threshold for macro-pore flow and surface flow |
| mactrsm | soil | - | 0 | 0.8 | Threshold fraction of soil water for macro-pore flow and surface runoff |
| mperc1 | soil | mm/h | 0.0208 | 4.17 | Maximum percolation capacity from soil layer 1 to soil layer 2 |
| mperc2 | soil | mm/h | 0.208 | 4.17 | Maximum percolation capacity from soil layer 2 to soil layer 3 |
| wcep1 | soil | - | 0.005 | 0.03 | Effective porosity as a fraction * |
| wcfc1 | soil | - | 0.02 | 0.08 | Fraction of soil water available for evapotranspiration but not for runoff * |
| The Number of Time Steps Included | PBIAS (%) | NSE (-) | |||
|---|---|---|---|---|---|
| HYPECOR | HYPEUA | HYPECOR | HYPEUA | ||
| Full period | 4127 | −10.8 | −3.7 | 0.84 | 0.84 |
| R = 0 mm | 1630 | −4.8 | −1.6 | 0.86 | 0.86 |
| 0 < R < 5 mm | 1837 | −11.5 | −7.1 | 0.84 | 0.83 |
| 5 < R < 10 mm | 362 | −15.1 | −2.8 | 0.85 | 0.85 |
| 10 < R < 15 mm | 185 | −19.2 | 1.6 | 0.80 | 0.84 |
| 15 < R < 20 mm | 64 | −24.9 | 6.1 | 0.76 | 0.82 |
| 20 < R < 25 mm | 23 | −29.5 | 16.5 | 0.72 | 0.77 |
| 25 < R < 30 mm | 11 | −26.6 | 33.4 | −0.20 | 0.74 |
| R > 30 mm | 15 | −45.4 | 21.4 | 0.47 | 0.73 |
| Indices | Value | Bias[%] | |||
|---|---|---|---|---|---|
| Qobs | HYPECOR | HYPEUA | HYPECOR | HYPEUA | |
| FMS | 0.773 | 0.711 | 0.618 | −8.1 | −20.0 |
| FHV | 192.1 | 166.9 | 166.8 | −13.1 | −13.2 |
| FHV | 466.1 | 411.4 | 417.3 | −11.7 | −10.5 |
| FHV | 384.1 | 350.2 | 357.3 | −8.8 | −7.0 |
| FHV | 266.9 | 254.2 | 262.5 | −4.8 | −1.7 |
| FHV | 195.4 | 188.9 | 198.7 | −3.3 | 1.7 |
| FHV | 144.7 | 134.0 | 147.6 | −7.4 | 2.0 |
| FLV | −803.6 | −929.7 | −891.6 | 15.7 | 10.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tanouchi, H.; Olsson, J.; Lindström, G.; Kawamura, A.; Amaguchi, H. Improving Urban Runoff in Multi-Basin Hydrological Simulation by the HYPE Model Using EEA Urban Atlas: A Case Study in the Sege River Basin, Sweden. Hydrology 2019, 6, 28. https://doi.org/10.3390/hydrology6010028
Tanouchi H, Olsson J, Lindström G, Kawamura A, Amaguchi H. Improving Urban Runoff in Multi-Basin Hydrological Simulation by the HYPE Model Using EEA Urban Atlas: A Case Study in the Sege River Basin, Sweden. Hydrology. 2019; 6(1):28. https://doi.org/10.3390/hydrology6010028
Chicago/Turabian StyleTanouchi, Hiroto, Jonas Olsson, Göran Lindström, Akira Kawamura, and Hideo Amaguchi. 2019. "Improving Urban Runoff in Multi-Basin Hydrological Simulation by the HYPE Model Using EEA Urban Atlas: A Case Study in the Sege River Basin, Sweden" Hydrology 6, no. 1: 28. https://doi.org/10.3390/hydrology6010028
APA StyleTanouchi, H., Olsson, J., Lindström, G., Kawamura, A., & Amaguchi, H. (2019). Improving Urban Runoff in Multi-Basin Hydrological Simulation by the HYPE Model Using EEA Urban Atlas: A Case Study in the Sege River Basin, Sweden. Hydrology, 6(1), 28. https://doi.org/10.3390/hydrology6010028





